On a Graph Associated to UP-Algebras

Abstract

In this article, we introduce the concept of graphs associated with commutative UP-algebra, which we say is a UP-graph whose vertices are the elements of commutative UP-algebra and whose edges are the association of two vertices, that is two elements from commutative UP-algebra. We also define a graph of equivalence classes of a commutative UP-algebra and prove some related results based on the algebraic properties of the graph. We show that two graphs are the same and complete bipartite if they are formed by equivalence classes of UP-algebra and the graph folding of commutative UP-algebra. An algorithm for checking whether a given set is a UP-algebra or not has also been given.

1. Introduction

In recent years, classical and non-classical algebra, as well as logical algebras have attracted the keen interest of researchers and have been widely considered as a strong tool for information systems and many other branches of computer sciences, including fuzzy information with rough and soft concepts. Many authors have studied graphs in classical structures, more precisely in commutative cases, e.g., commutative rings [1], commutative semirings [2], commutative semigroups [3], nearrings [4], Cayley vague graphs [5], etc. Beck [6] associated commutative rings and their zero divisor graphs $G\left(R\right)$. Jun and Lee [7] defined zero divisor graphs in BCK/BCI-algebras and showed related properties. Some properties of graphs related to BCH-algebras have been discussed by Hu and Li in [8], whereas Zahiri and Borzooei [9] defined a new graph of BCI-algebras X and showed that the graphs defined by Jun and Lee [7] and Zahiri and Borzooei [9] are the same. They also proved that the $\alpha$-divisor and p-semisimple part of a BCI algebra X is a quasi-ideal of X. The fuzzy logic of most logical algebras has been the recent choice of numerous researchers, including Hajek [10], who introduced the mathematics of fuzzy logic. Prabpayak and Leerawat [11] introduced KU-ideals, which can be considered to be an interesting idea in logical algebras. Yaqoob et al. [12] introduced cubic KU-ideals of KU-algebras. Roughness in KU-algebras was studied by Moin and Ali [13], whereas rough set theory has been applied to UP-algebras by Moin et al. [14]. Further, Mostafa et al. [15] defined graphs of commutative KU-algebras.

Iampan introduced the concept of UP-algebras [16], whereas Senapati et al. [17] represented UP-algebras in an inter-valued intuitionistic fuzzy environment. Senapati et al. [18] applied the cubic set structure in UP-algebras and proved the results based on them. Akram and Dudek [19] showed interval-valued fuzzy graphs. Akram and Davvaz [20] defined the concept of strong intuitionistic fuzzy graphs. Types of irregular bipolar fuzzy graphs and their applications were studied by Akram in [21].

In this paper, we introduce a (undirected) UP-graph of commutative UP-algebras and denote it by $G\left(A\right)$, whose vertices are the elements of UP-algebra A with the condition that the vertices $a,b\in A$ form an edge between them if and only if $a△b\in A=0.$ Further, it is shown that the graph of equivalence classes of A i.e., denoted by $G_E\left(A\right)$, and the graph folding of a commutative UP-algebra A are the same; more precisely, they form a complete bipartite graph.

2. Preliminaries

In this section, we shall consider concepts based on UP-algebras, UP-subalgebras, UP-ideals and other important terminologies with examples and some related results.

Definition 1.

[16] By a UP-algebra, we mean an algebra $(A,\ast ,0)$ of type $(2,0)$ with a single binary operation ∗ that satisfies the following identities: for any $x,y,z\in X,$

(UP1): $(y\ast z)\ast \left[\right(x\ast y)\ast (x\ast z\left)\right]=0,$

(UP2): $0\ast x=x,$

(UP3): $x\ast 0=0,$

(UP4): $x\ast y=y\ast x=0$ implies $x=y.$

Example 1.

[16] Let X be a universal set. Define a binary operation ∗ on the power set of X by putting $A\ast B=B\cap A^{\prime }$ = $A^{\prime }\cap B$ = $B-A$ for all $A,B\in P\left(X\right)$. Then, $\left(P\right(X);\ast ,\varnothing )$ is a UP-algebra, which is the power UP-algebra of Type 1.

Example 2.

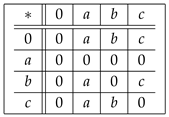
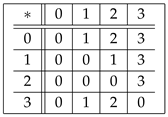
[16] Let X be a universal set. Define a binary operation ∗ on the power set of X by putting $A\ast B$ = $B\cup A^{\prime }$ = $A^{\prime }\cup B$∀ $A,B\in P\left(X\right)$. Then, $\left(P\right(X);\ast ,X)$ is a UP-algebra, which is a power UP-algebra of Type 2.

Example 3.

Let $A=\{0,a,b,c\}$ be a set in which ∗ is defined by the following Cayley table:

It is easy to see that $A=\{0,a,b,c\}$ is a UP-algebra.

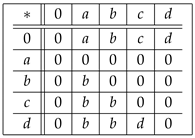
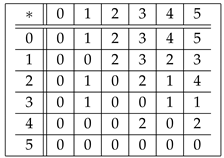
Example 4.

Let $A=\{0,a,b,c,d\}$ be a set in which ∗ is defined by the following Cayley table:

Here, $A=\{0,a,b,c,d\}$ is a UP-algebra.

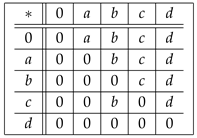
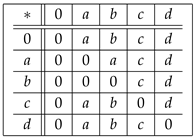
Example 5.

Let $A=\{0,a,b,c,d\}$ be a set in which ∗ is defined by the following Cayley table:

Here, $A=\{0,a,b,c,d\}$ is a UP-algebra.

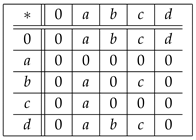
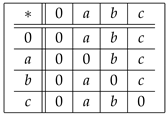
Example 6.

Let $A=\{0,a,b,c,d\}$ be a set in which ∗ is defined by the following Cayley table:

Here, $A=\{0,a,b,c,d\}$ is a UP-algebra.

Proposition 1.

In a UP-algebras A, the following properties hold for any $x,y,z\in A:$

(1)

$x\ast x=0$,

(2)

$x\ast y=0$ and $y\ast z=0\Rightarrow x\ast z=0,$

(3)

$x\ast y=0\Rightarrow (z\ast x)\ast (z\ast y)=0,$

(4)

$x\ast y=0\Rightarrow (y\ast z)\ast (x\ast z)=0,$

(5)

$x\ast (y\ast x)=0,$

(6)

$(y\ast x)\ast x=0⟺x=y\ast x$ and

(7)

$x\ast (y\ast y)=0$

We define a binary relation ${}^{\prime }{\le }^{\prime }$ in a UP-algebras A as $x\le y\iff x\ast y=0$. We observe that this binary relation ≤ forms a POS$(A,\le )$, where zero is the smallest element of A. The following conditions are true for $(A;\ast ,0)$ for all $x,y,z\in A$ with $(A,\le ).$

Proposition 2.

Let $A=(A,\ast ,0)$ be UP-algebras, then define a binary relation ≤ on A as follows: for all $x,y,z\in A$:

(1)

$x\le x$,

(2)

$x\le y$ and $y\le x\Rightarrow x=y,$

(3)

$x\le y$ and $y\le z\Rightarrow x\le z,$

(4)

$x\le y\Rightarrow z\ast x\le z\ast y,$

(5)

$x\le y\Rightarrow y\ast z\le x\ast z,$

(6)

$x\le y\ast x,$ and

(7)

$x\le y\ast y.$

Proposition 3.

Let $A=(A,\ast ,0)$ be UP-algebras, then define a binary relation ≤ on A as follows: for all $x,y,z\in A$:

(UP5): $(y\ast z)\ast (x\ast z)\le x\ast y.$

(UP6): $0\le x.$

(UP7): $x\le y,y\le x\Rightarrow x=y.$

(UP8): $y\ast x\le x.$

Proposition 4.

In a UP-algebra A, the given axioms are satisfied: for all $x,y,z\in A$:

(1)

$x\ast (y\ast z)=y\ast (x\ast z).$

(2)

$\left(\right(y\ast x)\ast x)\le y.$

Definition 2.

Let $A=(A,\ast ,0)$ be a UP-algebra. Then, a subset S of A is called the UP-subalgebras of A if the constant zero of A is in S and $(S,\ast ,0)$ itself forms a UP-algebra. Clearly, A and $\left\{0\right\}$ are UP-algebras of A.

Definition 3.

Let A be a UP-algebra. Then, a subset B of A is called a UP-ideal of A if it satisfies:

(i)

The constant zero of A is in B and

(ii)

for ant$x,y,z\in A,$ $x\ast (y\ast z)\in B$ and $y\in B\Rightarrow x\ast z\in B.$

Clearly, A and $\left\{0\right\}$ are UP-ideals of A.

Example 7.

Let $A=\{0,a,b,c,d\}$ be a set with operation *, which is defined in the table given in Example 5. We find that the subsets $\{0,a,b\}$ and $\{0,a,c\}$ are UP-ideals of A.

$A=(A;\ast ,0)$ is a UP-algebra here. Further, $\{0,a,b\}$ and $\{0,a,c\}$ are UP-ideals of A.

Definition 4.

Define $a△b=(b\ast a)\ast a,$ then A is said to be the commutative UP-algebra if $\forall a,b\in A,$ we get $(b\ast a)\ast a=(a\ast b)\ast b$, i.e., $a△b=b△a.$

Theorem 1.

For a UP-algebra $A,$ the following conditions are equivalent:

(1)

A is commutative,

(2)

$(b\ast a)\ast a\le (a\ast b)\ast b,$

(3)

$\left(\right(a\ast b)\ast b)\ast \left(\right(b\ast a)\ast a)=0.$

Proof. 

It is straightforward. ☐

Lemma 1.

If A is a commutative UP-algebra, then $a△(b\ast c)=(a△b)\ast (a△c).$

Proof. 

If A is a commutative UP-algebra, then we have, $(a△b)\ast (a△c)$ = $\left(\right(b\ast a)\ast a)\ast \left(\right(c\ast a)\ast a))$ $\le (c\ast a)\ast (b\ast a)\le b\ast c.$    (by (UP5))

Furthermore, $(a△b)\ast (a△c)\le (a△c)\le a.$   (by (UP8))

Hence, $(a△b)\ast (a△c)\le a△(b\ast c).$

For its converse part, by using (UP5) and Proposition 4 (1), we have, $(a△b)\ast (a△c)\ast (a△(b\ast c\left)\right)=\left(\right(b\ast a)\ast a)\ast \left(\right(c\ast a)\ast a))\ast ((b\ast c)\ast a)\ast a)\le \left(\right(c\ast a)\ast (b\ast a\left)\right)\ast (b\ast c)\le (b\ast c)\ast (b\ast c)=0.$

Hence, $a△(b\ast c)\le (a△b)\ast (a△c).$ Therefore, $a△(b\ast c)=(a△b)\ast (a△c).$ ☐

From now on, by A, we mean commutative UP-algebra unless otherwise stated.

Definition 5.

Let B be a subset of A. Then, the annihilator of B is defined by,

$$\mathrm{ann}\left(B\right)=\{x\in A:a△x=0\forall a\in B\}.$$

This is known as the UP-annihilator of B. If $B=\left\{a\right\},$ it is written as ann$\left(a\right).$

Lemma 2.

Let B be a subset of A and ann$\left(B\right)$ be a UP-annihilator of $B,$ then ann$\left(B\right)$ is an ideal of A.

Proof. 

Since $a△0=(0\ast a)\ast a=a\ast a=0,$ so $0\in \mathrm{ann}\left(B\right).$ Further, let $x\ast (y\ast z),$$y\in \mathrm{ann}\left(B\right),$ then $a△(x\ast (y\ast z\left)\right)=0.$ Hence, by Lemma 1, $a△(x\ast (y\ast z\left)\right)=(a△x)\ast (a△(y\ast z\left)\right)=(a△x)\ast (a△y\ast a△z)=(a△x)\ast (0\ast a△z)=(a△x)\ast (a△z)=a△(x\ast z)=0,$ which implies that $(x\ast z)\in \mathrm{ann}\left(B\right).$ Therefore, ann$\left(B\right)$ is an ideal of $A.$ ☐

Lemma 3.

If $B,C\subseteq A,$ then we have the following.

(1)

If $B\subseteq C,$ then $ann\left(C\right)\subseteq ann\left(B\right);$

(2)

$ann(B\cup C)=ann\left(B\right)\cap ann\left(C\right);$

(3)

$ann\left(B\right)\cup ann\left(C\right)\subseteq ann(B\cap C).$

Proof. 

(1) Suppose that $x\in \mathrm{ann}\left(C\right),$ so $(x\ast c)\ast c=0,\forall c\in C,$ but $B\subseteq C;$ hence $(x\ast b)\ast b=0,\forall b\in B.$ That is, $x\in \mathrm{ann}\left(B\right)$ implies $\mathrm{ann}\left(C\right)\subseteq \mathrm{ann}\left(B\right)$.

(2) Since $B\subseteq B\cup C$ and $C\subseteq B\cup C,$ so by Part (1), $\mathrm{ann}(B\cup C)\subseteq \mathrm{ann}\left(B\right),\mathrm{ann}\left(C\right),$ and hence, $\mathrm{ann}(B\cup C)\subseteq \mathrm{ann}\left(B\right)\cap \mathrm{ann}\left(C\right).$

Conversely, if $x\in \mathrm{ann}\left(B\right)\cap \mathrm{ann}\left(C\right),$ then $(x\ast b)\ast b=0,\forall b\in B$ and $(x\ast c)\ast c=0,\forall b\in C.$ For any $a\in B\cup C\Rightarrow a\in B\mathrm{or}a\in C$, and hence, $(x\ast a)\ast a=0\forall a\in B\cup C,$ we have $x\in \mathrm{ann}(B\cup C)$ implies $\mathrm{ann}\left(B\right)\cap \mathrm{ann}\left(C\right)\subseteq \mathrm{ann}(B\cup C).$

Therefore, $\mathrm{ann}(B\cup C)=\mathrm{ann}\left(B\right)\cap \mathrm{ann}\left(C\right).$

(3) We have $B\supset B\cap C,$$C\supset B\cap C$, so from (1), $ann\left(B\right)\subset ann(B\cap C)$ and $\mathrm{ann}\left(C\right)\subset \mathrm{ann}(B\cap C)\Rightarrow \mathrm{ann}\left(B\right)\cup \mathrm{ann}\left(C\right)\subseteq \mathrm{ann}(B\cap C).$ ☐

Lemma 4.

If B is a non-empty subset of A, then $ann\left(B\right)=\bigcap _{b\in B}ann\left(b\right).$

Proof. 

We have that $B=\bigcup _{b\in B}\left\{b\right\},$ so by Lemma 3 (2):

$$\mathrm{ann}\left(B\right)=\mathrm{ann}\{\bigcup _{b\in B}\left\{b\right\}\}=\bigcap _{b\in B}\mathrm{ann}\left(b\right).$$

 ☐

Definition 6.

Define a relation ∼ on A as $x\sim y⟺ann\left(x\right)=ann\left(y\right)$ $\forall x,y\in A.$

From the above definition, we obtained the following straightforward result.

Lemma 5.

The relation forms an equivalence relation on UP-algebra $A.$

3. Graphs of Commutative UP-Algebras

We shall introduce the graph and subgraph of UP-algebras A, as well as the graph and subgraph of equivalence classes of A. The set $(G,V,E)$ represents the graph of A, whereas the set $V\left(G\right)$ represents the set of vertices of G and $E\left(G\right)$ the set of edges. Graph G is said to be connected if there is a path between any two vertices, otherwise G is said to be disconnected. Further, G is said to be a complete graph if every two distinct vertices form exactly one edge. Graph G is said to be bipartite if its vertex set $V\left(G\right)$ can be partitioned into disjoint subsets $V_1$ and $V_2$ such that every edge of G joins a vertex of $V_1$ with a vertex of $V_2.$ A graph G is said to be a complete bipartite graph if every vertex in one bipartition subset is connected to every vertex in the other bipartition subset. The distance, $d(a,b)$ represents the length of the shortest path from the vertices a to $b.$ If there is no such path between a and b that forms the shortest path, then it is defined by $d(a,b)=\infty .$ The diameter of graph G is written as $diam\left(G\right)=max\left\{d\right(a,b):a,b\in V(G\left)\right\}.$

We say that the diameter of G is zero if there is only one vertex in $G.$ A connected graph with more than one vertex has a diameter of one if and only if each pair of distinct vertices forms an edge; such a graph is called a complete graph. The neighborhood of a vertex $a\in G$ is the set of the vertices in G adjacent to $a.$ In other words, $N\left(a\right)=\{b\in V(G):a-b\in E(G)$}. Later, we will see that, if $a\in A,$ then $N\left(a\right)=ann\left(a\right),\forall a\ne 0.$

For terminologies related to graphs and various examples, one can refer to [22,23]. A graph H is called a subgraph of G if $V\left(H\right)\subseteq V\left(G\right)$ and $E\left(H\right)\subseteq E\left(G\right).$ Any two graphs $G_1$ and $G_2$ are said to be isomorphic if there is a bijective mapping $f:V\left(G_1\right)\to V\left(G_2\right)$ in such a way that $a-b\in E\left(G_1\right)$, then $f\left(a\right)-f\left(b\right)\in E\left(G_2\right)$; otherwise, graphs are called non-isomorphic. A fan graph $F_n$ is a path $P_{n-1}\cup v_0$ where $v_0$ is an extra vertex connected to all vertices of the path $P_{n-1},$ where $P_{n-1}=\{v_1,v_2,\dots v_{n-1}$}.

Definition 7.

We associate a graph $G\left(A\right)$ corresponding to a commutative UP-algebra A, which is an undirected graph whose vertices are the elements of A and two distinct elements $a,b\in A$ are adjacent if and only if $a△b=0.$ A graph with this condition is said to be a UP-graph.

Theorem 2.

The graph $G\left(A\right)$ is a connected graph with diam$\left(G\right(A\left)\right)\le 3.$

Proof. 

Let $a,b\in A$ be any two distinct vertices of the graph $G\left(A\right).$ Then, we have the following two cases.

Case I: $a△b=0\Rightarrow d(a,b)=1.$

Case II: $a△b\ne 0.$ Then, there exists $c,d\in A-\{a,b\}$ with $c△a=d△b=0.$ If $c=d,$ then $a-c-b$ will form a path of length two; and hence, $d(a,b)=2.$ If $c\ne d$ and $c△d=0,$ then $a-c-d-b$ is a path of length three, and hence, $d(a,b)\le 3.$ In case $c△d\ne 0,$ then $a△(c△d)=0,$ $b△(c△d)=0;$ thus $a-c△d-b=0$ will be a path of length two, so $d(a,b)=2.$ In all these cases, diam$\left(G\right(A\left)\right)\le 3.$ From the above situations, there exists a path between any two distinct elements in A, and so, $G\left(A\right)$ is connected. ☐

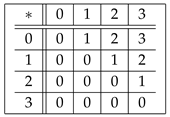
Example 8.

Let $A=\{0,1,2,3\}$ be a set in which ∗ is defined by the following Cayley table:

By Algorithm 1, given later, it is easy to observe that $(A,\ast ,0)$ is a commutative UP-algebra. By considering vertices $V\left(A\right)=\{0,1,2,3\},$ the graph of A is given below in Figure 1:

Figure 1. Graph of $G\left(A\right)$.

Algorithm 1: Algorithm for UP-algebras.

4. Graph of Equivalence Classes of a Commutative UP-Algebra A

We can easily construct the graph $G_E\left(A\right)$ of equivalence classes of A by using equivalence relation, as for any $a,b\in A,$ $a\sim b⟺\mathrm{ann}\left(a\right)=\mathrm{ann}\left(b\right).$ Therefore, if $v_1\sim v_2$ and $v_1△b=0\Rightarrow b\in \mathrm{ann}\left(v_1\right)=\mathrm{ann}\left(v_2\right)$, hence $v_2△b=0.$ We define equivalence classes of a as $\left[a\right]=\{f\in A:\mathrm{ann}(f)=\mathrm{ann}(a\left)\right\}.$

Lemma 6.

Let $\left\{\right[a]:a\in A\}$ be a set of equivalence classes of $A,$ where $\left[a\right]=\{f\in A:ann(f)=ann(a\left)\right\}.$ Then, $\left[a\right]△\left[b\right]=[a△b].$

Proof. 

We have that ann$\left(a\right)\subseteq \mathrm{ann}(a△b),$ ann$\left(b\right)\subseteq \mathrm{ann}(a△b),$ so $[a△b]\subseteq \left[a\right],\left[b\right].$ Next, we claim that $\left[a\right]△\left[b\right]\subseteq [a△b].$ Let $\left[t\right]\subseteq \left[a\right],\left[b\right].$ Then, ann$\left(a\right)\subseteq \mathrm{ann}\left(t\right),\mathrm{ann}\left(b\right)\subseteq \mathrm{ann}\left(t\right).$ Hence, we claim that ann$(a△b)\subseteq \mathrm{ann}\left(t\right).$ If $f\in \mathrm{ann}(a△b),$ then $f△a\in \mathrm{ann}\left(b\right)\subseteq \mathrm{ann}\left(t\right)\Rightarrow f△a△t=0;$ i.e., $f△t\in \mathrm{ann}\left(a\right)\subseteq \mathrm{ann}\left(t\right).$ Hence, $f△t=0;$ That is, $f\in \mathrm{ann}\left(t\right).$ Then, ann$(a△b)\subseteq \mathrm{ann}\left(t\right).$ Therefore, $\left[t\right]\subseteq [a△b]$ and $\left[a\right],\left[b\right]\subseteq [a△b].$ Hence $\left[a\right]△\left[b\right]=[a△b].$ ☐

Definition 8.

Graph $G_E\left(A\right)$ formed by equivalence classes of A is called simple whose vertices are the elements of equivalence class $\left\{\right[a];a\in A\}$, and two distinct classes $\left[a\right],\left[b\right]$ are adjacent in: $G_{E}A⟺\left[a\right]△\left[b\right]=\left\{0\right\}.$

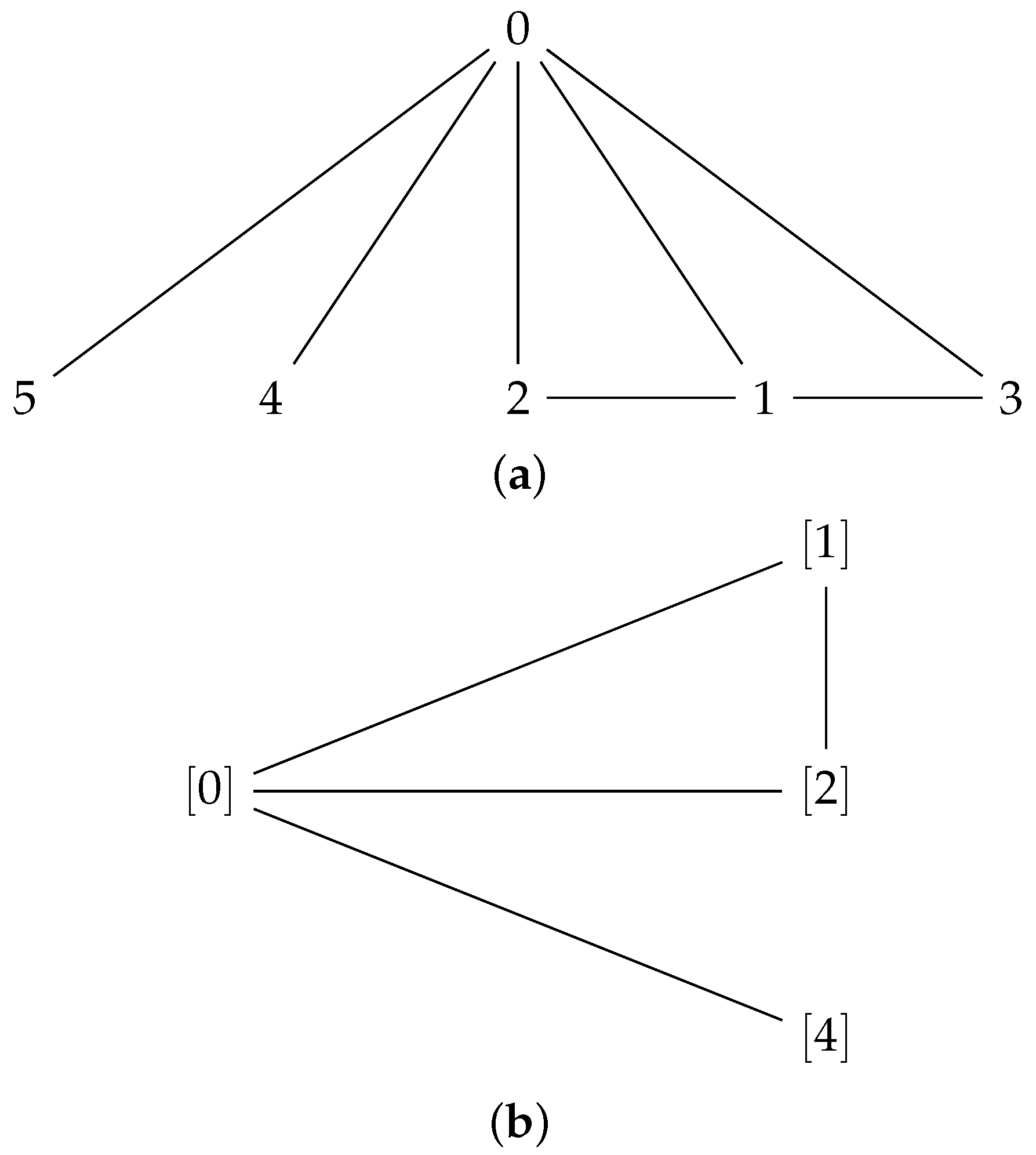
Example 9.

Let $A=\{0,1,2,3,4,5\}$ be a set in which ∗ is defined by the following Cayley table:

We find by Algorithm 1 that $A=(A;\ast ,0)$ is a commutative UP-algebra. Further, the graph of A whose set of vertices and edges are defined by $V\left(A\right)=\{0,1,2,3,4,5\},$ $E\left(A\right)=\left\{\right\{0,1\},\{0,2\},\{0,3\},\{0,4\},\{0,5\},\{1,2\},\{1,3\left\}\right\}$ and $V_E\left(A\right)=\{\left[0\right],\left[1\right],\left[2\right],\left[4\right]\}$ since ann$\left(0\right)=A,$ ann$\left(1\right)=\{0,2,3\}$ ann$\left(2\right)=ann\left(3\right)=\{0,1\},$ ann$\left(4\right)=ann\left(5\right)=\left\{0\right\},$ then $E\left(G_E\left(A\right)\right)=\{\{\left[0\right],\left[1\right]\},\{\left[0\right],\left[2\right]\},\{\left[0\right],\left[4\right]\},\{\left[1\right],\left[2\right]\}\}.$ The given Figure 2 shows the graph of $G\left(A\right)$ and $G_E\left(A\right).$

Figure 2. (a) Graph of $G\left(A\right)$; (b) graph of $G_E\left(A\right)$.

Lemma 7.

The following are true for $G_E\left(A\right)$ in a UP-algebra $A:$

(1)

$G_E\left(A\right)$ is a subgraph of $G\left(A\right);$

(2)

If $N\left(\right[0\left]\right)=A-\left\{0\right\},\forall a\in A,$ then $G\left(A\right)$ is a star graph.

Proof. 

It is straightforward. ☐

Theorem 3.

Let $G_E\left(A\right)$ be the graph of equivalence classes of $A.$ Then, for any distinct vertices $\left[a\right],\left[b\right]\in G_E\left(A\right),$ if $\left[a\right]$ and $\left[b\right]$ are connected by an edge, then ann$\left(a\right)$ and ann$\left(b\right)$ become distinct UP-annihilator ideals of $A.$

Proof. 

We consider ann$\left(a\right)$ = ann$\left(b\right),$ so $a\sim b.$ Hence, $\left[a\right]$ = $\left[b\right]$, which is a contradiction. That is, ann$\left(a\right)$ and ann$\left(b\right)$ are distinct UP-annihilator ideals of $A.$ ☐

The converse of above Theorem 3 is not true. In the above Example 9, it is easy to find that vertices [20,21] are distinct UP-annihilators, but there is no edge between them.

Theorem 4.

If $G\left(A\right)$ is complete or fan graph, then $G\left(A\right)\cong G_E\left(A\right).$

Proof. 

Consider $V\left(G\left(A\right)\right)=\{v_1,v_2,v_3,\dots v_n\}.$ Here, if $G\left(A\right)$ is the complete graph, then every pair of vertices of $G\left(A\right)$ is adjacent. As a result, we get that:

$$N\left(v_1\right)=\{v_2,v_3,\dots v_i\}\mathrm{for}i=2,3,4,\dots n.N\left(v_2\right)=\{v_1,v_3,\dots v_i\},\mathrm{for}i=1,3,4,\cdots n.$$

and $N\left(v_n\right)=\{v_1,v_2,\dots v_{n-1}\},$ for $i=1,3,4,\dots n.$ Therefore, we get that $ann\left(v_i\right)\ne ann\left(v_j\right)$ for all $i,j\in \{1,2,3,\dots ,n\}$ ⟹, every vertex of $G\left(A\right)$ is an equivalence class of $G\left(A\right)$, and so, the vertices of $G_E\left(A\right)$ are distinct and equal to the same number of vertices of $G\left(A\right);$ thus, there exists an isomorphic map $f:G\left(A\right)⟶G_E\left(A\right)$ such that $f\left(v_i\right)=\left[v_i\right]$ for each $i\in \{1,2,3,\dots ,n\}$ and the mapping of edges $f:E\left(G\left(A\right)\right)⟶E\left(G_E\left(A\right)\right)$, which maps the edges $f:E\left(G\left(A\right)\right)⟶E\left(G_E\left(A\right)\right)$, which map the edge $v_i-v_j$ in $E\left(G\right(A\left)\right)$ to the edge $\left[v_i\right]-\left[v_j\right]$ in $E\left(G_E\left(A\right)\right)$, which is a well-defined bijection, so $G\left(A\right)$ is complete. Therefore, $G\left(A\right)$ is isomorphic to $G_E\left(A\right).$

Next, to show that if $G\left(A\right)$ is a fan graph, then $G\left(A\right)$ is isomorphic to $G_E\left(A\right)$, if we consider that $G\left(A\right)$ is a fan graph, then $G\left(A\right)$ consists of a path $P_{n-1}=\{v_1,v_2,\dots v_{n-1}\}$ and a vertex $v_0$ such that $v_0$ is connected to all vertices of the path $P_{n-1}.$ Clearly,

$$N\left(v_0\right)=\{v_1,v_2,\dots v_{n-1}\},N\left(v_1\right)=\{v_0,v_2\},N\left(v_2\right)=\{v_0,v_1,v_3\}\dots N\left(v_n\right)=\{v_0,v_{n-1}\}.$$

Therefore, $ann\left(v_i\right)\ne ann\left(v_j\right)$ for all $i,j\in \{0,1,2,3,\dots ,n-1\}.$ Therefore, the vertices of $G_E\left(A\right)$ are distinct, and there is the same number of vertices of $G\left(A\right).$ Thus, finally, there exists an isomorphic map $f:G\left(A\right)⟶G_E\left(A\right)$ satisfying $f\left(v_i\right)=\left[v_i\right]$ for each $i\in \{1,2,3,\dots n\},$ and the mapping of edge $f:E\left(G\left(A\right)\right)⟶E\left(G_E\left(A\right)\right)$, which maps the edge $v_i-v_j$ in $G\left(A\right)$ to the edge $\left[v_i\right]-\left[v_j\right]$ in $G_E\left(A\right)$, which is a well-defined bijection, hence showing that $G\left(A\right)\cong G_E\left(A\right).$ ☐

Theorem 5.

If $G\left(A\right)$ is complete bipartite graph, then $G_E\left(A\right)$ is an edge.

Proof. 

We suppose that $G\left(A\right)$ is complete bipartite, whose vertex set is $V\left(G\left(A\right)\right)=\{v_1,v_2,\dots v_k,v_{k+1}\dots v_r\}.$ As $G\left(A\right)$ is complete bipartite, so we can split the vertices of $G\left(A\right)$ into two parts, say $V_1=\{v_1,v_2,v_3,\dots ,v_k\}$ and $V_2=\{v_{k+1},\dots v_r\}.$ Therefore, we have $E\left(G\left(A\right)\right)=\{v_1-v_{k+1},v_1-v_{k+2},\dots ,v_1-v_r,v_2-v_{k+1},\dots ,v_2-v_r,\dots ,v_k-v_{k+1},\dots ,v_k-v_r\}.$

Therefore, $N\left(v_1\right)=N\left(v_2\right)=\dots =N\left(v_k\right)=\{v_{k+1},v_{k+2},\dots ,v_r\}$ and $N\left(v_{k+1}\right)=N\left(v_{k+2}\right)=\dots =N\left(v_r\right)=\{v_1,v_2,\dots ,v_k\},$ which implies that there are two distinct equivalence classes $\left[v_1\right]$ and $\left[v_{k+1}\right]$ in $G_E\left(A\right)$, which are adjacent. Hence, $G_E\left(A\right)$ is an edge. ☐

Lemma 8.

Let $G_1$ and $G_2$ be two graphs of commutative UP-algebra and $G_1\cong G_2.$ For $a\in V\left(G_1\right),b\in V\left(G_2\right)$ if $f\left(a\right)=b,$ then $f\left(N\right(a\left)\right)=N\left(b\right).$

Proof. 

It is straightforward. ☐

Theorem 6.

If $G\left(A\right)\cong G\left(B\right)$ for corresponding to commutative UP-algebras A and $B,$ then $G_E\left(A\right)\cong G_E\left(B\right).$

Proof. 

Suppose that $V\left(G\left(A\right)\right)=\{v_1,v_2,v_3,\dots v_n\}$ and $V\left(G\left(B\right)\right)=\{u_1,u_2,u_3,\dots u_n\}$ such that there exists an isomorphism $f:G\left(A\right)⟶G\left(B\right)$ satisfying $f\left(v_i\right)=u_i$ for each $i=\{1,2,3,\dots n\}.$ Therefore, by Lemma 8, $f\left(N\left(u_i\right)\right)=N\left(u_i\right)$ for each i, so $f\left(ann\left(v_i\right)\right)=ann\left(u_i\right)$, and its edge mapping $f:E\left(G_E\left(A\right)\right)⟶E\left(G_E\left(B\right)\right),$ which maps the edge $\left[v_i\right]-\left[v_j\right]$ in $G_E\left(A\right)$ to the edge $\left[u_i\right]-\left[u_j\right]$ in $G_E\left(B\right),$ is a well-defined bijective map. Thus, $G_E\left(A\right)\cong G_E\left(B\right).$ ☐

The converse is not true, as is clear from the following example, where $G_E\left(A\right)\cong G_E\left(B\right)$ corresponding to two commutative UP-algebras A and B, but $G\left(A\right)\neg \cong G\left(B\right)$.

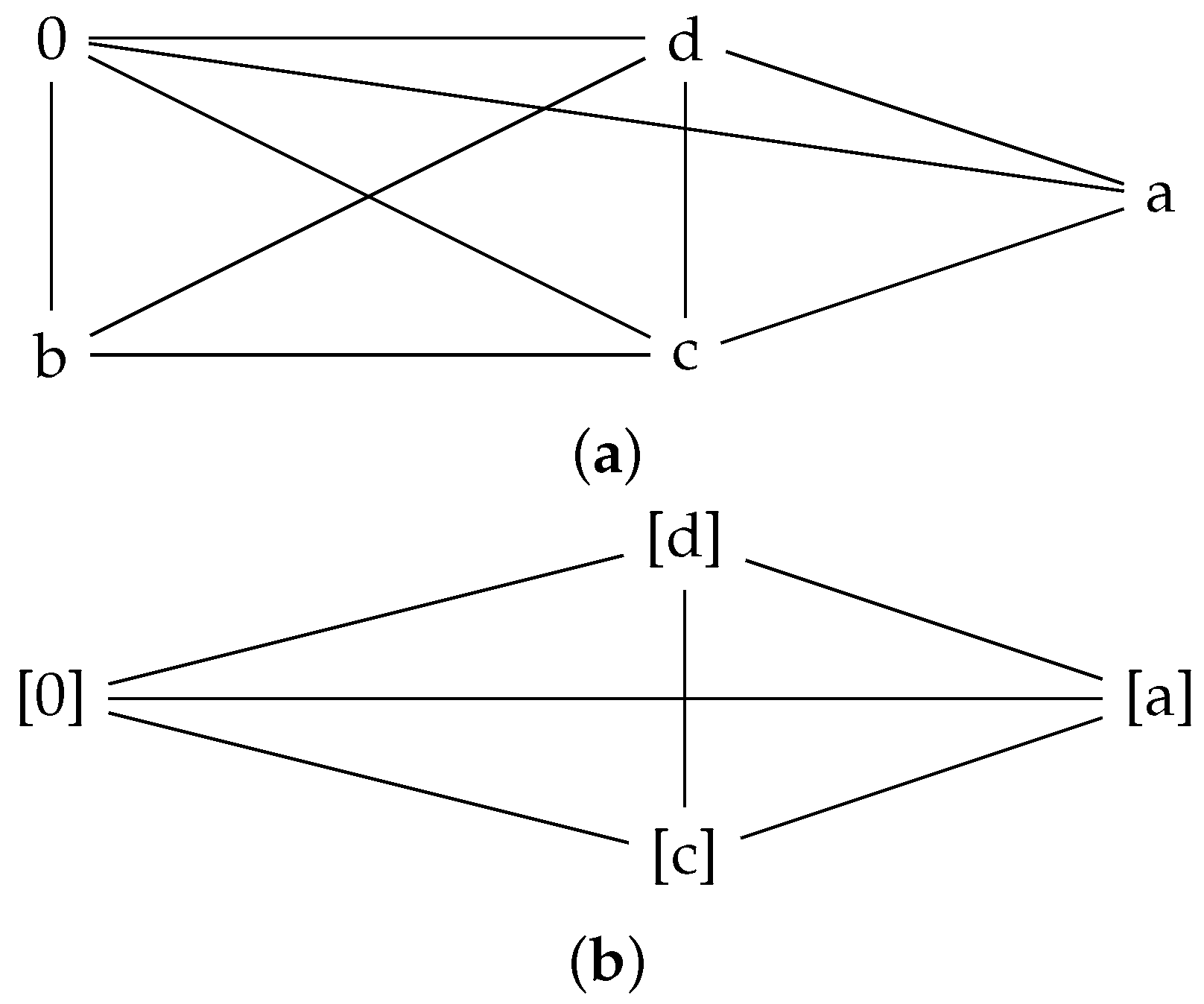
Example 10.

(a) Let $A=\{0,a,b,c,d\}$ be a set in which ∗ is defined by the following Cayley table:

By Algorithm 1, it is clear that $(A;\ast ,0)$ is a commutative UP-algebra. The corresponding graphs associated with A are given below in Figure 3a,b.

Figure 3. (a) Graph of $G\left(A\right)$; (b) graph of $G_E\left(A\right)$.

(b). Let $B=\{0,a,b,c\}$, then by Algorithm 1, it is clear that $(B;\ast ,0)$ is a commutative UP-algebra under the given Cayley table:

The graphs $G\left(B\right)$ and $G_E\left(B\right)$ are shown below in Figure 4a,b:

Figure 4. (a) Graph of $G\left(B\right)$; (b) graph of $G_E\left(B\right)$.

Clearly, the graphs $G_E\left(A\right)\cong G_E\left(B\right)$, whereas $G\left(A\right)\neg \cong G\left(B\right).$

5. Graph Folding

In this section, we shall discuss the graph folding of a graph of a commutative UP-algebra.

Definition 9.

[24] Let $G_1$ and $G_2$ be two graphs and $F:G_1⟶G_2$ be a continuous function. Then, F is called a graph map, if:

(1) 

For each vertex $v\in V\left(G_1\right),F\left(v\right)$ is a vertex in $V\left(G_2\right);$

(2) 

For each edge $e\in E\left(G_1\right),$ dim$\left(F\right(e\left)\right)\le dim\left(e\right).$

A graph map $F:G_1⟶G_2$ is called a graph folding if and only if F maps vertices to vertices and edges to edges. In other words, for $v\in V\left(G_1\right)$, we have $F\left(v\right)\in V\left(G_2\right)$ and for $e\in E\left(G_1\right),F\left(e\right)\in E\left(G_2\right).$ The graph folding is called non-trivial if and only if $|V\left(F\left(G_1\right)\right)|\le |V\left(G_1\right)|$ and $\left|E\right(F\left(G_1\right)|\le |E\left(G_1\right)|.$ Graph folding between two graphs $G_1$ and $G_2$ is denoted by $\eta (G_1,G_2)$, and for a simple graph $G_1$, it is denoted by $\eta \left(G_1\right).$

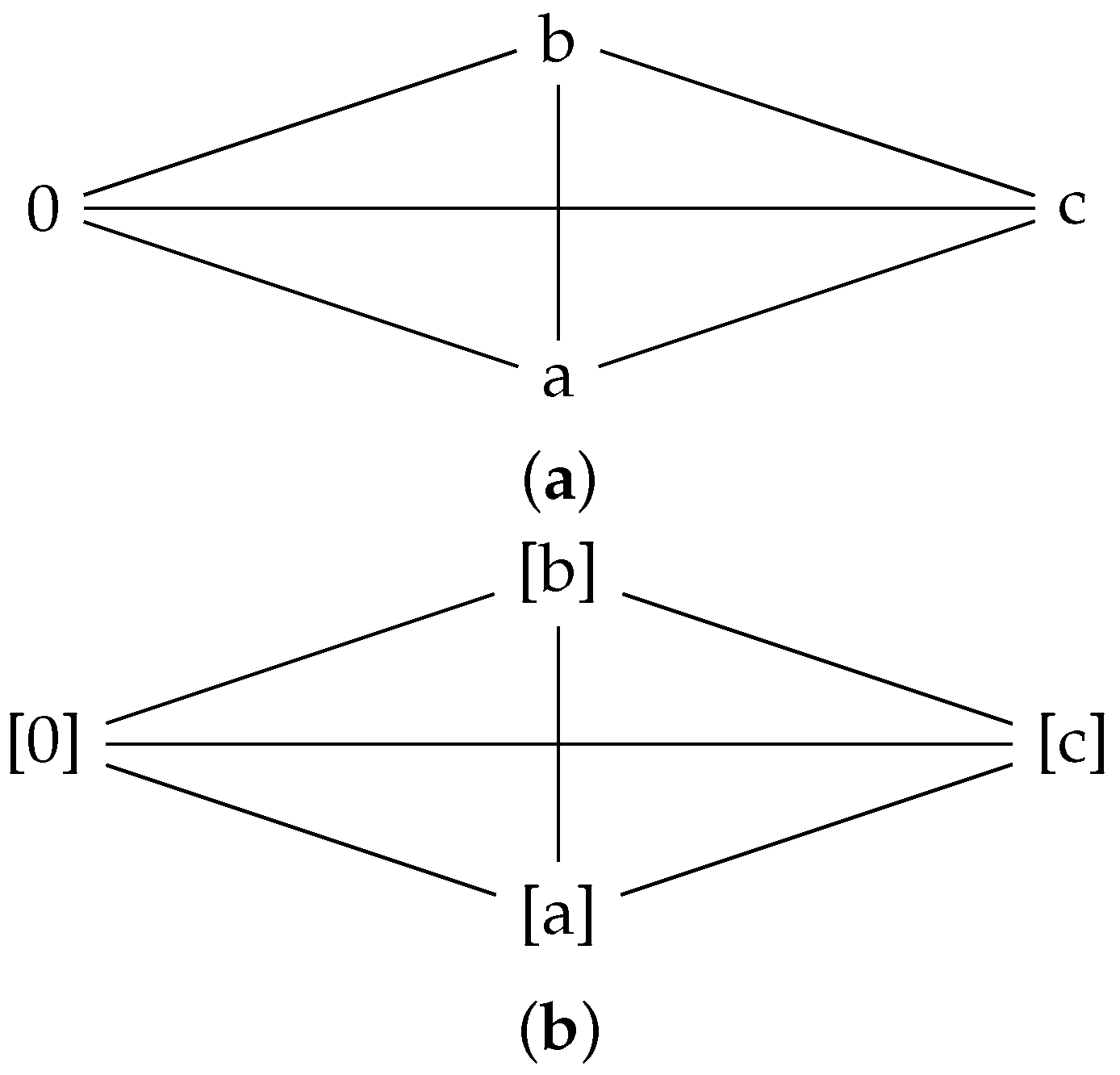
Example 11.

Let $A=\{0,1,2,3\}$ with ∗ as an operation defined by the Cayley table:

We note here that $(A;\ast ,0)$ is a commutative UP-algebra by Algorithm 1. For a graph of A, we have the set of vertices as $V\left(A\right)=\{0,1,2,3\}$ and the set of edges as,

$$E\left(A\right)=\{e_1=\{0,1\},e_2=\{0,2\},e_3=\{0,3\}\}.$$

The graph $G\left(A\right)$ is a complete bipartite and star graph. It is shown below in Figure 5.

Figure 5. Graph of $G\left(A\right)$.

Define a graph map $F:G\left(A\right)⟶G\left(A\right)$ by $F\left(0\right)=0,F\left(1\right)=F\left(2\right)=F\left(3\right)=1$ and $F\left(e_1\right)=F\left(e_2\right)=F\left(e_3\right)=e_1.$ Here, F is a graph folding satisfying $F\left(G\left(A\right)\right)=\overline{G}\left(A\right).$ The graph $\overline{G}\left(A\right)$ is shown below in Figure 6.

Figure 6. Graph of $\overline{G}\left(A\right)$.

Here, a complete bipartite or a star graph $G\left(A\right)$ can be folded onto an edge. We have a theorem based on the above statement.

Theorem 7.

Any complete bipartite graph $G\left(A\right)$ of A can be folded onto an edge.

Proof. 

Let $G\left(A\right)$ be a complete bipartite graph of a commutative UP-algebra A with the vertex set as $V\left(G\right)=\{v_1,v_2,v_3,\dots v_k,v_{k+1},\dots v_r\}.$ Since $G\left(A\right)$ is a bipartite graph, we can split vertex set $V\left(G\right)$ into two sets. $V_1=\{v_1,v_2,\dots v_k\}$, and $V_2=\{v_{k+1},\dots v_r\}.$ Since each vertex of $V_1$ is adjacent to each vertex of $V_2$ only by one edge, therefore $E\left(G\left(A\right)\right)=\{v_1-v_{k+1},v_1-v_{k+2},\dots ,v_1-v_r,v_2-v_{k+1},v_2-v_{k+2}\dots v_2-v_r,\dots ,v_k-v_{k+1},v_k-v_{k+2},\dots v_k-v_r\}.$ We define a graph folding map $F:G\left(A\right)\to G\left(A\right)$ as,

$$F\left(v_i\right)=\left\{\begin{array}{cc}\hfill v_1& \mathrm{if}i=1,2,3,\dots k\hfill \\ v_{k+1}\hfill & \mathrm{if}i=k+1,k+2,\dots r\hfill \end{array}\right..$$

Clearly, $F\left(G\right(A\left)\right)$ is the edge $v_1-v_{k+1}.$ ☐

The following corollary follows from Theorems 5 and 7.

Corollary 1.

Let A be a commutative UP-algebra. If $G\left(A\right)$ is the complete bipartite graph, then the graph $G_E\left(A\right)$ and the graph folding of A are the same graphs.

6. Conclusions

In this paper, we have introduced the associated graph of UP-algebra and have studied its algebraic properties. We have mainly taken two graphs $G\left(A\right)$ and $G_E\left(A\right)$ as the graph of A and its equivalence class. A number of results have been shown, for example if $G\left(A\right)$ is complete and a fan graph, then $G\left(A\right)\cong G_E\left(A\right).$ Furthermore, if $G\left(A\right)$ is complete bipartite graph, then $G_E\left(A\right)$ is an edge. We have shown that if $G\left(A\right)\cong G\left(B\right)$ for any two UP-algebra A and $B,$ then $G_E\left(A\right)\cong G_E\left(B\right)$, but its converse is not true in general.

As a result, we can say that the same concepts can be studied in different types of logical algebras.