Broken Bar Diagnosis for Squirrel Cage Induction Motors Using Frequency Analysis Based on MCSA and Continuous Wavelet Transform
Abstract
:1. Introduction
2. Related Works
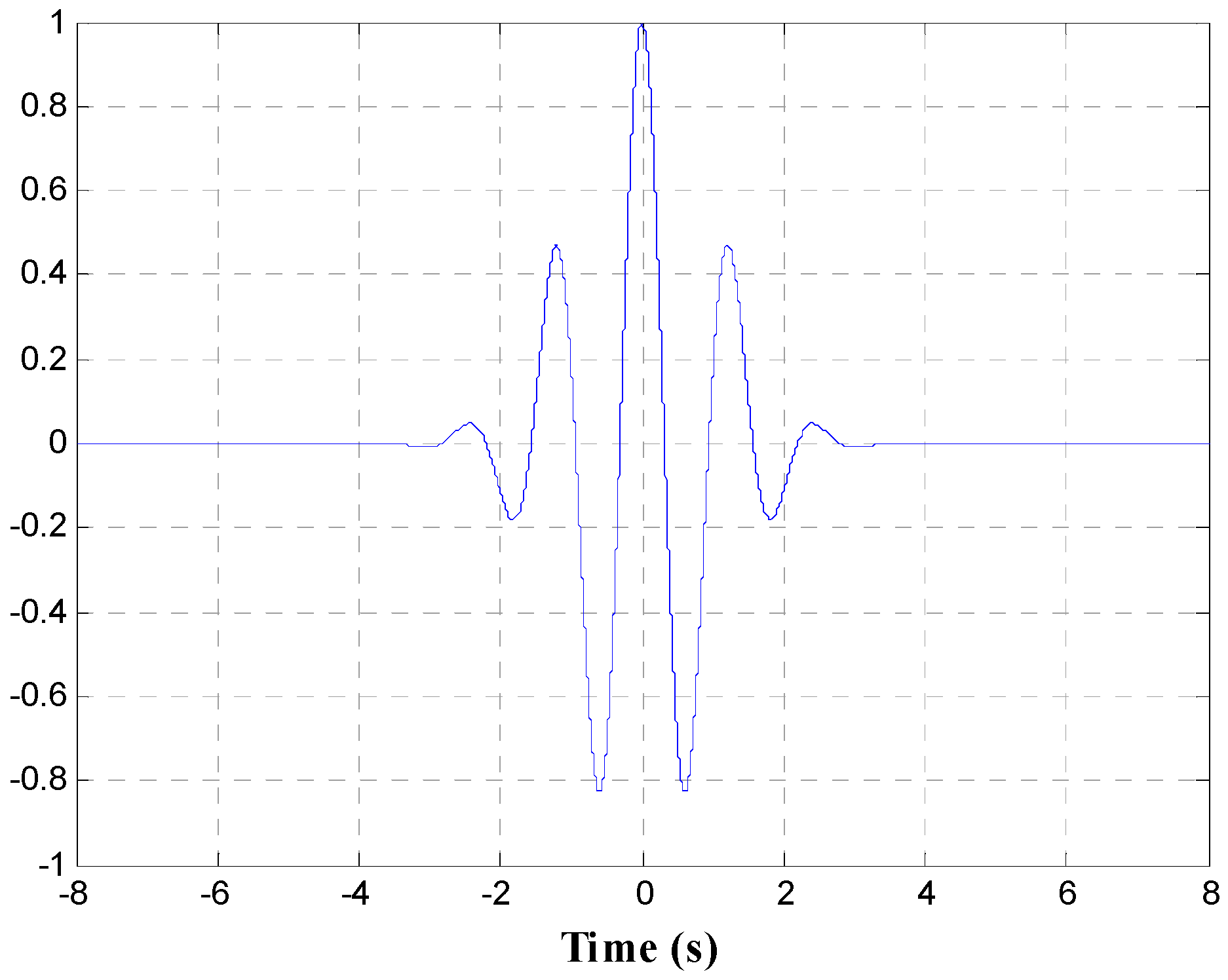
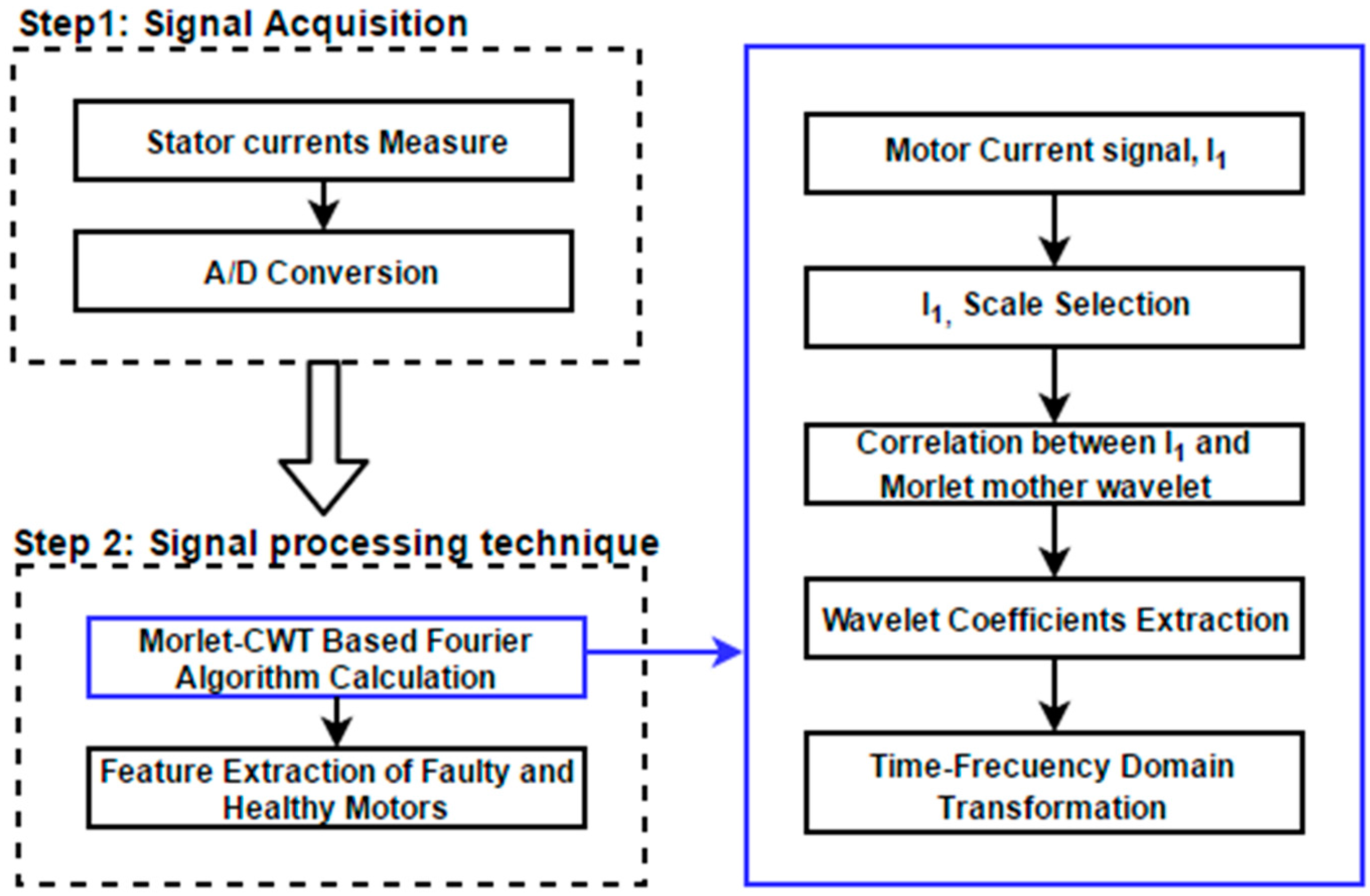
3. Proposed Approach
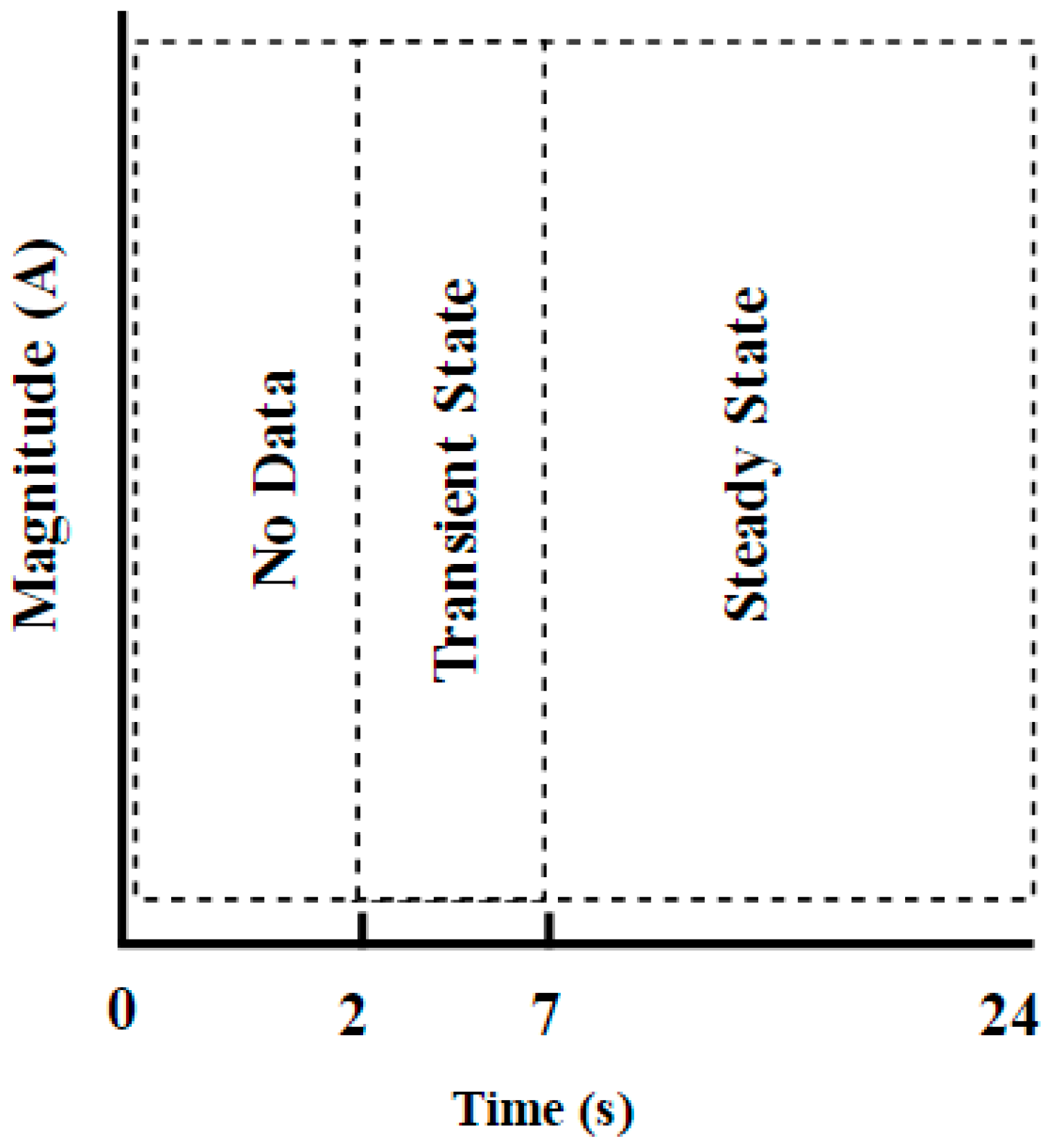
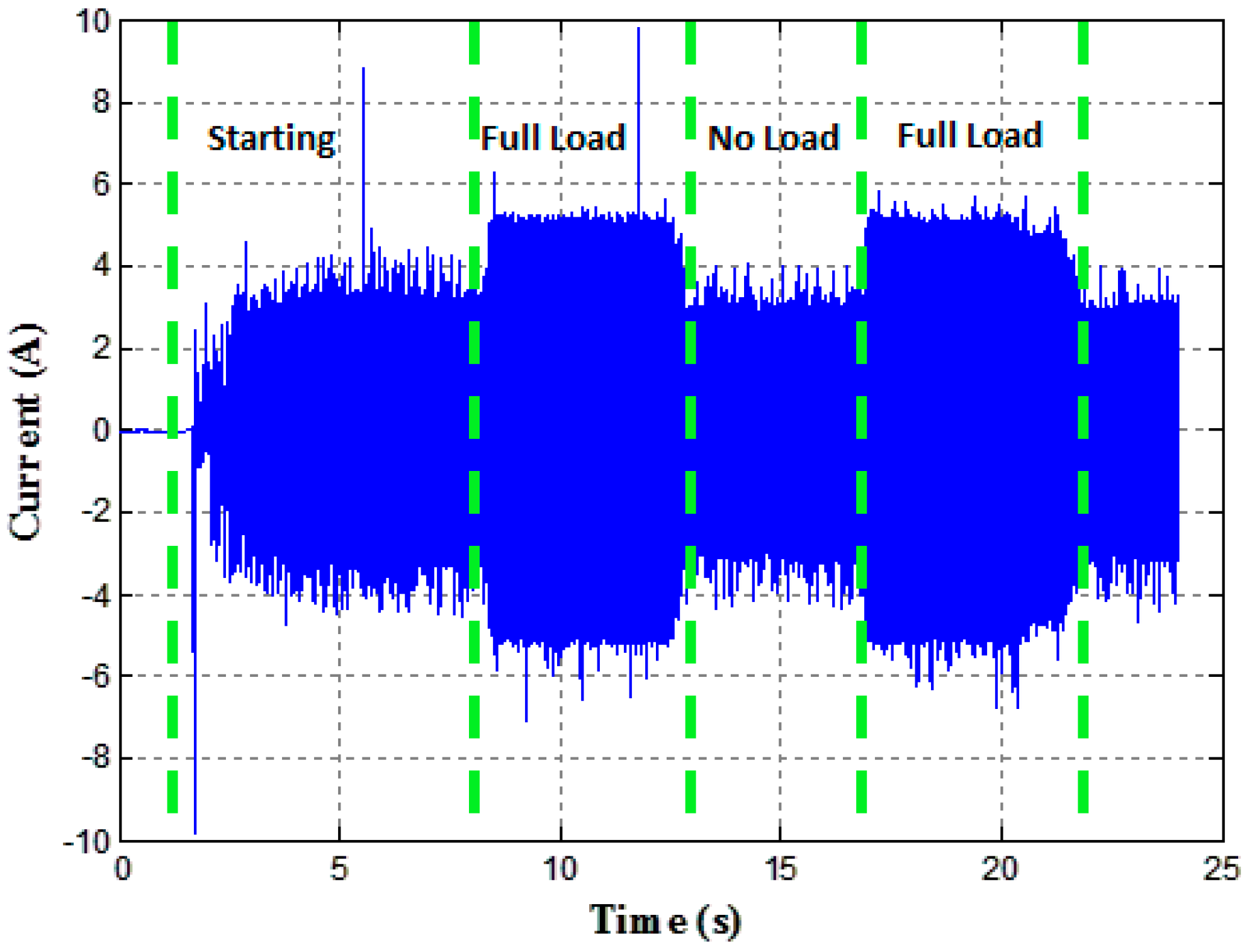
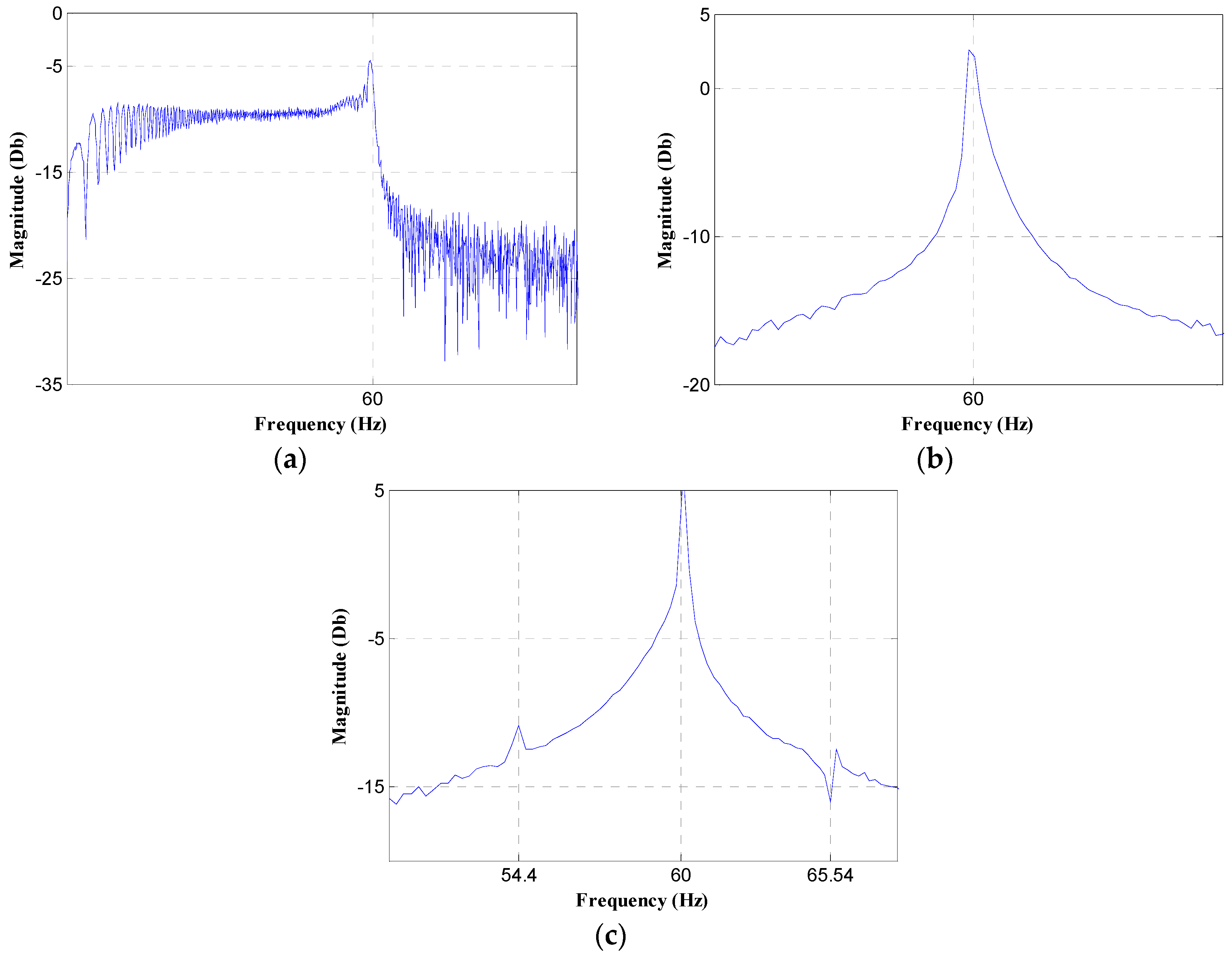
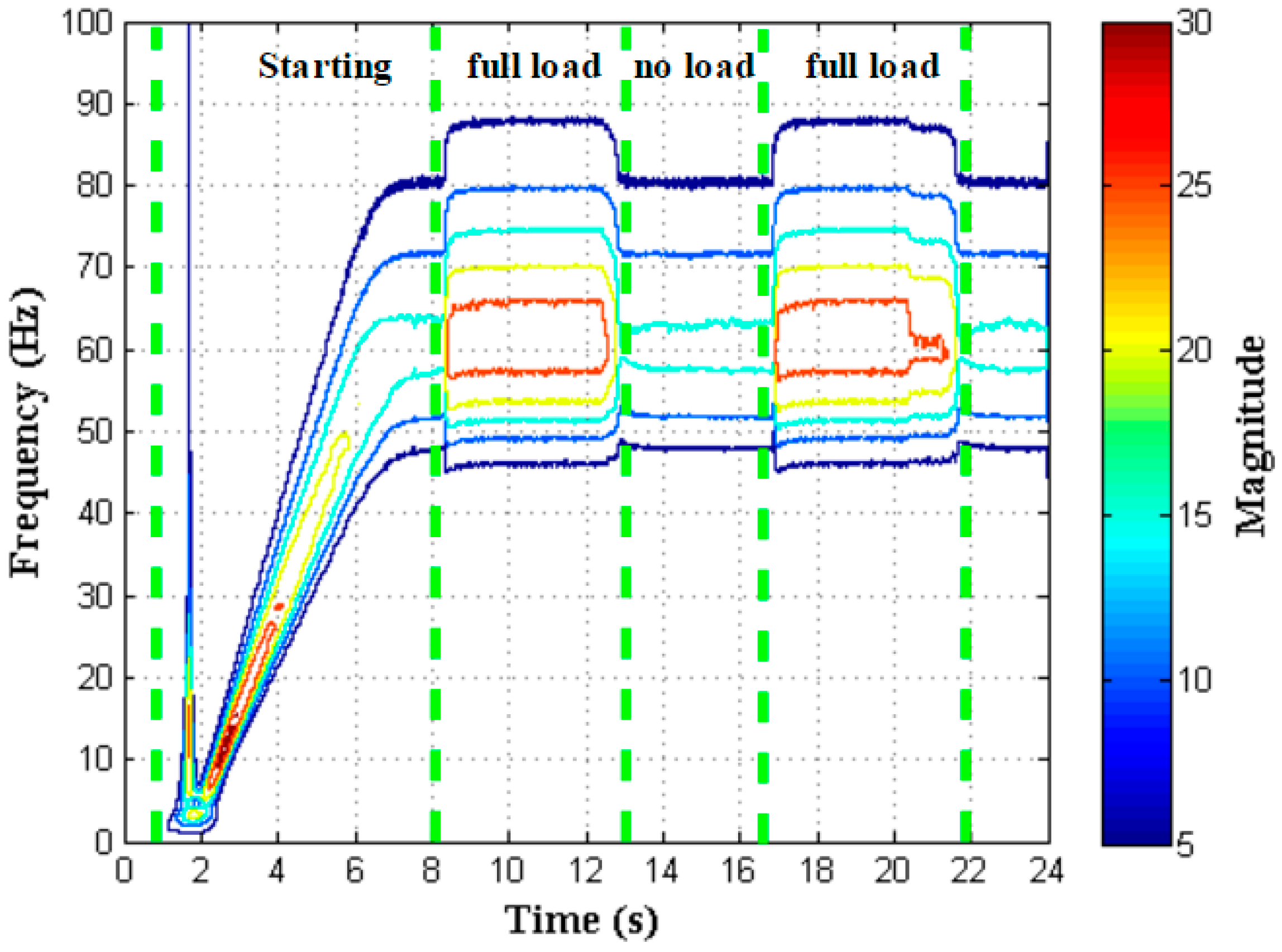
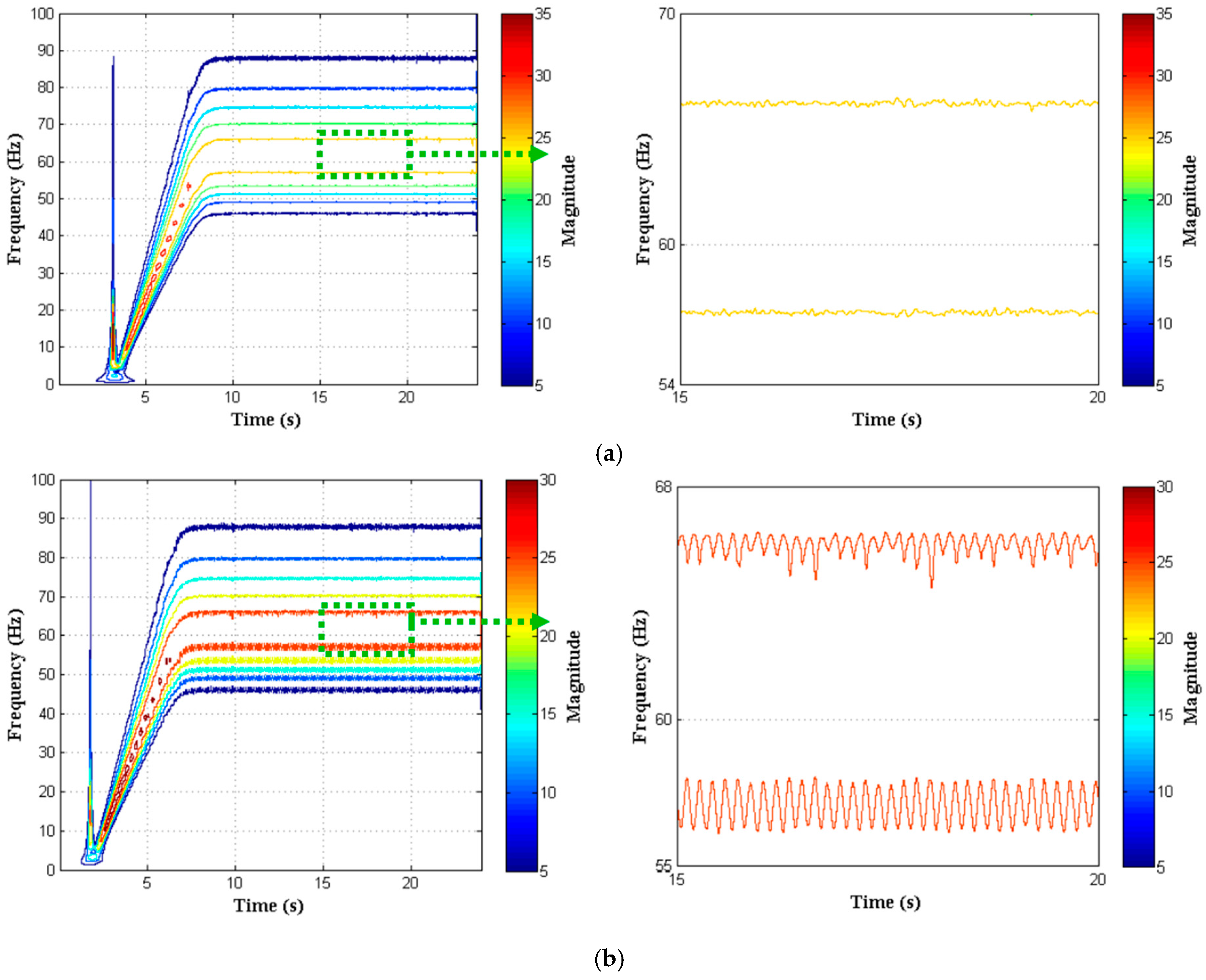
4. Experimental Validation Results and Comparison
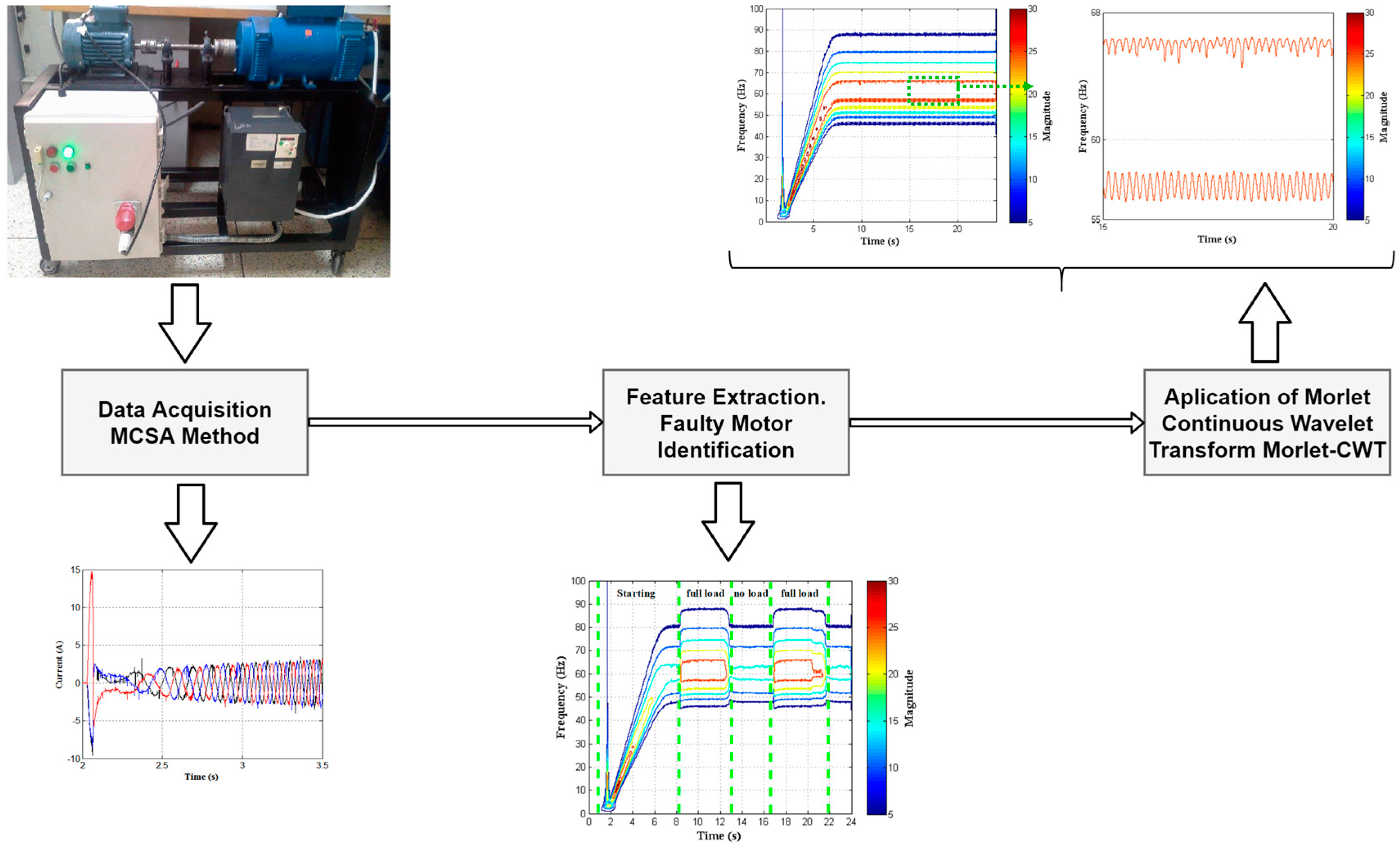
4.1. Motor Test Bench Configuration
4.2. Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Glowacz, A.; Glowacz, Z. Diagnosis of stator faults of the single-phase induction motor using acoustic signals. Appl. Acoust. 2017, 117, 20–27. [Google Scholar] [CrossRef]
- Puche-Panadero, R.; Pineda-Sanchez, M.; Riera-Guasp, M.; Roger-Folch, J.; Hurtado-Perez, E.; Perez-Cruz, J. Improved Resolution of the MCSA Method Via Hilbert Transform, Enabling the Diagnosis of Rotor Asymmetries at Very Low Slip. IEEE Trans. Energy Convers. 2009, 24, 52–59. [Google Scholar] [CrossRef]
- Nandi, S.; Toliyat, H.A.; Li, X. Condition monitoring and fault diagnosis of electrical motors—A review. IEEE Trans. Energy Convers. 2005, 20, 719–729. [Google Scholar] [CrossRef]
- Cusidó, J.; Romeral, L.; Ortega, J.A.; Garcia, A.; Riba, J. Signal injection as a fault detection technique. Sensors 2011, 11, 3356–3380. [Google Scholar] [CrossRef] [PubMed]
- Delgado, M.; Garcia, A.; Ortega, J.A.; Urresty, J.; Riba, J.R. Bearing diagnosis methodologies by means of common mode current. In Proceedings of the IEEE 13th European Conference on Power Electronics and Applications, Barcelona, Spain, 8–10 September 2009; pp. 1–10. [Google Scholar]
- Ceban, A.; Pusca, R.; Romary, R. Study of Rotor Faults in Induction Motors Using External Magnetic Field Analysis. IEEE Trans. Ind. Electron. 2012, 59, 2082–2093. [Google Scholar] [CrossRef]
- Bellini, A.; Filippetti, F.; Tassoni, C.; Capolino, G.-A. Advances in Diagnostic Techniques for Induction Machines. IEEE Trans. Ind. Electron. 2008, 55, 4109–4126. [Google Scholar] [CrossRef]
- Mustafa, M.O.; Nikolakopoulos, G.; Gustafsson, T. Broken bars fault diagnosis based on uncertainty bounds violation for three-phase induction motors. Int. Trans. Electr. Energy Syst. 2015, 25, 304–325. [Google Scholar] [CrossRef]
- Moussa, M.A.; Boucherma, M.; Khezzar, A. A Detection Method for Induction Motor Bar Fault Using Sidelobes Leakage Phenomenon of the Sliding Discrete Fourier Transform. IEEE Trans. Power Electron. 2017, 32, 5560–5572. [Google Scholar] [CrossRef]
- Thomson, W.T.; Fenger, M. Current signature analysis to detect induction motor faults. IEEE Ind. Appl. Mag. 2001, 7, 26–34. [Google Scholar] [CrossRef]
- Gyftakis, K.N.; Spyropoulos, D.V.; Kappatou, J.C.; Mitronikas, E.D. A Novel Approach for Broken Bar Fault Diagnosis in Induction Motors Through Torque Monitoring. IEEE Trans. Energy Convers. 2013, 28, 267–277. [Google Scholar] [CrossRef]
- Talhaoui, H.; Menacer, A.; Kessal, A.; Kechida, R. Fast Fourier and discrete wavelet transforms applied to sensorless vector control induction motor for rotor bar faults diagnosis. ISA Trans. 2014, 53, 1639–1649. [Google Scholar] [CrossRef] [PubMed]
- Glowacz, A.; Glowacz, Z. Diagnosis of the three-phase induction motor using thermal imaging. Infrared Phys. Technol. 2017, 81, 7–16. [Google Scholar] [CrossRef]
- Gaeid, K.S.; Ping, H.W.; Khalid, M.; Salih, A.L. Fault diagnosis of induction motor using MCSA and FFT. Electr. Electron. Eng. 2011, 1, 85–92. [Google Scholar]
- Kliman, G.B.; Stein, J. Methods of motor current signature analysis. Electr. Mach. Power Syst. 1992, 20, 463–474. [Google Scholar] [CrossRef]
- Elbouchikhi, E.; Choqueuse, V.; Trachi, Y.; Benbouzid, M. Induction machine bearing faults detection based on Hilbert-Huang transform. In Proceedings of the 2015 IEEE 24th International Symposium on Industrial Electronics (ISIE), Buzios, Brazil, 3–5 June 2015; pp. 843–848. [Google Scholar]
- Mehala, N.; Dahiya, R. Rotor faults detection in induction motor by wavelet analysis. Int. J. Eng. Sci. Technol. 2009, 1, 90–99. [Google Scholar]
- Nau, S.L.; Schmitz, D.; de Lima Pires, W. Methods to evaluate the quality of stator and rotor of electric motors. In Proceedings of the 2015 IEEE 10th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Guarda, Portugal, 1–4 September 2015; pp. 64–70. [Google Scholar]
- Keskes, H.; Braham, A. Recursive Undecimated Wavelet Packet Transform and DAG SVM for Induction Motor Diagnosis. IEEE Trans. Ind. Inform. 2015, 11, 1059–1066. [Google Scholar] [CrossRef]
- García-Escudero, L.A.; Duque-Perez, O.; Morinigo-Sotelo, D.; Perez-Alonso, M. Robust condition monitoring for early detection of broken rotor bars in induction motors. Expert Syst. Appl. 2011, 38, 2653–2660. [Google Scholar] [CrossRef]
- Chikouche, D.; Boukazzoula, N.; Rezki, M.; Ayad, M. Search of a robust defect signature in gear systems across adaptive Morlet wavelet of vibration signals. IET Signal Process. 2014, 8, 918–926. [Google Scholar]
- Garcia-Perez, A.; Romero-Troncoso, R.J.; Cabal-Yepez, E.; Osornio-Rios, R.A. The Application of High-Resolution Spectral Analysis for Identifying Multiple Combined Faults in Induction Motors. IEEE Trans. Ind. Electron. 2011, 58, 2002–2010. [Google Scholar] [CrossRef]
- Corral-Hernandez, J.A.; Antonino-Daviu, J.; Pons-Llinares, J.; Climente-Alarcon, V.; Frances-Galiana, V. Transient-Based Rotor Cage Assessment in Induction Motors Operating with Soft Starters. IEEE Trans. Ind. Appl. 2015, 51, 3734–3742. [Google Scholar] [CrossRef]
- Pons-Llinares, J.; Antonino-Daviu, J.A.; Riera-Guasp, M.; Lee, S.B.; Kang, T.; Yang, C. Advanced Induction Motor Rotor Fault Diagnosis Via Continuous and Discrete Time-Frequency Tools. IEEE Trans. Ind. Electron. 2015, 62, 1791–1802. [Google Scholar] [CrossRef]
- Farge, M. Wavelet Transforms and their Applications to Turbulence. Annu. Rev. Fluid Mech. 1992, 24, 395–458. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Cusido, J.; Rosero, J.A.; Cusido, M.; Garcia, A.; Ortega, J.A.; Romeral, L. On-Line System for Fault Detection in Induction Machines based on Wavelet Convolution. In Proceedings of the 2007 IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 17–21 June 2007; pp. 927–932. [Google Scholar]
- Mehrjou, M.R.; Mariun, N.; Marhaban, M.H.; Misron, N. Evaluation of Fourier and wavelet analysis for efficient recognition of broken rotor bar in squirrel-cage induction machine. In Proceedings of the 2010 IEEE International Conference on Power and Energy, Kuala Lumpur, Malaysia, 2–4 November 2010; pp. 740–743. [Google Scholar]
- Ece, D.G.; Başaran, M. Condition monitoring of speed controlled induction motors using wavelet packets and discriminant analysis. Expert Syst. Appl. 2011, 38, 8079–8086. [Google Scholar] [CrossRef]
- Haji, M.; Toliyat, H.A. Pattern recognition-a technique for induction machines rotor broken bar detection. IEEE Trans. Energy Convers. 2001, 16, 312–317. [Google Scholar] [CrossRef]
- Da Silva, I.N.; Godoy, W.F.; Lopes, T.D.; Goedtel, A.; Palácios, R.H.C. Application of intelligent tools to detect and classify broken rotor bars in three-phase induction motors fed by an inverter. IET Electr. Power Appl. 2016, 10, 430–439. [Google Scholar]
- Karmakar, S.; Chattopadhyay, S.; Mitra, M.; Sengupta, S. Induction Motor Fault Diagnosis Approach through Current Signature Analysis; Springer: Singapore, 2016; p. 182. [Google Scholar]
- Hernandez, J.C.; Antonino-Daviu, J.; Martinez-Gimenez, F.; Peris, A. Comparison of different wavelet families for broken bar detection in induction motors. In Proceedings of the 2015 IEEE International Conference on Industrial Technology (ICIT), Sevilla, Spain, 17–19 March 2015; pp. 3220–3225. [Google Scholar]
- Rangel-Magdaleno, J.; Ramirez-Cortes, J.; Peregrina-Barreto, H. Broken bars detection on induction motor using MCSA and mathematical morphology: An experimental study. In Proceedings of the 2013 IEEE International Instrumentation and Measurement Technology Conference (I2MTC), Minneapolis, MN, USA, 6–9 May 2013; pp. 825–829. [Google Scholar]
- Tallam, R.M.; Habetler, T.G.; Harley, R.G. Stator winding turn-fault detection for closed-loop induction motor drives. IEEE Trans. Ind. Appl. 2003, 39, 720–724. [Google Scholar] [CrossRef]
- Devi, N.R.; Sarma, D.V.S.S.S.; Rao, P.V.R. Diagnosis and classification of stator winding insulation faults on a three-phase induction motor using wavelet and MNN. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 2543–2555. [Google Scholar] [CrossRef]
- Menacer, A.; T-Said, M.S.d.N.; Benakcha, A.H.; Drid, S. Stator current analysis of incipient fault into asynchronous motor rotor bars using Fourier fast transform. J. Electr. Eng. 2004, 55, 122–130. [Google Scholar]
- Ahamed, S.K.; Sarkar, A.; Mitra, M.; Sengupta, S. Detection of Induction Motor Broken Bar Fault through Envelope Analysis Using Start-Up Current. Procedia Technol. 2012, 4, 646–651. [Google Scholar] [CrossRef]
- Spyropoulos, D.V.; Gyftakis, K.N.; Kappatou, J.; Mitronikas, E.D. The influence of the broken bar fault on the magnetic field and electromagnetic torque in 3-phase induction motors. In Proceedings of the 2012 20th International Conference on Electrical Machines, Marseille, France, 2–5 September 2012; pp. 1868–1874. [Google Scholar]
- Picazo-Rodenas, M.J.; Antonino-Daviu, J.; Climente-Alarcon, V.; Royo-Pastor, R.; Mota-Villar, A. Combination of Noninvasive Approaches for General Assessment of Induction Motors. IEEE Trans. Ind. Appl. 2015, 51, 2172–2180. [Google Scholar] [CrossRef]
- Singh, G.; Kumar, C.A.; Naikan, V.N.A. Effectiveness of Current Envelope analysis to detect broken rotor bar and inter turn faults in an inverter fed induction motor drive. In Proceedings of the 2015 International Conference on Power and Advanced Control Engineering (ICPACE), Bengalooru, India, 12–14 August 2015; pp. 191–194. [Google Scholar]
- Gyftakis, K.; Antonino-Daviu, J.; Garcia-Hernandez, R.; McCulloch, M.; Howey, D.; Cardoso, A. Comparative Experimental Investigation of the Broken Bar Fault Detectability in Induction Motors. In Proceedings of the 2015 IEEE 10th International Symposium on Diagnostics for Electrical Machines, Power Electronics and Drives (SDEMPED), Guarda, Portugal, 1–4 September 2015; pp. 461–467. [Google Scholar]
- Sapena-Bano, A.; Perez-Cruz, J.M.J.; Pineda-Sanchez, M.; Roger-Folch, J.; Riera-Guasp, M.; Puche-Panadero, R. Harmonic order tracking analysis: A novel method for the diagnosis of induction generators. In Proceedings of the 2014 International Conference on Electrical Machines (ICEM), Berlin, Germany, 2–5 September 2014; pp. 1765–1771. [Google Scholar]
- Kia, S.H.; Henao, H.; Capolino, G.-A. Diagnosis of broken-bar fault in induction machines using discrete wavelet transform without slip estimation. IEEE Trans. Ind. Appl. 2009, 45, 1395–1404. [Google Scholar] [CrossRef]
- Mehrjou, M.R.; Mariun, N.; Karami, M.; Noor, S.B.M.; Zolfaghari, S.; Misron, N.; Kadir, M.Z.A.A.; Radzi, M.A.M.; Marhaban, M.H. Wavelet-Based Analysis of MCSA for Fault Detection in Electrical Machine. In Wavelet Transform and Some of Its Real-World Applications; InTech: Rijeka, Croatia, 2015. [Google Scholar]
- Ngote, N.; Ouassaid, M.; Guedira, S.; Cherkaoui, M. On the Detection of Induction-Motor Rotor Fault by the Combined ‘Time Synchronous Averaging-Discrete Wavelet Transform’ Approach. J. Electr. Eng. Technol. 2015, 10, 2315–2325. [Google Scholar] [CrossRef]
- Li, D.Z.; Wang, W.; Ismail, F. A Spectrum Synch Technique for Induction Motor Health Condition Monitoring. IEEE Trans. Energy Convers. 2015, 30, 1348–1355. [Google Scholar] [CrossRef]
- El Bouchikhi, E.H.; Choqueuse, V.; Benbouzid, M. Induction machine faults detection using stator current parametric spectral estimation. Mech. Syst. Signal Process. 2015, 52–53, 447–464. [Google Scholar] [CrossRef]
- Pons-Llinares, J.; Antonino-Daviu, J.A.; Riera-Guasp, M.; Pineda-Sanchez, M.; Climente-Alarcon, V. Induction Motor Diagnosis Based on a Transient Current Analytic Wavelet Transform via Frequency B-Splines. IEEE Trans. Ind. Electron. 2011, 58, 1530–1544. [Google Scholar] [CrossRef]
- Komorowski, D.; Pietraszek, S. The Use of Continuous Wavelet Transform Based on the Fast Fourier Transform in the Analysis of Multi-channel Electrogastrography Recordings. J. Med. Syst. 2016, 40, 10. [Google Scholar] [CrossRef] [PubMed]


| Description | Value | Unit |
|---|---|---|
| Brand | ABB | – |
| Rated power | 1 | Hp |
| Rated current | 3.4 | A |
| Conection type | Delta | – |
| Rated voltage | 220 | V |
| Supply frequency | 60 | Hz |
| Nominal speed | 1705 | Rpm |
| Torque | 4.2 | Nm |
| Moment of inertia | 0.00174 | kg·m2 |
| Pole pairs | 2 | – |
| Number of bars | 22 | – |
| Number of Broken Bars | Frequency Bands | |||
|---|---|---|---|---|
| 56–58.5 Hz | 52.8–54.8 Hz | 50.5–52.5 Hz | 48.5–50 Hz | |
| 0 | 56.98 < f < 57.55 | 53.34 < f < 53.85 | 51.12 < f < 51.5 | 48.9 < f < 49.3 |
| ∆f = 0.57 | ∆f = 0.51 | ∆f = 0.42 | ∆f = 0.41 | |
| 1 | 57.41 < f < 58.35 | 53.5 < f < 54.5 | 51.2 < f < 51.8 | 48.9 < f < 49.5 |
| ∆f = 0.94 | ∆f = 0.98 | ∆f = 0.58 | ∆f = 0.59 | |
| 2 | 57.02 < f < 58.43 | 53.2 < f < 54.6 | 51 < f < 51.9 | 48.7 < f < 49.6 |
| ∆f = 1.41 | ∆f = 1.40 | ∆f = 0.93 | ∆f = 0.89 | |
| 3 | 56.23 < f < 58.35 | 52.82 < f < 54.79 | 50.7 < f < 51.2 | 48.5 < f < 49.8 |
| ∆f = 2.08 | ∆f = 1.97 | ∆f = 1.41 | ∆f = 1.32 | |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
,, D.G.; Aguilar, W.G.; Arcos-Aviles, D.; Sotomayor, D. Broken Bar Diagnosis for Squirrel Cage Induction Motors Using Frequency Analysis Based on MCSA and Continuous Wavelet Transform. Math. Comput. Appl. 2017, 22, 30. https://doi.org/10.3390/mca22020030
, DG, Aguilar WG, Arcos-Aviles D, Sotomayor D. Broken Bar Diagnosis for Squirrel Cage Induction Motors Using Frequency Analysis Based on MCSA and Continuous Wavelet Transform. Mathematical and Computational Applications. 2017; 22(2):30. https://doi.org/10.3390/mca22020030
Chicago/Turabian Style,, Danilo Granda, Wilbert G. Aguilar, Diego Arcos-Aviles, and Danny Sotomayor. 2017. "Broken Bar Diagnosis for Squirrel Cage Induction Motors Using Frequency Analysis Based on MCSA and Continuous Wavelet Transform" Mathematical and Computational Applications 22, no. 2: 30. https://doi.org/10.3390/mca22020030
APA Style,, D. G., Aguilar, W. G., Arcos-Aviles, D., & Sotomayor, D. (2017). Broken Bar Diagnosis for Squirrel Cage Induction Motors Using Frequency Analysis Based on MCSA and Continuous Wavelet Transform. Mathematical and Computational Applications, 22(2), 30. https://doi.org/10.3390/mca22020030







