Analysis of a Hand-Foot-Mouth Disease Model with Standard Incidence Rate and Estimation for Basic Reproduction Number
Abstract
:1. Introduction
2. Mathematical Model and Analysis
2.1. The Model
2.2. Local Stability Analysis
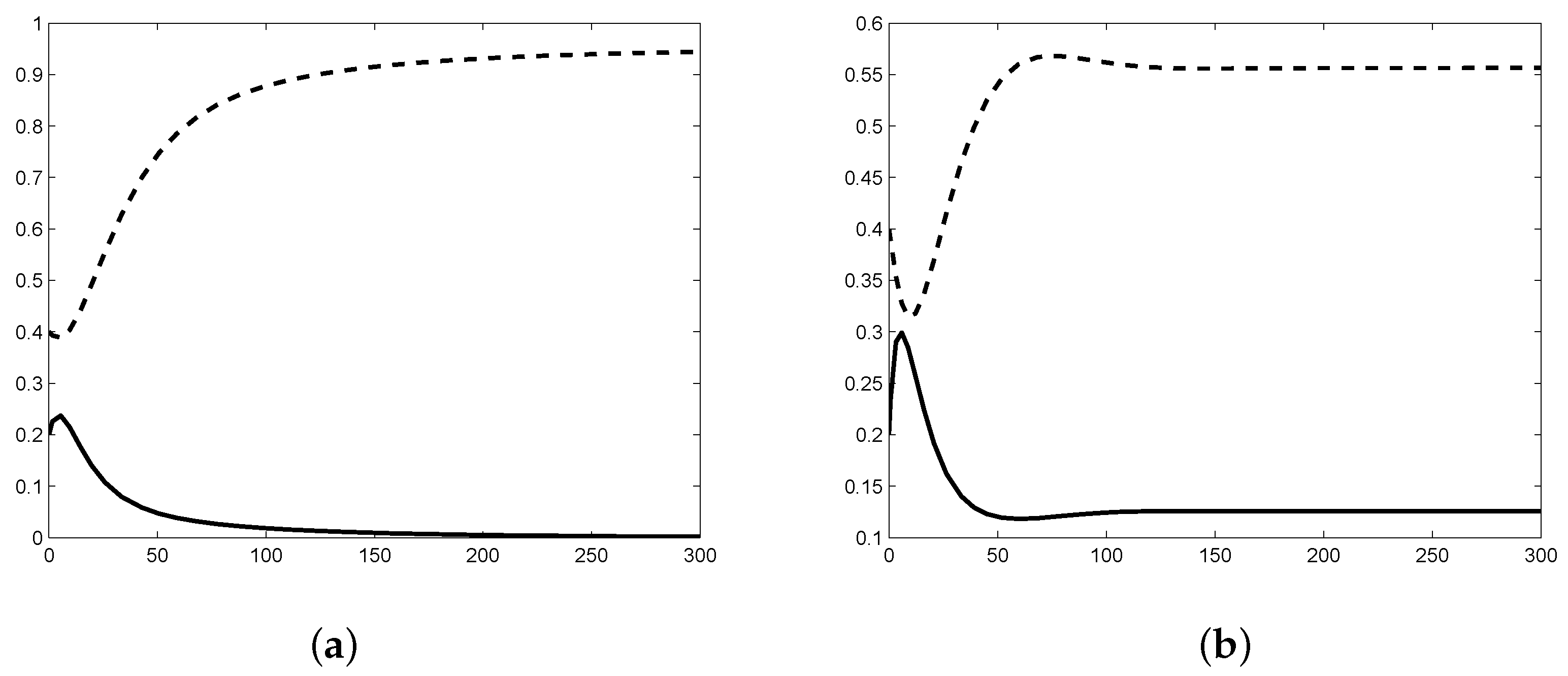
2.3. Numerical Simulation of Stability
3. Estimation of Basic Reproduction Number
3.1. Estimation Formula
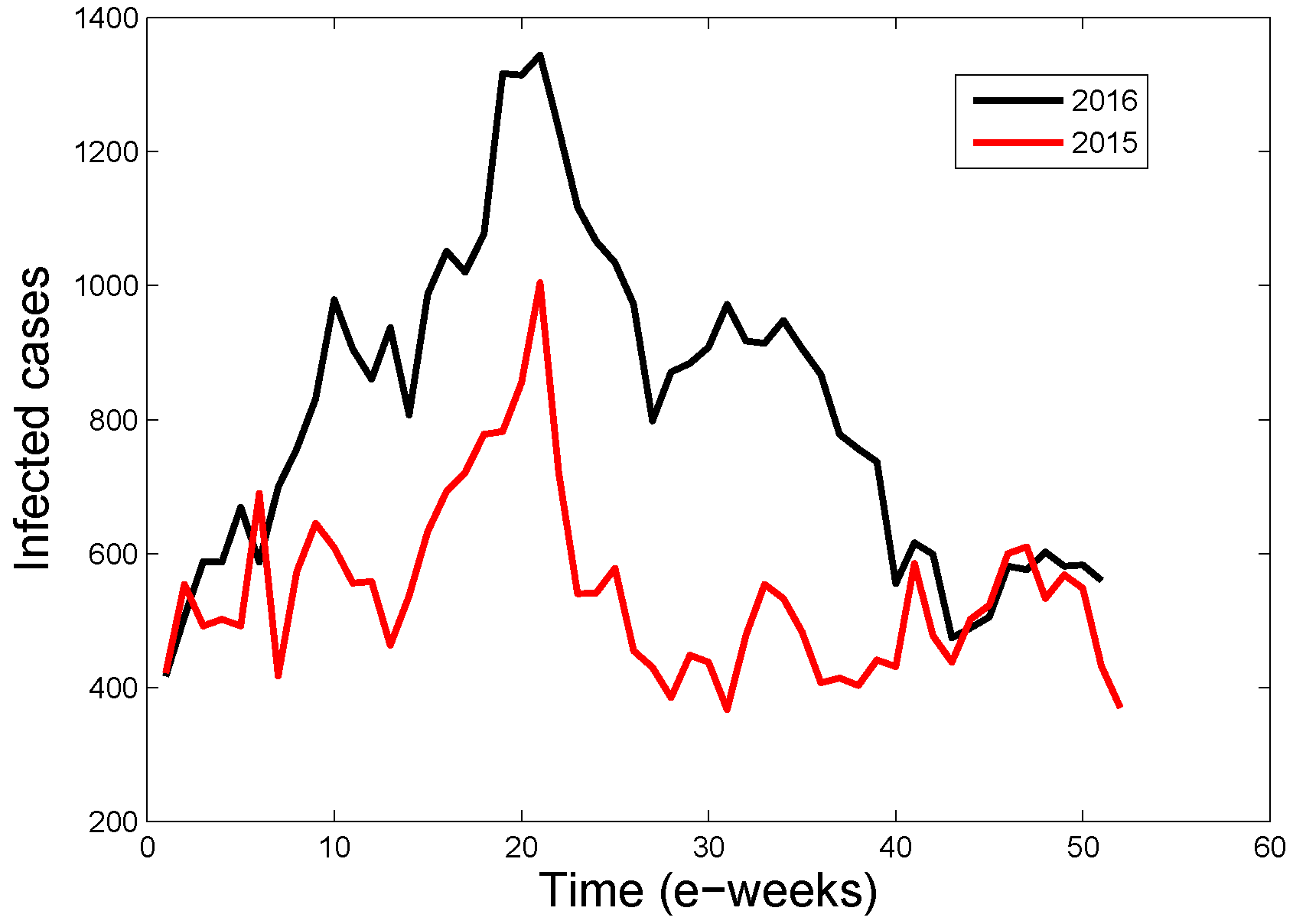
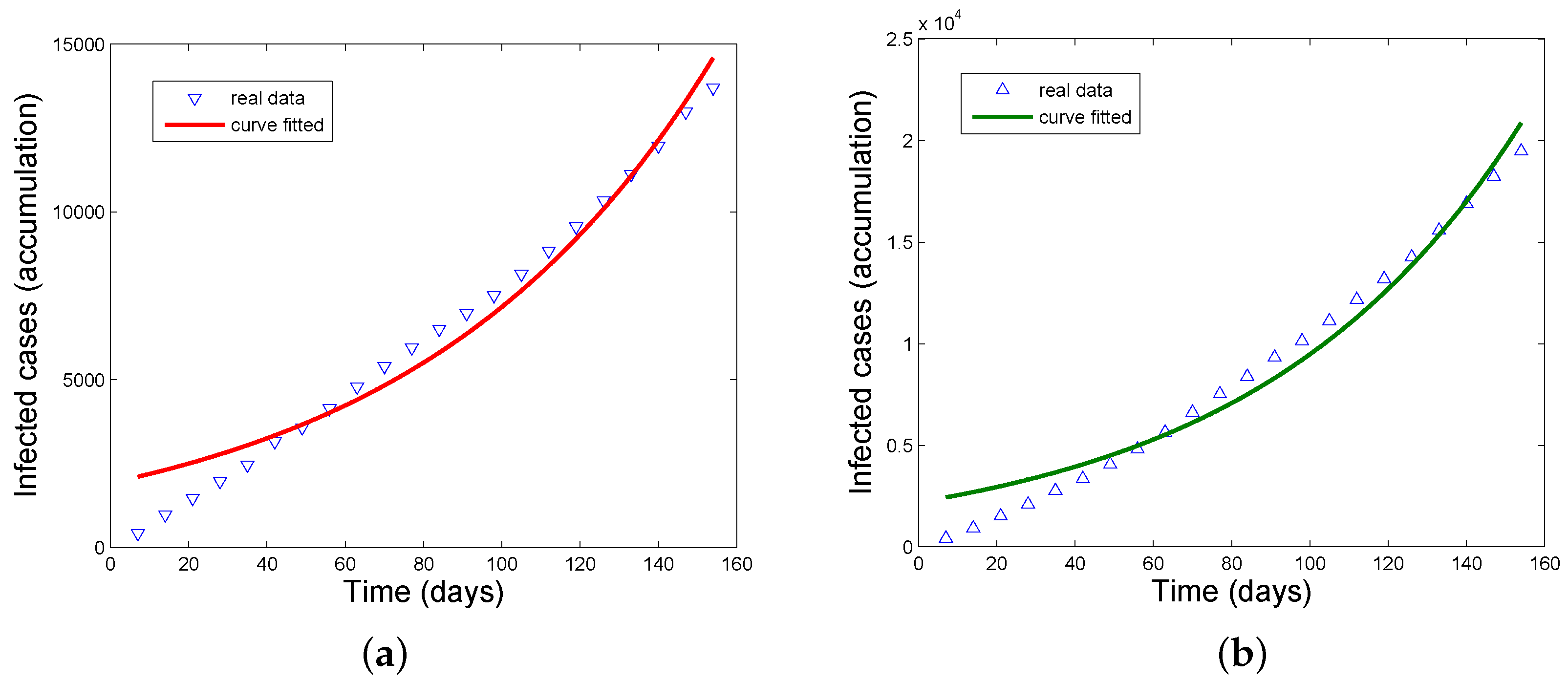
3.2. Application of the Estimation Formula
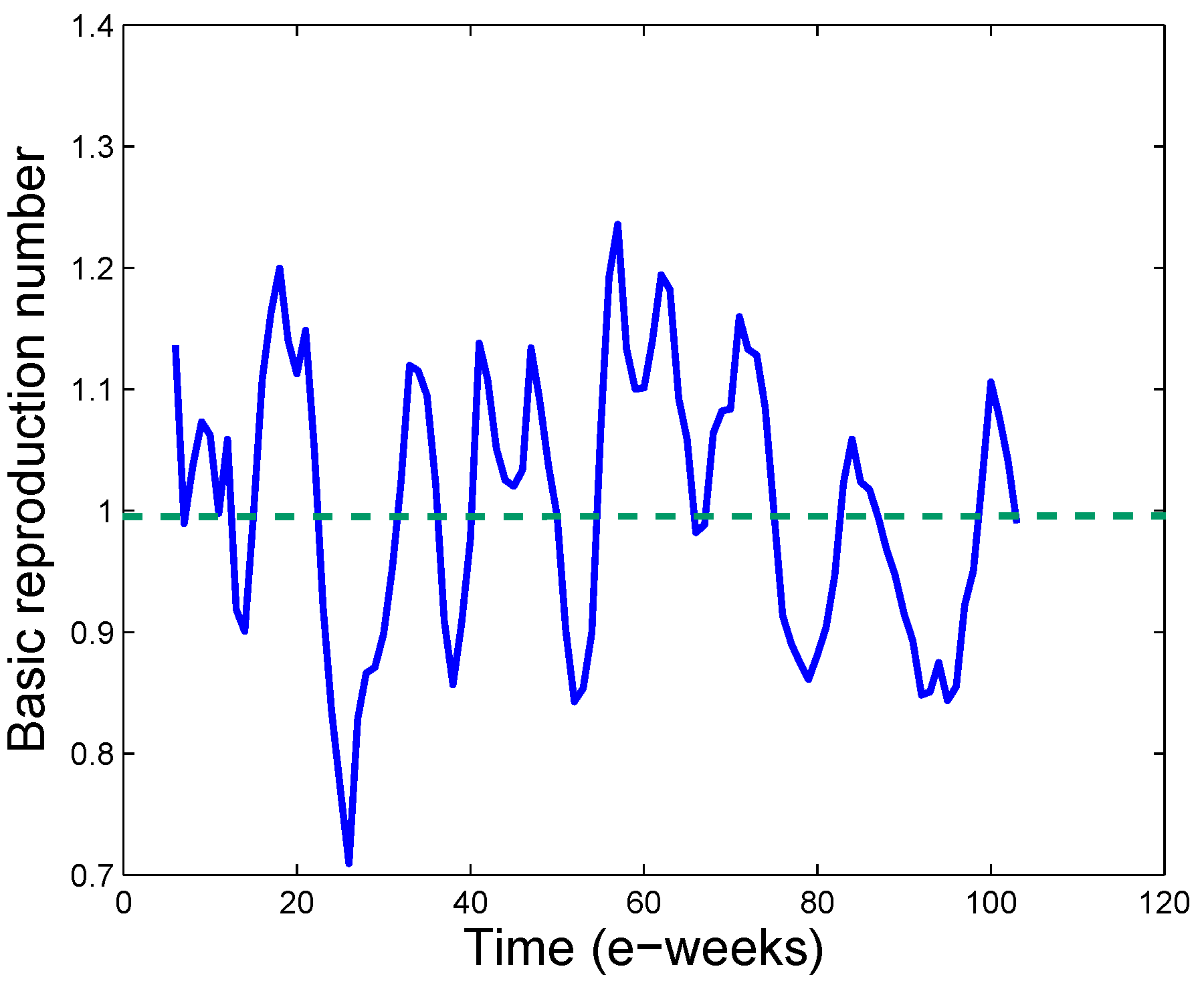
3.3. Real Time Estimation of
4. Discussion
Acknowledgments
Conflicts of Interest
References
- Yang, J.Y.; Chen, Y.M.; Zhang, F.Q. Stability analysis and optimal control of a hand-foot-mouth disease (HFMD) model. J. Appl. Math. Comput. 2013, 41, 99–117. [Google Scholar] [CrossRef]
- Zhu, Q.; Hao, Y.T.; Ma, J.Q.; Yu, S.C.; Wang, Y. Surveillance of hand, foot, mouth disease in Mainland China (2008–2009). Biomed. Environ. Sci. 2011, 24, 349–356. [Google Scholar] [PubMed]
- Lai, C.C.; Jiang, D.S.; Wu, H.M.; Chen, H.H. A dynamical model for the outbreaks of hand, foot and mouth diseases in Taiwan. Epidemiol. Infect. 2016, 144, 1500–1511. [Google Scholar] [CrossRef] [PubMed]
- Tinng, F.C.S.; Labadin, J. A Simple Deterministic Model for the Spread of Hand, Foot and Mouth Disease (HFMD) in Sarawak. In Proceedings of the 2008 Second Asia International Conference on Modelling and Simulation, Kuala, Lumpur, 13–15 May 2008; pp. 947–952. [Google Scholar]
- Zhu, Y.; Xu, B.; Lian, X.; Lin, W.; Zhou, Z.; Wang, W. A Hand-Foot-and-Mouth Disease Model with Periodic Transmission Rate in Wenzhou, China. Abstr. Appl. Anal. 2014, 234509. [Google Scholar] [CrossRef]
- Liu, J. Threshold dynamics for a HFMD epidemic model with periodic transmission rate. Nonlinear Dyn. 2011, 64, 89–95. [Google Scholar] [CrossRef]
- Roy, N.; Halder, N. Compartmental modeling of hand, foot and mouth infectious disease (HFMD). Res. J. Appl. Sci. 2010, 5, 177–182. [Google Scholar] [CrossRef]
- Urashima, M.; Shindo, N.; Okabe, M. Seasonal models of herpangina and hand-foot-mouth disease to simulate annual fluctuations in urban warming in Tokyo. Jpn. J. Infect. Dis. 2003, 56, 48–53. [Google Scholar] [PubMed]
- Samanta, G.P. Analysis of a delayed hand-foot-mouth disease epidemic model with pulse vaccination. Syst. Sci. Control Eng. 2014, 2, 61–73. [Google Scholar] [CrossRef]
- Sharma, S.; Samanta, G.P. Analysis of a hand-foot-mouth disease model. Int. J. Biomath. 2017, 10, 1750016. [Google Scholar] [CrossRef]
- Wang, W.D.; Zhou, Y.C.; Lu, Z.Y. Advances in Mathematical Biology; Science Press: Beijing, China, 2008. (In Chinese) [Google Scholar]
- Heesterbeek, J. A brief history of R0 and a recipe for its calculation. Acta Biotheor. 2002, 50, 189–204. [Google Scholar] [CrossRef] [PubMed]
- Hefferman, J.M.; Smith, R.J.; Wahl, L.M. Perspectives on the basic reproductive ratio. J. R. Soc. Interface 2005, 2, 281–293. [Google Scholar] [CrossRef] [PubMed]
- Anderson, R.M.; May, R.M. Infectious Diseases of Human: Dynamics and Control; Oxford University Press: Oxford, UK, 1991. [Google Scholar]
- Ministry of Public Health of Singapore. Available online:https://www.moh.gov.sg/content/moh_web/home/statistics/infectiousDiseasesStatistics/weekly_infectiousdiseasesbulletin.html (accessed on 5 January 2017).
- Samanta, G.P. A delayed hand-foot-mouth disease model with pulse vaccination strategy. Comp. Appl. Math. 2015, 34, 1131–1152. [Google Scholar] [CrossRef]
- Ministry of Public Health of Singapore. Available online:https://www.moh.gov.sg/content/moh_web/home/statistics/Health_Facts_Singapore/Population_And_Vital_Statistics.html (accessed on 5 January 2017).
- Favier, C.; Degallier, N.; Rosa-Freitas, M.G.; Boulanger, J.P.; Costa Lima, J.R.; Luitgards-Moura, J.F.; Menkès, C.E.; Mondet, B.; Oliveira, C.; Weimann, E.T.; et al. Early determination of the reproductive number for vector-borne diseases: The case of dengue in Brazil. Trop. Med. Int. Health 2006, 11, 332–340. [Google Scholar] [CrossRef] [PubMed]
| Parameter or Variable | Biological Implications | Value |
|---|---|---|
| S | number of susceptible individuals | variable |
| E | number of exposed individuals | variable |
| I | number of infective individuals | variable |
| R | number of recovered individuals | variable |
| N | total number of individuals, | variable |
| b | recruitment rate | demographical |
| transmission efficiency rate | estimated | |
| natural death rate | demographical | |
| loss of immunity rate | 0.07 [1,4] | |
| latent duration | estimated | |
| recovery rate | estimated |
© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, C. Analysis of a Hand-Foot-Mouth Disease Model with Standard Incidence Rate and Estimation for Basic Reproduction Number. Math. Comput. Appl. 2017, 22, 29. https://doi.org/10.3390/mca22020029
Wu C. Analysis of a Hand-Foot-Mouth Disease Model with Standard Incidence Rate and Estimation for Basic Reproduction Number. Mathematical and Computational Applications. 2017; 22(2):29. https://doi.org/10.3390/mca22020029
Chicago/Turabian StyleWu, Chunqing. 2017. "Analysis of a Hand-Foot-Mouth Disease Model with Standard Incidence Rate and Estimation for Basic Reproduction Number" Mathematical and Computational Applications 22, no. 2: 29. https://doi.org/10.3390/mca22020029
APA StyleWu, C. (2017). Analysis of a Hand-Foot-Mouth Disease Model with Standard Incidence Rate and Estimation for Basic Reproduction Number. Mathematical and Computational Applications, 22(2), 29. https://doi.org/10.3390/mca22020029





