Abstract
From the viewpoint of resource and energy-saving, the high extraction rate of alternating liquid–liquid flow (slug flow) is important given that it enables its novel use in extraction. Additionally, a specific extraction rate must be maintained for the practical application of slug flow to chemical extraction. Although slug flow is easily generated, controlling the slug length is difficult. In this study, two diaphragm pumps were interlocked to generate a slug flow. By linking the movement of the diaphragms of the two pumps, we could successfully and efficiently control the slug length, and the interlocking diaphragms could easily control the length of the aqueous and oil phase segments of the slug flow. The lengths of the aqueous and oil phases of the slug flow, which could not be quantitatively controlled, could be expressed in terms of the linear velocity of the liquid, the kinematic viscosity, and the tube diameter using the Reynolds number. This relation aids the extraction equipment design using slug flow. Furthermore, the mass transfer coefficient of extraction obtained using the slug flow generated by the developed device was similar to that obtained by the conventional method of a syringe pump. These results indicate that slug flow can be successfully applied to extraction processes.
1. Introduction
In the field of chemical processing, liquid–liquid extraction operations are essential for chemical production, metal ion recycling, and trace analysis [1]. In particular, lithium, the key ingredient in lithium-ion batteries, is currently extracted from natural minerals and salt water; this process is complex and consumes a significant amount of energy. Moreover, lithium consumption increased by 18% from 2018 to 2019, and the limited reserves and locations of lithium production indicate that lithium depletion is likely to be imminent. Consequently, technologies are being developed worldwide to recycle lithium from lithium-ion batteries. The extraction process is one of the most promising means to promote recycling [2]. Mixer–settler systems are typically used for liquid–liquid extraction, the structure and operation of which are relatively simple. However, the dispersed phases (aqueous or oil phases) that are micronized by the mixer require a long time (ranging from a few minutes to a few hours) to coalesce and separate into phases. Additionally, the use of extractants, such as di-(2-ethylhexyl)phosphoric acid (D2EHPA), N,N-diisopropyl-2-(octyl(phenyl)-N,N-diisobutylcarbamoyl methylphosphine oxide (CMPO), and 8-hydroxyquinoline, to accelerate the extraction process often yields chemical species with surfactant-like characteristics. Emulsions are generated during the mixer–settler extraction operation; thus, the separation of the aqueous and oil phases is highly time-consuming. Furthermore, liquid–liquid extraction equipment using the mixer-settler method tends to increase the volume of the equipment [3]. Recently, the drive to create a sustainable society has warranted a new solvent extraction method that saves energy, is more efficient than existing extraction methods, uses a small amount of solvent, and involves compact equipment.
The recent developments in microfabrication technology have highlighted the many advantages of using microflow devices for solvent extraction, which are expected to replace mixers and settlers. Microreactors, wherein the tube diameter is reduced to the order of millimeters or less, exhibit the following features [4,5,6,7]: (1) Mass transfer is efficient because of the narrow reaction space, and the diffusion distance is short; (2) the specific surface area per unit volume of the reactant is large, and thus the temperature can be finely controlled; and (3) the reaction time can also be finely controlled by tuning the flow rate and the length of the flow tube.
A fluid/reaction manipulation that exploits the characteristics of microreactors is known as slug flow. Slug flow represents a flow style obtained by alternating dissimilar phases that do not melt together in a microchannel. In addition to the abovementioned characteristics, slug flow exhibits the following three features from the viewpoint of chemical processes [8,9,10]: (1) Owing to the concentration renewal effect near the interface between the oil and aqueous phases, enhanced mixing occurs within each slug owing to the internal circulation flow and enhanced mass transfer between the two phases; (2) the size of each slug remains constant throughout the process, particularly in liquid–liquid extraction; and (3) the rapid separation of the liquid–liquid phase with a simple equipment design is feasible.
Thus, slug flow is a flow state that enhances the efficiency of microflow synthesis. The abovementioned features are also effective in separation operations; therefore, many studies have been conducted on solvent extraction using slug flow [11,12,13].
Slug flow can be easily generated using a T-shaped or Y-shaped pipe. However, although there are many reports [14,15,16,17,18,19] on the conditions of slug generation in liquid–liquid slug flow, there are only a few reports on controlling the length of each segment of the slug flow. As the length and shape of each segment are largely related to the mass transfer rate between the two liquids, controlling them is expected to facilitate system design when the slug flow is applied to the extraction operation. In extraction operations, it is desirable to have an optimum slug length that maximizes the combined effect of specific surface area and internal circulation. For non-extraction applications, a long slug length is desirable to avoid the mixing of components between slugs if a single slug is used as a tool for screening, for example, as a micro-batch reactor.
A slug flow generator that can independently control both the linear velocity and length of the slug was developed for the first time by linking two piezoelectric diaphragm pumps. The results of this study are expected to contribute toward equipment design and the setting of conditions for theoretical and practical use in the future, including the effect of linear flow velocity on the extraction rate for a given slug length. For example, Dessimoz et al. [14] showed that when the volumetric flow rates of the oil and water phases were equal, the linear velocity of the fluid was higher and the slug length was shorter, even though the slug lengths of the water and oil phases were same. They also concluded that the main parameters that influence the formation of the slug flow are physicochemical factors: the linear velocity of the liquid and the interfacial tension. In other words, the increase in interfacial tension and decrease in linear velocity favor slug flow. Higher linear velocities of the fluid result in faster extraction rates due to (1) the development of circulating flows within the segments of the aqueous and oil phases and (2) the larger surface area per unit volume due to shorter slug lengths. It is difficult to separate these two effects as influences on the extraction rate. Therefore, in this study, we attempted to fabricate a nest frame generator that can independently control the linear velocity and slug length. In addition, the use of a slug flow generator with an alternating pumping mechanism, such as this device, can be expected to further expand the conditions for slug generation. For example, slug generation can be expected even under conditions difficult with conventional methods (e.g., two-liquid systems with a small interfacial tension).
We also tried to clarify the quantitative relationship between the length of slug generated by this device and the flow conditions. Here, we aimed to investigate whether the velocity of the generated slug flow and slug length could be correlated with the frequency and voltage applied to the diaphragm motion using a piezoelectric element by interlocking two pumps. Therefore, we selected the aqueous cyclohexane system, which generates almost no emulsion and undergoes rapid phase separation. D2EHPA was chosen as the extractant for metal ions, and D2EHPA and sulfuric acid were added to alter the viscosity of the aqueous and oil phases, considering the practical use of recycling spent lithium-ion batteries in the future.
2. Materials and Methods
2.1. Concept of Slug Flow Generation
The concept of slug flow generation in this study is illustrated in Figure 1. Here, different insoluble liquids were supplied through channels A and B. In channel C, a flow state wherein the two phases flowed alternately (slug flow) was generated. Liquids A and B from inlets A and B, respectively, were merged in the T-junction pipe, and liquids A and B flowed alternately from outlet C. A slug flow with a controlled slug length (volume) could be generated by synchronizing and cyclically repeating the starting and stopping of liquid flow from inlets A and B (Figure 1).
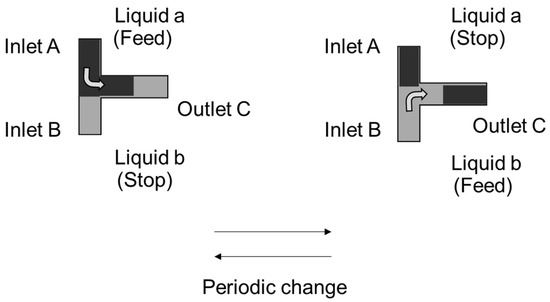
Figure 1.
Concept of mechanical generation of slug flow.
2.2. Slug Flow Generator
A piezoelectric micropump (PMP; APP-20KG, Takasago Electric Industry Co., Ltd., Nagoya, Aichi, Japan) with a piezoelectric material as the diaphragm pump was used to supply the liquids. Piezoelectric materials can generate mechanical strain when a voltage is applied, and the strain on the crystal varies according to the magnitude of the applied voltage. Thus, we can utilize this characteristic to operate the PMP as a diaphragm pump by periodically changing the applied voltage. Using the pump, the liquid can be continuously pumped out at a predetermined volumetric flow rate.
This PMP was used to supply the aqueous (A0–A3) and oil phases (O1–O4) listed in Table 1. By controlling the operation of these two PMPs, the supply of the oil phase was stopped when the water phase was fed to the T-pipe, and the collection of the oil phase was contained when the water phase was fed to the T-pipe. The voltage and frequency were considered the control parameters for PMP operation, corresponding to the magnitudes of the amplitude and the frequency of the diaphragm pump oscillation, respectively. In practice, the operation of the PMP was computer-controlled to alternately discharge the aqueous and oil phases (Figure 1).

Table 1.
Viscosity and kinematic viscosity of the solutions used in this experiment.
2.3. Experimental Operation for Slug Flow Generation
The experimental setup used in this study is illustrated in Figure 2. A controller was used to control the two PMPs, and a predetermined frequency and voltage were applied to generate a slug flow by merging the aqueous and oil phases in the T-junction tube. Each aqueous and oil phase was stored in a separating funnel and fed to the PMPs in a downflow manner. A check valve was installed to reduce the mutual influence of the PMPs. The slug flow was directed through a polytetrafluoroethylene (PTFE) tube with an inner diameter of 1 mm, and the flow was photographed. The liquid released from the outlet of the PTFE tube was weighed in a female cylinder, and the volumetric flow rate and linear velocity of the liquid were calculated based on its volume, the length of the PTFE tube, and time.
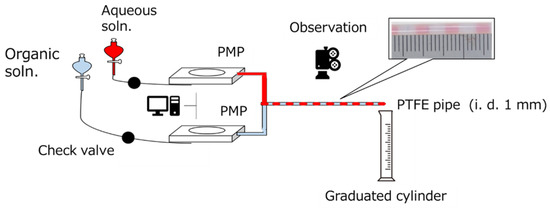
Figure 2.
Experimental setup. Solutions listed in Table 1 were stored in a dispensing funnel and connected to a PMP using tubing with a check valve. A controller was used to control the diaphragm of the PMP. Aqueous and oil solutions were combined in a polypropylene T-type connector with an inner diameter of 1 mm. After merging, the liquid formed a slug flow and flowed through the transparent PTFE tube. We measured the slug length by first video recording the slug flow and then converting it into a still image.
2.4. Reagents
Pure water, which was distilled and subjected to ion-exchange treatment and organic matter removal by activated carbon, was used as the aqueous phase. Bis(2-ethylhexyl) hydrogen phosphate (D2EHPA; molecular formula: (C8H17O)2PO2H, molecular weight: 322.4, FUJIFILM Wako Pure Chemical Corporation, Osaka, Japan), which is often used as an extractant in the solvent extraction of metal ions, was used to adjust the viscosity. For visualization, new coccin (C20H11N2Na3O10S3; molecular weight: 604.47, Fujifilm Wako Pure Chemicals) was used as a water-soluble red dye in the aqueous phase (approximately 10 mg/1000 mL water).
The viscosity of the oil phase could affect the supply of liquid by the diaphragm pump. Therefore, D2EHPA was dissolved in cyclohexane, and solutions of different viscosities were prepared. The viscosity of each solution was measured at room temperature (20–25 °C) using a tuning-fork oscillating viscometer (SV-10, A&D Company Ltd., Tokyo, Japan). The viscosities of organic solvents commonly used in organic synthesis are generally in the range of 0.3–2.00 mPa·s. In this study, we prepared an oil phase with a viscosity that was slightly higher than this range. The viscosity and kinematic viscosity of the oil phases prepared by dissolving D2EHPA in cyclohexane are listed in Table 1. From the comparison of the physical properties of A0 and A1 in Table 1, it can be seen that the impact of 1 mM LiCl on the aqueous phase liquid properties is negligible. Although Li is transported from O1 to O4, the impact on the oil phase liquid properties seems small compared to that when over 40 mM D2EHPA is dissolved in the solution.
3. Results and Discussion
3.1. Construction and Validation of Model for Slug Length Calculation
3.1.1. Model Based on the Additivity of the Liquid Discharged in One Stroke of a PMP Diaphragm
The effect of liquid kinematic viscosity on the volumetric flow rate was investigated using a single PMP. Using the A1 solution as the aqueous phase and O1–O4 (0.75–2.26 mPa∙s) as the oil phases, the relationship between the frequency of the diaphragm and the volume flow rate was determined (Figure 3). As the frequency of the diaphragm pump increased, the volume flow rate of each liquid increased linearly. However, this relationship was not directly proportional. Furthermore, with an increasing kinematic viscosity of the liquid, the volume flow rate decreased. Thus, it is suggested that the kinematic viscosity of the liquid affects the amount of liquid discharged from the pump.
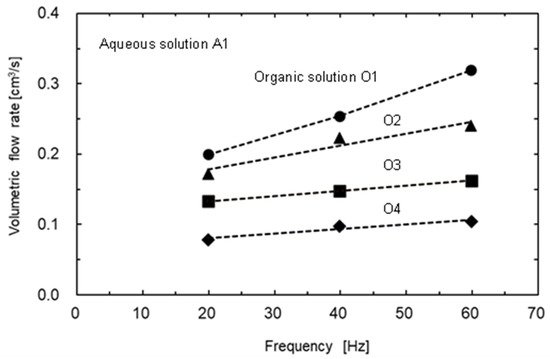
Figure 3.
Effect of frequency on volumetric flow rate under various kinematic viscosities of oil phase.
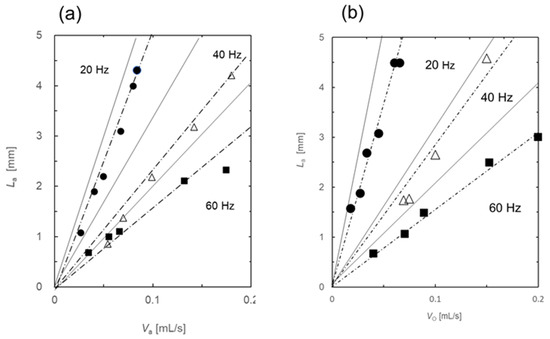
Two pumps were used to generate a slug flow using a PTFE tube with an inner diameter and length of 1 mm and 60 cm, respectively. Here, A1 and O1 were used as the aqueous and oil phases, respectively. The amplitude width of the diaphragm pump was altered by adjusting the voltage applied to the piezoelectric element, and consequently, the flow rate was varied. The relationship between the slug length and the flow rate in the aqueous and oil phases is depicted in Figure 4. At all frequencies, the volume per slug, and thus, the slug length, increased with increasing flow rate. Furthermore, with increasing frequency, the number of times the valves of the PMP opened and closed increased, thereby reducing the slug length. In the conventional method of generating slug flow by pumping two liquids at a fixed rate, the slug length demonstrates a one-to-one relationship with the flow rate. The device proposed in this study could overcome this limitation.
We considered the equation for the slug length generated by the PMP. If the slug length is [mm], the volumetric flow rate is [mL/s], and the set frequency of the device is f [Hz], Equation (1) can be established as follows:
where [mL] denotes the volume per piece of slug; subscript “i” represents either an a (aqueous phase) or o (oil phase). Assuming that the slug length is [mm] and the cross-sectional pipe area is S [mm2], Equation (2) is established as follows:
From Equations (1) and (2), Equation (3) is obtained as the (ideal) relationship between and that can be measured.
where d [mm] denotes the inner diameter of the pipe. The experimental values of the slug length for both the aqueous and oil phases were smaller than the values calculated using Equation (3) (Figure 4).
These results can be interpreted as the effect of the kinematic viscosity of the liquid, i.e., a lower pumping rate leads to a shorter slug length, which, in turn, leads to an apparent increase in the PMP frequency. Because it is difficult to independently analyze the effects of the amplitude and frequency, we introduce the term “effective frequency” (f′ [Hz]) as the apparent frequency to comprehensively evaluate these. Here, f′ was obtained by correlating the straight-line slope with the experimental values in Figure 4, replacing f with f′ in Equation (1).
f′ was determined from the slope of the approximate straight-line plot of the experimental values, and the relationship between f and f′ was obtained for the aqueous and oil phases, respectively (Figure 5a,b).
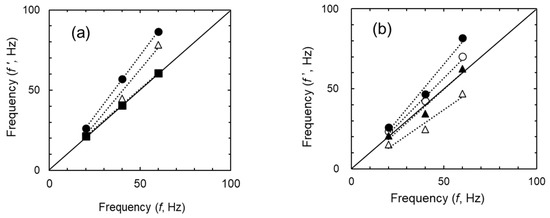
In both the oil (Figure 5a) and aqueous (Figure 5b) phases, a linear relationship was observed between f and f′. The slope of the line is represented by Pi (=f′/f). The correlation between Pi and the physical properties of the liquid is depicted in Figure 6. A linear relationship was obtained between Pi and the kinematic viscosity and density of the liquid.
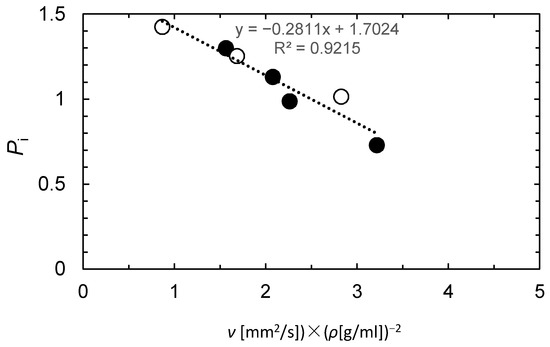
Figure 6.
Effect of the kinematic viscosities of the oil and aqueous phases on parameter Pi; ● oil phase; ○ aqueous phase.
Using the kinematic viscosity of each solution, we calculated f′ from the approximate equation Pi = −0.281 × ν [mm2/s] (ρ[g/mL])−2 + 1.70. We observed that there was a good correlation between the volume flow rate and the length of the slug for the solutions used in this experiment. Figure 6 depicts a slight difference between the Pi values for the oil phase (●) and aqueous phase (○), which may be due to the hydrophobic nature of the tube used in the experiment.
The parameter P tended to decrease with increasing kinematic viscosity and density for both the aqueous and oil phases. This may be due to the difficulty of liquid movement preventing the pump diaphragm from supplying the liquid in motion. However, because the P seems to depend on the diaphragm shape, it is expected to vary, although this trend is not dissimilar for each device.
In addition, the surface characteristics of the tube may have an effect, which will be clarified in future studies.
The correlation equation obtained here is represented by a single dotted line in Figure 4, comparing the calculated slug length with the experimental results. The calculated and experimentally measured results are in good agreement, indicating that the slug length can be controlled by tuning the frequency (oscillation frequency) and voltage (amplitude), which determine the motion of the diaphragm of the PMP.
3.1.2. Effect of Various Conditions on Slug Length
As clarified in the previous section, the slug length is proportional to the linear flow velocity (u). For example, as the μ value of the liquid increases, the flow rate decreases, and thus, the slug length decreases. In addition, if the inner diameter (d) of the pipe increases, Li decreases. The correlation of the relationships between u, μ, d, and can facilitate equipment design. Therefore, the data obtained thus far were arranged to correlate Li with the Reynolds number, Re, of the liquid, which was calculated using Equation (4).
For pure solvents, the density of each solution required for Re was calculated using the values from [20], whereas the concentration was used in the case of solutions, assuming that the volume change during solute dissolution is negligible. ui [m/s] represents the linear flow velocity and d denotes the inner diameter of the channel that leads to the pump. The relationship between Re and slug length (Li) for each d value of the channel, through which the slug flows, is depicted in Figure 7. The frequency was set at 40 Hz. Li and d exhibited a linear relationship for d = 1 and 2 mm. Here, the solutions were A1 for the aqueous phase and O1–O4 for the oil phase, which are shown in Table 1.
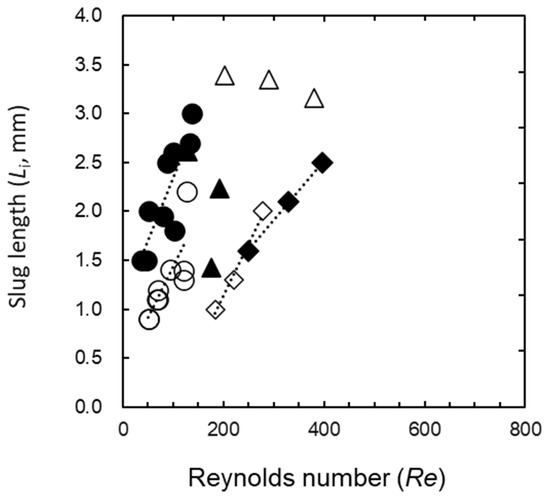
Figure 7.
Relationship between Re and Li; ○ and ●: 1 mm; ◇ and ◆: 2 mm; △ and ▲: 3 mm; open: aqueous phase; filled: oil phase.
In contrast, although slug flow was generated for d = 3 mm, it was unstable and of uneven length, likely because it required multiple strokes to be generated, i.e., the slug volume increased. The progress per stroke decreased with increasing values of d. Therefore, we considered the case in which d = 1 and 2 mm. If the d value of the extraction tube does not affect the amount of liquid supplied by the PMP, the volume per slug (Li d2π/4) is constant. Therefore, Li is considered to be inversely proportional to the cross-sectional area of the tube, i.e., the square of the inner diameter d. Considering that Re and Li are positively correlated, Equation (5) can be written as
where α and n are constants. Transforming Equation (5), we obtain Equation (6) as follows:
Even if d is varied, the slug length can be predicted and controlled by calculating α based on the experimental values. Figure 8 depicts a plot with Re on the horizontal axis and Lid2 on the vertical axis. A good linear relationship was observed for d = 1 mm and 2 mm, where α = 0.024 mm3.
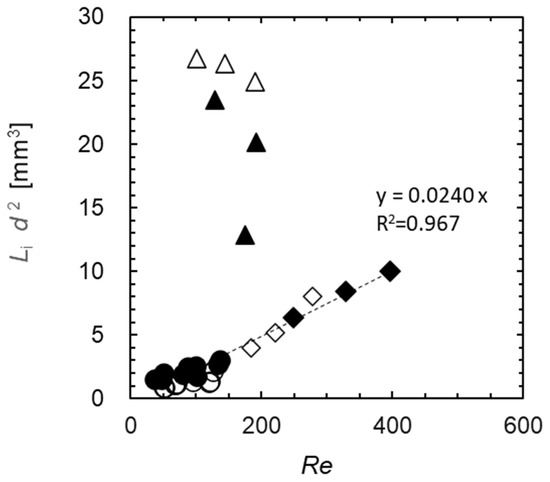
Figure 8.
Relationship between Re and Lid2; ○ and ● 1 mm; ◇ and ◆ 2 mm; △ and ▲ 3 mm; open: aqueous phase; filled: oil phase.
The following equation can be used as an estimation formula, where the left-hand side represents the volume per slug (Lid2π/4) and α′ = 0.019 mm3.
Yao et al. [21] reported the slug length of a liquid–liquid system generated in the line of sight of a T-junction to be an interphase with the diameter of the pipe and the measured volume flow ratio of the aqueous and oil phases of the liquid. In this study, we found the slug flow generated by interlocking the diaphragms of two pumps to be in step with the Reynolds number. It is suggested that the physicochemical parameters affecting the length of the slug flow are different depending on the generation of the slug flow. Having found the possibility of correlation with the Reynolds number, we would like to clarify the relationship with the interfacial force between liquids in the future.
3.2. Extraction Experiment
We compared the extraction rate of the slug flow generated by the interlocking of the two diaphragm PMPs used in this study with that of a syringe pump, which is often used in slug flow research. In this experiment, a commercially available syringe pump (KDS410, KD Scientific Inc., Holliston, MA, USA) was used instead of a diaphragm-type piezo pump (Figure 2). The A1 solution was used for the aqueous phase and the O2 solution was used for the oil phase. The mass transfer capacity factor KLa was calculated using the method proposed by Kashid et al. [15].
The mass transfer rate N [mol/(L·s)] is expressed by Equation (8):
where t [s] denotes the extraction time, KLa [1/s] the overall mass transfer capacity coefficient, and C [mol/L] and C* [mol/L] denote the lithium-ion concentrations in the aqueous phase at a given time and at equilibrium, respectively. Integrating with t yields Equation (9):
where A represents the integration constant. Then, solving Equation (8) with the initial condition C = C0 at t = 0 yields Equation (10):
Equation (9) is converted to Equation (11):
Here, E(=100 × (C0 − C)/C0) [%] and E*(=100 × (C0 − C*)/C0) [%] denote the extraction rate at a given time and at equilibrium, respectively; the data obtained from the palindromic extraction experiment were used for E*. Based on Equation (9), KLa was obtained from the slope of the plot with time t on the horizontal axis and −ln(1−E/E*) on the vertical axis.
Figure 9 depicts the effect of the liquid flow velocity U [m/s] on the overall mass transfer coefficient, KLa, using a piezo micropump (●) and a syringe pump (○) (via the method shown in [22]). The slug flow generated by the interlocking of the two diaphragm piezo pumps used in this study could achieve the same extraction rate as that of the syringe pump frequently used in previous studies. KLa tended to increase with increasing U, suggesting that circulation flow occurred in each fluid, which is a characteristic of slug flow.
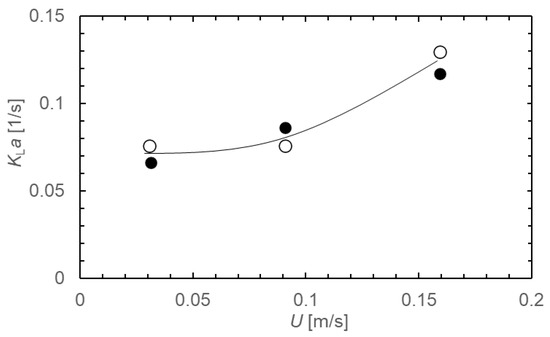
Figure 9.
Effect of flow rate on overall mass transfer capacity coefficient (KLa) by a piezo micropump (●) or syringe pump (○).
4. Conclusions
Slug flow provides the benefit of a high-speed extraction operation and is desirable for controlling the extraction rate and setting the slug shape (length) during the process design for practical applications. In this study, we attempted to generate a slug flow using two PMPs with an interlocked diaphragm pump operation. Our results indicated that by regulating the voltage and frequency applied to the piezoelectric diaphragm pumps, the liquid flow rate and the apparent frequency could control the slug length. When the generated slug flow was stable, the slug length could be correlated with the Reynolds number and kinematic viscosity of the liquid. Additionally, the mass transfer coefficient of the slug flow generated by the proposed device was the same as that of the slug flow generated by the conventional method of using a syringe pump. Hence, these results are expected to pave the way for practical applications of slug flow in liquid–liquid extraction processes for improved efficiency. The developed device can be used to vary the length of the slug flow at a given linear velocity; therefore, it can clarify the effect of the linear velocity on the extraction rate while maintaining a constant specific surface area. It is expected that the knowledge gained from this study will be useful for designing specific equipment. In this study, the effect of the material of the tube is not clarified. The parameters may change depending on whether the tube is hydrophobic or hydrophilic. These aspects can be studied in the future.
Author Contributions
Conceptualization, A.M.; methodology, A.M. and H.A.; validation, A.M., T.F. and S.-i.K.; formal analysis, A.M., T.F. and S.-i.K.; investigation, A.M., H.A. and K.K.; data curation, A.M.; writing—original draft preparation, A.M.; writing—review and editing, A.M., T.F. and S.-i.K.; visualization, A.M.; supervision, A.M.; project administration, A.M.; funding acquisition, A.M. All authors have read and agreed to the published version of the manuscript.
Funding
The authors wish to thank the New Energy and Industrial Technology Development Organization (NEDO) for providing financial support (project number JPNP19004) for this study.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
This paper is based on the results obtained from project JPNP19004 subsidized by the New Energy and Industrial Technology Development Organization (NEDO).
Conflicts of Interest
There are no conflict of interest to declare.
Nomenclature
| A | the integration constant |
| α | proportional constant [-] (=) |
| α′ | proportional constant [-] (=) |
| C | the lithium-ion concentration in the aqueous phase at a given time [mol/L] |
| C0 | the initial concentration of lithium-ion in the aqueous phase [mol/L] |
| C* | the lithium-ion concentration in the aqueous phase at equilibrium [mol/L] |
| d | the inner diameter of the pipe [mm] |
| E | the extraction rate (=100 × (C0 − C)/C0 [%]) |
| E* | the extraction rate at equilibrium [%] (=100 × (C0 − C*)/C0 [%]) |
| f | set frequency of the device [Hz] |
| f′ | effective frequency [Hz] |
| KLa | the overall mass transfer capacity coefficient [1/s] |
| slug length [mm] | |
| N | mass transfer rate [mol/(L·s)] |
| Re | Reynolds number [-] |
| proportional constant [-] (=f′/f) | |
| S | cross-sectional pipe area [mm2] |
| t | extraction time [s] |
| U | linear flow velocity [m/s] |
| ui | linear flow velocity [m/s] |
| volumetric flow rate [mL/s] | |
| denotes the volume per piece of slug [mL] | |
| ν | kinetic viscosity [mm2/s] |
| ρ | density [g/mL] |
| subfix | |
| i | either a (aqueous phase) or o (oil phase) |
| L | liquid |
| 0 | initial condition |
References
- Angeli, P.; Ortega, E.G.; Tsaoulidis, D.; Earle, M. Intensified liquid–liquid extraction technologies in small channels: A review. Johns. Matthey Technol. Rev. 2019, 63, 299–310. [Google Scholar] [CrossRef]
- Bae, H.; Kim, Y. Technologies of lithium recycling from waste lithium ion batteries: A review. Mater. Adv. 2021, 2, 3234–3250. [Google Scholar] [CrossRef]
- Pinto, G.A.; Durão, F.O.; Fiúza, A.M.A.; Guimarães, M.M.B.L.; Novais Madureira, C.M. Design optimisation study of solvent extraction: Chemical reaction, mass transfer and mixer-settler hydrodynamics. Hydrometallurgy 2004, 74, 131–147. [Google Scholar] [CrossRef]
- Dummann, G.; Quittmann, U.; Gröschel, L.; Agar, D.W.; Wörz, O.; Morgenschweis, K. The capillary-microreactor: A new reactor concept for the intensification of heat and mass transfer in liquid–liquid reactions. Catal. Today 2003, 79–80, 433–439. [Google Scholar] [CrossRef]
- Hessel, V.; Löwe, H.; Schönfeld, F. Micromixers—A review on passive and active mixing principles. Chem. Eng. Sci. 2005, 60, 2479–2501. [Google Scholar] [CrossRef]
- Mills, P.L.; Quiram, D.J.; Ryley, J.F. Microreactor technology and process miniaturization for catalytic reactions—A perspective on recent developments and emerging technologies. Chem. Eng. Sci. 2007, 62, 6992–7010. [Google Scholar] [CrossRef]
- Wong, S.; Ward, M.; Wharton, C. Micro T-mixer as a rapid mixing micromixer. Sens. Actuators B 2004, 100, 359–379. [Google Scholar] [CrossRef]
- Antony, R.; Giri Nandagopal, M.S.; Sreekumar, N.; Rangabhashiyam, S.; Selvaraju, N. Liquid–liquid slug flow in a microchannel reactor and its mass transfer properties—A review. Bull. Chem. React. Eng. Catal. 2014, 9, 207–223. [Google Scholar] [CrossRef]
- Sotowa, K. Fluid behavior and mass transport characteristics of gas–liquid and liquid–liquid flows in microchannels. J. Chem. Eng. Jpn. 2014, 47, 213–224. [Google Scholar] [CrossRef]
- Ramji, S.; Rakesh, A.; Pushpavanam, S. Modelling mass transfer in liquid-liquid slug flow in a microchannel. Chem. Eng. J. 2019, 364, 280–291. [Google Scholar] [CrossRef]
- Tiwari, A.; Rajesh, V.M.; Yadav, S. Biodiesel production in micro-reactors: A review. Energy Sustain. Dev. 2018, 43, 143–161. [Google Scholar] [CrossRef]
- Vandermeersch, T.; Gevers, L.; De Malsche, W. A robust multistage mesoflow reactor for liquid–liquid extraction for the separation of Co/Ni with Cyanex 272. Sep. Purif. Technol. 2016, 168, 32–38. [Google Scholar] [CrossRef]
- He, Y.; Guo, S.; Chen, K.; Li, S.; Zhang, L.; Yin, S. Sustainable green production: A review of recent development on rare earths extraction and separation using microreactors. ACS Sustain. Chem. Eng. 2019, 7, 17616–17626. [Google Scholar] [CrossRef]
- Dessimoz, A.-L.; Cavin, L.; Renken, A.; Kiwi-Minsker, L. Liquid–liquid two-phase flow patterns and mass transfer characteristics in rectangular glass microreactors. Chem. Eng. Sci. 2008, 63, 4035–4044. [Google Scholar] [CrossRef]
- Kashid, M.N.; Harshe, Y.M.; Agar, D.W. Liquid–liquid slug flow in a capillary: an alternative to suspended drop or film contactors. Ind. Eng. Chem. Res. 2007, 46, 8420–8430. [Google Scholar] [CrossRef]
- Miki, Y.; Matsumoto, S.; Takada, N.; Kaneko, A.; Abe, Y. Effects of flow rate on formation behavior of two-phase slug flow in a microchannel T-junction. Jpn. J. Multiph. Flow 2014, 27, 591–598. [Google Scholar] [CrossRef][Green Version]
- Qian, J.; Li, X.; Wu, Z.; Jin, Z.; Sunden, B. A comprehensive review on liquid–liquid two-phase flow in microchannel: Flow pattern and mass transfer. In Microfluidics and Nanofluidics, 5th ed.; Perry, R.H., Chilton, C.H., Eds.; McGraw-Hill Chemical Engineering Series; McGraw-Hill: New York, NY, USA, 2019; Volume 23, p. 20. [Google Scholar] [CrossRef]
- Takada, N.; Matsumoto, J.; Matsumoto, S. Prediction of two-phase slug flow patterns in microchannel with T-junction. Jpn. J. Multiph. Flow 2014, 28, 32–38. [Google Scholar] [CrossRef][Green Version]
- Thorsen, T.; Roberts, R.W.; Arnold, F.H.; Quake, S.R. Dynamic pattern formation in a vesicle-generating microfluidic device. Phys. Rev. Lett. 2001, 86, 4163–4166. [Google Scholar] [CrossRef] [PubMed]
- Perry, R.H.; Chilton, C.H. (Eds.) Chemical Engineers’ Handbook, 5th ed.; McGraw-Hill Chemical Engineering Series; McGraw-Hill: New York, NY, USA, 1973. [Google Scholar]
- Yao, C.; Liu, Y.; Xu, C.; Zhao, S.; Chen, G. Formation of liquid-liquid slug flow in a microfluidic T-junction: Effects of fluid properties and leakage flow. AIChE J. 2018, 64, 346–357. [Google Scholar] [CrossRef]
- Hirayama, Y.; Hinoue, M.; Tokumoto, H.; Matsuoka, A.; Noishiki, K.; Muto, A. Liquid–Liquid Extraction and Separation of Cobalt and Lithium Ions Using a Slug Flow Microreactor. J. Chem. Eng. Jpn. 2018, 51, 222–228. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).