1. Introduction
Anthropogenic emission of carbon species is projected to disrupt the Earth’s climate over the coming decades. Carbon Capture and Storage (CCS) is thereby gaining importance as a strategy to prevent carbon emissions from reaching the atmosphere. This is particularly relevant for those industrial sectors that can hardly avoid the use of carbon, like steel making. In this context, sorption-enhanced reactive processes (SERPs) are receiving increasing attention as strategic technologies to accelerate CCS implementation in such industrial sectors [
1,
2,
3,
4]. SERPs are integrated conversion/separation processes that achieve a greater product yield from equilibrium-limited reactions by adsorbing one of the product species on a solid surface [
5].
Gas adsorption is a well-established industrial process for the separation and purification of gases [
1,
5,
6,
7,
8,
9]. It is widely applied, as an example, to separate H
2 and O
2, respectively, from natural gas reformate and air [
6,
8,
9]. During an adsorption process, a gas species, or adsorbate, is selectively transferred to a solid surface. Subsequently, this gas species is recovered by regenerating the solid material, or sorbent. Regeneration can be achieved by heating the sorbent to higher temperatures or by lowering the adsorbate partial pressures [
9,
10].
Various SERP concepts have been proposed and investigated for the conversion of methane- or syngas-like mixtures to H
2, with simultaneous capture of CO
2 [
11,
12,
13,
14,
15,
16]. Among these processes, the sorption-enhanced water gas shift (SEWGS) process shows significant potential to capture CO
2 with low costs and energy penalties [
4,
13]. In the SEWGS process, CO
2 is selectively adsorbed to shift the thermodynamic equilibrium of the water gas shift reaction (WGS) towards the production of H
2 Equation (1).
The implementation of SEWGS as pre-combustion capture technology has been assessed on the treatment of coal and natural gas-derived syngas for the production of electricity or hydrogen. More recently, the conversion of carbon-rich steelworks arising gases to a low-carbon hydrogen fuel gas has been more intensively investigated [
15,
17,
18,
19,
20,
21,
22].
As carbon dioxide emissions from iron and steel making are considered to be among the hardest to abate [
2,
23], SEWGS development is rapidly moving towards higher technology readiness levels (TRL) in this field of use [
14,
24,
25]. In the recently concluded H2020 STEPWISE project, a SEWGS process was developed and piloted at TRL 6 for the treatment of blast furnace gas (BFG). In the STEPWISE pilot, a single column pilot reactor can be exposed up to 800 Nm
3/h of BFG, which is directly supplied from the SSAB blast furnace in Luleå, Sweden [
14]. More recently, the STEPWISE pilot has been used to demonstrate the production of methanol from its BFG-derived H
2 and CO
2 streams in the H2020 FReSMe project [
26]. Further pilot campaigns at TRL 6 are planned as part of the currently on-going H2020 C4U project [
27], and plans for the construction of a first multi-columns pilot have begun as part of the H2020 INITIATE project [
25].
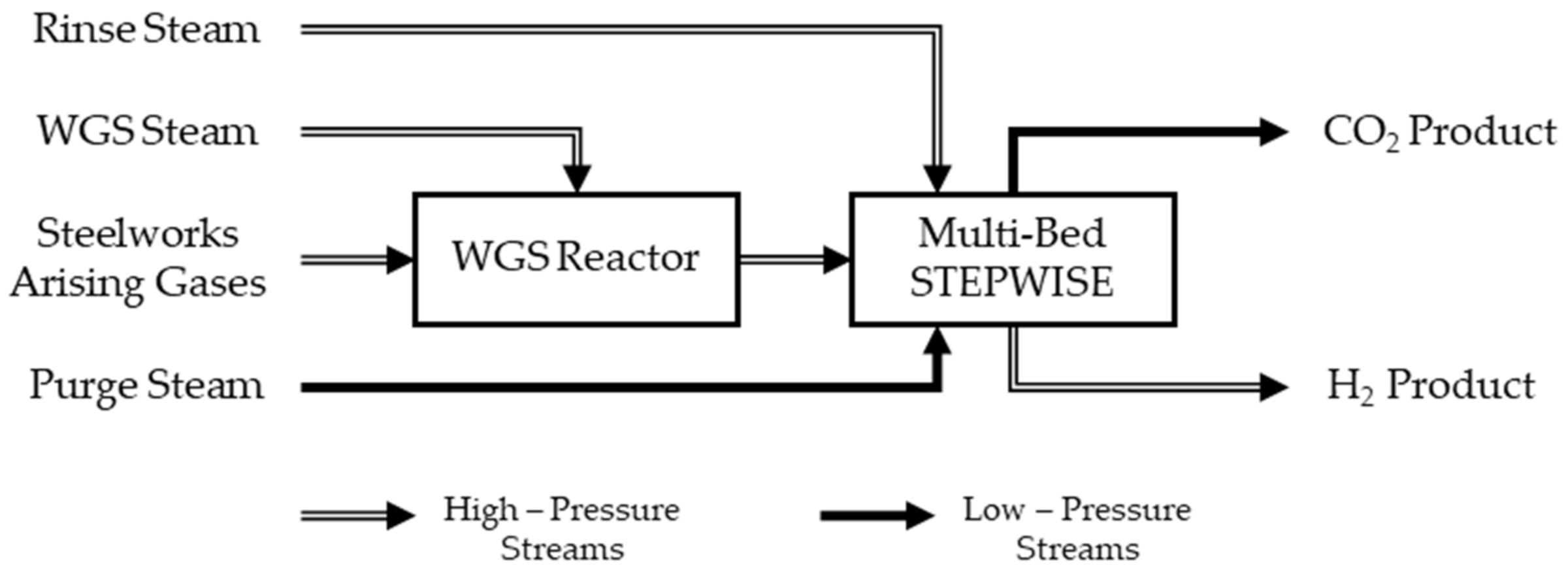
Essentially, when industrially relevant scales are considered, STEPWISE is designed to work as a multi-bed pressure swing adsorption (PSA)-like technology, as illustrated in
Figure 1 [
14,
19]. The STEPWISE reactive columns are packed with a potassium-promoted hydrotalcite-based (K-HTC) CO
2 sorbent. This functions at temperatures between 300 and 550 °C [
14]. Hydrotalcites are especially interesting as SEWGS sorbents due to their good hydrothermal stability, high selectivity towards CO
2 adsorption, fast sorption kinetics, and stable cyclic performances [
12,
13,
28,
29,
30,
31,
32]. Furthermore, hydrotalcites are catalytically active towards CO conversion by WGS reaction and allow the simultaneous co-adsorption of acid gases [
33].
In a typical STEPWISE multi-bed layout, an initial single stage WGS reactor (pre WGS) converts part of the incoming CO. Deep conversion of CO is not required, thereby avoiding multiple reactive and intercooling stages [
14]. High-pressure (HP) steam is supplied as a reactant to the pre-WGS. Additional HP steam is added to the STEPWISE unit to increase the sharpenss of the CO
2 separation by rinsing the sorbent with a steam front [
12,
34,
35,
36]. Low-pressure (LP) steam is used as purging agent to regenerate the sorbent and recover the CO
2 product at low pressures [
12]. Both the rinse and purge steam amounts are usually expressed in relation to the amount of carbon fed (i.e., CO and CO
2) through steam-to-carbon ratios (S/C) [
12,
24,
35,
36,
37].
Generally, for any given pre-shifted feed gas composition, the main process parameters of STEPWISE include the following: (1) sorbent bed properties (bed void fraction, particle size, particle porosity, density); (2) reactor column sizes (length and diameter); (3) temperature and pressure conditions; and (4) amount of carbon fed as CO and CO2, which we express here in terms of gas-hourly-space-velocity (GHSVc) and (5) S/C ratios.
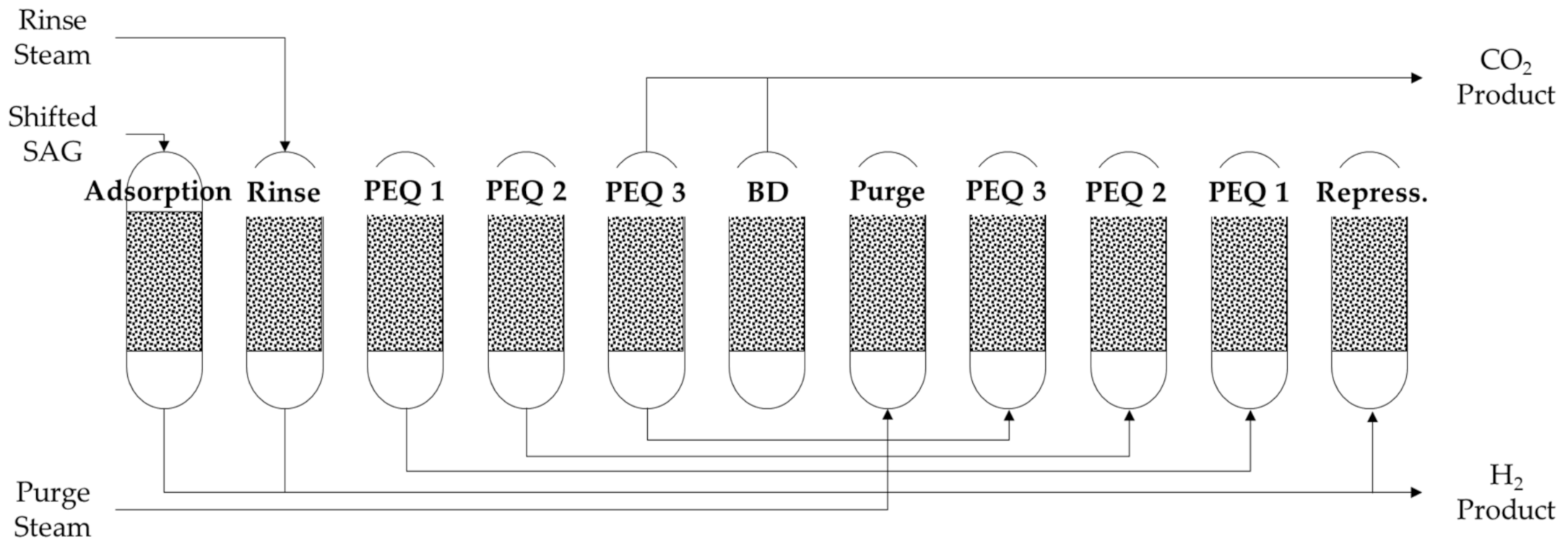
In addition to these process parameters, a Skarstrom cycle needs to be designed [
38]. This is essentially a pre-programmed sequence of steps, which allows to operate semi-batch PSA-like processes on a continuous mode [
5,
9,
10,
39]. Cycle steps, such pressure equalizations (PEQs), rinse, and blow down (BD), which are valid for the STEPWISE technologies, are described extensively by previous authors [
12,
35,
36,
37]. The parallel optimization of the Skarstrom cycle, or cycle design, and the process parameters is central to achieve high separation performances at low processing costs for STEPWISE, as for any other PSA-like technology [
5,
8,
9,
39].
1.1. Optimization of SEWGS Based Processes via Computer Simulations
Typically, the optimal design of PSA technologies aims to (1) maximize separation performances (i.e., product recovery and purity); (2) optimize energy performances; and (3) minimize processing costs [
40]. When PSA physical models are used, this results in a mixed nonlinear integer optimization problem with partial differential and algebraic equation (PDAE) integration. The use of accurate physical models to conduct this optimization is thereby known to be computationally expensive and intricated. However, this is also more suited to generate new process knowledge in contrast to reduced order models [
39,
41,
42,
43,
44].
When physical models are used, the main challenge is to optimize both process parameters, like pressure and steam inputs, and the cycle design. Different approaches are available to deal with this challenge. Some authors make use of process superstructures [
45,
46]. Others fix either the process parameters or the cycle design [
47,
48,
49,
50]. Alternatively, the problem complexity is reduced by solving ideal single column cycles. These cycles do not meet multi-bed schedule constrains and do not account for the required number of columns or idle times. However, the study of ideal single column cycles is found useful to generate process insights at the initial stage of the design. This approach is taken by Casas (2013) and Streb (2020), as an example, to highlight the effects of process parameters and individual step times on capture performances [
51,
52,
53].
Concerning SEWGS optimization, the necessity of generating new process knowledge has driven different authors to focus mostly on using physical models to execute parametric sensitivities with pre-specified cycle designs [
12,
24,
35,
36,
37]. First, Reijers et al. (2011) conducted a parametric sensitivity on cycle time, feed flow rate, and purge and rinse steam flows, with a fixed six-column cycle design, including one feed co-current pressure equalization, feed countercurrent rinse, feed countercurrent blow down, feed-countercurrent repressurization with partial recycle of the light H
2 product, and an idle step [
37]. An alternative eight-column cycle was studied by Boon et al. (2015). This cycle presents three feed countercurrent PEQs, feed-co-current rinse, and no idle steps in comparison to Reijers’s one [
12]. A single-column full PDAE model is implemented on MATLAB and used to analyze separation performances over varying total cycle time, rinse, and purge steam flow amounts. The same cycle but with three feed co-current PEQs and feed countercurrent rinse steps is studied by Jansen et al. (2011), analyzing SEWGS separation performances for different purge and rinse flows [
24].
As pointed out by Boon et al. (2015), Reijers observed that carbon purity (CP) and carbon capture ratio (CCR) rise proportionally with the supplied rinse and purge steam amounts although with reducing gain after a certain point. However, it is not possible simultaneously to increase both CCR and CP by modifying only one variable, as CP drops with higher purge as well as CCR with higher rinse [
12]. Only under specific regimes, CP may also rise with a higher purge input [
12]. According to Boon et al. (2015), CP is strongly influenced by the progression of the CO
2 front during the adsorption step [
12]. In most cases, a higher purge amount will cause the bed to be more deeply regenerated at the beginning of adsorption step. A cleaner bed will then further reduce the CO
2 front progression, and consequently the CP [
12].
More recently, Najmi et al. (2016) studied a multi-train configuration, including two trains of eight columns [
36]. In that work, both feed flow rate and steam inputs are varied with a fixed cycle design. Interestingly, it is concluded that a modification of the rinse and purge steam inputs is not sufficient by itself to maintain CO
2 recovery and purity unchanged, while feed flow rate is varied. Accordingly, it is indicated that the duration of the adsorption step should be changed as well. This new duration is needed to compensate for the varying progression of the CO
2 front during the adsorption step. However, following the influence of the purge steam input on the progression of the CO
2 front that was inferred by Boon et al. (2015), it shall be possible to retain separation performances without necessarily changing the cycle time as well.
1.2. Aim of This Work
In this study, we expand the work of previous authors on the role of the rinse and purge steam amounts to achieve high separation performance by SEWGS with hydrotalcite-based sorbents. An investigation on the effect of the adsorption pressure is also added. Specifically, we aim to show the influence of the selected process parameters (rinse steam, purge steam, and adsorption pressure) over the progression and shape of the CO2 front over different cycle steps. This is done to demonstrate the retention of high separation performances at different feed carbon loads.
2. Materials and Methods
2.1. Parametric Approach
A systematic parametric approach is devised to analyze the STEPWISE separation performance at different feed pressure and steam inputs (
Figure 2). The parametric approach comprises two steps: (1) a basis of design step, where an ideal single column schedule with null idle times is fixed, together with other basic process parameters and bed properties; and (2) a process parameters optimization step, whereby parametric sensitivities are conducted to achieve evaluate separation performances.
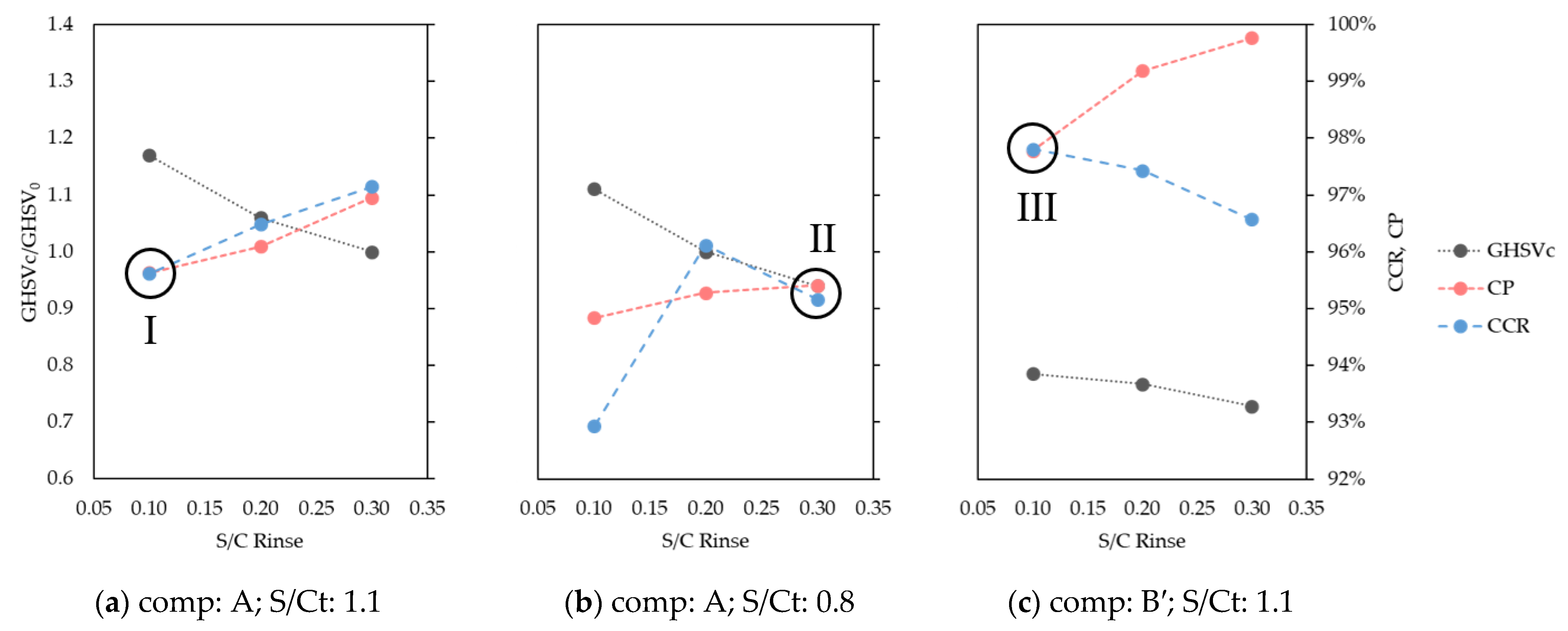
Separation performances are measured with Carbon Capture Ratio (CCR) and Carbon Purity (CP) indicators, as defined in Equations (2) and (3). Process parameters are systematically varied in order to find operating points whereby CCR and CP are (almost) equal. These points lie on the diagonal of a CCR/CP Pareto chart and are referred as Pareto diagonal solutions or diagonal solutions.
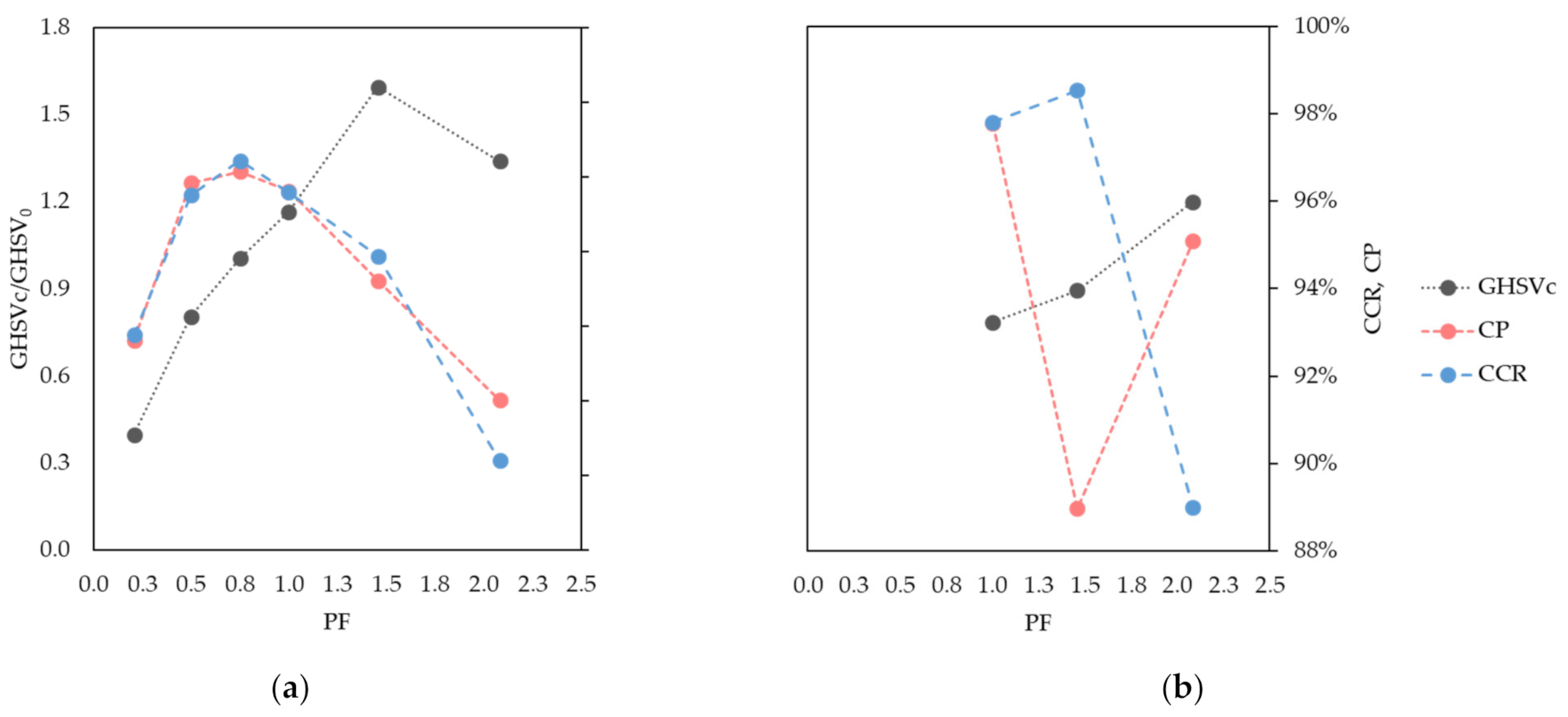
The systematic identification of diagonal solutions is proposed as a method to rapidly evaluate different sets of process parameters in terms of separation performances. Essentially, the solution space order is reduced by combining CO2 recovery and purity into a single indicator. For each set of parameters, diagonal solutions are then searched by tuning the feed carbon loading, which is expressed as carbon gas hourly space velocity (GHSVc) and is defined in Equation (10).
Although the diagonal solutions do not necessarily match those optimum solutions that best compromise between CCR and CP, maximize efficiency, or minimize costs, this approach is proposed to facilitate the identification and comparison of different operating points. It is therefore used to highlight how the studied parameters affect capture performances rather than to find their optimal design values.
Additionally, in order to show the trade-off between system throughput and energy consumption, the system is re-parametrized in terms of S/C variations. Instead of the conventional study of system performance in terms of S/Cr and S/Cp [
12,
24,
35,
36,
37,
54], a new variable is introduced to systematically track rinse and purge steam distribution at a fix total steam consumption. This is called the rinse-to-purge ratio (R/P), and it is defined according to Equation (8). It is important to realize that rinse and purge steam have different pressure qualities. This difference is not highlighted in the results of this study, as the aim is to highlight the process influence of steam inputs and carbon load on separation performance.
Since we intend to focus on studying the steam and pressure role on the reactor performances, individual step times and cycle time are not parametrized. This is done to facilitate a broad mapping of the studied parameters. Therefore, only ideal single-column capture performances are presented, while the required number of columns or idle times are not determined.
2.2. Basic Assumptions
The assumed STEPWISE column characteristics are presented in
Table 1. Two steelworks arising gases (SAG) mixtures are used to define the inlet gas specifications of the pre WGS reactor (
Table 2). Based on these two mixtures, four different inlet compositions are derived to conduct STEPWISE simulations (
Table 3). Compositions are named with letters.
STEPWISE feed compositions are obtained from the respective SAG mixtures with Aspen Plus software. Specifically, the pre WGS reactor is modelled with an adiabatic Gibbs reactor block. Inlet temperature is fixed at 340 °C, while different shift intensities are assumed by using steam to CO ratios (S/CO) from 1.5 to 1.9 at pre WGS inlet. The Peng Robinson equation of states (EOS) is used to conduct these calculations. The pressure value is fixed at the desired inlet pressure of the STEPWISE reactor, as outlined in
Table 1.
Composition A is derived from a mixture of blast furnace gas (BFG) and basic oxygen furnace gas (BOFG). This mixture is computed using the availability and composition of these gases, as specified by Hooey et al. (2013) [
55]. The same shift intensity is used for all cases with this composition. Concerning compositions B′, B″, and B‴, composition values are obtained for different shift intensities, driven by different steam-to-carbon-monoxide (S/CO) inputs at the simulated pressure levels.
Concerning cycle design, the assumed ideal single-column cycle structure with zero idle times is depicted in
Figure 3. In terms of steps, this is equivalent to the structure that is proposed by Boon et al. (2015) [
12]. The cycle includes adsorption and rinse steps at the same high-pressure level. The rinse step is co-current with the feed. Subsequently, three co-current pressure equalization steps occur, to be followed by countercurrent blow-down and purge steps. Column pressure is then increased countercurrently with the pressure equalization products. At last, repressurization is conducted with a partial reflux of light H
2 product. Total cycle time is kept unchanged to evaluate S/C ratios and adsorption pressure performances. As mentioned earlier, individual step times variations to minimize number of columns and meet multi-bed scheduling constraints are outside the scope of this work.
2.3. Parametric Studies
Three parametric studies were conducted. These are summarized in
Table 4 by showing the respective manipulated variables. Each study correspond to a series of STEPWISE simulations.
In the first study, GHSVc was kept constant, as done in some previous works [
12,
24,
37], while R/P ratio and total steam consumptions were varied.
In a second study, GHSVc was systematically varied, trying to achieve the pareto diagonal solution for different R/P ratios and total steam consumption, according to the proposed methodology. Some simulations were conducted on the feed composition B′, which was derived from a pure pre-shifted BOFG.
Finally, pressure variations were similarly analyzed in a third study on both BFG/BOFG and pure BOFG derived gases. Pressure and GHSVc are reported with dimensionless figures (i.e., PF in Equation (9) and GHSVr in Equation (11)) by using the reference values that are reported in
Table 5.
2.4. Models
A STEPWISE column mathematical model was developed and implemented in MATLAB. This model is largely based on the previously presented SEWGS model by Boon et al. (2015) [
12,
56]. Specifically, it includes:
Continuity, momentum, energy, and species balances;
WGS reaction kinetics and equilibrium relationships;
Adsorption and desorption kinetics represented by linear driving force (LDF) method;
CO
2-H
2O dual interaction model with the K-HTC sorbent, which includes multi-site adsorption and nanopore condensation effects, as described by Coenen et al. (2017) and Boon et al. (2015), respectively [
32,
57];
Heat or reaction and heat of adsorption formulations [
12];
Valve equations;
Pressure drop factor by Ergun approximation;
Ideal gas law equation of states (EOS);
Gas physical property models, including gaseous species’ heat conductivity, specific heat capacity, diffusivity, viscosity, and density relationships;
Axial dispersion; and
Bed to wall radial heat transfer coefficient.
The resulting set of PDAE was solved numerically. Equations were discretized over the time and space according to the method of lines. Space discretization included a combination of upwind, central difference, and Barton schemes, as outlined by Boon et al. (2015) [
56]. Time integration as achieved with a first-order Euler scheme. Uniform grids of 200 and 50 points were used, respectively, for space and time.
A cycle routine was added to the column model. The routine can sequentially simulate the various steps of an ideal single-column cycle by varying flow directions and boundary conditions, according to a prespecified cycle structure. Consequently, the model solution includes all relevant column transient profiles over time and space for each cycle step.
2.5. Definitions
Throughout this study, the following definitions apply:
4. Conclusions
In this work, we studied the steam and pressure requirements to achieve high CO2 purity and recovery with the STEPWISE technology. Reactor performances were evaluated via numerical simulations and structured parametric sensitivities. These were executed over a range of S/C and pressure input values. For each set of input parameters, the diagonal Pareto solution (i.e., CCR = CP) was searched by varying the inlet carbon loading (i.e., GHSVc).
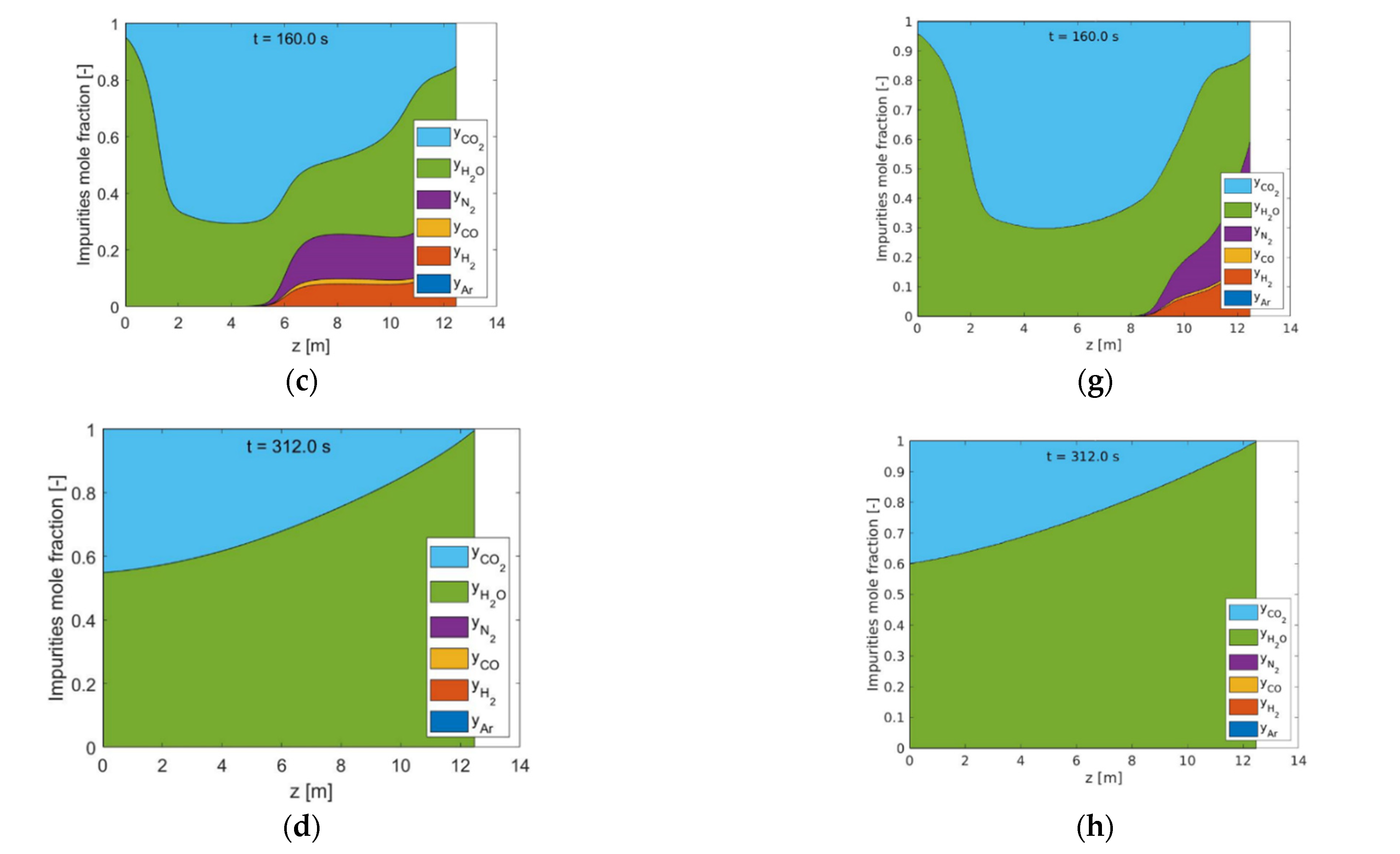
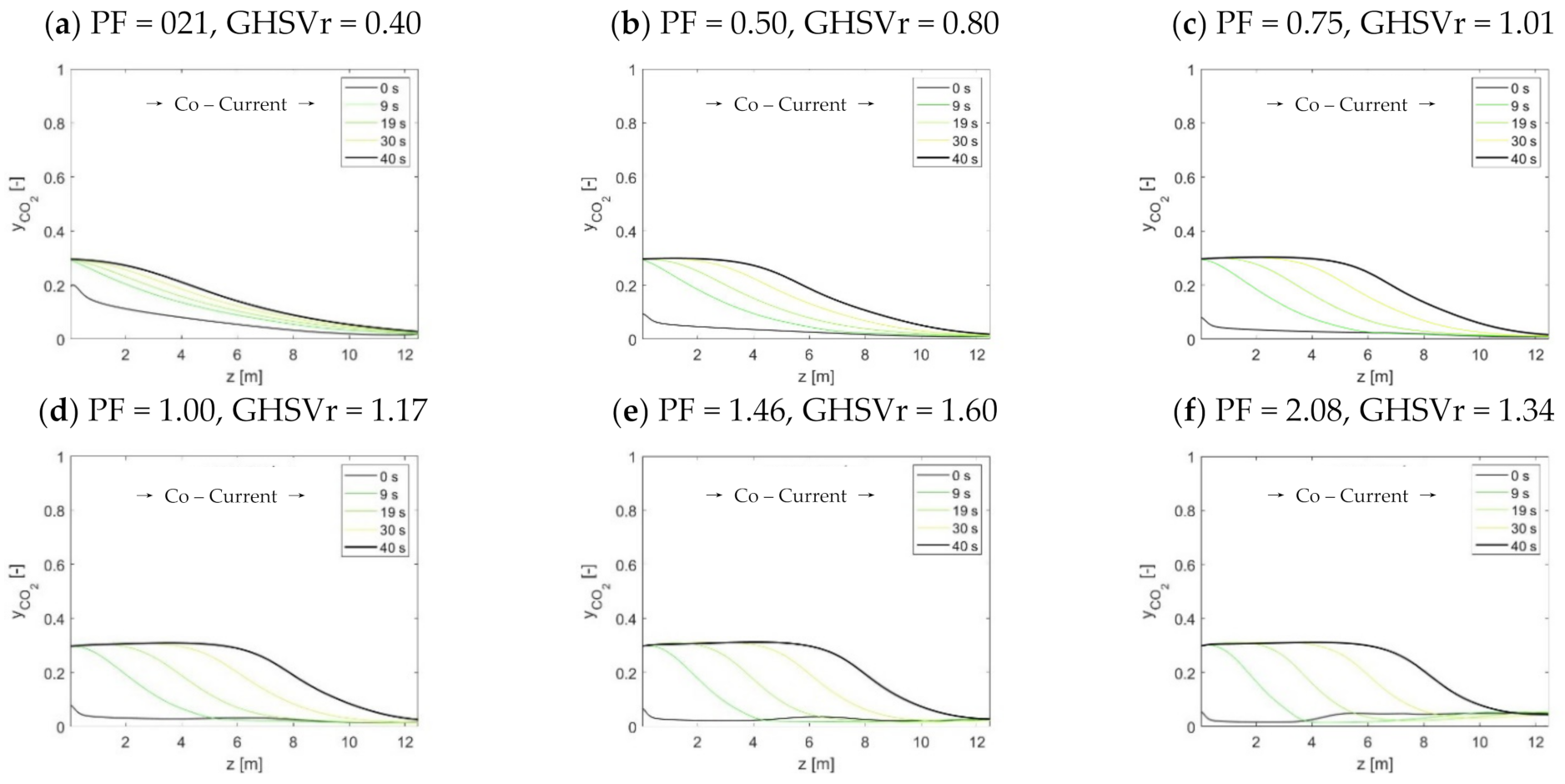
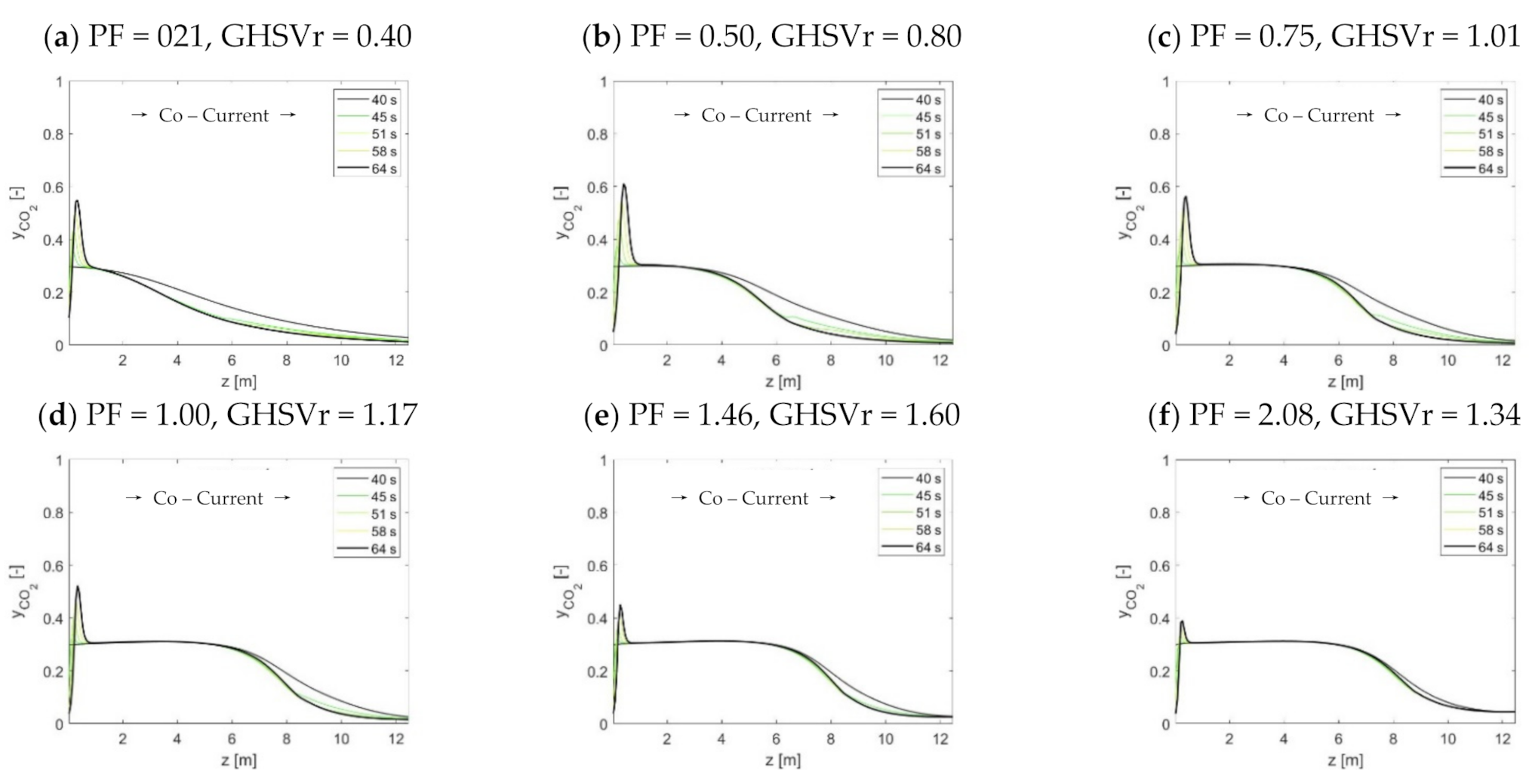
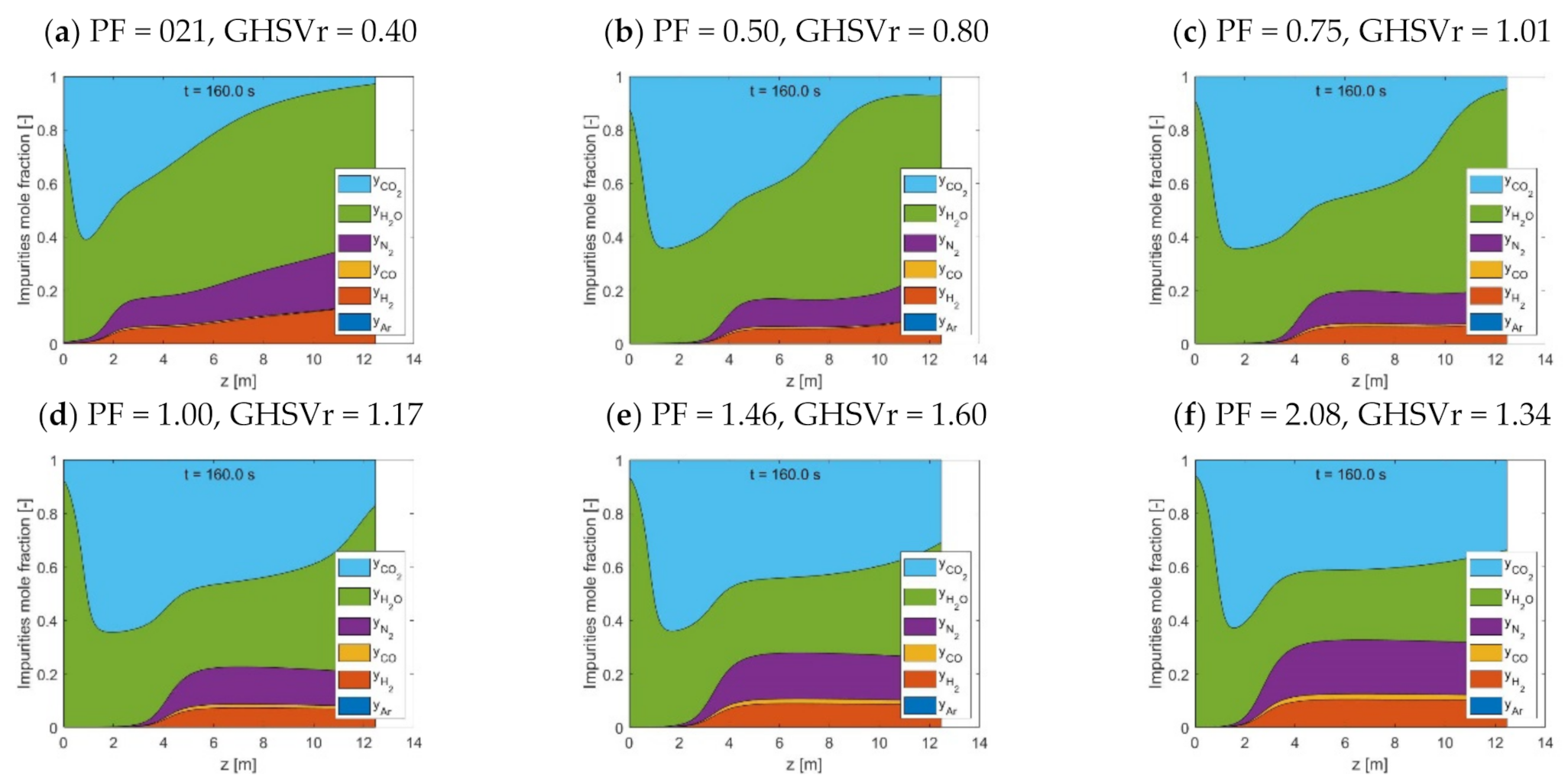
The use of HP rinse and LP purge steam amounts are confirmed to increase the flexibility of STEPWISE in achieving deep CO2 separation. Higher CCR and CP were directly obtained by increasing simultaneously the R/P and S/Ct ratios. The diagonal solution was maintained at ~95% even when carbon loading was decreased by 20%. This was achieved by increasing the R/P ratio, while the S/Ct was reduced from 1.1 to 0.8. The combination of a higher R/P ratio with a lower S/Ct improved the rinse effectiveness at the expense of a less-performing purge. These effects balance the reduced CO2 front progression that follows a lower GHSVc, as shown by column concentration profiles. Therefore, steam consumption and throughput can be traded off by tuning the R/P ratio while keeping all other parameters unchanged, including cycle time. It is important that future energy and economic optimization consider the R/P parameter, including the different quality of these two stem inputs.
As the adsorption pressure increases, larger GHSVc are found at the diagonal separation performances. During the adsorption step, a higher pressure improves both the width and progression of the MTZ, thereby improving the GHSVc. Conversely, an optimum pressure value was found where the Pareto diagonal solution peaks. This is the point that best compromises between rinse front progression, adsorptive rinse, and cross-over intensities. The peaking shape of the diagonal solutions over pressure implies that milder feed gas compression can be implemented by reducing the GHSVc, while the separation performance is retained. As capture performance above 90% is achieved over a broad range of pressure values (from 12 to 50 bar), STEPWISE could be adapted to fit process integration schemes that minimize the processing costs of different applications.
A superior separation performance was also achieved with a higher inlet steam content. This change comes with a reduction of the GHSVc, and it appears to be valid over a range of feed pressure values. Consequently, optimal R/P ratio and feed pressure values can be expected to depend on the initially available HP steam within the feed gas. This shall be more extensively investigated in future studies, together with the impact of different cycle structures (e.g., number of PEQ, type and number of refluxes).