Effect of Geometrical Parameters on Extraction Efficiency of the Annular Centrifugal Contactor
Abstract
1. Introduction
2. Materials and Methods
2.1. Chemicals
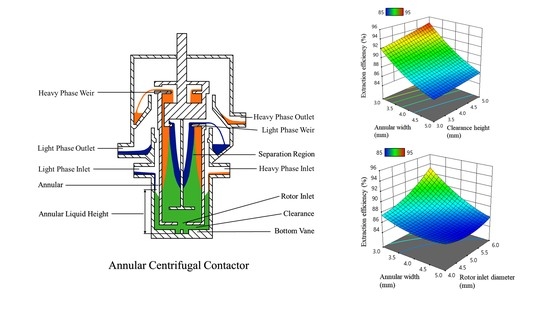
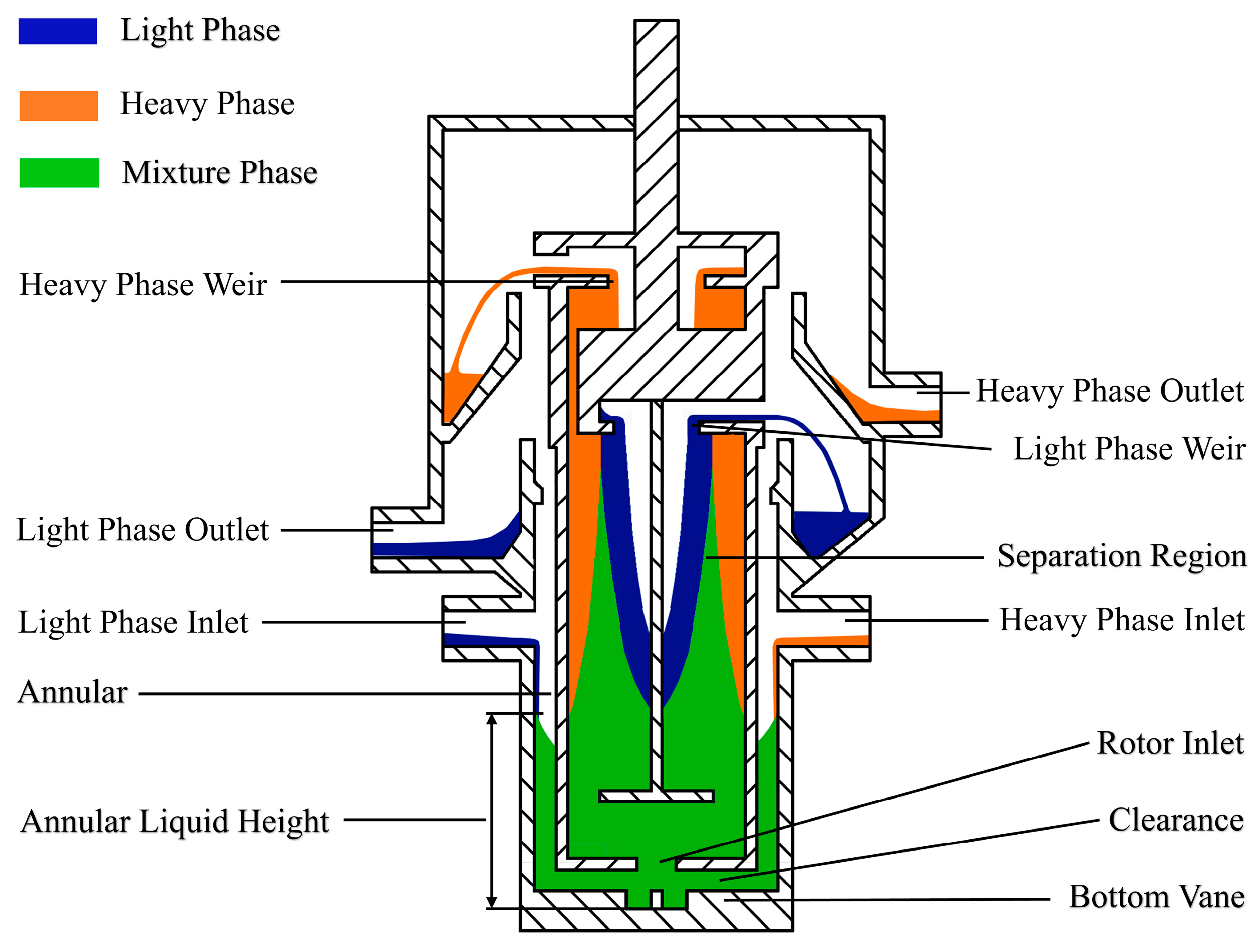
2.2. Annular Centrifugal Contactor
2.3. Experimental Design
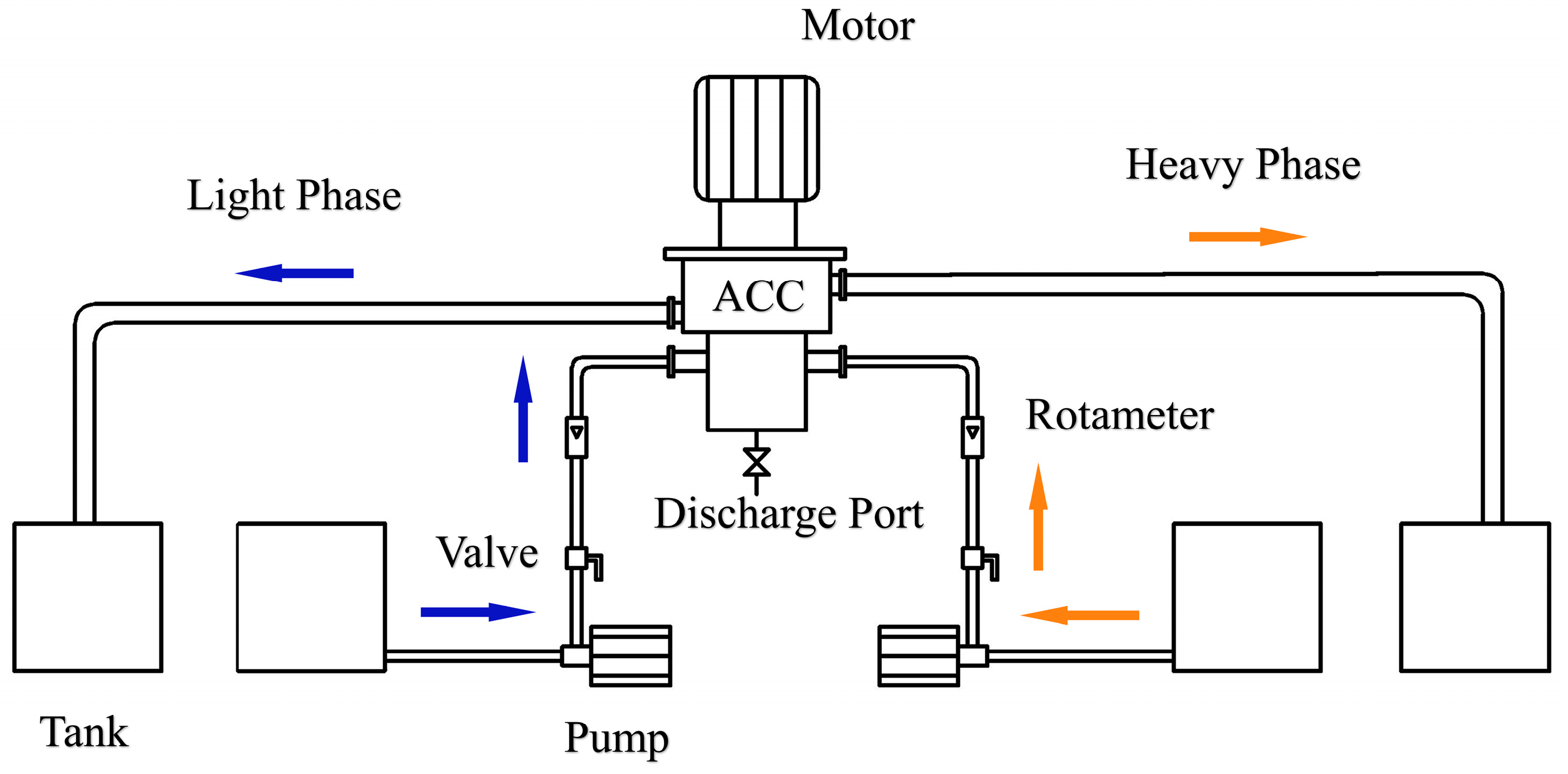
2.4. Methods
2.5. Extraction Efficiency
3. Results and Discussion
3.1. Effect of Geometrical Parameters on Extraction Efficiency
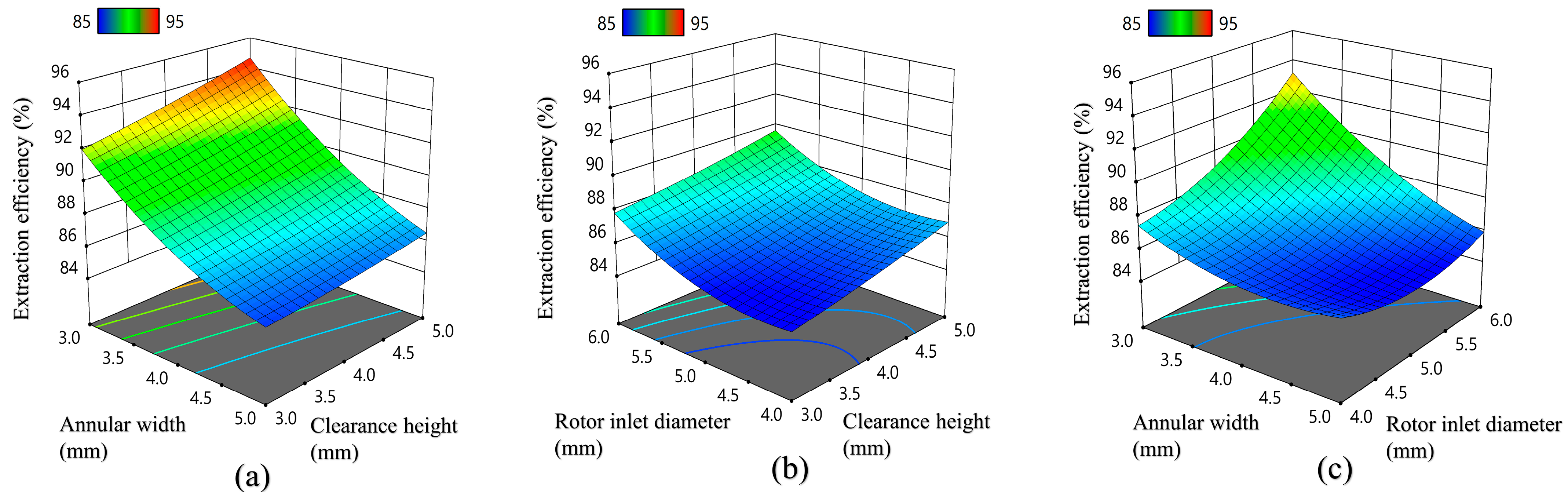
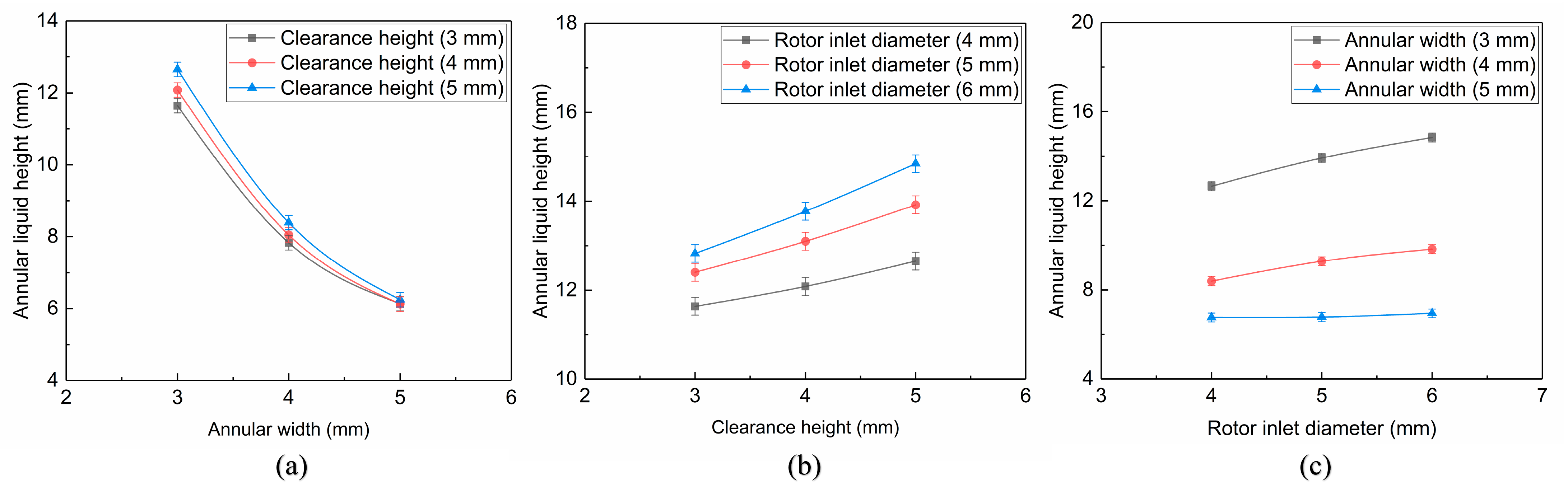
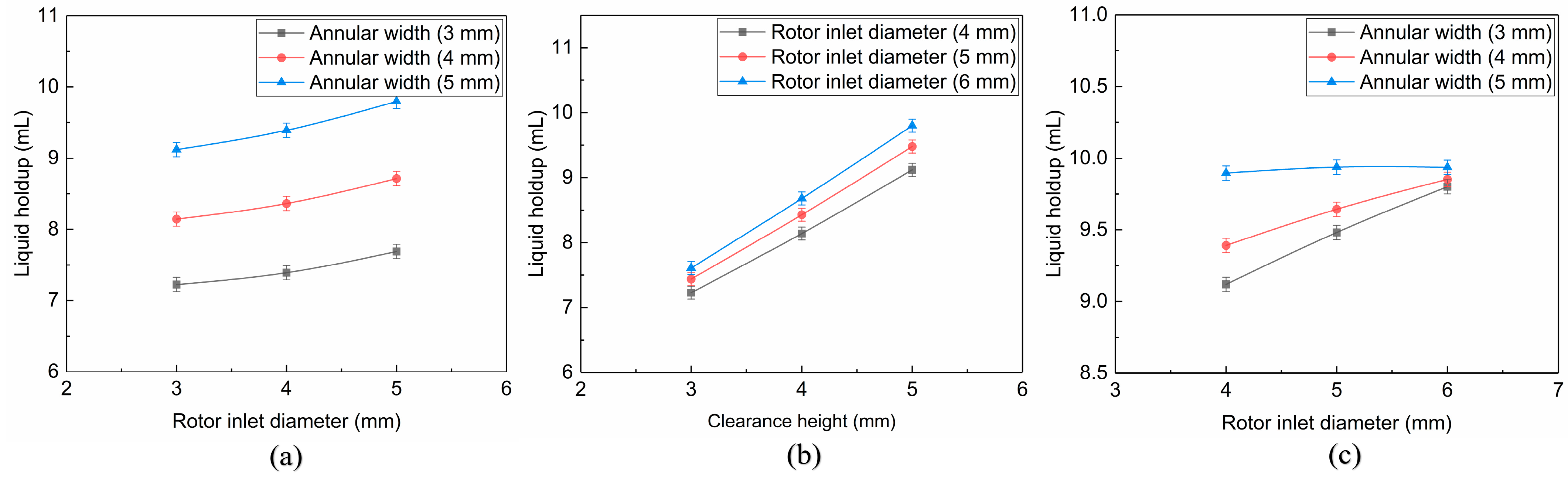
3.1.1. Annular Width
3.1.2. Clearance Height
3.1.3. Rotor Inlet Diameter
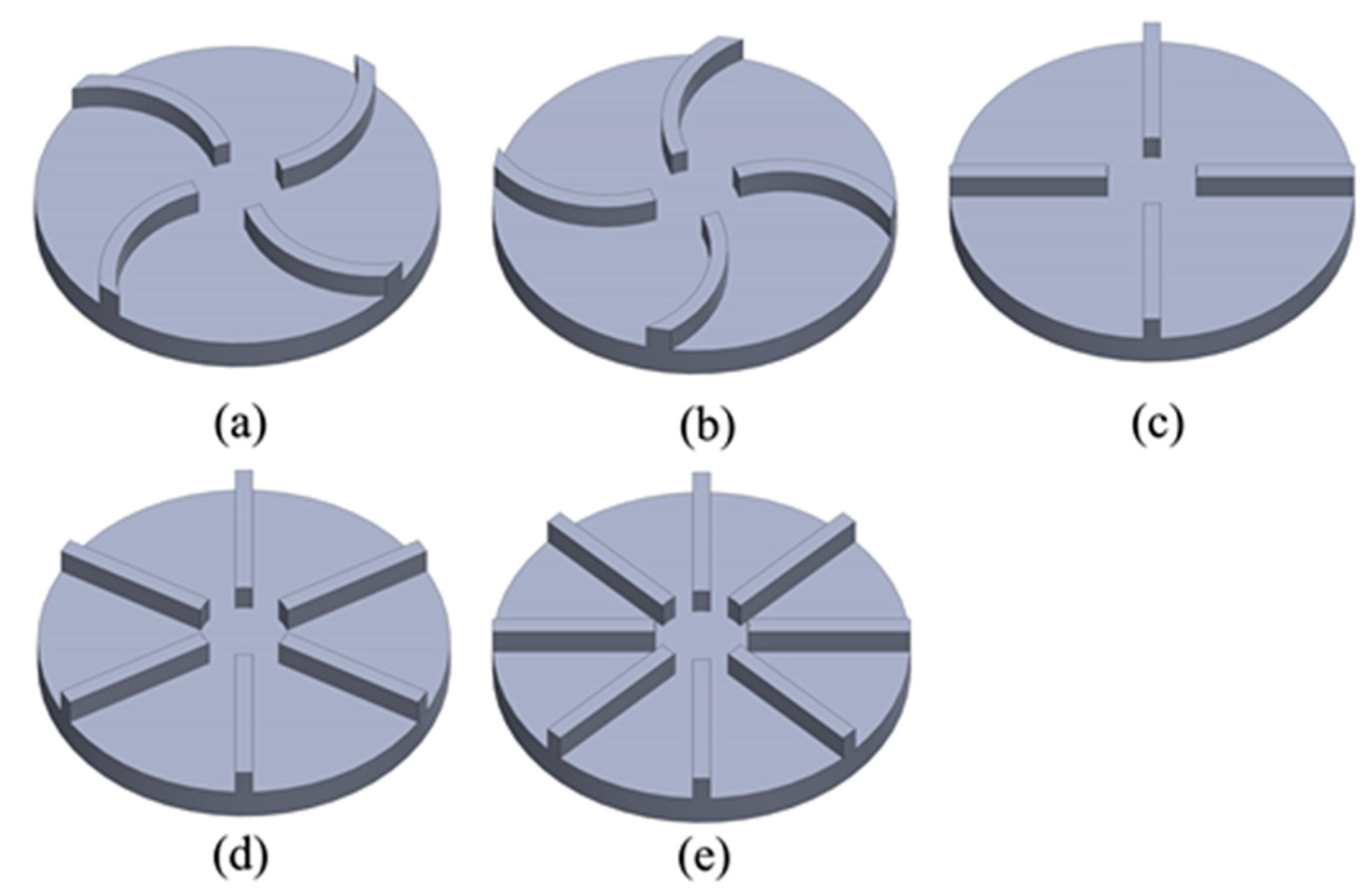
3.1.4. Bottom Vane
3.2. Response Surface Model Explanation of Each Factor Affecting the EO
∂2EO/(∂d∂Hc) = −0.416
∂2EO/(∂Hc∂Din) = −0.0554
∂2EO/(∂Din∂d) = −1.46
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ramaswamy, S.; Huang, H.J.; Ramarao, B.V. Separation and Purification Technologies in Biorefineries, 1st ed.; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 2013; pp. 61–70. [Google Scholar]
- Manousi, N.; Plastiras, O.E.; Kalogiouri, N.P.; Zacharis, C.K.; Zachariadis, G.A. Metal-Organic Frameworks in Bioanalysis: Extraction of Small Organic Molecules. Separations 2021, 8, 60. [Google Scholar] [CrossRef]
- Vedantam, S.; Joshi, J.B. Annular Centrifugal Contactors—A Review. Chem. Eng. Res. Des. 2006, 84, 522–542. [Google Scholar]
- Duan, W.H.; Sun, T.X.; Wang, J.C. An Industrial-Scale Annular Centrifugal Contactor for the TRPO Process. Nucl. Sci. Tech. 2018, 29, 1–9. [Google Scholar] [CrossRef]
- Davis, M.W.; Weber, E.J. Liquid-Liquid Extraction between Rotating Concentric Cylinders. Ind. Eng. Chem. Res. 1960, 52, 929–934. [Google Scholar] [CrossRef]
- Xu, J.Q.; Duan, W.H.; Zhou, X.Z.; Zhou, J.Z. Extraction of Phenol in Wastewater with Annular Centrifugal Contactors. J. Hazard. Mater. 2005, 131, 98–102. [Google Scholar] [CrossRef] [PubMed]
- Holeschovsky, U.B.; Cooney, C.L. Quantitative Description of Ultrafiltration in A Rotational Filtration Device. AIChE J. 1991, 37, 1219–1226. [Google Scholar] [CrossRef]
- Cao, S.; Duan, W.H.; Wang, C.Q. Effects of Structure Parameters on the Hydraulic Performance of the 20 Annular Centrifugal Contactor. Energy Procedia 2013, 39, 461–466. [Google Scholar] [CrossRef][Green Version]
- Nicholas, B.; Wyatt, T.J.; O’Hern, B.S. Drop-Size Distributions and Spatial Distributions in an Annular Centrifugal Contactor. AIChE J. 2013, 59, 2219–2226. [Google Scholar]
- Chen, H.L.; Wang, J.C.; Duan, W.H. Hydrodynamic Characteristics of 30% TBP/Kerosene-HNO3 Solution System in an Annular Centrifugal Contactor. Nucl. Sci. Tech. 2019, 30, 47–58. [Google Scholar] [CrossRef]
- Zhao, M.M.; Cao, S.; Duan, W.H. Effects of Some Parameters on Mass-Transfer Efficiency of a Φ20 mm Annular Centrifugal Contactor for Nuclear Solvent Extraction Processes. Prog. Nucl. Energy 2014, 74, 154–159. [Google Scholar] [CrossRef]
- Xu, Y.; Tang, K.; Bai, Z.S.; Wang, H.L. Hydrodynamic and Mass-Transfer Characteristics of Annular Centrifugal Contactors on the Caprolactam Recovery from Waste Liquor. Appl. Mech. Mater. 2013, 330, 792–798. [Google Scholar] [CrossRef]
- Birdwell, J.F.; Anderson, K.K. Evaluation of Mass Transfer Performance for Caustic-Side Solvent Extraction of Cesium in A Conventional 5-cm Centrifugal Contactor; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2002.
- Leonard, R.A.; Regalbuto, M.C.; Aase, S.B.; Arafat, H.A.; Falkenberg, J.R. Hydraulic Performance of a 5-cm CINC Contactor for Caustic-Side Solvent Extraction; Argonne National Laboratory: Oak Ridge, TN, USA, 2002.
- Wardle, K.E.; Allen, T.R.; Anderson, M.H.; Swaney, R.E. Experimental Study of the Hydraulic Operation of an Annular Centrifugal Contactor with Various Mixing Vane Geometries. AIChE J. 2010, 56, 1960–1974. [Google Scholar] [CrossRef]
- Attimarad, M.; Elgorashe, R.E.E.; Subramaniam, R.; Islam, M.M.; Venugopala, K.N.; Nagaraja, S.; Balgoname, A.A. Development and Validation of Rapid RP-HPLC and Green Second-Derivative UV Spectroscopic Methods for Simultaneous Quantification of Metformin and Remogliflozin in Formulation Using Experimental Design. Separations 2020, 7, 59. [Google Scholar] [CrossRef]
- Faraji, N.; Zhang, Y.; Ray, A.K. Optimization of Lactoperoxidase and Lactoferrin Separation on an Ion-Exchange Chromatography Step. Separations 2017, 4, 10. [Google Scholar] [CrossRef]
- Silva, V. Statistical Approaches with Emphasis on Design of Experiments Applied to Chemical Processes, 1st ed.; BoD–Books on Demand: Norderstedt, Germany, 2018; pp. 157–166. [Google Scholar]
- Kadam, B.D.; Joshi, J.B.; Koganti, S.B.; Patil, R.N. Hydrodynamic and Mass Transfer Characteristics of Annular centrifugal contactors. Chem. Eng. Res. Des. 2007, 86, 233–244. [Google Scholar] [CrossRef]
- Taylor, G.I. Stability of a Viscous Liquid Contained Between Two Rotating Cylinders. Philos. Trans. R. Soc. Lond. A 1923, 223, 289–343. [Google Scholar]
- Chandrasekhar, S. The Stability of Spiral Flow between Rotating Cylinders. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1962, 263, 57–91. [Google Scholar]
- Wardle, K.E. Summary Report on Liquid-Liquid Contactor Scoping Experiments and Validation Test Case Definition; Argonne National Laboratory: Oak Ridge, TN, USA, 2012.
- Arafat, H.A.; Hash, M.C.; Hebden, A.S.; Leonard, R.A. Characterization and Recovery of Solvent Entrained during the Use of Centrifugal Contactors; Argonne National Laboratory: Oak Ridge, TN, USA, 2001.
- Bernstein, G.J.; Grosvenor, D.E.; Lenc, J.F.; Levitz, N.M. Development and Performance of a High-Speed, Long-Rotor Centrifugal Contactor for Application to Reprocessing LMFBR Fuels; Argonne National Laboratory: Oak Ridge, TN, USA, 1973.
- Wardle, K.E.; Allen, T.R.; Swaney, R. Computational Fluid Dynamics (CFD) Study of the Flow in an Annular Centrifugal Contactor. Sep. Sci. Tech. 2008, 41, 2225–2244. [Google Scholar] [CrossRef]
- Wardle, K.E. FY12 Summary Report on Liquid-Liquid Contactor Experiments for CFD Model Validation; Argonne National Laboratory: Oak Ridge, TN, USA, 2012.
- Wardle, K.E.; Allen, T.R.; Anderson, M.H. Analysis of the Effect of Mixing Vane Geometry on the Flow in an Annular Centrifugal Contactor. AIChE J. 2009, 55, 2244–2259. [Google Scholar] [CrossRef]
- Birdwell, J.F.; Anderson, K.K. Evaluation of 5-cm Centrifugal Contactor Hydraulic and Mass Transfer Performance for Caustic-Side Solvent Extraction of Cesium; Argonne National Laboratory: Oak Ridge, TN, USA, 2001.
- Le, A.V.; Parks, S.E.; Nguyen, M.H.; Roach, P.D. Optimised Extraction of Trypsin Inhibitors from Defatted Gac (Momordica Cochinchinensis Spreng) Seeds for Production of a Trypsin Inhibitor-Enriched Freeze Dried Powder. Separations 2019, 6, 8. [Google Scholar] [CrossRef]
| Parameters | Level | ||||
|---|---|---|---|---|---|
| −Alpha | −1 | 0 | 1 | +Alpha | |
| Annular width, d/mm | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Clearance height, Hc/mm | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| Rotor inlet diameter, Din/mm | 4.0 | 4.0 | 5.0 | 6.0 | 6.0 |
| Source | Sum of Squares | DF | Mean Square | F-Value | p-Value |
|---|---|---|---|---|---|
| Model | 159 | 9 | 19.0 | 19.0 | <0.0001 |
| d | 77.4 | 1 | 77.4 | 82.8 | <0.0001 |
| Hc | 15.2 | 1 | 15.2 | 16.2 | 0.0002 |
| Din | 20.2 | 1 | 20.2 | 21.6 | 0.0009 |
| d × Hc | 1.40 | 1 | 1.40 | 1.50 | 0.249 |
| d × Din | 17.1 | 1 | 17.1 | 18.3 | 0.0016 |
| Hc × Din | 0.0245 | 1 | 0.0245 | 0.0262 | 0.874 |
| d2 | 22.6 | 1 | 22.6 | 24.2 | 0.0006 |
| Hc2 | 0.368 | 1 | 0.368 | 0.394 | 0.544 |
| Din2 | 5.42 | 1 | 5.42 | 5.80 | 0.0368 |
| Residual | 9.35 | 10 | 0.934 | ||
| Lack of fit | 7.66 | 5 | 1.53 | 4.54 | 0.0612 |
| Pure error | 1.69 | 5 | 0.338 |
| Bottom Vane Structure | Liquid Holdup Vm/mL | Extraction Efficiency EO/% |
|---|---|---|
| 4 anti-clockwise covered vanes, 4ACV | 7.61 ± 0.11 | 89.3 ± 0.9 |
| 4 clockwise covered vanes, 4CV | 9.50 ± 0.18 | 94.5 ± 0.8 |
| 4 straight vanes, 4V | 8.23 ± 0.21 | 92.3 ± 0.5 |
| 6 straight vanes, 6V | 7.73 ± 0.14 | 90.0 ± 0.8 |
| 8 straight vanes, 8V | 7.55 ± 0.16 | 87.1 ± 0.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Su, Y.; Tang, J.; Yang, X.; Wang, R. Effect of Geometrical Parameters on Extraction Efficiency of the Annular Centrifugal Contactor. Separations 2021, 8, 102. https://doi.org/10.3390/separations8070102
Su Y, Tang J, Yang X, Wang R. Effect of Geometrical Parameters on Extraction Efficiency of the Annular Centrifugal Contactor. Separations. 2021; 8(7):102. https://doi.org/10.3390/separations8070102
Chicago/Turabian StyleSu, Yigang, Jianxin Tang, Xiaoxia Yang, and Rijie Wang. 2021. "Effect of Geometrical Parameters on Extraction Efficiency of the Annular Centrifugal Contactor" Separations 8, no. 7: 102. https://doi.org/10.3390/separations8070102
APA StyleSu, Y., Tang, J., Yang, X., & Wang, R. (2021). Effect of Geometrical Parameters on Extraction Efficiency of the Annular Centrifugal Contactor. Separations, 8(7), 102. https://doi.org/10.3390/separations8070102