Abstract
The movement of the gas–liquid interface caused by the movement of the bubble position will have an impact on the starting conditions for particle migration. This article quantifies the influence of moving bubbles on the starting conditions of particle migration in non-Newtonian fluids, and it aims to better understand the influence of bubbles moving in non-Newtonian fluids on particle migration to achieve more effective control. First, the forces and moments acting on the particles are analyzed; then, fluid dynamics, non-Newtonian fluid mechanics, extended DLVO (Derjaguin Landau Verwey Overbeek theory), surface tension, and friction are applied on the combined effects of particle migration. Then, we reasonably predict the influence of gas–liquid interface movement on particle migration in non-Newtonian fluids. The theoretical results show that the movement of the gas–liquid interface in non-Newtonian fluids will increase the separation force acting on the particles, which will lead to particle migration. Second, we carry out the particle migration experiment of moving bubbles in non-Newtonian fluid. Experiments show that when the solid–liquid two-phase flow is originally stable, particle migration occurs after the bubble movement is added. This phenomenon shows that the non-Newtonian fluid with bubble motion has stronger particle migration ability. Although there are some errors, the experimental results basically support the theoretical data.
1. Introduction
The development of the world economy is highly dependent on the extraction and production of energy. Safe and efficient energy extraction is an important issue of today’s era. Natural resources such as oil and weather do not accumulate in large areas such as rivers and lakes, but they are mainly stored in small pores, voids, or caves in rocks. Among them, the oil is gathered in the reservoir, and its storage state can be imagined as an oily stone, rather than being similar to an oil depot. During the mining process, the flow of fluid and the migration of particles in the crevices are inevitable and will cause some difficulties in production. Most oil and gas fields with loose formations or relatively loose have sand production. Sand production shortens the life of oil and gas wells, wears downhole and surface equipment tools (such as pumps, separators, heaters, pipelines, etc.), bridges or blocks well bores, reduces oil and gas well production, and forces oil wells to stop production. The migration and rearrangement of particles can cause groundwater surges, which can cause mining accidents and pollution in the mine. For these reasons, studying the movement laws of particles in fluids and making reasonable predictions and guidance on actual production has become a key issue for improving production safety and increasing production efficiency.
With the deepening of the particle migration, people have conducted extensive research on particle migration for many years. In 1987, Leighton and Acrivos studied the migration of spherical particles in uneven flow [1]. In 2005, Timberlake and Morris conducted an experimental study on a fluid containing spherical particles flows freely on the surface of an angled plane under gravity [2]. In 2010, Rossana et al. discussed the migration law of particles in an elastic suspension medium and found that migration is affected by particle size, properties, and arrangement structure [3]. In 2015, Gaojin et al. numerically analyzed the particle migration law in the channel when the viscoelastic fluid is in a pressure-driven state [4]. In 2019, the Euler–Lagrangian modeling method by Sharaf et al. studied particle distribution, heat transfer, and flow field generated in nano-scale fluid flow in narrow parallel plane channels [5].
In summary, for many years, people have been engaged in the study of particle migration in the flow field, and they have tried to predict and guide the actual production work. However, there is still a lack of research on particle migration in non-Newtonian fluids. This study aims to improve the understanding of the particle migration mechanism in non-Newtonian fluids during foam migration. Unlike the solid–liquid two-phase flow, when the bubbles move with the fluid, the particles will encounter the gas–liquid interface. This change will increase the force acting on the particles and have an effect on the migration of the particles. First, we analyze the forces and moments acting on the particles. Theoretical calculation of the starting conditions of particles in non-Newtonian fluids are presented. Subsequently, laboratory experiments were performed to determine the movement of particles in non-Newtonian fluids with bubble movement and collect data. Finally, the theoretical calculations are compared with the experimental data, and the migration law of particles in the non-Newtonian fluid with bubble motion is summarized.
2. Theoretical Calculation
2.1. Analysis of Forces Acting on Particles
The dispersed gas moves in the fluid and gathers into discontinuous bubbles. In order to facilitate the understanding of the starting conditions of the particles in the non-Newtonian fluid, the force acting on the particles is accurately calculated, and the following assumptions are made: the particles are perfectly spherical, the particles are in contact, the surface is uniform, and the laminar flow is continuous and uniform.
When a particle is in a non-Newtonian fluid with bubbles, four situations will occur: (1) the particle is only under the action of the fluid, (2) the particle is in contact with the advancing bubble, (3) the particle is inside the bubble, and (4) the particles are in contact with the leaving bubbles. For case 1, the forces acting on the particles include hydrodynamic force, contact force, and friction force. For cases 2 and 4, additional forces such as surface tension forces also act on the particles. For case 3, the particles are only subject to contact force and friction force. Both contact force and friction force hinder the migration of particles, while hydrodynamic force and surface tension help particles leave the fracture surface. This article mainly discusses situations 1, 2, and 4, as shown in Figure 1.
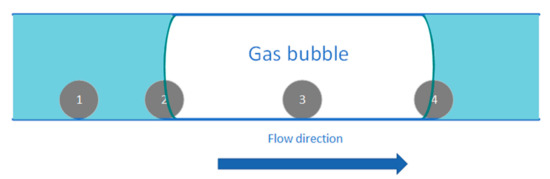
Figure 1.
Four states of particles in non-Newtonian fluid.
2.1.1. The Force on the Particle in the Fluid
When the particle is in the first state, the particle is subjected to contact force Fa, lift Fl, resistance Fd, and friction force Ff, as shown in Figure 2.
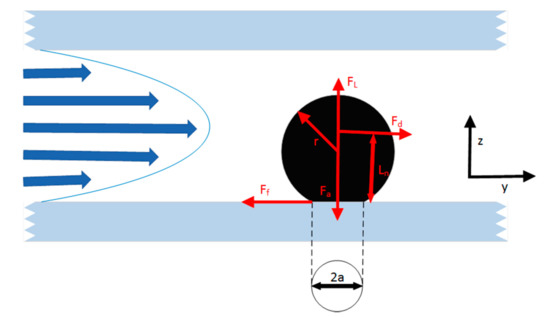
Figure 2.
Force of particles in fluid.
When the sphere is on a smooth plane, according to people’s research, when the fluid flows through the particles in a laminar state, a complex flow field will be formed. The fluid performs linear shearing motion around the particles and can be obtained by applying force on the particles. The following mathematical expression is obtained, the laminar fluid will form the resistance of Fd to spherical particles on the smooth surface. The expression is [6,7,8]:
where is the viscosity of the liquid, r is the radius of the spherical particle, and is the velocity of the liquid relative to the center of the spherical particle.
A uniform fluid flows through the spherical particles at a stable speed and shears the spherical particles. The fluid velocity parallel to the flow direction and at the center the spherical particles is used as the speed reference. There is an upward lift perpendicular to the contact surface between the particle and the smooth plane. Therefore, the following expression can be made. When the fluid flows through the spherical particles in a laminar flow state and performs a shearing motion, an upward lift Fl will be generated where is the liquid density. The expression is [8]:
Under the extended DLVO theory, there are several forces that act between the smooth surface and the spherical particles. They are Lifshitz van der Waals (LW) force, electrostatic (EDL) force, Born force, and Lewis acid base (AB) force. The interaction of several forces forms the total contact force between the smooth surface and the spherical particle. In this paper, the force acting on the smooth surface and the spherical particle is called the contact force. The magnitude of the contact force Fa is determined by the following conditions: the distance between the spherical particles and the smooth surface, and the energy of the interaction between the smooth surface and the spherical particles [9]. The expression is:
where is the total energy of the interaction between the spherical particle and the smooth plane, h is the vertical distance between the two, is the EDL force, is the LW force, is the AB force, and is the Born force.
The friction force Ff can be determined by using the Coulomb friction law, where fs is the static friction coefficient, which is usually 0.5 to 0.8 for rock materials [10]; and Fn is the net force perpendicular to the surface.
2.1.2. The Force Exerted by the Particle and the Bubble
When bubbles encounter particles, surface tension is generated, as shown in Figure 3.
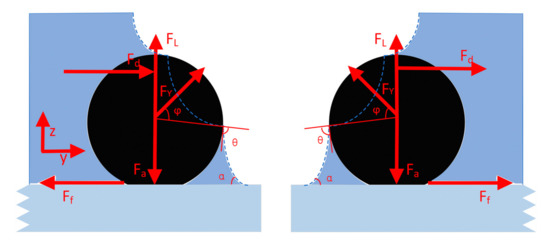
Figure 3.
The force on the particle when it encounters the gas–liquid interface.
When the gas–liquid interface passes through the particles, the surface tension is generated and perpendicular to the gas–liquid interface [11,12].
The tension formed by the contact between the gas–liquid interface and the particles is , the angle between the tension formed by the liquid surface and the particle liquid surface when the gas–liquid interface advances or retreats is , and the liquid surface and the particle liquid surface form tension when the gas–liquid interface advances or retreats, which has a complementary angle of . When < , the surface tension is toward the center of the particle, and when > , the surface tension is away from the center of the particle. For the case where α < 90° [13,14], Fγ reaches its maximum value at = /2. The maximum surface tension in the z direction is , and the maximum surface tension in the y direction is . It can be understood as the following formula:
In fact, the moving bubbles do not directly contact the fracture surface, but there is a consistent film between the particles and gas–liquid interface, as described by Bretherton [15]. The number of capillaries can determine the thickness of the film δ, which can be given as [16]:
The Hamaker constant in the gas–water fracturing system is A.
2.2. Various Forces on the Particles
When particles are in a non-Newtonian fluid with bubbles moving, they only contact the fluid most of the time. This paper mainly studies the particle migration caused by rolling.
The power-law fluid is a kind of non-Newtonian fluid. Assuming the liquid is a power-law fluid, the following formula can be given:
To make the particles rollable, the torque for particle migration needs to be greater than that for preventing particle migration. When the torque is equal, the particles are in a critical condition of migration. The formula for torque balance is as follows:
The liquidity index will affect the calculation result when the value of n is 4/7. Substituting the known conditions into the moment balance formula, the initial pressure gradient of particle migration is:
If the particles do not migrate under the action of the fluid, the particles will encounter bubbles, which can be considered by the following formula:
RF_z is the ratio of forces in the z direction, RF_y is the ratio of forces in the y direction, and R_p is the ratio of torsional forces. When the first case R_p ≤ 1, RF_z ≤ 1, and RF_y ≤ 1 are met, the particles cannot start. When the second case R_p > 1, RF_z > 1, or RF_y > 1 is met, the particles will migrate from the smooth surface by rolling, lifting, or sliding, respectively.
3. Laboratory Experiment
3.1. Experiment Preparation
First, the common rock particles obtained from the mine site are sieved, and those of the qualified particle size are obtained by using a test sieve. Then, they are placed in a vacuum at 75 °C for 36 h. Finally, a dry box is used to store them to prevent moisture until the test. In order to imitate the actual fluid and facilitate observation, this experiment uses polyacrylamide solution to simulate non-Newtonian fluid, prepares polyacrylamide solutions of different concentrations, and uses a rheometer to measure the fluidity index and consistency coefficient of polyacrylamide solutions of different concentrations.
The contact angle is measured. The dynamic contact angle of the particles on the plane was measured at 25 °C. The background solution is increased at a constant acceleration rate. Then, it decreases at the same rate. The advancing and retreating contact angles are regarded as fixed points during the measurement. The average value is obtained by multiple measurements under the same conditions. It is assumed that the contact angles on the particle and the plane are the same. The measured advancing contact angle and receding contact angle are 83.6° and 41.7°, respectively. Then, we measured the static contact angle of the liquid on the plane at 25 °C and used a syringe to put the liquid on the polished surface and measure it with a goniometer. Then, we placed the same amount of liquid at different positions on the polishing surface and took the average of multiple measurements. The contact angle obtained is 61°.
The schematic diagram of the experimental device for particle migration in non-Newtonian fluid bubble motion is shown in Figure 4. It is mainly composed of a fluid reservoir, syringe pump, injector, pressure sensor, flat simulation device, microscope, video recorder, information acquisition system, and temperature controller. The fluid reservoir is used to provide and collect the test–use sub-Newtonian fluid. The syringe pump pushes the syringe with a stable speed piston to make the injection liquid speed constant, and the pump injects the non-Newtonian fluid into the flat simulation device at a stable flow rate. The injector is connected to the pipeline through a three-way valve. Usually, the tee and injector channels are closed. When gas needs to be introduced, the three-way and ejector channel are opened. The injector injects a certain amount of gas into the system to create a gas–liquid interface in the simulation device. The pressure sensor measures the injection pressure at the inlet, and the microscope and video recorder observe and record the particle migration. The information collection system collects and records various data in the experiment. The temperature controller uses a civil air conditioner to keep the temperature in the test state within the required range. The experimental device diagram is shown in Figure 5.
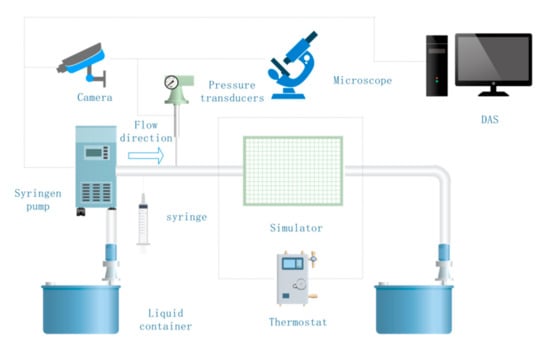
Figure 4.
Schematic diagram of the experimental device for particle migration in non-Newtonian fluid bubble motion.

Figure 5.
Laboratory equipment.
3.2. Experiment Procedure
A particle migration experiment with and without bubbles is carried out in a non-Newtonian fluid to determine the influence of the gas–liquid interface on particle migration. The sample is placed in the device after being put in the solution under vacuum for 2 days, and we injected the non-Newtonian fluid for a period of time. After it stabilized, we confirmed that there were no bubbles in the device. Then, we maintained the fluid in stable injection conditions for 2 h to establish stable conditions. Then, we increased the pressure and maintained it for 1 h each time. Afterwards, we collected the effluent liquid and measured the particle quality after drying. Then, we observed the remaining condition of the particles from the microscope, cycled several times, and obtained the migration law of the particles under the influence of the fluid. To illustrate the influence of the gas–liquid interface on the particles, the inert gas was injected into the pipe from the syringe to make bubbles in the device. After that, the effluent liquid was collected and dried, and the pellet quality was measured. The remaining particles were observed from the microscope.
4. Starting Conditions of Particles under the Action of Fluid
4.1. The Influence of Non-Newtonian Fluid Parameters on Mechanics
The change of non-Newtonian fluid parameters will affect the force of the particles to a certain extent. When the non-Newtonian fluid parameters change, several main forces acting on the particles will rise or fall. These effects will change the starting conditions of the particles. The consistency coefficient will affect the lift and drag, and the increase of the consistency coefficient will increase the lift and drag at the same time. As shown in Figure 6, when the consistency coefficient increases, the curve will move up significantly.
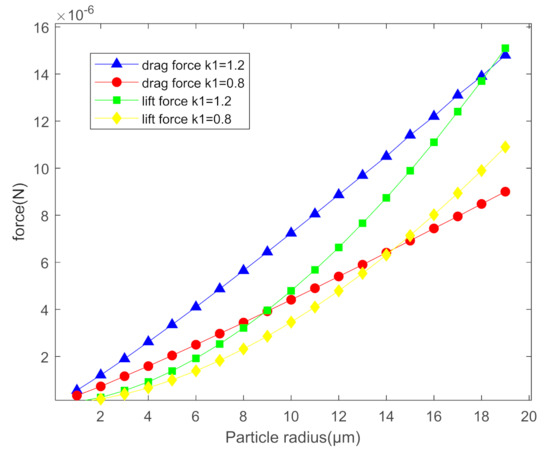
Figure 6.
Changes in lift and drag under the influence of consistency coefficient.
4.2. Newtonian and Non-Newtonian Fluids
Non-Newtonian fluids have an impact on the starting conditions of particle migration due to their own properties. Different from Newtonian fluid, both the fluidity index and the consistency coefficient in non-Newtonian fluids will have a certain effect on the migration of particles. As shown in Figure 7, when k1 is 1.2 and n is 0.57 in a non-Newtonian fluid, the curve moves up significantly.
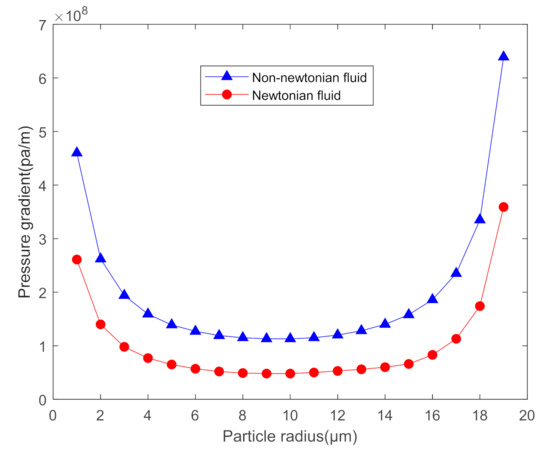
Figure 7.
Pressure gradient curve of Newtonian fluid and non-Newtonian fluid.
4.3. Separation of Particles Caused by Liquid
When only liquid and solid phases act, the particles are affected by drag, lift, friction, and contact force. Once the pressure gradient changes, the migration conditions of various particle sizes will gradually be reached.
- (1)
- As shown in Figure 8, the increase in fluidity index has an impact on the starting conditions of the particles. As the fluidity index increases, the pressure gradient curve decreases overall. When H = 40 μm, K1 = 1.2, and n increases from 0.57 to 0.8, the minimum pressure gradient in the pressure gradient curve is reduced by 51%.
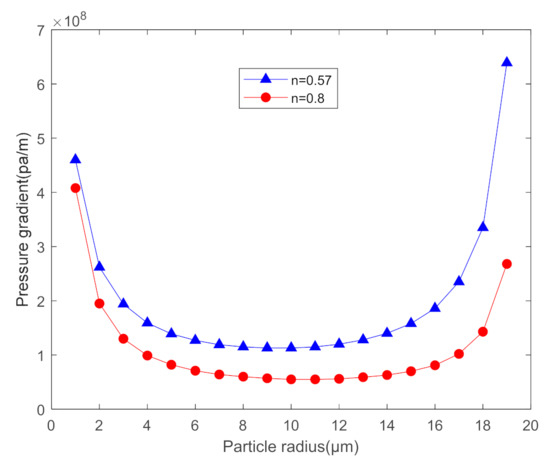 Figure 8. Pressure gradient curve under the influence of fluidity index.
Figure 8. Pressure gradient curve under the influence of fluidity index. - (2)
- As shown in Figure 9, the consistency coefficient has a significant effect on the pressure gradient curve. The increase in the consistency coefficient causes the pressure gradient curve to move upwards horizontally, and the lowest point of the conditions for particle activation rises. When H = 40 μm, n = 0.57, and K1 increases from 0.8 to 1.2, the lowest point of the pressure gradient curve becomes 166% of the original.
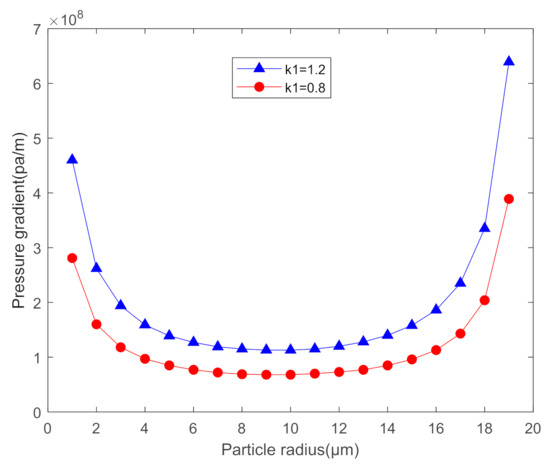 Figure 9. The effect of consistency coefficient on pressure gradient curve.
Figure 9. The effect of consistency coefficient on pressure gradient curve.
As shown in Figure 10, the theoretical prediction data are obviously different from the experimental data. There are many reasons for the error of the theoretical prediction result and the experimental result. The theoretical model simplifies the actual situation. The spherical particles and smooth surfaces do not conform to the actual situation. However, the theoretical data are in line with the trend of the experimental data, which explains to a certain extent the starting conditions of the particles in the non-Newtonian fluid.
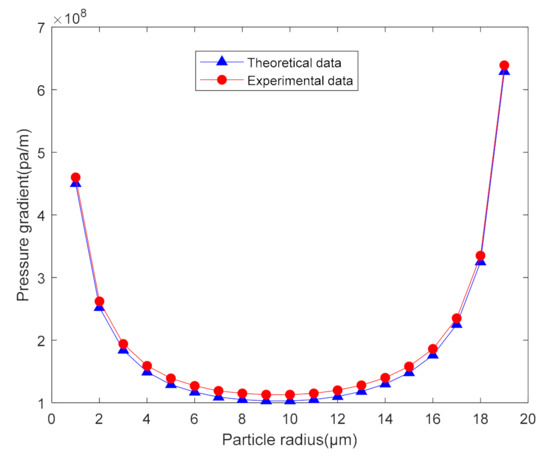
Figure 10.
The difference between theoretical data and experimental data.
4.4. Particle Migration Due to Bubbles
When the bubbles meet the particles, the gas–liquid interface generates tension on the particles, the particles generate friction and contact force with the smooth surface, and the fluid generates lift and resistance to the particles. When the first case R_p ≤ 1, RF_z ≤ 1, and RF_y ≤ 1 are met. The particles cannot start. When the second case R_p > 1, RF_z > 1, or RF_y > 1 is met. Then, the particles will migrate from the smooth surface by rolling, lifting, or sliding, respectively. At the same time, the larger the ratio, the easier the particle migration. Whether the particles are in contact with the advancing gas–liquid interface or the receding gas–liquid interface, they will detach from the surface, lift, and move with the fluid, as shown in Figure 11 and Figure 12.
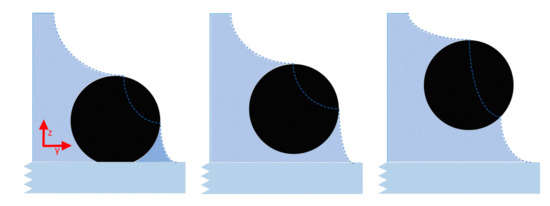
Figure 11.
Particles detach from the surface when they meet the front inlet liquid interface, lift up, and move with the fluid.
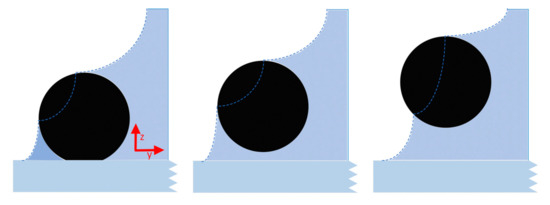
Figure 12.
Particles detach from the surface when encountering a receding gas–liquid interface, lift up, and move with the fluid.
As shown in Figure 13 and Figure 14, the movement of the gas-liquid interface causes the particles to migrate on a large scale after fluid power cannot make the particles migrate. Due to the presence of bubbles, the gas–liquid interface causes surface tension to act on the particles, which makes the particles migrate. According to theoretical calculations, when particles are affected by air bubbles, the particle force will be experienced as several times the force generated by only the fluid. The particles should all migrate. Through experiments and observations, it was found that the moving bubbles caused a large number of particles to migrate, but the experimental results did not fully meet expectations, and the particles could not fully migrate as predicted. After the bubbles passed, a large number of particles remained on the surface. The error is mainly due to the following reasons: (1) The particle shape is highly irregular, not an ideal spherical shape. (2) The surface of the particles is uniform, but the actual surface has physical heterogeneity.
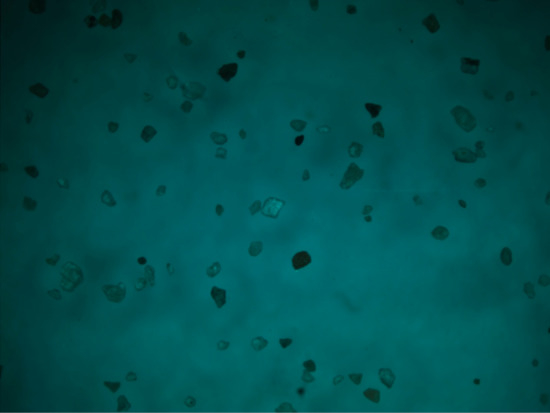
Figure 13.
Particles in non-Newtonian fluids.
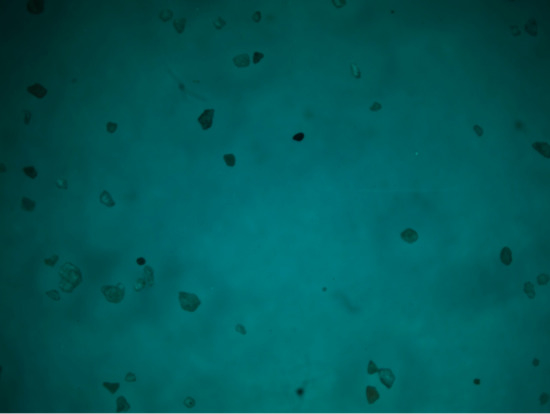
Figure 14.
Particles in a non-Newtonian fluid with bubble motion.
5. Conclusions
The migration of particles is a long process, including particles detaching from the surface, lifting, and moving with the fluid. As the primary prerequisite for determining whether particles can migrate, we mainly study the separation of particles from the surface. This paper studies the migration laws of particles in non-Newtonian fluids through theory and experiment. First, we compare the particle migration modes in the fluid and then study the changes in particle migration conditions caused by changes in parameters in various non-Newtonian fluids. Finally, bubbles were added to the system to study the influence of the gas–liquid interface on particle migration, and we draw the following conclusions:
- The experimental results show that the non-Newtonian fluid with bubbles has a much greater ability to mobilize particles than the non-Newtonian fluid without bubbles.
- In a real environment, the particle shape is very complex, and the sharp points are very obvious. The sharp part causes great damage to the force generated by the bubble. The composition of the particles is complex and not uniform. These actual conditions, which are different from theoretical assumptions, have caused errors between experiment and theory. However, the theory still explains that non-Newtonian fluids containing bubbles have stronger particle mobilization capabilities than pure non-Newtonian fluids.
- The starting conditions for particle migration are affected by the non-Newtonian fluid coefficient. When the consistency coefficient increases, the pressure gradient curve moves upward. When the fluidity index increases, the pressure gradient curve decreases. In actual production, measuring the coefficients of non-Newtonian fluids has instructive significance for predicting the difficulty of particle migration.
Author Contributions
Conceptualization, J.S. and X.Z.; Data curation, J.S.; Funding acquisition, X.Z.; Writing—original draft, J.S.; Writing—review & editing, J.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Natural Science Foundation of China, grant number 51574161. The APC was funded by Natural Science Foundation of China.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data included in this study are available upon request by contact with the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Leighton, D.; Acrivos, A. The shear-induced migration of particles in concentrated suspensions. J. Fluid Mech. 1987, 181, 415. [Google Scholar] [CrossRef]
- Timberlake, B.D.; Morris, J.F. Particle migration and free-surface topography in inclined plane flow of a suspension. J. Fluid Mech. 2005, 538, 309. [Google Scholar] [CrossRef]
- Pasquino, R.; Snijkers, F.; Grizzuti, N.; Vermant, J. The effect of particle size and migration on the formation of flow-induced structures in viscoelastic suspensions. Rheol. Acta 2010, 49, 993–1001. [Google Scholar] [CrossRef]
- Li, G.; McKinley, G.H.; Ardekani, A.M. Dynamics of particle migration in channel flow of viscoelastic fluids. J. Fluid Mech. 2015, 785, 486–505. [Google Scholar] [CrossRef]
- Sharaf, O.Z.; Al-Khateeb, A.N.; Kyritsis, D.C.; Abu-Nada, E. Numerical investigation of nanofluid particle migration and convective heat transfer in microchannels using an Eulerian–Lagrangian approach. J. Fluid Mech. 2019, 878, 62–97. [Google Scholar] [CrossRef]
- O’Neill, M. A sphere in contact with a plane wall in a slow linear shear flow. Chem. Eng. Sci. 1968, 23, 1293–1298. [Google Scholar] [CrossRef]
- Goldman, A.; Cox, R.; Brenner, H. Slow viscous motion of a sphere parallel to a plane wall—I Motion through a quiescent fluid. Chem. Eng. Sci. 1967, 22, 637–651. [Google Scholar] [CrossRef]
- Saffman, P.G. The lift on a small sphere in a slow shear flow. J. Fluid Mech. 1965, 22, 385–400. [Google Scholar] [CrossRef]
- Bergendahl, J.; Grasso, D. Prediction of colloid detachment in a model porous media: Thermodynamics. AIChE J. 1999, 45, 475–484. [Google Scholar] [CrossRef]
- Jaeger, J.C. The frictional properties of joints in rock. Pure Appl. Geophys. 1959, 43, 148–158. [Google Scholar] [CrossRef]
- Leenaars, A.F.M.; O’Brien, S.B.G. Particle removal from silicon substrates using surface tension forces. Philips J. Res. 1989, 44, 183–209. [Google Scholar]
- Gómez Suárez, C.; Noordmans, J.; van der Mei, H.C.; Busscher, H.J. Removal of colloidal particles from quartz collector surfaces as stimulated by the passage of liquid-air interfaces. Langmuir 1999, 15, 5123–5127. [Google Scholar] [CrossRef]
- Noordmans, J.; Wit, P.J.; Van Der Mei, H.C.; Busscher, H.J. Detachment of polystyrene particles from collector surfaces by surface tension forces induced by air-bubble passage through a parallel plate flow chamber. J. Adhes. Sci. Technol. 1997, 11, 957–969. [Google Scholar] [CrossRef]
- Aramrak, S.; Flury, M.; Harsh, J.B. Detachment of Deposited Colloids by Advancing and Receding Air-Water Interfaces. Langmuir 2011, 27, 9985–9993. [Google Scholar] [CrossRef] [PubMed]
- Bretherton, F.P. The motion of long bubbles in tubes. J. Fluid Mech. 1961, 10, 166–188. [Google Scholar] [CrossRef]
- Lazouskaya, V.; Wang, L.-P.; Or, D.; Wang, G.; Caplan, J.L.; Jin, Y. Colloid mobilization by fluid displacement fronts in channels. J. Colloid Interface Sci. 2013, 406, 44–50. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).