Iterative Multivariate Peaks Fitting—A Robust Approach for The Analysis of Non-Baseline Resolved Chromatographic Peaks
Abstract
:1. Introduction
2. Results
2.1. Theory
- 0.
- Initialization step. The average of the signal Yav(t) as a function of time is calculated by averaging all the channels. Next, the time at the maximum response for Yav and the variance assuming a single peak is measured. In the first column, the matrix P is populated with a constant (constant baseline drift), and in the second column, the initial peak profile. Finally, the starting matrix P is estimated using the initial measured position and variance with the selected mathematical function (by default PMG1). Additional fitting parameters, if any, are set to their minimum values. All columns in P are normalized to one (H0 = 1 in Equation (4)).
- 1.
- Optimization step. The minimization function is obtained by estimating X, Xest using:
- 2.
- Iteration step. The average residua between X and Xest are measured. Then, a new column is added to P corresponding to a new peak. The position of the peaks depends on the residual, while its shape is the average of all other peaks.
- 3.
- Optimization and termination conditions. Before optimization, and to avoid local minima, the variance of all peaks is decreased by a set factor. The optimization (step 1) is repeated, and the termination conditions are tested. If validated, the routine is stopped; otherwise, the algorithm loops to step 2.
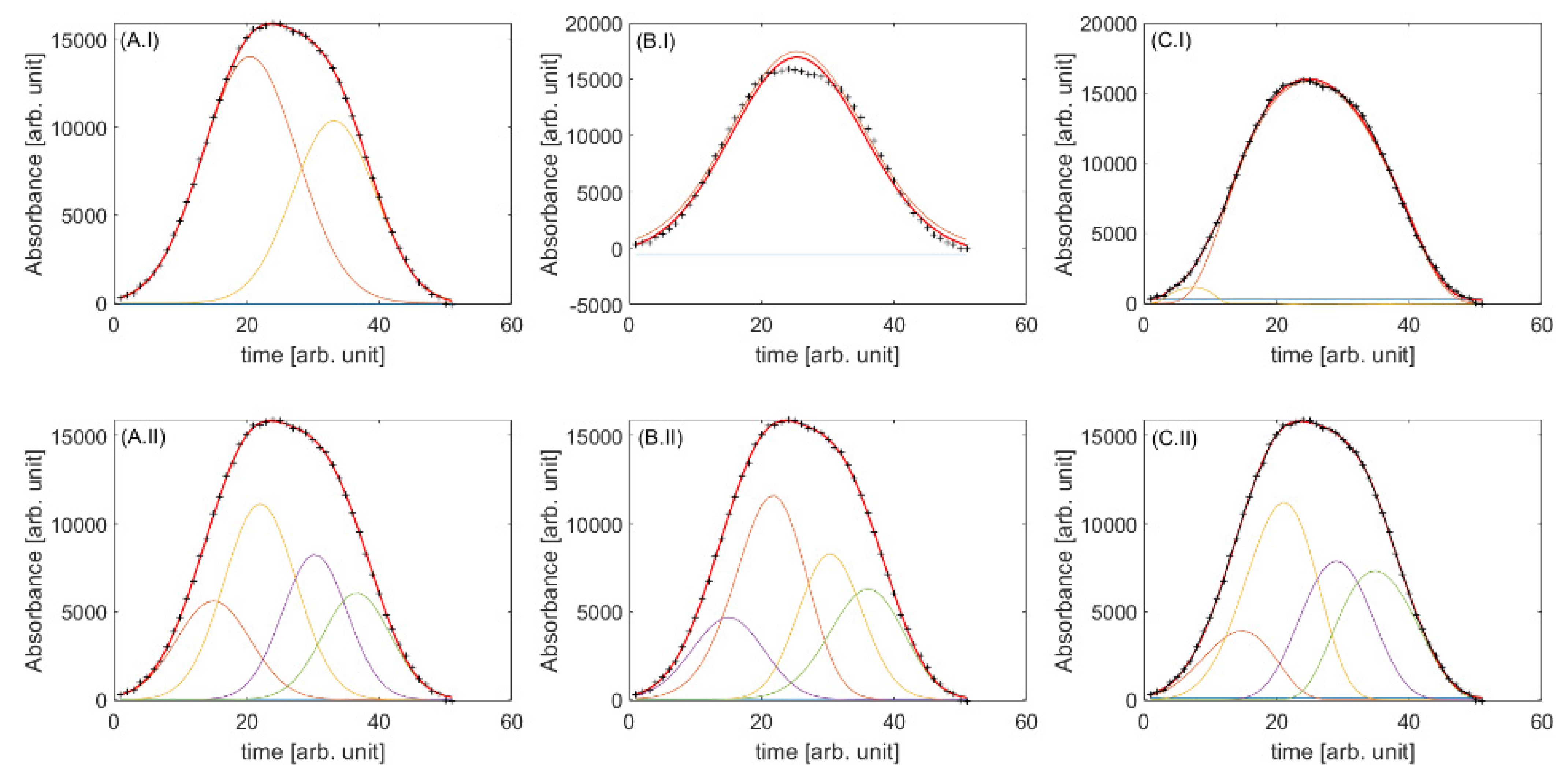
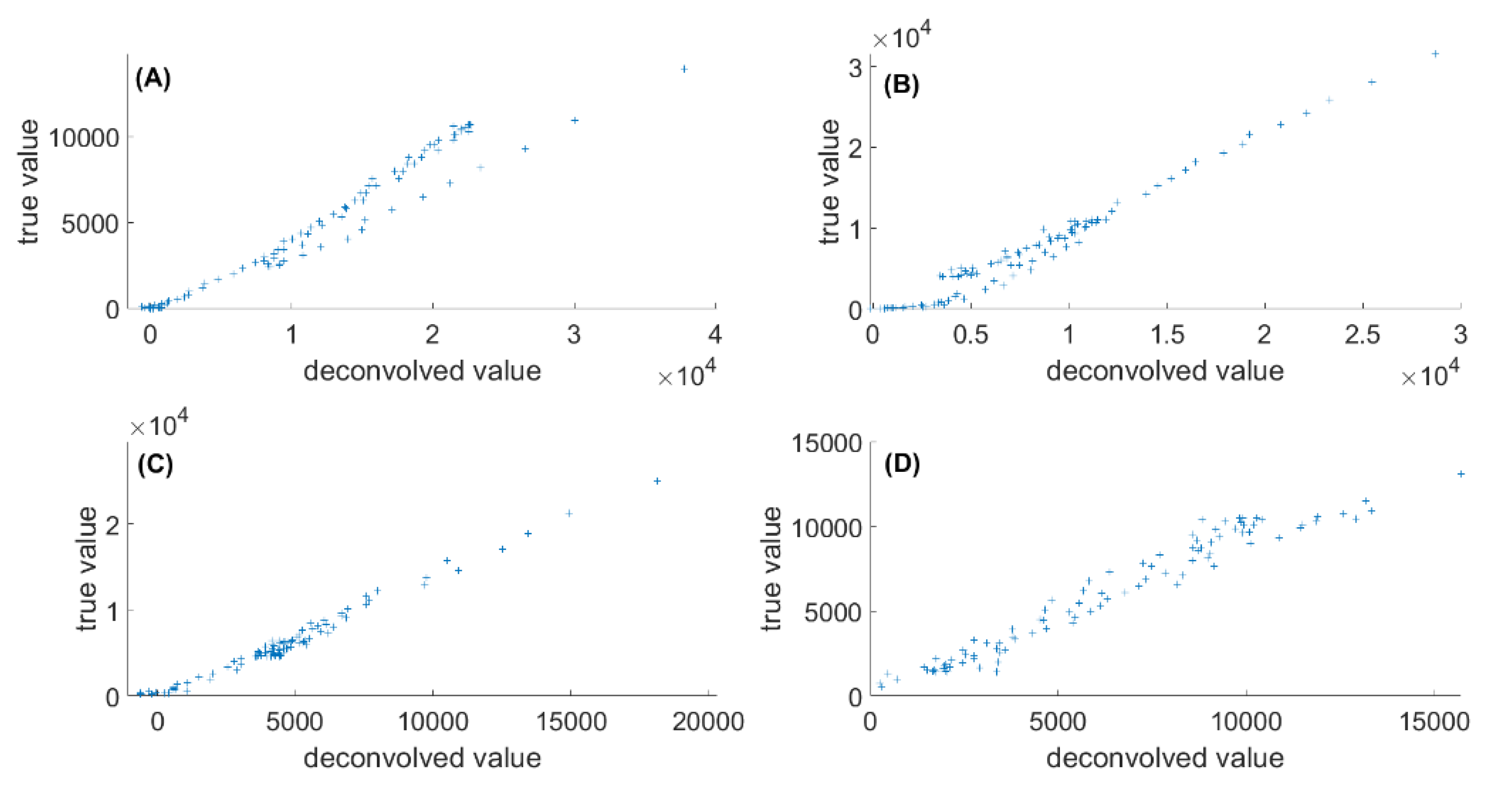
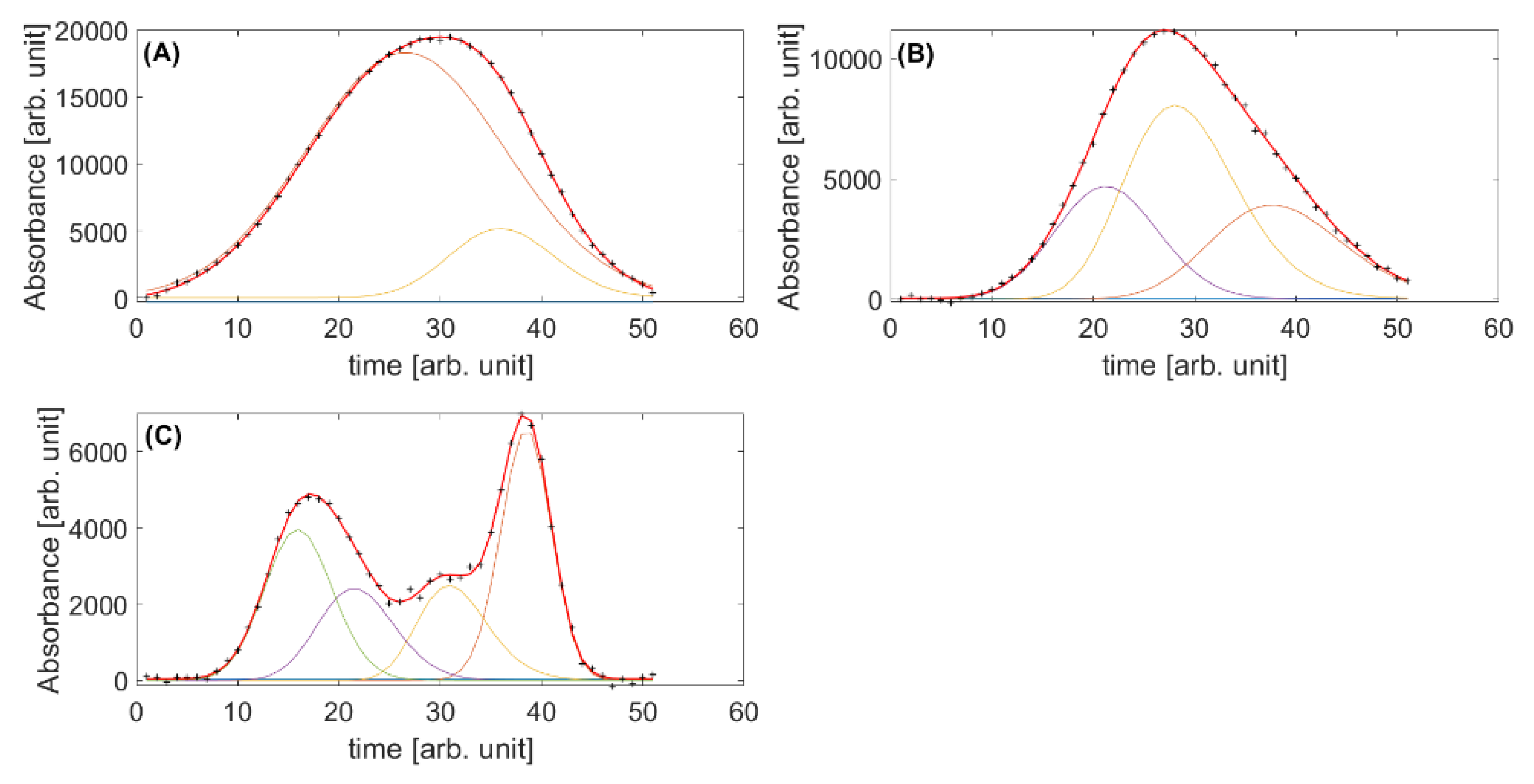
2.2. Validation with Simulated Data
2.2.1. Exploration of Data
2.2.2. First-Order vs. Second-Order Iterative Peak Fitting
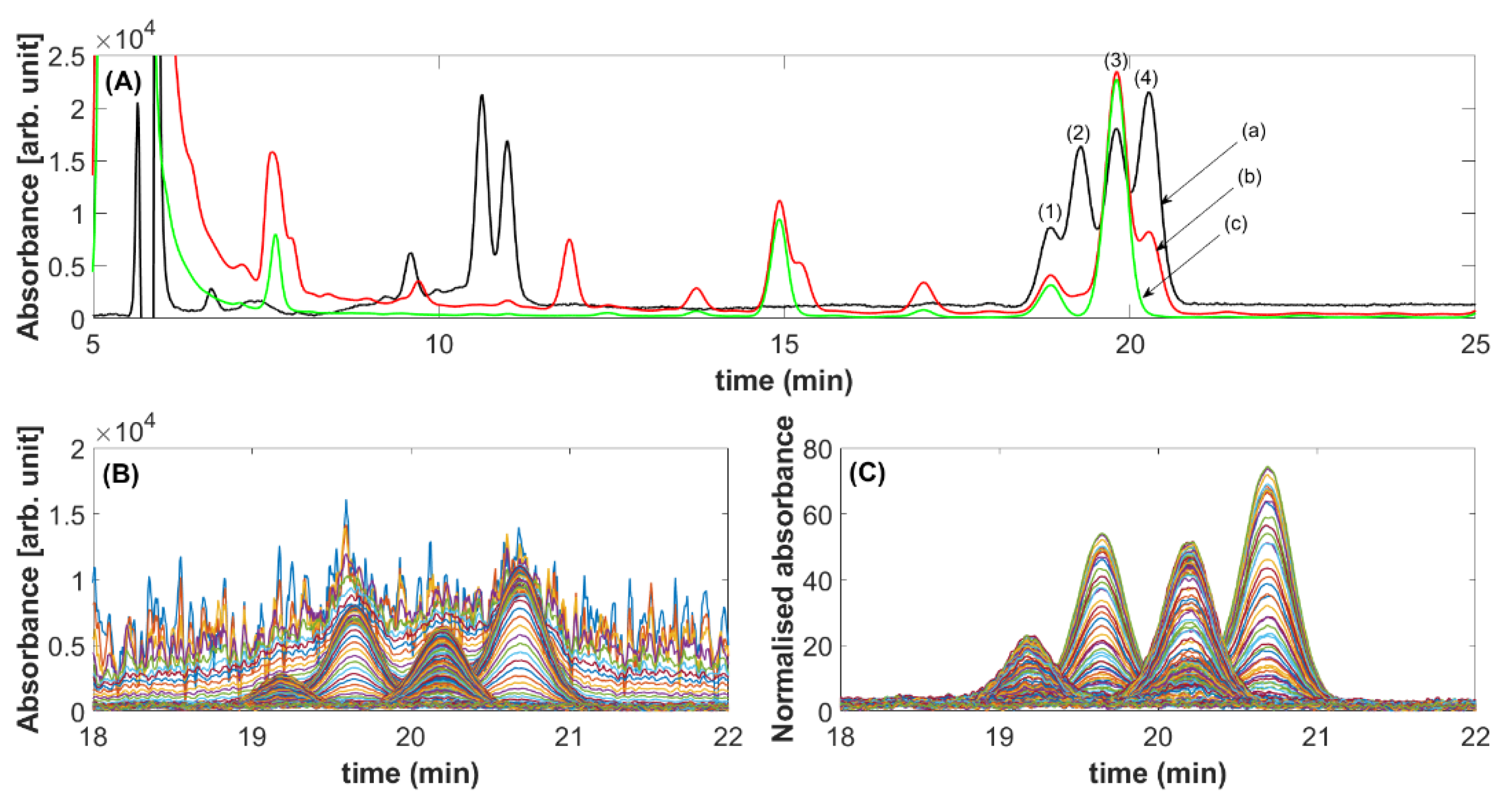
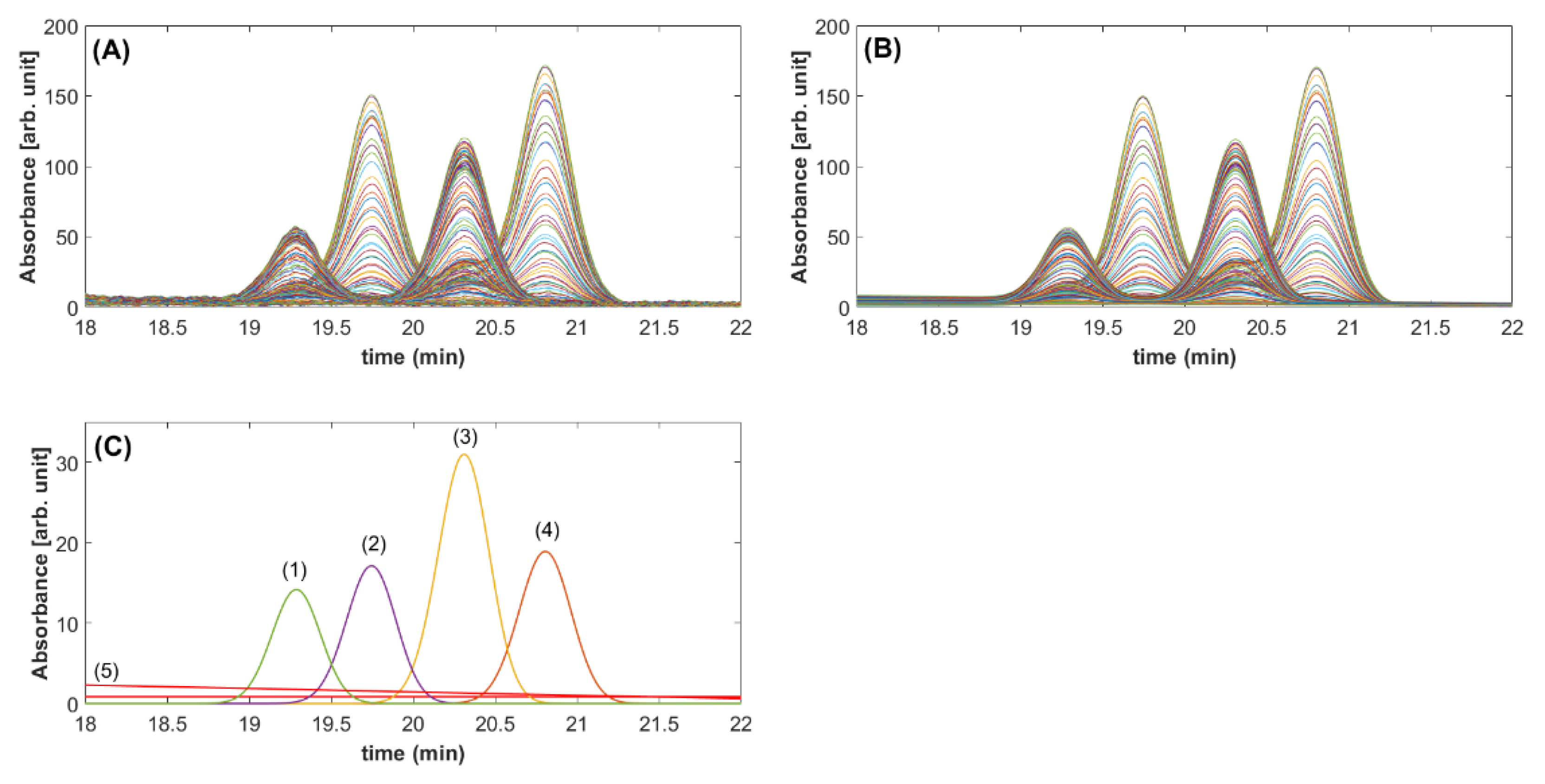
2.3. Validation with HPLC-DAD Separation of Diterpene in Coffee
3. Discussion
4. Materials and Methods
4.1. Simulated Data
4.2. Real Data
4.3. Programming and Software
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
- Options.maxPeaks = 20; Termination condition for the number of peaks. If Options.maxPeaks is obtained, the function stops.
- Options.Function = ‘PMG1’; Mathematical function to be used (‘Gauss’, ‘PMG1’ or ‘PMG2’).
- Options.LoopMe = 5; Number of times fminserach or fminunc can be repeated until convergence is reached.
- Options.RecursiveLoop = 0.95; Termination condition for the MSSR, the algorithm will stop if MSSRn > Options.RecursiveLoop* if MSSRn-1, where MSSRn is the mean sum squared residuals obtained with n peaks after optimization.
- Options.InitialFactor = [1 0.7 0.4]; Multiplicative factor for the initial peak shape before minimization. If Options.InitialFactor is not a single value, all values will be tested.
- Options.MinResolution = 0; Termination condition. If two peaks have a resolution lower than Options.MinResolution, the function stops.
- Options.Penalisation = true; If Options. Penalization is true, a penalization factor for negative intensities is used before calculating the MSSR.
- Options.PenalisationWeight = 1.5; Penalisation factor.
- Options.Constrained.SharedParameters = ‘None’; Constrain on the peak shape: ‘None’, ‘Partial’ or ‘Full’. If ‘None’ peak shapes are independ from each other, if ‘Full’ all peak shapes are the same, if ‘Partial’ peaks variance will fluctuate with a range set by Options.Constrained.Limits.
- Options.Constrained.Limits = 1.5; Should be superior at 1, only used if Options.Constrained.SharedParameters = ‘Partial’.
- Options.PointsPerPeaks = [25 75]; the average number of points per peak, used to smooth the residual when adding a new peak and avoid spikes. More than one value can be used to induce variations in the position of the new peaks and avoid local minima.
- Options.MinMax = 0.05; Termination condition. If the maximum intensity of any peak is lower than Options.MinMax time the intensity of the most intense peak the function stops.
- Options.Robust = false; If this option is used, an additional peak will still be tested when a termination condition is true. If with additional peaks the termination is not true anymore, the algorithms will continue.
- Model.Peaks is a structure that contain the name of the mathematical function, the fitting parameters, the intensity at each channel and the baseline intensity.
- FittedChannels is a [mxkxn] matrix with the intensity as a function of time for each element.
- Stats is a structure with the Options used, the computing time, the number of peaks separated, the end conditions and the means sum square residual.
- myModel is a [mxk] matrix with the normalized peaks model.
References
- Vessman, J.; Stefan, R.I.; van Staden, J.F.; Danzer, K.; Lindner, W.; Burns, D.T.; Fajgelj, A.; Müller, H. Selectivity in analytical chemistry (IUPAC Recommendations 2001). Pure Appl. Chem. 2001, 73, 1381–1386. [Google Scholar] [CrossRef]
- Dyson, N.; Green, J.D. Chromatographic Integration Methods; RSC Chromatography Monographs; Royal Society of Chemistry: Cambridge, UK, 1991; Volume 249, ISBN 978-0-85404-510-5. [Google Scholar]
- Barth, H.G. Chromatography Fundamentals, Part VIII: The Meaning and Significance of Chromatographic Resolution. LCGC N. Am. 2019, 37, 824–828. [Google Scholar]
- Chen, Y.; Zou, C.; Bin, J.; Yang, M.; Kang, C. Multilinear mathematical separation in chromatography. Separations 2021, 8, 31. [Google Scholar] [CrossRef]
- Wahab, M.F.; Hellinghausen, G.; Armstrong, D.W. The Progress Made in Peak Processing. LC GC Eur. 2019, 32, 22–28. [Google Scholar]
- Romanenko, S.V.; Stromberg, A.G.; Pushkareva, T.N. Modeling of analytical peaks: Peaks properties and basic peak functions. Anal. Chim. Acta 2006, 580, 99–106. [Google Scholar] [CrossRef]
- Caballero, R.D.; García-Alvarez-Coque, M.C.; Baeza-Baeza, J.J. Parabolic-Lorentzian modified Gaussian model for describing and deconvolving chromatographic peaks. J. Chromatogr. A 2002, 954, 59–76. [Google Scholar] [CrossRef]
- Purushothaman, S.; Ayet San Andrés, S.; Bergmann, J.; Dickel, T.; Ebert, J.; Geissel, H.; Hornung, C.; Plaß, W.R.; Rappold, C.; Scheidenberger, C.; et al. Hyper-EMG: A new probability distribution function composed of Exponentially Modified Gaussian distributions to analyze asymmetric peak shapes in high-resolution time-of-flight mass spectrometry. Int. J. Mass Spectrom. 2017, 421, 245–254. [Google Scholar] [CrossRef]
- Di Marco, V.B.; Bombi, G.G. Mathematical functions for the representation of chromatographic peaks. J. Chromatogr. A 2001, 931, 1–30. [Google Scholar] [CrossRef]
- Harris, D.C. Nonlinear Least-Squares Curve Fitting with Microsoft Excel Solver. J. Chem. Educ. 1998, 75, 119. [Google Scholar] [CrossRef]
- Erny, G.L.; Bergström, E.T.; Goodall, D.M.; Grieb, S. Predicting Peak Shape in Capillary Zone Electrophoresis: A Generic Approach to Parametrizing Peaks Using the Haarhoff−Van der Linde (HVL) Function. Anal. Chem. 2001, 73, 4862–4872. [Google Scholar] [CrossRef]
- Phillips, M.L.; White, R.L. Dependence of Chromatogram Peak Areas Obtained by Curve-Fitting on the Choice of Peak Shape Function. J. Chromatogr. Sci. 1997, 35, 75–81. [Google Scholar] [CrossRef] [Green Version]
- Li, J. Comparison of the capability of peak functions in describing real chromatographic peaks. J. Chromatogr. A 2002, 952, 63–70. [Google Scholar] [CrossRef]
- Vemi, A. Testing the capability of a polynomial-modified gaussian model in the description and simulation of chromatographic peaks of amlodipine and its impurity in ion-interaction chromatography. J. Sep. Sci. 2014, 37, 1797–1804. [Google Scholar] [CrossRef]
- Wahab, M.F.; O’Haver, T.C.; Gritti, F.; Hellinghausen, G.; Armstrong, D.W. Increasing chromatographic resolution of analytical signals using derivative enhancement approach. Talanta 2019, 192, 492–499. [Google Scholar] [CrossRef]
- Wahab, M.F.; Berthod, A.; Armstrong, D.W. Extending the power transform approach for recovering areas of overlapping peaks. J. Sep. Sci. 2019, 42, 3604–3610. [Google Scholar] [CrossRef] [PubMed]
- Dasgupta, P.K.; Chen, Y.; Serrano, C.A.; Guiochon, G.; Liu, H.; Fairchild, J.N.; Shalliker, R.A. Black Box Linearization for Greater Linear Dynamic Range: The Effect of Power Transforms on the Representation of Data. Anal. Chem. 2010, 82, 10143–10150. [Google Scholar] [CrossRef] [PubMed]
- Erny, G.L.; Moeenfard, M.; Alves, A. Liquid chromatography with diode array detection combined with spectral deconvolution for the analysis of some diterpene esters in Arabica coffee brew. J. Sep. Sci. 2015, 38, 612–620. [Google Scholar] [CrossRef] [Green Version]
- Ahmadi, G.; Tauler, R.; Abdollahi, H. Multivariate calibration of first-order data with the correlation constrained MCR-ALS method. Chemom. Intell. Lab. Syst. 2015, 142, 143–150. [Google Scholar] [CrossRef]
- Ruckebusch, C.; Blanchet, L. Multivariate curve resolution: A review of advanced and tailored applications and challenges. Anal. Chim. Acta 2013, 765, 28–36. [Google Scholar] [CrossRef]
- De Juan, A.; Vander Heyden, Y.; Tauler, R.; Massart, D.L. Assessment of new constraints applied to the alternating least squares method. Anal. Chim. Acta 1997, 346, 307–318. [Google Scholar] [CrossRef]
- Monago-Maraña, O.; Pérez, R.L.; Escandar, G.M.; Muñoz De La Peña, A.; Galeano-Díaz, T. Combination of Liquid Chromatography with Multivariate Curve Resolution-Alternating Least-Squares (MCR-ALS) in the Quantitation of Polycyclic Aromatic Hydrocarbons Present in Paprika Samples. J. Agric. Food Chem. 2016, 64, 8254–8262. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Torres-Lapasió, J.R.; Baeza-Baeza, J.J.; García-Alvarez-Coque, M.C. A Model for the Description, Simulation, and Deconvolution of Skewed Chromatographic Peaks. Anal. Chem. 1997, 69, 3822–3831. [Google Scholar] [CrossRef]
- Boqué, R.; Ferré, J. Using second-order data in chromatographic analysis. LC GC Eur. 2004, 17, 402–407. [Google Scholar]
- Nikitas, P.; Pappa-Louisi, A.; Papageorgiou, A. On the equations describing chromatographic peaks and the problem of the deconvolution of overlapped peaks. J. Chromatogr. A 2001, 912, 13–29. [Google Scholar] [CrossRef]
- Shanno, D.F. Conditioning of Quasi-Newton Methods for Function Minimization. Math. Comput. 1970, 24, 647. [Google Scholar] [CrossRef]
- Find Minimum of Unconstrained Multivariable Function Using Derivative-Free Method—MATLAB Fminsearch. Available online: https://www.mathworks.com/help/matlab/ref/fminsearch.html (accessed on 30 July 2021).
- Lagarias, J.C.; Reeds, J.A.; Wright, M.H.; Wright, P.E. Convergence Properties of the Nelder--Mead Simplex Method in Low Dimensions. SIAM J. Optim. 1998, 9, 112–147. [Google Scholar] [CrossRef] [Green Version]
- Find Minimum of Unconstrained Multivariable Function—MATLAB Fminunc. Available online: https://www.mathworks.com/help/optim/ug/fminunc.html (accessed on 30 July 2021).
- Erny, G.L.; Calisto, V.; Esteves, V.I. Noise normalisation in capillary electrophoresis using a diode array detector. J. Sep. Sci. 2011, 34, 1703–1707. [Google Scholar] [CrossRef]
- Moeenfard, M.; Erny, G.L.; Alves, A. Determination of diterpene esters in green and roasted coffees using direct ultrasound assisted extraction and HPLC–DAD combined with spectral deconvolution. J. Food Meas. Charact. 2020, 14, 1451–1460. [Google Scholar] [CrossRef]
- Misra, S.; Wahab, M.F.; Patel, D.C.; Armstrong, D.W. The utility of statistical moments in chromatography using trapezoidal and Simpson’s rules of peak integration. J. Sep. Sci. 2019, 42, 1644–1657. [Google Scholar] [CrossRef] [PubMed]
- Multivariate Curve Resolution Homepage. Available online: http://www.mcrals.info/ (accessed on 28 July 2021).
- Erny, G. glerny/itMPF: Iterative Multivariate Peak Fitting v1.0; Zenodo: Geneva, Switzerland, 2021. [Google Scholar] [CrossRef]

| Method | FOM | KO 2 | CO 3 | KP 4 | CP 5 |
|---|---|---|---|---|---|
| A | r2 | 0.99990 | 0.99991 | 0.99997 | 0.99980 |
| LOQ1 (mg/L) | 5.5 | 5.0 | 3.8 | 7.6 | |
| B | r2 | 0.99979 | 0.99991 | 0.99996 | 0.99972 |
| LOQ (mg/L) | 7.7 | 5.0 | 5.0 | 8.9 | |
| C | r2 | 0.99995 | NA | 0.99998 | NA |
| LOQ (mg/L) | 3.7 | NA | 3.1 | NA |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Erny, G.L.; Moeenfard, M.; Alves, A. Iterative Multivariate Peaks Fitting—A Robust Approach for The Analysis of Non-Baseline Resolved Chromatographic Peaks. Separations 2021, 8, 178. https://doi.org/10.3390/separations8100178
Erny GL, Moeenfard M, Alves A. Iterative Multivariate Peaks Fitting—A Robust Approach for The Analysis of Non-Baseline Resolved Chromatographic Peaks. Separations. 2021; 8(10):178. https://doi.org/10.3390/separations8100178
Chicago/Turabian StyleErny, Guillaume Laurent, Marzieh Moeenfard, and Arminda Alves. 2021. "Iterative Multivariate Peaks Fitting—A Robust Approach for The Analysis of Non-Baseline Resolved Chromatographic Peaks" Separations 8, no. 10: 178. https://doi.org/10.3390/separations8100178
APA StyleErny, G. L., Moeenfard, M., & Alves, A. (2021). Iterative Multivariate Peaks Fitting—A Robust Approach for The Analysis of Non-Baseline Resolved Chromatographic Peaks. Separations, 8(10), 178. https://doi.org/10.3390/separations8100178






