Numerical Simulation of Fluid Dynamics in a Monolithic Column
Abstract
:1. Introduction
2. Numerical Method
3. Results and Discussion
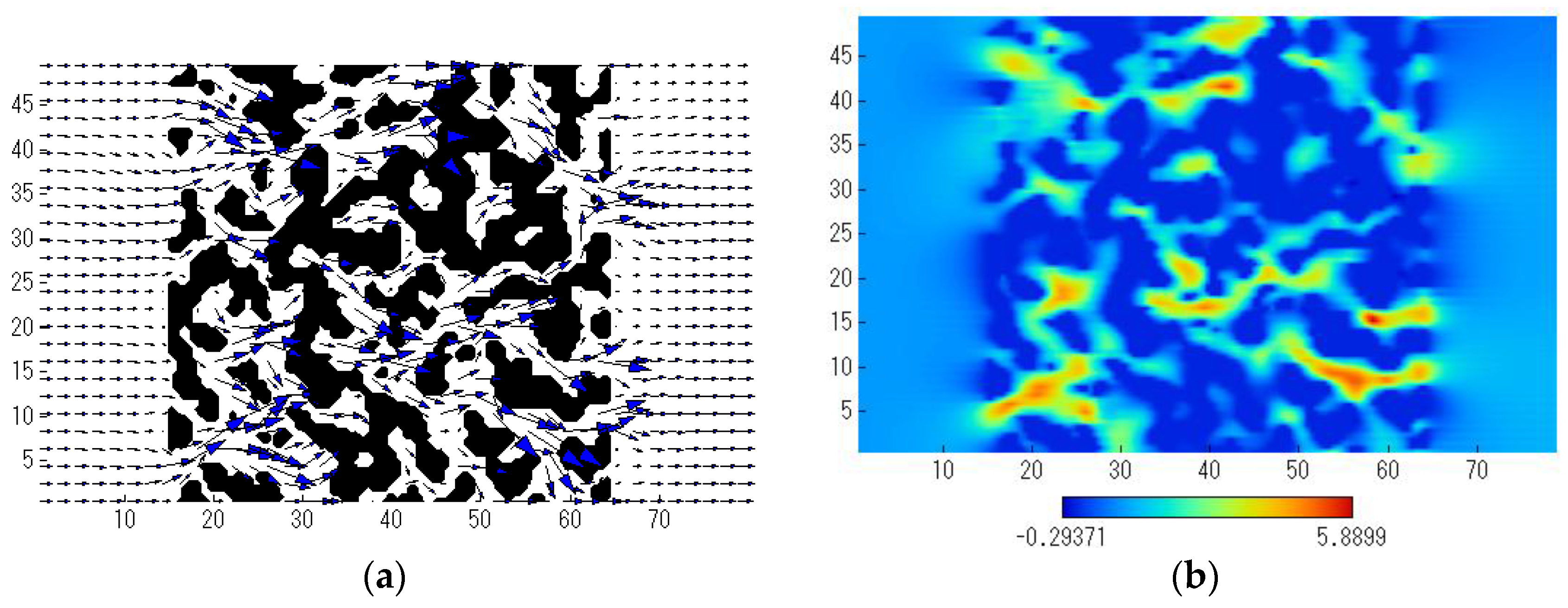
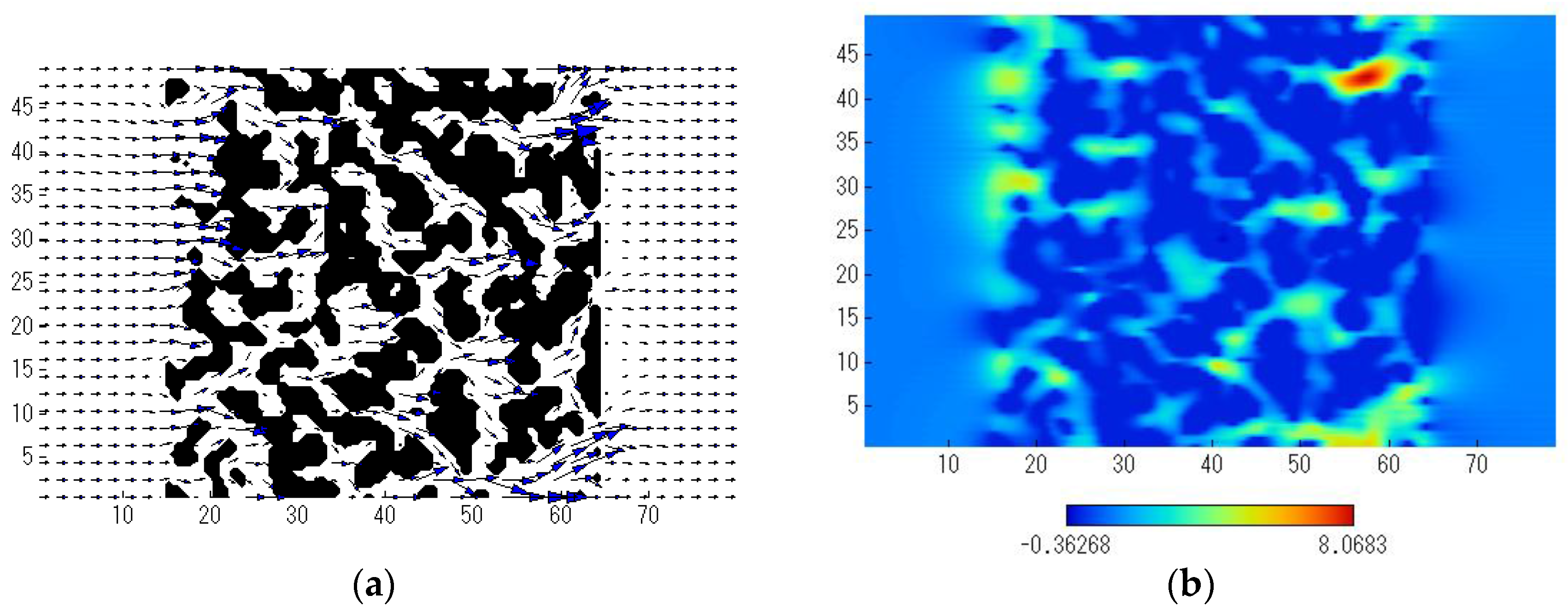
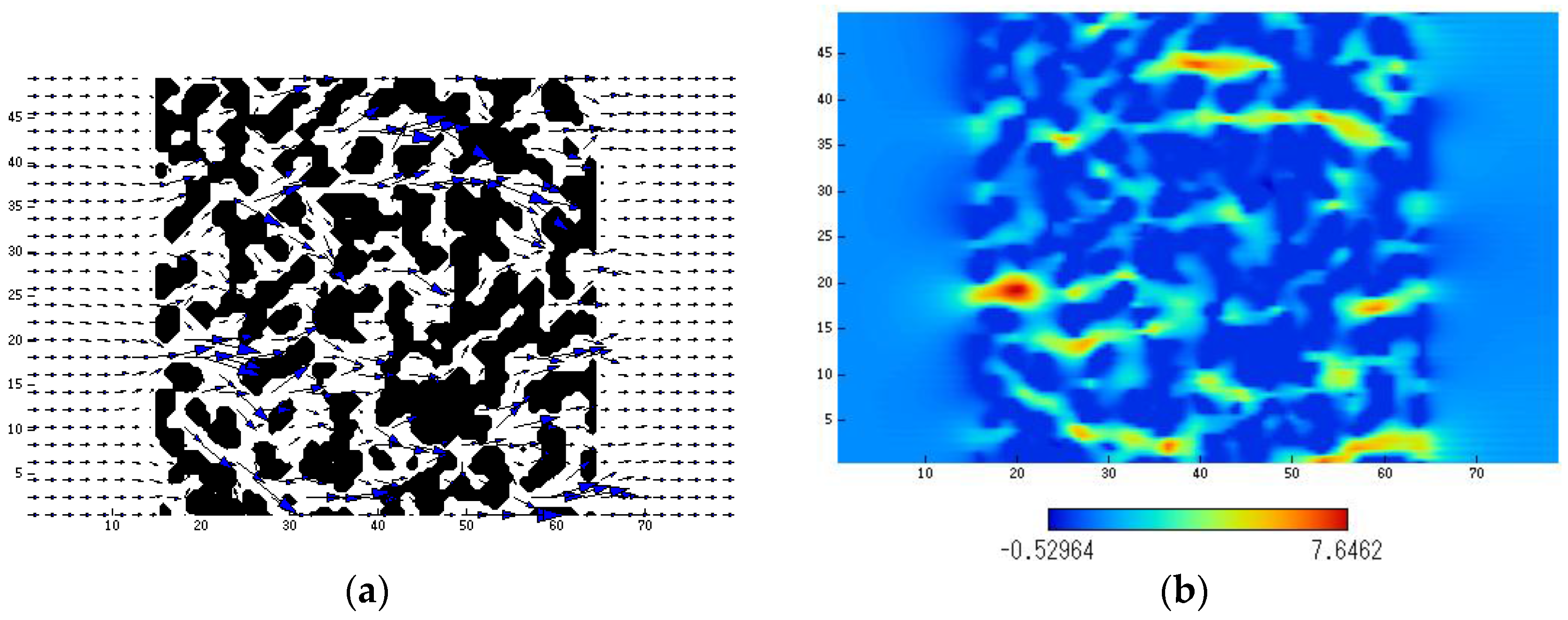
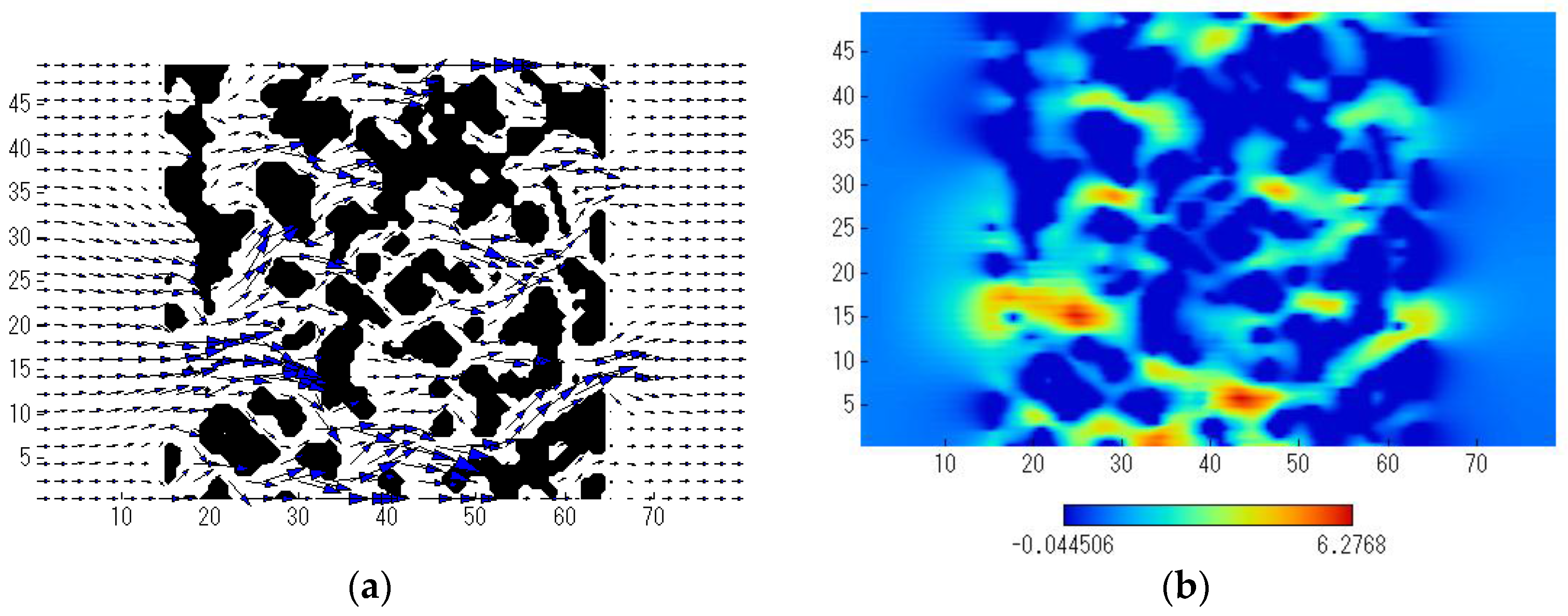
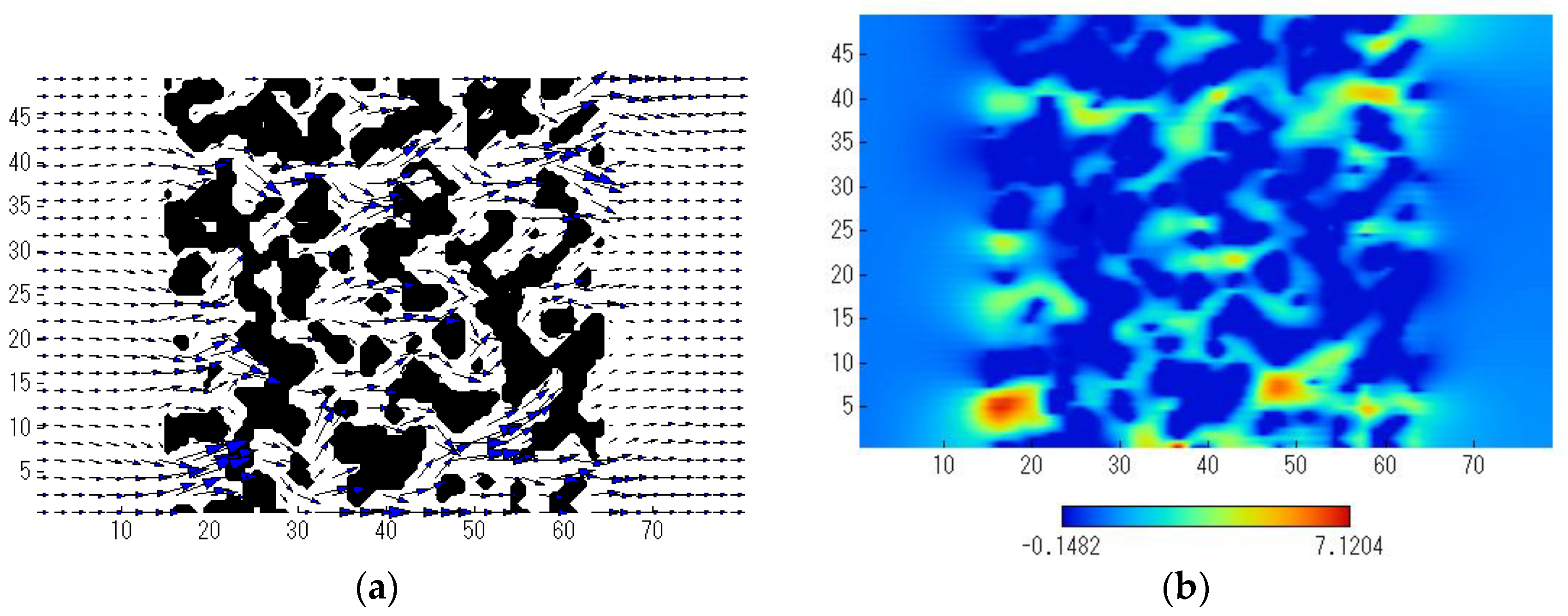
3.1. Flow Field
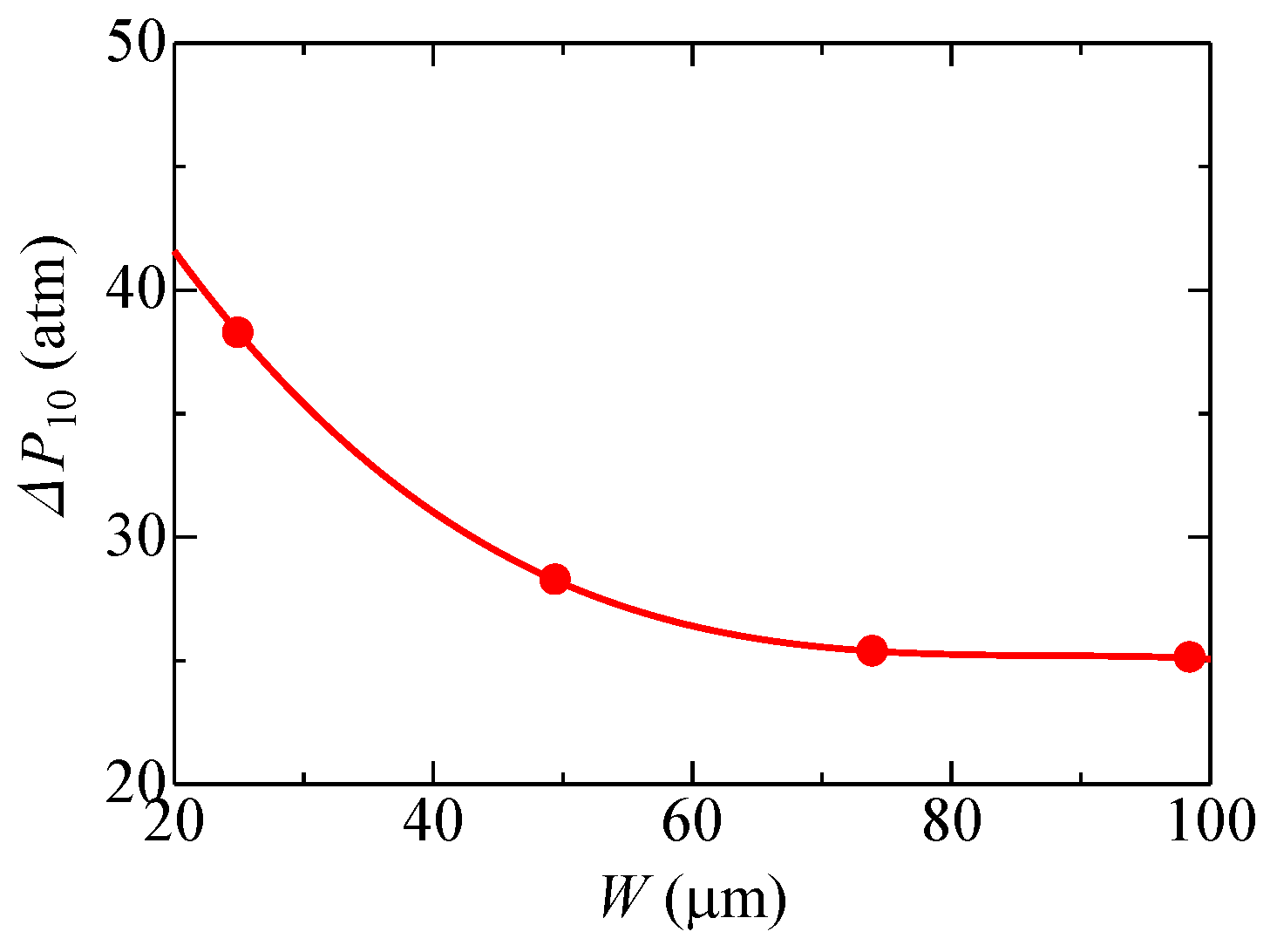
3.2. Channel Length
3.3. Velocity Distribution
4. Conclusions
- (a)
- When the height (width) of the numerical domain was 49 μm or greater, the pressure drop was saturated. The order of the magnitudes of the pressure drop was M03 > M01 > M02 > M05 > M04. The pressure drop was smaller as the porosity and/or the pore size increased.
- (b)
- When particles were added to the flow, the trajectory of each particle was examined in order to evaluate the flow path length. Consequently, the flow path length was almost constant regardless of the column type, and was approximately 1.2 times larger than the thickness of the column.
- (c)
- The maximum flow velocity in the X direction increased with the pressure drop. The change in the flow direction was larger as the pressure drop increased. As a result, when the structure of the column substrate was more complicated, the change in the flow direction became larger, resulting in the larger pressure drop.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Umemura, T.; Kamiya, S.; Itoh, A.; Chiba, K.; Haraguchi, H. Preparation and characterization of methacrylate-based semi-micro monoliths for high-throughput bioanalysis. Anal. Bioanal. Chem. 2006, 386, 566–571. [Google Scholar] [CrossRef] [PubMed]
- Shu, S.; Kobayashi, H.; Kojima, N.; Sabarudin, A.; Umemura, T. Preparation and characterization of lauryl methacrylate-based monolithic microbore column for reversed-phase liquid chromatography. J. Chromatogr. A 2011, 1218, 5228–5234. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Doolen, G.D. Lattice Boltzmann method for fluid flows. Ann. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- Yamamoto, K.; Komiyama, R.; Umemura, T. Numerical simulation on flow in column chromatography. Int. J. Mod. Phys. C 2014, 24, 1–7. [Google Scholar] [CrossRef]
- Yamamoto, K.; Satake, S.; Yamashita, H.; Takada, N.; Misawa, M. Lattice Boltzmann simulation on flow with soot accumulation in diesel particulate filter. Int. J. Mod. Phys. C 2007, 18, 528–535. [Google Scholar] [CrossRef]
- Yamamoto, K.; Satake, S.; Yamashita, H.; Takada, N.; Misawa, M. Fluid simulation and X-ray CT images for soot deposition in a diesel filter. Eur. Phys. J. 2009, 171, 205–212. [Google Scholar] [CrossRef]
- Yamamoto, K.; Yamauchi, K.; Takada, N.; Misawa, M.; Furutani, H.; Shinozaki, O. Lattice Boltzmann simulation on continuously regenerating diesel filter. Philos. Trans. A R. Soc. Lond. 2011, 369, 2584–2591. [Google Scholar] [CrossRef] [PubMed]
- Yamamoto, K.; Matsui, K. Diesel exhaust after-treatment by silicon carbide fiber filter. Fibers 2014, 2, 128–141. [Google Scholar] [CrossRef]
- Zou, Q.; He, X. On pressure and velocity boundary conditions for the lattice Boltzmann BGK model. Phys. Fluids 1997, 9, 1591–1598. [Google Scholar] [CrossRef]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Interphase transport in isothermal systems. In Transport Phenomena, 2nd ed.; Wiley: New York, NY, USA, 1960. [Google Scholar]
- Imai, Y.; Miki, T.; Ishikawa, T.; Aoki, T.; Yamauchi, T. Deposition of micrometer particles in pulmonary airways during inhalation and breath holding. J. Biomech. 2012, 45, 1809–1815. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Meng, L.; Pittman, E.N.; Etheredge, A.; Hubbard, K.; Trinidad, D.A.; Kato, K.; Ye, X.; Calafat, A.M. Quantification of urinary mono-hydroxylated metabolites of polycyclic aromatic hydrocarbons by on-line solid phase extraction-high performance liquid chromatography-tandem mass spectrometry. Anal. Bioanal. Chem. 2016. [Google Scholar] [CrossRef] [PubMed]

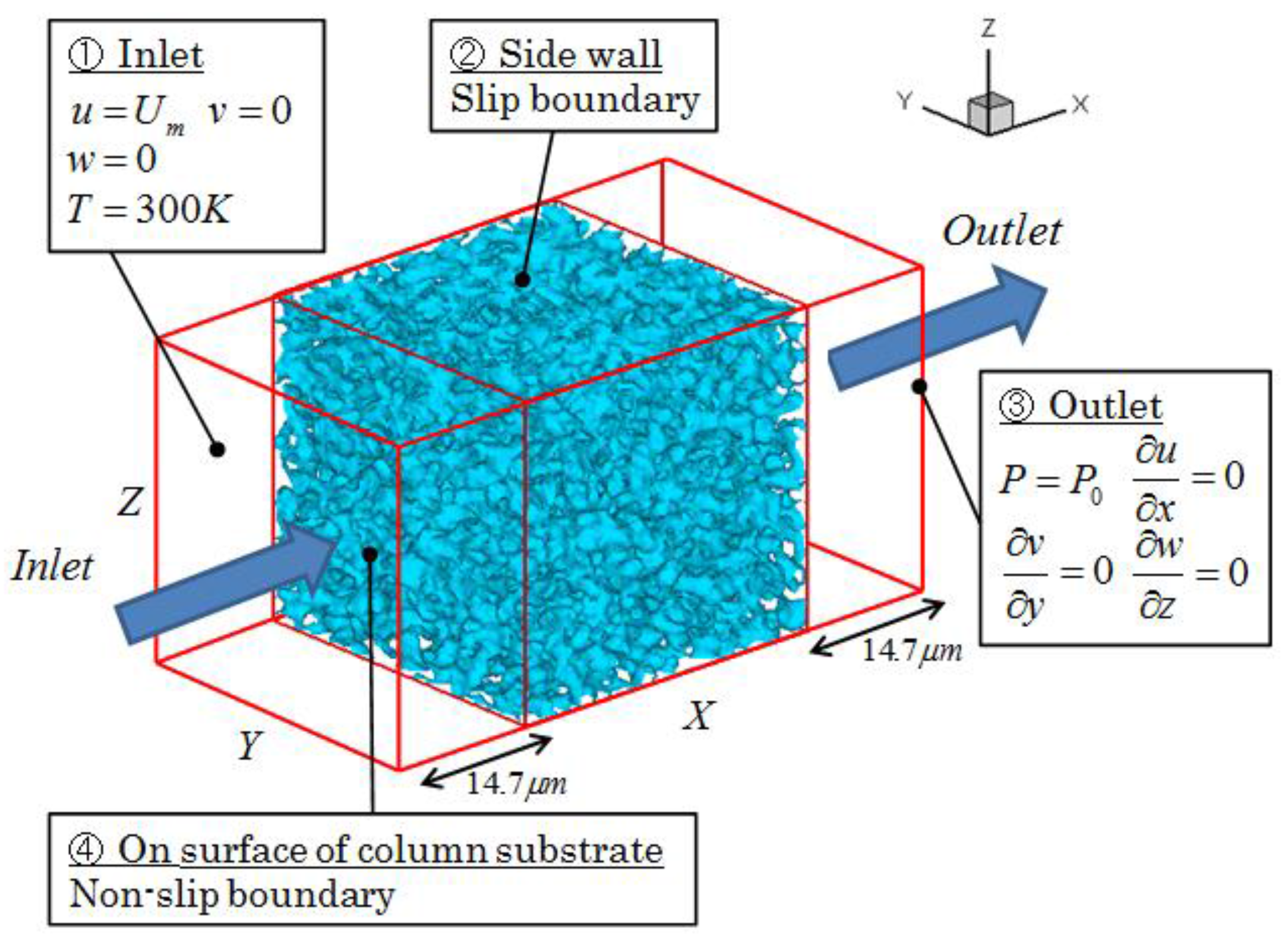
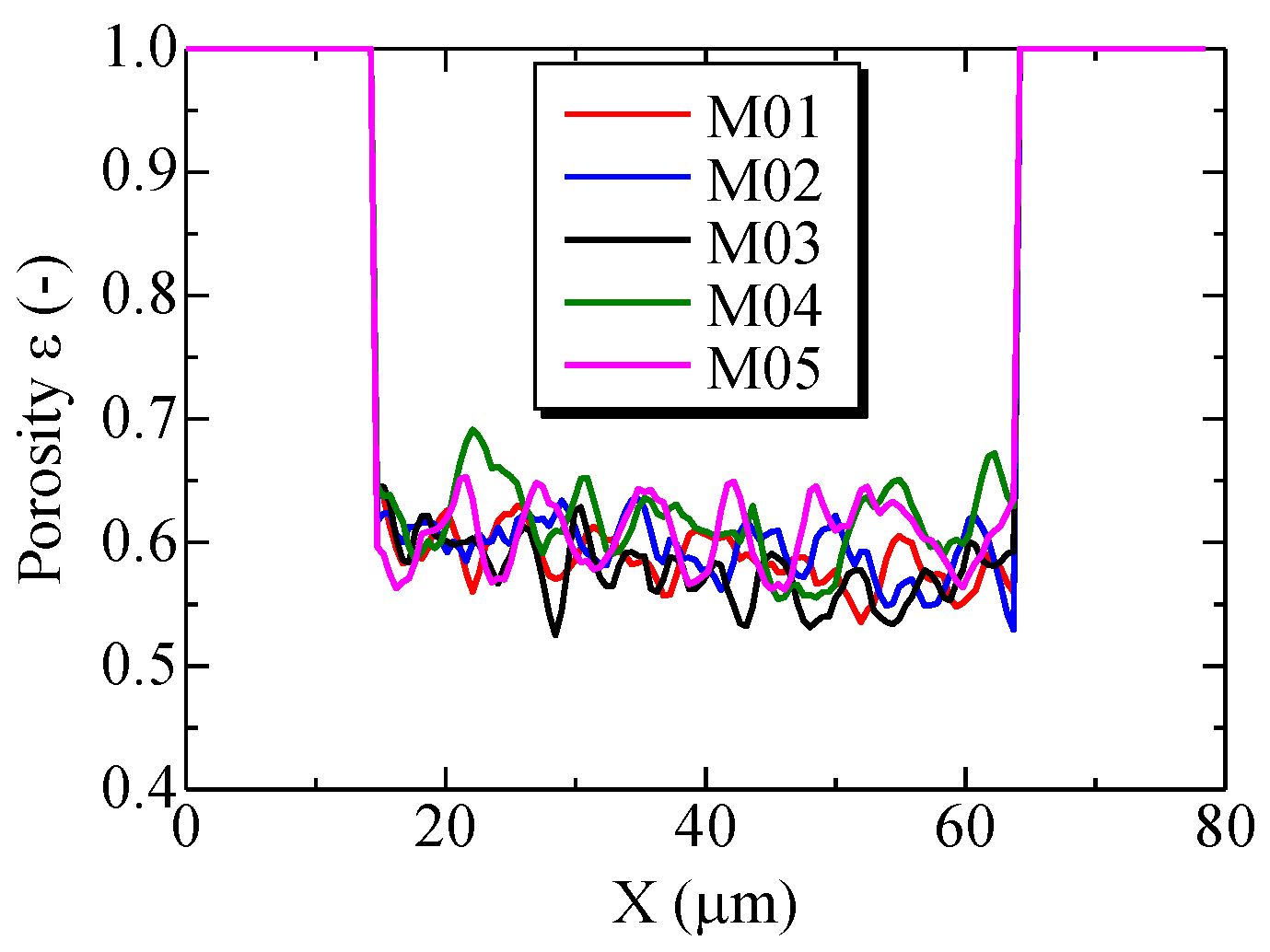
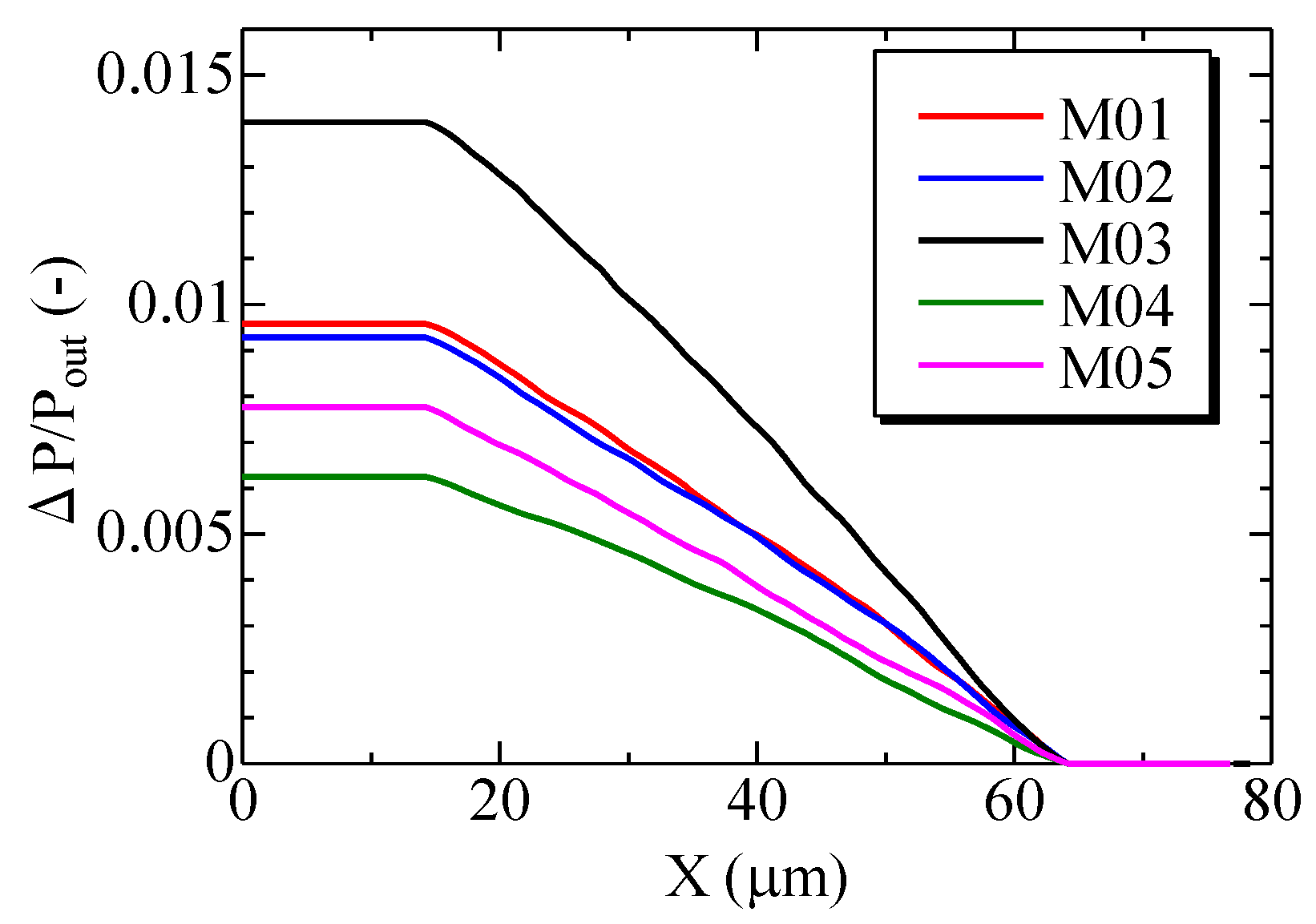
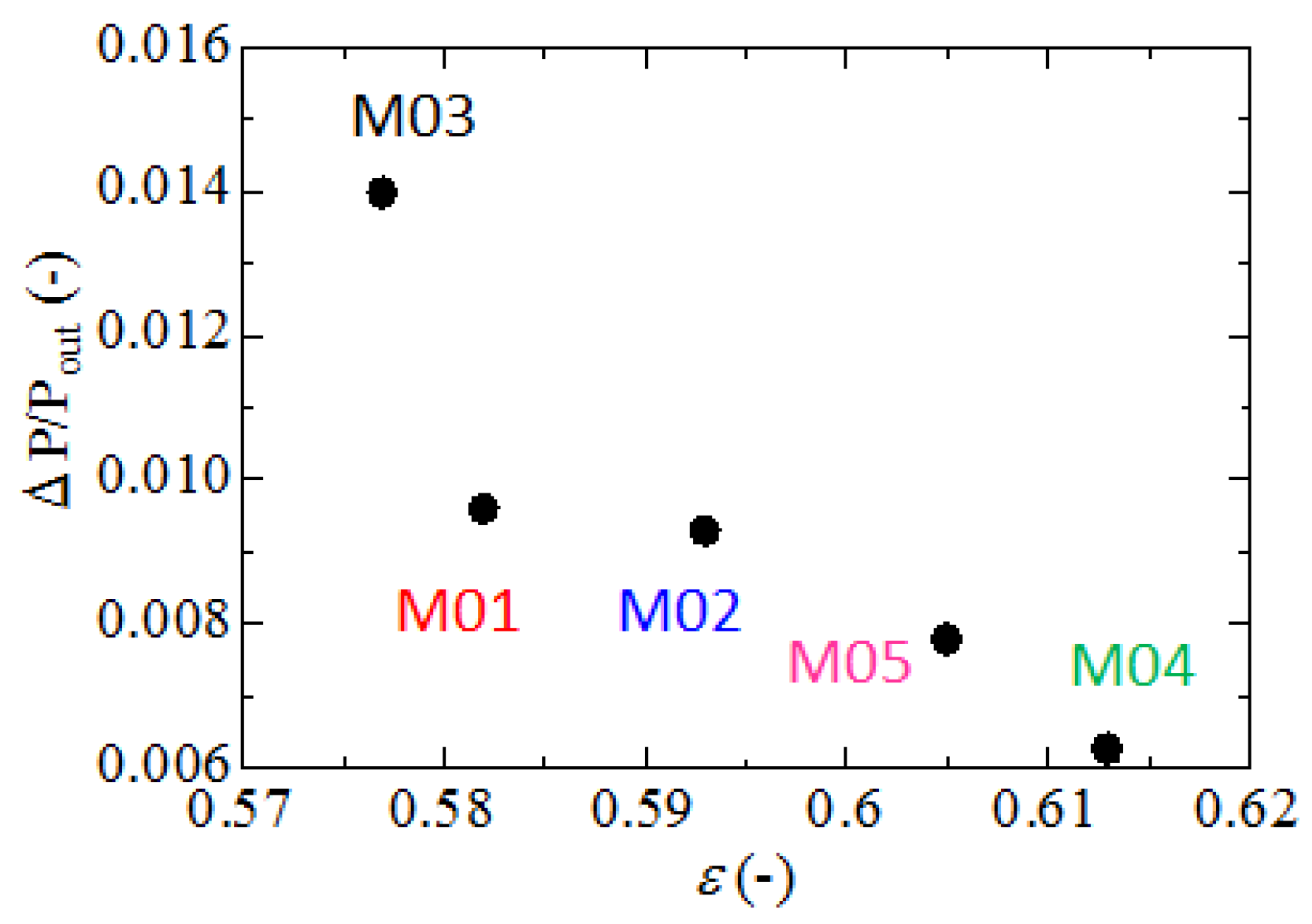
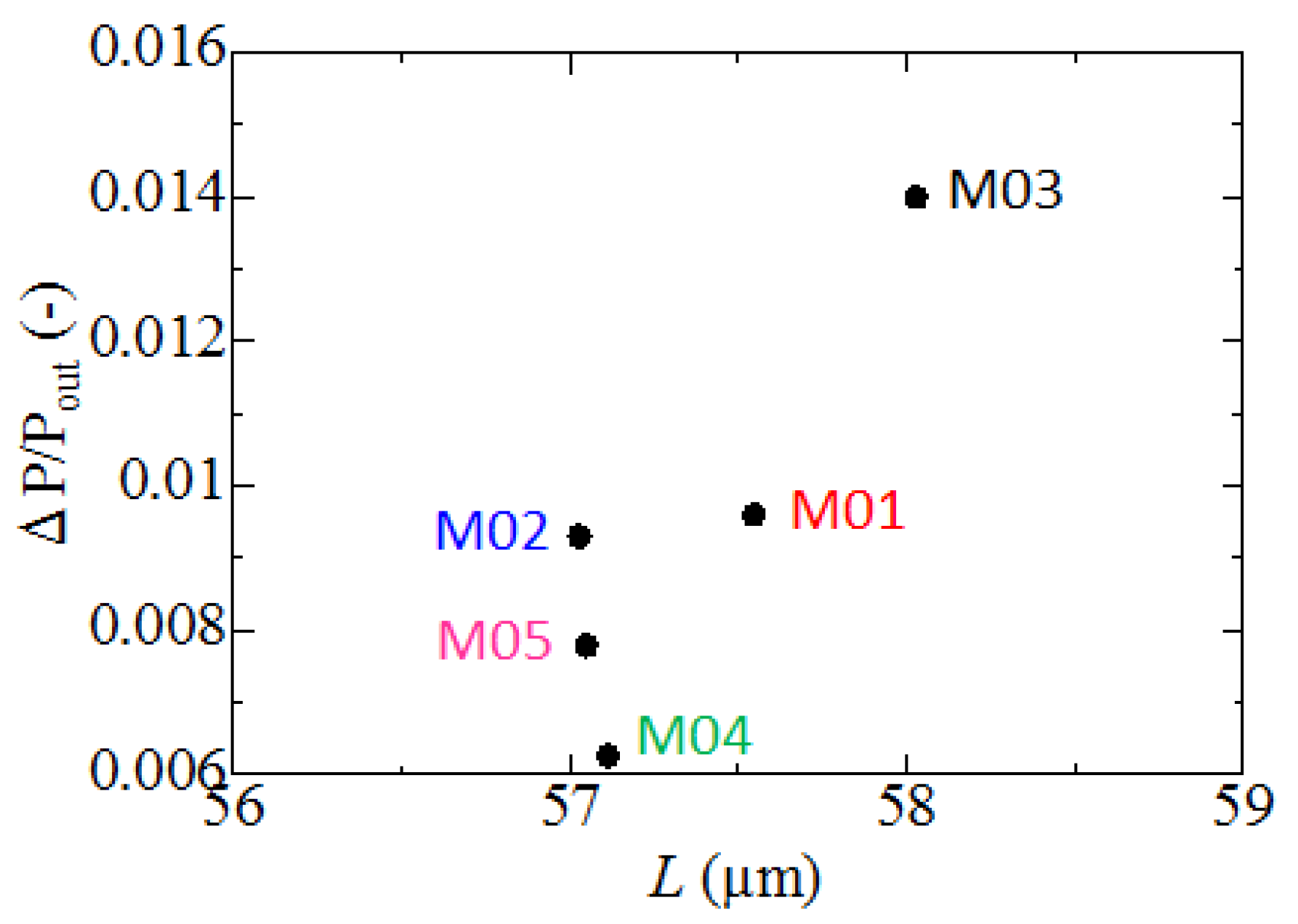

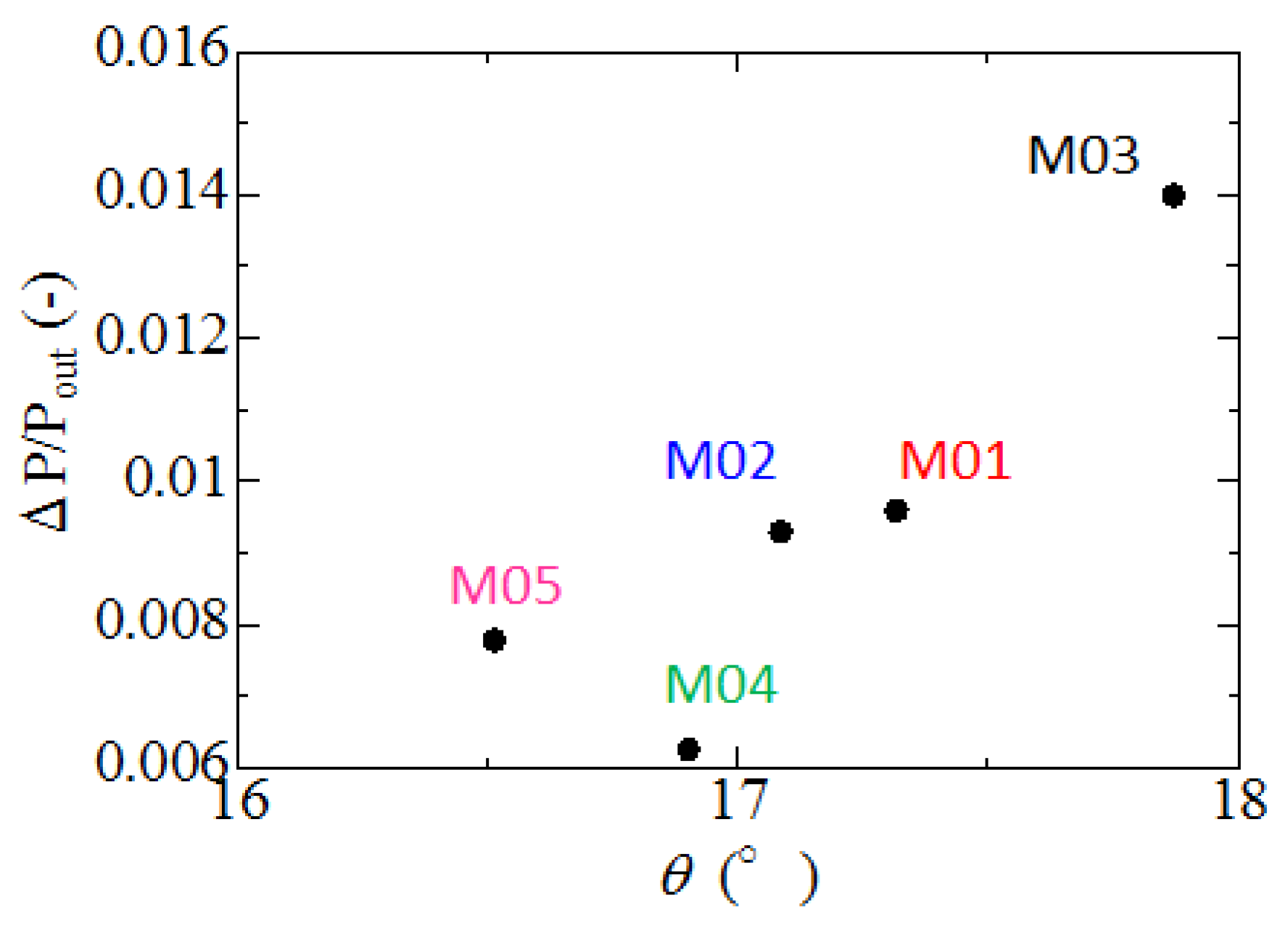
| No. | Ratio of Cross-Linker | Reactor Vessel for Polymerization Reaction | Reaction Temperature | Porosity ε | Pore Size Dp |
|---|---|---|---|---|---|
| M01 | 10% | SUS a pipe | 60 °C | 0.582 | 4.43 μm |
| M02 | 25% | SUS a pipe | 60 °C | 0.593 | 4.28 μm |
| M03 | 10% | SUS a pipe | 90 °C | 0.577 | 4.01 μm |
| M04 | 10% | PEEK b tube | 60 °C | 0.613 | 4.65 μm |
| M05 | 10% | PEEK b tube | 90 °C | 0.605 | 4.56 μm |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yamamoto, K.; Tajima, Y. Numerical Simulation of Fluid Dynamics in a Monolithic Column. Separations 2017, 4, 3. https://doi.org/10.3390/separations4010003
Yamamoto K, Tajima Y. Numerical Simulation of Fluid Dynamics in a Monolithic Column. Separations. 2017; 4(1):3. https://doi.org/10.3390/separations4010003
Chicago/Turabian StyleYamamoto, Kazuhiro, and Yuuta Tajima. 2017. "Numerical Simulation of Fluid Dynamics in a Monolithic Column" Separations 4, no. 1: 3. https://doi.org/10.3390/separations4010003
APA StyleYamamoto, K., & Tajima, Y. (2017). Numerical Simulation of Fluid Dynamics in a Monolithic Column. Separations, 4(1), 3. https://doi.org/10.3390/separations4010003





