Composition- and Temperature-Dependent Solubility of Sinomenine Hydrochloride in Ethanol–Water Mixtures

Abstract

Sinomenine Hydrochloride is a bioactive alkaloid extracted from the root and stem of the medicinal plant sinomenium acutum, and is widely used to treat rheumatoid arthritis. Relevant studies were consulted, and the solubility data of Sinomenine Hydrochloride in ethanol–water mixed solvent have not been reported. It is essential to choose a proper solvent in the process of crystallization that has a significant influence on the purity and productivity. Therefore, it is necessary to determine the solubility of Sinomenine Hydrochloride under the conditions of different ratios of ethanol–water mixed solvent and temperature. In this study, the solubility of Sinomenine Hydrochloride in ethanol–water mixed solvent was determined using high-performance liquid chromatography within the temperature range of 283.15 K–308.15 K. At the same time, the CNIBS/R-K model, Modified Apelblat model, Yaws model, and Apelblat–Jouyban–Acree model were used to fit the solubility data, and the relevant thermodynamic parameters were calculated using the Van’t Hoff model. The results showed that the solubility of Sinomenine Hydrochloride was higher in pure water than in pure ethanol. Moreover, with the increase in the mass fraction of ethanol in the mixed solvent, the solubility of Sinomenine Hydrochloride showed a trend of increasing first and then decreasing. When the ethanol–water ratio was 5:5, the solubility of the compound reached the maximum. In addition, experimental data showed that the solubility of Sinomenine Hydrochloride was affected by temperature. In the experimental temperature range, the solubility increased with the increase in temperature. Among these four solubility models, the CNIBS/R-K model had the best fitting effect; the maximum RAD and RMSD were 4.622 × 10⁻³ and 4.079 × 10⁻³, respectively. The thermodynamic model fitting results showed that the predicted values were in good agreement with the experimental data, and the thermodynamic parameters ΔHd, ΔSd, and ΔGd were all positive values. This indicated that the dissolution of Sinomenine Hydrochloride in the ethanol–water mixture was a non-spontaneous and endothermic process. A proper ratio of ethanol–water and temperature improved the solubility of Sinomenine Hydrochloride. The data determined in this study can provide basic data for the industrial purification of Sinomenine Hydrochloride.

1. Introduction

Sinomenine is a bioactive alkaloid extracted from the root and stem of medicinal plant sinomenium acutum (Thunb.) Rehd et Wils. [1], which has anti-inflammatory, immunosuppressive, anti-arrhythmic, and other curative effects [2,3]. It has been widely used in clinical medicine to treat rheumatoid arthritis, malignant tumor, nephropathy, and other diseases in China, Japan, and other Asian countries [4,5,6,7,8] and has a remarkable clinical effect and high cure rate. At present, Sinomenine Hydrochloride, which is the hydrochloride form of sinomenine with better water solubility, is used as the active pharmaceutical ingredient (API) to make pharmaceutical preparations of tablets, pills, capsules, or injections [9,10], and other new dosage forms have also been developed in recent years [11,12,13]. The structural formula of Sinomenine Hydrochloride (CAS No. 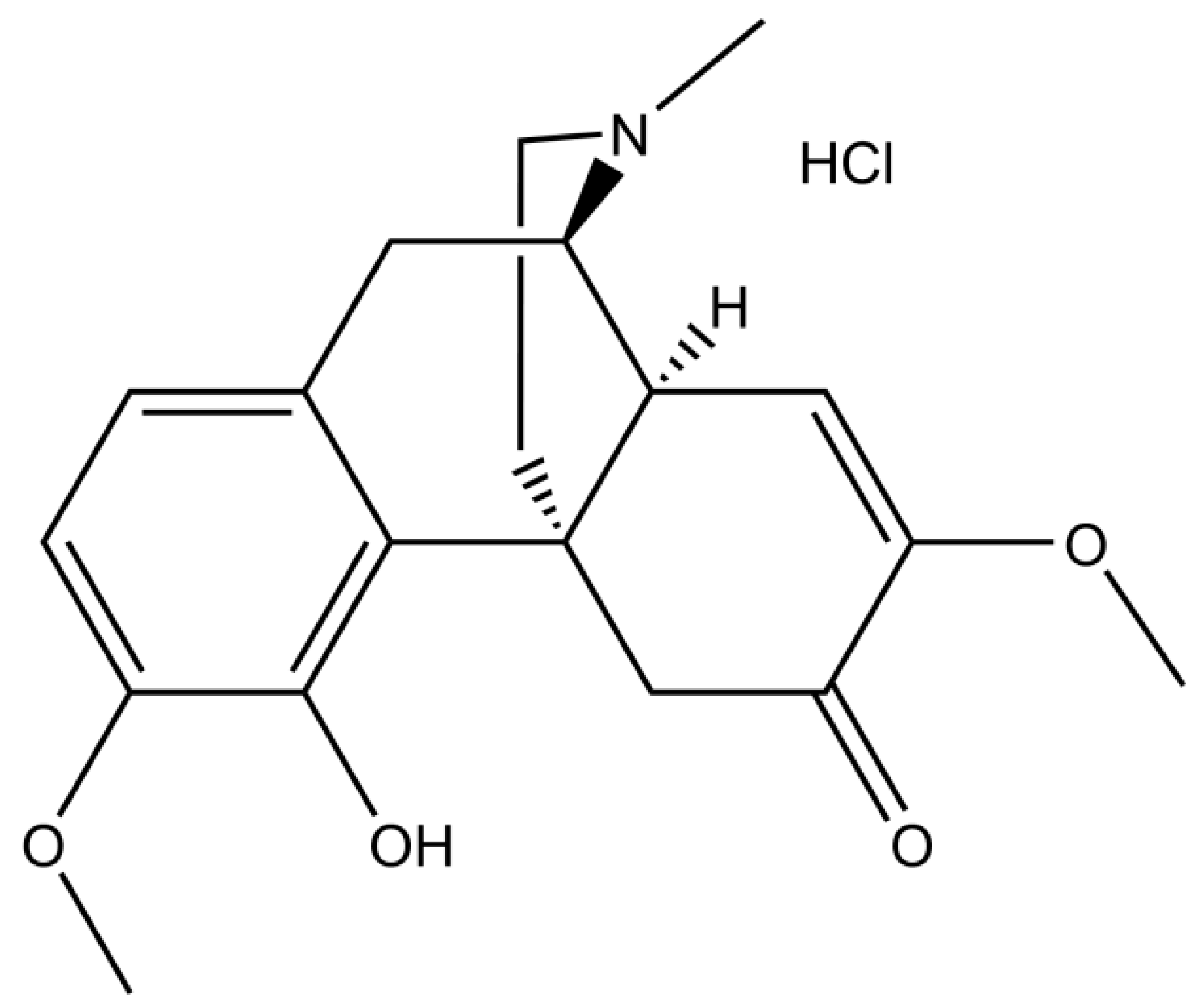6080-33-7) is shown in Figure 1 [14].

Clinical application has shown that Sinomenine Hydrochloride can improve the curative effect when combined with a variety of drugs. However, some toxic reactions to Sinomenine Hydrochloride have been reported in recent years, in particular, anaphylactic shock. The safety of drugs depends not only on the toxicological properties of APIs, but also on the toxicological properties of impurities in the drug substance. The purity of Sinomenine Hydrochloride is also an important factor in its quality control. It is essential to choose a proper solvent in the process of crystallization that has a significant influence on the purity and productivity. Moreover, solubility data is an important factor to be able to optimize the crystallization process [15]. Ethanol is usually used as a solvent in the crystallization process of Sinomenine Hydrochloride. Relevant studies were consulted and the solubility data of Sinomenine Hydrochloride in ethanol–water mixed solvent have not been reported. Therefore, it is necessary to determine the solubility of Sinomenine Hydrochloride under the conditions of different ratios of ethanol–water mixed solvent and temperature.

In this study, the solubility of Sinomenine Hydrochloride in ethanol–water mixed solvent systems with different proportions was determined at different temperatures (283.15, 288.15, 293.15, 298.15, 303.15, 308.15 K). The CNIBS/R-K model, Modified Apelblat model, Yaws model, and Apelblat–Jouyban–Acree model were used to fit the solubility data. Compared to the activity coefficient method, the empirical equations do not require many thermodynamic parameters. These characteristics make it suitable for the solubility simulation calculation of some substances for which thermodynamic parameters are not easily obtained. The thermodynamic parameters of Sinomenine Hydrochloride in these solvents were calculated from the measured solubility data using the modified version of the Van’t Hoff model. The determined data can provide a reference for the industrial purification of Sinomenine Hydrochloride.

2. Experimental

2.1. Materials

Sinomenine Hydrochloride standard was purchased from Shanghai Yuanye Biotechnology Co., Ltd. (Shanghai, China) with a purity of 98.0%. Sinomenine Hydrochloride was provided by Hunan Zhengqing Pharmaceutical Group Co., Ltd. (Huaihua, China) with a minimum purity of 98.0%. Purified water was prepared by a Milli-Q water purifier (Millipore, Bedford, MA, USA). The pH of the water was measured at 298.15 K using a sartorius PB-30 pH meter (Beijing, China) with three-point calibration immediately prior to use, giving pH = [6.98 ± 0.005]. All reagents used, like ethanol and acetonitrile, were of analytical grade. Sodium dihydrogen phosphate was purchased from Chemart Tianjin Chemical Technology Co., Ltd. (Tianjin, China).

2.2. Instruments

The following instruments were used to conduct the experiments: Intelligent Thermostatic Culture Oscillator (HNY- 2102C, manufactured by Tianjin Ounuo Instrument Co., Ltd., Tianjin, China), Digital Display Thermostatic Water Bath (XMTD- 204, manufactured by Shanghai Yuejin Medical Device Co., Ltd., Shanghai, China), Cryogenic Coolant Circulation Pump (DLSB- 5 L/25, manufactured by Tianjin Konuo Instrument Equipment Co., Ltd., Tianjin, China), 1/100 K Electronic Balance (METTLER AE 240, manufactured by Mettler Toledo, Columbus, OH, USA), High-performance liquid chromatography apparatus (Waters ACQuity Arc, manufactured by Waters, Milford, MA, USA), and a Liquid Chromatography Column (Plus C18-A, 4.6 × 250 mm, 5 μm, manufactured by Diamonsil, Beijing, China).

2.3. Solubility Measurements

The solubility of Sinomenine Hydrochloride in mixture solvents (water–ethanol) was measured by the equilibrium method, similarly to previous reports in the literature [16,17,18]. For each target composition, 10.00 g of the ethanol–water binary mixture was prepared gravimetrically to achieve an ethanol mole fraction $x_A$ (

Table 1. The solubilities of Sinomenine Hydrochloride in solvents with different ethanol–water mole fractions at temperatures ranging from 283.15 to 308.15 K (P = 0.1 MPa) ^a.

${\mathit{x}}_{\mathit{A}}$	${\mathit{\chi }}_{\mathit{e}}$
	283.15 K	288.15 K	293.15 K	298.15 K	303.15 K	308.15 K
0.000	0.722	0.741	0.773	0.788	0.824	0.830
0.033	0.756	0.777	0.813	0.826	0.834	0.876
0.072	0.788	0.810	0.842	0.856	0.886	0.901
0.117	0.821	0.840	0.870	0.882	0.905	0.917
0.171	0.851	0.866	0.891	0.900	0.921	0.929
0.236	0.869	0.880	0.900	0.909	0.929	0.935
0.317	0.869	0.881	0.899	0.906	0.922	0.936
0.419	0.864	0.866	0.884	0.903	0.915	0.927
0.553	0.812	0.823	0.855	0.866	0.887	0.908
0.735	0.742	0.749	0.784	0.806	0.834	0.863
1.000	0.511	0.532	0.586	0.632	0.634	0.714

^a ${\chi }_e$ stands for the experimentally mole fraction solubility of Sinomenine Hydrochloride; $x_A$ stands for the molar concentration of ethanol in the mixed solvent. The relative standard uncertainty for pressure is 0.05, for temperature is 0.1 K, for ${\chi }_e$ is 0.01, and for $x_A$ is 0.005.

). The Sinomenine Hydrochloride samples were added to the mixed solvent in a 10 mL stoppered tube. They were placed in a thermostatic shaking box and shaken for 24 h to obtain a supersaturated solution. Then, the supersaturated solutions were put in a constant temperature water bath for 5 days, and the sample solution reached the solid–liquid equilibrium state at this temperature (the preliminary results showed that 24 h + 5 d was sufficient to reach the equilibrium condition). The supernatant was passed through a pre-warmed 0.22 μm PTFE syringe filter to obtain a particle-free, saturated solution of Sinomenine Hydrochloride. The saturated solutions were diluted 100 times, and then the High-Performance Liquid Chromatography (HPLC) was used to measure the concentration of Sinomenine Hydrochloride in the saturated solution.

The experiment was repeated three times under the same conditions to minimize the experimental errors, and the mean value was used as the final result to calculate the mole fraction solubility. The mole fraction solubility of Sinomenine Hydrochloride in different mixed solvents was expressed by ${\chi }_e$, and was calculated according to Equation (1). The initial molar concentration of ethanol in the mixed solvent was expressed by $x_A$, and was calculated according to Equation (2).

$${\chi }_e={\displaystyle \frac{m_1∕M_1}{m_1∕M_1+m_2∕M_2+m_3∕M_3}}$$

(1)

$$x_A={\displaystyle \frac{m_2∕M_2}{m_2∕M_2+m_3∕M_3}}$$

(2)

where m₁, m₂, and m₃, respectively, represent the mass of Sinomenine Hydrochloride, ethanol, and water; and M₁, M₂, and M₃, respectively, represent the molar mass of Sinomenine Hydrochloride, ethanol, and water.

2.4. Analytical Methods

The contents of Sinomenine Hydrochloride in the equilibrium mixture were determined by HPLC on a Diamonsil Plus C18-A, (4.6 mm × 250 mm, 5 μm) chromatographic column. Referring to the content determination method of Sinomenine Hydrochloride in the Chinese Pharmacopoeia (2020 Ed), with 0.78% sodium dihydrogen phosphate (mass ratio) as the mobile phase A and acetonitrile as the mobile phase B, it was eluted with mobile phase A/mobile phase B (88:12, volume percent) for 15 min [19]. The flow rate was 1 mL/min, the injection volume was 5 μL, the column temperature was 303 K, and the detection wavelength was 265 nm.

2.5. Powder X-Ray Diffraction

To assess potential solid-state transformations and the crystallinity of Sinomenine Hydrochloride during the experiments, the excess solid remaining in the suspension was characterized by powder X-ray diffraction (PXRD). PXRD patterns were collected on a Bruker D8 Advance instrument (Bruker AXS GmbH, Karlsruhe, Germany) using Cu Kα radiation (λ = 1.5406 Å) operated at 40 kV and 40 mA. Data were acquired over 2θ = 10–50° with a step size of 0.02° and a scan rate of 10° min⁻¹.

3. Result and Discussion

3.1. Experimental Results

3.1.1. PXRD Analysis

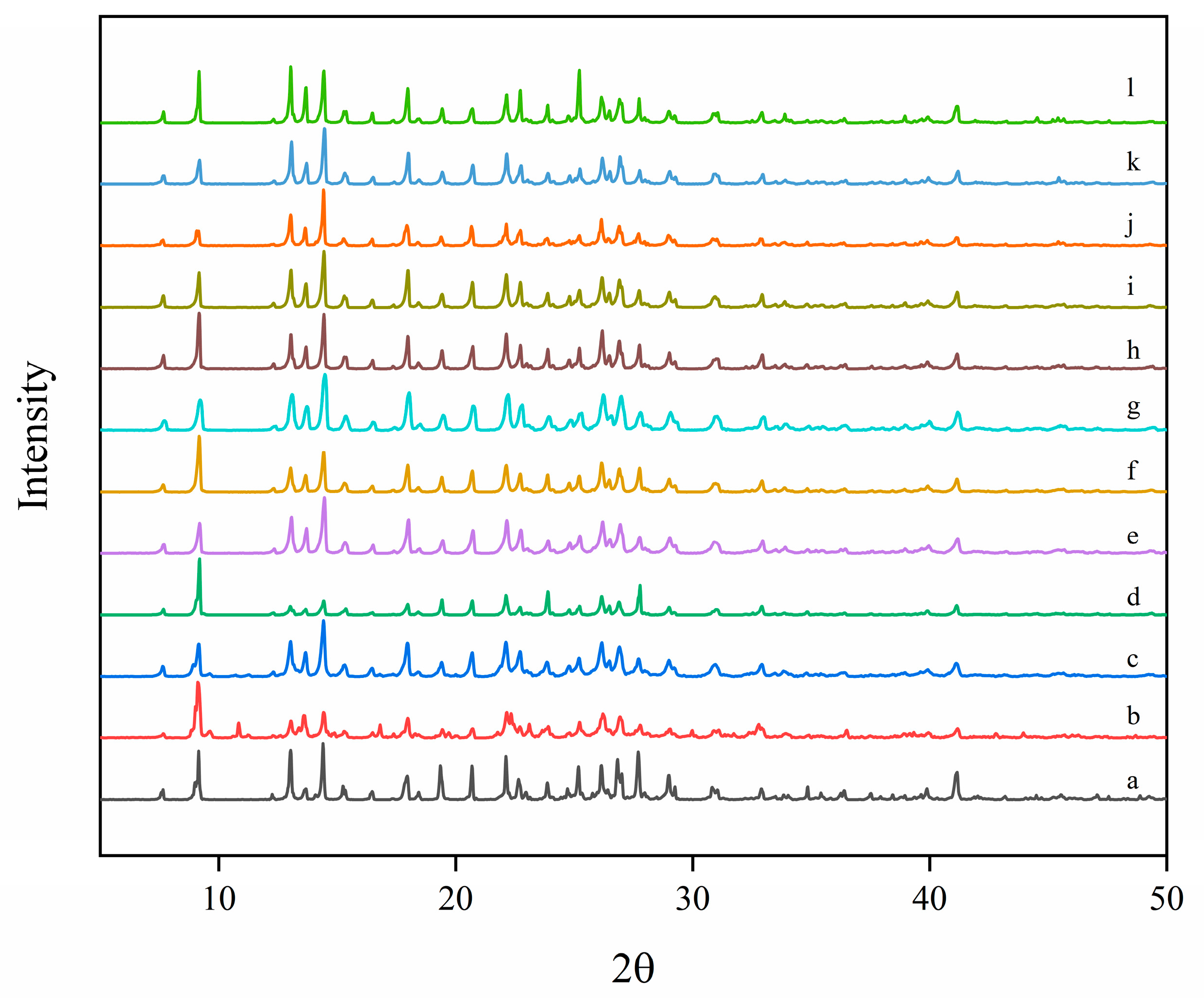
The PXRD patterns of the equilibrated bottom-phase solid of Sinomenine Hydrochloride and the neat material are shown in Figure 2. In both cases, peaks occur at the same characteristic 2θ positions (Figure 2). The coincidence of peak positions indicates that Sinomenine Hydrochloride remained in the same crystalline form throughout the experiments, with no transformation to polymorphic or amorphous phases.

3.1.2. Linear Relation Investigation

Sinomenine Hydrochloride was precisely weighed and dissolved in water, and the standard solutions of 2.00 × 10³ μg/ mL, 1.00 × 10³ μg/ mL, 5.00 × 10² μg/ mL, 2.50 × 10² μg/ mL, 1.25 × 10² μg/ mL, 62.50 μg/ mL, 31.25 μg/ mL were obtained. The peak area of Sinomenine Hydrochloride was detected by HPLC. Taking the peak area as Y and the concentration of Sinomenine Hydrochloride as X to carry out linear regression with Origin 9.0 software, the regression equation of Sinomenine Hydrochloride was obtained, Y = 3.000 × 10⁶ X − 7.426 × 10³ (r = 0.999). The results showed that the method could accurately quantify Sinomenine Hydrochloride in the concentration range of 0.03 mg/mL–2.00 mg/mL.

3.1.3. Solubility Data of Sinomenine Hydrochloride

The mole fraction solubility of Sinomenine Hydrochloride at different temperatures (283.15 K, 288.15 K, 293.15 K, 298.15 K, 303.15 K, 308.15 K) and different proportions of ethanol–water (0:10–10:0) mixed solvents is shown in Table 1. The results show that the mole fraction solubility of Sinomenine Hydrochloride in ethanol–water mixed solvent was affected by solvent composition and temperature change.

The solubility of Sinomenine Hydrochloride in pure water higher was than that in pure ethanol, and the solubility of Sinomenine Hydrochloride increased first and then decreased with the increase in the molar mass of ethanol in the ethanol–water solvent system. When the ratio of ethanol–water was 5:5 (by mass), the solubility value reached its maximum. The underlying mechanism may be that Sinomenine Hydrochloride is an ionic, strongly polar solute. Introducing a small amount of ethanol into water weakens bulk water structuring and modifies the local solvent microenvironment around the solute. Ethanol is enriched in the first solvation shell (preferential solvation), which lowers the solute activity coefficient and thus increases the mole fraction solubility. As the ethanol mole fraction increases further, the mixture dielectric constant drops and ionic hydration becomes less favorable; ion–dipole stabilization and dissociation are weakened, the activity coefficient rises, and the mole fraction solubility decreases. The interplay of these effects produces the observed maximum at $x_A$ ≈ 0.24–0.32 and is consistent with the minimum Gibbs free energy of dissolution (ΔG_d) inferred from our correlations.

In addition, the equilibrium solubility of the Sinomenine Hydrochloride was also affected by the temperature. It is clear that Sinomenine Hydrochloride had the lowest solubility value when the temperature was 283.15 K, and the solubility gradually increased as the temperature increased. These results indicate that the proper ratio of ethanol–water and temperature improved the solubility of Sinomenine Hydrochloride in the recrystallization process.

3.2. Solubility Data Correlation

Compared to the activity coefficient method, empirical equations do not require many thermodynamic parameters. These characteristics make them suitable for the solubility simulation calculation of some substances for which thermodynamic parameters are not easily obtained [20,21]. When the solubility is not known, the equilibrium solubility simulation with a high degree of fit is helpful to accurately predict the solubility of compounds.

In this study, the CNIBS/R-K model, Modified Apelblat model, Yaws model, and Apelblat–Jouyban–Acree model were used to correlate the equilibrium solubility data of Sinomenine Hydrochloride. The prediction ability of models was represented by the values of relative average deviation (RAD) and root mean square deviation (RMSD) [22]. The calculation of these values is represented in Equations (3) and (4).

$$RAD={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N\left(\left|{\displaystyle \frac{x_i^c-x_i^e}{x_i^e}}\right|\right)$$

(3)

$$RMSD={\left[{\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{\left(x_i^c-x_i^e\right)}^2\right]}^{{\displaystyle \frac{1}{2}}}$$

(4)

where $x_i^c$ represents the predicted value of the model; $x_i^e$ represents the measured value of the experiment; and N represents the number of data.

3.2.1. CNIBS/ R-K Model

When the solution is in an ideal state, the CNIBS/R-K model can be used to investigate the relationship between the solubility of solute and binary solvent systems at the same thermodynamic temperature, and was first proposed by Acree et al. [23,24]. The formula of the equation is shown in Equation (5).

$$ln{x}_e=x_{A}ln{\left(x_e\right)}_A+x_{B}n{\left(x_e\right)}_B+x_A{x}_B{\sum }_{i=0}^N{S}_i{\left(x_A-x_B\right)}^i$$

(5)

where $x_A$ is the mole fraction composition of ethanol in the solvent mixture and $x_B$ is the mole fraction composition of water in the solvent mixture.${\left(x_e\right)}_A$ is the mole fraction solubility of Sinomenine Hydrochloride in ethanol. ${\left(x_e\right)}_B$ is the mole fraction solubility of Sinomenine Hydrochloride in water. $x_e$ is the mole fraction solubility of Sinomenine Hydrochloride in the solvent mixture. $S_i$ is the model constant and N refers to the number of “curve-fit” parameters. The value of N is 2 and $x_B=1-x_A$. By substituting them into Equation (5), a new equation can be obtained [25].

$$ln{x}_e=ln{\left(x_e\right)}_B+\left(ln{\left(x_e\right)}_A-ln{\left(x_e\right)}_B+{(S}_0-S_1+S_2\right)x_A+\left({-S}_0+3S_1-5S_2\right){\left(x_A\right)}^2+\left(-{2S}_1+8S_2\right){\left(x_A\right)}^3+\left(-4S_2\right){\left(x_A\right)}^4$$

(6)

By introducing a constant term to Equation (6), it can be further simplified to produce Equation (7):

$$\mathit{ln}{\chi }_e=B_0+B_1 x_A+B_2 x_A^2+B_3{ x}_A^3+B_4{ x}_A^4$$

(7)

where $B_0$, $B_1$, $B_2$, $B_3$, and $B_4$ are the model parameters calculated through regression analysis.

By substituting the solubility data of Sinomenine Hydrochloride into Equation (7), some model parameters were obtained through precise calculation, and the specific values are listed in

Table 2. Parameter-fitting results of the CNIBS/R-K model for Sinomenine Hydrochloride at different temperatures.

T/K	Parameters of CNIBS/R-K Model
	B0	B1	B2	B3	B4	r	103 RAD	103 RMSD
283.15	−0.33	1.63	−4.68	5.38	−2.67	0.999	3.622	2.916
288.15	−0.30	1.57	−4.68	5.47	−2.69	1.000	1.114	0.909
293.15	−0.25	1.42	−4.43	5.39	−2.66	0.999	2.203	1.813
298.15	−0.23	1.30	−3.97	4.69	−2.25	0.998	3.043	2.636
303.15	−0.20	1.27	−4.25	5.58	−2.86	0.995	4.337	3.726
308.15	−0.18	1.12	−3.74	4.84	−2.39	0.995	4.622	4.079

. The smaller the values of RAD and RMSD, the better the predictive ability of the model. The R² of this model was not less than 0.990. All RAD values were less than 4.622 × 10⁻³, and all RMSD values were less than 4.079 × 10⁻³. They indicate that the model has a good predictive ability and can be used to predict the solubility of Sinomenine Hydrochloride in ethanol–water mixed solvents.

3.2.2. Modified Apelblat Model

For a binary mixed solid–liquid equilibrium system, the solubility can be expressed by Equation (8).

$${\chi }_e={\displaystyle \frac{f_e}{{\gamma }_e{f}_e^{\theta }}}$$

(8)

$f_e$ is the amount of solute in the solution; ${\gamma }_e$ is the activity coefficient of the solute; and $f_e^{\theta }$ is the standard fugacity. The fugacity ratio of the pure solute can be calculated by thermodynamic equation that is shown in Equation (9).

$$ln\left({\displaystyle \frac{1}{{\chi }_e{\gamma }_e}}\right)={\displaystyle \frac{{△}_{fus}H}{R{T}_t}}\left({\displaystyle \frac{T_t}{T}}-1\right)-{\displaystyle \frac{△C_P}{R}}\left({\displaystyle \frac{T_t}{T}}-1\right)+{\displaystyle \frac{△C_P}{R}}ln{\displaystyle \frac{T_t}{T}}$$

(9)

T is the absolute temperature; T_t is the triple point temperature of the solute, and the melting temperature is often used to replace the triple point temperature in practical calculation; ${△}_{fus}H$ is the Melting enthalpy of the solute;$△C_P$ is the hot melt difference of solid–liquid equal pressure; and R is the ideal gas constant.

When the solution is relatively dilute,${\gamma }_e$ can be regarded as the infinite dilution activity coefficient ${\chi }_e^{\theta }$. The relationship between the infinite dilution activity coefficient and temperature is shown in Equation (10):

$$\mathit{ln}{\chi }_e^{\theta }=A+B/T$$

(10)

Equations (8)–(10) are combined to obtain Equation (11).

$$ln{x}_e=\left[{\displaystyle \frac{{△}_{fus}H}{R{T}_t}}+{\displaystyle \frac{△C_P}{R}}\left(1+ln{T}_t\right)-A\right]-\left[\left({\displaystyle \frac{{△}_{fus}H}{R{T}_t}}+{\displaystyle \frac{△C_P}{R}}\right)T_t+B\right]{\displaystyle \frac{1}{T}}-{\displaystyle \frac{△C_P}{R}}lnT$$

(11)

Equation (11) can also be expressed as Equation (12) [26].

$$\mathit{ln}{\chi }_e=A+B/T+Cln\left(T\right)$$

(12)

where T is the thermodynamic temperature; and A, B, and C are the model parameters of Modified Apelblat model, and can be obtained by fitting the solubility data.

The Modified Apelblat model is mainly used to investigate the relationship between the solubility and thermodynamic temperature of a solute in an ideal solution.

The values of the model parameters obtained through calculation are shown in

Table 3. Parameter-fitting results of the Modified Apelblat model for Sinomenine Hydrochloride in ethanol–water mixed solvent.

${\mathit{x}}_{\mathit{A}}$	Parameters of Modified Apelblat Model
	A	B	C	r	103 RAD	103 RMSD
0.000	46.11	−2486.35	−6.67	0.986	6.089	2.718
0.033	10.85	−897.39	−1.41	0.970	7.066	3.694
0.072	38.60	−2117.35	−5.55	0.994	3.557	1.605
0.117	54.57	−2751.20	−7.98	0.993	3.049	1.385
0.171	40.87	−2078.20	−5.97	0.991	5.341	2.555
0.236	15.71	−926.80	−2.23	0.989	77.083	51.683
0.317	−7.09	90.03	1.18	0.994	1.503	0.866
0.419	−33.48	1245.26	5.12	0.980	3.512	1.664
0.553	−11.25	152.39	1.86	0.988	3.476	1.872
0.735	−90.12	3500.56	13.72	0.9991	4.363	2.294
1.000	−61.49	1727.16	9.69	0.969	1.966	8.880

. The R² of this model was not less than 0.939, which indicated that the result was strong. In addition, the RAD was less than 7.708 × 10⁻², and the RMSD was less than 5.168 × 10⁻², indicating that the prediction ability of the Modified Apelblat model was poorer than that of the CNIBS/R-K model.

3.2.3. Yaws Model

Like the Modified Apelblat model, the Yaws model is also used to investigate the relationship between the solubility and thermodynamic temperature of a solute in an ideal solution. A₁, B₁, and C₁ are the parameters of the model [27]. The equation is shown in Equation (13).

$$\mathit{ln}{\chi }_e=A_1+B_1/T+C_1/T^2$$

(13)

The values of model parameters obtained through calculation are shown in

Table 4. Parameter-fitting results of the Yaws model for Sinomenine Hydrochloride in ethanol–water mixed solvent.

${\mathit{x}}_{\mathit{A}}$	Parameters of Yaws Model
	A1	B1	C1	r	103 RAD	103 RMSD
0.000	−1.76	1407.48	−283,942.00	0.991	24.400	19.550
0.033	0.61	−3.07	−70,577.90	0.982	7.044	3.692
0.072	−1.31	1153.96	−240,690.00	0.996	3.571	1.608
0.117	−2.77	1951.94	−346,307.00	0.994	3.069	1.390
0.171	−2.00	1432.88	−258,132.00	0.994	3.072	1.337
0.236	−0.27	369.33	−94,166.30	0.993	2.889	1.244
0.317	1.34	−596.39	50,075.45	0.996	1.512	0.867
0.419	3.43	−1826.71	230,010.50	0.988	3.483	1.654
0.553	2.13	−954.31	82,250.02	0.993	3.473	1.871
0.735	8.56	−4643.34	604,018.80	0.994	4.317	2.277
1.000	8.09	−3952.86	416,046.30	0.982	18.999	8.845

. The R² of this model was not less than 0.964, the RAD was less than 2.440 × 10⁻², and the RMSD was less than 1.955 × 10⁻². The prediction ability of the Yaws model is not significantly different from that of the Modified Apelblat model.

3.2.4. Apelblat–Jouyban–Acree Model

The Apelblat–Jouyban–Acree model is obtained by combining the Modified Apelblat model and the Jouyban–Acree model. It is a three-dimensional model of solute solubility in binary solvents, solvent composition, and dissolution temperature [28] The equation is shown in Equation (14), where A₂, B₂, C₂, A₃, B₃, C₃, S₀, S₁, and S₂ are the parameters of the model.

$$ln{x}_e=x_A\left(A_2+{\displaystyle \frac{B_2}{T}}+C_{2}lnT\right)+x_B\left(A_3+{\displaystyle \frac{B_3}{T}}+C_{3}lnT\right)+{\displaystyle \frac{x_A{x}_B}{T}}{\sum }_{i=0}^N{S}_i{\left(x_A-x_B\right)}^i$$

(14)

After the equation fitting, the values of the parameters A₂, B₂, C₂, A₃, B₃, C₃, S₀, S₁, and S₂ are −86.24, 3121.73, 13.21, 43.08, −2170.28, −6.33, 0.98, −0.03, and 0.64, respectively. The r is 0.991. The RAD and RMSD values are 1.16 × 10² and 1.47 × 10², respectively. The prediction ability of the Apelblat–Jouyban–Acree model is poorer than that of the CNIBS/R-K model, when the solubility of Sinomenine Hydrochloride was measured in different ethanol–water mixed solvents within the temperature range of 283.15 K–308.15 K. 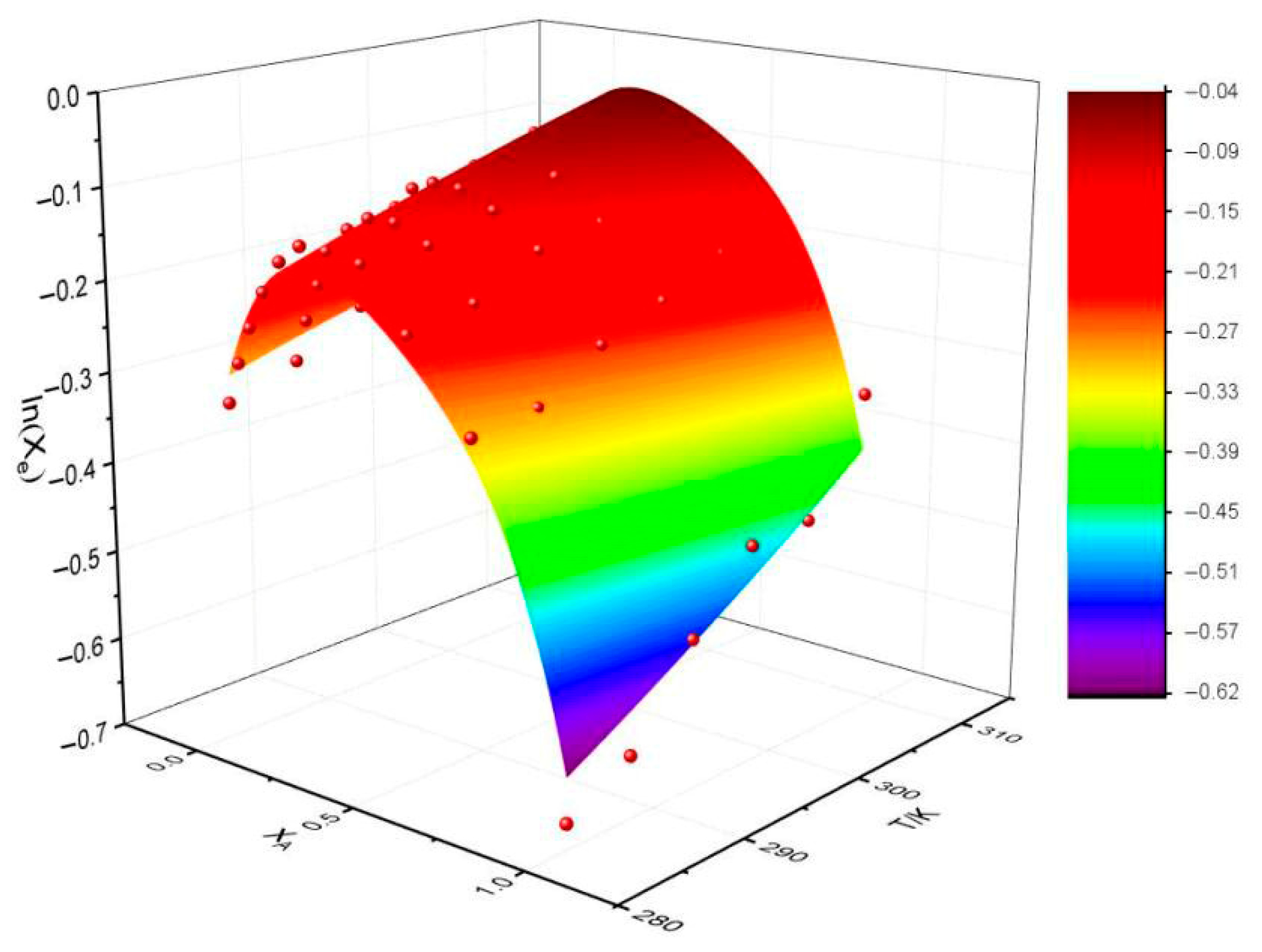Figure 3 shows the relationship between the predicted values of the model and the actual values. When the temperature is 298.15 K, the solubility of Sinomenine Hydrochloride falls on the curved surface, and the fitting result is the best. However, the rest of the points are outside of the surface. This result is consistent with poor RAD and RMSD values. Overall, the prediction ability of the CNIBS/R-K model is the best.

3.3. Thermodynamic Parameter Calculation

Melting enthalpy (Δ_fusH) and melting entropy (Δ_fusS) can be obtained using the Van‘t Hoff model in ideal solution [29], but the enthalpy and entropy of the mixtures cannot be ignored in non-ideal solution. Melting enthalpy is replaced by dissolving enthalpy (ΔH_d), and melting entropy is replaced by dissolving entropy (ΔS_d). The formula is shown in Equation (15) [30].

$$\mathit{ln}{x}_e=-{\displaystyle \frac{{\Delta H}_d}{RT}}+{\displaystyle \frac{{\Delta S}_d}{R}}$$

(15)

where R is gas molar constant; ΔH_d is the dissolving enthalpy of Sinomenine Hydrochloride; ΔS_d is the dissolving entropy of Sinomenine Hydrochloride; and T is thermodynamic temperature.

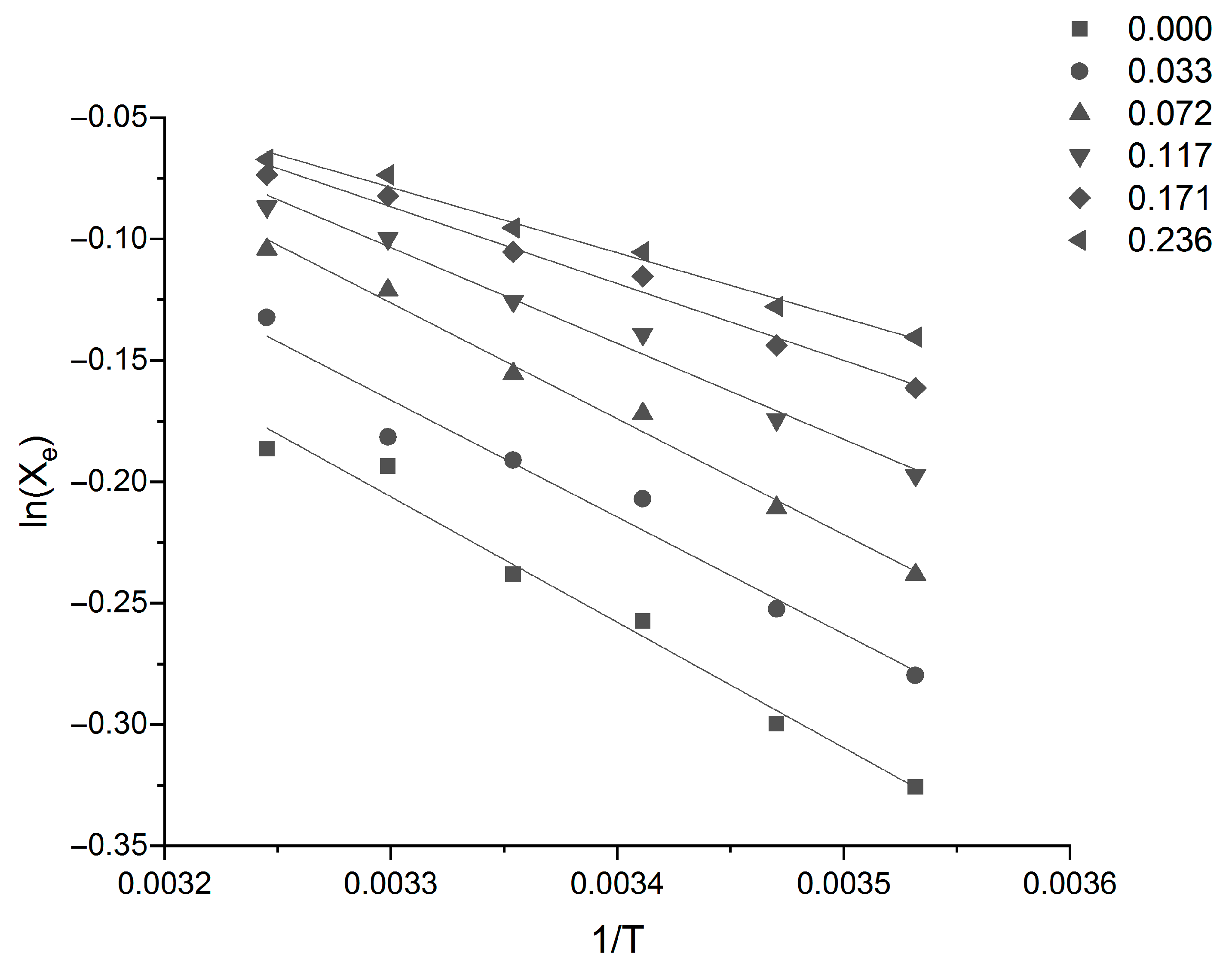
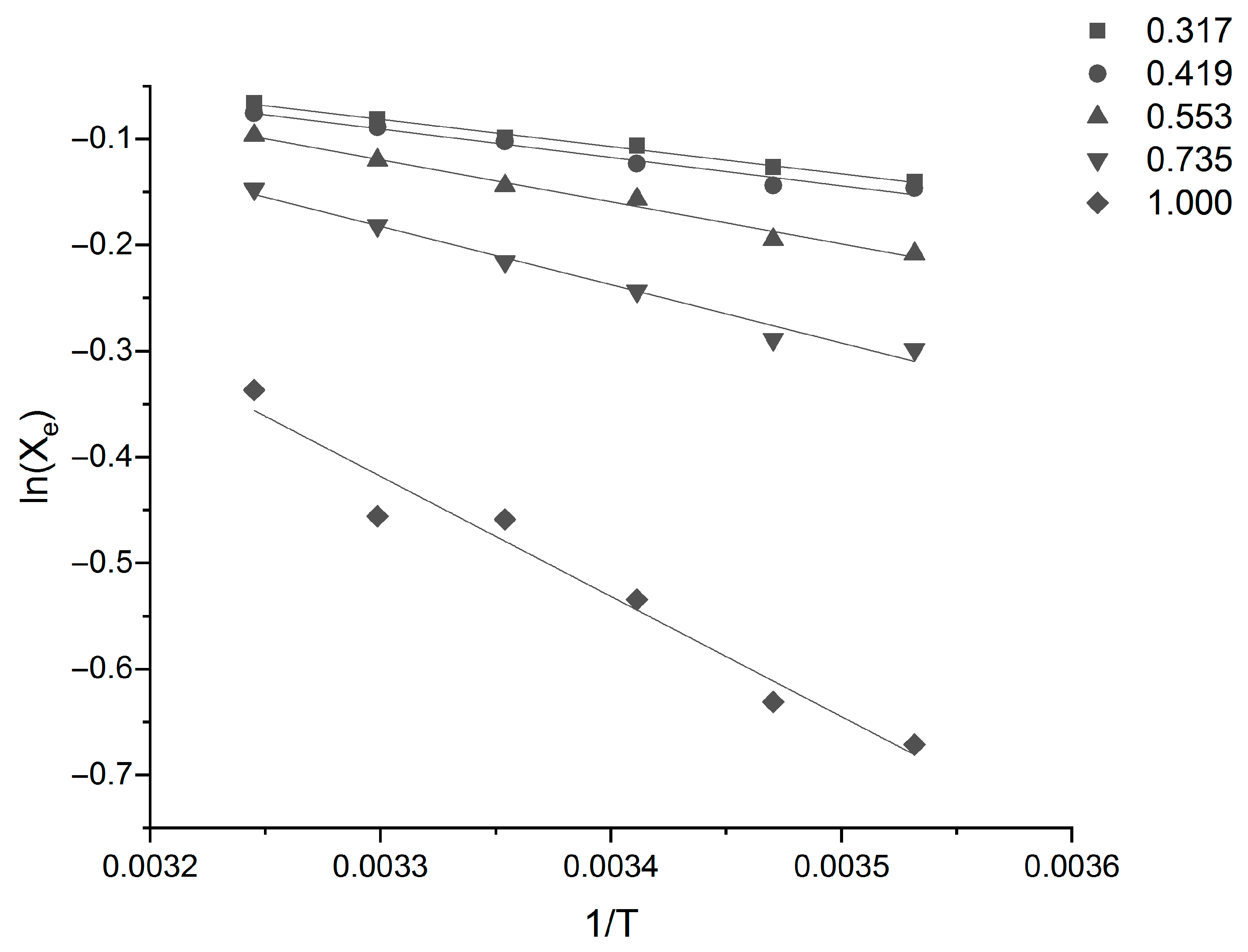
Equation (15) was used to fit the data, and the related thermodynamic parameters of Sinomenine Hydrochloride can be calculated from the linear fit of ln Xe against 1/T in Figure 4 and Figure 5. The values of the parameters are listed in

Table 5. Thermodynamic parameters of Sinomenine Hydrochloride in different ethanol–water mixed solvents at the mean temperature (Tmean = 295.65 K).

${\mathit{x}}_{\mathit{A}}$	ΔHd (kJ·mol−1) ± SE	ΔSd (J·mol−1·K−1) ± SE	ΔGd (kJ·mol−1) ± u
0.000	4.299 ± 0.300	12.471 ± 1.017	0.615 ± 0.009
0.033	3.991 ± 0.385	11.789 ± 1.304	0.509 ± 0.011
0.072	3.963 ± 0.187	12.030 ± 0.634	0.409 ± 0.005
0.117	3.268 ± 0.188	9.927 ± 0.637	0.336 ± 0.005
0.171	2.643 ± 0.166	7.998 ± 0.561	0.281 ± 0.005
0.236	2.238 ± 0.134	6.734 ± 0.452	0.248 ± 0.004
0.317	2.151 ± 0.092	6.418 ± 0.311	0.255 ± 0.003
0.419	2.213 ± 0.190	6.551 ± 0.643	0.278 ± 0.005
0.553	3.318 ± 0.197	9.960 ± 0.667	0.376 ± 0.006
0.735	4.592 ± 0.317	13.643 ± 1.073	0.562 ± 0.009
1.000	9.480 ± 0.932	27.810 ± 3.155	1.265 ± 0.027

SE(ΔH_d) and SE(ΔS_d) are the standard errors of the slope and intercept from the Van’t Hoff fit of ln x₁ vs. 1/T (OLS, n = 6). Standard uncertainty u(ΔG_d) is obtained by error propagation (including the covariance between ΔH_d and ΔS_d).

.

The changes in Gibbs free energy (ΔG_d) for the dissolution of Sinomenine Hydrochloride in different solvents were also calculated using the Gibbs−Helmholtz equation shown in Equations (16) and (17) [31].

$$△G=△H-T_{mean}△S$$

(16)

$$T_{mean}={\displaystyle \frac{n}{\sum _1^n\frac{1}{T_i}}}$$

(17)

where $T_i$ represents the thermodynamic temperature; and n represents the number of points of temperature. This experiment was conducted at six temperatures, so n = 6.

The results of the thermodynamic parameters, including ΔH_d, ΔG_d, and ΔS_d, for the dissolution of Sinomenine Hydrochloride in ethanol–water mixture at different temperatures, are presented in Table 5. All of the ΔH_d values are positive values, and the ΔH_d of Sinomenine Hydrochloride first decreases and then increases with increasing ethanol mole fraction in the ethanol–water solvent system. This shows that the dissolution behavior of Sinomenine Hydrochloride in ethanol–water mixed solvent is endothermic, and the interactions between solvent molecules and Sinomenine Hydrochloride molecules are much stronger than those between the solvent–solvent and solute–solute molecules. This is also the reason why the solubility of Sinomenine Hydrochloride in the mixed solvent increases with the increase in temperature. The ΔS_d values are positive in different proportions of ethanol–water mixed solvents. This indicates that the dissolution process of Sinomenine Hydrochloride is entropically driven in the solvent. In addition, all of the ΔG_d values are also positive values. This indicates that the dissolution process of Sinomenine Hydrochloride is apparently not spontaneous in the range of temperature (283.15 K–308.15 K). The greater the ΔG_d value, the weaker the solubility. The value of ΔG_d first decreases and then increases with increasing ethanol mole fraction in the ethanol–water mixed solvent, and the change trend is the same as the solubility data of Sinomenine Hydrochloride in this study, which indicates that the data obtained in this study is consistent with the theoretical values.

4. Conclusions

The solubilities of Sinomenine Hydrochloride in ethanol–water mixed solvent systems were determined at different temperatures (from 283.15 K to 308.15 K) under atmospheric pressure. The experimental results indicated that the solubility of Sinomenine Hydrochloride in pure water was higher than that in pure ethanol. When the proportion of ethanol in the mixed solvent increases, the solubility first increases and then decreases. Further, the solubility was the largest when the ethanol–water ratio was 5:5 (by mass), and the solubility increased with the increase in temperature. The results indicated that a proper ratio of ethanol–water and temperature improved the solubility of Sinomenine Hydrochloride in the process of Sinomenine Hydrochloride recrystallization. Sinomenine Hydrochloride can be dissolved at $x_A$ ≈ 0.24–0.32 and T = 308.15 K to exploit the solubility maximum, and then crystallization can be induced by cooling to 283.15 K and/or by shifting the solvent composition away from the maximum toward ethanol-richer mixtures. However, practical industrial implementation should still take all relevant conditions into comprehensive consideration. The CNIBS/R-K model, Modified Apelblat model, Yaws model, and Apelblat–Jouyban–Acree model were applied to mathematically describe the solubility of Sinomenine Hydrochloride. The CNIBS/R-K model has the best fitting effect, the maximum values of RAD and RMSD were 4.622 × 10⁻³ and 4.079 × 10⁻³, respectively. The dissolution of Sinomenine Hydrochloride ethanol–water mixed solvent systems was confirmed to be endothermic and not spontaneous based on the obtained thermodynamic parameters. This study can be regarded as the basic data of the separation and purification process of Sinomenine Hydrochloride.