A Study on Improving Separation Efficiency Through Weir Curvature Optimization in an FWKO with a Dish-Head Inlet

Abstract

The Free Water Knock Out (FWKO) vessel is a critical device in the oil sands treatment process, responsible for separating water, oil, and gas. This study investigates the gas–oil interface within the FWKO and analyzes the flow characteristics of the unresolved mixture near the interface. To enhance the separation efficiency by increasing the residence time of the mixture, a concave-shaped weir was introduced. Numerical simulations were conducted using ANSYS Fluent 2023 R1, applying the Volume of Fluid (VOF) model to capture the multiphase flow behavior. Optimization was performed using a genetic algorithm, and the optimal weir curvature with a minor radius of 0.017333 m and a major radius of 0.19032 m yielded the highest separation efficiency. The model incorporating the optimized weir demonstrated a 1.26% improvement in separation efficiency compared to the reference model, and a 2.13% improvement over the baseline model without curvature. These findings confirm that applying curvature to the traditionally flat weir can achieve higher separation efficiency. Moreover, improving separation efficiency through such a simple geometric modification demonstrates significant economic effectiveness.

1. Introduction

The demand for petroleum resources continues to rise, but conventional extraction methods alone are no longer sufficient to meet global energy needs. As a result, unconventional oil production technologies have gained attention, with oil sands plants in particular being highlighted due to their vast potential reserves and steadily increasing output. Oil sands are deeply buried in a highly viscous state, and extraction is typically carried out using the Steam-Assisted Gravity Drainage (SAGD) process. This method involves injecting high-temperature steam into the oil sands reservoir to reduce viscosity, thereby enabling oil recovery [1,2,3,4].

The SAGD process produces a mixture of water, oil, and gas, which must be separated to obtain clean oil. For this purpose, a Free Water Knock Out (FWKO) unit is used. The FWKO is a gravity separator that utilizes density differences to achieve phase separation. Its basic principle is that bitumen enters the vessel and, during its residence time, separates based on the density difference between oil and water. Oil accumulates at the top and is discharged over the weir.

The key factors determining the separation performance of the FWKO include residence time, oil–water interfacial area, density difference between the fluids, and the presence of slugging flow [5]. Without altering the inflow conditions or operating parameters, improving the separation efficiency through geometric modifications of the FWKO mainly involves increasing the residence time or expanding the interfacial area, thus allowing more time and space for phase separation.

Various studies have been conducted to enhance FWKO separation efficiency. Kang et al. [6] numerically demonstrated that changing the curvature and area of the vane distributor at the inlet alters the internal flow field, thereby improving oil–water separation. Son et al. [7] showed through CFD that increasing the thickness of a porous baffle reduces the average flow velocity and increases the residence time, enhancing separation performance. Some studies have attempted to improve separation efficiency by modifying the shape of the weir. Jung and Kim [8] numerically analyzed the impact of weir angle on separator performance, confirming that increasing the angle expands the oil–water interfacial area and improves separation. Yang et al. [9] investigated the effects of weir top geometry and fluid viscosity on separation efficiency, showing that changes in weir top shape increased the air–oil interface and prolonged residence time. However, while existing studies primarily focus on increasing interfacial area through weir shape modification, little attention has been given to controlling the flow of the mixture to increase residence time. Therefore, this study is not aimed at merely enlarging the interfacial area through weir geometry modification, but instead proposes a new design strategy that passively controls the flow of the unresolved mixture to increase residence time, thereby offering a differential contribution compared to previous research.

The genetic algorithm (GA) is a global optimization technique capable of finding effective solutions in complex and nonlinear search spaces. It is not constrained by the form or differentiability of the objective function and can flexibly handle various constraints and discrete variables. GA searches multiple candidate solutions simultaneously, making it less prone to local optima and highly suitable for solving multi-objective optimization problems through Pareto-optimal solutions. [10,11,12,13] Due to these advantages, GA has been widely applied in engineering optimization and is often combined with CFD. For example, Zheng et al. [14] integrated GA and CFD using a Windows socket-based platform to optimize the porosity distribution of multilayer porous inserts in tubular heat exchangers, demonstrating improved thermo-hydraulic performance. Similarly, Liu et al. [15] conducted a CFD-based NSGA-II multi-objective optimization of a plate-fin heat exchanger for hydraulic retarders, confirming enhanced heat transfer and reduced flow resistance.

This study aims to improve the separation efficiency of the FWKO by modifying the shape of the weir. First, the flow behavior at the gas–oil interface is examined, as the fluid in this region directly flows over the weir, making it a critical zone for separation. Then, design variables and candidate weir geometries are selected to enhance separation efficiency. Finally, the optimal weir shape is derived using a genetic algorithm.

2. Numerical Analysis

This section presents the geometry and mesh of the FWKO used for numerical simulation, followed by a description of the governing equations and boundary conditions applied in the analysis. Subsequently, the flow characteristics of the mixture at the gas–oil interface are examined, based on interface analysis, and an appropriate weir geometry is selected to enhance the separation efficiency.

2.1. Three-Phase Separator Model

As the analysis model, a horizontal-type FWKO was considered, as shown in Figure 1. Compared to vertical-type FWKOs, the horizontal configuration offers a longer residence time, leading to higher separation efficiency. To further improve performance, a porous baffle and a dish-head type inlet device were installed [16,17]. These components reduce the kinetic energy of the incoming mixture, enabling greater separation efficiency through extended residence time. The pressure vessel has a length of L = 1.63 m and a diameter of D = 0.3328 m.

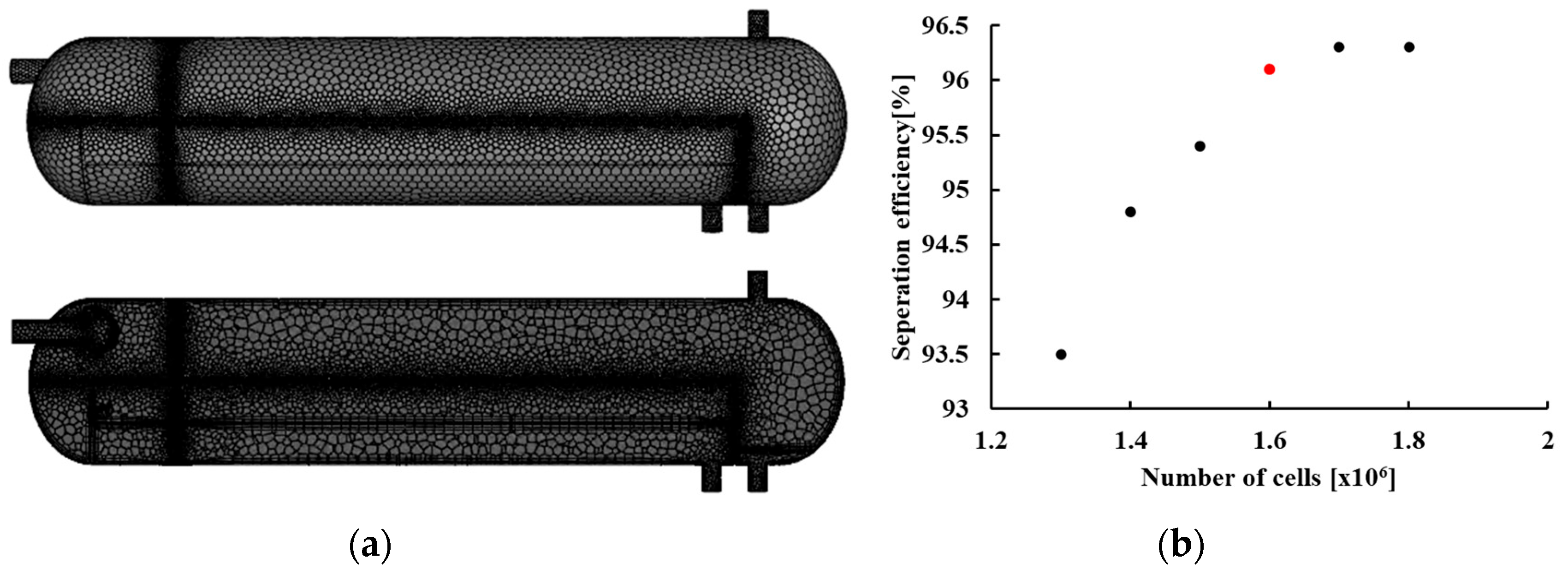
The mesh used in the simulation is shown in Figure 2. In the FWKO, the unresolved oil–water mixture crossing over the weir along with the oil at the gas–oil interface leads to a decrease in separation efficiency. Therefore, to accurately capture the behavior near the gas–oil interface, a refined mesh was applied in this region. As shown in the figure, the mesh is densely distributed around the perforated baffle and the gas–oil interface. In addition, to precisely analyze the effect of weir geometry on separation performance, the mesh near the weir was also densely generated. Based on the results of a grid dependency test (GDT), the total number of mesh elements was determined to be 1.6 million. The GDT results are also presented in Figure 2, where the optimal mesh number is indicated in red. The minimum orthogonal quality is 0.3, and the maximum skewness is 0.85. The Y⁺ value for evaluating near-wall viscous flow behavior in the turbulence model is 1.0308.

2.2. Equations

In this study, numerical analysis was performed using the commercial software ANSYS Fluent 2023 R1. For turbulence modeling, the realizable k-ε model was employed, and to simulate multiphase flow, the volume of fluid (VOF) method based on the Eulerian–Eulerian approach was applied. The VOF model is a widely used multiphase flow technique for tracking the interface between immiscible fluids. It enables accurate tracking of the free surface based on the volume fraction in each cell without requiring mesh deformation, ensuring high numerical stability. This method is effectively applied to a variety of engineering problems such as wave motion, droplet formation, and free-surface flows [18,19]. The following equations represent the governing equations used in the numerical simulation.

The continuity equation for each phase _q is expressed as follows. Here, ${\alpha }_q$ denotes the volume fraction of phase $q$, ${\rho }_q$ represents the density of phase $q$, and ${\mathrm{v}}_q$ indicates the velocity vector of phase q.

$${\displaystyle \frac{\partial }{\partial t}}\left({\alpha }_q{\rho }_q\right)+\nabla ·\left({\alpha }_q{\rho }_q{\mathbf{v}}_{q}k\right)=0$$

(1)

The momentum equation for each phase is expressed as follows. Here, $\mathrm{p}$ denotes the pressure, ${\tau }_q$ is the viscous stress tensor, $\mathbf{g}$ is the gravitational acceleration, and ${\mathrm{F}}_q$ represents the interfacial interaction force between phases.

$${\displaystyle \frac{\partial }{\partial t}}\left({\alpha }_q{\rho }_q{\mathbf{v}}_q\right)+\nabla ·\left({\alpha }_q{\rho }_q{\mathbf{v}}_q{\mathbf{v}}_q\right)=-{\alpha }_q\nabla \mathrm{p}+\nabla ·\left({\alpha }_q{\tau }_q\right)+{\alpha }_q{\rho }_q\mathbf{g}+{\mathbf{F}}_q$$

(2)

The surface tension model is considered as an additional term in the VOF method, and the surface tension force can be expressed as follows. Here, $\sigma$ is the surface tension coefficient, and ${\kappa }^{\prime }$ denotes the curvature.

$${\mathbf{F}}_{surface}=\sigma {\kappa }^{\prime }\nabla {\alpha }_q$$

(3)

In the realizable k-ε model, the transport equations for the turbulent kinetic energy (k) and the turbulent dissipation rate (ε) are given as follows. Here, ${\mu }_t$ is the turbulent viscosity, $G_k$ is the production term of turbulent kinetic energy, $G_b$ is the buoyancy term, ${\sigma }_k$ and ${\sigma }_{\epsilon }$ are empirical turbulent model constants, $C_1$ and $C_2$ are empirical coefficients, and S denotes the magnitude of the strain rate tensor.

$${\displaystyle \frac{\partial }{\partial t}}\left(\rho k\right)+\nabla ·\left(\rho k\mathbf{v}\right)=\nabla ·\left({\displaystyle \frac{{\mu }_t}{{\sigma }_k}}\nabla k\right)+G_k+G_b-\rho \epsilon$$

(4)

$${\displaystyle \frac{\partial }{\partial t}}\left(\rho \epsilon \right)+\nabla ·\left(\rho \epsilon \mathbf{v}\right)=\nabla ·\left({\displaystyle \frac{{\mu }_t}{{\sigma }_{\epsilon }}}\nabla \epsilon \right)+C_1{S}_{\epsilon }-C_2\rho {\displaystyle \frac{{\epsilon }^2}{k+\sqrt{\nu \epsilon }}}$$

(5)

In multiphase flow using the VOF method, the volume fraction tracking equation is expressed as follows.

$${\displaystyle \frac{\partial {\alpha }_q}{\partial t}}+\mathbf{v}·{\nabla \alpha }_q=0$$

(6)

2.3. Boundary Conditions

In the FWKO, a mixture of water, oil, and air enters through the inlet, and each phase is discharged through its designated outlet. The physical properties of each phase are presented in

Table 1. Material properties.

Phase	Density [kg/m3]	Viscosity [Pa∙s]	Surface Tension [N/m]
Gas	1.225	1.7894 × 10−5	-
Oil	830	0.1	0.027 (with gas)
Water	998.2	0.001003	0.072 (with gas) 0.04 (with oil)

. Under the FWKO operating conditions considered in this study (approximately 100–120 °C), the interfacial tension significantly decreases as temperature increases, making the local adhesion effects negligible compared with viscous and gravitational forces. In addition, the Bond number is sufficiently large, confirming that gravitational forces dominate over interfacial tension. Therefore, the wall-adhesion effect was neglected in this work, consistent with prior studies [20] and with the general modeling practice for FWKO.

At the inlet where the mixture enters, the flow velocity was calculated and set to satisfy 60 BPD with an SOR of 2.2. The air outlet was defined with a gauge pressure of 0, while the oil and water outlets were assigned constant pressure values to simulate the effect of valves installed in actual FWKO systems for maintaining the interface level. According to Behin and Azimi [21], the highest separation efficiency is achieved when the oil–water interface is maintained at half the diameter of the vessel, which was reflected in the boundary condition settings. Detailed values are provided in

Table 2. Boundary conditions.

BC	Phase	Variable	Value
Inlet	Mixture	Velocity	0.31056 m/s
Outlet	Gas	Gauge pressure	0 Pa
	Oil	Static pressure	677.44 Pa
	Water	Static pressure	1983.78 Pa

.

To facilitate faster convergence, initial conditions were defined using patching, as shown in Figure 3. The water region was initialized from the bottom of the vessel up to half the height of the weir, while the oil region was set directly above the water region, extending up to the full height of the weir. Furthermore, to avoid backflow of oil at the oil outlet during the initial stage of the simulation, the outlet region was also patched accordingly.

2.4. Analysis of the Gas–Oil Interface

In this section, a numerical simulation was performed on the FWKO model without any curvature applied to the weir, based on the conditions described earlier. The gas–oil interface behavior was examined accordingly. To validate the accuracy of the simulation results, a comparison was made with a previous study [20] that analyzed separation efficiency under the same FWKO geometry but with different baffle designs. The reference study [20] validated its numerical model using experimental data from an earlier work, thereby providing a reliable basis for comparison. The simulation conducted under identical conditions in the present study showed minimal deviation in separation efficiency compared to the prior study, confirming that the present numerical model was qualitatively validated.

Flow behavior within the FWKO was observed over a simulation time of 800 s. The separation efficiency ($\eta$) was calculated using the average values from 700 to 800 s, as expressed in Equation (9). Here, N represents the number of time steps between 700 and 800 s, ${\dot{m}}_{oil}$ is the mass flow rate of oil at the oil outlet, and ${\dot{m}}_{water}$ is the mass flow rate of water discharged through the oil outlet. The separation efficiency for the model without weir curvature was found to be 95.31%.

$$\eta ={\displaystyle \frac{1}{N}}\sum _{t=700}^{800}{\displaystyle \frac{{\dot{m}}_{oil}}{\left({\dot{m}}_{oil}+{\dot{m}}_{water}\right)}}$$

(7)

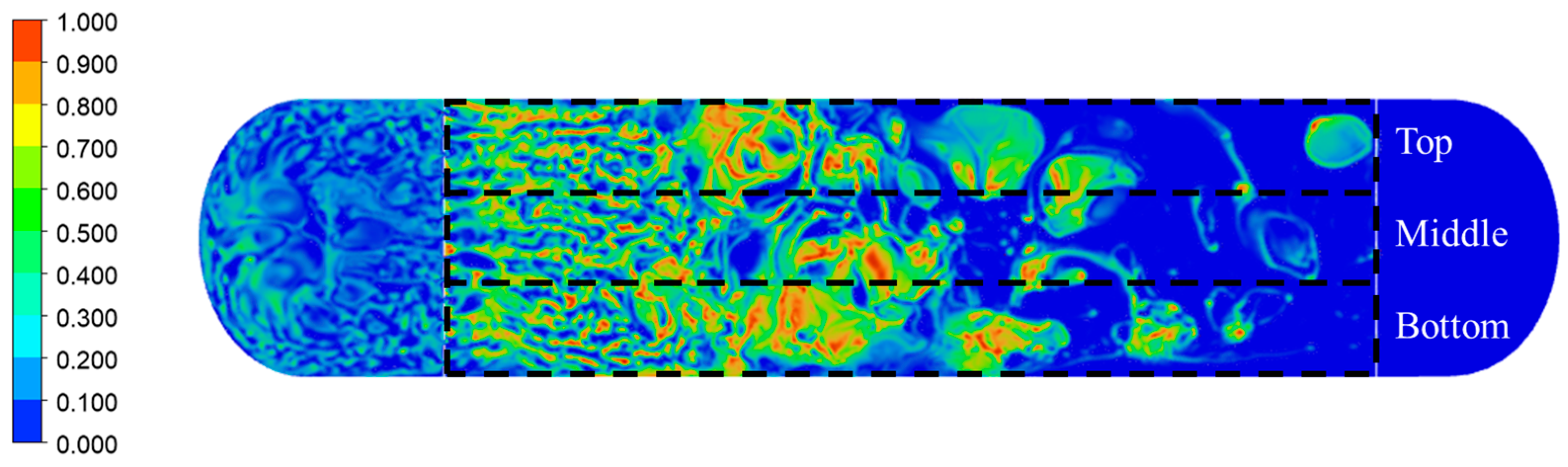
As shown in Figure 4, in the FWKO without weir curvature, the unresolved oil–water mixture flows along the wall and exits toward the oil outlet at the gas–oil interface. It was observed that the average water content in the mixture near the wall was approximately 15.6% higher than that at the center of the interface, as shown in

Table 3. Water volume fraction distribution at the gas–oil Interface.

Location	Water Volume Fraction		Difference [%]
Top	0.2467	0.2520 (average)	15.60%
Bottom	0.2573
Middle	0.2126

, indicating significant phase imbalance and incomplete separation near the boundary.

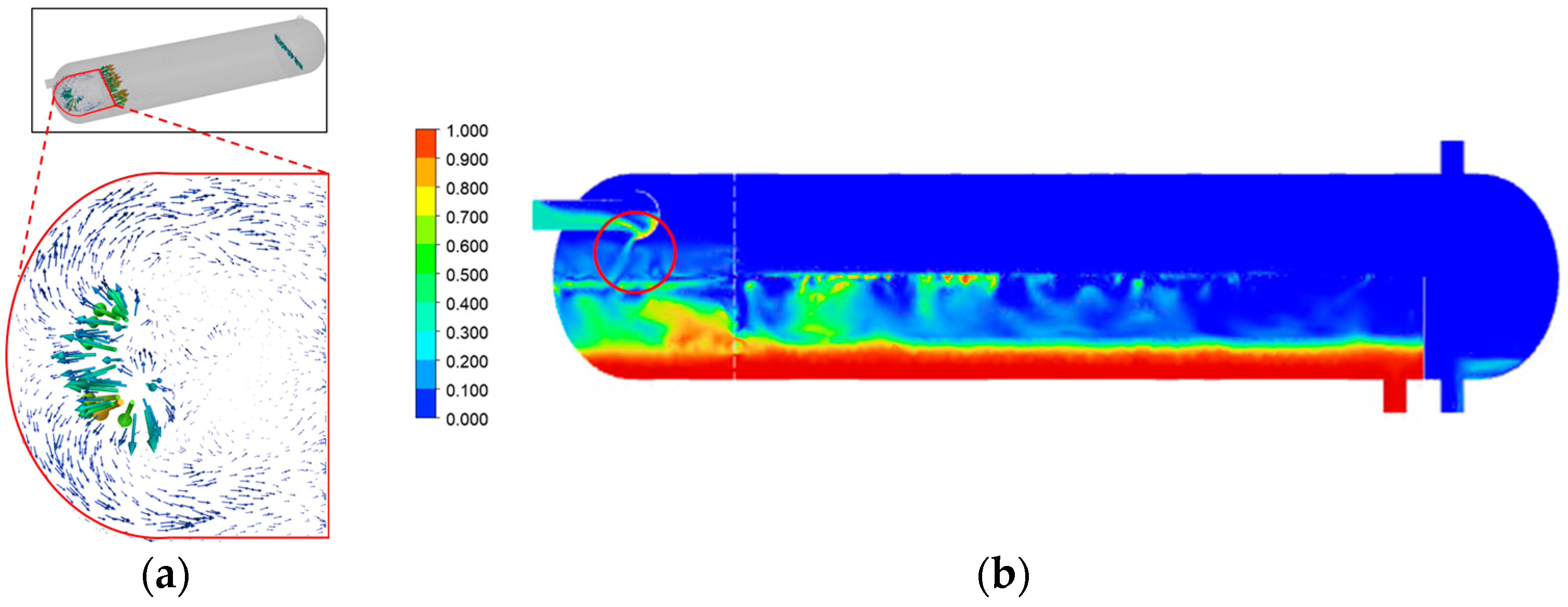
Figure 5a shows the velocity vectors of the incoming mixture at the inlet. As seen in Figure 5a,b, the mixture enters, collides with the dish head(as indicated by the red circle in Figure 5b), and then strikes the front wall of the FWKO before flowing along the wall surface. This indicates that the flow behavior of the mixture inside the FWKO is significantly influenced by the inlet configuration. When the mixture enters in the direction of the front wall, as in the case with the dish head inlet, it flows along the wall surface, resulting in wall-guided flow within the FWKO.

This section confirms through gas–oil interface analysis that the unresolved mixture predominantly remains near the wall region of the interface. Based on this observation, introducing curvature to the weir to raise its height near the wall can help control the wall-guided flow of the mixture. This is expected to increase residence time and contribute to improved separation efficiency.

3. Optimization

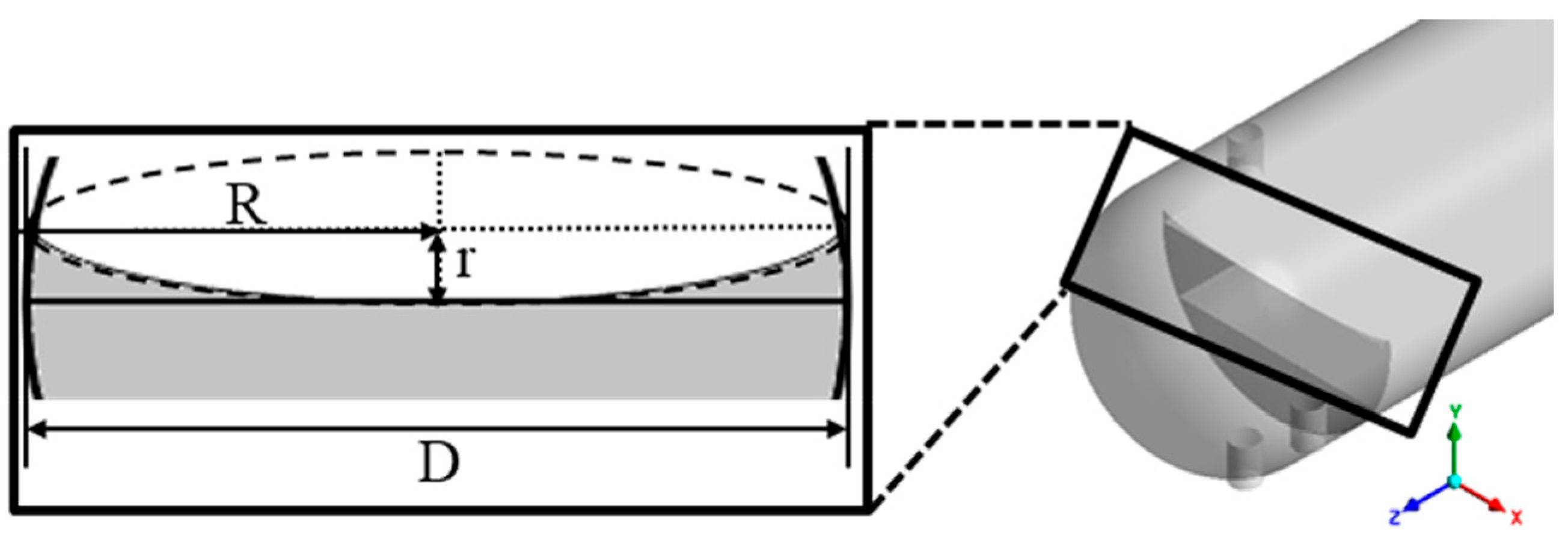
This section presents the optimization of a concave weir shape based on the previous analysis. To identify the optimal curvature of the concave weir, an elliptical profile was applied. The minor radius r, which determines the height near the wall, and the major radius R, which defines the curvature, were selected as the geometric design variables. Equation (8) represents the equation of an ellipse, and Equation (9) describes the curvature $\kappa$ as a function of position. As can be seen from both equations, the curvature at each point on the ellipse is determined by the lengths of the major and minor axes.

$${\displaystyle \frac{x^2}{R^2}}+{\displaystyle \frac{y^2}{r^2}}=1$$

(8)

$$\kappa ={\displaystyle \frac{r^2·R^2}{{\left(R^2{y}^2+r^2{x}^2\right)}^{3/2}}}$$

(9)

The weir geometry was designed by placing an ellipse with major radius R and minor radius r tangent to the top surface of the weir. The ellipse was trimmed at the intersection with the vessel wall, resulting in increased weir height near the wall, as shown in Figure 6.

In this section, the optimization of the major radius R and the minor radius r is carried out to achieve the highest separation efficiency of the FWKO. Before proceeding with the optimization, a reference model was analyzed by setting the major radius R to 0.1664 m, which is half the diameter of the FWKO vessel, and the minor radius to 0.02 m. Numerical simulation was then performed based on these parameters.

3.1. Design of Experiment (DoE)

Next, a design of experiments (DoE) was conducted to examine the correlation between the design variables $R$ and $r$ and the separation efficiency, with the goal of identifying an optimal design point. The DoE type was Latin hypercube sampling (LHS) with CCD (Central Composite Design) samples. The LHS method is particularly effective for simulations with high experimental or computational costs, as it ensures a well-distributed sampling with fewer points compared to traditional grid-based methods, enabling efficient experimental planning [22,23,24]. The CCD-based DoE generates y sample points according to the number of design variables k′, as described in Equation (10). Based on the reference values of R = 0.1664 m and r = 0.02 m, a total of 9 design combinations were created, as shown in

Table 4. DoE results at the design points.

Case	R [m]	$\mathbf{r} \left[\mathbf{m}\right]$	$\mathit{\eta }$
1	0.18167	0.016667	0.9646
2	0.19167	0.025556	0.9653
3	0.17167	0.012222	0.9537
4	0.18833	0.03	0.9460
5	0.175	0.043333	0.9515
6	0.19833	0.021111	0.9590
7	0.185	0.047778	0.9348
8	0.195	0.038889	0.9486
9	0.17833	0.034444	0.9567

. A constraint was imposed to ensure that R does not fall below 0.1664 m, the radius of the FWKO vessel.

$$y=2^{k\prime }+2k^{\prime }+1$$

(10)

3.2. Response Surface Method (RSM)

The response surface methodology (RSM) was used to approximate the relationship between separation efficiency and the design variables based on data obtained from numerical simulations. Among various RSM techniques, non-parametric regression (NPR) was adopted in this study. NPR utilizes kernel functions to estimate values based on local information, offering the advantage of smoothly connecting data and effectively predicting function values at specific points [25,26,27]. As shown in the graph in Figure 7a, the predicted values obtained using NPR are plotted against the observed values from numerical simulations. The close alignment of the data points along the diagonal indicates that the NPR model provides reliable predictions for the present analysis.

In addition, quantitative indicators related to model reliability were evaluated. The coefficient of determination (R²) was found to be 0.999 (best value = 1), and the root mean square error (RMSE) was 0.0003 (best value = 0), further confirming the high accuracy and reliability of the model.

The sensitivity analysis results using NPR are presented in Figure 7b. In the graph, the horizontal axis represents the normalized values of the input variables (scaled relative to their full range), and the vertical axis indicates the separation efficiency. As explained in Section 3.1, since R cannot be smaller than the radius of the FWKO vessel, only values above 0.5 (represented by the dotted line) are meaningful. R shows a nonlinear trend, initially decreasing and then increasing. Similarly, $r$ also exhibits a non-monotonic behavior, following a curve that decreases and then rises. These results indicate that both variables have a nonlinear relationship with separation efficiency, rather than a simple linear one. Based on this, it can be inferred that the optimal value of $R$ likely exists in the region greater than the reference value of 0.1664 m, while the optimal value of $r$ is likely to be found in a region smaller than the reference value of 0.02 m.

3.3. Genetic Algorithm

To optimize the weir geometry, the screening method based on a genetic algorithm was applied. The objective was to maximize separation efficiency, with the constraints set as separation efficiency < 1, $r$ < 0.1664 m, and $R$ > 0.1664 m. The optimization predicted the optimal values of $r$ and $R$ to be 0.017333 m and 0.19032 m, respectively, with a separation efficiency of 97.51%. To validate the result, a numerical simulation was performed under the same conditions, yielding an actual separation efficiency of 97.34%. The prediction error was only 0.17%, confirming the high accuracy. Compared to the reference model, the optimized model showed a 1.26% improvement in separation efficiency.

Table 5. Comparison of five models’ results.

Case	$\mathit{\eta }$	Difference [%]	$\mathbf{Curvature} \left[{\mathbf{m}}^{-1}\right]$
Model without curvature	0.9531	-	-
Reference model	0.9613	0.860	416
Optimized model	0.9734	2.13	633
Model with the smallest curvature (Case 7)	0.9348	1.92	81
Model with the largest curvature (Case 3)	0.9537	0.0630	1149

compares the non-curved model, reference model, optimized model, and the models with the smallest and largest curvature from the DoE results. The “difference” column shows the percentage change in separation efficiency relative to the non-curved model, and the final column lists the curvature measured at the point on the weir closest to the center of the ellipse.

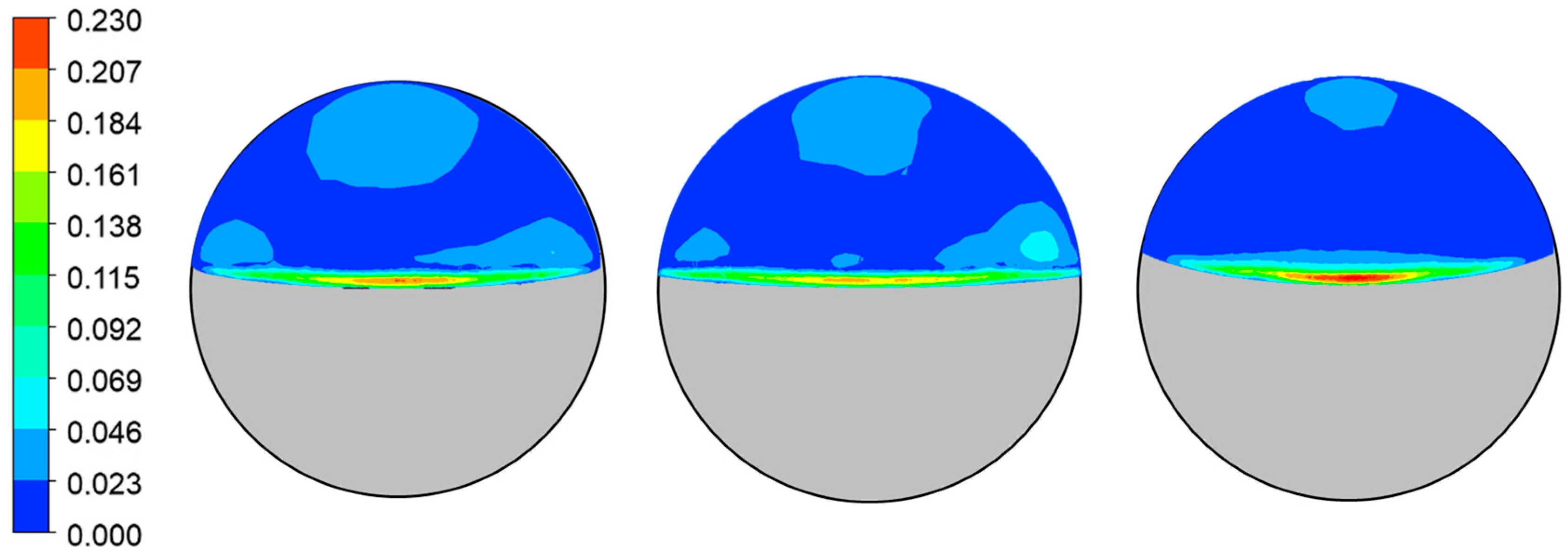
The analysis shows that as curvature increases (the weir becomes more concave), separation efficiency initially improves and then drops sharply. The improvement occurs because the curved weir redirects the flow along the gas–oil interface, increasing residence time. The subsequent decline in efficiency is due to the narrowed flow passage above the weir caused by excessive curvature, which accelerates the flow and results in the unresolved mixture exiting before sufficient separation occurs. Figure 8 presents velocity contours over the top of each weir, with the gray region indicating the weir. Case 7, which had the lowest separation efficiency, shows relatively high velocity over the weir.

To better examine the effect of weir curvature, Case 3 from the DoE, which had the largest curvature (most gradual slope), was analyzed. The curvature was 1149 [m⁻¹], and the separation efficiency was 95.37%. This result indicates that higher curvature does not always lead to better separation. As seen in the non-curved model, the presence and proper design of curvature are critical factors, and optimal separation performance can be achieved by selecting an appropriate curvature.

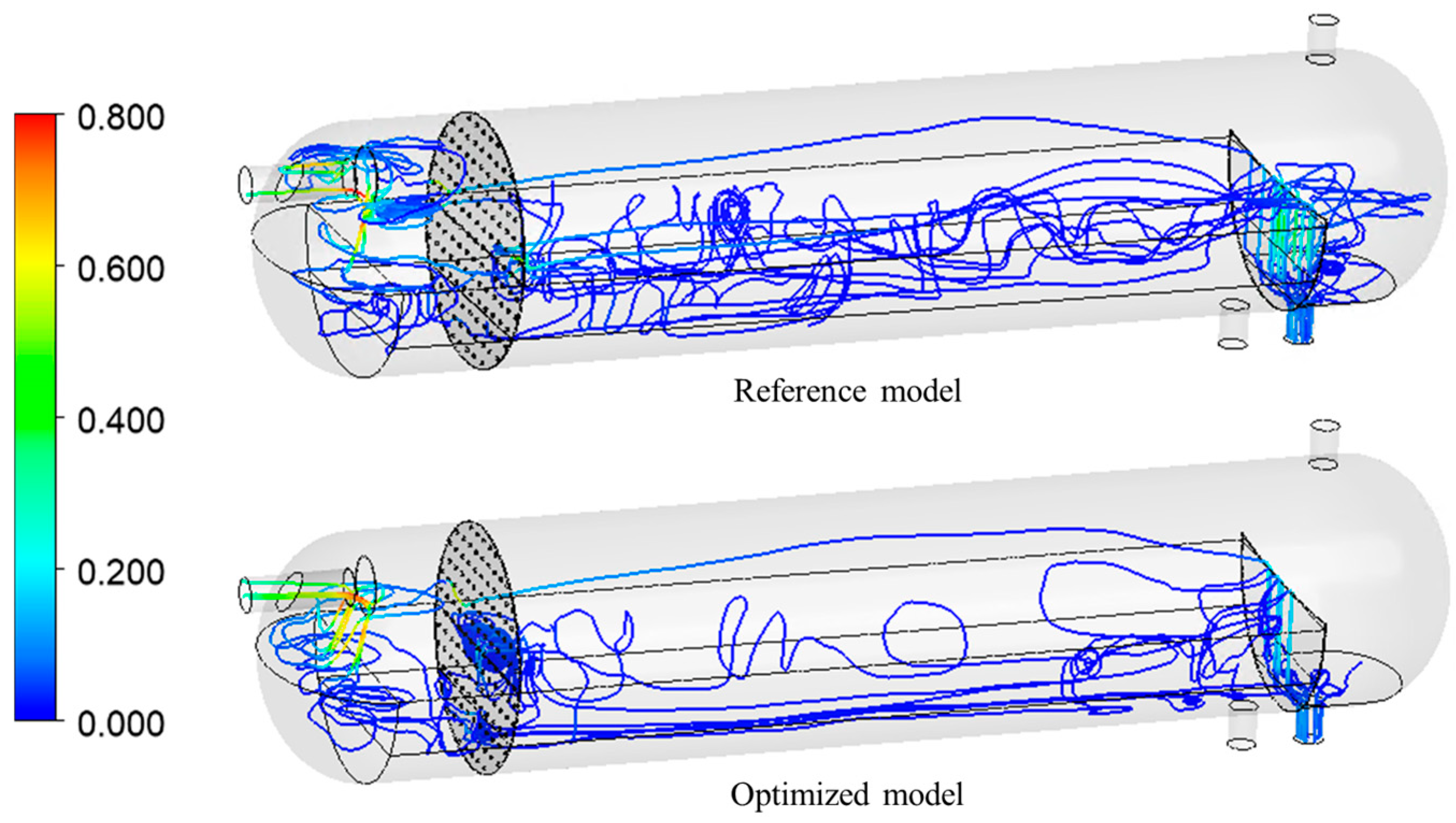
Figure 9 presents the velocity streamlines of both the reference and optimized models. In the reference model, the streamlines are highly intertwined and chaotic, indicating that the flow is unstable and strongly mixed inside the FWKO. Such disordered motion increases interphase mixing, thereby lowering the stability of the oil–water interface and reducing the separation efficiency. In contrast, the optimized model exhibits relatively straight and stable streamlines directed toward the outlet, demonstrating that the flow is more uniform and less turbulent. This streamlined flow reduces unnecessary mixing, enhances interface stability, and ultimately leads to improved separation performance compared to the reference model.

Finally, Figure 10 compares the mixture residence time and turbulence intensity near the weir for the reference and optimized models. The residence time was measured based on the point at which the mixture first crossed the weir. In the optimized model, the residence time increased from 243 s to 250 s, a gain of 7 s. This indicates that the change in weir curvature altered the flow structure at the gas–oil interface, allowing the mixture to remain inside the FWKO for a longer duration. The increase in residence time contributed to improved flow stability and a reduction in turbulence intensity. Specifically, the turbulence intensity measured just before the weir was noticeably lower in the optimized model compared to the reference model. According to Kim [20], turbulence intensity plays a critical role in promoting oil–water mixing inside the FWKO. As turbulence weakens, interphase mixing is suppressed and a more distinct interface can form. Therefore, the observed increase in residence time and corresponding reduction in turbulence intensity in the optimized model indicate enhanced interface stability, which ultimately supports improved separation efficiency.

4. Conclusions

In this study, the flow characteristics at the gas–oil interface were first analyzed to improve the separation efficiency of the FWKO. The analysis revealed that due to the dish-head inlet configuration, the unresolved mixture predominantly flows along the vessel wall. Based on this finding, curvature was introduced to the weir to increase its height near the wall, thereby redirecting the wall-guided flow and increasing the residence time of the mixture. For optimal design, the major and minor radii ($R, r$) of the elliptical weir were selected as design variables, and nine design points were generated using Latin hypercube sampling (LHS)-based DoE. Sensitivity analysis and optimal point identification were conducted using non-parametric regression (NPR) and the screening method. As a result, the model incorporating the optimized weir curvature showed improvements in separation efficiency of 1.26% compared to the reference model, 2.13% compared to the non-curved baseline model, and 3.97% compared to the lowest-efficiency design point. It was also found that separation efficiency does not follow a simple linear trend with curvature but is instead influenced by a nonlinear interaction between flow deflection intensity and velocity changes. These results provide a practical design strategy for improving separation performance through internal flow control in FWKO systems. In particular, under dish-head inlet configurations where the unresolved mixture predominantly flows along the vessel wall, moderately increasing the wall-side curvature provides an effective strategy to stabilize the gas–oil interface and secure sufficient residence time, thereby improving separation efficiency. The behavior of the mixture at the gas–oil interface is affected by various factors, such as the geometry and operating conditions of the FWKO, and thus the weir curvature cannot be determined as a fixed value. Hence, the curvature optimization strategy proposed in this study is recommended for practical FWKO design. This study demonstrates the effectiveness of coupling CFD with optimization techniques, offering a scalable approach for other multiphase separation systems in the oil sands industry and beyond.