Vapor Liquid Equilibrium Measurement and Distillation Simulation for Azeotropic Distillation Separation of H₂O/EM Azeotrope

Abstract

Since H₂O and Ethylene Glycol Monomethyl Ether (EM) form a minimum-boiling azeotrope, 1-pentanol, 1-hexanol, and 1-heptanol are selected as entrainers to separate the azeotropic mixture (H₂O/EM) using azeotropic distillation. The binary vapor liquid equilibrium (VLE) data were determined at 101.3 kPa, including H₂O/EM, EM/1-pentanol, EM/1-hexanol, EM/1-heptanol, H₂O/1-pentanol, H₂O/1-hexanol and H₂O/1-heptanol. Meanwhile, the Herington area test was used to validate the thermodynamic consistency of the experimental binary data. The VLE data for the experimental binary system were analyzed using the NRTL, UNIQUAC, and Wilson activity coefficient models, showing excellent agreement between predictions and measurements. Finally, molecular simulations were employed to calculate interaction energies between components, providing insights into the VLE behavior. The azeotropic distillation process was simulated using Aspen Plus to evaluate the separation performance and determine the optimal operating parameters. Therefore, this study provides guidance and a foundational basis for the separation of H₂O/EM systems at 101.3 kPa.

1. Introduction

EM, also known as methyl cellosolve, is an important chemical raw material [1], Due to the presence of both hydrophobic and hydrophilic functional groups in this compound, it is widely utilized in diverse industrial and commercial applications, including household products, paints, inks [2], coatings, cleaning solutions and biochemical applications [1,3]. Since the H2O/EM system forms a completely miscible binary azeotrope, specialized distillation methods must be employed for separation, including extractive distillation [4,5], azeotropic distillation [6,7], and salting-out distillation [8]. In this study, 1-pentanol, 1-hexanol, and 1-heptanol were selected as azeotropic agents to separate the H₂O/EM azeotropic mixture. The advantages of azeotropic distillation in this separation process lie in its ability to break azeotropic limitations, technological maturity, and high purity of the final product. Compared to alternative technologies such as extraction and membrane separation, azeotropic distillation demonstrates strong competitiveness due to its reliability and high product purity.

Currently, there are no experimental reports on VLE data for entrainer screening in the H₂O/EM azeotropic system. To separate the azeotropic mixture using azeotropic distillation and selected entrainers, binary isobaric VLE data for the systems are required (H₂O/EM, EM/1-pentanol, EM/1-hexanol, EM/1-heptanol, H₂O/1-pentanol, H₂O/1-hexanol and H₂O/1-heptanol). Numerous studies have reported binary VLE data for the H₂O/EM azeotropic system. Bejarano [9] studied the system under varying pressures (74.5 kPa, 101.3 kPa, and 134.0 kPa). Ochi K [10] reported data for the H₂O/1-hexanol system under the 101.3 kPa, Krishnaiah reported the vapor liquid equilibrium data for EM/1-pentanol at 40 kPa and 95 kPa [11], and in NIST, there are binary VLE data for H₂O/1-pentanol at 101.3 kPa. Notably, the NIST database currently lacks data for the following binary systems at 101.3 kPa (EM/1-pentanol, EM/1-hexanol, EM/1-heptanol, and H₂O/1-heptanol).

In this work, binary VLE data were measured at 101.3 kPa for the following systems (H₂O/EM, EM/1-pentanol, EM/1-hexanol, EM/1-heptanol, H₂O/1-pentanol, H₂O/1-hexanol and H₂O/1-heptanol). The measured binary VLE data were validated for thermodynamic consistency using the Herington area test [12]. The experimental data were correlated with the Non-Random Two-Liquid (NRTL) [13], Universal Quasi-Chemical (UNIQUAC) [14], and Wilson activity coefficient models [15,16]. The azeotropic distillation process was simulated using Aspen Plus to evaluate the separation performance and determine the optimal operating parameters.

2. Experiment

2.1. Chemicals

A summary of the data for these chemicals is given in

Table 1. Details of the chemicals.

Chemical	Molecular Formula	CAS No.	Mass Fraction	Purification Method	Source	Analysis Method
ethylene glycol monomethyl ether	C3H8O2	109-86-4	>0.995	none	Shandong Keyuan Biochemical Co., Ltd. (Heze, China)	GC
1-pentanol	C5H12O	71-41-0	>0.990	none	Shandong Keyuan Biochemical Co., Ltd.	GC
1-hexanol	C6H14O	111-27-3	>0.990	none	Shanghai Meryer Co., Ltd. (Shanghai, China)	GC
1-heptanol	C7H16O	111-70-6	>0.990	none	Shanghai Meryer Co., Ltd.	GC
water	H2O	7732-18-5	>0.990	none	Hangzhou Wahaha Group Co., Ltd. (Hangzhou, China)	GC

. All chemicals used in this study were used without further purification.

2.2. Apparatus and Experimental Procedure for VLE Data Collection

The binary VLE data were determined using a modified Othmer distill [17,18], As shown in Figure 1. The effectiveness of the entire experimental setup was validated through previously conducted and published studies [19]. Prior to the experiments, the temperature and pressure measurement system of the Othmer boiling point apparatus was calibrated using a standard substance (H₂O). Subsequently, standard samples of known concentration were prepared, and a GC analytical calibration curve was established. VLE experiments were then conducted for verification to ensure the reliability of the experimental setup. As seen in Figure 2, the experimental data show good agreement with literature values [9] under comparable conditions, providing an independent validation of existing data. The experimental data will be further fitted in the following sections.

During measurements, temperature fluctuations of the mixture remained within 0.10 K over approximately 100 min, confirming the attainment of equilibrium. In the procedure, the mixture in the equilibrium still was heated at the bottom to generate vapor, which was then condensed in a spherical condenser. The condensed liquid flowed back into the still, where it was reheated to boiling, cycling repeatedly until equilibrium was achieved. After the system stabilized at equilibrium, liquid-phase and vapor-phase samples were extracted using microsyringes for chromatographic analysis.

2.3. Experimental Procedures

The vapor-phase and liquid-phase samples were analyzed by gas chromatography (GC), with an injection volume of 0.4 μL for each analysis. The gas chromatographic analytical conditions are listed in

Table 2. Details of GC.

Project	Characteristic	Description
Column	Type	Packing column
	Specification	Porapak Q (3 mm × 2 m)
Carrier gas	Specification	H2 (99.999%, mass fraction)
	Flow rate	40 cm3/min
Detector	Type	Thermal conductivity detector (TCD)
	Temperature	523 K
Injector	Temperature	523 K
Column	Temperature	503 K

.

2.4. Molecular Simulation Methods

As a pivotal computational method, molecular simulation uncovers the fundamental properties and dynamic processes of substances at the atomic level, providing crucial insights into mechanisms that underpin material behavior and complementing experimental observations. Its essence lies in reconstructing the dynamic processes of the microscopic world through mathematical models and algorithms. Molecular modeling facilitates the simulation of experimentally inaccessible information, including inter-molecular interactions and molecular dynamics trajectories. This method has been applied to studies of adsorption processes [20,21], crystallization processes [22,23], and phase equilibrium processes [24,25]. Interaction energies among system components can be quantified using molecular simulations that employ density functional theory.

The theoretical quantum chemical calculations were performed using the Gaussian 16 software package. Geometry optimization and subsequent vibrational frequency calculations for the studied complexes were performed at the B3LYP-D3BJ/TZVP level. The optimized geometries were established as local minima on the potential energy surface (PES) through vibrational frequency analysis, which confirmed the absence of imaginary frequencies, thereby excluding saddle points or transition states. The B3LYP-D3BJ/TZVP [26] level of theory has been widely validated as a reliable approach for predicting molecular electrostatic potentials and solvation surface charge distributions. All quantum chemical calculations in this study were performed under gas-phase conditions. While this method efficiently provides molecular electronic structures and optimized geometries, it is crucial to emphasize its inherent limitation: it does not account for solvation effects in liquid-phase environments. The interaction energy (denoted as E_inter), a fundamental measure of binding affinity in the optimized complexes, was evaluated according to the standard definition [25]. It is calculated as the energy difference between the complex and its constituent monomers at their optimized geometries within the complex (Equation (1)) [26]:

$$E_{inter} = E_{AB} - E_A - E_B .$$

(1)

Among them, E_AB, E_A, and E_B represent the total energies of the complex (A+B), monomer A, and monomer B, respectively. The energy mixing (ΔE) is related to the overheating enthalpy, which can be defined as the difference between the interaction energy of mixed molecules and the interaction energy of pure components. To model the energetic consequences of intermolecular interactions upon mixing, Equation (2) provides the fundamental framework for computing the system’s energy perturbation:

$$\Delta E = {2E}_{AB} - E_{AA} - E_{BB}.$$

(2)

If the calculated value of ΔE is zero, the system is considered athermal (ideal mixing). If there is a significant deviation from zero, it indicates a greater deviation from ideality.

3. Experimental Results and Discussion

3.1. VLE Data of Binary Systems

Under low-pressure or medium-pressure conditions, the expressions for VLE [27,28] are as follows:

$${\gamma }_i={\displaystyle \frac{P{y}_i}{{P_i}^s{x}_i}}.$$

(3)

Among them, x_i and y_i represent the mole fractions of component i in the liquid and vapor phases, respectively, P denotes the system pressure, and P_i^s is the saturation vapor pressure of pure component i, which can be calculated using the Extended Antoine Equation [29] from Aspen V12 Plus. Compared to the standard Antoine equation [30], the additional parameters introduced in the Extended Antoine Equation enhance its flexibility and allow it to describe the entire vapor pressure curve.

Table 3. Parameters for the extended Antoine equation.

Component	C1i	C2i	C3	C4i	C5i	C6i	C7i	C8i	C9i
EM	62.6982	−7444.7	0	0	−6.581	8.883 × 10−18	6	188.15	597.6
1-pentanol	107.842	−10,643	0	0	−12.858	1.249 × 10−17	6	195.56	588.1
1-hexanol	128.512	−12,288	0	0	−15.732	1.270 × 10−17	6	228.55	611.3
1-heptanol	140.5020	−13,466	0	0	−17.353	1.128 × 10−17	6	239.15	632.3
H2O	66.7412	−7258.2	0	0	−7.304	4.165 × 10−6	2	273.16	647.1

lists the Antoine parameters for C₁ to C₉. Extended Antoine Equation Calculation:

$${lnp}_i=C_{1i}+{\displaystyle \frac{C_{2i}}{T+C_{3i}}}+C_{4i}+C_{5i}lnT+C_{6i}{T}^{C^{7i}}for C_{8i}\le T\le C_{9i}.$$

(4)

Among them, T (K) represents the system temperature, and P (kPa) denotes the system pressure. Based on the calculations using the above formulas and parameters,

Table 4. Binary VLE data for H₂O (1)/EM (2).

T/K	x1	y1	γ1	γ2
373.15	1.0000	1.0000	1.0025	-
373.15	0.9759	0.9719	0.9985	2.6402
373.15	0.9426	0.9367	0.9962	2.5050
373.15	0.8969	0.8914	0.9963	2.3911
373.15	0.8602	0.8564	0.9980	2.3319
373.25	0.7906	0.7999	1.0107	2.1606
373.25	0.6930	0.7348	1.0591	1.9538
373.35	0.6202	0.6862	1.1014	1.8616
373.75	0.5148	0.6206	1.1831	1.7366
373.95	0.4514	0.5870	1.2672	1.6599
374.25	0.3800	0.5315	1.3486	1.6482
375.25	0.3286	0.4884	1.3832	1.6036
375.85	0.2791	0.4548	1.4845	1.5581
376.55	0.2323	0.4142	1.5856	1.5333
377.85	0.1866	0.3576	1.6286	1.5158
379.65	0.1393	0.3037	1.7411	1.4582
381.15	0.1110	0.2563	1.7523	1.4316
382.65	0.0925	0.2257	1.7604	1.3870
384.65	0.0716	0.1753	1.6520	1.3494
387.25	0.0444	0.1401	1.9513	1.2535
388.85	0.0391	0.1097	1.6492	1.2242
390.95	0.0247	0.0897	1.9957	1.1517
393.85	0.0117	0.0395	1.6871	1.0928
397.15	0.0000	0.0000	-	1.0134

,

Table 5. Binary VLE data for EM (1)/1-pentanol (2).

T/K	x1	y1	γ1	γ2
410.65	0.0000	0.0000	-	1.0101
408.45	0.0683	0.1099	1.1609	1.0374
406.95	0.1363	0.1815	1.0038	1.0818
405.35	0.2053	0.3082	1.1857	1.0488
404.15	0.2942	0.4081	1.1357	1.0524
402.05	0.4364	0.5607	1.1202	1.0516
400.85	0.5371	0.6438	1.0839	1.0823
400.25	0.5924	0.6909	1.0742	1.0891
399.85	0.6641	0.7482	1.0505	1.0918
398.95	0.7639	0.8215	1.0307	1.1370
398.75	0.7962	0.8452	1.0237	1.1505
398.15	0.8249	0.8749	1.0420	1.1055
397.15	1.0000	1.0000	1.0134	-

,

Table 6. Binary VLE data for EM (1)/1-hexanol (2).

T/K	x1	y1	γ1	γ2
430.15	0.0000	0.0000	-	0.9936
424.65	0.0874	0.2152	1.1321	1.0164
419.75	0.1732	0.4001	1.2116	1.0065
414.55	0.2594	0.5148	1.2020	1.0839
411.05	0.3742	0.6295	1.1253	1.1069
407.95	0.4508	0.7147	1.1599	1.0850
406.35	0.5161	0.7522	1.1177	1.1335
405.05	0.5730	0.7894	1.0979	1.1450
403.85	0.6256	0.8268	1.0915	1.1232
402.95	0.6805	0.8583	1.0701	1.1138
401.65	0.7422	0.8886	1.0566	1.1390
400.65	0.8029	0.9124	1.0338	1.2169
399.75	0.8483	0.9363	1.0323	1.1888
397.15	1.0000	1.0000	1.0134	-

,

Table 7. Binary VLE data for EM (1)/1-heptanol (2).

T/K	x1	y1	γ1	γ2
448.15	0.0000	0.0000	-	1.0153
438.15	0.0497	0.2507	1.6423	1.0869
431.95	0.1003	0.4040	1.5310	1.1158
423.75	0.1921	0.5930	1.4533	1.1212
417.15	0.2890	0.7399	1.4423	1.0310
412.15	0.3839	0.8284	1.3986	0.9461
408.15	0.4695	0.8895	1.3780	0.8254
406.25	0.5215	0.9289	1.3701	0.6344
403.65	0.6005	0.9408	1.3019	0.7020
402.85	0.6307	0.9462	1.2768	0.7131
401.65	0.6801	0.9517	1.2350	0.6153
397.15	1.0000	1.0000	1.0134	-

,

Table 8. Binary VLE data for H₂O (1)/1-pentanol (2).

T/K	x1	y1	γ1	γ2
411.15	0.0000	0.0000	-	0.9937
381.55	0.0272	0.3064	8.4329	2.0641
379.55	0.0430	0.4375	8.1540	1.8444
374.15	0.0764	0.4701	5.9515	2.2514
371.95	0.1032	0.5569	5.6443	2.1293
369.25	0.1381	0.5553	4.6402	2.4990
369.15	0.1499	0.5798	4.4790	2.4050
369.15	0.1508	0.5690	4.3686	2.4696
369.15	0.2226	0.5696	2.9639	2.6933
369.15	0.3074	0.5641	2.1253	3.0622
368.75	0.4183	0.5823	1.6358	3.5559
368.75	0.5180	0.5772	1.6358	3.5559
368.75	0.5743	0.5517	1.1291	5.2140
368.75	0.6948	0.5673	0.9597	7.0187
369.05	0.7991	0.5880	0.8554	10.0224
369.05	0.9480	0.5600	0.6867	41.3464
373.15	1.0000	1.0000	1.0025	-

,

Table 9. Binary VLE data for H₂O (1)/1-hexanol (2).

T/K	x1	y1	γ1	γ2
429.65	0.0000	0.0000	-	1.0092
382.15	0.0507	0.6301	9.1174	2.2674
373.35	0.0988	0.6500	6.5472	3.3602
371.85	0.2226	0.6862	3.2371	3.7465
370.85	0.2985	0.6805	2.4819	4.4326
370.75	0.4211	0.6933	1.7991	5.1807
370.75	0.4981	0.6850	1.5027	6.1370
370.75	0.6091	0.6750	1.2110	8.1298
370.85	0.7271	0.7059	1.0570	10.4880
370.75	0.7558	0.6904	0.9981	12.3998
370.75	0.8713	0.7032	0.8820	22.5461
370.95	0.9790	0.6840	0.7580	145.7353
373.15	1.0000	1.0000	1.0025	-

and

Table 10. Binary VLE data for H₂O (1)/1-heptanol (2).

T/K	x1	y1	γ1	γ2
448.15	0.0000	0.0000	-	1.0153
377.45	0.0479	0.8020	14.4234	3.1665
374.65	0.1002	0.8034	7.6239	3.8227
372.25	0.1499	0.8032	5.5486	4.5727
372.05	0.2001	0.8285	4.3168	4.2776
372.05	0.2926	0.8352	2.9760	4.6481
371.85	0.4253	0.8392	2.0725	5.6389
372.15	0.5162	0.8429	1.6965	6.4471
371.95	0.6230	0.8310	1.3960	8.9871
372.15	0.6868	0.8301	1.2560	10.7639
371.95	0.7911	0.8359	1.1058	15.7493
372.15	0.9780	0.8400	0.8924	144.3722
373.15	1.0000	1.0000	1.0025	-

present the experimentally obtained binary VLE data and activity coefficients (γi). As observed in Table 8, Table 9 and Table 10, activity coefficients (γ) exhibit abnormally high values in some cases. This can be attributed to the significant difference between the strong hydrogen bonding among H₂O molecules and the pronounced hydrophobicity of the long alkyl chain of alcohol molecules. This leads directly to highly non-ideal behavior in the liquid phase and a strong tendency for liquid-phase splitting (partial miscibility). In dilute aqueous solutions, alcohol molecules exhibit extremely high fugacity, indicating a substantial tendency to “escape” from the liquid phase, which is reflected as activity coefficients γ >> 1.

3.2. Thermodynamic Consistency Test for the Experimental Data (Herington Integral Method)

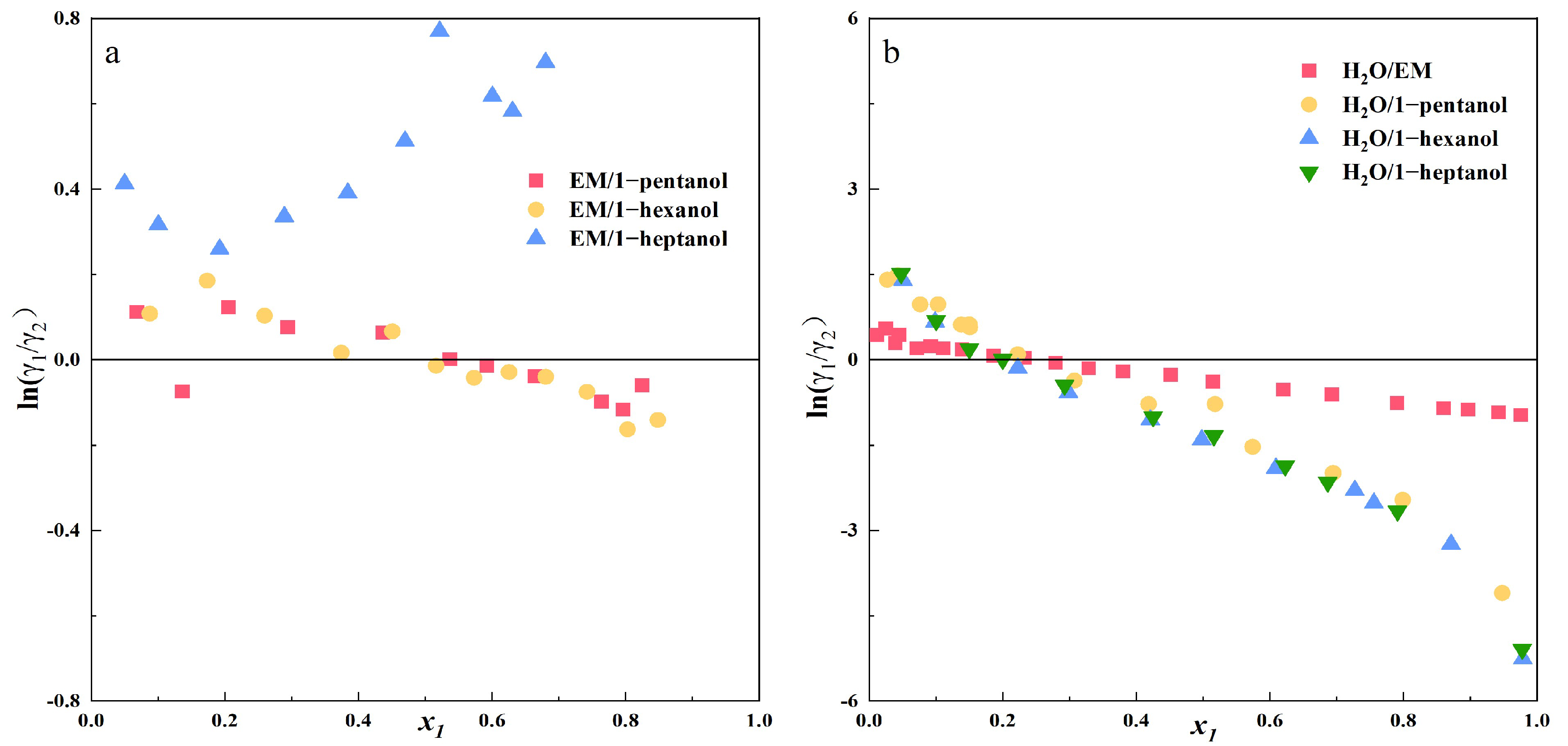
To ensure the accuracy and reliability of the measured VLE data, thermodynamic consistency tests must be performed on the experimental data. Common methods include the integral test, differential test, and slope method. To assess adherence to the Gibbs-Duhem equation, the thermodynamic consistency of the experimental phase equilibrium data was rigorously evaluated via Herington area test [31]. The Herington method is a semi-empirical approach that involves plotting x₁ against ln(γ₁/γ₂) (as shown in Figure 3) and defining and examining the relationship between D and J. The specific steps are as follows:

$$D={\displaystyle \frac{{\int }_{x_i=0}^{x_i=1}ln\frac{{\gamma }_2}{{\gamma }_1}d{x}_i}{{\int }_{x_i=0}^{x_i=1}\left|ln\frac{{\gamma }_2}{{\gamma }_1}\right|d{x}_i}}\times 100,$$

(5)

$$J=150\times {\displaystyle \frac{T_{max}-T_{min}}{T_{min}}}.$$

(6)

Among them, T_max (K) corresponds to the maximum temperature of the system. T_min (K) corresponds to the minimum temperature of the system.

The calculation results are presented in

Table 11. Result of Herrington integral test.

Binary System	|D − J|
H2O/EM	5.9450
EM/1-pentanol	6.6655
EM/1-hexanol	2.8024
EM/1-heptanol	2.4528
H2O/1-pentanol	8.0924
H2O/1-hexanol	8.8198
H2O/1-heptanol	8.1581

, D − J represents the criterion for evaluating thermodynamic consistency using the Herington integral test method. If |D − J| < 10, the data exhibits reasonable reliability. As shown in Table 11, the measured VLE data for the binary system demonstrate reliable consistency.

3.3. Correlation of Binary VLE Data

To validate experimental data, the VLE data obtained from experiments were correlated using the NRTL, UNIQUAC, and Wilson activity coefficient models, which appear in Equations (7)–(9). The calculated correlated binary interaction parameters are listed in

Table 12. The correlated binary interaction parameters (a_ij; a_ji; b_ij; b_ji), standard deviations of vapor compositions (δ_y1) and temperatures (δ_T).

System	Model	Correlation Paramenters				RMSD
		aij	aji	bij/K	bji/K	δy1	δT
H2O/EM	NRTL	−13.7500	6.3087	5804.2600	−2612.2645	0.0076	0.3232
	UNIQUAC	1.1661	0.1903	−141.1685	−619.4664	0.0067	0.3062
	WILSON	−3.3899	9.4101	1387.1798	−4020.3589	0.0067	0.3117
EM/1-pentanol	NRTL	2.9908	−0.1247	−916.6271	−100.2345	0.0097	0.2624
	UNIQUAC	−1.5565	0.5743	470.7308	−125.3232	0.0097	0.2610
	WILSON	0.01484	−2.6222	159.0824	742.3043	0.0097	0.2623
EM/1-hexanol	NRTL	11.9088	−8.4514	−4512.7373	3221.0569	0.0112	0.3033
	UNIQUAC	−4.4627	4.7822	1812.4600	−1970.3248	0.0116	0.3105
	WILSON	7.07436	−9.9947	−2752.0434	3841.7263	0.0114	0.3072
EM/1-heptanol	NRTL	29.5548	13.9507	−10,000.0000	−6383.2185	0.0104	0.1710
	UNIQUAC	−25.5473	−1.65054	9051.5620	1090.3780	0.0170	0.3527
	WILSON	−4.5029	−15.8153	2264.3243	−7550.6066	0.0290	0.2730
H2O/1-pentanol	NRTL	24.0611	16.9207	−7482.0249	−6082.7347	0.0403	0.6400
	UNIQUAC	−2.7402	−9.6022	818.2867	3461.7929	0.0408	0.6558
	WILSON	−0.3626	−48.9978	−148.4263	−10,000.0000	0.0375	0.7109
H2O/1-hexanol	NRTL	27.4105	1.2408	−8543.0889	−417.7151	0.0803	1.0454
	UNIQUAC	−2.0196	−0.6236	621.4692	70.4286	0.7994	0.9868
	WILSON	16.5498	−80.0000	−6504.2841	−10,000.0000	0.0351	0.4534
H2O/1-heptanol	NRTL	633.9445	62.9729	−147,929.7011 147,929.70110	−9545.9276	0.0308	0.7138
	UNIQUAC	−27.0665	−27.3470	10,000.0000	10,000.0000	0.0289	0.7988
	WILSON	−27.4899	−80.0000	10,000.0000	−10,000.0000	0.0274	0.3687

, and a comparison between experimental and predicted data is shown in Figure 4. To quantify model prediction fidelity, root mean square deviations (RMSD) of vapor-phase mole fractions and equilibrium temperatures were computed via Equations (10) and (11), serving as key metrics for thermodynamic model validity.

NRTL:

$$\mathrm{l}\mathrm{n}{\gamma }_i={\displaystyle \frac{{\sum }_{j=1}^n{x}_{ji}{G}_{ji}{x}_j}{{\sum }_{k=1}^n{G}_{ki}{x}_k}}+\sum _{j=1}^n\left({\displaystyle \frac{x_j{G}_{ij}}{{\sum }_{k=1}^n{G}_{kj}{x}_k}}\right)\left({\tau }_{ij}-{\displaystyle \frac{{\sum }_{l=1}^n{\tau }_{lj}{G}_{lj}{x}_l}{{\sum }_{k=1}^n{G}_{kj}{x}_k}}\right),$$

(7)

where ${\tau }_{ij}=a_{ij}+{\displaystyle \frac{b_{ij}}{T}};G_{ij}=\mathrm{e}\mathrm{x}\mathrm{p}(-{\alpha }_{ij}{\tau }_{ij})$.

UNIQUAC:

$$\mathrm{l}\mathrm{n}{\gamma }_i=\mathrm{l}\mathrm{n}{\displaystyle \frac{{\varphi }_i}{x_i}}+{\displaystyle \frac{z}{2}}{q}_i\mathrm{l}\mathrm{n}{\displaystyle \frac{{\theta }_i}{{\varphi }_i}}+l_i+{\displaystyle \frac{{\varphi }_i}{x_i}}\sum _{j=1}^n{x}_j{l}_j+q_i^t\left(1-\mathrm{l}\mathrm{n}{t}_i^t-{\displaystyle \frac{{\sum }_{j=1}^n{\theta }_j{\tau }_{ij}}{t_j^t}}\right),$$

(8)

where ${\tau }_{ij}=\mathrm{e}\mathrm{x}\mathrm{p}\left(a_{ij}+{\displaystyle \frac{b_{ij}}{T}}\right)$.

Wilson:

$$\mathrm{l}\mathrm{n}{\gamma }_i=1-\mathrm{l}\mathrm{n}\left(\sum _{j=1}^n{A}_{ij}{x}_j\right)-\sum _{k=1}^n\left({\displaystyle \frac{x_k{A}_{ki}}{{\sum }_{j=1}^n{A}_{kj}{x}_j}}\right),$$

(9)

where $A_{ij}=a_{ij}+{\displaystyle \frac{b_{ij}}{T}}$.

$$\mathrm{RMSD}\left({\mathrm{y}}_{\mathrm{i}}\right)=\sqrt{{\displaystyle \frac{{\sum }_i^N{\left(y_{i,\mathit{exp}}-y_{i,\mathit{cal}}\right)}^2}{N}} }$$

(10)

$$\mathrm{RMSD}(T_{\mathrm{i}})=\sqrt{{\displaystyle \frac{{\sum }_i^N{\left(T_{i,\mathit{exp}}-T_{i,\mathit{cal}}\right)}^2}{N}} }$$

(11)

The experimental results indicate that the investigated H₂O–long-chain alcohol system exhibits highly non-ideal behavior. During the correlation process, although the NRTL model demonstrated the best correlation accuracy within the experimental data range, the optimized binary interaction parameters exhibited abnormally large absolute values. This clearly reveals the inherent mathematical limitations of local composition models in describing such extremely non-ideal systems characterized by strong asymmetry and a tendency for liquid-phase splitting. These abnormal parameters likely result from over-parameterization, where the model forces a perfect fit to a limited dataset, leading to physically meaningless values. Consequently, the obtained model parameters should be used strictly for interpolation within the experimental data range. Extrapolation for predictions is strongly discouraged, as it would yield unreliable results.

As indicated by the binary correlated interaction parameters and root mean square deviations (RMSD) listed in the table, all three activity coefficient models can satisfactorily correlate the H₂O/EM system. The figure demonstrates that each model is capable of describing this thermodynamic system with reasonable accuracy. Moreover, 1-pentanol, 1-hexanol, and 1-heptanol are all able to break the azeotropic system of H₂O/EM. Data indicate that the mass fractions of H₂O in their azeotropes with water are approximately 56%, 68%, and 83%, respectively.

From the experimental data, the azeotropic temperature of H₂O and EM is 99.9 °C, and the boiling point of the new azeotrope formed by the azeotrope and H₂O should be lower than that of the original azeotrope, while the temperature difference between the new azeotrope formed by 1-hexanol and 1-heptanol and H₂O is too small compared with the original azeotropic temperature, which will cause separation difficulties. Secondly, the larger the proportion of H₂O in the azeotropic composition, the less azeotropic dose required to remove the H₂O from the system, that is, the less separation load, which is more conducive to reducing the energy consumption of the subsequent distillation column. It can be seen from

Table 13. Physical properties of azeotropes in H₂O and different substances (P = 101.325 kPa).

Azeotropic Substances	1-Pentanol	1-Hexanol	1-Heptanol
Boiling point/°C	138	157	176
Azeotropic temperature/°C	95.9	97.9	99.2
Azeotropic Composition (H2O)/wt%	56	68	83

that the azeotropic composition of the three azeotropic agents accounts for a large proportion of H₂O. In summary, 1-pentanol is the best choice among the three azeotropes.

3.4. Molecular Interaction Simulation

Molecular interaction energy simulations depicted in Figure 5 enabled the calculation of ΔE via Equation (2), yielding values of −6.348 kJ/mol for H₂O/EM, 3.058 kJ/mol for EM/1-pentanol, 3.115 kJ/mol for EM/1-hexanol, 3.162 kJ/mol for EM/1-heptanol, −4.691 kJ/mol for H₂O/1-pentanol, −4.701 kJ/mol for H₂O/1-hexanol, and −4.694 kJ/mol for H₂O/1-heptanol. Systems exhibiting negative deviations (H₂O/EM, H₂O/1-pentanol, H₂O/1-hexanol, and H₂O-1-heptanol; all ΔE < 0) corresponded to minimum H₂O activity coefficients of 0.9962, 0.6867, 0.7580. Conversely, systems showing positive deviations (EM/1-pentanol, EM/1-hexanol, and EM/1-heptanol; all ΔE > 0) displayed maximum EM activity coefficients of 1.1857, 1.2116. Critically, these molecular simulation outcomes demonstrate quantitative consistency with experimental VLE data across all investigated systems.

4. Separation of H₂O/EM via Azeotropic Distillation

4.1. Process Flow

To verify the feasibility of the selected entrainer for the separation, a process flow simulation was conducted. The wastewater from a pesticide plant contains 88 wt% H₂O, 10 wt% methyl cellosolve, and 2 wt% methanol. The simulated process flow is shown in Figure 6. With a feed flow rate of 1000 kg/h, the stream first enters T1, the light-ends removal column. The primary objective of T1 is to remove the light component (methanol) from the feedstock, with the distillate obtaining the light component at a mass fraction ≥ 0.999. The bottom mixture then proceeds to T2, the azeotropic distillation column (COL-MAIN). Here, under the influence of the entrainer 1-pentanol, H₂O is entrained and carried overhead. This overhead vapor is condensed and separated in a decanter (DECANTER). The upper organic phase, primarily consisting of n-pentanol, is returned to the azeotropic distillation column, with any lost entrainer being replenished. The lower aqueous phase enters the solvent recovery column (COL-REC). The bottom product from COL-REC is methyl cellosolve with a mass fraction ≥ 0.999. Simultaneously, the bottom stream of the solvent recovery column (COL-REC) produces H₂O with a mass fraction ≥ 0.999, while its distillate is an azeotropic mixture of H₂O and the entrainer. This distillate is subsequently recycled back to the azeotropic distillation column (COL-MAIN) for reuse.

4.2. Process Parameter Optimization

In the distillation process, key process parameters such as the feed flow rate of the entrainer, the number of theoretical stages, the feed stage location of the feedstock, and the reflux ratio have a crucial impact on the separation efficiency. Column T3, the solvent recovery column, is relatively straightforward to optimize; therefore, the primary focus was on optimizing columns T1 and T2. Sensitivity analysis on the process parameters related to columns T1 and T2 was conducted using Aspen Plus. The process was optimized by minimizing the estimated reboiler duty (Q), the thermal energy consumption. However, this represents only a preliminary stage of process evaluation. The results are shown in Figure 6 and Figure 7.

As shown in Figure 7, the optimal dosage of the entrainer is 805.3 kg/h, at which point the separation target (i.e., an EM purity of 0.999) is achieved.

As can be seen from Figure 8, by integrating the optimization results of both the light-ends removal column T1 and the azeotropic distillation column T2 systems, the optimal process parameters for this azeotropic distillation system can be determined, as summarized in

Table 14. Results of Process Parameter Optimization.

Optimization Results	Light-Ends Removal Column T1	Azeotropic Distillation Column T2	Solvent Recovery Column T3
Number of Theoretical Stages	49	24	6
Feed Stage Location	14	13 (FEED2)	3
Reflux Ratio	6	4	1
Total Duty/kW	170.27	7498.98	105.65
Column Pressure/kPa	101.325	101.325	101.325
Entrainer Feed Rate/(kg/h)	/	805.3	/

.

5. Conclusions

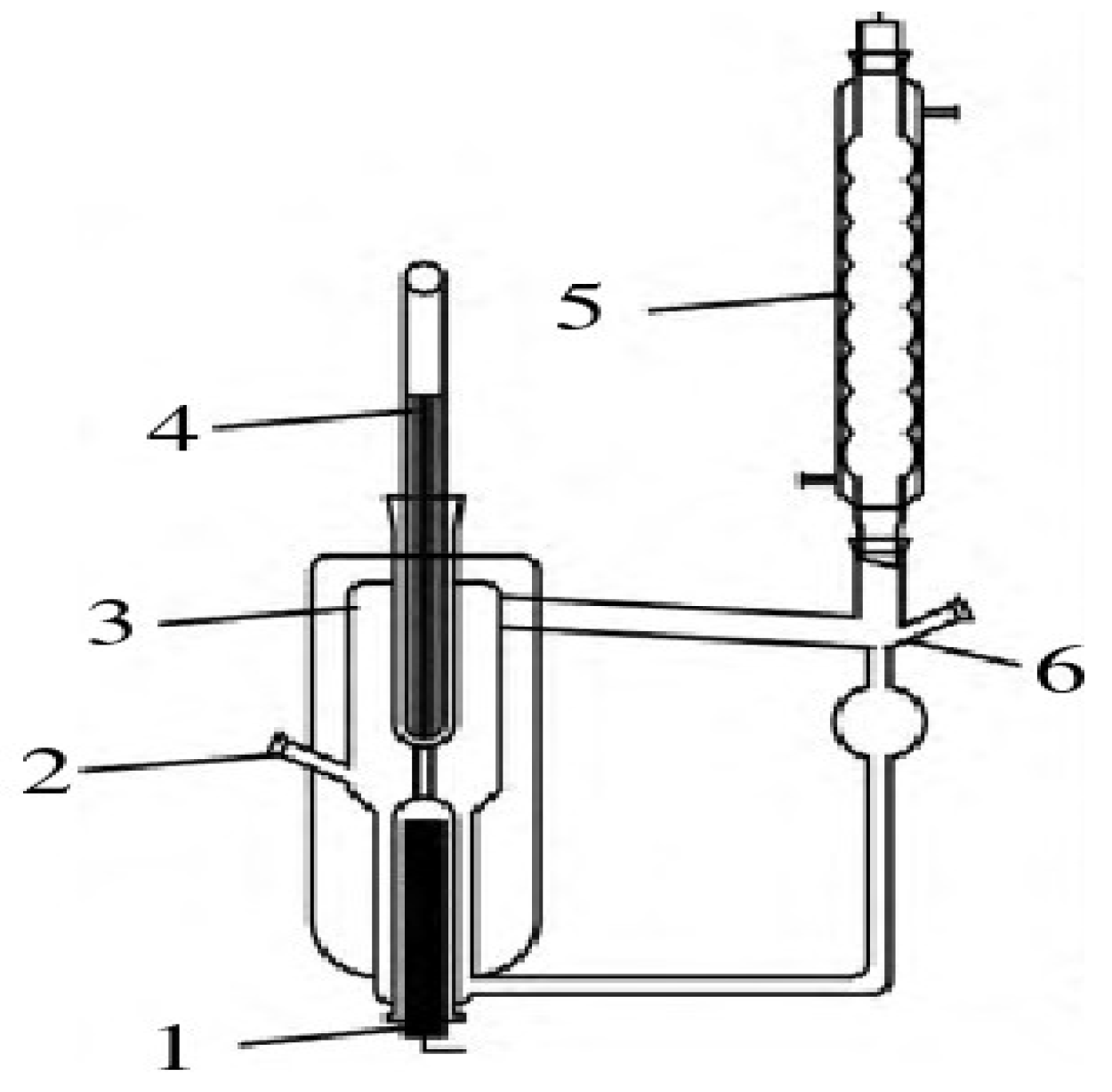
VLE data for seven binary systems were measured at atmospheric pressure using a modified Othmer still, filling a significant data gap. All experimental data passed the thermodynamic consistency test via Herington’s area method. Using the Aspen Plus process simulation software, the parameters for the NRTL, UNIQUAC, and Wilson activity coefficient models were regressed, yielding parameter sets applicable at atmospheric pressure. The results indicate that all three activity coefficient models can satisfactorily correlate the H₂O/EM system. Molecular interaction energy simulations agreed with the experimental VLE data, confirming the reliability of the data provided in this work. The analysis shows that 1-pentanol is the optimal choice among the three evaluated entrainers.

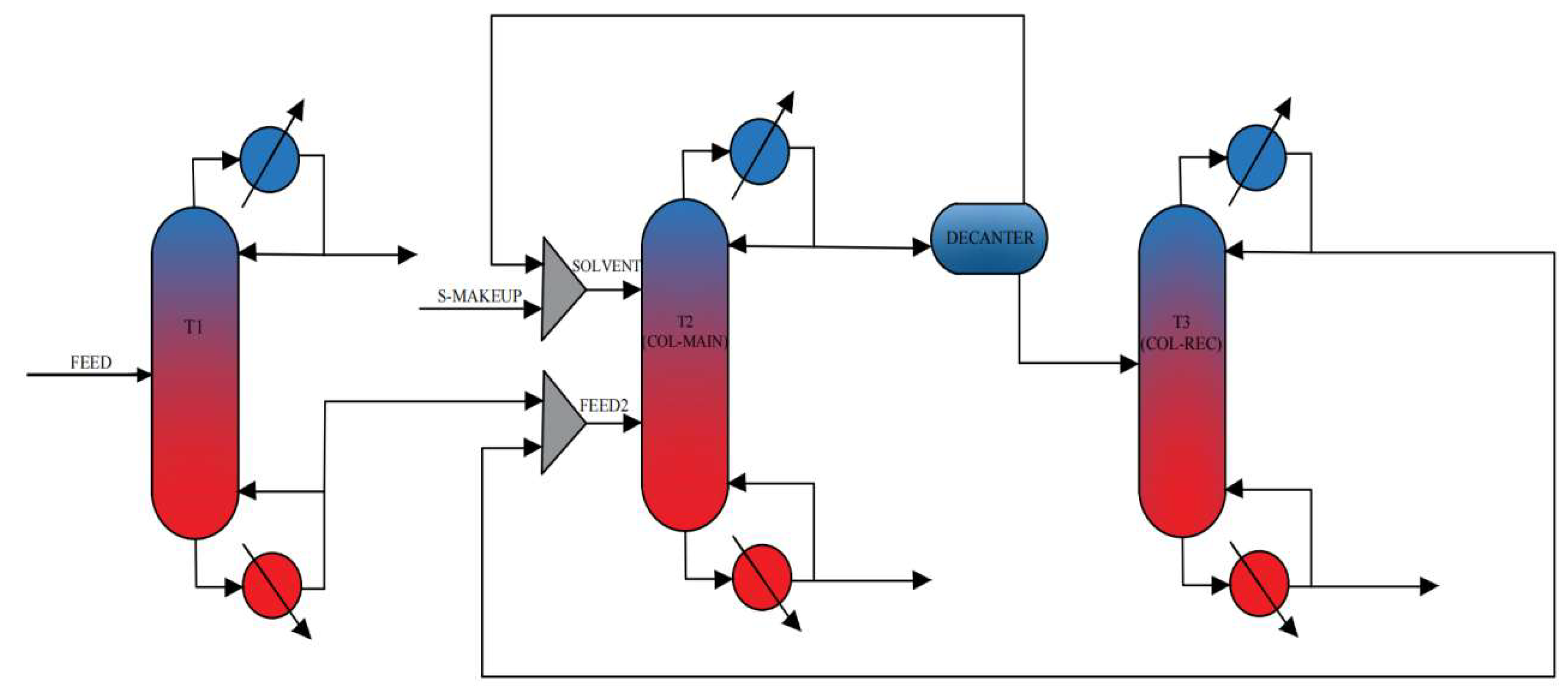
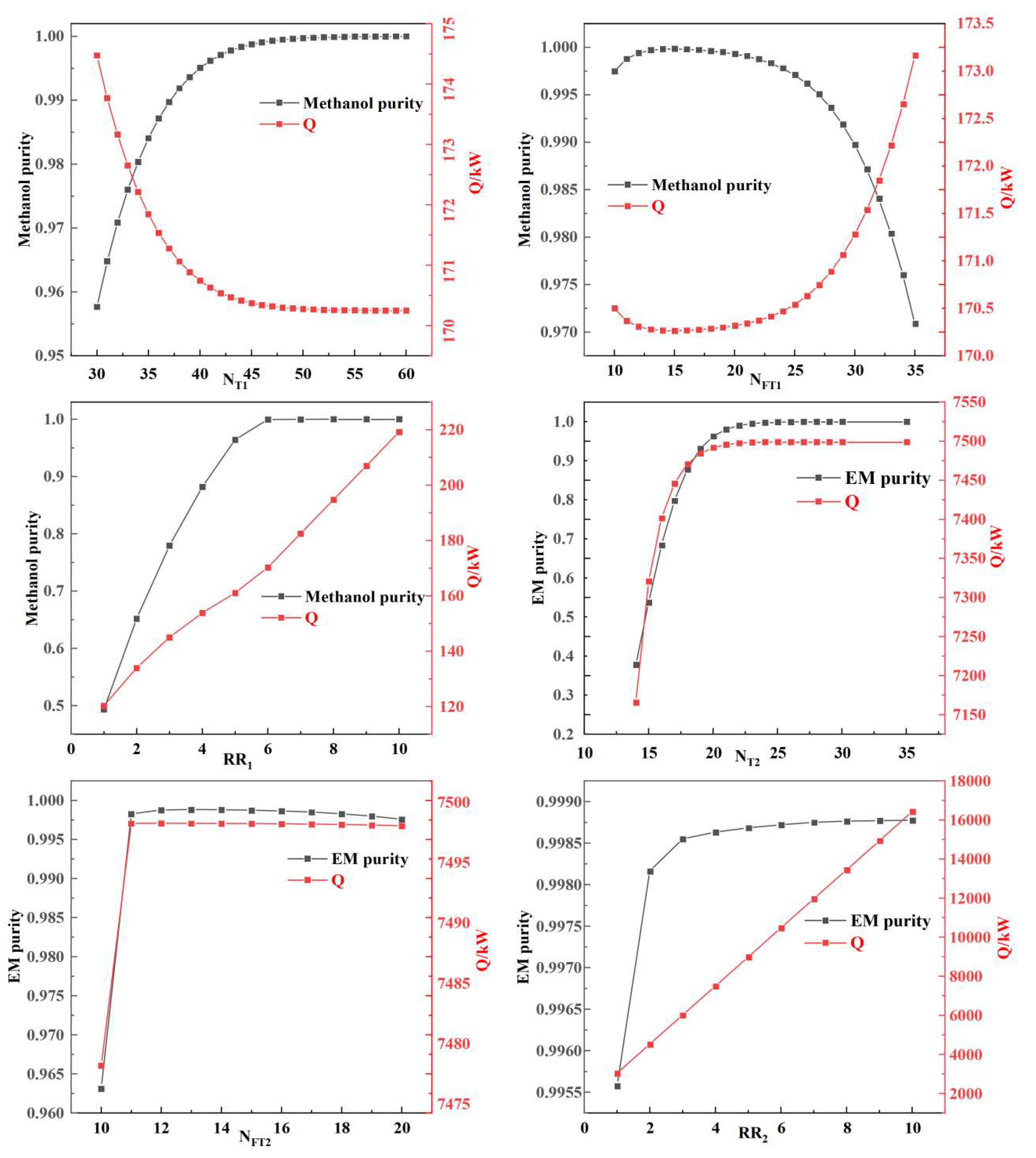
Subsequently, the azeotropic distillation process was simulated using Aspen Plus to evaluate the separation performance and identify the optimal operating parameters. This simulation provided the foundation for conceptual process design and preliminary thermodynamic assessment. Upon finalizing the conceptual design, addressing operational challenges such as emulsion formation and entrainer loss will become critical obstacles to overcome during subsequent detailed engineering design and pilot-scale scaling. These issues represent key focus areas for future work.