Mineral Extraction from Mixed Brine Solutions
Abstract
1. Introduction
1.1. Sulfate Minerals
1.2. The Economic Value of the Sulfate Minerals
1.3. Treatment Methods of High Saline Brine Solutions
2. The Calculating Model to Examine the Potential for Extracting SMs from Mixed Solutions
f γ = Aϕ {[I^(0.5)/(1 + 1.2*I^(0.5)]+ [ (2/1.2)*ln{ 1 + 1.2*I^(0.5)}]
QS(MX) = [M2+] brine * [X2−] brine
3. Result and Discussion
3.1. Analysis of Water Samples Collected
3.2. The Chemical Composition of HSBSs and Doha East SW
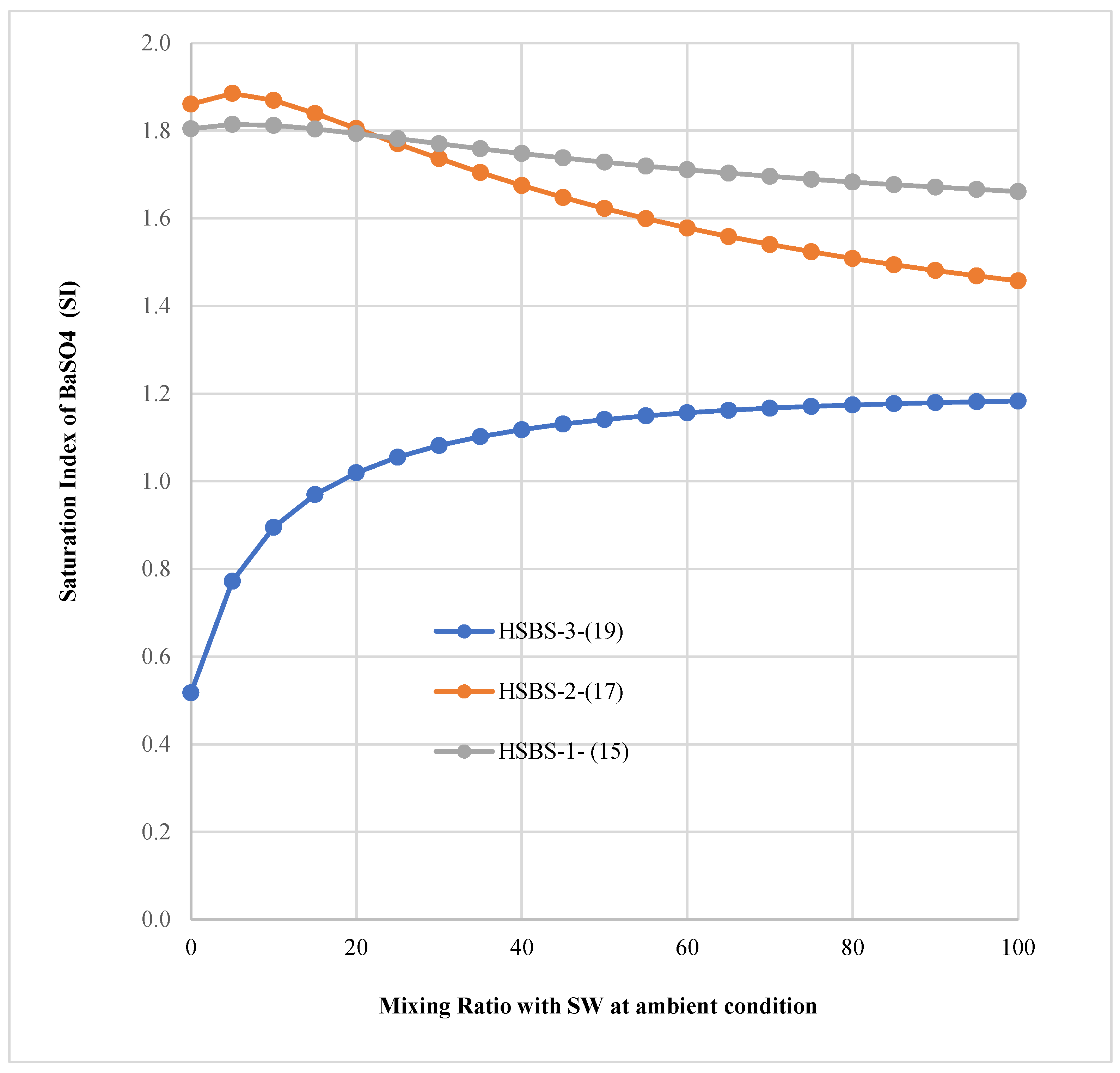
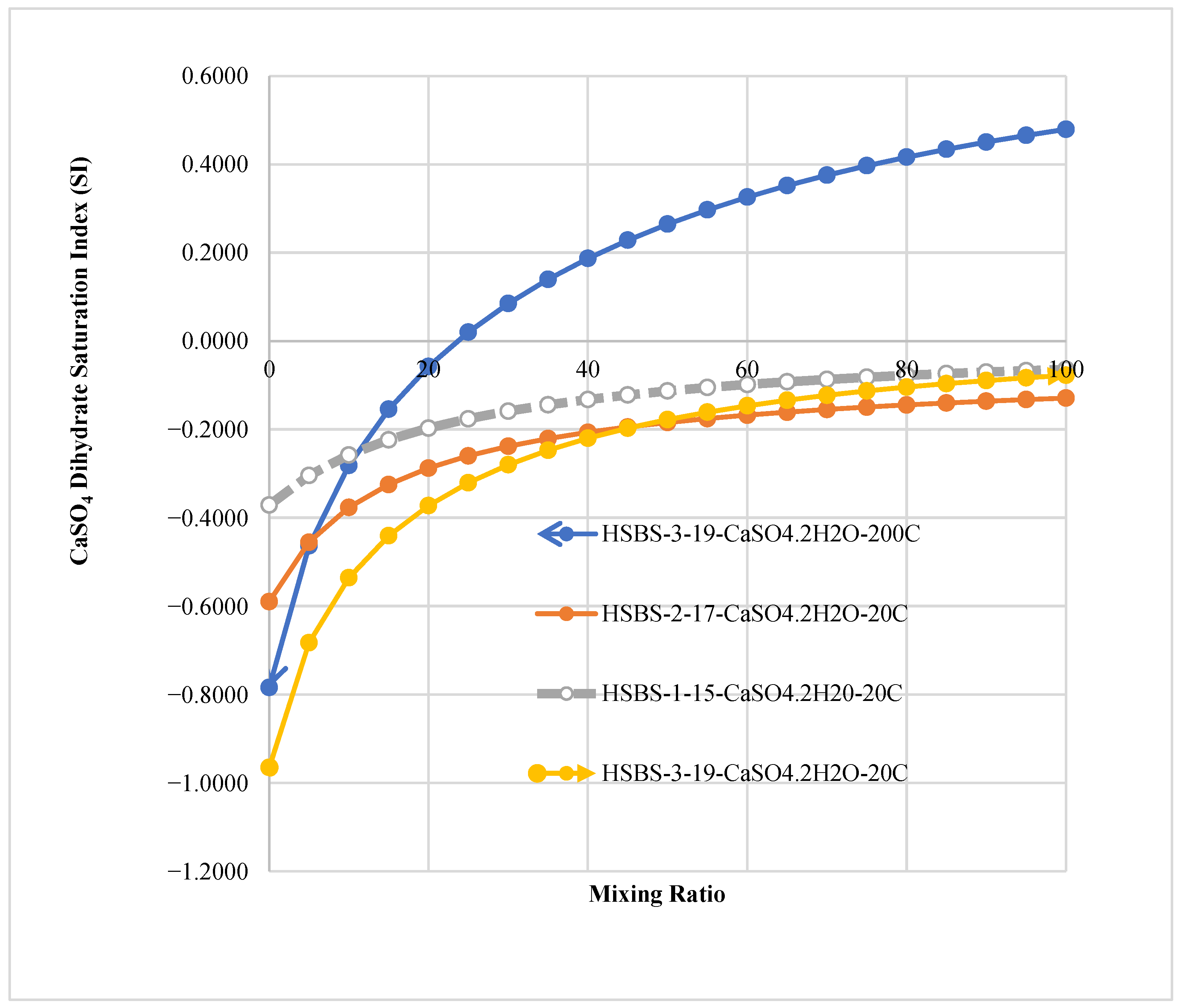
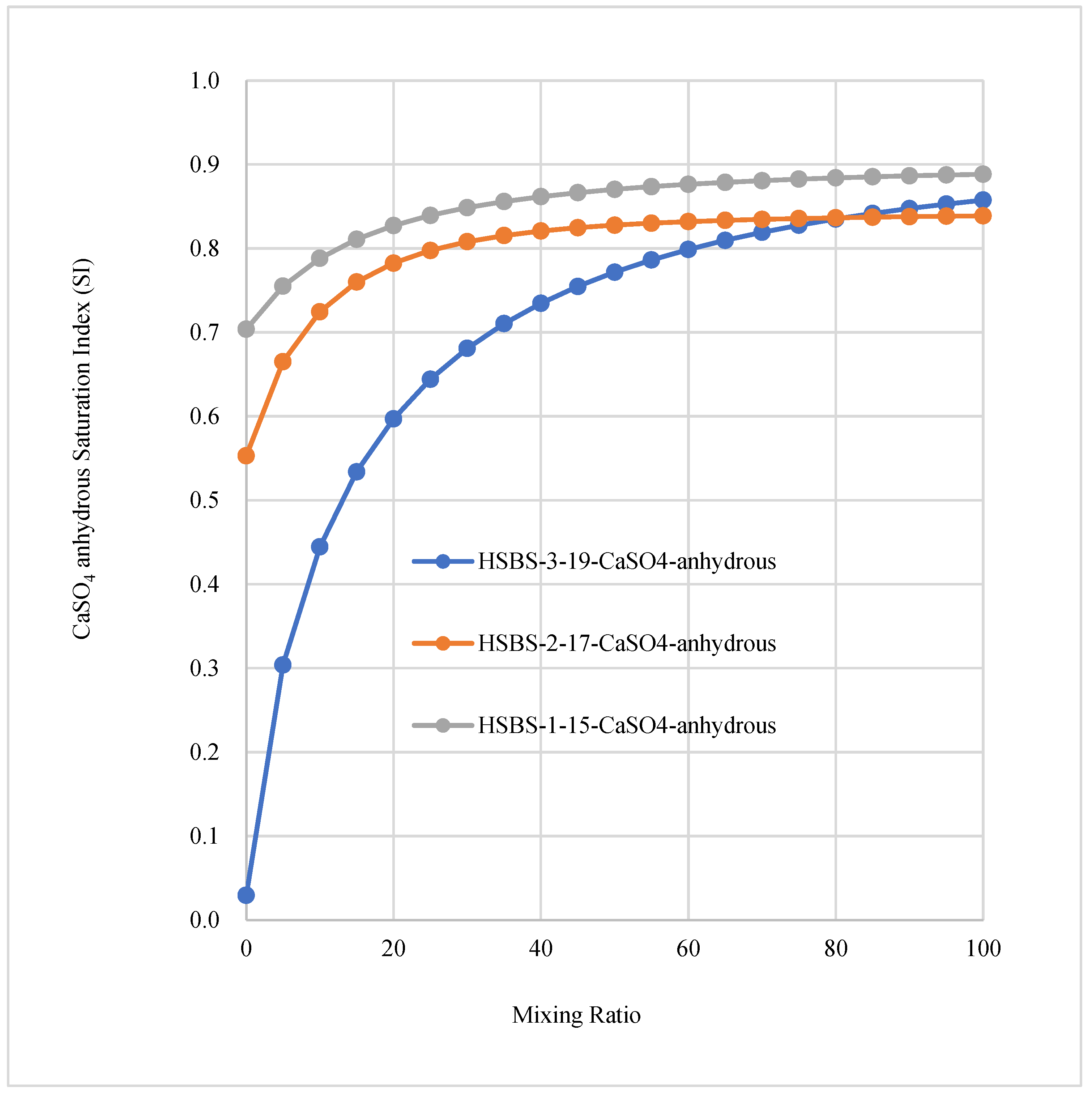
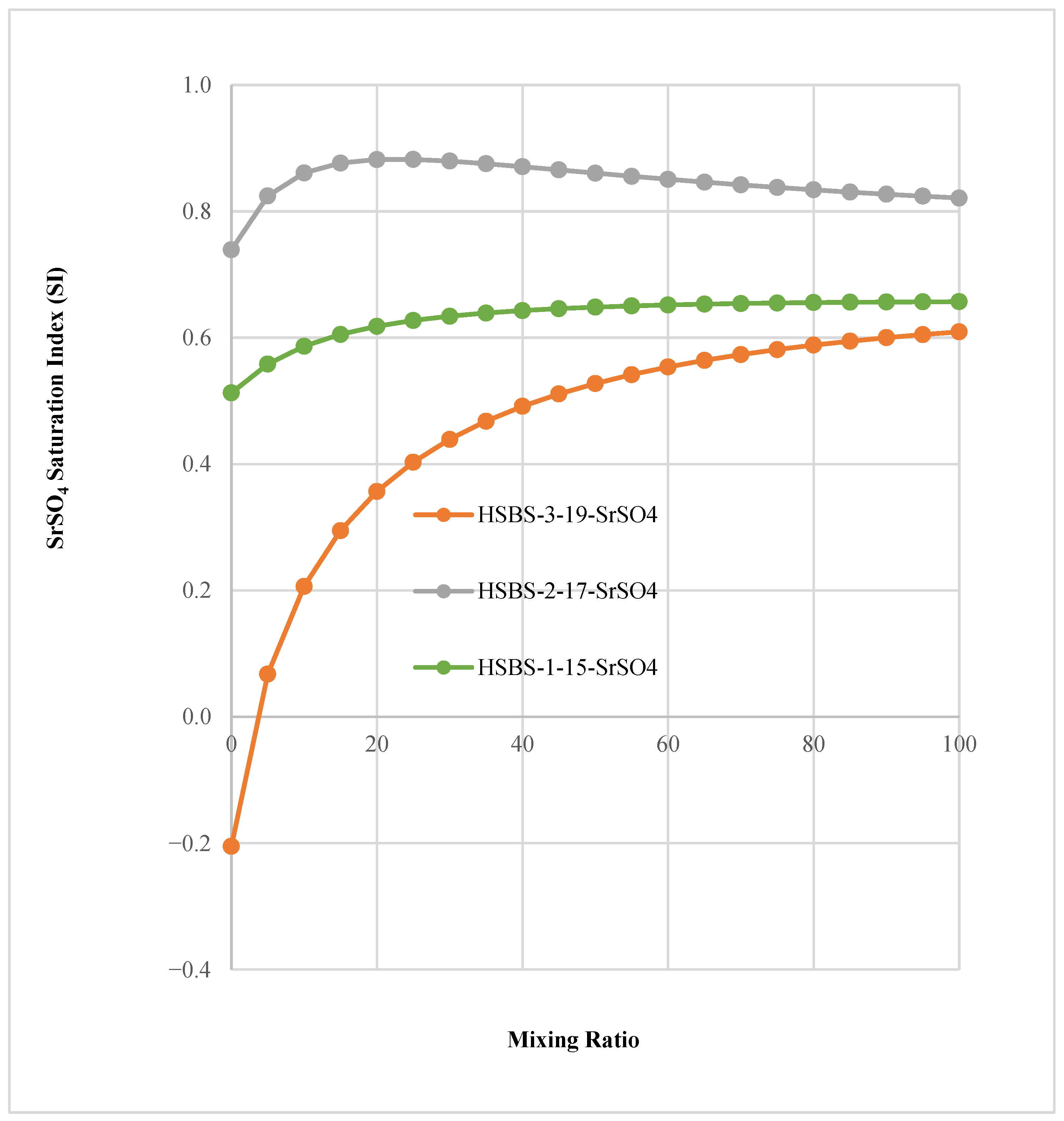
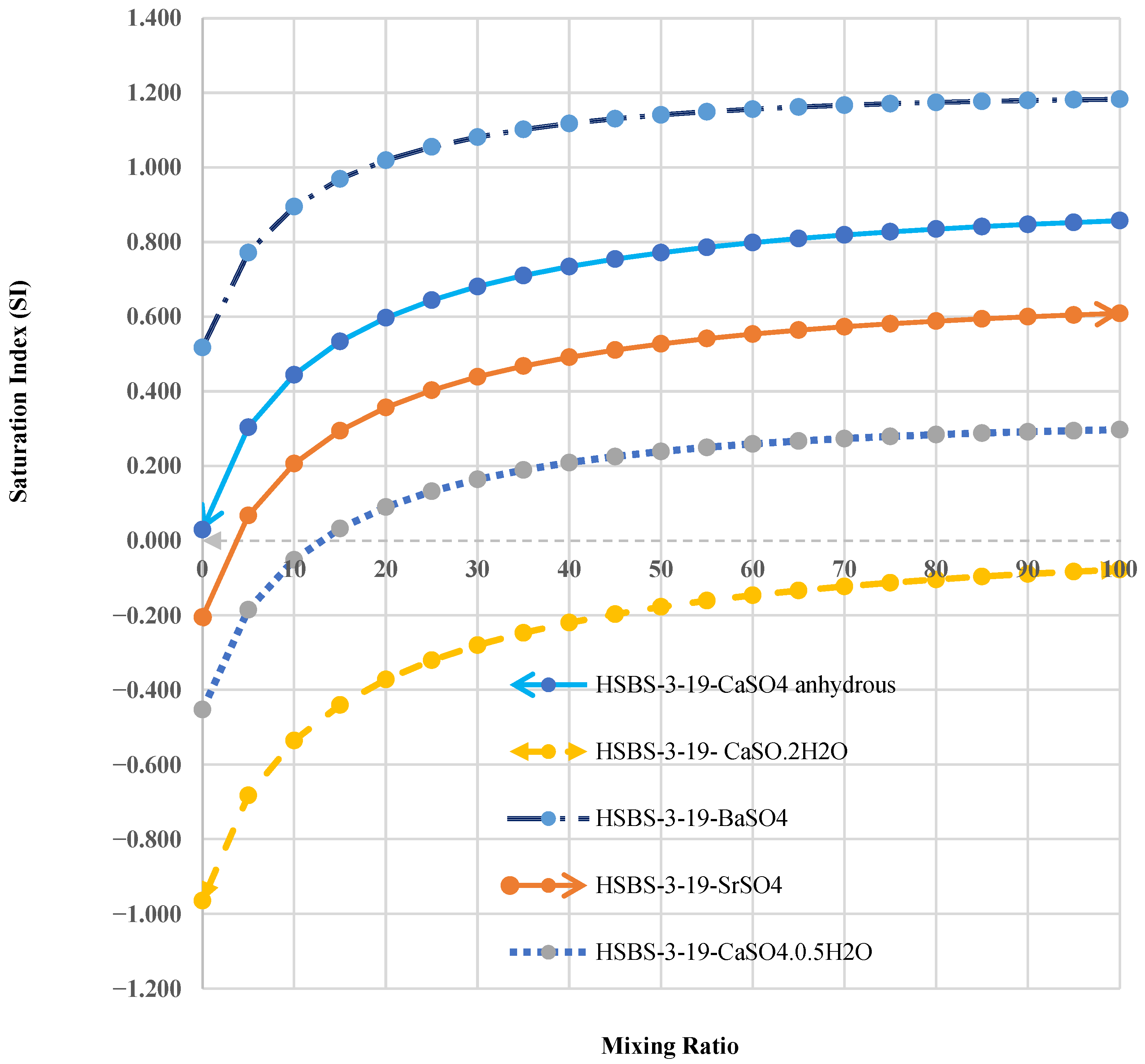
3.3. The Saturation Index of SMs in Mixed Solutions
3.4. Sulfate Mineral Extraction
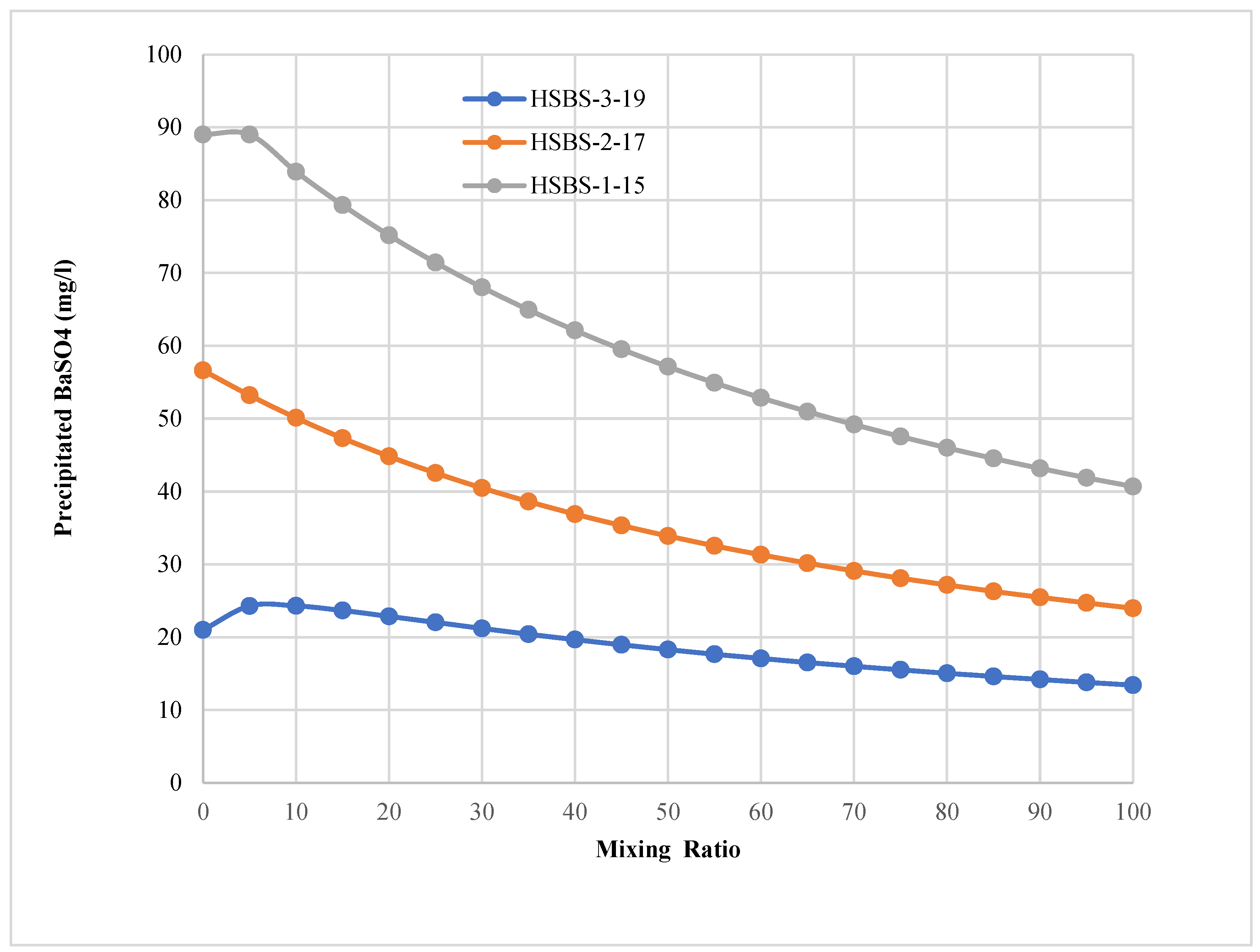
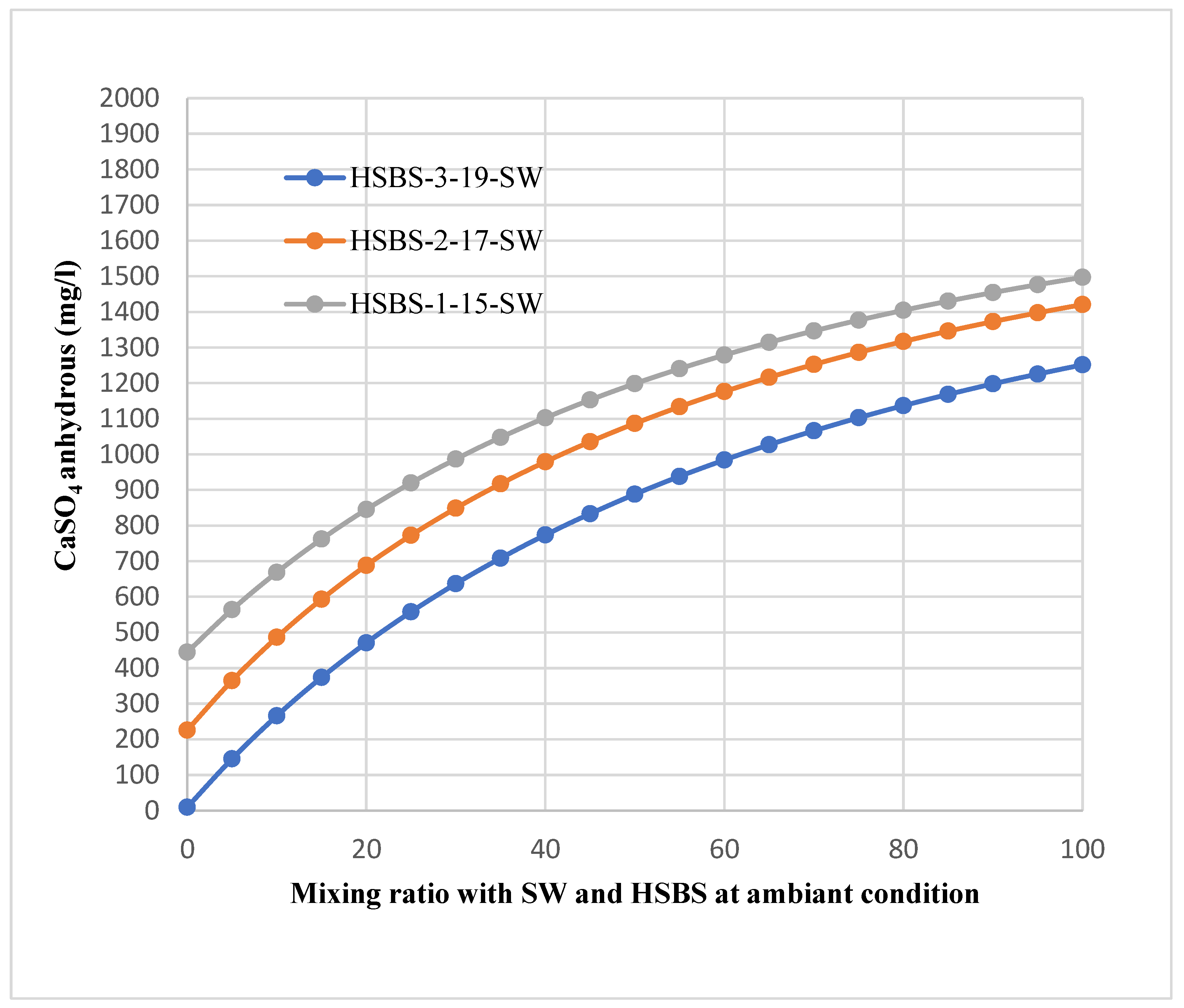
3.5. The Expected Quantity of the SMs Precipitated
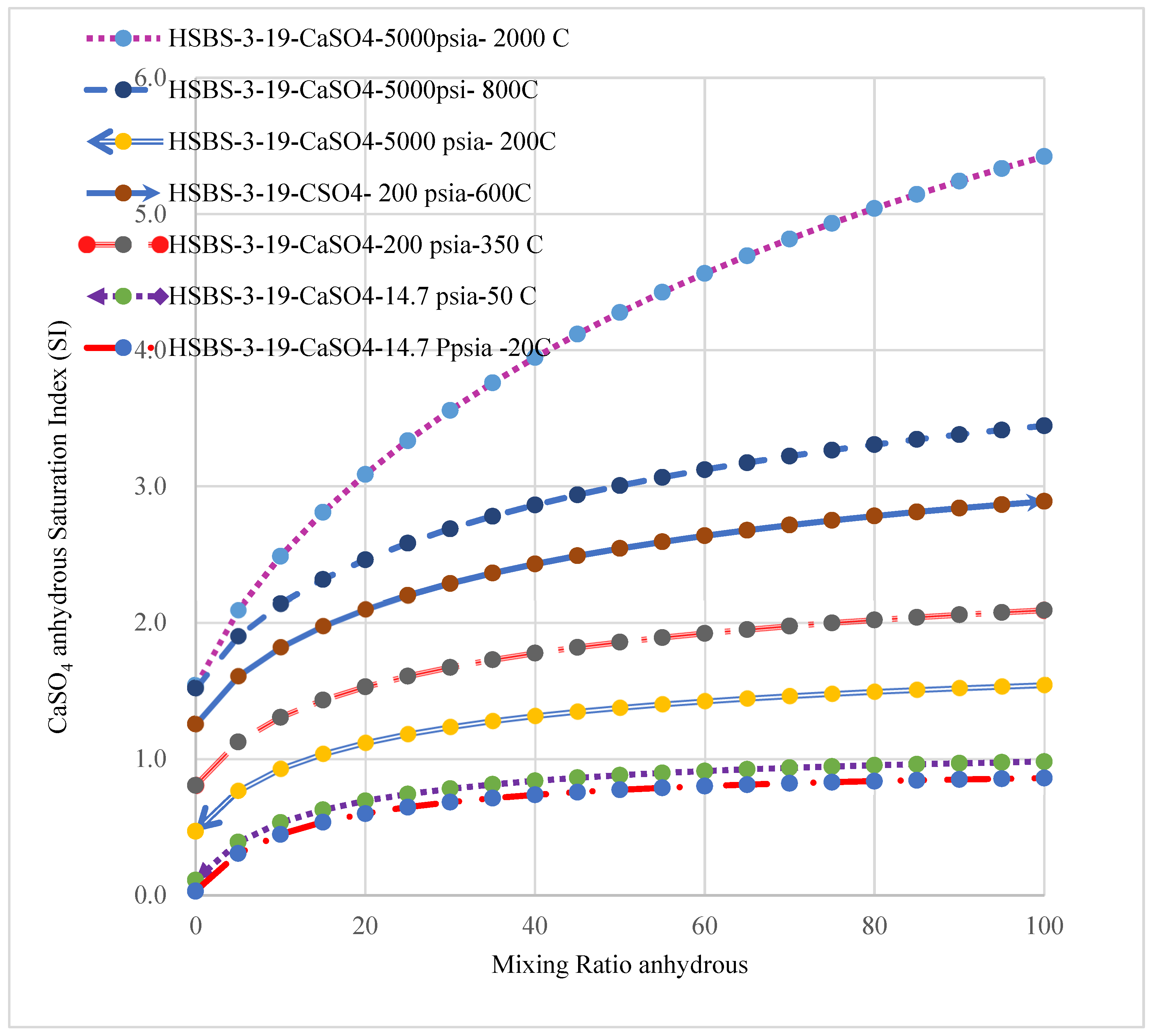
3.6. The Effect of Temperature and Pressure on the Precipitation of SMs
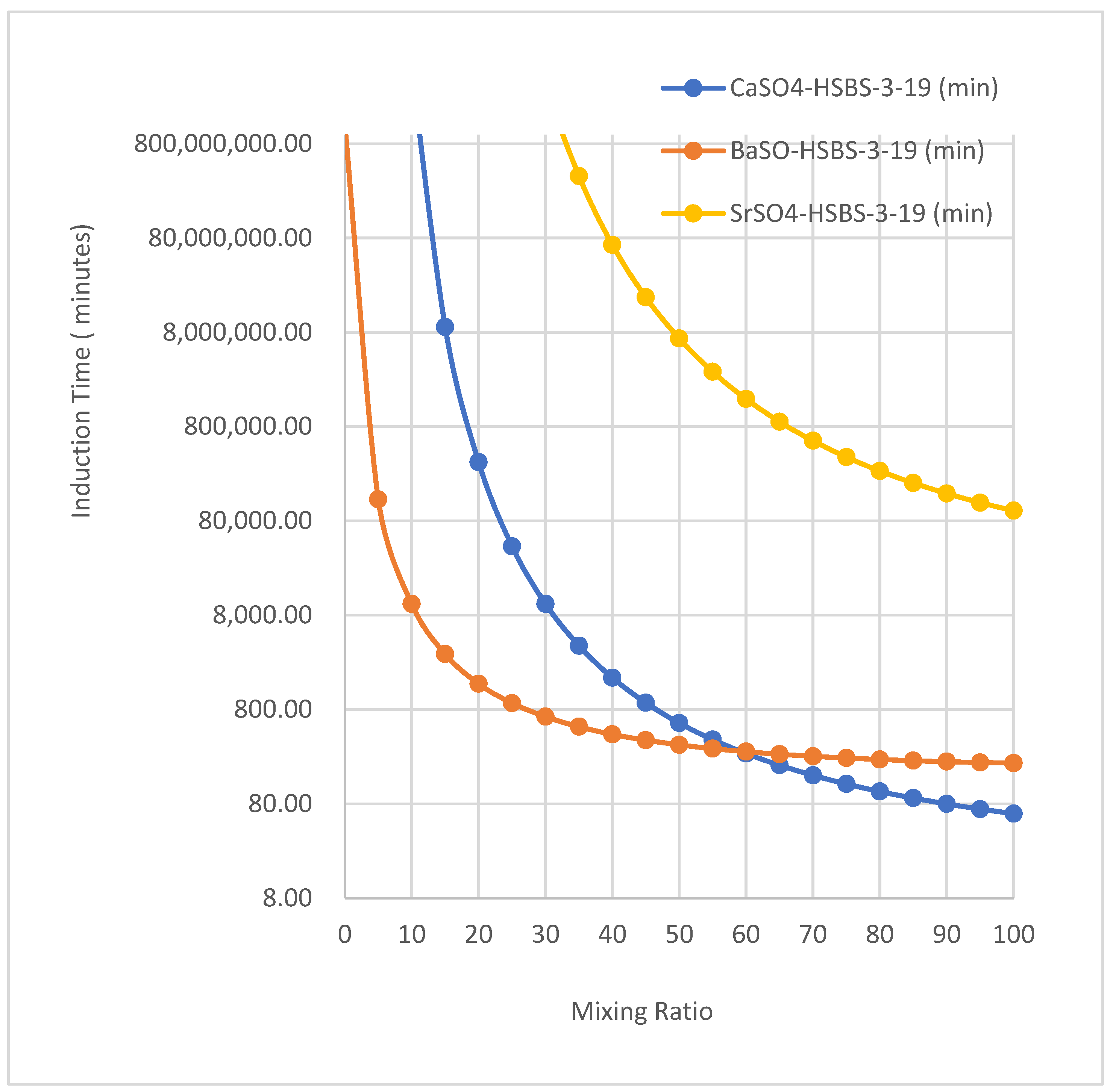
3.7. The Induction Time Required for Precipitation
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B. Sample Calculation of Figs
| Mixing Ratio | Volume | Total Volume | Volume | mg/L | mg/L | mg/L | mg/L | mg/L | mg/L | mg/L | mg/L | mg/L | mg/L |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| % | SW | After Mixing of HSBS | HSBS | CO32− | HCO3− | Na+ | K+ | Mg2+ | Ca2+ | Cl− | SO42− | Ba2+ | Sr2+ |
| 0 | 0.00 | 1.00 | 1.00 | 0.00 | 214 | 63,577 | 2180 | 1924 | 9232 | 98,000 | 175 | 30 | 360 |
| 5 | 0.05 | 1.05 | 1.00 | 0.00 | 210 | 61,328 | 2104 | 1906 | 8841 | 94,534 | 348 | 29 | 343 |
| 10 | 0.10 | 1.10 | 1.00 | 0.00 | 206 | 59,284 | 2035 | 1889 | 8486 | 91,383 | 506 | 27 | 328 |
| 15 | 0.15 | 1.15 | 1.00 | 0.00 | 203 | 57,417 | 1972 | 1873 | 8162 | 88,505 | 650 | 26 | 315 |
| 20 | 0.20 | 1.20 | 1.00 | 0.00 | 200 | 55,706 | 1915 | 1859 | 7865 | 85,868 | 782 | 25 | 302 |
| 25 | 0.25 | 1.25 | 1.00 | 0.00 | 197 | 54,132 | 1862 | 1846 | 7592 | 83,442 | 903 | 24 | 291 |
| 30 | 0.30 | 1.30 | 1.00 | 0.00 | 194 | 52,679 | 1813 | 1834 | 7339 | 81,202 | 1015 | 23 | 280 |
| 35 | 0.35 | 1.35 | 1.00 | 0.00 | 192 | 51,334 | 1768 | 1823 | 7106 | 79,128 | 1119 | 22 | 270 |
| 40 | 0.40 | 1.40 | 1.00 | 0.00 | 190 | 50,084 | 1725 | 1813 | 6889 | 77,202 | 1215 | 22 | 261 |
| 45 | 0.45 | 1.45 | 1.00 | 0.00 | 188 | 48,921 | 1686 | 1804 | 6687 | 75,409 | 1305 | 21 | 252 |
| 50 | 0.50 | 1.50 | 1.00 | 0.00 | 186 | 47,836 | 1650 | 1795 | 6498 | 73,736 | 1388 | 20 | 244 |
| 55 | 0.55 | 1.55 | 1.00 | 0.00 | 184 | 46,820 | 1615 | 1786 | 6322 | 72,171 | 1467 | 19 | 237 |
| 60 | 0.60 | 1.60 | 1.00 | 0.00 | 182 | 45,868 | 1583 | 1779 | 6156 | 70,703 | 1540 | 19 | 230 |
| 65 | 0.65 | 1.65 | 1.00 | 0.00 | 181 | 44,974 | 1553 | 1771 | 6001 | 69,324 | 1609 | 18 | 223 |
| 70 | 0.70 | 1.70 | 1.00 | 0.00 | 179 | 44,132 | 1525 | 1764 | 5855 | 68,027 | 1674 | 18 | 217 |
| 75 | 0.75 | 1.75 | 1.00 | 0.00 | 178 | 43,338 | 1498 | 1758 | 5717 | 66,803 | 1735 | 17 | 211 |
| 80 | 0.80 | 1.80 | 1.00 | 0.00 | 176 | 42,589 | 1473 | 1752 | 5587 | 65,648 | 1793 | 17 | 206 |
| 85 | 0.85 | 1.85 | 1.00 | 0.00 | 175 | 41,879 | 1449 | 1746 | 5464 | 64,555 | 1847 | 16 | 201 |
| 90 | 0.90 | 1.90 | 1.00 | 0.00 | 174 | 41,208 | 1426 | 1740 | 5347 | 63,520 | 1899 | 16 | 196 |
| 95 | 0.95 | 1.95 | 1.00 | 0.00 | 173 | 40,570 | 1405 | 1735 | 5236 | 62,537 | 1948 | 15 | 191 |
| 100 | 1.00 | 2.00 | 1.00 | 0.00 | 172 | 39,965 | 1385 | 1730 | 5131 | 61,604 | 1995 | 15 | 187 |
| mol/L | mol/L | mol/L | mol/L | mol/L | mol/L | mol/L | mol/L | mol/L |
|---|---|---|---|---|---|---|---|---|
| HCO3− | Na+ | K+ | Mg2+ | Ca2+ | Cl− | SO42− | Ba2+ | Sr2+ |
| 0.003500 | 2.764217 | 5.45 × 10−2 | 7.91 × 10−2 | 2.30 × 10−1 | 2.76 | 1.82 × 10−3 | 2.20 × 10−4 | 4.11 × 10−3 |
| 0.003435 | 2.666445 | 5.26 × 10−2 | 7.84 × 10−2 | 2.21 × 10−1 | 2.67 | 3.62 × 10−3 | 2.09 × 10−4 | 3.92 × 10−3 |
| 0.003376 | 2.577561 | 5.09 × 10−2 | 7.77 × 10−2 | 2.12 × 10−1 | 2.58 | 5.26 × 10−3 | 2.00 × 10−4 | 3.75 × 10−3 |
| 0.003321 | 2.496406 | 4.93 × 10−2 | 7.71 × 10−2 | 2.04 × 10−1 | 2.50 | 6.76 × 10−3 | 1.91 × 10−4 | 3.59 × 10−3 |
| 0.003272 | 2.422014 | 4.79 × 10−2 | 7.65 × 10−2 | 1.96 × 10−1 | 2.42 | 8.13 × 10−3 | 1.83 × 10−4 | 3.45 × 10−3 |
| 0.003226 | 2.353574 | 4.65 × 10−2 | 7.60 × 10−2 | 1.89 × 10−1 | 2.35 | 9.40 × 10−3 | 1.76 × 10−4 | 3.32 × 10−3 |
| 0.003184 | 2.290398 | 4.53 × 10−2 | 7.55 × 10−2 | 1.83 × 10−1 | 2.29 | 1.06 × 10−2 | 1.69 × 10−4 | 3.19 × 10−3 |
| 0.003145 | 2.231902 | 4.42 × 10−2 | 7.50 × 10−2 | 1.77 × 10−1 | 2.23 | 1.16 × 10−2 | 1.63 × 10−4 | 3.08 × 10−3 |
| 0.003109 | 2.177584 | 4.31 × 10−2 | 7.46 × 10−2 | 1.72 × 10−1 | 2.18 | 1.26 × 10−2 | 1.57 × 10−4 | 2.98 × 10−3 |
| 0.003075 | 2.127012 | 4.22 × 10−2 | 7.42 × 10−2 | 1.67 × 10−1 | 2.13 | 1.36 × 10−2 | 1.52 × 10−4 | 2.88 × 10−3 |
| 0.003044 | 2.079812 | 4.12 × 10−2 | 7.38 × 10−2 | 1.62 × 10−1 | 2.08 | 1.44 × 10−2 | 1.47 × 10−4 | 2.79 × 10−3 |
| 0.003014 | 2.035656 | 4.04 × 10−2 | 7.35 × 10−2 | 1.58 × 10−1 | 2.04 | 1.53 × 10−2 | 1.42 × 10−4 | 2.70 × 10−3 |
| 0.002987 | 1.994261 | 3.96 × 10−2 | 7.32 × 10−2 | 1.54 × 10−1 | 1.99 | 1.60 × 10−2 | 1.37 × 10−4 | 2.62 × 10−3 |
| 0.002961 | 1.955374 | 3.88 × 10−2 | 7.29 × 10−2 | 1.50 × 10−1 | 1.96 | 1.67 × 10−2 | 1.33 × 10−4 | 2.55 × 10−3 |
| 0.002936 | 1.918775 | 3.81 × 10−2 | 7.26 × 10−2 | 1.46 × 10−1 | 1.92 | 1.74 × 10−2 | 1.29 × 10−4 | 2.48 × 10−3 |
| 0.002913 | 1.884267 | 3.75 × 10−2 | 7.23 × 10−2 | 1.43 × 10−1 | 1.88 | 1.81 × 10−2 | 1.26 × 10−4 | 2.41 × 10−3 |
| 0.002892 | 1.851676 | 3.68 × 10−2 | 7.21 × 10−2 | 1.39 × 10−1 | 1.85 | 1.87 × 10−2 | 1.22 × 10−4 | 2.35 × 10−3 |
| 0.002871 | 1.820847 | 3.62 × 10−2 | 7.18 × 10−2 | 1.36 × 10−1 | 1.82 | 1.92 × 10−2 | 1.19 × 10−4 | 2.29 × 10−3 |
| 0.002852 | 1.791641 | 3.57 × 10−2 | 7.16 × 10−2 | 1.33 × 10−1 | 1.79 | 1.98 × 10−2 | 1.16 × 10−4 | 2.23 × 10−3 |
| 0.002833 | 1.763932 | 3.51 × 10−2 | 7.14 × 10−2 | 1.31 × 10−1 | 1.76 | 2.03 × 10−2 | 1.13 × 10−4 | 2.18 × 10−3 |
| 0.002816 | 1.737609 | 3.46 × 10−2 | 7.12 × 10−2 | 1.28 × 10−1 | 1.74 | 2.08 × 10−2 | 1.10 × 10−4 | 2.13 × 10−3 |
| MLIf*Z^4 | MLIf*Z^1 | ML*Z^2 | ML*Z^2 | MLIf*Z^1 | ML*Z^2 | ML*Z^2 | ML*Z^2 | SUM(Mli*Z^2) | Ionic Strength (Mixture) |
|---|---|---|---|---|---|---|---|---|---|
| Na+ | K+ | Mg2+ | Ca2+ | Cl− | SO42− | Ba2+ | Sr2+ | Sum (ion.Z^Equivalence) | 0.5 *SUM |
| 3.35 | 6.61 × 10−2 | 3.84 × 10−1 | 1.12 | 3.35 | 8.84 × 10−3 | 1.07 × 10−3 | 1.99 × 10−2 | 8.31 | 4.15 |
| 3.21 | 6.34 × 10−2 | 3.78 × 10−1 | 1.06 | 3.21 | 1.75 × 10−2 | 1.01 × 10−3 | 1.89 × 10−2 | 7.97 | 3.98 |
| 3.08 | 6.09 × 10−2 | 3.72 × 10−1 | 1.01 | 3.08 | 2.52 × 10−2 | 9.57 × 10−4 | 1.79 × 10−2 | 7.66 | 3.83 |
| 2.97 | 5.86 × 10−2 | 3.67 × 10−1 | 9.69 × 10−1 | 2.97 | 3.22 × 10−2 | 9.10 × 10−4 | 1.71 × 10−2 | 7.39 | 3.69 |
| 2.86 | 5.66 × 10−2 | 3.62 × 10−1 | 9.28 × 10−1 | 2.86 | 3.85 × 10−2 | 8.67 × 10−4 | 1.63 × 10−2 | 7.14 | 3.57 |
| 2.77 | 5.48 × 10−2 | 3.58 × 10−1 | 8.92 × 10−1 | 2.77 | 4.42 × 10−2 | 8.28 × 10−4 | 1.56 × 10−2 | 6.91 | 3.45 |
| 2.68 | 5.31 × 10−2 | 3.54 × 10−1 | 8.58 × 10−1 | 2.68 | 4.95 × 10−2 | 7.93 × 10−4 | 1.50 × 10−2 | 6.70 | 3.35 |
| 2.60 | 5.15 × 10−2 | 3.50 × 10−1 | 8.27 × 10−1 | 2.60 | 5.43 × 10−2 | 7.60 × 10−4 | 1.44 × 10−2 | 6.51 | 3.25 |
| 2.53 | 5.01 × 10−2 | 3.47 × 10−1 | 7.99 × 10−1 | 2.53 | 5.88 × 10−2 | 7.30 × 10−4 | 1.38 × 10−2 | 6.33 | 3.17 |
| 2.46 | 4.88 × 10−2 | 3.44 × 10−1 | 7.73 × 10−1 | 2.46 | 6.29 × 10−2 | 7.02 × 10−4 | 1.33 × 10−2 | 6.17 | 3.09 |
| 2.40 | 4.76 × 10−2 | 3.41 × 10−1 | 7.48 × 10−1 | 2.40 | 6.67 × 10−2 | 6.77 × 10−4 | 1.29 × 10−2 | 6.02 | 3.01 |
| 2.34 | 4.65 × 10−2 | 3.38 × 10−1 | 7.26 × 10−1 | 2.34 | 7.02 × 10−2 | 6.53 × 10−4 | 1.24 × 10−2 | 5.88 | 2.94 |
| 2.29 | 4.54 × 10−2 | 3.36 × 10−1 | 7.05 × 10−1 | 2.29 | 7.35 × 10−2 | 6.31 × 10−4 | 1.20 × 10−2 | 5.75 | 2.87 |
| 2.24 | 4.44 × 10−2 | 3.33 × 10−1 | 6.85 × 10−1 | 2.24 | 7.66 × 10−2 | 6.10 × 10−4 | 1.17 × 10−2 | 5.63 | 2.81 |
| 2.19 | 4.35 × 10−2 | 3.31 × 10−1 | 6.67 × 10−1 | 2.19 | 7.95 × 10−2 | 5.90 × 10−4 | 1.13 × 10−2 | 5.51 | 2.76 |
| 2.14 | 4.26 × 10−2 | 3.29 × 10−1 | 6.49 × 10−1 | 2.14 | 8.22 × 10−2 | 5.72 × 10−4 | 1.10 × 10−2 | 5.41 | 2.70 |
| 2.10 | 4.18 × 10−2 | 3.27 × 10−1 | 6.33 × 10−1 | 2.10 | 8.47 × 10−2 | 5.55 × 10−4 | 1.07 × 10−2 | 5.31 | 2.65 |
| 2.06 | 4.10 × 10−2 | 3.25 × 10−1 | 6.18 × 10−1 | 2.06 | 8.71 × 10−2 | 5.39 × 10−4 | 1.04 × 10−2 | 5.21 | 2.61 |
| 2.03 | 4.03 × 10−2 | 3.24 × 10−1 | 6.03 × 10−1 | 2.03 | 8.94 × 10−2 | 5.24 × 10−4 | 1.01 × 10−2 | 5.12 | 2.56 |
| 1.99 | 3.96 × 10−2 | 3.22 × 10−1 | 5.90 × 10−1 | 1.99 | 9.15 × 10−2 | 5.09 × 10−4 | 9.84 × 10−3 | 5.04 | 2.52 |
| 1.96 | 3.90 × 10−2 | 3.21 × 10−1 | 5.77 × 10−1 | 1.96 | 9.35 × 10−2 | 4.96 × 10−4 | 9.59 × 10−3 | 4.96 | 2.48 |
| Pressure | Pressure | Temp. | Temp. | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Psia | Bar | C | K | C1 | C2 | C3 | C4 | i^0.5 | C6 | C7 | C8 | log Kco | Kco |
| 2.668 × 10−4 | 2.209 × 10−3 | 4.984 × 10−3 | 2.794 × 10−1 | 9.601 × 10−2 | −1.942 × 10−3 | 2.775 × 10−3 | 2.772 × 10−1 | 0.093804 | 3.719 × 10−1 | 1.609 × 10−2 | |||
| 2.522 × 10−4 | 4.365 × 10−3 | 4.721 × 10−3 | 2.657 × 10−1 | 9.440 × 10−2 | −4.113 × 10−3 | 3.557 × 10−4 | 2.613 × 10−1 | 0.090033 | 3.476 × 10−1 | 1.861 × 10−2 | |||
| 2.392 × 10−4 | 6.298 × 10−3 | 4.485 × 10−3 | 2.533 × 10−1 | 9.295 × 10−2 | −6.059 × 10−3 | −1.813 × 10−3 | 2.470 × 10−1 | 0.086653 | 3.258 × 10−1 | 2.120 × 10−2 | |||
| 2.274 × 10−4 | 8.041 × 10−3 | 4.272 × 10−3 | 2.422 × 10−1 | 9.165 × 10−2 | −7.814 × 10−3 | −3.769 × 10−3 | 2.341 × 10−1 | 0.083605 | 3.062 × 10−1 | 2.383 × 10−2 | |||
| 2.168 × 10−4 | 9.620 × 10−3 | 4.079 × 10−3 | 2.321 × 10−1 | 9.046 × 10−2 | −9.404 × 10−3 | −5.542 × 10−3 | 2.225 × 10−1 | 0.080842 | 2.884 × 10−1 | 2.648 × 10−2 | |||
| 2.071 × 10−4 | 1.106 × 10−2 | 3.903 × 10−3 | 2.229 × 10−1 | 8.939 × 10−2 | −1.085 × 10−2 | −7.155 × 10−3 | 2.119 × 10−1 | 0.078328 | 2.722 × 10−1 | 2.913 × 10−2 | |||
| 1.982 × 10−4 | 1.237 × 10−2 | 3.743 × 10−3 | 2.145 × 10−1 | 8.840 × 10−2 | −1.217 × 10−2 | −8.631 × 10−3 | 2.021 × 10−1 | 0.076028 | 2.574 × 10−1 | 3.175 × 10−2 | |||
| 1.900 × 10−4 | 1.358 × 10−2 | 3.595 × 10−3 | 2.068 × 10−1 | 8.750 × 10−2 | −1.339 × 10−2 | −9.985 × 10−3 | 1.932 × 10−1 | 0.073918 | 2.438 × 10−1 | 3.432 × 10−2 | |||
| 1.825 × 10−4 | 1.469 × 10−2 | 3.459 × 10−3 | 1.997 × 10−1 | 8.667 × 10−2 | −1.451 × 10−2 | −1.123 × 10−2 | 1.850 × 10−1 | 0.071974 | 2.313 × 10−1 | 3.685 × 10−2 | |||
| 1.756 × 10−4 | 1.572 × 10−2 | 3.334 × 10−3 | 1.932 × 10−1 | 8.590 × 10−2 | −1.554 × 10−2 | −1.238 × 10−2 | 1.774 × 10−1 | 0.070179 | 2.197 × 10−1 | 3.930 × 10−2 | |||
| 1.692 × 10−4 | 1.667 × 10−2 | 3.218 × 10−3 | 1.871 × 10−1 | 8.518 × 10−2 | −1.650 × 10−2 | −1.345 × 10−2 | 1.704 × 10−1 | 0.068514 | 2.090 × 10−1 | 4.167 × 10−2 | |||
| 1.632 × 10−4 | 1.755 × 10−2 | 3.110 × 10−3 | 1.814 × 10−1 | 8.452 × 10−2 | −1.739 × 10−2 | −1.444 × 10−2 | 1.639 × 10−1 | 0.066967 | 1.990 × 10−1 | 4.395 × 10−2 | |||
| 1.577 × 10−4 | 1.838 × 10−2 | 3.009 × 10−3 | 1.762 × 10−1 | 8.390 × 10−2 | −1.822 × 10−2 | −1.537 × 10−2 | 1.578 × 10−1 | 0.065525 | 1.897 × 10−1 | 4.614 × 10−2 | |||
| 1.525 × 10−4 | 1.915 × 10−2 | 2.915 × 10−3 | 1.712 × 10−1 | 8.333 × 10−2 | −1.900 × 10−2 | −1.623 × 10−2 | 1.521 × 10−1 | 0.064179 | 1.810 × 10−1 | 4.823 × 10−2 | |||
| 1.476 × 10−4 | 1.987 × 10−2 | 2.827 × 10−3 | 1.666 × 10−1 | 8.279 × 10−2 | −1.972 × 10−2 | −1.704 × 10−2 | 1.468 × 10−1 | 0.062918 | 1.729 × 10−1 | 5.021 × 10−2 | |||
| 1.430 × 10−4 | 2.055 × 10−2 | 2.744 × 10−3 | 1.623 × 10−1 | 8.228 × 10−2 | −2.040 × 10−2 | −1.780 × 10−2 | 1.418 × 10−1 | 0.061736 | 1.653 × 10−1 | 5.207 × 10−2 | |||
| 1.387 × 10−4 | 2.118 × 10−2 | 2.666 × 10−3 | 1.583 × 10−1 | 8.181 × 10−2 | −2.104 × 10−2 | −1.851 × 10−2 | 1.371 × 10−1 | 0.060624 | 1.581 × 10−1 | 5.383 × 10−2 | |||
| 1.347 × 10−4 | 2.178 × 10−2 | 2.593 × 10−3 | 1.544 × 10−1 | 8.136 × 10−2 | −2.164 × 10−2 | −1.919 × 10−2 | 1.327 × 10−1 | 0.059577 | 1.514 × 10−1 | 5.547 × 10−2 | |||
| 1.309 × 10−4 | 2.234 × 10−2 | 2.524 × 10−3 | 1.508 × 10−1 | 8.093 × 10−2 | −2.221 × 10−2 | −1.982 × 10−2 | 1.285 × 10−1 | 0.058590 | 1.450 × 10−1 | 5.699 × 10−2 | |||
| 1.273 × 10−4 | 2.288 × 10−2 | 2.459 × 10−3 | 1.474 × 10−1 | 8.053 × 10−2 | −2.275 × 10−2 | −2.042 × 10−2 | 1.245 × 10−1 | 0.057657 | 1.390 × 10−1 | 5.840 × 10−2 | |||
| 1.239 × 10−4 | 2.338 × 10−2 | 2.397 × 10−3 | 1.442 × 10−1 | 8.016 × 10−2 | −2.326 × 10−2 | −2.099 × 10−2 | 1.208 × 10−1 | 0.056774 | 1.333 × 10−1 | 5.969 × 10−2 |
| C Ba2+ | C SO42− | C Sr2+ | C Ca2+ | C Mg2+ | Ba2+-SO42− | Sr2+-SO42− | Ca2+-SO42− | Mg2+-SO42− | Sum (M-SO42−) | Kco*(M-SO42−) |
|---|---|---|---|---|---|---|---|---|---|---|
| 2.668 × 10−4 | 2.209 × 10−3 | 4.984 × 10−3 | 2.794 × 10−1 | 9.601 × 10−2 | −1.942 × 10−3 | 2.775 × 10−3 | 2.772 × 10−1 | 0.093804 | 3.719 × 10−1 | 1.609 × 10−2 |
| 2.522 × 10−4 | 4.365 × 10−3 | 4.721 × 10−3 | 2.657 × 10−1 | 9.440 × 10−2 | −4.113 × 10−3 | 3.557 × 10−4 | 2.613 × 10−1 | 0.090033 | 3.476 × 10−1 | 1.861 × 10−2 |
| 2.392 × 10−4 | 6.298 × 10−3 | 4.485 × 10−3 | 2.533 × 10−1 | 9.295 × 10−2 | −6.059 × 10−3 | −1.813 × 10−3 | 2.470 × 10−1 | 0.086653 | 3.258 × 10−1 | 2.120 × 10−2 |
| 2.274 × 10−4 | 8.041 × 10−3 | 4.272 × 10−3 | 2.422 × 10−1 | 9.165 × 10−2 | −7.814 × 10−3 | −3.769 × 10−3 | 2.341 × 10−1 | 0.083605 | 3.062 × 10−1 | 2.383 × 10−2 |
| 2.168 × 10−4 | 9.620 × 10−3 | 4.079 × 10−3 | 2.321 × 10−1 | 9.046 × 10−2 | −9.404 × 10−3 | −5.542 × 10−3 | 2.225 × 10−1 | 0.080842 | 2.884 × 10−1 | 2.648 × 10−2 |
| 2.071 × 10−4 | 1.106 × 10−2 | 3.903 × 10−3 | 2.229 × 10−1 | 8.939 × 10−2 | −1.085 × 10−2 | −7.155 × 10−3 | 2.119 × 10−1 | 0.078328 | 2.722 × 10−1 | 2.913 × 10−2 |
| 1.982 × 10−4 | 1.237 × 10−2 | 3.743 × 10−3 | 2.145 × 10−1 | 8.840 × 10−2 | −1.217 × 10−2 | −8.631 × 10−3 | 2.021 × 10−1 | 0.076028 | 2.574 × 10−1 | 3.175 × 10−2 |
| 1.900 × 10−4 | 1.358 × 10−2 | 3.595 × 10−3 | 2.068 × 10−1 | 8.750 × 10−2 | −1.339 × 10−2 | −9.985 × 10−3 | 1.932 × 10−1 | 0.073918 | 2.438 × 10−1 | 3.432 × 10−2 |
| 1.825 × 10−4 | 1.469 × 10−2 | 3.459 × 10−3 | 1.997 × 10−1 | 8.667 × 10−2 | −1.451 × 10−2 | −1.123 × 10−2 | 1.850 × 10−1 | 0.071974 | 2.313 × 10−1 | 3.685 × 10−2 |
| 1.756 × 10−4 | 1.572 × 10−2 | 3.334 × 10−3 | 1.932 × 10−1 | 8.590 × 10−2 | −1.554 × 10−2 | −1.238 × 10−2 | 1.774 × 10−1 | 0.070179 | 2.197 × 10−1 | 3.930 × 10−2 |
| 1.692 × 10−4 | 1.667 × 10−2 | 3.218 × 10−3 | 1.871 × 10−1 | 8.518 × 10−2 | −1.650 × 10−2 | −1.345 × 10−2 | 1.704 × 10−1 | 0.068514 | 2.090 × 10−1 | 4.167 × 10−2 |
| 1.632 × 10−4 | 1.755 × 10−2 | 3.110 × 10−3 | 1.814 × 10−1 | 8.452 × 10−2 | −1.739 × 10−2 | −1.444 × 10−2 | 1.639 × 10−1 | 0.066967 | 1.990 × 10−1 | 4.395 × 10−2 |
| 1.577 × 10−4 | 1.838 × 10−2 | 3.009 × 10−3 | 1.762 × 10−1 | 8.390 × 10−2 | −1.822 × 10−2 | −1.537 × 10−2 | 1.578 × 10−1 | 0.065525 | 1.897 × 10−1 | 4.614 × 10−2 |
| 1.525 × 10−4 | 1.915 × 10−2 | 2.915 × 10−3 | 1.712 × 10−1 | 8.333 × 10−2 | −1.900 × 10−2 | −1.623 × 10−2 | 1.521 × 10−1 | 0.064179 | 1.810 × 10−1 | 4.823 × 10−2 |
| 1.476 × 10−4 | 1.987 × 10−2 | 2.827 × 10−3 | 1.666 × 10−1 | 8.279 × 10−2 | −1.972 × 10−2 | −1.704 × 10−2 | 1.468 × 10−1 | 0.062918 | 1.729 × 10−1 | 5.021 × 10−2 |
| 1.430 × 10−4 | 2.055 × 10−2 | 2.744 × 10−3 | 1.623 × 10−1 | 8.228 × 10−2 | −2.040 × 10−2 | −1.780 × 10−2 | 1.418 × 10−1 | 0.061736 | 1.653 × 10−1 | 5.207 × 10−2 |
| 1.387 × 10−4 | 2.118 × 10−2 | 2.666 × 10−3 | 1.583 × 10−1 | 8.181 × 10−2 | −2.104 × 10−2 | −1.851 × 10−2 | 1.371 × 10−1 | 0.060624 | 1.581 × 10−1 | 5.383 × 10−2 |
| 1.347 × 10−4 | 2.178 × 10−2 | 2.593 × 10−3 | 1.544 × 10−1 | 8.136 × 10−2 | −2.164 × 10−2 | −1.919 × 10−2 | 1.327 × 10−1 | 0.059577 | 1.514 × 10−1 | 5.547 × 10−2 |
| 1.309 × 10−4 | 2.234 × 10−2 | 2.524 × 10−3 | 1.508 × 10−1 | 8.093 × 10−2 | −2.221 × 10−2 | −1.982 × 10−2 | 1.285 × 10−1 | 0.058590 | 1.450 × 10−1 | 5.699 × 10−2 |
| 1.273 × 10−4 | 2.288 × 10−2 | 2.459 × 10−3 | 1.474 × 10−1 | 8.053 × 10−2 | −2.275 × 10−2 | −2.042 × 10−2 | 1.245 × 10−1 | 0.057657 | 1.390 × 10−1 | 5.840 × 10−2 |
| 1.239 × 10−4 | 2.338 × 10−2 | 2.397 × 10−3 | 1.442 × 10−1 | 8.016 × 10−2 | −2.326 × 10−2 | −2.099 × 10−2 | 1.208 × 10−1 | 0.056774 | 1.333 × 10−1 | 5.969 × 10−2 |
| ∑(M-Cso4) | B | C1 | C2 | C3 | C4 | C5 | C6 | At Equilibrium |
|---|---|---|---|---|---|---|---|---|
| sum∑ (M-SO42−) | Kco*(∑(M-SO42−)) | Kco* ((∑M-SO42−)^2) | Kco*C SO42−*4 | 1.000 | 2.000 | 3.000 | 2^0.5 | [SO42−] |
| 3.719 × 10−1 | 1.609 × 10−2 | 5.985 × 10−3 | 3.825 × 10−4 | −1.016 | 1.032 | 1.016 | 0.000 | 2.174 × 10−3 |
| 3.476 × 10−1 | 1.861 × 10−2 | 6.470 × 10−3 | 9.352 × 10−4 | −1.019 | 1.038 | 1.019 | 0.000 | 4.284 × 10−3 |
| 3.258 × 10−1 | 2.120 × 10−2 | 6.908 × 10−3 | 1.640 × 10−3 | −1.021 | 1.043 | 1.022 | 0.001 | 6.165 × 10−3 |
| 3.062 × 10−1 | 2.383 × 10−2 | 7.297 × 10−3 | 2.504 × 10−3 | −1.024 | 1.048 | 1.025 | 0.001 | 7.849 × 10−3 |
| 2.884 × 10−1 | 2.648 × 10−2 | 7.637 × 10−3 | 3.534 × 10−3 | −1.026 | 1.054 | 1.028 | 0.002 | 9.364 × 10−3 |
| 2.722 × 10−1 | 2.913 × 10−2 | 7.927 × 10−3 | 4.734 × 10−3 | −1.029 | 1.059 | 1.031 | 0.002 | 1.073 × 10−2 |
| 2.574 × 10−1 | 3.175 × 10−2 | 8.170 × 10−3 | 6.105 × 10−3 | −1.032 | 1.064 | 1.035 | 0.003 | 1.198 × 10−2 |
| 2.438 × 10−1 | 3.432 × 10−2 | 8.367 × 10−3 | 7.648 × 10−3 | −1.034 | 1.070 | 1.038 | 0.004 | 1.311 × 10−2 |
| 2.313 × 10−1 | 3.685 × 10−2 | 8.521 × 10−3 | 9.363 × 10−3 | −1.037 | 1.075 | 1.041 | 0.005 | 1.414 × 10−2 |
| 2.197 × 10−1 | 3.930 × 10−2 | 8.633 × 10−3 | 1.125 × 10−2 | −1.039 | 1.080 | 1.045 | 0.005 | 1.508 × 10−2 |
| 2.090 × 10−1 | 4.167 × 10−2 | 8.708 × 10−3 | 1.330 × 10−2 | −1.042 | 1.085 | 1.048 | 0.006 | 1.595 × 10−2 |
| 1.990 × 10−1 | 4.395 × 10−2 | 8.747 × 10−3 | 1.551 × 10−2 | −1.044 | 1.090 | 1.051 | 0.007 | 1.676 × 10−2 |
| 1.897 × 10−1 | 4.614 × 10−2 | 8.754 × 10−3 | 1.788 × 10−2 | −1.046 | 1.094 | 1.055 | 0.009 | 1.750 × 10−2 |
| 1.810 × 10−1 | 4.823 × 10−2 | 8.731 × 10−3 | 2.040 × 10−2 | −1.048 | 1.099 | 1.058 | 0.010 | 1.818 × 10−2 |
| 1.729 × 10−1 | 5.021 × 10−2 | 8.682 × 10−3 | 2.307 × 10−2 | −1.050 | 1.103 | 1.061 | 0.011 | 1.882 × 10−2 |
| 1.653 × 10−1 | 5.207 × 10−2 | 8.608 × 10−3 | 2.589 × 10−2 | −1.052 | 1.107 | 1.064 | 0.012 | 1.942 × 10−2 |
| 1.581 × 10−1 | 5.383 × 10−2 | 8.512 × 10−3 | 2.884 × 10−2 | −1.054 | 1.111 | 1.067 | 0.014 | 1.997 × 10−2 |
| 1.514 × 10−1 | 5.547 × 10−2 | 8.398 × 10−3 | 3.192 × 10−2 | −1.055 | 1.114 | 1.070 | 0.015 | 2.049 × 10−2 |
| 1.450 × 10−1 | 5.699 × 10−2 | 8.266 × 10−3 | 3.512 × 10−2 | −1.057 | 1.117 | 1.073 | 0.016 | 2.098 × 10−2 |
| 1.390 × 10−1 | 5.840 × 10−2 | 8.119 × 10−3 | 3.844 × 10−2 | −1.058 | 1.120 | 1.076 | 0.018 | 2.143 × 10−2 |
| 1.333 × 10−1 | 5.969 × 10−2 | 7.959 × 10−3 | 4.187 × 10−2 | −1.060 | 1.123 | 1.079 | 0.020 | 2.186 × 10−2 |
| SW | Constant (Equation (13)) | [Ba2+] | [Mg2+] | [Ca2+] | [Sr2+] |
|---|---|---|---|---|---|
| Mixing Ratio | 1 + Kco([SO42−]) | [Ba2+] at Equilibrium | [Mg2+] at Equilibium | [Ca2+] at Equilibium | [Sr2+] at Equilibium |
| 0 | 1.0001 | 2.67 × 10−4 | 9.60 × 10−2 | 2.79 × 10−1 | 4.98 × 10−3 |
| 5 | 1.0002 | 2.52 × 10−4 | 9.44 × 10−2 | 2.66 × 10−1 | 4.72 × 10−3 |
| 10 | 1.0004 | 2.39 × 10−4 | 9.29 × 10−2 | 2.53 × 10−1 | 4.48 × 10−3 |
| 15 | 1.0006 | 2.27 × 10−4 | 9.16 × 10−2 | 2.42 × 10−1 | 4.27 × 10−3 |
| 20 | 1.0009 | 2.17 × 10−4 | 9.04 × 10−2 | 2.32 × 10−1 | 4.08 × 10−3 |
| 25 | 1.0011 | 2.07 × 10−4 | 8.93 × 10−2 | 2.23 × 10−1 | 3.90 × 10−3 |
| 30 | 1.0015 | 1.98 × 10−4 | 8.83 × 10−2 | 2.14 × 10−1 | 3.74 × 10−3 |
| 35 | 1.0018 | 1.90 × 10−4 | 8.73 × 10−2 | 2.06 × 10−1 | 3.59 × 10−3 |
| 40 | 1.0023 | 1.82 × 10−4 | 8.65 × 10−2 | 1.99 × 10−1 | 3.45 × 10−3 |
| 45 | 1.0027 | 1.75 × 10−4 | 8.57 × 10−2 | 1.93 × 10−1 | 3.32 × 10−3 |
| 50 | 1.0032 | 1.69 × 10−4 | 8.49 × 10−2 | 1.86 × 10−1 | 3.21 × 10−3 |
| 55 | 1.0037 | 1.63 × 10−4 | 8.42 × 10−2 | 1.81 × 10−1 | 3.10 × 10−3 |
| 60 | 1.0043 | 1.57 × 10−4 | 8.35 × 10−2 | 1.75 × 10−1 | 3.00 × 10−3 |
| 65 | 1.0048 | 1.52 × 10−4 | 8.29 × 10−2 | 1.70 × 10−1 | 2.90 × 10−3 |
| 70 | 1.0055 | 1.47 × 10−4 | 8.23 × 10−2 | 1.66 × 10−1 | 2.81 × 10−3 |
| 75 | 1.0061 | 1.42 × 10−4 | 8.18 × 10−2 | 1.61 × 10−1 | 2.73 × 10−3 |
| 80 | 1.0068 | 1.38 × 10−4 | 8.13 × 10−2 | 1.57 × 10−1 | 2.65 × 10−3 |
| 85 | 1.0075 | 1.34 × 10−4 | 8.08 × 10−2 | 1.53 × 10−1 | 2.57 × 10−3 |
| 90 | 1.0082 | 1.30 × 10−4 | 8.03 × 10−2 | 1.50 × 10−1 | 2.50 × 10−3 |
| 95 | 1.0090 | 1.26 × 10−4 | 7.98 × 10−2 | 1.46 × 10−1 | 2.44 × 10−3 |
| 100 | 1.0098 | 1.23 × 10−4 | 7.94 × 10−2 | 1.43 × 10−1 | 2.37 × 10−3 |
| SW | [M2+][SO42−] = IAP | LOG([Ba2+][SO42−]) | [BaSO4] | [BaSO4] |
|---|---|---|---|---|
| Mixing Ratio | [Ba2+][SO42−] | log (IAP) of BaSO4 | Pksp | Saturation Index (SI) |
| 0 | 5.80 × 10−7 | −6.2366 | 6.7541 | 0.5174 |
| 5 | 1.08 × 10−6 | −5.9664 | 6.7382 | 0.7718 |
| 10 | 1.47 × 10−6 | −5.8315 | 6.7265 | 0.8950 |
| 15 | 1.78 × 10−6 | −5.7486 | 6.7182 | 0.9695 |
| 20 | 2.03 × 10−6 | −5.6929 | 6.7124 | 1.0195 |
| 25 | 2.22 × 10−6 | −5.6537 | 6.7088 | 1.0551 |
| 30 | 2.37 × 10−6 | −5.6253 | 6.7069 | 1.0816 |
| 35 | 2.49 × 10−6 | −5.6045 | 6.7064 | 1.1019 |
| 40 | 2.57 × 10−6 | −5.5892 | 6.7071 | 1.1179 |
| 45 | 2.64 × 10−6 | −5.5781 | 6.7087 | 1.1306 |
| 50 | 2.69 × 10−6 | −5.5701 | 6.7110 | 1.1409 |
| 55 | 2.72 × 10−6 | −5.5647 | 6.7140 | 1.1493 |
| 60 | 2.75 × 10−6 | −5.5612 | 6.7175 | 1.1563 |
| 65 | 2.76 × 10−6 | −5.5593 | 6.7213 | 1.1621 |
| 70 | 2.76 × 10−6 | −5.5587 | 6.7255 | 1.1669 |
| 75 | 2.76 × 10−6 | −5.5591 | 6.7300 | 1.1709 |
| 80 | 2.75 × 10−6 | −5.5604 | 6.7347 | 1.1743 |
| 85 | 2.74 × 10−6 | −5.5624 | 6.7395 | 1.1771 |
| 90 | 2.72 × 10−6 | −5.5650 | 6.7444 | 1.1795 |
| 95 | 2.70 × 10−6 | −5.5680 | 6.7495 | 1.1814 |
| 100 | 2.68 × 10−6 | −5.5715 | 6.7545 | 1.1830 |
| Amount | Amount | |
|---|---|---|
| Precipitated | Precipitated | |
| Mixing Ratio | mol/L | mg/L |
| 0 | 0.00018 | 21 |
| 5 | 0.00021 | 24 |
| 10 | 0.00021 | 24 |
| 15 | 0.00020 | 24 |
| 20 | 0.00020 | 23 |
| 25 | 0.00019 | 22 |
| 30 | 0.00018 | 21 |
| 35 | 0.00018 | 20 |
| 40 | 0.00017 | 20 |
| 45 | 0.00016 | 19 |
| 50 | 0.00016 | 18 |
| 55 | 0.00015 | 18 |
| 60 | 0.00015 | 17 |
| 65 | 0.00014 | 17 |
| 70 | 0.00014 | 16 |
| 75 | 0.00013 | 16 |
| 80 | 0.00013 | 15 |
| 85 | 0.00013 | 15 |
| 90 | 0.00012 | 14 |
| 95 | 0.00012 | 14 |
| 100 | 0.00012 | 13 |
| Mixing Ratio | Induction Time | Induction Time |
|---|---|---|
| KAN Equation | KAN Equation | |
| sec | min | |
| 0 | 73,876,414,107.62 | 1,231,273,568.46 |
| 5 | 8,127,659.26 | 135,460.99 |
| 10 | 633,403.88 | 10,556.73 |
| 15 | 185,416.07 | 3090.27 |
| 20 | 89,969.12 | 1499.49 |
| 25 | 56,010.45 | 933.51 |
| 30 | 40,178.40 | 669.64 |
| 35 | 31,484.08 | 524.73 |
| 40 | 26,164.84 | 436.08 |
| 45 | 22,655.40 | 377.59 |
| 50 | 20,209.40 | 336.82 |
| 55 | 18,433.23 | 307.22 |
| 60 | 17,102.59 | 285.04 |
| 65 | 16,081.59 | 268.03 |
| 70 | 15,283.69 | 254.73 |
| 75 | 14,651.52 | 244.19 |
| 80 | 14,145.66 | 235.76 |
| 85 | 13,738.26 | 228.97 |
| 90 | 13,409.14 | 223.49 |
| 95 | 13,143.33 | 219.06 |
| 100 | 12,929.54 | 215.49 |
References
- MEWRE. Statistical Year Book; Ministry of Electricity and Water and Renewable energy (MEWRE): Kuwait City, Kuwait, 2022.
- Drioli, E.; Curcio, E.; Di Profio, G. Integrated Membrane Operations for Seawater Desalination and Salt Produc-tion. Desalination 2004, 167, 1–11. [Google Scholar]
- Altmann, T.; Attenborough, A.; Kenny, C. Extraction of Sodium Chloride from Seawater Using Nanofiltration. UK Patent Application GB 2395946 A, 17 November 2004. [Google Scholar]
- Wang, H.; Zhong, Y.; Du, B.; Zhao, Y.; Wang, M. Recovery of both magnesium and lithium from high Mg/Li ratio brines using a novel process. Hydrometallurgy 2017, 175, 102–108. [Google Scholar] [CrossRef]
- Al-Sairfi, H.; Koshuriyan, M.; Ahmed, M. Performance feasibility study of direct contact membrane distillation systems in the treatment of seawater and oilfield-produced brine: The effect of hot- and cold-channel depth. Desalin. Water Treat. 2023, 313, 26–36. [Google Scholar] [CrossRef]
- Wallace, P.S. Zero Discharge Water Desalination Plant with Minerals Extraction Integrated with Natural Gas Combined Cycle Power Generation. Patent US20110198285A1, 18 August 2011. [Google Scholar]
- Hou, J.; Alghunaimi, F.; Han, M.; Aljuryyed, N. Removal of High-Concentration Sulfate from SeaWater by Ettringite Precipitation. J. Chem. 2022, 8723962. [Google Scholar] [CrossRef]
- Jeppesen, T.; Shu, L.; Keir, G.; Jegatheesan, V. Metal recovery from reverse osmosis concentrate. J. Clean. Prod. 2009, 17, 703–707. [Google Scholar] [CrossRef]
- Dawoud, M.A.; Al-Mulla, M.M. Environmental Impacts of Seawater Desalination: Arabian Gulf Case Study. Int. J. Environ. Sustain. 2012, 1, 22–37. [Google Scholar] [CrossRef]
- Morillo, J.; Usero, J.; Rosado, D.; El Bakouri, H.; Riaza, A.; Bernaola, F.-J. Comparative study of brine management technologies for desalination plants. Desalination 2014, 336, 32–49. [Google Scholar] [CrossRef]
- BinMerdhah, A.B. Inhibition of barium sulfate scale at high-barium formation water. J. Pet. Sci. Eng. 2012, 90–91, 124–130. [Google Scholar] [CrossRef]
- Bageri, B.S.; Mahmoud, M.A.; Shawabkeh, R.A.; Al-Mutairi, S.H.; Abdulraheem, A. Toward a complete removal of barite scale using a chelating agent and catalysts. Arab. J. Sci. Eng. 2017, 42, 1667–1674. [Google Scholar] [CrossRef]
- Gamal, H.; Al-Afnan, S.; Elkatatny, S.; Bahgat, M. Barium Sulfate Scale Removal at Low-Temperature. Geofluids 2021, 2021, 1–12. [Google Scholar] [CrossRef]
- Ali, A.M.; Messaoud, H. Barium Sulphate Deposits. Energy Procedia 2018, 157, 879–891. [Google Scholar] [CrossRef]
- Boerlage, S.F.E.; Kennedy, M.D.; Witkamp, J.G.; Van Der Hoek, P.J.; Schippers, J.C. BaSO4 solubility prediction in reverse osmosis membrane systems. J. Membr. Sci. 1999, 159, 47–59. [Google Scholar] [CrossRef]
- Boerlage, S.F.S.; Kennedy, M.D.; Bremere, I.; Witkamp, G.J.; Van der Hoek, J.P.; Schippers, J.C. The scaling po-tential of barium sulphate in reverse osmosis system. J. Membr. Sci. 2002, 197, 251–268. [Google Scholar] [CrossRef]
- Antony, A.; Le-Clench, P. Barium sulfate(BaSO4), fouling due to. In Encyclopedia of Membrane; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1–2. [Google Scholar]
- Kamari, A.; Gharagheizi, F.; Bahadori, A.; Mohammadi, A.H. Rigorous modeling for prediction of barium sulfate (barite) deposition in oilfield brines. Fluid Phase Equilibria 2014, 366, 117–126. [Google Scholar] [CrossRef]
- Cabrera, S.M.; Winnubst, L.; Richter, H.; Voigt, I.; McCutcheon, J.; Nijmeijer, A. Performance evaluation of an industrial ceramic nanofiltration unit for wastewater treatment in oil production. Water Res. 2022, 220, 118593. [Google Scholar] [CrossRef]
- Jian, C. Solubility and solubility constant of barium sulfate in aqueous sodium sulfate solutions between 0 and 80c. J. Solut. Chem. 1995, 25, 105–111. [Google Scholar] [CrossRef]
- Monnin, C. A thermodynamic model for the solubility of barite and celestite in electrolyte solutions and seawater to 200 °C and to 1 kbar. Chem. Geol. 1999, 153, 187–209. [Google Scholar] [CrossRef]
- Yan, Y.; Yu, T.; Song, J.; Wu, B.; Qu, C. A review of prediction methods for oilfield produced water scaling. In 3rd International Conference on Green Energy and Sustainable Development IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2021; Volume 651, p. 032052. [Google Scholar]
- Mitchell, W.R.; Grist, M.D.; Boyle, J.M. Chemical treatments associated with North Sea projects. J. Pet. Technol. SPE 1980, 7880, 904–912. [Google Scholar] [CrossRef]
- Lindlof, C.J.; Stoffer, G.K. A case study of sea water injection incompatibility. J. Pet. Technol. 1983, 35, 1256–1262. [Google Scholar] [CrossRef]
- Shuler, J.P.; Freitas, A.E.; Bowker, A.K. Selection and application of BaSO4 scale inhibitors for a CO2 flood, Rangely Weber Sand Unit, Colorado. Soc. Pet. Eng. SPE 1991, 18973, 1–8. [Google Scholar] [CrossRef]
- IMARC Group. Barite Pricing Report: Q2 2025. Available online: https://www.imarcgroup.com/barite-pricing-report (accessed on 18 May 2025).
- McRae, M.E. Barite. In Mineral Commodity Summaries 2022; US Geological Survey: Reston, VA, USA, 2022; pp. 30–31. [Google Scholar]
- Corrêa, L.F.; Hao, J.; Neerup, R.; Almeida, S.; Shi, M.; Thomsen, K.; Fosbøl, P.L. Review of barium sulphate solubility measurements. Geothermics 2022, 104, 102465. [Google Scholar] [CrossRef]
- Miranda, M.A.; Ghosh, A.; Mahmodi, G.; Xie, S.; Shaw, M.; Kim, S.; Krzmarzick, M.J.; Lampert, D.J.; Aichele, C.P. Treatment and Recovery of High-Value Elements from Produced Water. Water 2022, 14, 880. [Google Scholar] [CrossRef]
- Olajire, A.A. Recent advances on the treatment technology of oil and gas produced water for sustainable energy industry-mechanistic aspects and process chemistry perspectives. Chem. Eng. J. Adv. 2020, 4, 100049. [Google Scholar] [CrossRef]
- Mahbouba, Z.N.; Abdulkhalik, M.K.; Mussa, J.H. Characteristics and management of produced water in Al-Ahdab oil field. In Material Science and Engineering; IOP Publishing: Reston, VA, USA, 2021; pp. 1094–12090. [Google Scholar] [CrossRef]
- Al Salem, F.; Thiemann, T. Variability in Quantity and Salinity of Produced Water from an Oil Production in South Kuwait. Engineering 2024, 16, 8–23. [Google Scholar] [CrossRef]
- Al-Hubail, J.; El-Dash, K. Managing disposal of water produced with petroleum in Kuwait. J. Environ. Manag. 2006, 79, 43–50. [Google Scholar] [CrossRef]
- Isemin, A.I.; Inyang, P.N.; Okoro, D.M. Oil field produced water treatment. Pet. Eng. 2015, 86, 35395–35397. [Google Scholar]
- Bahadori, A.; Zahedi, G.; Zendehboudi, S. Estimation of potential barium sulfate precipitation in oilfield using a simple predictive tool. Environ. Prog. Sustain. Energy 2012, 32, 860–865. [Google Scholar] [CrossRef]
- Kausley, S.B.; Malhotra, C.P.; Pandit, A.B. Treatment and reuse of shale gas wastewater: Electrocoagulation system for enhanced removal of organic contamination and scale causing divalent cations. J. Water Process. Eng. 2017, 16, 149–162. [Google Scholar] [CrossRef]
- Udeagbara, S.; Isehunwa, S.; Okereke, N.; Oguamah, I.U.; Kerunwa, A.; Nwanwe, O.; Arellano-Garcia, H. Treatment of produced water from Niger Delta oil fields using sequential mixture of bio-adsorbents. Cogent Eng. 2021, 8, 1939927. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, X.; Ren, X.; Tang, Q.; Fang, S.; Duan, M. Oil aerated flocs formation assisted by a flocculant for heavy oil produced water treatment. J. Water Process. Eng. 2022, 49, 103141. [Google Scholar] [CrossRef]
- Alomar, T.; Hameed, B.; Usman, M.; Almomani, F.; Ba-Abbad, M.; Khraisheh, M. Recent advances on the treatment of oil fields produced water by adsorption and advanced oxidation processes. J. Water Process. Eng. 2022, 49, 103034. [Google Scholar] [CrossRef]
- Ali, A.; Quist-Jensen, C.A.; Macedonio, F.; Drioli, E. Application of Membrane Crystallization for recovery of minerals from produced water. Membranes 2015, 5, 772–792. [Google Scholar] [CrossRef] [PubMed]
- Al-Salmi, M.; Laqbabi, M.; Al-Obaidan, S.; Al-Maamari, R.S.; Khayet, M.; Al-Abri, M. Application of membrane distillation for the treatment of oil produced water. Desalination 2020, 494, 114678. [Google Scholar] [CrossRef]
- Mero, J.L. The Mineral Resources of the Sea. Geol. Mag. 1965, 102, 565. [Google Scholar] [CrossRef]
- Dickinson, W.; Sanders, L. Noval barium sulfate scale inhibitor for use in high Iron environments. In Proceedings of the Society of Petroleum Engineers (SPE) Latin America and Caribbean Petroleum Engineering Conference, SPE-153613-MS, Mexico City, Mexico, 16–18 April 2012. [Google Scholar]
- Quist-Jensen, C.; Macedonio, F.; Drioli, E. Membrane crystallization for salts recovery from brine—An experimental and theoretical analysis. Desalin. Water Treat. 2016, 57, 7593–7603. [Google Scholar] [CrossRef]
- Kim, J.K.; Hong, S. Recovery of water and minerals from shale gas produced water by membrane distillation crystallization. Water Res. 2018, 129, 447–459. [Google Scholar] [CrossRef]
- Pramanik, B.K.; Thangavadivel, K.; Shu, L.; Jegatheesan, V. A critical review of membrane crystallization for the purification of water and recovery of minerals. Rev. Environ. Sci. Bio/Technol. 2016, 15, 411–439. [Google Scholar] [CrossRef]
- Zhu, B.; Wilson, S.; Zeyen, N.; Raudsepp, M.J.; Zolfaghari, A.; Wang, B.; Rostron, B.J.; Snihur, K.N.; von Gunten, K.; Harrison, A.L.; et al. Unlocking the potential of hydraulic fracturing flowback and produced water for CO2 removal via mineral carbonation. Appl. Geochem. 2022, 142, 105345. [Google Scholar] [CrossRef]
- Curico, E.; Drioli, E. Membrane Distillation and Related Operations—A Review. Sep. Purif. Rev. 2005, 34, 35–86. [Google Scholar] [CrossRef]
- Salmón, I.R.; Luis, P. Membrane crystallization via membrane distillation. Chem. Eng. Process. Process. Intensif. 2018, 123, 258–271. [Google Scholar] [CrossRef]
- Al-Sairfi, H.; Koshuriyan, M.; Ahmed, M. Membrane distillation of saline feeds and produced water: A comparative study of an air-gap and vacuum-driven modules. Desalin. Water Treat. 2024, 317, 100145. [Google Scholar] [CrossRef]
- Cheng, W.; Li, Z.; Cheng, F. Solubility of Li2CO3 in Na–K–Li–Cl brines from 20 to 90 °C. J. Chem. Thermodyn. 2013, 67, 74–82. [Google Scholar] [CrossRef]
- Guide to Best Practices for Ocean CO2 Measurements; Dickson, A.G.; Sabine, C.L.; Christian, J.R. (Eds.) PICES Special Publication. U.S. Department of Commerce, NO-AA; 2007. Available online: https://www.pmel.noaa.gov/co2/files/dickson_thecarbondioxidesysteminseawater_equilibriumchemistryandmeasurementspp17-40.pdf (accessed on 20 May 2025).
- Meijer, J.; Van Rosmalen, G. Solubilities and supersaturations of calcium sulfate and its hydrates in seawater. Desalination 1984, 51, 255–305. [Google Scholar] [CrossRef]
- Haynes, W.M. (Ed.) CRC Handbook of Chemistry and Physics, 103rd ed.; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Ksp Table: Solubility Product Constants. Department of Chemistry, University of Massachusetts Amherst: Amherst, MA, USA. Available online: https://owl.oit.umass.edu/departments/Chemistry/appendix/Ksp.html (accessed on 8 September 2025).
- Logunov, A.V.; Kopyrin, V.A.; Portnyagin, A.L.; Deneko, M.V. Analysis of the application for the magnetohydrodynamic effect in the hydrocarbon production. J. Phys. Conf. Ser. 2020, 1441, 012023. [Google Scholar] [CrossRef]
- Pitzer, K.S.; Mayorga, G. Thermodynamics of electrolytes. II. Activity and osmotic coefficients for strong electrolytes with one or both ions univalent. J. Phys. Chem. 1973, 77, 2300–2308. [Google Scholar] [CrossRef]
- Pitzer, K.S.; Mayorga, G. Thermodynamics of electrolytes. III. Activity and osmotic coefficients for 2-2 electrolytes. J. Solut. Chem. 1974, 3, 539–546. [Google Scholar] [CrossRef]
- Pitzer, K.S. Activity Coefficients in Electrolyte Solutions, 2nd ed.; CRC Press: Boca Raton, FL, USA, 1991. [Google Scholar]
- Ulfsbo, A.; Abbas, Z.; Turner, D.R. Activity coefficients of a simplified seawater electrolyte at varying salinity (5–40) and temperature (0 and 25 °C) using Monte Carlo simulations. Mar. Chem. 2015, 171, 78–86. [Google Scholar] [CrossRef]
- Møller, P. Parameters and temperature dependencies for the Pitzer equation applied to aqueous sodium chloride solutions. J. Geochim. Cosmochim. Acta 1988, 52, 1341–1346. [Google Scholar]
- Simoes, M.C.; Hughes, K.J.; Ingham, D.B.; Ma, L.; Pourkashanian, M. Estimation of the Pitzer Parameters for 1–1, 2–1, 3–1, 4–1, and 2–2 Single Electrolytes at 25 °C. J. Chem. Eng. Data 2016, 61, 2536–2554. [Google Scholar] [CrossRef]
- Monnin, C.; Galinier, C. The solubility of celestite and barite in electrolyte solutions and natural waters at 25 °C: A thermodynamic study. Chem. Geol. 1988, 71, 283–296. [Google Scholar] [CrossRef]
- Oddo, J.E.; Tomson, M.B. Simplified Calculation of CACO3 Saturation at High Temperatures and Pressures in Brine Solutions. J. Pet. Technol. 1982, 34, 1583–1590. [Google Scholar] [CrossRef]
- Odd, J.E.; Tomas, M.B. Why Scale Forms in the Oil Field and Methods to Predict It, SPE Production and Facilities. Soc. Pet. Eng. 1994, 9, 47–54. [Google Scholar]
- Al-Bazali, T. Insight into Debye Hückel length (κ−1): Smart gravimetric and swelling techniques reveals discrepancy of diffuse double layer theory at high ionic concentrations. J. Pet. Explor. Prod. Technol. 2022, 12, 461–471. [Google Scholar] [CrossRef]
- Abrams, D.S.; Prausnitz, J.M. Statistical thermodynamics of liquid mixtures: A new expression for the excess Gibbs energy of partly or completely miscible systems. AIChE J. 1975, 21, 116–128. [Google Scholar] [CrossRef]
- Thomsen, K.; Ilita, M.C.; Rasmussen, P. Extended UNIQUAC model for correlation and prediction of va-por-liquid-liquid-solid equilibria in aqueous salt system containing non-electrolytes. Part-B alcohol-water-salt systems. Chem. Eng. Sci. 2004, 59, 3631–3647. [Google Scholar] [CrossRef]
- Qi, C.; Xie, Z. ScaleChem scaling prediction software used in oil well scaling and protection in Heyangshan oil area. In Proceedings of the 2022 Global Conference on Robotics, Artificial Intelligence and Information Technology (GCRAIT), Chicago, IL, USA, 30–31 July 2022. [Google Scholar]
- Moghadasi, J.; Sharif, A.; Müuller-Steinhagen, H.; Jamialahmadi, M. Prediction of Scale Formation Problems in Oil Reservoirs and Production Equipment due to Injection of Incompatible Waters. Dev. Chem. Eng. Miner. Process. 2006, 14, 545–566. [Google Scholar] [CrossRef]
- Collins, F.C.; Leineweber, J.P. The Kinetics of the Homogeneous Precipitation of Barium Sulfate. J. Phys. Chem. 1956, 60, 389–394. [Google Scholar] [CrossRef]
- Davis, J.A.; Collins, E.A. Solubility of Barium and Strontium Sulfate in Strong Electrolyte Solutions. Environ. Sci. Technol. 1971, 10, 1039–1043. [Google Scholar] [CrossRef]
- Nancollas, G.H.; Liu, S.T. Crystal Growth and Dissolution of Barium Sulfate. Soc. Pet. Eng. J. 1975, 509, 516. [Google Scholar] [CrossRef]
- Templeton, C.C.; Rodgers, J.C. Prediction of Anhydrite Precipitation in Field Water-Heating Systems. J. Pet. Technol. 1960, 20, 423–432. [Google Scholar] [CrossRef]
- Amiri, M.; Moghadasi, J. The prediction of calcium carbonate and calcium sulfate scale formation in Iranian oil-fields at different mixing rations of injection water with formation water. Pet. Sci. Technol. 2012, 30, 223–236. [Google Scholar] [CrossRef]
- Samira, H.; Esmaeilzadeh, F. Calculating Scaling Tendency and Scaling Index to Predicting the Formation Minerals Deposit in the Oil Field. In Proceedings of the 3rd International Conference on Research in Engineering, Science and Technology, Batumi, Georgia, 5 June 2016. [Google Scholar]
- Kan, A.T.; Tomson, M.B. Scale Prediction for Oil and Gas Production. SPE J. 2012, 17, 362–378. [Google Scholar] [CrossRef]
- Ruiz-Agudo, C.; Putin’s, C.V.; Ruiz-Agudo, E.; Putin’s, A. The influence of pH on barite nucleation and growth. Chem. Geol. 2015, 391, 7–18. [Google Scholar] [CrossRef]
- American Public Health Association; American Water Works Association; Water Environment Federation. 4110 B. Determination of Anions by Ion Chromatography. In Standard Methods for the Examination of Water and Wastewater, 23rd ed.; American Public Health Association: Washington, DC, USA, 2017. [Google Scholar]
- ASTM D1067-92(1996); Standard Test Methods for Acidity or Alkalinity of Water. ASTM International: West Conshohocken, PA, USA, 1996.
- ASTM D6919-17; Standard Test Method for Determination of Dissolved Alkali and Alkaline Earth Cations and Ammonium in Water and Wastewater by Ion Chromatography. ASTM International: West Conshohocken, PA, USA, 2017.
- American Public Health Association; American Water Works Association; Water Environment Federation. 3120 B. Inductively Coupled Plasma (ICP) Method. In Standard Methods for the Examination of Water and Wastewater, 23rd ed.; American Public Health Association: Washington, DC, USA, 2017. [Google Scholar]
- Moghadasi, J.; Jamialahmadi, M.; Müller-Steinhagen, H.; Sharif, A. Scale Formation in Oil Reservoir and Production Equipment during Water Injection Kinetics of CaSO4 and CaCO3 Crystal Growth and Effect on Formation Damage. In Proceedings of the SPE European Formation Damage Conference, Hague, The Netherlands, 13–14 May 2003. [Google Scholar] [CrossRef]
| Mineral | Solubility in Water (g/100 mL) @ 20 °C | Ksp @ 25 °C (Approximate) | References |
|---|---|---|---|
| Li2CO3 | 1.33 | 5.3 × 10−4 | [51] |
| CaCO3 | 6.6 × 10−4 | 3.3 × 10−9 to 8.7 × 10−9 | [52] |
| CaSO4·2H2O | 0.21 to 0.27 | 3.14 × 10−5 | [53] |
| SrSO4 | 0.0138 | 3.2 × 10−7 | [54] |
| BaSO4 | 2.44 × 10−4 | 1.1 × 10−10 | [54,55] |
| Mg(OH)2 | 9 × 10−4 | 1.5 × 10−11 | [54,55] |
| NaCl | 35.9 | Highly soluble | [56] |
| KCl | 34.4 | Highly soluble | [56] |
| MgCl2 | 54.3 | Highly soluble | [56] |
| CaCl2 | 74.5 | Highly soluble | [54] |
| BaCl2 | 35.7 | Highly soluble | [56] |
| Parameters | AVG | MAX | MIN | STDEV | RSD |
|---|---|---|---|---|---|
| SW | Doha East | Doha East | Doha East | Doha East | Doha East |
| pH | 7.70 | 8.10 | 7.50 | 0.21 | 2.74 |
| TDS | 48,529 | 49,200 | 48,020 | 419.77 | 0.86 |
| HCO3− | 130.0 | 132.0 | 128.6 | 1.09 | 0.83 |
| Na+ | 16,352 | 16,945 | 15,850 | 323.11 | 1.97 |
| K+ | 586 | 620 | 540 | 24.05 | 4.10 |
| Mg2+ | 1536 | 1700 | 1450 | 71.44 | 4.65 |
| Ca2+ | 1029 | 1200 | 970 | 54.69 | 5.31 |
| Cl− | 25,207 | 26,500 | 24,450 | 592.82 | 2.35 |
| Sr2+ | 13.2 | 14.5 | 12.3 | 0.708 | 5.34 |
| Ba2+ | 0.007 | 0.008 | 0.006 | 0.0005 | 6.65 |
| SO42− | 3815 | 4000 | 3649 | 77.4 | 2.02 |
| PH | TDS | HCO3− | Na+ | K+ | Mg2+ | Ca2+ | Cl− | SO42− | Ba2+ | Sr2+ | NO3− | F− | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| mg/L | mg/L | mg/L | mg/L | mg/L | mg/L | mg/L | mg/L | mg/L | mg/L | mg/L | mg/L | ||
| AVG | 6.4 | 175,793 | 213.5 | 63,557 | 2180 | 1924 | 9232 | 98,000 | 175 | 30.2 | 360 | 16.2 | 4.5 |
| MAX | 6.8 | 182,600 | 225.5 | 66,085 | 2500 | 2010 | 9450 | 99,150 | 180 | 31.2 | 410 | 17.5 | 5.3 |
| MIN | 6.2 | 173,800 | 205.8 | 60,339 | 1900 | 1850 | 9140 | 95,760 | 165 | 29.6 | 320 | 15.2 | 3.8 |
| STDEV | 0.1 | 2893 | 5.1 | 1148 | 170 | 37 | 83 | 730 | 3.9 | 0.4 | 19 | 0.7 | 0.4 |
| RSD | 2.2 | 2.0 | 2.4 | 1.8 | 7.8 | 1.9 | 0.9 | 0.7 | 2.2 | 1.2 | 5.3 | 4.1 | 9.2 |
| SEM | 0.03 | 631.00 | 1.10 | 250.6 | 37.20 | 8.00 | 18.0 | 159.40 | 0.9 | 0.08 | 4.10 | 0.10 | 0.10 |
| U (95%) | 0.1 | 1263 | 2.2 | 501 | 74 | 16 | 36 | 319 | 1.7 | 0.2 | 8 | 0.3 | 0.2 |
| CI upper | 6.5 | 177,056 | 215.7 | 64,058 | 2255 | 1940 | 9268 | 98,318 | 176 | 30.4 | 368 | 16.5 | 4.7 |
| CI lower | 6.3 | 174,530 | 211.3 | 63,056 | 2106 | 1908 | 9196 | 97,681 | 173.4 | 30.0 | 352 | 15.9 | 4.3 |
| PH | TDS | HCO3− | Na+ | K+ | Mg2+ | Ca2+ | Cl− | SO42− | Ba2+ | Sr2+ | NO3− | F− | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| mg/L | mg/L | mg/L | mg/L | mg/L | mg/L | mg/L | mg/L | mg/L | mg/L | mg/L | mg/L | ||
| AVG | 6.3 | 243,212 | 183 | 96,923 | 5085 | 2720 | 9156 | 149,400 | 328 | 49.1 | 653 | 34 | 4.0 |
| MAX | 6.6 | 248,300 | 185 | 97,650 | 5250 | 2780 | 9590 | 150,400 | 340 | 50.2 | 680 | 43 | 4.4 |
| MIN | 5.6 | 240,100 | 181 | 96,100 | 4950 | 2680 | 9000 | 148,600 | 300 | 47.2 | 620 | 32 | 3.7 |
| STDEV | 0.24 | 1805.67 | 1.19 | 482.03 | 72.50 | 27.61 | 125.0 | 473.3 | 10.3 | 0.6 | 15.3 | 2.8 | 0.2 |
| RSD | 3.76 | 0.74 | 0.65 | 0.50 | 1.43 | 1.02 | 1.36 | 0.32 | 3.1 | 1.3 | 2.34 | 8.21 | 4.5 |
| SEM | 0.05 | 394.03 | 0.26 | 105.19 | 15.82 | 6.03 | 27.27 | 103.28 | 2.3 | 0.14 | 3.33 | 0.61 | 0.04 |
| U (95%) | 0.10 | 788.06 | 0.52 | 210.38 | 31.64 | 12.05 | 54.54 | 206.56 | 4.6 | 0.3 | 6.67 | 1.22 | 0.1 |
| CI upper | 6.4 | 244,000 | 183.5 | 97,134 | 5117 | 2732 | 9211 | 149,607 | 332.3 | 49.4 | 660 | 35 | 4.1 |
| CI lower | 6.2 | 242,424 | 182.5 | 96,713 | 5054 | 2708 | 9102 | 149,193 | 323.0 | 48.8 | 647 | 33 | 3.9 |
| pH | TDS | HCO3− | Na+ | K+ | Mg2+ | Ca2+ | Cl− | SO42− | Ba2+ | Sr2+ | NO3− | F− | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| mg/L | mg/L | mg/L | mg/L | mg/L | mg/L | mg/L | mg/L | mg/L | mg/L | mg/L | mg/L | ||
| AVG | 5.6 | 197,999 | 171 | 83,299 | 2620 | 2715 | 9603 | 128,400 | 610.25 | 82.31 | 400.00 | 10.98 | 4.10 |
| MAX | 6.0 | 199,869 | 173 | 83,810 | 2710 | 2760 | 9680 | 130,800 | 630.00 | 84.10 | 450.00 | 12.10 | 4.50 |
| MIN | 5.5 | 195,899 | 169 | 82,800 | 2560 | 2680 | 9550 | 125,900 | 580.00 | 80.50 | 370.00 | 9.50 | 3.80 |
| STDEV | 0.13 | 860.43 | 0.93 | 266.36 | 32.23 | 23.82 | 30.50 | 967.99 | 12.82 | 0.84 | 23.66 | 0.57 | 0.17 |
| RSD | 2.349 | 0.43 | 0.54 | 0.32 | 1.23 | 0.88 | 0.32 | 0.75 | 2.10 | 1.02 | 5.92 | 5.15 | 4.26 |
| SEM | 0.029 | 187.76 | 0.20 | 58.12 | 7.03 | 5.20 | 6.66 | 211.23 | 2.87 | 0.19 | 5.16 | 0.12 | 0.04 |
| U (95%) | 0.058 | 375.52 | 0.40 | 116.25 | 14.07 | 10.40 | 13.31 | 422.47 | 5.73 | 0.37 | 10.33 | 0.25 | 0.08 |
| CI upper | 5.7 | 198,375 | 171 | 83,416 | 2634 | 2725 | 9616 | 128,823 | 615.98 | 82.68 | 410.33 | 11.23 | 4.17 |
| CI lower | 5.6 | 197,624 | 170 | 83,183 | 2606 | 2705 | 9590 | 127,978 | 604.52 | 81.94 | 389.67 | 10.73 | 4.02 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salman, M.A.; Ahmed, M.; Al-Sairfi, H.; Al-Foudari, Y. Mineral Extraction from Mixed Brine Solutions. Separations 2025, 12, 266. https://doi.org/10.3390/separations12100266
Salman MA, Ahmed M, Al-Sairfi H, Al-Foudari Y. Mineral Extraction from Mixed Brine Solutions. Separations. 2025; 12(10):266. https://doi.org/10.3390/separations12100266
Chicago/Turabian StyleSalman, M. A., M. Ahmed, H. Al-Sairfi, and Y. Al-Foudari. 2025. "Mineral Extraction from Mixed Brine Solutions" Separations 12, no. 10: 266. https://doi.org/10.3390/separations12100266
APA StyleSalman, M. A., Ahmed, M., Al-Sairfi, H., & Al-Foudari, Y. (2025). Mineral Extraction from Mixed Brine Solutions. Separations, 12(10), 266. https://doi.org/10.3390/separations12100266







