Abstract
The pitch-diameter ratio is an important design indicator affecting the separation performance of spirals. Based on the numerical simulation method, this paper systematically investigated the variation of flow hydrodynamic parameters in the spiral concentrator with the regulation of the pitch-diameter ratio. The radial distribution and variation trend of hematite and quartz particles with different particle sizes are further analyzed. Additionally, the separation indices of hematite and quartz with different particle size combinations were predicted. The results show that the tangential velocity, maximum radial velocity, velocity shear rate, and Reynolds number of fluid in each region decrease with the increase of the pitch-diameter ratio. The range of laminar flow gradually expands as the pitch-diameter ratio increases. There are significant differences in depth of water, ratio of inward and outward flows, and secondary flow velocity in different regions. Some flow hydrodynamic parameters at the inner trough reach relative equilibrium at a pitch-diameter ratio of 0.675. Hematite and quartz particles form a selective distribution in the trough surface, which comprehensively reflects the density effect, particle size effect, following flow effect of fine particles, and the effect of interstitial trickling of high-density fine particles. Fine hematite and coarse quartz form a large amount of misplaced material, and there is a corresponding mixing area. With the increase in pitch-diameter ratio, coarse and fine hematite particles migrate inward and outward, respectively. With the increase in pitch-diameter ratio, the misplaced amount of quartz on the inner trough decreases, but the outward migration distance of coarse quartz is smaller. Increasing the pitch-diameter ratio is beneficial to the separation of combined feedings of coarse hematite and quartz but unfavorable to that of fine hematite and quartz. The maximum separation efficiency of coarse hematite and fine quartz can reach 85.74%, and the iron grade of the inner product can reach 65.96% when the pitch-diameter ratio is 0.675 and the splitter location is 115 mm. The changing trend of separation indices in this feeding is closely related to the variation of fluid parameters and the change in the radial distribution of single mineral particles. The research results can provide references for the structural design of spirals, the selection of feed particle size, and the adjustment of splitter location.
1. Introduction
A spiral concentrator is one of the thin flow film gravity equipment based on the combined action of centrifugal force and gravity and widely used in production processes such as iron ore processing, coal washing, rare earth element preconcentration, and waste resource utilization. It can produce qualified concentrates or provide high-quality raw materials for subsequent separation operations through a short process under suitable conditions, playing an important role in improving separation and economic indices [1,2,3,4]. Since the application of spirals, there has been active research on its sorting theory, structural design, process operation, and other aspects. In recent years, the research methods for spirals have tended to be diverse, creating beneficial conditions for fully utilizing their unique advantages.
Among the working parameters that affect the separation performance of spirals, the structural parameters often have a more fundamental regulatory effect on the flow field characteristics and particle behavior. Once the structural parameters of the spiral concentrator are determined, they are rarely adjusted during production operations [5,6,7,8,9,10]. Therefore, optimizing and designing structural parameters such as cross-sectional geometry, diameter, and pitch based on the properties of the materials to be separated is usually the primary task before their application. After installation and production, the separation indices can be further improved by adjusting the operating parameters such as feed flow rate, feed solid mass concentration, and splitter position.
In order to provide good dynamic conditions for the materials transport without pressure in the spiral concentrator, the trough surface must have an appropriate longitudinal inclination angle. Pitch is a structural parameter that determines the longitudinal inclination angle of a spiral concentrator. The relative size of pitch is usually characterized by the ratio of pitch to diameter—the pitch-diameter ratio (P/D). The pitch-diameter ratio not only affects the primary flow velocity, depth of water, and particle velocity of the slurry in the trough surface but also determines the height of the spiral concentrator, which has an undeniable impact on the layout of production equipment and the investment and construction of factory buildings [5,11]. Researchers have drawn many valuable conclusions from investigating the impact of pitch on material separation performance. For example, when dealing with materials with larger particle sizes and higher density, using a large pitch can ensure good pulp fluidity and separation accuracy [5]. Adopting a small pitch-diameter ratio and extending the number of spiral turns can improve the separation effect of fine-grained materials [12]. In addition, Liu et al. found that reducing the pitch-diameter ratio can enhance the separation performance of spirals for materials with low density differences. The spirals with a pitch-diameter ratio of 0.36 have been used in the preconcentration of vanadium shale and the gravity concentration of fine apatite, achieving good separation and economic indices [13,14]. These conclusions can provide a reference for the selection of pitch for specific materials. However, the inherent relationship between structural parameters, the internal flow field, and particle separation behavior still needs to be further revealed.
In recent years, the vigorous development of numerical simulation technologies such as CFD has provided strong support for the visualization and quantification of the flow field and particle separation processes in spirals. A high-precision numerical model can not only significantly reduce the cost of structural design and separation experiments but also provide greater possibilities for further research on separation theory based on the large amount of qualitative and quantitative data. Furthermore, numerical simulation technology makes it easier to identify the effects of different variables on the flow field characteristics and the particle motion behavior of spirals, thereby providing a scientific basis for structural optimization [15,16,17,18]. From the perspective of fluid flow, the film flow field in the spirals belongs to open channel flow. Therefore, a reasonable selection of a multiphase flow model is crucial to successfully simulating the flow field characteristics and particle movement behavior. At present, the VOF model is usually used to predict the characteristics of the water flow field in spirals [19]. For the simulation of particle systems, the multiphase flow model involves the Euler–Lagrange and Euler–Euler methods. Among them, the Euler–Lagrange method hardly considers the influence of particles on the fluid and is only suitable for qualitative tracking the motion trajectory of a small number of particles, so it is not suitable for separation conditions with high particle concentration [20]. In addition, when the Euler–Euler method is used to predict the free interface of slurry, the problem of numerical dispersion will occur, so this method cannot be applied to systems with high particle concentrations [21,22,23]. Recently, the authors’ research team proposed a Eulerian Multi-fluid VOF multiphase flow model that combines the advantages of the Euler–Euler model and the VOF interface tracking model, realizing the prediction of high concentration particulate flow in spirals [24]. However, there is currently relatively little numerical simulation work on the pitch [25,26]. The understanding formed only focuses on the flow field characteristics of water flow, so the mechanism of the influence of pitch on the migration behavior of particles in the slurry and the interaction between particles and flow fluid still needs to be explored.
Based on the above research background, with the help of a high-precision numerical model of flow field and particle motion in spirals established by the author’s research team in the early stages [17,24], this paper systematically investigates the influence of the pitch-diameter ratio on the flow hydrodynamic parameters and the radial distribution of solid particles in the trough surface of the spiral concentrator. The variation of flow spreading, spatial distribution of velocity and flow regime, and distribution of hematite and quartz particles in different regions with the regulation of pitch-diameter ratio are investigated. Further, the separation indices of hematite and quartz with different particle size combinations are predicted by adjusting the splitter location to investigate the suitable feeding particle size conditions and the splitter location. The regulatory effect of the pitch-diameter ratio on the separation indices under combined feedings of different particle sizes is consequently analyzed.
2. Test Method
2.1. Geometric Parameters of the Spiral Concentrator
The cubic parabolic spiral concentrator is used as the experimental object, with an outer radius (R) of 200 mm, an inner radius (r0) of 35 mm, a pitch (P) of 240 mm, and a number of spiral turns of 3.25. The cross-sectional curve equation is shown in equation (1):
The cross-sectional geometry is shown in Figure 1.
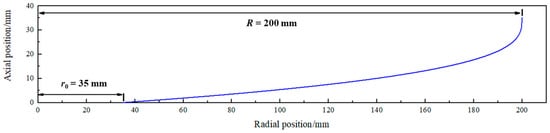
Figure 1.
Cross-sectional geometry of the spiral concentrator.
2.2. Solid Particle Properties
In this paper, hematite and quartz are selected as separation materials, and the densities were set to 4950 kg/m3 and 2650 kg/m3, respectively. By referring to the feeding particle size composition of the spiral concentrator at the production site (Qidashan Iron Ore Processing Plant), the particle sizes of quartz and hematite used in this work were both set to 90 μm and 38 μm, to represent coarse and fine particles in the gravity concentration operation, respectively. Numerical experiments were conducted on the spiral concentrator to separate hematite and quartz particles using a mixed feeding method with a total solid mass concentration of 20% and a mass ratio of 1.87:1.87:1:1 (hematite of 90 μm; hematite of 38 μm; quartz of 90 μm; and quartz of 38 μm) and a feeding iron grade of 45.6%.
2.3. Numerical Model and Experimental Conditions
Firstly, the VOF multiphase flow model and the RNG k-ε turbulence model were used to simulate the spreading process of the flow layer inside the spiral concentrator to obtain a clear gas-liquid interface and a converging stable flow field [17,18,19]. On this basis, a Eulerian Multi-fluid VOF model considering the Bagnold effect is used to simulate the particles motion [24]. The Eulerian Multi-fluid VOF model is a coupled model of the VOF model and the Euler–Euler model [27], which can achieve synchronous simulation of gas-liquid continuous interface and particle discrete phase behavior. For the interphase forces, the main considerations are drag force FD and lift force FL. The liquid-solid drag and gas-liquid drag are predicted by the Gidaspow model [28] and the symmetric model [29], respectively. The lifting model adopts the Bagnold empirical formula and is loaded into the lift coefficient module through the UDF (user-defined function). The equation is as follows [24]:
where N is the Bagnold number, and its expression is as follows:
where λ is the linear concentration, expressed as follows:
where C0 is the maximum possible volume concentration of solids, which is set to 0.63 in the simulation; C is the volume concentration of solids; ρp is the particle density; dp is the particle diameter; is the shearing rate; and μ is the viscosity of the liquid.
When simulating the gas-liquid two-phase flow using the VOF model, the initial computational domain should be filled with air with zero velocity, and the inlet velocity of the liquid phase should be set at the inlet. Then, the flow field is initialized, and the calculation begins. When simulating the gas-liquid-solid multiphase flow using the Eulerian Multi-fluid VOF model, the initial flow field is obtained based on the calculation results of the VOF model. On this basis, the particle phase is added, and the flow field properties of the particles are set before starting the calculation. When performing numerical simulation of gas-liquid two-phase flow, the coupling solution algorithm for pressure field and velocity field adopts the SIMPLE algorithm. When performing numerical simulation of gas-liquid-solid multiphase flow, the coupling solution algorithm for pressure field and velocity field adopts the Phase Coupled SIMPLE algorithm. The spatial discretization formats for other convective terms are shown in Table 1.

Table 1.
Spatial discretization formats of different numerical test models.
The accuracy of the above numerical models has been verified and corrected through flow morphology testing and actual separation experiments of solid particles [17,24].
Under the conditions of maintaining a constant inlet flow rate of 12 L/min and other structural parameters, a total of 5 sets of numerical experiments were conducted with different pitch-diameter ratios. The comparison of the pitch-diameter ratio is shown in Table 2.

Table 2.
Pitch-diameter ratio comparison table.
The computational domain mesh with a pitch of 240 mm is illustrated in Figure 2. Due to the consistent mesh division method for each turn, only one turn is displayed to improve clarity. After conducting mesh independence experiments, the appropriate number of hexahedral meshes was determined to be 1, 037, 036. The boundary of the computational domain is divided into inlet, up-wall, down-wall, and outlet. The boundary condition for the inlet is set to velocity inlet. Since the outlet contacts air directly, it is set to the pressure outlet, where the pressure is set to the standard atmospheric pressure. In addition, in the outlet, the return volume fraction of air is set to 1, and the water phase return coefficient is set to 0. The up-wall is in contact with air, setting up a free-slip wall. The down-wall is set to the no-slip wall.

Figure 2.
Mesh division of the calculation domain of the spiral concentrator model.
2.4. Extraction and Characterization of Simulation Data
According to the splitter location of the laboratory spiral concentrator and the product band division ratio in production, the trough surface is divided radially outward into the inner trough (r = 35–80 mm), the middle trough (r = 80–140 mm), and the outer trough (r = 140–200 mm). The extracted flow hydrodynamic parameters include: depth of water H (i.e., total water depth at a certain radial position or absolute water depth), relative water depth h/H (h is the actual water depth value of a certain fluid particle), tangential velocity, and radial velocity. The maximum value of radial velocity is used to characterize the intensity of secondary flow. The split ratio of inward and outward flows can be judged by the change in reversal position (the relative water depth position when the radial velocity is zero) of secondary flow. The flow regime is characterized by the Reynolds number Re. For investigating the changes in flow velocity, three radial positions of 60 mm, 120 mm, and 180 mm are selected to represent the flow field characteristics of the inner, middle, and outer troughs, respectively.
For extracting the simulation data of particles, the inner, middle, and outer troughs are further divided into two narrower intervals along the spiral trough surface (at the end of the third turn). Therefore, there are a total of 6 intervals (r1–r6): r1 = 35–57.5 mm, r2 = 57.5–80 mm, r3 = 80–110 mm, r4 = 110–140 mm, r5 = 140–170 mm, and r6 = 170–200 mm. Under different simulation conditions, the mass flow rates of hematite and quartz particles were extracted, respectively, and the particle yields in the six radial intervals were calculated in turn. Then, the radial distribution characteristics of hematite and quartz were analyzed. On this basis, the iron grade of each concentrate product and the corresponding separation efficiency were calculated at different splitter locations. The separation efficiency is an important index used to evaluate the separation performance of the spirals, which is defined as the difference between the recovery of valuable minerals and the recovery of gangue minerals in the concentrate [30].
where is the separation efficiency, is the recovery of valuable minerals, and is the recovery of gangue minerals. As hematite and quartz minerals are used in the test, the recovery rate is equal to the yield. The width of the concentrate band is determined by the radial coordinates of the splitter location.
3. Results and Discussion
3.1. Variations of Flow Hydrodynamic Parameters inside the Spiral Concentrator with Different Pitch-Diameter Ratios
3.1.1. Effect of Pitch-Diameter Ratio on the Depth of Flow Film
For the open thin film flow system, the depth of the flow film determines the space for particle separation. The radial distribution of the depth of flow film at the troughs of each turn end with different pitch-diameter ratios is shown in Figure 3.
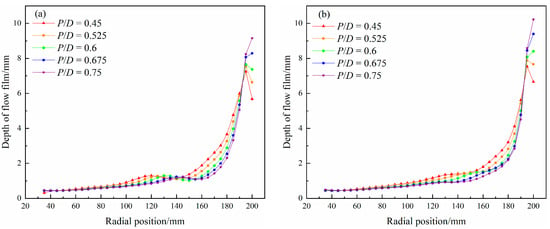
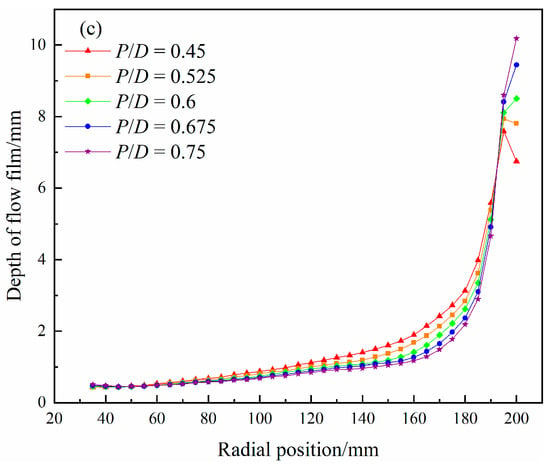
Figure 3.
Radial distribution of the depth of flow film with different pitch-diameter ratios. (a) The end of the first turn; (b) the end of the second turn; and (c) the end of the third turn.
From Figure 3, it can be seen that the flow film inside the spiral trough surface is thin in the inner and middle troughs and thick in the outer trough. It is consistent with relevant measured data, proving the reliability and accuracy of the numerical model adopted. Comparing the curve shapes at the troughs, it can be found that as the number of spiral turns increases, the flow film shape becomes more stable, and the influence of the pitch-diameter ratio on the depth of the flow film becomes clearer. In the third turn, where the flow film reaches stability, as the pitch-diameter ratio increases, the depth of the flow film in the middle and outer troughs gradually decreases, especially in the outer trough of 140–180 mm. However, the maximum flow film thickness (7.6–10.19 mm) increases with the increase of the pitch-diameter ratio. The depth of flow film in the inner trough is all below 0.7 mm, and the regulatory effect of the pitch-diameter ratio is also relatively small.
3.1.2. Effect of Pitch-Diameter Ratio on the Distribution of Flow Velocity
Due to the combined effects of centrifugal force, a component of gravity along the inclined plane, and frictional force, the flow gradually forms two motion forms in the spiral channel, which are the primary downward rotating flow and the lateral secondary flow. The fluid motion characteristics comprehensively affect the force, motion, and bending results of particles [31,32].
The tangential and radial velocities of fluid particles at the three representative radial positions with different pitch-diameter ratios were extracted to characterize the primary flow intensity and secondary flow distribution, respectively. The trends of the two velocities along the relative water depth are shown in Figure 4 and Figure 5, respectively. Considering that the flow film shape has reached a fully developed stable state at the end of the third turn and the secondary flow often tends to stabilize after the second turn, both the flow velocity component data at the end of the third turn have been extracted.
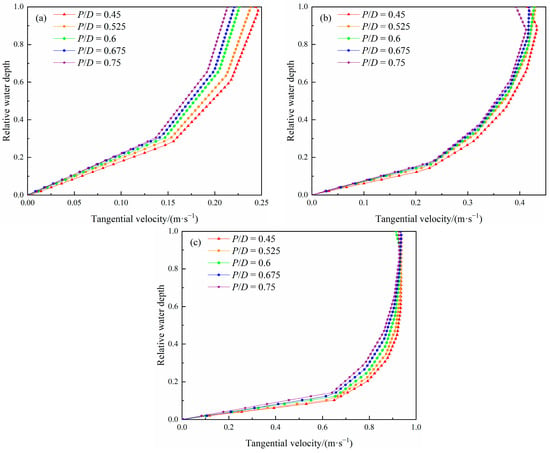
Figure 4.
Distribution of tangential velocity along relative water depth with different pitch-diameter ratios. (a) Inner trough (r/R = 0.3); (b) middle trough (r/R = 0.6); and (c) outer trough (r/R = 0.9).
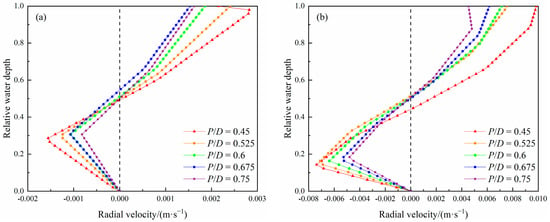
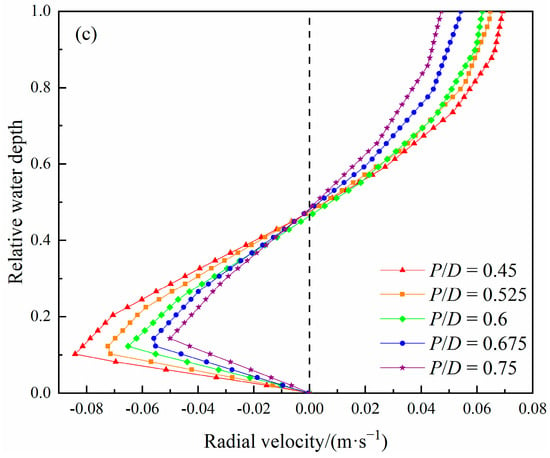
Figure 5.
Distribution of radial velocity along relative water depth with different pitch-diameter ratios. (a) Inner trough (r/R = 0.3); (b) middle trough (r/R = 0.6); and (c) outer trough (r/R = 0.9).
From Figure 4, it can be seen that the tangential velocity of fluid particles in the inner, middle, and outer troughs continuously increases from the bottom of the trough upwards and shows a linear, sharply increasing trend near the bottom of the trough. As the water depth rises, the increase in velocity tends to flatten out. The position in depth where trend changes depend on the radial position of fluid particles. The greater the radial position of the fluid particle is outward, the smaller the relative water depth corresponding to the velocity trend inflection point, and the higher the tangential velocity shear rate. In addition, the maximum tangential velocity of the fluid particles increases radially outward. Therefore, when the pitch-diameter ratio is regulated, the variation of the tangential velocity distribution characteristics of fluid is related to the spatial position of fluid particles.
From Figure 4a, it can be clearly seen that the tangential velocity of the fluid particles at the inner trough decreases gradually with the increase of the pitch-diameter ratio. As the position in depth moves up, the tangential velocity variation becomes more sensitive. It means that the closer it is to the water surface, not only does the centrifugal force increase, but the geometric parameters of the spiral concentrator also have a more significant impact on flow particles. From Figure 4b,c, it can be observed that the tangential velocity of fluid particles in the middle and outer troughs also decreases with increasing pitch-diameter ratio, but the decrease of the velocity in the middle trough is smaller than that in the inner trough, while the decrease of the velocity in the outer trough is nearly consistent with that in the inner fluid. The tangential velocity in the outer trough reaches its maximum below the water surface line (with a relative water depth of 0.72–0.94), and the velocity curves converge at a point (with a tangential velocity value of 0.93 m/s and a corresponding relative water depth of 0.86). As the relative water depth increases from 0.86, the flow tangential velocity remains unchanged or slightly decreases.
From Figure 5, it can be seen that the radial velocity magnitude of fluid particles is much smaller than the tangential velocity. Compared to different radial positions, the radial velocities in the inner and middle troughs are much lower than those in the outer trough. The maximum velocity of inward and outward flows with different pitch-diameter ratios is shown in Table 3.

Table 3.
Maximum radial velocity of inward and outward flow with different pitch-diameter ratios.
It can be seen from Table 3 that the intensity of the secondary flow gradually increases from the inside to the outside. The intensity of the outward flow at the inner trough is significantly higher than that of the inward flow. The intensity of the outward flow at the middle trough is slightly higher than that of the inward flow. The intensity of the inward flow at the outer trough is higher than that of the outward flow. It indicates that the characteristic of secondary flow is closely related to fluid spatial position. In addition, as the radial position moves outward, the relative water depth corresponding to the maximum inward velocity gradually decreases, indicating that the shear rate of the inward velocity gradually increases from the inside to the outside. It is consistent with the shear rate distribution characteristics of tangential velocity. The reversal position of the secondary flow is in the range of 0.45 to 0.55. The reversal positions in the inner trough are relatively high and scattered, while those in the middle and outer troughs are slightly low and relatively concentrated. Further statistical analysis is conducted on the reversal positions of the secondary flow with different pitch-diameter ratios, and the results are presented in Table 4.

Table 4.
Reversal positions of secondary flow with different pitch-diameter ratios.
Figure 5a shows that as the pitch-diameter ratio increases, the shear rate of the inward velocity in the inner trough gradually decreases, and the maximum inward velocity relatively decreases. Meanwhile, the reversal position of the secondary flow moves up, which only moves downwards at the maximum pitch-diameter ratio of 0.75, indicating that the maximum split ratio of the inward flow is obtained at a pitch-diameter ratio of 0.675 (Table 3). The variation in the maximum radial velocity of outward flow is related to the reversal position. As the pitch-diameter ratio increases, it decreases continuously and reaches its minimum value at a pitch-diameter ratio of 0.675. It indicates that as the pitch-diameter ratio increases, the intensity of inward and outward flow at the inner trough weakens, and an equilibrium point exists.
Figure 5b,c indicate that the variation of radial velocity at the middle and outer troughs is consistent with that at the inner trough. The monotonicity between the pitch-diameter ratio and the maximum velocity of inward and outward flow is clearer, so there is no inflection point of variation. Except for the pitch-diameter ratio of 0.45, the reversal positions (see Table 4 for details) of the secondary flow at the middle trough are all concentrated at the relative water depths of 0.51 or 0.50, while the reversal positions at the outer trough are almost located below 0.50, also with a relatively concentrated distribution. It indicates that the influence of the pitch-diameter ratio on the split ratio of inward and outward flow at the middle and outer troughs is relatively insignificant.
3.1.3. Variation of Flow Regime Distribution Characteristics with Different Pitch-Diameter Ratios
During the operation of the spiral concentrator, the fluid flow regime is divided into three forms: laminar flow, transitional flow, and turbulent flow along the radial direction from inside to outside. The flow regime determines the normal force supporting the suspension of particles, affecting particle loosening and stratification. The flow regime distribution in a spiral concentrator can be determined according to the Reynolds number (Re) of open channel flow, and its expression is as follows:
where V is the mean velocity of the fluid; is the mean depth of the flow film; ρ is the fluid density; and μ is the viscosity of the fluid. The judgment criteria for laminar flow, transitional flow, and turbulence are Re ≤ 400, 400 < Re < 2000, and Re ≥ 2000, respectively [20]. The distribution curve of Reynolds number with different pitch-diameter ratios at the end of the third turn is shown in Figure 6.
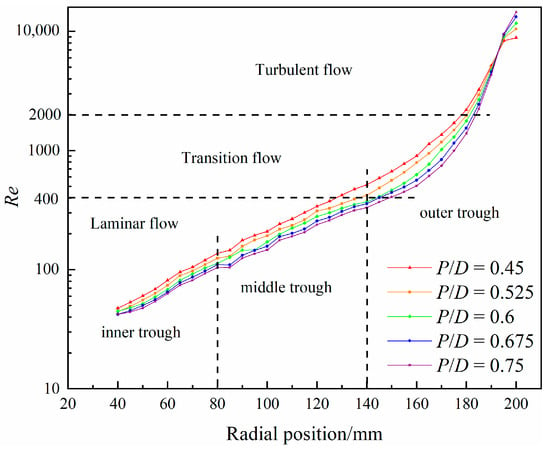
Figure 6.
Distribution of Reynolds number along radial position with different pitch-diameter ratios.
From Figure 6, it can be seen that Re gradually increases from the inside to the outside along the trough surface. In the inner and middle troughs, the Re shows a linear growth trend, developing from laminar flow to transitional flow gradually. At the junction of the middle and outer troughs (r = 140 mm), the growth rate of Re increases. Finally, the flow regime develops into complete turbulence approximately around r = 180 mm (20 mm within the outer trough endpoint). Taking P/D = 0.45 as an example, the width of laminar flow is around 90 mm, almost covering the inner and middle troughs. The range of transition flow and turbulence is relatively narrow, mainly located at the outer trough.
As the pitch-diameter ratio increases, Re gradually decreases, especially at the middle and outer troughs, so the distribution width of laminar flow expands outward while the width of transition flow and turbulence flow slightly narrows. The specific change is shown in Figure 7.
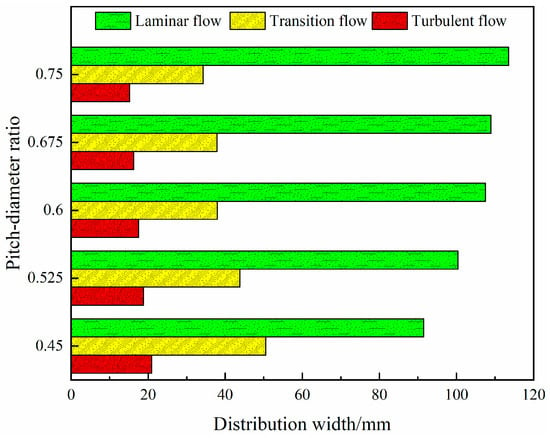
Figure 7.
Flow regime distribution with different pitch-diameter ratios.
In addition, under different pitch-diameter ratios, the radial variation trend of Re in the inner and middle troughs is linear, and the growth rate is similar. However, Re at the outer trough changes from a uniform linear growth to a steep increasing trend, and the growth rate at each location is positively correlated with the pitch-diameter ratio. Finally, it intersects at the same position (approximately r = 190 mm) and continues to grow outward. From the position of r = 195 mm (5 mm inside the outer edge endpoint) outward, Re increases as the pitch-diameter ratio increases. These trends are consistent with those of the depth of the flow film in Figure 3.
The above research on the flow field characteristics shows that the depth of the flow film in the spiral concentrator increases from inside to outside, and the tangential velocity of the primary flow, the radial velocity of the secondary flow, the velocity shear rate, and the Re also increase relatively. The hydrodynamic parameters are highly correlated. After increasing the pitch-diameter ratio, the flow film in the middle and outer troughs becomes thinner, while the depth of the flow film at the inner trough remains almost unchanged. The tangential velocity, maximum radial velocity, velocity shear rate, and Re in most of the radial regions show a clear decreasing trend with increasing pitch diameter ratio, resulting in an outward expansion of the laminar flow distribution width. The reversal position of the secondary flow at the inner trough moves up with an increase in the pitch-diameter ratio, and all reach equilibrium points at the pitch-diameter ratio of 0.675. The influence of the pitch-diameter ratio on the reversal positions of the secondary flow at the middle and outer troughs is relatively small, indicating that the influence of the pitch-diameter ratio on the split ratio is closely related to the spatial position of the fluid.
It should be noted that the depth of flow film at the outer trough of r = 190–200 mm increases sharply with the increase in pitch-diameter ratio (see Figure 8), resulting in an increase in the local flow area. Meanwhile, the velocity is also positively correlated with the pitch-diameter ratio as well as the depth of the flow layer. The increase in flow rate at the outer trough offsets the decrease in flow rate in other thin flow film regions. Therefore, the flow rate on the entire flow surface is constant. A series of complex variations of flow hydrodynamic parameters in a spiral concentrator with the regulation of pitch-diameter ratio will have an important impact on particle movement, radial distribution, and separation indices.
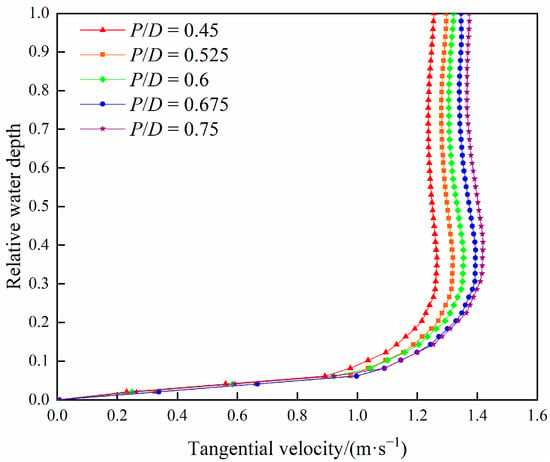
Figure 8.
Distribution of tangential velocity along relative water depth at r = 190 mm with different pitch-diameter ratios.
3.2. Prediction of Particle Separation Indices with Different Pitch-Diameter Ratios
3.2.1. Yield Distribution of Hematite and Quartz Particles in Different Radial Intervals
The yields of four types of particles were extracted within six radial intervals at the end of the third turn. The spatial distribution characteristics of hematite and quartz particles with different particle sizes and their changes with the adjustment of the pitch-diameter ratio are systematically investigated. The results are shown in Figure 9.
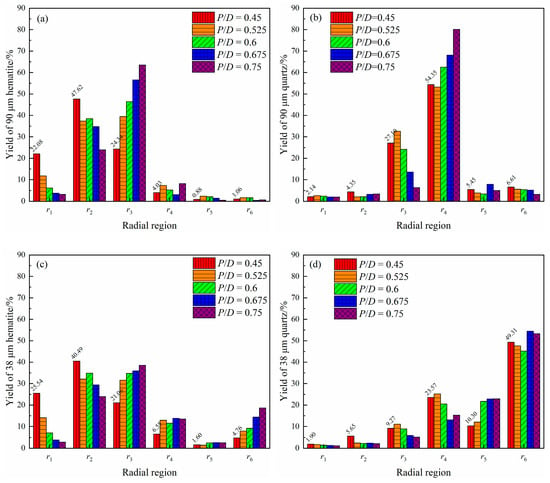
Figure 9.
Yield distribution of particles in various radial regions at the end of the third turn with different pitch-diameter ratios. (a) 90 μm hematite particles; (b) 90 μm quartz particles; (c) 38 μm hematite particles; and (d) 38 μm quartz particles.
It can be seen from Figure 9 that most of the hematite particles gather in three microregions at the inner trough. The yield of hematite is higher in the r2 and r3 regions but lower in the r1 region. When the pitch-diameter ratio is 0.45, the total yield of the two particle sizes of hematite in the three regions (r1–r3) is 94.04% and 87.09%, respectively. The yield of 38 μm hematite particles in the three regions (r1–r3) is about 7% lower than that of 90 μm hematite particles, which is mainly related to the fact that the distribution of 38 μm hematite in the r4 and r6 regions is relatively high. The majority of coarse and fine quartz particles are concentrated in the r4–r6 region, with a total yield of 66.41% and 83.18%, respectively. The main distribution intervals of coarse and fine quartz are the r4 and r6 regions, respectively. It indicates that the aggregation interval of coarse quartz is more inward. Additionally, the yield of coarse quartz in the hematite accumulation area (r3) is 17.83% higher than that of fine quartz, indicating that coarse quartz is more likely to lead to a reduction in iron concentrate quality.
The above analysis indicates that hematite and quartz particles form an obvious selective distribution due to the difference in density during the evolution of the flow field. If the splitter is set near the center of the trough surface (r = 110 mm), the density separation effect can be achieved. However, there is a certain amount of misplaced particles with different pitch-diameter ratios.
In the quartz accumulation area, the misplaced yield of fine hematite is higher than that of coarse hematite. In the hematite accumulation area, the misplaced yield of coarse quartz is higher than that of fine quartz. Therefore, the movement and distribution of fine hematite and coarse quartz are the key factors affecting the optimization of structural parameters. The misplaced coarse quartz particles are mainly distributed in the r3 region of the hematite accumulation area, and the misplaced fine hematite particles are mainly distributed in the r4 and r6 regions of the quartz accumulation area.
As shown in Figure 9a,c, the yield of hematite in the r3 region increases with the increase of the pitch-diameter ratio, in which the increase of 90 μm hematite is higher. The yield of hematite in the r1 and r2 regions generally decreases with the increase in pitch-diameter ratio. The 38 μm misplaced hematite in quartz accumulation areas (r4, r5, and r6 regions) increases with the increase of pitch-diameter ratio, with the misplaced amount of 38 μm hematite being relatively higher in the r6 region. For quantitative analysis, the yielded change values of hematite in each region are listed in Table 5 and Table 6.

Table 5.
Variation values of 90 μm hematite particles yielded in different radial regions.

Table 6.
Variation values of 38 μm hematite particle yield in different radial regions.
It can be observed from the data in Table 5 and Table 6 that when the pitch-diameter ratio is adjusted upward on the basis of 0.45, the total distribution law of 90 μm hematite in its accumulation area shows a fluctuation change. The lowest value was 88.63% (94.04% − 5.41%) when the pitch-diameter ratio was 0.525, and the maximum value was 95.05% (88.63% + 2.37% + 4.05%) when the pitch-diameter ratio was 0.675. The other two yield ratios were similar (91% and 90.65%) and lower than the distribution rate at a 0.45 pitch-diameter ratio. The total distribution law of 38 μm hematite in the accumulation area showed a significant continuous decreasing trend with the increase of the pitch-diameter ratio. Although under the pitch-diameter ratio of the benchmark 38 μm hematite yield, the yield of fine hematite in this area declines more sharply due to the effect of interstitial trickling in the r1 area, compared to hematite of 90 μm and its increased pitch-diameter ratio. Considering the variation of hematite yield in the quartz accumulation area, coarse-grained hematite migrates inward from the r4 area at the appropriate pitch-diameter ratio, which increases the possibility of improving the quality of iron concentrate products, while fine-grained hematite migrates to the quartz accumulation area, obviously with the increase in pitch-diameter ratio. When the pitch-diameter ratio is adjusted from 0.45 to 0.525, fine-grained hematite migrates mainly to the r4 area. When the pitch-diameter ratio continues to increase from 0.525, it further migrates to the r6 region, which increases the loss of iron minerals and makes it difficult to select the location of the product splitter.
It can be seen from the variation trend of quartz yield with the pitch-diameter ratio in Figure 9b,d that the yield of 90 μm quartz particles in the main accumulation area r4 shows an obvious increase trend, while that in the main accumulation area r3 shows a decrease trend (only increases when the pitch-diameter ratio is regulated from 0.45 to 0.525). The results show that increasing the pitch-diameter ratio will promote the coarse-grained quartz migration from inside to outside. The yield of 38 μm quartz particles in the main accumulation area r6 decreased slightly and then increased significantly with the increase of the pitch-diameter ratio; the yield in r5 shows a continuous increasing trend, and that in r4 shows a general decreasing trend. The yield of 38 μm quartz in the hematite accumulation areas r1, r2, and r3 also showed a slight but clear decreasing trend. In conclusion, increasing the pitch-diameter ratio can reduce the misplaced amount of quartz particles in the hematite accumulation area, and it is beneficial to improve the purity of iron concentrate products to a certain extent. The variation values of quartz particles yielded with the regulation of pitch-diameter ratio are shown in Table 7 and Table 8.

Table 7.
Variation values of 90 μm quartz particle yield in different radial microzones.

Table 8.
Variation values of 38 μm quartz particle yield in different radial microzones.
The data in Table 7 and Table 8 show that the total misplaced amount of quartz in the hematite accumulation area decreases with the increase of the pitch-diameter ratio on the whole, and the misplaced material of coarse quartz increases slightly when the pitch-diameter ratio is regulated from 0.45 to 0.525. In contrast, coarse-grained quartz has a greater reduction in misplaced amounts than fine-grained quartz, but it mainly migrates to r4, while fine-grained quartz migrates to r5 and r6. When the pitch-diameter ratio is regulated to 0.675 and 0.75, the misplaced amount of fine quartz can be reduced to 9.57% and 8.51%, and that of coarse quartz can be reduced to 18.85% and 11.76%. It can be seen that under the regulation of pitch-diameter ratio, there is little difference in the minimum misplaced amount between the two. However, since the region r4, to which the coarse quartz migrated, belongs to the central miscible region, it is difficult to say whether the index is ideal when the product separation line is set in this region.
Based on the above analysis, the coarse-grained hematite migrates to the inside of the center of the trough surface, while the fine-grained hematite migrates to the outside of the center with the increase of the pitch-diameter ratio, resulting in more losses in the outermost region. The regulation of the pitch-diameter ratio has an obvious effect on reducing the misplaced amount of coarse and fine quartz within the center of the trough surface, but the coarse quartz has a small outward migration displacement and little distance from the accumulation area of hematite. Therefore, since the yield and iron grade of concentrate are very sensitive to the movement of the splitter location, it is necessary to comprehensively evaluate the control effect of the pitch-diameter ratio with the help of the prediction results of the separation indices under different working parameters.
3.2.2. Prediction of the Concentrate Grade and Separation Efficiency at Different Splitter Locations
In order to observe the separation indices of hematite and quartz with different particle sizes more directly, the splitter location was adjusted under the conditions of different pitch-diameter ratios, and the iron grade and separation efficiency of the concentrate (products inner to the trough surface) were extracted, respectively. The predicted results are shown in Figure 10 and Figure 11.
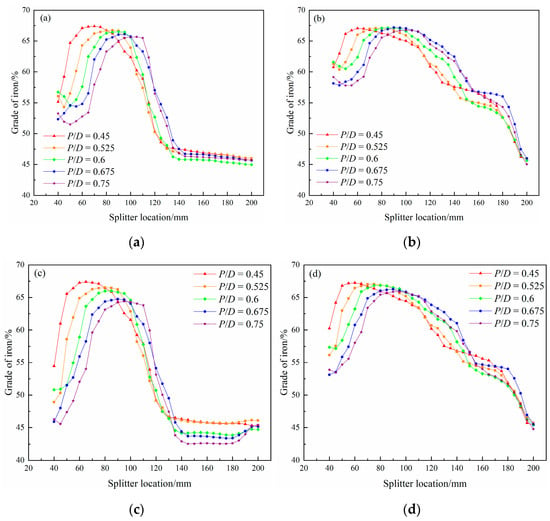
Figure 10.
Influence of splitter location on iron grade of concentrate with different pitch-diameter ratios. (a) 90 μm hematite particles + 90 μm quartz particles; (b) 90 μm hematite particles + 38 μm quartz particles; (c) 38 μm hematite particles + 90 μm quartz particles; and (d) 38 μm hematite particles + 38 μm quartz particles.
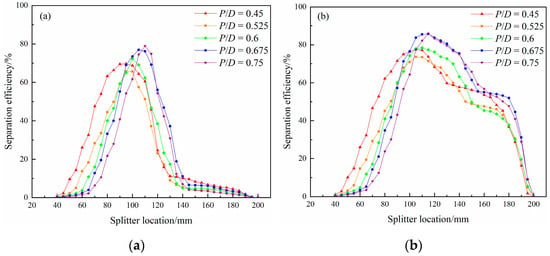
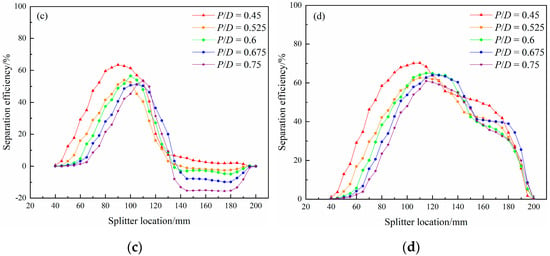
Figure 11.
Influence of splitter location on particle separation efficiency with different pitch-diameter ratios. (a) 90 μm hematite particles + 90 μm quartz particles; (b) 90 μm hematite particles + 38 μm quartz particles; (c) 38 μm hematite particles + 90 μm quartz particles; and (d) 38 μm hematite particles + 38 μm quartz particles.
As can be seen from Figure 10 and Figure 11, iron grade curves and separation efficiency curves were distributed in a peak shape as the splitter location moved outward; that is, there were the highest concentrate grade, the highest separation efficiency, and the best splitter location.
The curves in Figure 10 show that, with the regulation of the pitch-diameter ratio, the highest iron grade obtained by each combined feeding is distributed in the range of 64.42–67.40%, and the optimal splitter location shifts outward with the increase of the pitch-diameter ratio, but all of them are concentrated in the interval within the center point of the trough surface (60–105 mm). The variation trend of the maximum iron grade of concentrate products with the regulation of the pitch-diameter ratio was as follows: when 90 μm hematite and 38 μm quartz were combined for feeding (Figure 10b), the highest iron grades obtained at each pitch-diameter ratio were particularly similar, reaching 66.75–67.18% approximately. Under other combined feedings, the maximum iron grade of concentrate decreased with the increase of the pitch-diameter ratio. Among them, the maximum iron grade of 38 μm hematite and 90 μm quartz decreased to less than 65% when the pitch-diameter ratio was 0.75, which is related to their misplacement.
The prediction results for concentrate grade show that, under the condition of a low pitch-diameter ratio, higher concentrate quality can be obtained with the combined feedings. With the increase in the pitch-diameter ratio, the combined feedings of coarse hematite and fine quartz can still obtain higher concentrate quality by moving the splitter location outward. However, for other combined feedings, although moving the splitter location outward helps to reach the highest concentrate grade under a fixed pitch-diameter ratio, the highest iron grade decreases significantly with the increase of the pitch-diameter ratio. In the working parameter range of the spiral concentrator adopted in the experiment, coarse-grained hematite is easier to obtain high-quality concentrate than feedings of fine-grained hematite, and fine-grained quartz has less interference on the accurate recovery of hematite than coarse-grained quartz. The prediction results for concentrate grade are consistent with the radial distribution characteristics of particles.
As can be seen from the sub-graphs in Figure 11, the maximum separation efficiency of the four particle combinations is 69.71%, 77.56%, 63.45%, and 70.26%, respectively, at the base pitch-diameter ratio (0.45). The separation efficiency of feedings of coarse-grained hematite and quartz is significantly higher than that of feedings of fine-grained hematite and quartz (about 8%). The separation efficiency of a coarse quartz-hematite feeding system is lower than that of a fine quartz-hematite feeding system (about 8%). When the pitch-diameter ratio is regulated, the maximum separation efficiency achieved by different feedings changes to a certain extent, but the variation trend is different.
For the combination of 90 μm hematite and quartz of any particle size, the maximum separation efficiency decreases slightly when the pitch-diameter ratio is 0.525 and then increases obviously with the increase of the pitch-diameter ratio. Finally, the maximum separation efficiency reaches equilibrium when the pitch-diameter ratio is increased to 0.675 and 0.75 and the optimal splitter location shifts outward. The maximum separation efficiencies of 90 μm hematite and 38 μm quartz are very close to each other (85.75% and 85.93%) at high pitch-diameter ratios, but the trend of the curve near the peak is more moderate when the pitch-diameter ratio is 0.675, which can ensure that the separation efficiency will not change abruptly when the splitter location is adjusted within a certain range, so as to facilitate the industrial operation. The maximum separation efficiency of 90 μm hematite and 90 μm quartz is 76.96% and 78.91%, respectively, but it is still about 8% lower than the maximum separation efficiency of 90 μm hematite and 38 μm quartz. The common feature is that the trend near the curve peak is more moderate when the pitch-diameter ratio is 0.675. The optimal separation results of coarse-grained hematite and quartz are highly correlated with the equilibrium of the inner fluid dynamics parameters when the pitch-diameter ratio is 0.675, which is also consistent with the significant reduction of quartz particle misplacement.
For the combination of 38 μm hematite and quartz of each size, the maximum separation efficiency decreased significantly when the pitch-diameter ratio increased from 0.45 to 0.525. When the pitch-diameter ratio increased again, the maximum separation efficiency showed a slight fluctuation, but it did not exceed the index obtained at the pitch-diameter ratio of 0.45. The lowest indices were found at larger pitch-diameter ratios (0.675 and 0.75), which were closely related to the yield variation of 38 μm hematite in different radial regions.
The variation of concentrate grade and separation efficiency can be judged by a comprehensive adjustment of pitch-diameter ratio and splitter position. The separation indices of coarse-grained hematite–quartz feedings are obviously higher than those of fine-grained hematite–quartz feedings. For hematite of any size, better separation indices are obtained by being combined with fine quartz, and the concentrate grade and separation efficiency are positively correlated. Increasing the pitch-diameter ratio is favorable to the combined feeding of coarse hematite and quartz but unfavorable to that of fine hematite and quartz. Table 9 shows the highest separation efficiency, corresponding splitter location, and iron grade of the concentrate obtained at each feeding at appropriate pitch-diameter ratios.

Table 9.
Optimum separation index and corresponding working parameters of each feed ore combination.
The predicted data in Table 9 show that when the pitch-diameter ratio increases to 0.675, the feedings of 90 μm hematite and quartz can obtain a better separation index, and the splitter location should be set at r = 115 mm and 105 mm. At the pitch-diameter ratio of 0.45, the maximum separation efficiency of feedings of 38 μm hematite and quartz is obtained at the splitter locations of r = 110 mm and 90 mm. To obtain a higher concentrate grade, the splitter location needs to be moved inward to the inner region. In addition, when coarse-grained quartz is used as the gangue mineral, the splitter location needs to be more inward, which is closely related to its higher misplacement amount in the hematite accumulation area.
4. Conclusions
- (1)
- Under the fixed working parameters, the depth of the flow film, the tangential velocity, the radial velocity, the velocity shear rate, and the Re increase from inside to outside, indicating a highly positive correlation between the distribution characteristics of flow hydrodynamic parameters. With the increase of the pitch-diameter ratio, the tangential velocity, maximum radial velocity, velocity shear rate, and Re of the fluid in each region decrease significantly, and the laminar flow range extends outward;
- (2)
- There are significant differences in the influence of the pitch-diameter ratio on the depth of the flow film, the split ratio of the inward and outward flows, and the radial velocity in different radial regions. The effect of the pitch-diameter ratio on the depth of flow film in the inner trough is slight, while the reversal position of the secondary flow moves up and the intensity of secondary flow weakens as the pitch-diameter ratio increases, reaching equilibrium at a pitch-diameter ratio of 0.675. In the middle and outer troughs, the depth of the flow film decreases with the increase of the pitch-diameter ratio, the maximum velocity of the secondary flow significantly decreases without an equilibrium point, and the variation trend of the reversal position of secondary flow is also not significant;
- (3)
- With the evolution of the flow field, hematite and quartz particles form a selective distribution feature of high-density particles inside and low-density particles outside at the end of the third turn. The density effect can be clearly described. Meanwhile, the movement of fine particles following the fluid and the interstitial trickling of high-density fine particles are obvious, implying the multiphase flow model adopted is highly reliable;
- (4)
- Fine hematite and coarse quartz form a large amount of mismatch, and the main mismatching areas are one third of the middle trough and one sixth of the outer trough. With the increase in pitch-diameter ratio, coarse and fine hematite migrate to the inner and outer troughs, respectively. Additionally, the mismatch amount of quartz in the inner trough decreases, but the migrating distance of coarse quartz is smaller;
- (5)
- The separation indices of the combined feedings of coarse hematite and fine quartz are the highest when adjusting the splitter location at different pitch-diameter ratios. When the pitch-diameter ratio increases to 0.675, the separation efficiency maximum increases to the equilibrium point, and its variation trend is relatively gentle when the splitter location is adjusted near the equilibrium point, making it more convenient for industrial operations. The changing trend of the separation indices is closely related to the variation of the flow hydrodynamic parameters and provides a basis for spiral design;
- (6)
- Increasing the pitch-diameter ratio is unfavorable for the separation between the fine hematite and the fine/coarse quartz, and the maximum separation efficiency is obtained under the condition of a pitch-diameter ratio of 0.45. When coarse quartz is used as a gangue mineral, the optimum splitter location needs to be adjusted inward, which is closely related to the high mismatch rate of coarse quartz in the hematite accumulation area.
Author Contributions
Conceptualization, S.G.; methodology, X.Z.; validation, L.M. and Q.Z.; investigation, Q.Z.; writing—original draft preparation, S.G. and X.Z.; writing—review and editing, S.G. and X.Z.; visualization, L.M.; supervision, W.L. All authors have read and agreed to the published version of the manuscript.
Funding
National Natural Science Foundation of China [51974065, 52274257], Fundamental Research Funds for the Central Universities [N2201008, N2201004].
Data Availability Statement
Data sharing not applicable. No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
We appreciate the technical support provided by the Department of Mineral Processing Engineering, School of Resources and Civil Engineering, Northeastern University for this project.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| P | Pitch of the spiral concentrator, mm. |
| D | Diameter of the spiral concentrator, mm. |
| R | Outer radius of the spiral concentrator, mm. |
| r0 | Inner radius of the spiral concentrator, mm. |
| FD | Drag force, N. |
| FL | Lift force, N. |
| d | Diameter, μm. |
| N | Bagnold number. |
| C0 | Maximum possible volume concentration of solids. |
| C | Volume concentration of solids. |
| r | Radial position, mm. |
| h | Actual water depth value, mm. |
| H | Absolute water depth, mm. |
| Es | Separation efficiency, %. |
| Rv | Recovery of valuable minerals, %. |
| Rg | Recovery of gangue minerals, %. |
| V | Mean velocity of the fluid, m/s. |
| Mean depth of flow film, mm. | |
| Greek letters | |
| λ | Linear concentration. |
| ρ | Density, kg/m3. |
| µ | Fluid viscosity, kg/(m·s). |
| Subscripts | |
| p | Particle. |
References
- Bazin, C.; Sadeghi, M.; Bourassa, M.; Roy, P.; Lavoie, F.; Cataford, D.; Rochefort, C.; Gosselin, C. Size recovery curves of minerals in industrial spirals for processing iron oxide ores. Miner. Eng. 2014, 65, 115–123. [Google Scholar] [CrossRef]
- Holland-Batt, A.B. The effect of feed rate on the performance of coal spirals. Coal Prep. 1994, 14, 199–222. [Google Scholar] [CrossRef]
- Khanchi, A.R.; Sedighi, H.; Ansar, S.; Fasihi, J. Preconcentration of rare earth elements from Iranian monazite ore by spiral concentrator using multi-response optimization method. Int. J. Miner. Sci. Technol. 2014, 24, 117–121. [Google Scholar] [CrossRef]
- Dehaine, Q.; Filippov, L.O. Modelling heavy and gangue mineral size recovery curves using the spiral concentration of heavy minerals from kaolin residues. Powder Technol. 2016, 292, 331–341. [Google Scholar] [CrossRef]
- Holland-Batt, A.B. Some design considerations for spiral concentrators. Miner. Eng. 1995, 8, 1381–1395. [Google Scholar] [CrossRef]
- Sadeghi, M.; Bazin, C.; Renaud, M. Radial distribution of iron oxide and silica particles in the reject flow of a spiral concentrator. Int. J. Miner. Process. 2016, 153, 51–59. [Google Scholar] [CrossRef]
- Tripathy, S.K.; Murthy, Y.R. Modeling and optimization of spiral concentrator for separation of ultrafine chromite. Powder Technol. 2012, 4, 151–162. [Google Scholar] [CrossRef]
- Nienaber, E.C.; Auret, L. Spiral concentrator interface monitoring through image processing: Optimization for parameter selection. IFAC-PapersOnLine 2016, 49, 102–107. [Google Scholar] [CrossRef]
- Nienaber, E.C.; McCoy, J.T.; Auret, L. Spiral concentrator interface monitoring through image processing: A statistical learning approach. IFAC-PapersOnLine 2017, 50, 53–58. [Google Scholar] [CrossRef]
- Ye, G.; Huo, Y.; Li, C.; Deng, C.; Yu, Y.; Huang, G.; Ma, L. A comparative study of trough profile and operating parameters performance in spiral concentrator. Int. J. Coal Prep. Util. 2021, 41, 678–691. [Google Scholar] [CrossRef]
- Davies, P.O.J.; Goodman, R.H.; Deschamps, J.A. Recent developments in spiral design, construction and application. Miner. Eng. 1991, 4, 437–456. [Google Scholar] [CrossRef]
- Boucher, D.; Deng, Z.; Leadbeater, T.W.; Langlois, R.; Waters, K.E. Speed analysis of quartz and hematite particles in a spiral concentrator by PEPT. Miner. Eng. 2016, 91, 86–91. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Y.M.; Liu, T.; Cai, Z.L.; Sun, K. Preconcentration of vanadium from stone coal by gravity using fine mineral spiral. Minerals 2016, 6, 82. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Y.M.; Liu, T.; Cai, Z.L.; Chen, T.J.; Sun, K. Beneficiation of a sedimentary phosphate ore by a combination of spiral gravity and direct-reverse flotation. Minerals 2016, 6, 38. [Google Scholar] [CrossRef]
- Doheim, M.A.; Gawad, A.F.A.; Mahran, G.M.A.; Abu-Ali, M.H.; Rizk, A.M. Computational prediction of water-flow characteristics in spiral concentrators: Part I, flow depth and turbulence intensity. J. Eng. Sci. 2008, 36, 935–950. [Google Scholar] [CrossRef]
- Doheim, M.A.; Gawad, A.F.A.; Mahran, G.M.A.; Abu-Ali, M.H.; Rizk, A.M. Computational prediction of water-flow characteristics in spiral concentrators: Part II, the primary and secondary flows. J. Eng. Sci. 2008, 36, 951–961. [Google Scholar] [CrossRef]
- Meng, L.; Gao, S.; Wei, D.; Cui, B.; Shen, Y.; Song, Z.; Yuan, J. Effects of cross-sectional geometry on flow characteristics in spiral concentrators. Sep. Sci. Technol. 2021, 56, 2967–2977. [Google Scholar] [CrossRef]
- Meng, L.; Gao, S.; Wei, D.; Cui, B.; Shen, Y.; Song, Z. Investigation on the evolution of flow field stability in a spiral concentrator. Miner. Eng. 2021, 174, 107224. [Google Scholar] [CrossRef]
- Matthews, B.W.; Fletcher, C.A.J.; Partridge, A.C.; Vasquez, S. Computations of curved free surface water flow on spiral concentrators. J. Hydraul. Eng. 1999, 125, 1126–1139. [Google Scholar] [CrossRef]
- Matthews, B.W.; Fletcher, C.A.J.; Partridge, A.C. Computational simulation of fluid and dilute particulate flows on spiral concentrators. Appl. Math. Model. 1998, 22, 965–979. [Google Scholar] [CrossRef]
- Matthews, B.W.; Fletcher, C.A.J.; Partridge, T.C. Particle flow modelling on spiral concentrators: Benefits of dense media for coal processing? In Second International Conference on CFD in the Minerals and Process Industries; CSIRO: Melbourne, Australia, 1999; pp. 211–216. [Google Scholar]
- Doheim, M.A.; Gawad, A.F.A.; Mahran, G.M.A.; Abu-Ali, M.H.; Rizk, A.M. Numerical simulation of particulate-flow in spiral concentrators: Part I. low solids concentration (0.3% & 3% solids). Appl. Math. Model. 2013, 37, 198–215. [Google Scholar] [CrossRef]
- Mahran, G.M.A.; Doheim, M.A.; Abu-Ali, M.H.; Gawad, A.F.A. CFD simulation of particulate flow in a spiral concentrator. Mater. Test. 2015, 57, 811–816. [Google Scholar] [CrossRef]
- Gao, S.; Meng, L.; Zhou, X.; Shen, Y.; Cui, B.; Song, Z. Design of partial cross-sectional geometry and prediction of separation performance in the spiral concentrator. Sep. Sci. Technol. 2022, 57, 2127–2144. [Google Scholar] [CrossRef]
- Wang, J.W.; Andrews, J.R.G. Numerical simulations of liquid flow on spiral concentrators. Miner. Eng. 1994, 7, 1363–1385. [Google Scholar] [CrossRef]
- Ye, G.; Ma, L.; Alberini, F.; Xu, Q.; Huang, G.; Yu, Y. Numerical studies of the effects of design parameters on flow fields in spiral concentrators. Int. J. Coal Prep. Util. 2022, 42, 67–81. [Google Scholar] [CrossRef]
- Ĉerne, G.; Petelin, S.; Tiselj, I. Coupling of the interface tracking and the two-fluid models for the simulation of incompressible two-phase flow. J. Comput. Phys. 2001, 171, 776–804. [Google Scholar] [CrossRef]
- Hou, D.X.; Cui, B.Y.; Zhao, Q.; Wei, D.Z.; Song, Z.G.; Feng, Y.Q. Research on the structure of the cylindrical hydrocyclone spigot to mitigate the misplacement of particles. Powder Technol. 2021, 387, 61–71. [Google Scholar] [CrossRef]
- Akhlaghi, M.; Mohammadi, V.; Nouri, N.M.; Taherkhani, M.; Karimi, M. Multi-Fluid VOF model assessment to simulate the horizontal air-water intermittent flow. Chem. Eng. Res. Des. 2019, 152, 48–59. [Google Scholar] [CrossRef]
- Mishra, B.K.; Tripathy, A.A. Preliminary study of particle separation in spiral concentrators using DEM. Int. J. Miner. Process. 2010, 94, 192–195. [Google Scholar] [CrossRef]
- Holtham, P.N. Primary and secondary fluid velocities on spiral concentrators. Miner. Eng. 1992, 5, 79–91. [Google Scholar] [CrossRef]
- Holtham, P.H. Particle transport in gravity concentrators and the Bagnold effect. Miner. Eng. 1992, 5, 205–221. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).