Arithmetic Proficiency Across Adulthood: Cognitive and Subjective Influences
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
2.2. Neuropsychological Background Assessment
2.3. Objective Arithmetic Measures
2.4. Subjective Arithmetic Measures
2.5. Procedure
2.6. Statistical Analysis
3. Results
3.1. Outcomes in Neuropsychological Background Tests
3.2. Objective Arithmetic Outcomes
3.3. Subjective Arithmetic Outcomes
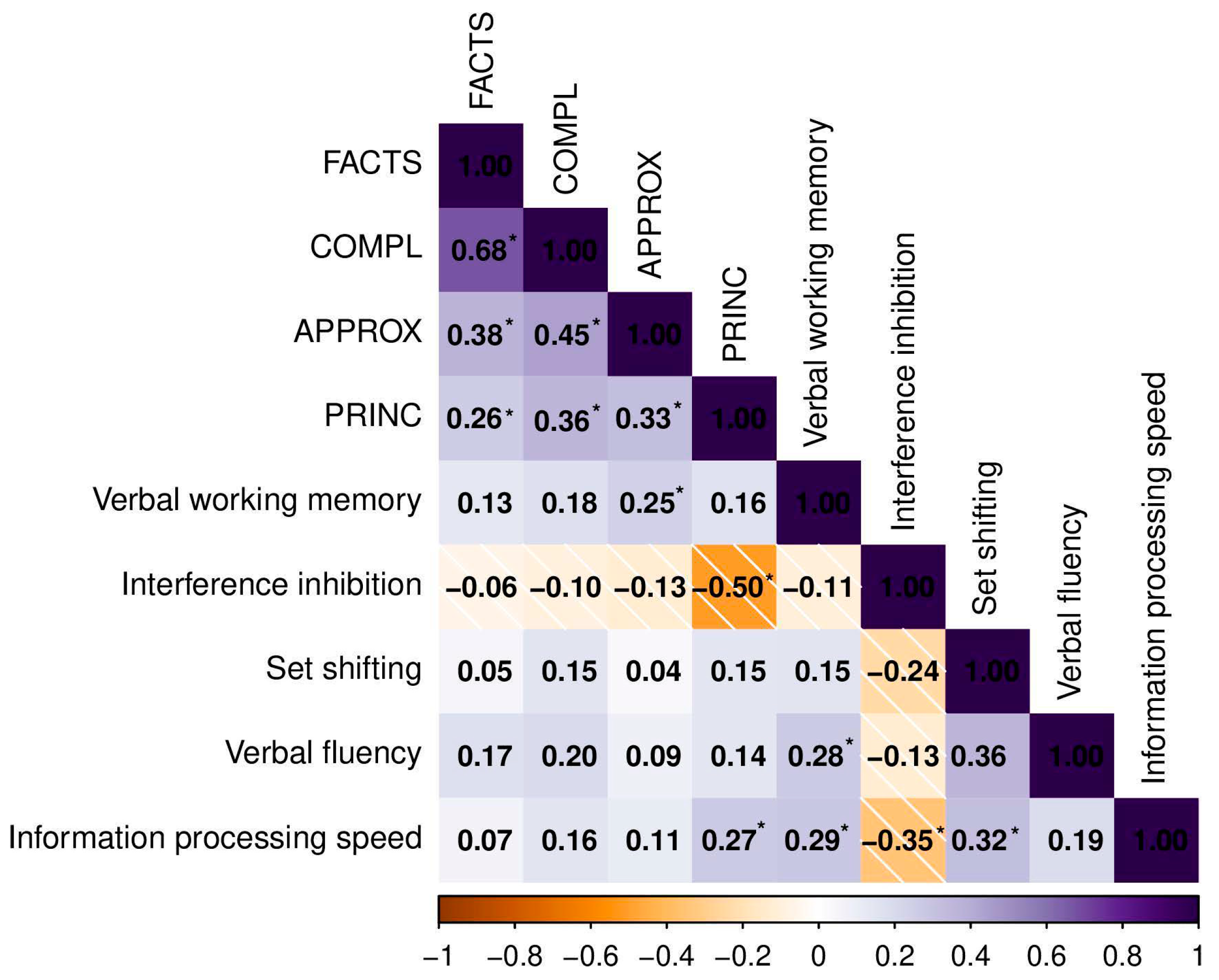
3.4. Correlation Analysis
3.4.1. Correlations with Demographic Variables
3.4.2. Correlations with Domain-General Cognitive Factors
3.4.3. Correlations with Subjective Arithmetic Outcomes
3.5. Hierarchical Regression Analysis
3.5.1. Simple Calculations
3.5.2. Exact Complex Calculations
3.5.3. Approximate Complex Calculations
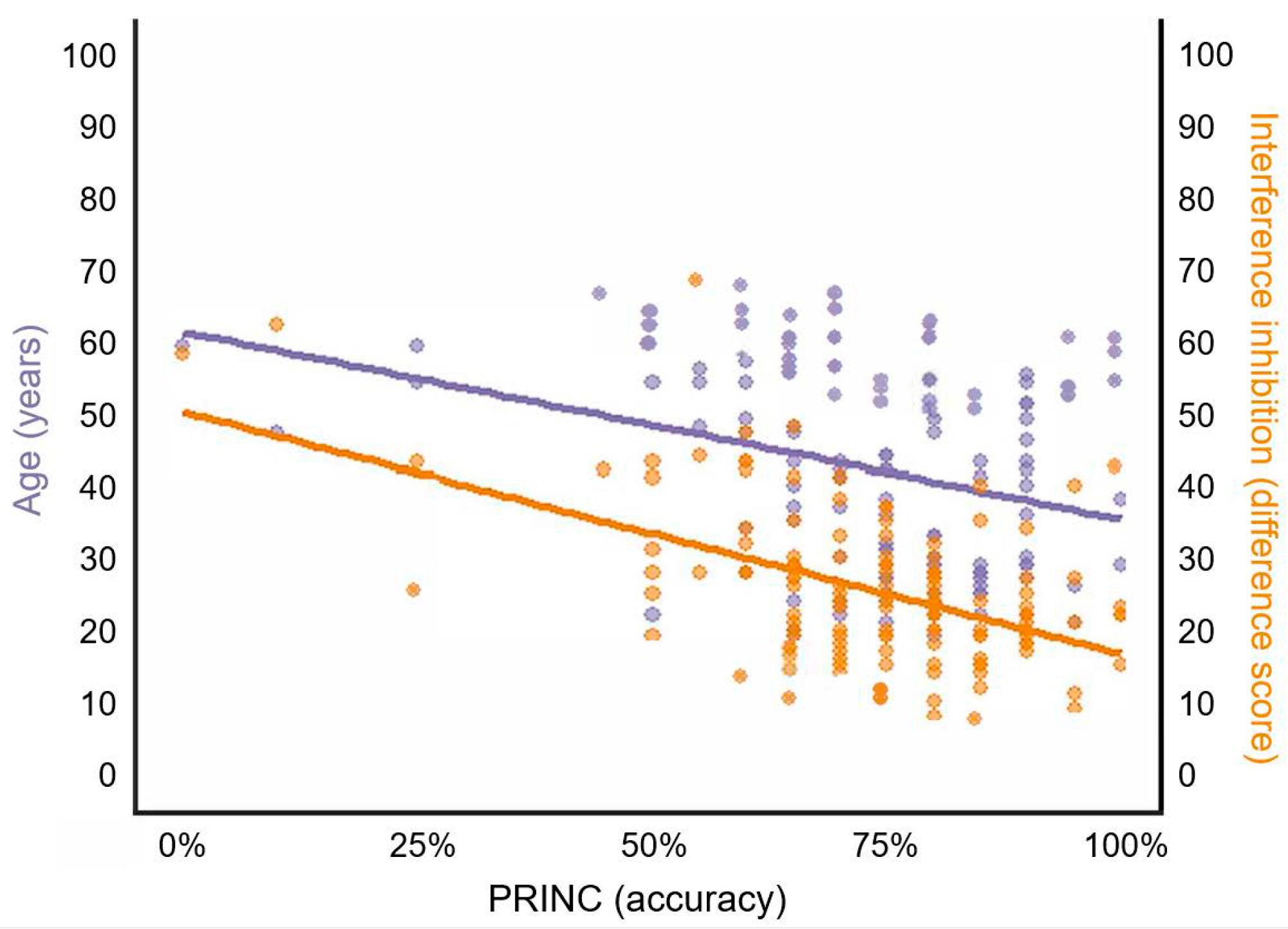
3.5.4. Arithmetic Principles
4. Discussion
4.1. Demographic Factors
4.2. Domain-General Cognitive Factors
4.3. Subjective Arithmetic Factors
4.4. Predictors of Arithmetic Performance
4.5. Limitations and Strengths
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aschenbrenner, S., Tucha, O., & Lange, K. W. (2000). Regensburger Wortflüssigkeits-Test (RWT). Hogrefe. [Google Scholar]
- Ashcraft, M. H. (2002). Math anxiety: Personal, educational, and cognitive consequences. Current Directions in Psychological Science, 11(5), 181–185. [Google Scholar] [CrossRef]
- Avcil, M., & Artemenko, C. (2025). Development of arithmetic across the lifespan: A registered report. Developmental Psychology. in press. [Google Scholar] [CrossRef]
- Barroso, C., Ganley, C. M., McGraw, A. L., Geer, E. A., Hart, S. A., & Daucourt, M. C. (2021). A meta-analysis of the relation between math anxiety and math achievement. Psychological Bulletin, 147(2), 134–168. [Google Scholar] [CrossRef]
- Bäumler, G. (1985). Farbe-Wort-Interferenztest (FWIT) nach J. R. Stroop—Handanweisung. Hogrefe. [Google Scholar]
- Bull, R., & Lee, K. (2014). Executive functioning and mathematics achievement. Child Development Perspectives, 8(1), 36–41. [Google Scholar] [CrossRef]
- Carey, E., Hill, F., Devine, A., & Szücs, D. (2016). The chicken or the egg? The direction of the relationship between mathematics anxiety and mathematics performance. Frontiers in Psychology, 6, 1987. [Google Scholar] [CrossRef] [PubMed]
- Chen, E. H., & Bailey, D. H. (2021). Dual-task studies of working memory and arithmetic performance: A meta-analysis. Journal of Experimental Psychology: Learning, Memory, and Cognition, 47(2), 220–233. [Google Scholar] [CrossRef] [PubMed]
- Chow, J. C., & Ekholm, E. (2019). Language domains differentially predict mathematics performance in young children. Early Childhood Research Quarterly, 46, 179–186. [Google Scholar] [CrossRef]
- Christou, C., & Papageorgiou, E. (2007). A framework of mathematics inductive reasoning. Learning and Instruction, 17(1), 55–66. [Google Scholar] [CrossRef]
- Cohen, J. (1988). Statistical power analysis for the behavioral sciences (2nd ed.). Lawrence Erlbaum Associates. [Google Scholar]
- Cragg, L., Keeble, S., Richardson, S., Roome, H. E., & Gilmore, C. (2017). Direct and indirect influences of executive functions on mathematics achievement. Cognition, 162, 12–26. [Google Scholar] [CrossRef]
- Delazer, M. (2003). Neuropsychological findings on conceptual knowledge of arithmetic. In The development of arithmetic concepts and skills: Constructing adaptive expertise (pp. 385–407). Lawrence Erlbaum Associates Publishers. [Google Scholar]
- Delazer, M., Girelli, L., Granà, A., & Domahs, F. (2003). Number processing and calculation—Normative data from healthy adults. The Clinical Neuropsychologist, 17(3), 331–350. [Google Scholar] [CrossRef]
- Desoete, A. (2015). Cognitive predictors of mathematical abilities and disabilities. In R. C. Kadosh, & A. Dowker (Eds.), The Oxford handbook of numerical cognition (pp. 915–932). Oxford University Press. [Google Scholar]
- Devine, A., Fawcett, K., Szűcs, D., & Dowker, A. (2012). Gender differences in mathematics anxiety and the relation to mathematics performance while controlling for test anxiety. Behavioral and Brain Functions, 8(1), 33. [Google Scholar] [CrossRef]
- Di Martino, P., & Zan, R. (2010). ‘“Me and maths”: Towards a definition of attitude grounded on students’ narratives’. Journal of Mathematics Teacher Education, 13(1), 27–48. [Google Scholar] [CrossRef]
- Donelle, L., Hoffman-Goetz, L., & Arocha, J. F. (2007). Assessing health numeracy among community-dwelling older adults. Journal of Health Communication, 12(7), 651–665. [Google Scholar] [CrossRef] [PubMed]
- Dowker, A., Sarkar, A., & Looi, C. Y. (2016). Mathematics anxiety: What have we learned in 60 years? Frontiers in Psychology, 7, 508. [Google Scholar] [CrossRef] [PubMed]
- Dowker, A., & Sheridan, H. (2022). Relationships between mathematics performance and attitude to mathematics: Influences of gender, test anxiety, and working memory. Frontiers in Psychology, 13, 814992. [Google Scholar] [CrossRef]
- Duverne, S., & Lemaire, P. (2005). Aging and mental arithmetic. In J. I. D. Campbell (Ed.), Handbook of mathematical cognition (pp. 397–411). Psychology Press. [Google Scholar]
- Faul, F., Erdfelder, E., Lang, A.-G., & Buchner, A. (2007). G*Power 3: A flexible statistical power analysis program for the social, behavioral, and biomedical sciences. Behavior Research Methods, 39(2), 175–191. [Google Scholar] [CrossRef]
- Folstein, M. F., Folstein, S. E., & McHugh, P. R. (1975). Mini-mental state. Journal of Psychiatric Research, 12(3), 189–198. [Google Scholar] [CrossRef] [PubMed]
- Gilmore, C., Keeble, S., Richardson, S., & Cragg, L. (2015). The role of cognitive inhibition in different components of arithmetic. ZDM, 47(5), 771–782. [Google Scholar] [CrossRef]
- Guiso, L., Monte, F., Sapienza, P., & Zingales, L. (2008). Diversity. Culture, gender, and math. Science, 320(5880), 1164–1165. [Google Scholar] [CrossRef]
- Hart, S. A., & Ganley, C. M. (2019). The nature of math anxiety in adults: Prevalence and correlates. Journal of Numerical Cognition, 5(2), 122–139. [Google Scholar] [CrossRef]
- Hawes, Z. C. K., Gilligan-Lee, K. A., & Mix, K. S. (2022). Effects of spatial training on mathematics performance: A meta-analysis. Developmental Psychology, 58(1), 112–137. [Google Scholar] [CrossRef]
- Härting, C., Markowitsch, H. J., Neufeld, U., Calabrese, P., Deisinger, K., & Kessler, J. (2000). Wechsler gedächtnis test—Revidierte Fassung: Deutsche adaption der revidierten fassung der wechsler-memory scale. Huber. [Google Scholar]
- Henschel, S., & Roick, T. (2017). Relationships of mathematics performance, control and value beliefs with cognitive and affective math anxiety. Learning and Individual Differences, 55, 97–107. [Google Scholar] [CrossRef]
- Hernández De La Hera, J. M., Morales-Rodríguez, F. M., Rodríguez-Gobiet, J. P., & Martínez-Ramón, J. P. (2023). Attitudes toward mathematics/statistics, anxiety, self-efficacy and academic performance: An artificial neural network. Frontiers in Psychology, 14, 1214892. [Google Scholar] [CrossRef] [PubMed]
- Herrmann, C., Buss, U., & Snaith, R. P. (1995). Hospital anxiety and depression scale-german version (HADS-D). Huber. [Google Scholar]
- Hinault, T., & Lemaire, P. (2016). Age-related changes in strategic variations during arithmetic problem solving. In Progress in brain research (Vol. 227, pp. 257–276). Elsevier. [Google Scholar] [CrossRef]
- Hodzik, S., & Lemaire, P. (2011). Inhibition and shifting capacities mediate adults’ age-related differences in strategy selection and repertoire. Acta Psychologica, 137(3), 335–344. [Google Scholar] [CrossRef]
- Hyde, J. S., & Mertz, J. E. (2009). Gender, culture, and mathematics performance. Proceedings of the National Academy of Sciences of the United States of America, 106(22), 8801–8807. [Google Scholar] [CrossRef]
- Justicia-Galiano, M. J., Martín-Puga, M. E., Linares, R., & Pelegrina, S. (2017). Math anxiety and math performance in children: The mediating roles of working memory and math self-concept. British Journal of Educational Psychology, 87(4), 573–589. [Google Scholar] [CrossRef]
- Knops, A., Nuerk, H.-C., & Göbel, S. M. (2017). Domain-general factors influencing numerical and arithmetic processing. Journal of Numerical Cognition, 3(2), 112–132. [Google Scholar] [CrossRef]
- LeFevre, J., Fast, L., Skwarchuk, S., Smith-Chant, B. L., Bisanz, J., Kamawar, D., & Penner-Wilger, M. (2010). Pathways to mathematics: Longitudinal predictors of performance. Child Development, 81(6), 1753–1767. [Google Scholar] [CrossRef]
- Lehrl, S. (2005). Mehrfachwahl-Wortschatz-Intelligenztest: MWT-B (5th ed.). Spitta. [Google Scholar]
- Liebert, R. M., & Morris, L. W. (1967). Cognitive and emotional components of test anxiety: A distinction and some initial data. Psychological Reports, 20(3), 975–978. [Google Scholar] [CrossRef]
- Lipnevich, A. A., Preckel, F., & Krumm, S. (2016). Mathematics attitudes and their unique contribution to achievement: Going over and above cognitive ability and personality. Learning and Individual Differences, 47, 70–79. [Google Scholar] [CrossRef]
- Mather, M. (2016). The affective neuroscience of aging. Annual Review of Psychology, 67(1), 213–238. [Google Scholar] [CrossRef]
- Mather, M., & Carstensen, L. L. (2005). Aging and motivated cognition: The positivity effect in attention and memory. Trends in Cognitive Sciences, 9(10), 496–502. [Google Scholar] [CrossRef] [PubMed]
- OECD. (2024). Do adults have the skills they need to thrive in a changing world? Survey of adult skills 2023. OECD. [Google Scholar] [CrossRef]
- Petermann, F., Jäncke, L., & Waldmann, H.-C. (2016). Neuropsychological assessment battery deutschsprachige adaptation der Neuropsychological Assessment Battery (NAB) von Robert A. Stern und Travis White. Hogrefe. [Google Scholar]
- Raghubar, K. P., Barnes, M. A., & Hecht, S. A. (2010). Working memory and mathematics: A review of developmental, individual difference, and cognitive approaches. Learning and Individual Differences, 20(2), 110–122. [Google Scholar] [CrossRef]
- Reyna, V. F., Nelson, W. L., Han, P. K., & Dieckmann, N. F. (2009). How numeracy influences risk comprehension and medical decision making. Psychological Bulletin, 135(6), 943–973. [Google Scholar] [CrossRef]
- Ritchie, S. J., & Bates, T. C. (2013). Enduring links from childhood mathematics and reading achievement to adult socioeconomic status. Psychological Science, 24(7), 1301–1308. [Google Scholar] [CrossRef]
- Rossi, S., Xenidou-Dervou, I., & Cipora, K. (2023). Emotions and mathematics: Anxiety profiles and their influence on arithmetic performance in university students. Royal Society Open Science, 10(10), 230861. [Google Scholar] [CrossRef]
- Rossi, S., Xenidou-Dervou, I., Simsek, E., Artemenko, C., Daroczy, G., Nuerk, H., & Cipora, K. (2022). Mathematics–gender stereotype endorsement influences mathematics anxiety, self-concept, and performance differently in men and women. Annals of the New York Academy of Sciences, 1513(1), 121–139. [Google Scholar] [CrossRef]
- Salthouse, T. A., & Coon, V. E. (1994). Interpretation of differential deficits: The case of aging and mental arithmetic. Journal of Experimental Psychology: Learning, Memory, and Cognition, 20(5), 1172–1182. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Smith, A. (1973). Symbol digit modalities test [Dataset]. APA PsycTests. [Google Scholar]
- Spelke, E. S. (2005). Sex differences in intrinsic aptitude for mathematics and science? A critical review. American Psychologist, 60(9), 950–958. [Google Scholar] [CrossRef] [PubMed]
- Spreng, R. N., & Turner, G. R. (2019). The shifting architecture of cognition and brain function in older adulthood. Perspectives on Psychological Science, 14(4), 523–542. [Google Scholar] [CrossRef]
- Tapia, M. (1996, November 6). The attitudes toward mathematics instrument. Annual Meeting of the Mid-South Educational Research Association, Tuscaloosa, Alabama. [Google Scholar]
- Zamarian, L., López-Rolón, A., & Delazer, M. (2007a). Neuropsychological case studies on arithmetic processing. In D. B. Berch, & M. M. M. Mazzocco (Eds.), Why is math so hard for some children? The nature and origins of mathematical learning difficulties and disabilities (pp. 245–263). Paul H. Brookes Publishing Co. [Google Scholar]
- Zamarian, L., Scherfler, C., Kremser, C., Pertl, M.-T., Gizewski, E., Benke, T., & Delazer, M. (2018). Arithmetic learning in advanced age. PLoS ONE, 13(2), e0193529. [Google Scholar] [CrossRef]
- Zamarian, L., Semenza, C., Domahs, F., Benke, T., & Delazer, M. (2007b). Alzheimer’s disease and mild cognitive impairment: Effects of shifting and interference in simple arithmetic. Journal of the Neurological Sciences, 263(1–2), 79–88. [Google Scholar] [CrossRef] [PubMed]
- Zamarian, L., Stadelmann, E., Nürk, H.-C., Gamboz, N., Marksteiner, J., & Delazer, M. (2007c). Effects of age and mild cognitive impairment on direct and indirect access to arithmetic knowledge. Neuropsychologia, 45(7), 1511–1521. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J., Cheung, S. K., Wu, C., & Meng, Y. (2018). Cognitive and affective correlates of Chinese children’s mathematical word problem solving. Frontiers in Psychology, 9, 2357. [Google Scholar] [CrossRef] [PubMed]

| Max. Score | M | SD | Min | Max | |
|---|---|---|---|---|---|
| FACTS (% correct) | 100 | 88.9 | 9.8 | 57.5 | 100.0 |
| COMPL (% correct) | 100 | 76.7 | 15.1 | 22.5 | 100.0 |
| APPROX (% correct) | 100 | 56.8 | 20.5 | 0.0 | 91.7 |
| PRINC (% correct) | 100 | 73.5 | 16.2 | 0.0 | 100.0 |
| Affective math anxiety (individual median) | 4 | 1.3 | 0.5 | 1 | 3 |
| Cognitive math anxiety (individual median) | 4 | 1.3 | 0.5 | 1 | 3 |
| Math self-concept (individual median) | 4 | 2.8 | 0.7 | 1 | 4 |
| Attitudes Toward Mathematics (individual median) | 4 | 3.3 | 0.6 | 2 | 4 |
| FIN (individual median) | 10 | 6.1 | 2.2 | 1 | 10 |
| Unstandardized Coefficients | Standardized Coefficients | Collinearity | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | B | SE | Beta (β) | t | P | Tolerance | VIF | ||
| FACTS | 1 | (Intercept) | 0.749 | 0.037 | 20.198 | <0.001 | |||
| Education | 0.010 | 0.003 | 0.312 | 3.772 | <0.001 | 1.000 | 1.000 | ||
| 2 | (Intercept) | 0.534 | 0.041 | 13.170 | <0.001 | ||||
| Education | 0.001 | 0.002 | 0.028 | 0.394 | 0.694 | 0.809 | 1.235 | ||
| COMPL | 0.413 | 0.051 | 0.631 | 8.114 | <0.001 | 0.681 | 1.468 | ||
| APPROX | 0.040 | 0.036 | 0.084 | 1.128 | 0.261 | 0.749 | 1.336 | ||
| PRINC | 0.000 | 0.043 | 0.000 | −0.003 | 0.998 | 0.833 | 1.200 | ||
| 3 | (Intercept) | 0.534 | 0.064 | 8.312 | <0.001 | ||||
| Education | 0.001 | 0.002 | 0.034 | 0.469 | 0.640 | 0.793 | 1.262 | ||
| COMPL | 0.398 | 0.054 | 0.609 | 7.371 | <0.001 | 0.608 | 1.646 | ||
| APPROX | 0.033 | 0.036 | 0.068 | 0.913 | 0.363 | 0.737 | 1.357 | ||
| PRINC | 0.001 | 0.046 | 0.001 | 0.015 | 0.988 | 0.719 | 1.391 | ||
| Affective math anxiety | −0.008 | 0.018 | −0.037 | −0.454 | 0.650 | 0.630 | 1.588 | ||
| Cognitive math anxiety | −0.001 | 0.017 | −0.005 | −0.058 | 0.954 | 0.607 | 1.646 | ||
| Math self-concept | −0.014 | 0.011 | −0.094 | −1.304 | 0.195 | 0.795 | 1.259 | ||
| Attitudes Toward Mathematics | 0.014 | 0.011 | 0.086 | 1.210 | 0.229 | 0.822 | 1.216 | ||
| FIN | 0.003 | 0.003 | 0.067 | 0.927 | 0.356 | 0.784 | 1.276 | ||
| COMPL | 1 | (Intercept) | 0.360 | 0.065 | 5.507 | <0.001 | |||
| Education | 0.021 | 0.004 | 0.430 | 5.612 | <0.001 | 0.992 | 1.008 | ||
| Sex (f = 1, m = 2) | 0.079 | 0.023 | 0.265 | 3.455 | <0.001 | 0.992 | 1.008 | ||
| 2 | (Intercept) | −0.264 | 0.086 | −3.072 | 0.003 | ||||
| Education | 0.009 | 0.003 | 0.189 | 2.936 | 0.004 | 0.820 | 1.219 | ||
| Sex (f = 1, m = 2) | 0.038 | 0.018 | 0.127 | 2.091 | 0.038 | 0.922 | 1.085 | ||
| FACTS | 0.796 | 0.100 | 0.521 | 7.943 | <0.001 | 0.793 | 1.262 | ||
| APPROX | 0.093 | 0.049 | 0.127 | 1.885 | 0.062 | 0.752 | 1.330 | ||
| PRINC | 0.121 | 0.059 | 0.130 | 2.058 | 0.042 | 0.858 | 1.166 | ||
| 3 | (Intercept) | −0.254 | 0.110 | −2.300 | 0.023 | ||||
| Education | 0.008 | 0.003 | 0.151 | 2.271 | 0.025 | 0.769 | 1.300 | ||
| Sex (f = 1, m = 2) | 0.025 | 0.019 | 0.085 | 1.321 | 0.189 | 0.826 | 1.211 | ||
| FACTS | 0.759 | 0.104 | 0.496 | 7.319 | <0.001 | 0.737 | 1.357 | ||
| APPROX | 0.087 | 0.050 | 0.118 | 1.743 | 0.084 | 0.742 | 1.348 | ||
| PRINC | 0.106 | 0.063 | 0.114 | 1.675 | 0.096 | 0.735 | 1.361 | ||
| Affective math anxiety | −0.005 | 0.025 | −0.017 | −0.222 | 0.824 | 0.612 | 1.633 | ||
| Cognitive math anxiety | −0.015 | 0.023 | −0.047 | −0.629 | 0.531 | 0.606 | 1.651 | ||
| Math self-concept | 0.010 | 0.016 | 0.039 | 0.598 | 0.551 | 0.809 | 1.236 | ||
| Attitudes Toward Mathematics | 0.024 | 0.015 | 0.105 | 1.586 | 0.115 | 0.772 | 1.295 | ||
| FIN | 0.002 | 0.005 | 0.027 | 0.408 | 0.684 | 0.777 | 1.287 | ||
| Unstandardized Coefficients | Standardized Coefficients | Collinearity | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Model | B | SE | Beta (β) | t | p | Tolerance | VIF | ||
| APPROX | 1 | (Intercept) | 0.276 | 0.077 | 3.584 | <0.001 | |||
| Education | 0.022 | 0.006 | 0.321 | 3.893 | <0.001 | 1.000 | 1.000 | ||
| 2 | (Intercept) | 0.168 | 0.089 | 1.893 | 0.061 | ||||
| Education | 0.019 | 0.006 | 0.285 | 3.450 | <0.001 | 0.965 | 1.036 | ||
| Verbal working memory | 0.021 | 0.009 | 0.193 | 2.335 | 0.021 | 0.965 | 1.036 | ||
| 3 | (Intercept) | −0.259 | 0.154 | −1.683 | 0.095 | ||||
| Education | 0.009 | 0.006 | 0.132 | 1.583 | 0.116 | 0.816 | 1.225 | ||
| Verbal working memory | 0.015 | 0.008 | 0.139 | 1.790 | 0.076 | 0.943 | 1.061 | ||
| FACTS | 0.239 | 0.214 | 0.115 | 1.120 | 0.265 | 0.536 | 1.865 | ||
| COMPL | 0.317 | 0.150 | 0.233 | 2.114 | 0.036 | 0.466 | 2.144 | ||
| PRINC | 0.205 | 0.103 | 0.162 | 1.997 | 0.048 | 0.855 | 1.170 | ||
| 4 | (Intercept) | −0.249 | 0.154 | −1.616 | 0.108 | ||||
| Education | 0.009 | 0.006 | 0.131 | 1.578 | 0.117 | 0.816 | 1.225 | ||
| Verbal working memory | 0.014 | 0.008 | 0.133 | 1.718 | 0.088 | 0.939 | 1.065 | ||
| FACTS | 0.217 | 0.215 | 0.104 | 1.011 | 0.314 | 0.531 | 1.884 | ||
| COMPL | 0.304 | 0.150 | 0.223 | 2.022 | 0.045 | 0.463 | 2.159 | ||
| PRINC | 0.170 | 0.108 | 0.135 | 1.576 | 0.118 | 0.771 | 1.297 | ||
| FIN | 0.008 | 0.008 | 0.087 | 1.026 | 0.307 | 0.792 | 1.263 | ||
| PRINC | 1 | (Intercept) | 0.741 | 0.074 | 9.965 | <0.001 | |||
| Age | −0.003 | 0.001 | −0.286 | −3.484 | <0.001 | 0.998 | 1.002 | ||
| Education | 0.010 | 0.004 | 0.187 | 2.285 | 0.024 | 0.998 | 1.002 | ||
| 2 | (Intercept) | 0.853 | 0.134 | 6.347 | <0.001 | ||||
| Age | −0.002 | 0.001 | −0.139 | −1.594 | 0.113 | 0.723 | 1.383 | ||
| Education | 0.007 | 0.004 | 0.123 | 1.612 | 0.109 | 0.948 | 1.055 | ||
| Interference inhibition | −0.006 | 0.001 | −0.428 | −5.300 | <0.001 | 0.844 | 1.185 | ||
| Information processing speed | 0.001 | 0.002 | 0.031 | 0.341 | 0.734 | 0.687 | 1.455 | ||
| 3 | (Intercept) | 0.649 | 0.151 | 4.284 | <0.001 | ||||
| Age | −0.002 | 0.001 | −0.136 | −1.618 | 0.108 | 0.687 | 1.455 | ||
| Education | −0.001 | 0.004 | −0.025 | −0.312 | 0.755 | 0.784 | 1.275 | ||
| Interference inhibition | −0.006 | 0.001 | −0.415 | −5.455 | <0.001 | 0.840 | 1.191 | ||
| Information processing speed | 0.000 | 0.001 | 0.011 | 0.125 | 0.900 | 0.683 | 1.465 | ||
| FACTS | 0.086 | 0.161 | 0.052 | 0.530 | 0.597 | 0.504 | 1.982 | ||
| COMPL | 0.238 | 0.111 | 0.221 | 2.147 | 0.034 | 0.457 | 2.186 | ||
| APPROX | 0.117 | 0.063 | 0.148 | 1.845 | 0.067 | 0.758 | 1.320 | ||
| 4 | (Intercept) | 0.611 | 0.146 | 4.197 | <0.001 | ||||
| Age | −0.002 | 0.001 | −0.131 | −1.633 | 0.105 | 0.687 | 1.456 | ||
| Education | −0.002 | 0.004 | −0.037 | −0.483 | 0.630 | 0.772 | 1.296 | ||
| Interference inhibition | −0.006 | 0.001 | −0.411 | −5.619 | <0.001 | 0.826 | 1.210 | ||
| Information processing speed | 0.000 | 0.001 | −0.023 | −0.283 | 0.778 | 0.665 | 1.503 | ||
| FACTS | 0.053 | 0.155 | 0.033 | 0.344 | 0.731 | 0.497 | 2.011 | ||
| COMPL | 0.161 | 0.109 | 0.150 | 1.479 | 0.142 | 0.431 | 2.319 | ||
| APPROX | 0.084 | 0.061 | 0.107 | 1.379 | 0.170 | 0.741 | 1.349 | ||
| Math self-concept | 0.027 | 0.018 | 0.111 | 1.514 | 0.133 | 0.830 | 1.205 | ||
| FIN | 0.018 | 0.005 | 0.240 | 3.320 | 0.001 | 0.850 | 1.177 | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the University Association of Education and Psychology. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Goettfried, E.; Thaler, K.; Delazer, M.; Basso, D.; Piazza, M.; Knoflach, M.; Zamarian, L. Arithmetic Proficiency Across Adulthood: Cognitive and Subjective Influences. Eur. J. Investig. Health Psychol. Educ. 2025, 15, 84. https://doi.org/10.3390/ejihpe15050084
Goettfried E, Thaler K, Delazer M, Basso D, Piazza M, Knoflach M, Zamarian L. Arithmetic Proficiency Across Adulthood: Cognitive and Subjective Influences. European Journal of Investigation in Health, Psychology and Education. 2025; 15(5):84. https://doi.org/10.3390/ejihpe15050084
Chicago/Turabian StyleGoettfried, Elisabeth, Katharina Thaler, Margarete Delazer, Demis Basso, Manuela Piazza, Michael Knoflach, and Laura Zamarian. 2025. "Arithmetic Proficiency Across Adulthood: Cognitive and Subjective Influences" European Journal of Investigation in Health, Psychology and Education 15, no. 5: 84. https://doi.org/10.3390/ejihpe15050084
APA StyleGoettfried, E., Thaler, K., Delazer, M., Basso, D., Piazza, M., Knoflach, M., & Zamarian, L. (2025). Arithmetic Proficiency Across Adulthood: Cognitive and Subjective Influences. European Journal of Investigation in Health, Psychology and Education, 15(5), 84. https://doi.org/10.3390/ejihpe15050084








