Psychometric Network Model Recovery: The Effect of Sample Size, Number of Items, and Number of Nodes
Abstract
1. Introduction
1.1. From Psychometric Networks to Gaussian Graphical Models
1.2. The Cross-Disciplinary Utility of Gaussian Graphical Models
1.3. The Landscape of Network Estimation Algorithms
- The Ising Model. For binary data (e.g., present/absent symptoms), the Ising model, originating from statistical physics, is the appropriate analogue to the GGM. It is equivalent to a log-linear model with only pairwise interactions and can be estimated using penalized logistic regression (Marsman et al., 2018).
- Mixed Graphical Models (MGMs). Real-world datasets in health and social sciences often contain a mix of variable types (e.g., continuous, categorical, count). MGMs extend the graphical modeling framework to handle such heterogeneous data, estimating a single network of conditional dependencies across different variable domains (Altenbuchinger et al., 2020).
- EBICglasso. The graphical LASSO (glasso, Friedman et al., 2008) is a penalized maximum likelihood method that uses an l1 penalty to shrink small partial correlations to exactly zero. The magnitude of this penalty is controlled by a tuning parameter, λ. To select the optimal model from the set of networks estimated with different λ values, the Extended Bayesian Information Criterion (EBIC, Foygel & Drton, 2010) is often employed. EBIC (Chen & Chen, 2008) modifies the standard BIC by adding a hyperparameter (ranging from 0 to 1), which tunes the penalty for model complexity. Higher values of γ impose a stronger penalty on denser networks, favoring sparser models and helping to control the false positive rate. This combined procedure is commonly known as EBICglasso (Epskamp, 2017), and has been a dominant approach in psychometrics (Isvoranu & Epskamp, 2023).
- Alternative GGM Estimators: The dominance of EBICglasso is not without critique. Some research suggests that in the low-dimensional settings (p ≪ n) common in psychology, its advantages diminish, and it may be outperformed by other methods. Non-regularized methods, based on multiple regression with stepwise selection or bootstrapping, have been proposed as alternatives that can offer better control over false positives (Williams et al., 2019). Furthermore, Bayesian methods for GGM estimation provide a framework for quantifying uncertainty about both the network structure and its parameters (Franco et al., 2024).
1.4. The Present Study
2. Materials and Methods
3. Results
3.1. Invertible and Non-Empty Matrices
3.2. Effect of Simulated Conditions on Network Indicators
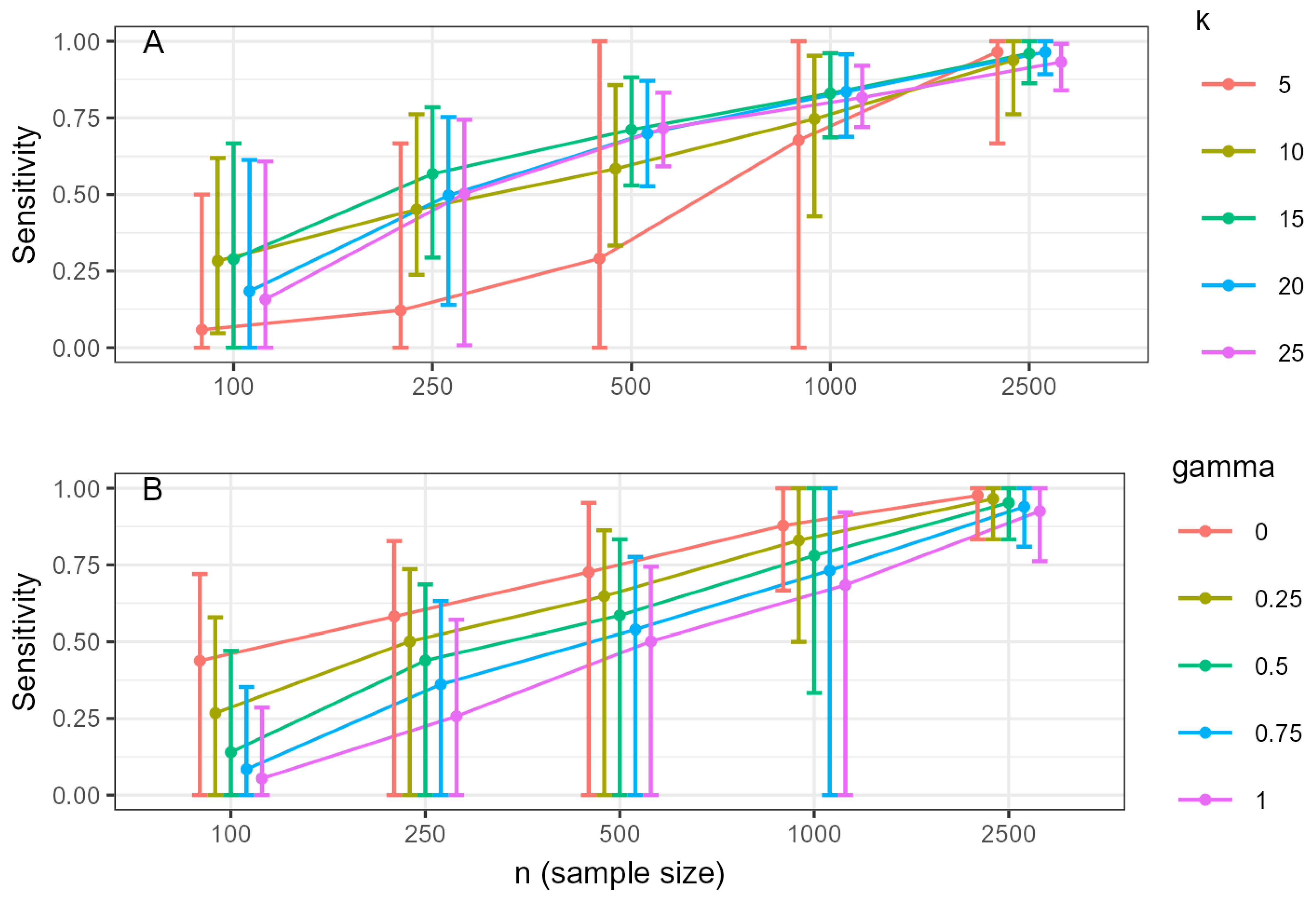
3.3. Estimated Network Accuracy
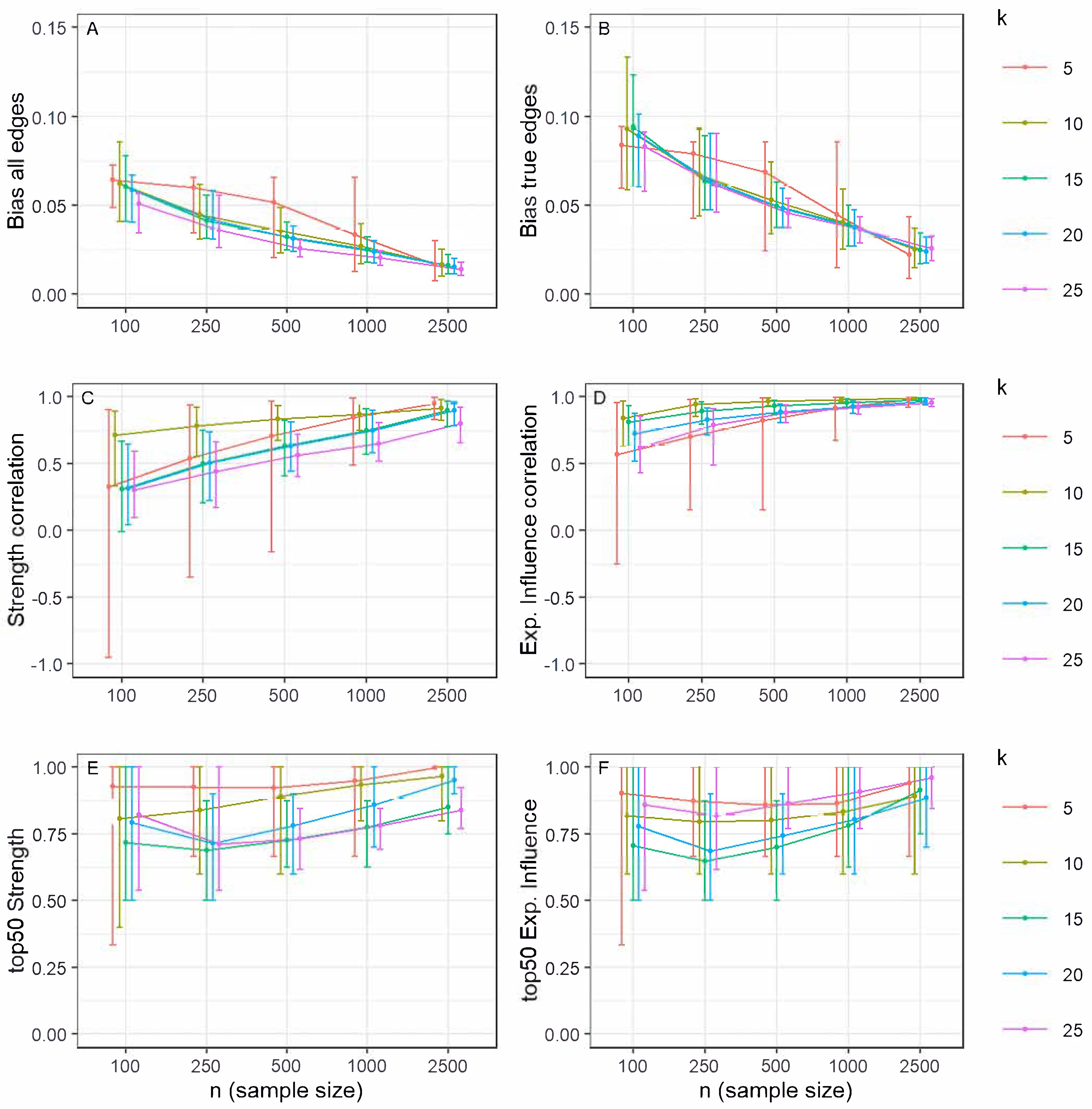
3.4. Edge Weight Estimation Accuracy
3.5. Centrality Index Accuracy
4. Discussion
4.1. Main Findings
4.2. Comparison with Existing Literature
4.3. Limitations and Future Directions
4.4. Practical Recommendations and Conclusions
- For exploratory research where the goal is to discover potential connections and maximize sensitivity, use lower values of (γ ≤ 0.25).
- For confirmatory research or studies where the priority is to minimize false positives and identify only the most robust connections, use higher values (γ ≥ 0.5).
- Be aware that the impact of γ decreases substantially in very large samples (n ≥ 1000).
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BFI | Big Five Inventory |
| 1 | The median absolute deviation (MAD) between the edge weights of the true network and the weight of the estimated network was used as a bias indicator. |
References
- Altenbuchinger, M., Weihs, A., Quackenbush, J., Grabe, H. J., & Zacharias, H. U. (2020). Gaussian and Mixed Graphical Models as (multi-)omics data analysis tools. Biochimica et Biophysica Acta (BBA)-Gene Regulatory Mechanisms, 1863(6), 194418. [Google Scholar] [CrossRef]
- Chen, J., & Chen, Z. (2008). Extended Bayesian information criteria for model selection with large model spaces. Biometrika, 95(3), 759–771. [Google Scholar] [CrossRef]
- Christensen, A. P., & Golino, H. (2021). Factor or network model? Predictions from neural networks. Journal of Behavioral Data Science, 1(1), 85–126. [Google Scholar] [CrossRef]
- Constantin, M. (2022). powerly: Sample size analysis for psychological networks and more (Versión 1.8.6) [Software]. Available online: https://cran.r-project.org/web/packages/powerly/index.html (accessed on 14 October 2024).
- Constantin, M. A., Schuurman, N. K., & Vermunt, J. K. (2023, July 10). A general Monte Carlo method for sample size analysis in the context of network models. Psychological Methods. advance online publication. [Google Scholar] [CrossRef]
- Cramer, A. O. J., Waldorp, L. J., van der Maas, H. L. J., & Borsboom, D. (2010). Comorbidity: A network perspective. Behavioral and Brain Sciences, 33(2–3), 137–150. [Google Scholar] [CrossRef] [PubMed]
- Cronbach, L. J. (1990). Essentials of psychological testing (5th ed.). Harper & Row. [Google Scholar]
- de Ron, J., Robinaugh, D. J., Fried, E. I., Pedrelli, P., Jain, F. A., Mischoulon, D., & Epskamp, S. (2022). Quantifying and addressing the impact of measurement error in network models. Behaviour Research and Therapy, 157, 104163. [Google Scholar] [CrossRef]
- Epskamp, S. (2017). Brief report on estimating regularized gaussian networks from continuous and ordinal data. arXiv, arXiv:1606.05771. [Google Scholar] [CrossRef]
- Epskamp, S., Borsboom, D., & Fried, E. I. (2018a). Estimating psychological networks and their accuracy: A tutorial paper. Behavior Research Methods, 50(1), 195–212. [Google Scholar] [CrossRef]
- Epskamp, S., Cramer, A. O. J., Waldorp, L. J., Schmittmann, V. D., & Borsboom, D. (2012). qgraph: Network visualizations of relationships in psychometric data. Journal of Statistical Software, 48, 1–18. [Google Scholar] [CrossRef]
- Epskamp, S., Kruis, J., & Marsman, M. (2017a). Estimating psychopathological networks: Be careful what you wish for. PLoS ONE, 12(6), e0179891. [Google Scholar] [CrossRef]
- Epskamp, S., Rhemtulla, M., & Borsboom, D. (2017b). Generalized network psychometrics: Combining network and latent variable models. Psychometrika, 82(4), 904–927. [Google Scholar] [CrossRef]
- Epskamp, S., Waldorp, L. J., Mõttus, R., & Borsboom, D. (2018b). The gaussian graphical model in cross-sectional and time-series data. Multivariate Behavioral Research, 53(4), 453–480. [Google Scholar] [CrossRef]
- Fisher, R. A. (1936). Statistical methods for research workers (6th ed.). Oliver and Boyd. [Google Scholar]
- Foygel, R., & Drton, M. (2010, December 6–9). Extended Bayesian information criteria for Gaussian graphical models. 24rd International Conference on Neural Information Processing Systems (Vol. 1, pp. 604–612), Vancouver, BC, Canada. [Google Scholar]
- Franco, V. R., Barros, G. W. F., & Jiménez, M. (2024). A generalized approach for Bayesian Gaussian graphical models. Advances in Psychology, 2, e533499. [Google Scholar] [CrossRef]
- Friedman, J., Hastie, T., & Tibshirani, R. (2008). Sparse inverse covariance estimation with the graphical lasso. Biostatistics, 9(3), 432–441. [Google Scholar] [CrossRef] [PubMed]
- Golino, H., & Epskamp, S. (2017). Exploratory graph analysis: A new approach for estimating the number of dimensions in psychological research. PLoS ONE, 12(6), e0174035. [Google Scholar] [CrossRef] [PubMed]
- Hoekstra, R. H. A., Epskamp, S., Finnemann, A., & Borsboom, D. (2024). Unlocking the potential of simulation studies in network psychometrics: A tutorial. Available online: https://osf.io/preprints/psyarxiv/4j3hf_v1 (accessed on 1 September 2025).
- Huth, K., Haslbeck, J., Keetelaar, S., van Holst, R., & Marsman, M. (2025). Statistical evidence in psychological networks. OSF. [Google Scholar] [CrossRef]
- Isvoranu, A.-M., & Epskamp, S. (2023). Which estimation method to choose in network psychometrics? Deriving guidelines for applied researchers. Psychological Methods, 28(4), 925–946. [Google Scholar] [CrossRef]
- Johal, S. K., & Rhemtulla, M. (2023). Comparing estimation methods for psychometric networks with ordinal data. Psychological Methods, 28(6), 1251–1272. [Google Scholar] [CrossRef]
- Lakens, D. (2013). Calculating and reporting effect sizes to facilitate cumulative science: A practical primer for t-tests and ANOVAs. Frontiers in Psychology, 4, 863. [Google Scholar] [CrossRef]
- Leme, D. E. d. C., Alves, E. V. d. C., Lemos, V. d. C. O., & Fattori, A. (2020). Network analysis: A multivariate statistical approach for health science research. Geriatrics, Gerontology and Aging, 14(1), 43–51. [Google Scholar] [CrossRef]
- Marsman, M., Borsboom, D., Kruis, J., Epskamp, S., van Bork, R., Waldorp, L. J., van der Maas, H. L. J., & Maris, G. (2018). An Introduction to Network Psychometrics: Relating Ising Network Models to Item Response Theory Models. Multivariate Behavioral Research, 53(1), 15–35. [Google Scholar] [CrossRef]
- R Core Team. (2024). R: A language and environment for statistical computing. R Foundation for Statistical Computing. Available online: https://www.R-project.org/ (accessed on 28 April 2024).
- Revelle, W. (2022). psych: Procedures for psychological, psychometric, and personality research (Versión 2.2.5) [Software]. Available online: https://CRAN.R-project.org/package=psych (accessed on 20 July 2022).
- Rual, J.-F., Venkatesan, K., Hao, T., Hirozane-Kishikawa, T., Dricot, A., Li, N., Berriz, G. F., Gibbons, F. D., Dreze, M., Ayivi-Guedehoussou, N., Klitgord, N., Simon, C., Boxem, M., Milstein, S., Rosenberg, J., Goldberg, D. S., Zhang, L. V., Wong, S. L., Franklin, G., … Vidal, M. (2005). Towards a proteome-scale map of the human protein–protein interaction network. Nature, 437(7062), 1173–1178. [Google Scholar] [CrossRef]
- Schmittmann, V. D., Cramer, A. O. J., Waldorp, L. J., Epskamp, S., Kievit, R. A., & Borsboom, D. (2013). Deconstructing the construct: A network perspective on psychological phenomena. New Ideas in Psychology, 31(1), 43–53. [Google Scholar] [CrossRef]
- Skrondal, A. (2000). Design and analysis of monte carlo experiments: Attacking the conventional wisdom. Multivariate Behavioral Research, 35(2), 137–167. [Google Scholar] [CrossRef]
- Van Der Maas, H. L. J., Dolan, C. V., Grasman, R. P. P. P., Wicherts, J. M., Huizenga, H. M., & Raijmakers, M. E. J. (2006). A dynamical model of general intelligence: The positive manifold of intelligence by mutualism. Psychological Review, 113, 842–861. [Google Scholar] [CrossRef]
- Williams, D. R., Rhemtulla, M., Wysocki, A. C., & Rast, P. (2019). On nonregularized estimation of psychological networks. Multivariate Behavioral Research, 54(5), 719–750. [Google Scholar] [CrossRef]
- Zhao, H., & Duan, Z.-H. (2019). Cancer genetic network inference using gaussian graphical models. Bioinformatics and Biology Insights, 13, 1177932219839402. [Google Scholar] [CrossRef]

| Independent Variables | Values |
| Type of data (d) | Continuous |
| Ordinal | |
| Sample size (n) | 100 |
| 250 | |
| 500 | |
| 1000 | |
| 2500 | |
| Network size (number of nodes) (k) | 5 |
| 10 | |
| 15 | |
| 20 | |
| 25 | |
| Value of gamma (γ) | 0.00 |
| 0.25 | |
| 0.50 | |
| 0.75 | |
| 1.00 | |
| Dependent Variables | Evaluation Metric |
| Estimated network accuracy | Sensitivity |
| Specificity | |
| Edge weight estimation accuracy | Estimation bias for all edges |
| Estimation bias for true edges | |
| Centrality index accuracy | Correlation between the true and estimated node strength |
| Ratio of nodes correctly identified within the top 50% in strength | |
| Correlation between the true and estimated node expected influence | |
| Ratio of nodes correctly identified within the top 50% in expected influence |
| k\n | 100 | 250 | 500 | 1000 | 2500 |
|---|---|---|---|---|---|
| 5 | 99.9 | 100 | 100 | 100 | 100 |
| 10 | 99.7 | 99.9 | 100 | 100 | 100 |
| 15 | 96.5 | 99.9 | 100 | 100 | 100 |
| 20 | 82.7 | 99.9 | 100 | 100 | 100 |
| 25 | 42.8 | 99.4 | 100 | 100 | 100 |
| k | n\γ | 0 | 0.25 | 0.50 | 0.75 | 1 |
|---|---|---|---|---|---|---|
| 5 | 100 | 52.2 | 35.1 | 25.8 | 19.8 | 15.8 |
| 250 | 67.3 | 52.2 | 40.8 | 32.1 | 26.2 | |
| 500 | 86.4 | 75.4 | 62.2 | 52.2 | 43.6 | |
| 1000 | 99.6 | 98.8 | 94.4 | 88.1 | 79.5 | |
| 2500 | 100.0 | 100.0 | 100.0 | 100.0 | 99.8 | |
| 10 | 100 | 99.7 | 99.7 | 99.7 | 99.1 | 95.5 |
| 250 | 99.9 | 99.9 | 99.9 | 99.9 | 99.9 | |
| 15 | 100 | 96.5 | 96.5 | 95.5 | 85.5 | 64.8 |
| 250 | 99.9 | 99.9 | 99.9 | 99.9 | 99.9 | |
| 20 | 100 | 82.7 | 82.3 | 70.4 | 45.0 | 27.8 |
| 250 | 99.9 | 99.9 | 99.9 | 99.9 | 99.9 | |
| 25 | 100 | 42.8 | 41.3 | 23.6 | 13.4 | 8.0 |
| 250 | 99.4 | 99.4 | 99.4 | 99.4 | 98.2 |
| (1) Sensitivity | (2) Specificity | (3) Bias of All Edges | (4) Bias of True Edges | (5) r Strength | (6) r Expected Influence | (7) Top-50% Strength | (8) Top-50% Expected Influence | |
|---|---|---|---|---|---|---|---|---|
| d | 0.001 | 0.066 | 0.103 | 0.059 | 0.072 | 0.097 | 0.004 | 0.005 |
| k | 0.412 | 0.217 | 0.483 | 0.060 | 0.442 | 0.539 | 0.166 | 0.439 |
| γ | 0.434 | 0.299 | 0.331 | 0.352 | 0.119 | 0.141 | 0.010 | 0.025 |
| n | 0.915 | 0.392 | 0.927 | 0.914 | 0.701 | 0.779 | 0.216 | 0.341 |
| d × k | 0.002 | 0.003 | 0.009 | 0.008 | 0.015 | 0.003 | 0.004 | 0.006 |
| d × γ | 0.002 | 0.011 | 0.026 | 0.008 | 0.009 | 0.011 | 0.003 | 0.001 |
| d × n | 0.025 | 0.007 | 0.041 | 0.030 | 0.015 | 0.009 | 0.001 | 0.001 |
| k × γ | 0.050 | 0.020 | 0.004 | 0.003 | 0.087 | 0.012 | 0.024 | 0.047 |
| k × n | 0.352 | 0.089 | 0.215 | 0.209 | 0.173 | 0.154 | 0.146 | 0.203 |
| n × γ | 0.219 | 0.134 | 0.020 | 0.015 | 0.015 | 0.015 | 0.004 | 0.010 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the University Association of Education and Psychology. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ávalos-Tejeda, M.; Calderón, C. Psychometric Network Model Recovery: The Effect of Sample Size, Number of Items, and Number of Nodes. Eur. J. Investig. Health Psychol. Educ. 2025, 15, 235. https://doi.org/10.3390/ejihpe15110235
Ávalos-Tejeda M, Calderón C. Psychometric Network Model Recovery: The Effect of Sample Size, Number of Items, and Number of Nodes. European Journal of Investigation in Health, Psychology and Education. 2025; 15(11):235. https://doi.org/10.3390/ejihpe15110235
Chicago/Turabian StyleÁvalos-Tejeda, Marcelo, and Carlos Calderón. 2025. "Psychometric Network Model Recovery: The Effect of Sample Size, Number of Items, and Number of Nodes" European Journal of Investigation in Health, Psychology and Education 15, no. 11: 235. https://doi.org/10.3390/ejihpe15110235
APA StyleÁvalos-Tejeda, M., & Calderón, C. (2025). Psychometric Network Model Recovery: The Effect of Sample Size, Number of Items, and Number of Nodes. European Journal of Investigation in Health, Psychology and Education, 15(11), 235. https://doi.org/10.3390/ejihpe15110235







