Approximation Possibilities of Fuzzy Control Surfaces for Purpose of Implementation into Microcontrollers
Abstract
:1. Introduction
2. Differential Drive Kinematics
2.1. Control Task
2.2. Control Quality Criterions
2.3. Approximation of Surfaces
- the coordinates x, y, z from each point Q = [x, y, z] which lies on the area, conform to the equation,
- each Q point on the x, y, z of which Q = [x, y, z] from which the coordinates conform to the equation, represents a point of area [28].
2.4. EN20 Mobile Robot
3. Results
3.1. Identification of EN20 Robot Dynamics
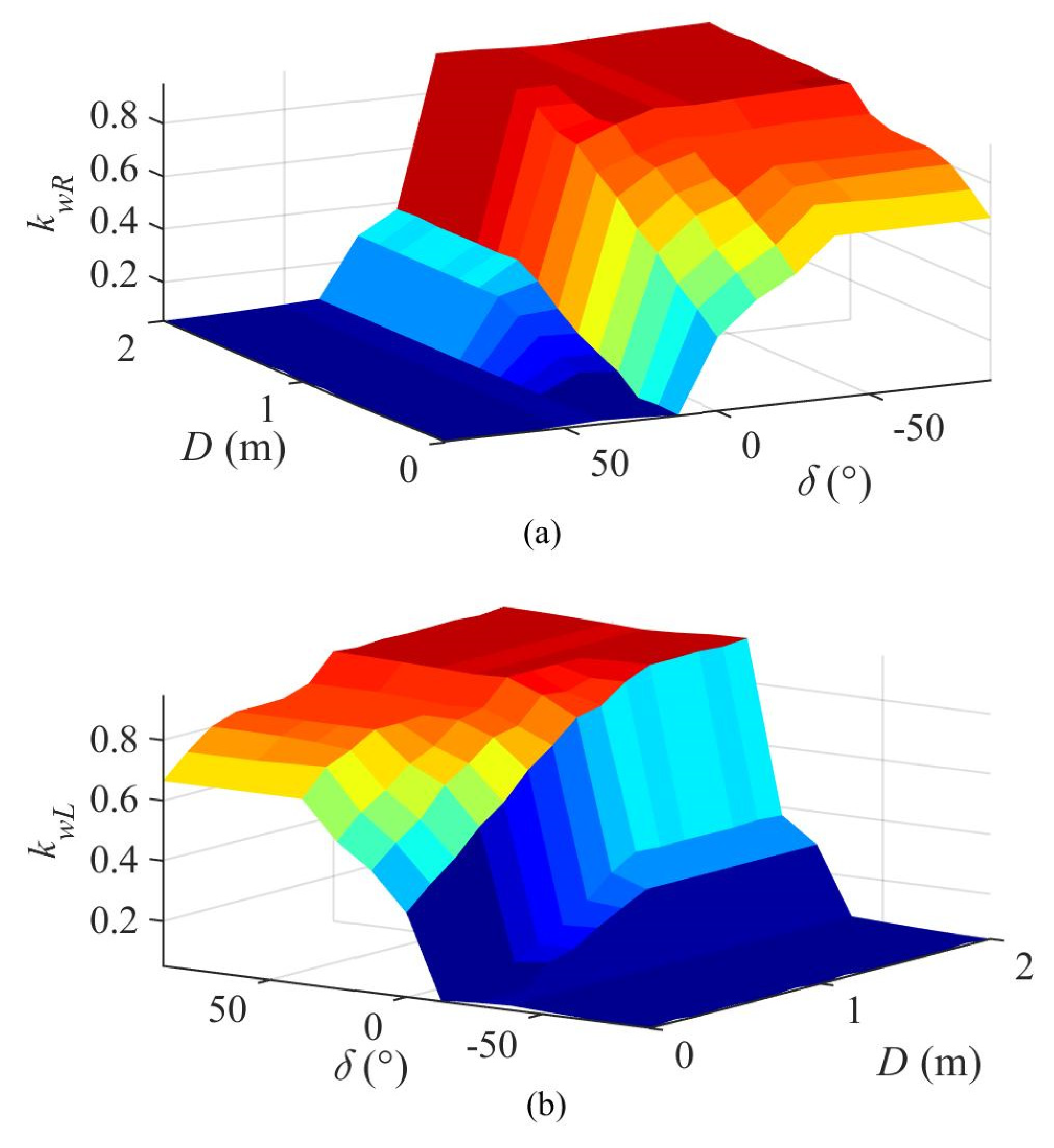
3.2. Fuzzy Controller
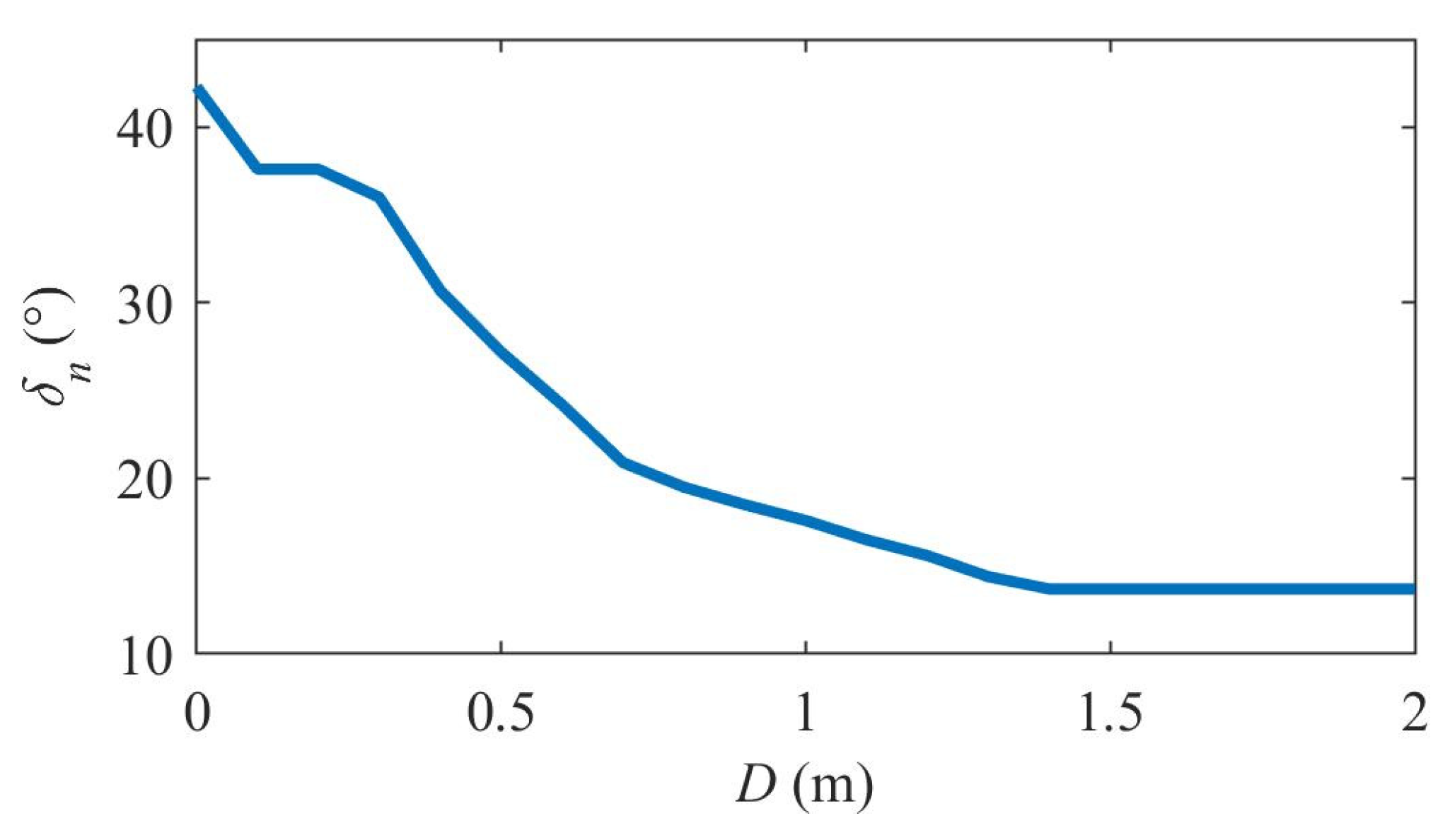
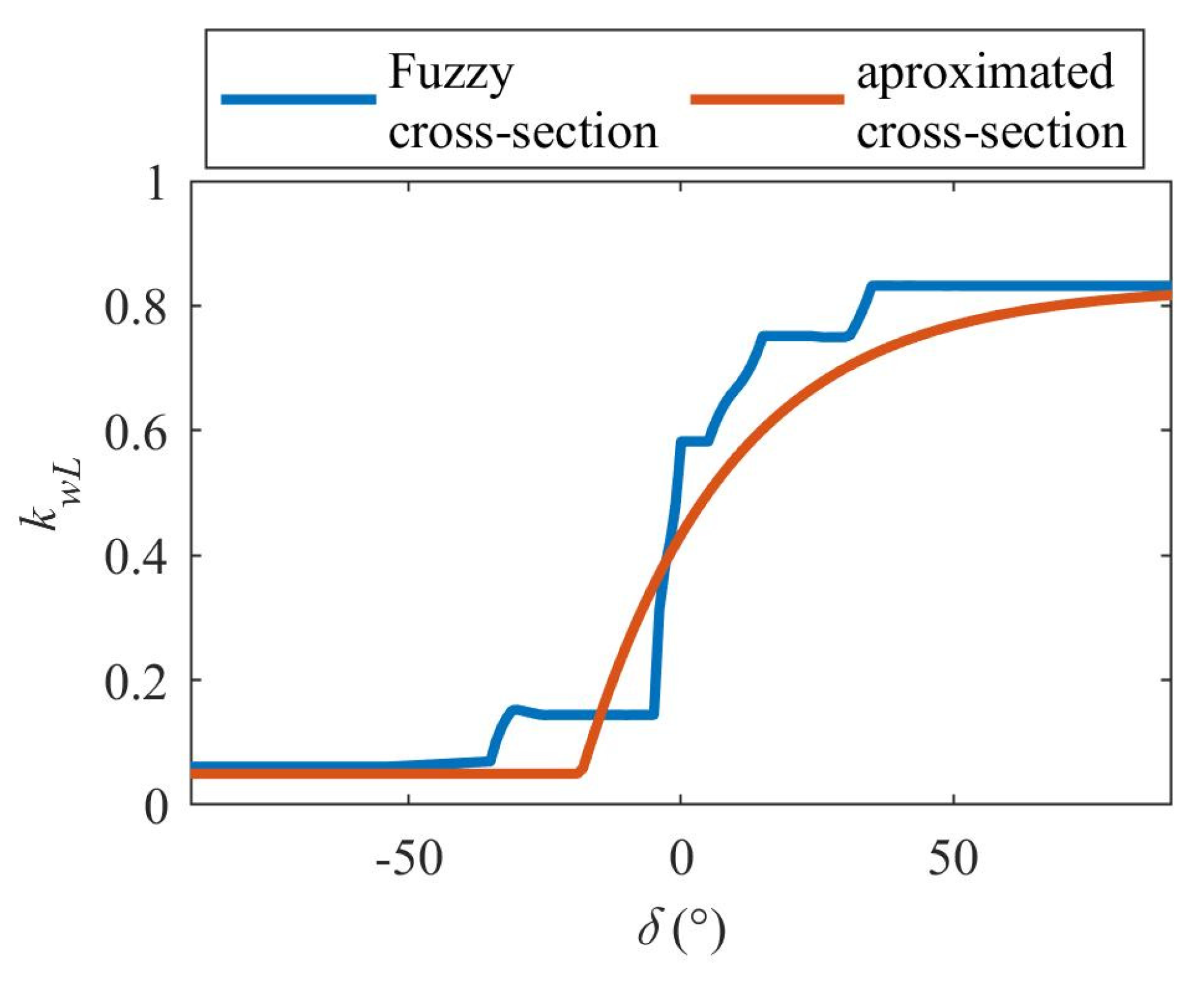
3.3. Approximation of Fuzzy Control Surfaces Using a Table
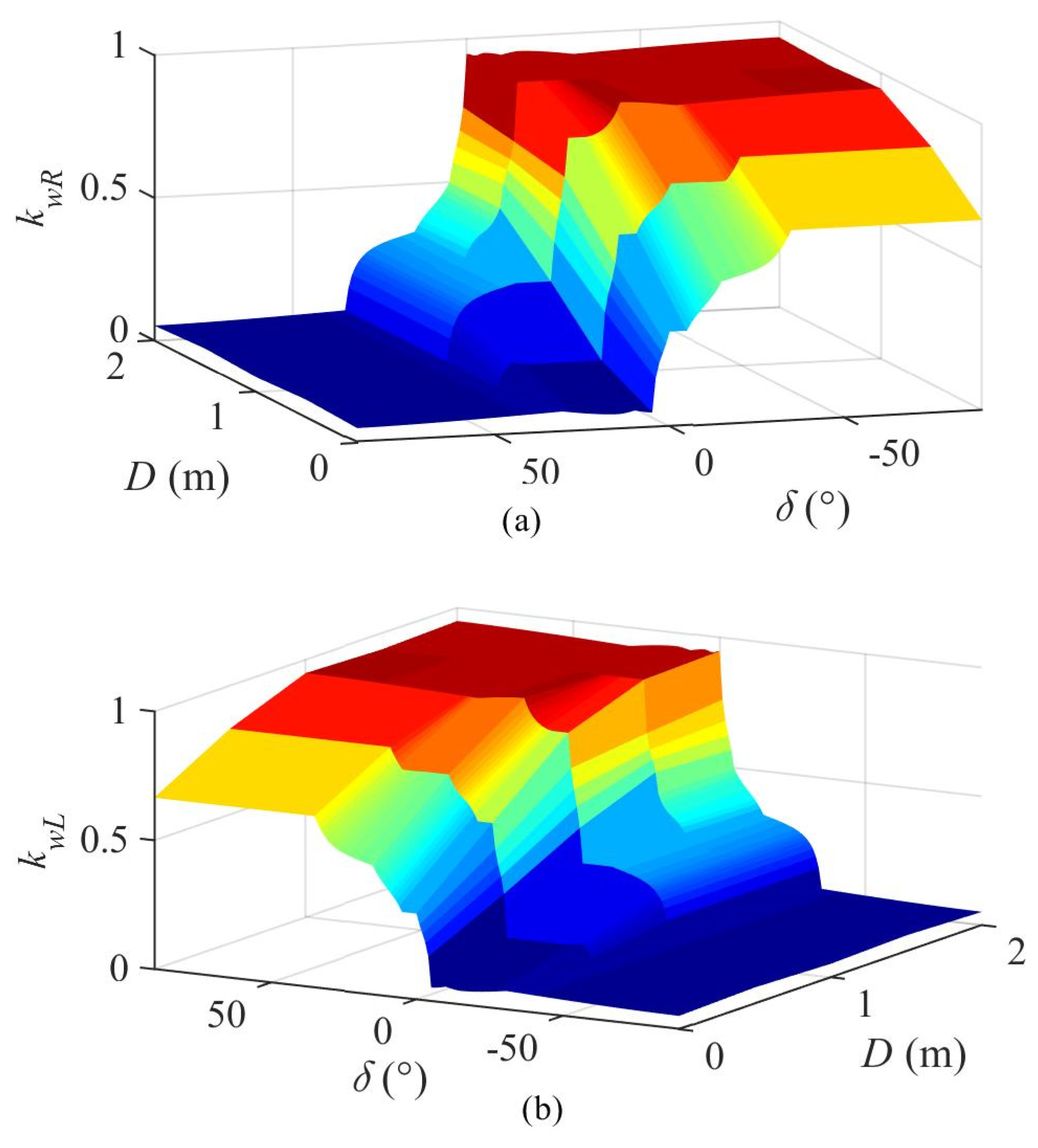
3.4. Approximation of Fuzzy Control Surfaces through a Polynomial
3.5. Approximation of Fuzzy Control Surfaces through Exponential Function
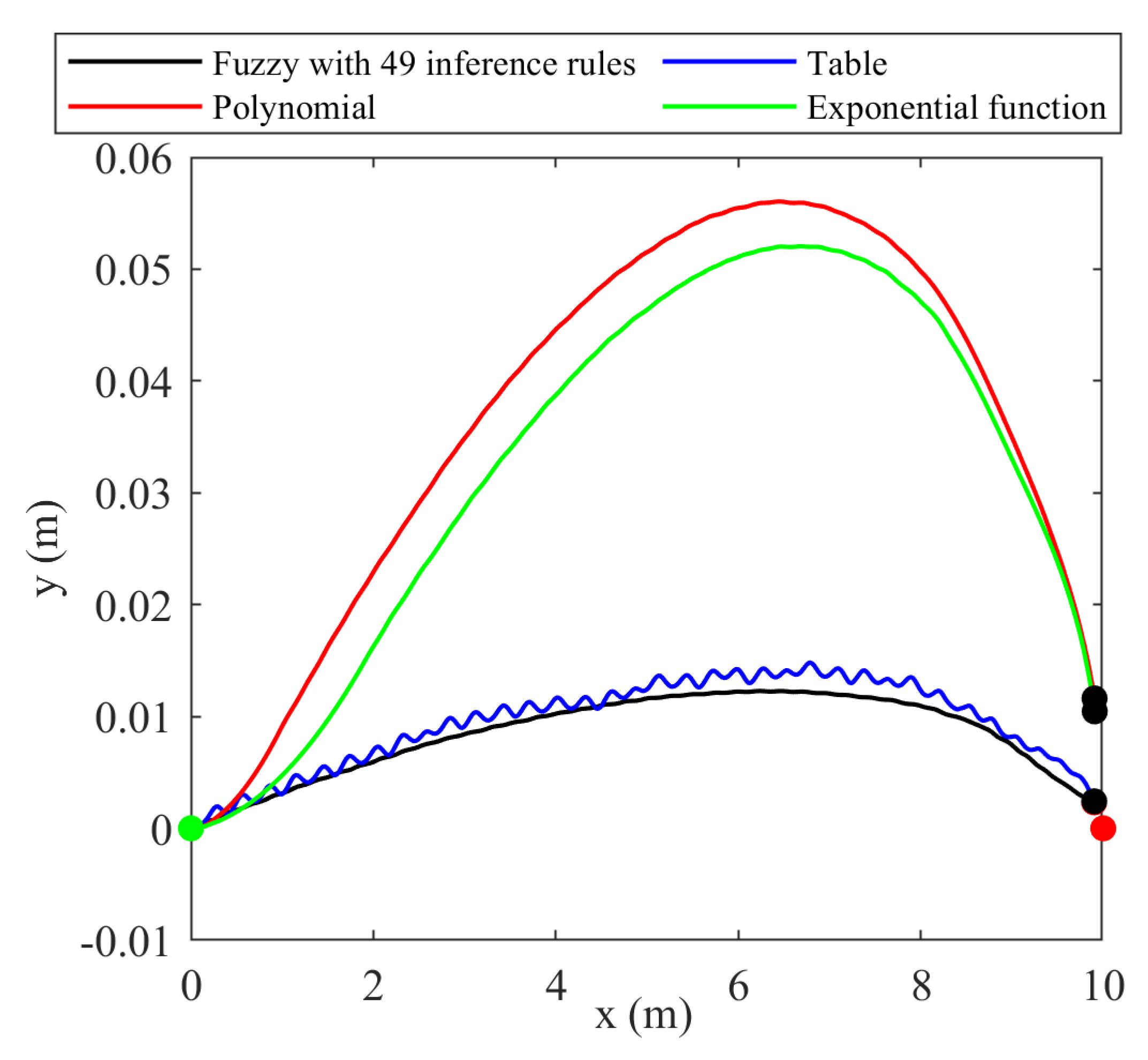
3.6. Real-World Testing
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rubio, F.; Valero, F.; Llopis-Albert, C. A review of mobile robots: Concepts, methods, theoretical framework, and applications. Int. J. Adv. Robot. Syst. 2019, 16, 1–22. [Google Scholar] [CrossRef] [Green Version]
- Zadeh, L.A. From computing with numbers to computing with words: From manipulation of measurements to manipulation of perceptions. In The Dynamics of Judicial Proof; MacCrimmon, M., Tillers, P., Eds.; Physica: Heidelberg, Germany, 2002; Volume 94, pp. 81–117. [Google Scholar] [CrossRef]
- Omrane, H.; Masmoudi, M.S.; Masmoudi, M. Fuzzy Logic Based Control for Autonomous Mobile Robot Navigation. Comp. Int. Neurosci. 2016, 2016, 9548482. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Castillo, O. Interval Type-2 Mamdani Fuzzy Systems for Intelligent Control. In Combining Experimentation and Theory Studies in Fuzziness and Soft Computing; Trillas, E., Bonissone, P., Magdalena, L., Kacprzyk, J., Eds.; Springer: Berlin, Germany, 2012; pp. 163–177. [Google Scholar] [CrossRef]
- Masmoudi, M.S.; Krichen, N.; Masmoudi, M.; Derbel, N. Fuzzy logic controllers design for omnidirectional mobile robot navigation. Appl. Soft Comput. 2016, 49, 901–919. [Google Scholar] [CrossRef]
- Bai, Z.; Lu, Y.; Li, Y. Method of Improving Lateral Stability by Using Additional Yaw Moment of Semi-Trailer. Energies 2020, 13, 6317. [Google Scholar] [CrossRef]
- Urrea, C.; Páez, F. Designand Comparison of Strategies for Level Control in a Nonlinear Tank. Processes 2021, 9, 735. [Google Scholar] [CrossRef]
- García-Sánchez, J.R.; Tavera-Mosqueda, S.; Silva-Ortigoza, R.; Hernández-Guzmán, V.M.; Marciano-Melchor, M.; Rubio, J.d.J.; Ponce-Silva, M.; Hernández-Bolaños, M.; Martínez-Martínez, J. A Novel Dynamic Three-Level Tracking Controller for Mobile Robots Considering Actuators and Power Stage Subsystems: Experimental Assessment. Sensors 2020, 20, 4959. [Google Scholar] [CrossRef]
- García-Sánchez, J.R.; Tavera-Mosqueda, S.; Silva-Ortigoza, R.; Hernández-Guzmán, V.M.; Sandoval-Gutiérrez, J.; Marcelino-Aranda, M.; Taud, H.; Marciano-Melchor, M. Robust Switched Tracking Control for Wheeled Mobile Robots Considering the Actuators and Drivers. Sensors 2018, 18, 4316. [Google Scholar] [CrossRef] [Green Version]
- Serrano, M.E.; Scaglia, G.J.E.; Rómoli, S.; Mut, V.; Godoy, S. Trajectory tracking controller based on numerical approximation under control actions constraints. In Proceedings of the 2014 IEEE Biennial Congress of Argentina (ARGENCON), San Carlos de Bariloche, Argentina, 11–13 June 2014; pp. 37–42. [Google Scholar] [CrossRef]
- Serrano, M.E.; Godoy, S.A.; Rómoli, S.; Scaglia, G.J.E. A Numerical Approximation-Based Controller for Mobile Robots with Velocity Limitation. Asian J. Control 2017, 19, 2165–2177. [Google Scholar] [CrossRef]
- Oltean, S.E.; Dulău, M.; Puskas, R. Position control of Robotino mobile robot using fuzzy logic. In Proceedings of the IEEE International Conference on Automation, Quality and Testing, Robotics (AQTR), Cluj-Napoca, Romania, 28–30 May 2010. [Google Scholar] [CrossRef]
- Faisal, M.; Hedjar, R.; Sulaiman, M.A.; Al-Mutib, K. Fuzzy Logic Navigation and Obstacle Avoidance by a Mobile Robot in an Unknown Dynamic Environment. Int. J. Adv. Rob. Syst. 2013, 10, 37. [Google Scholar] [CrossRef]
- Štefek, A.; Pham, V.T.; Krivanek, V.; Pham, K.L. Optimization of Fuzzy Logic Controller Used for a Differential Drive Wheeled Mobile Robot. Appl. Sci. 2021, 11, 6023. [Google Scholar] [CrossRef]
- Kósa, P.; Olejár, M.; Palková, Z.; Hrubý, D.; Cviklovič, V.; Harničárová, M.; Valícek, J. The effect of the number of inference rules of a fuzzy controller on the quality of control of a mobile robot. MATEC Web Conf. 2019, 299, 05002. [Google Scholar] [CrossRef] [Green Version]
- Abdalla, M.; Al-Jarrah, T. Optimal Fuzzy Controller: Rule Base Optimizer Generation. Jrn. Contr. Eng. Appl. Inf. 2018, 20, 76–86. [Google Scholar]
- Muniz, L.; Carmo, M.; Santos, M.; Santos, A.; Mercorelli, P. Case Study: Aspects of Fuzzy Controller Implementation in Embedded Systems. In Proceedings of the International Conference on Mathematics and Computers in Science and Engineering (MACISE), Madrid, Spain, 18–20 January 2020; pp. 155–158. [Google Scholar] [CrossRef]
- Purwanto, F.H.; Utami, E.; Pramono, E. Implementation and Optimization of Server Room Temperature and Humidity Control System using Fuzzy Logic Based on Microcontroller. J. Phys. Conf. Ser. 2018, 1140, 012050. [Google Scholar] [CrossRef]
- Ridwan, M.; Taryo, T. Implementation of Fuzzy Logic Controller for Pressure Sensor Calibration Chamber. Int. J. Automot. Mech. Eng. 2021, 18, 8825–8832. [Google Scholar] [CrossRef]
- Uzunovic, T.; Turkovic, I. Implementation of microcontroller based fuzzy controller. In Proceedings of the 6th IEEE International Conference Intelligent Systems, Sofia, Bulgaria, 6–8 September 2012; pp. 310–315. [Google Scholar] [CrossRef]
- Carvajal, O.; Castillo, O. Implementation of a Fuzzy Controller for an Autonomous Mobile Robot in the PIC18F4550 Microcontroller. In Hybrid Intelligent Systems in Control, Pattern Recognition and Medicine; Springer: Cham, Switzerland, 2020; Volume 827, pp. 315–325. [Google Scholar] [CrossRef]
- Abood, M.S.; Thajeel, I.K.; Alsaedi, E.M.; Hamdi, M.M.; Mustafa, A.S.; Rashid, S.A. Fuzzy Logic Controller to control the position of a mobile robot that follows a track on the floor. In Proceedings of the 4th International Symposium on Multidisciplinary Studies and Innovative Technologies (ISMSIT), Istanbul, Turkey, 22–24 October 2020; pp. 1–7. [Google Scholar] [CrossRef]
- Olejár, M.; Hrubý, D.; Lukáč, O. Methods of Control of Microclimatic Conditions in Enclosed Spaces and Their Influence on Electricity Saving, 1st ed.; Slovak University of Agriculture in Nitra: Nitra-Chrenová, Slovakia, 2009; pp. 74–141. (In Slovak) [Google Scholar]
- Sekaj, I. Fuzzy Logic Controllers and Their Replacement by a Non-Fuzzy Approximation Algorithm. IFAC Proc. Vol. 1997, 30, 363–368. [Google Scholar] [CrossRef]
- Dombi, J.; Hussain, A. A new approach to fuzzy control using the distending function. J. Process. Control 2020, 86, 16–29. [Google Scholar] [CrossRef]
- Peri, V. Fuzzy Logic Controller for an Autonomous Mobile Robot. Master’s Thesis, Cleveland State University, Cleveland, OH, USA, 2005. Available online: https://academic.csuohio.edu/embedded/Publications/Thesis/Mohan%20Thesis.pdf (accessed on 21 April 2021).
- Vacho, L.; Olejár, M.; Hrubý, D.; Cviklovič, V.; Valíček, J.; Palková, Z.; Harničárová, M.; Tozan, H. Identification of Dynamics of Movement of the Differential Mobile Robotic Platform Controlled by Fuzzy Controller. Teh. Vjesn. 2019, 26, 1642–1649. [Google Scholar] [CrossRef]
- Holmes, M.H. Introduction to the Foundations of Applied Mathematics, 1st ed.; Springer: New York, NY, USA, 2009; pp. 205–264. [Google Scholar]
- Cviklovič, V.; Olejár, M.; Hrubý, D.; Lukáč, O. Odometry in Navigation of Autonomous Mobile Robots, 1st ed.; SUA: Nitra, Slovakia, 2013; pp. 30–68. [Google Scholar]
- Zajkowski, K.; Rusica, I.; Palkova, Z. The use of CPC theory for energy description of two nonlinear receivers. In Proceedings of the 22nd International Conference on Innovative Manufacturing Engineering and Energy (IManE&E), Chisinau, Moldova, 31 May–2 June 2018. [Google Scholar] [CrossRef]
- Caraveo, C.; Valdez, F.; Castillo, O. A New Meta-Heuristics of Optimization with Dynamic Adaptation of Parameters Using Type-2 Fuzzy Logic for Trajectory Control of a Mobile Robot. Algorithms 2017, 10, 85. [Google Scholar] [CrossRef] [Green Version]
- Mikleš, J.; Fikar, M. Process Modelling, Identification, and Control, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 221–251. [Google Scholar]




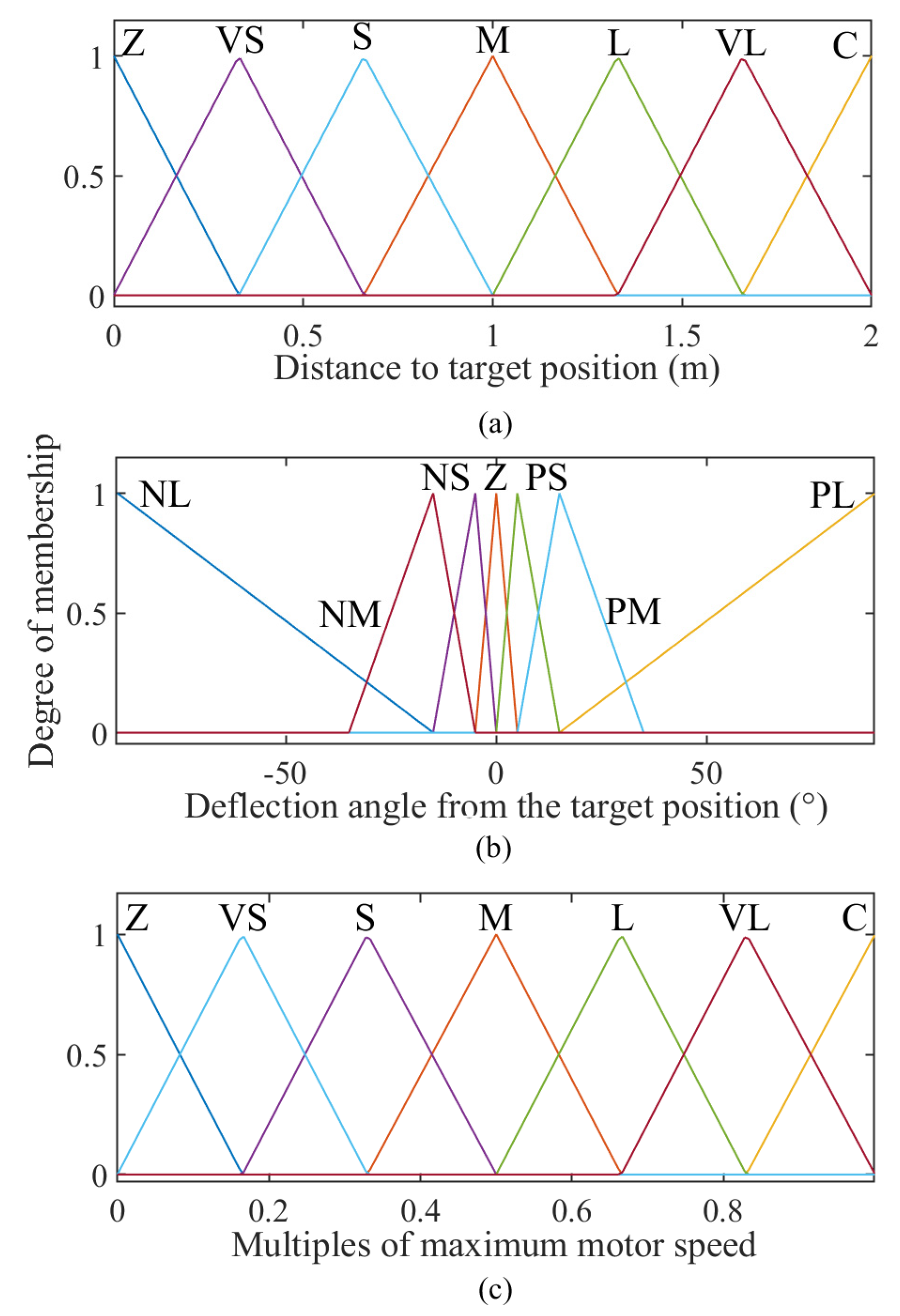




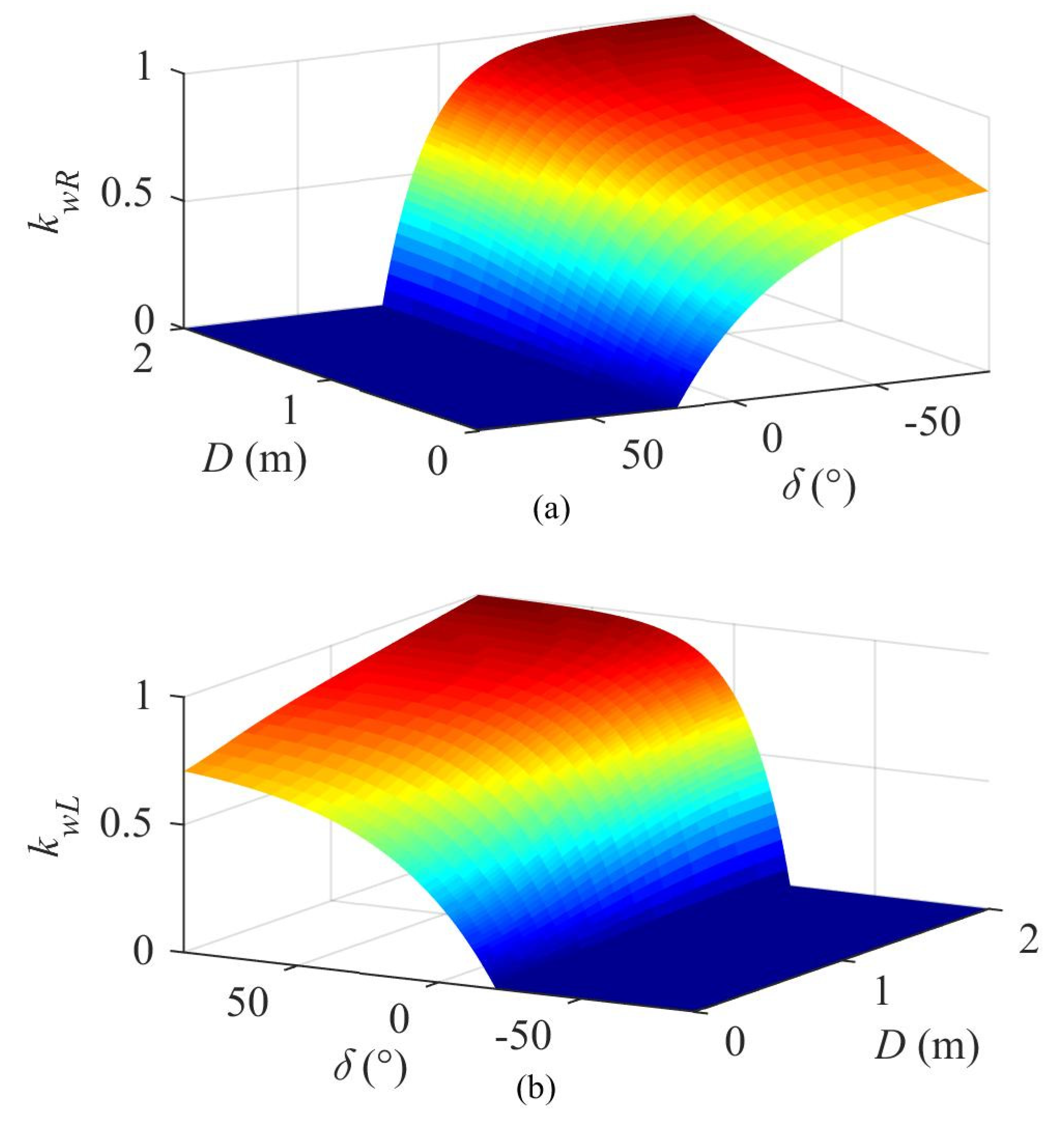


| Distance to Target Position D (m) | Deflection Angle from the Target Position δ (°) | Multiples of Maximum Right and Left Motor Speeds kwR, kwL |
|---|---|---|
| Z—zero distance | Z—zero angle | Z—zero multiple |
| VS—very small distance | PS—positive small angle | VS—very small multiple |
| S—small distance | PM—positive middle angle | S—small multiple |
| M—middle distance | PL—positive large angle | M—middle multiple |
| L—large distance | NS—negative small angle | L—large multiple |
| VL—very large distance | NM—negative middle angle | VL—very large multiple |
| C—colossal distance | NL—negative large angle | C—colossal multiple |
| Control Method | Control Time treg (s) | Absolute Error Control Area IAE | Squared Error Control Area ISE |
|---|---|---|---|
| Fuzzy with 49 inference rules | 40.032 | 3.329 | 0.529 |
| Table with kD = 0.5 m and kδ = 1° | 40.113 | 3.392 | 0.538 |
| Polynomial with m = 1 and n = 5 | 42.482 | 5.107 | 0.982 |
| Exponential function with m = 1, n = 6 and δ0 = −20° | 43.216 | 3.651 | 0.537 |
| Parameter | Fuzzy Controller | Table Approximation | Polynomial Approximation | Exponential Function Approximation |
|---|---|---|---|---|
| Average computation time (ms) | 1224.4 | 0.033 | 1.992 | 2.490 |
| Memory occupation (%) | 4 | 8 | 2 | 2 |
| RAM occupation (%) | 18 | 4 | 2 | 2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olejár, M.; Marko, D.; Lukáč, O.; Harničárová, M.; Valíček, J. Approximation Possibilities of Fuzzy Control Surfaces for Purpose of Implementation into Microcontrollers. Processes 2021, 9, 1602. https://doi.org/10.3390/pr9091602
Olejár M, Marko D, Lukáč O, Harničárová M, Valíček J. Approximation Possibilities of Fuzzy Control Surfaces for Purpose of Implementation into Microcontrollers. Processes. 2021; 9(9):1602. https://doi.org/10.3390/pr9091602
Chicago/Turabian StyleOlejár, Martin, Dušan Marko, Ondrej Lukáč, Marta Harničárová, and Jan Valíček. 2021. "Approximation Possibilities of Fuzzy Control Surfaces for Purpose of Implementation into Microcontrollers" Processes 9, no. 9: 1602. https://doi.org/10.3390/pr9091602
APA StyleOlejár, M., Marko, D., Lukáč, O., Harničárová, M., & Valíček, J. (2021). Approximation Possibilities of Fuzzy Control Surfaces for Purpose of Implementation into Microcontrollers. Processes, 9(9), 1602. https://doi.org/10.3390/pr9091602








