Computational Fluid Dynamics Modelling of Liquid–Solid Slurry Flows in Pipelines: State-of-the-Art and Future Perspectives
Abstract
:1. Introduction
1.1. Engineering Aspects and Physical Features of Slurry Pipe Transport
1.2. Modeling of Slurry Pipe Flows
1.3. The Potential of Computational Fluid Dynamics
1.4. Scope and Structure of This Paper
2. CFD Modelling Approaches
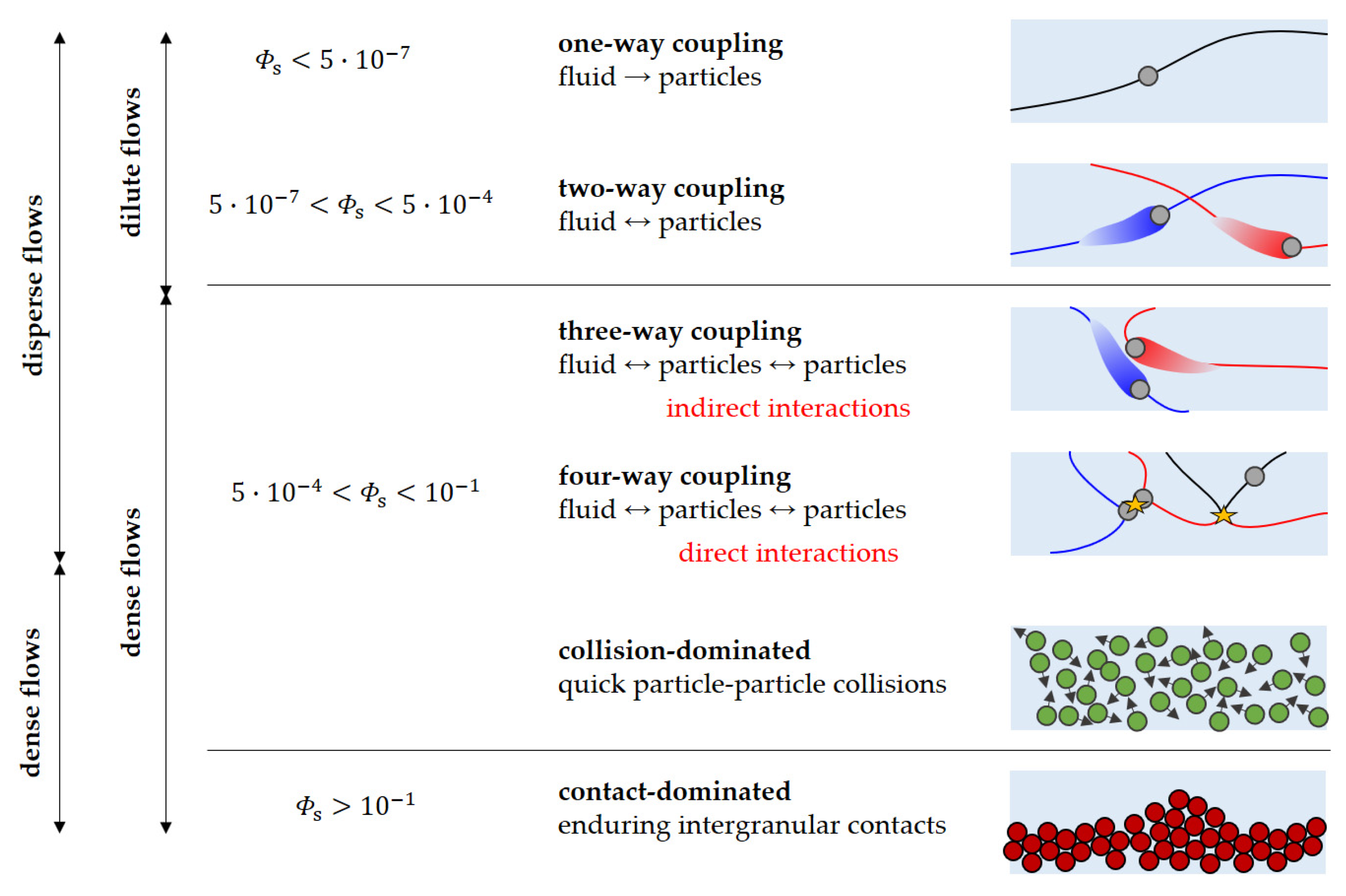
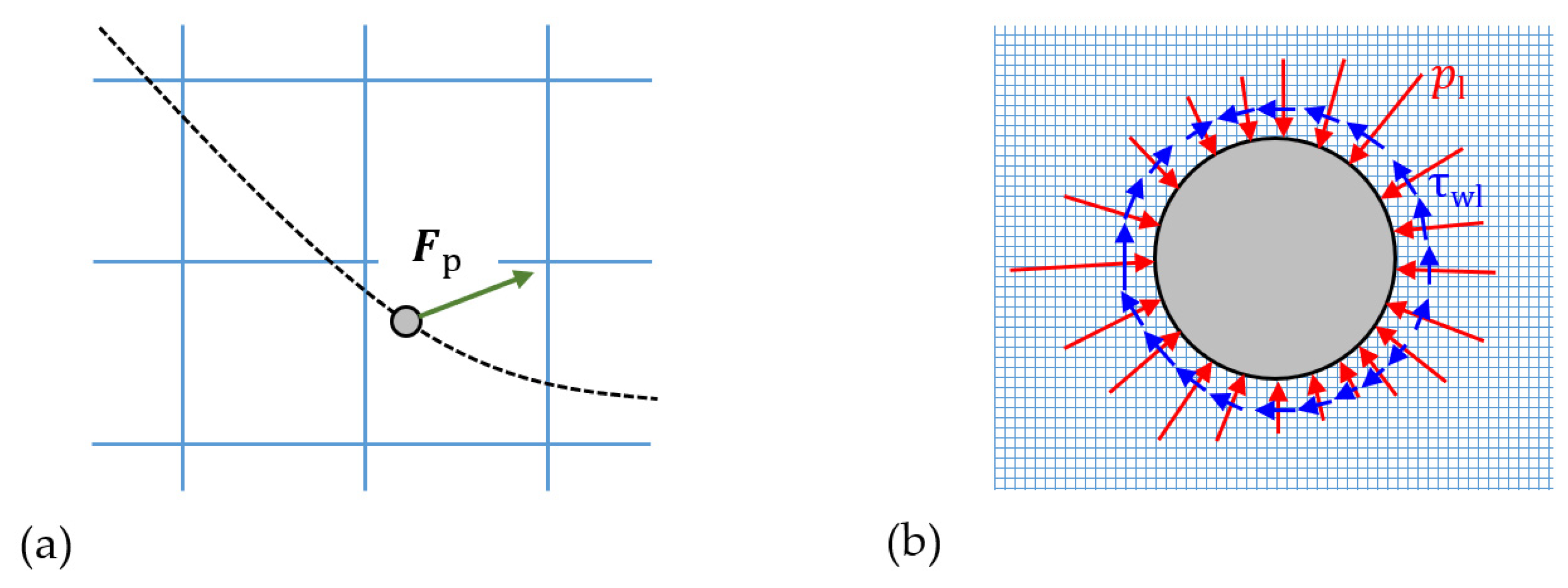
2.1. Eulerian–Lagrangian Modelling
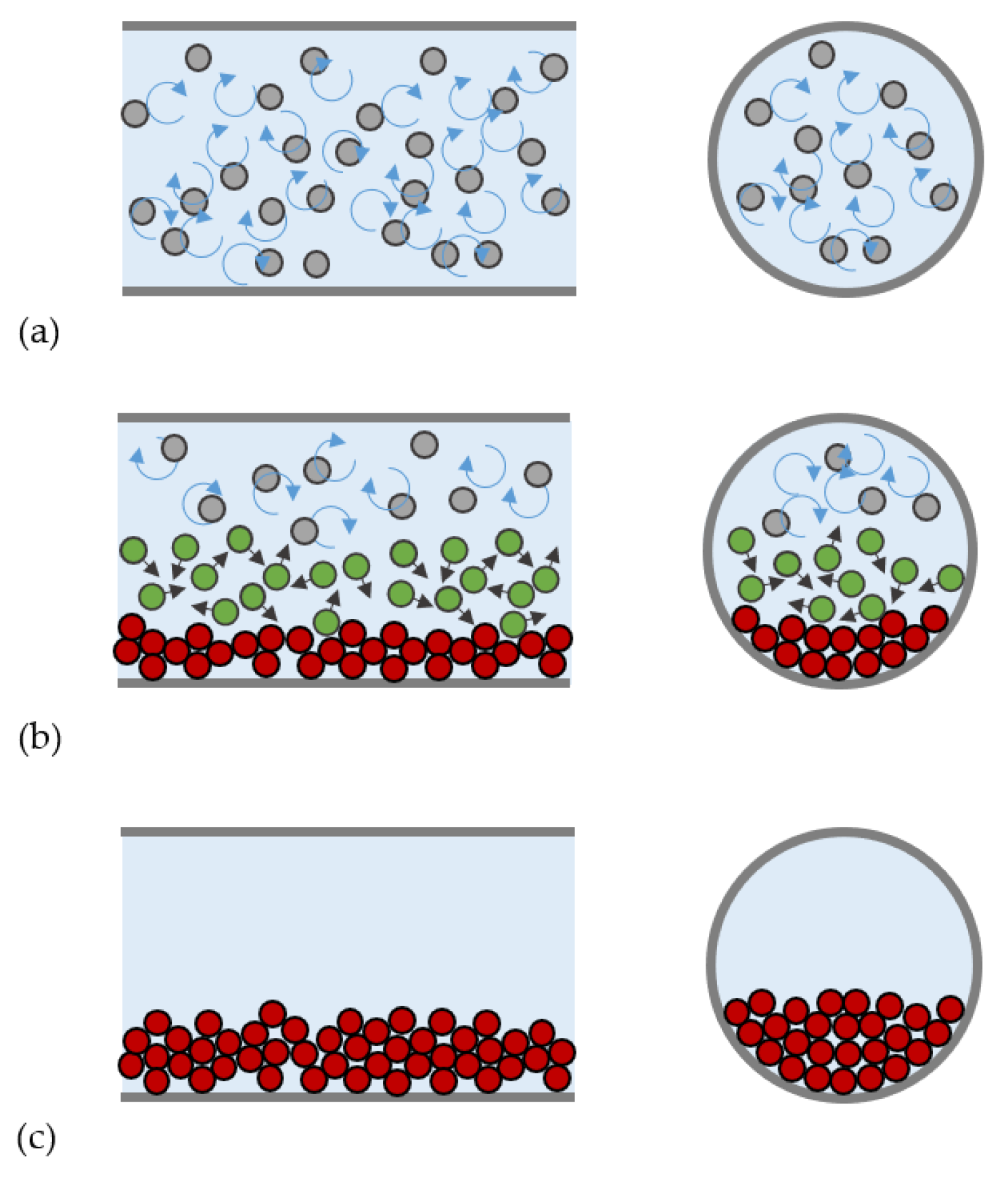
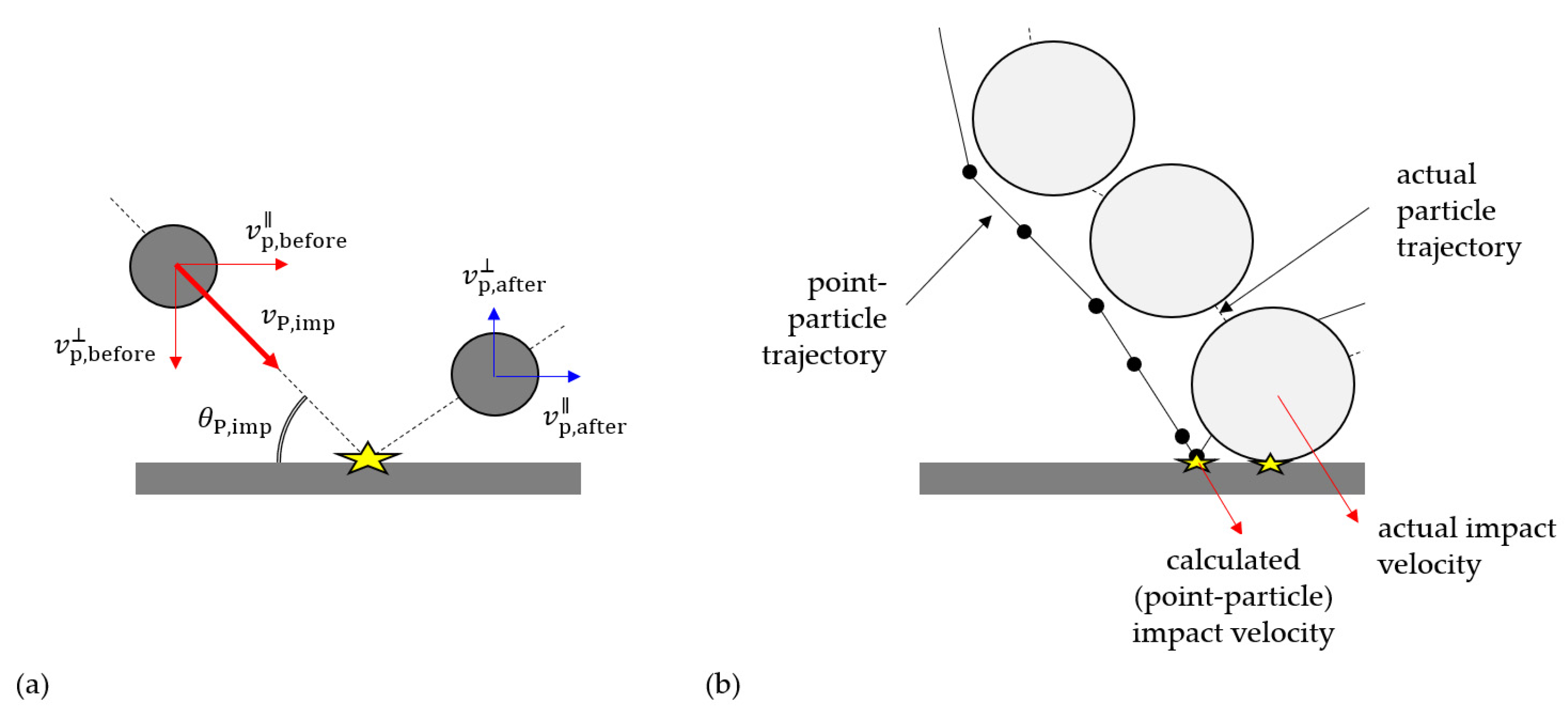
2.1.1. One-Way Coupled Slurry Flows
2.1.2. Two and Four-Way Coupled Slurry Flows
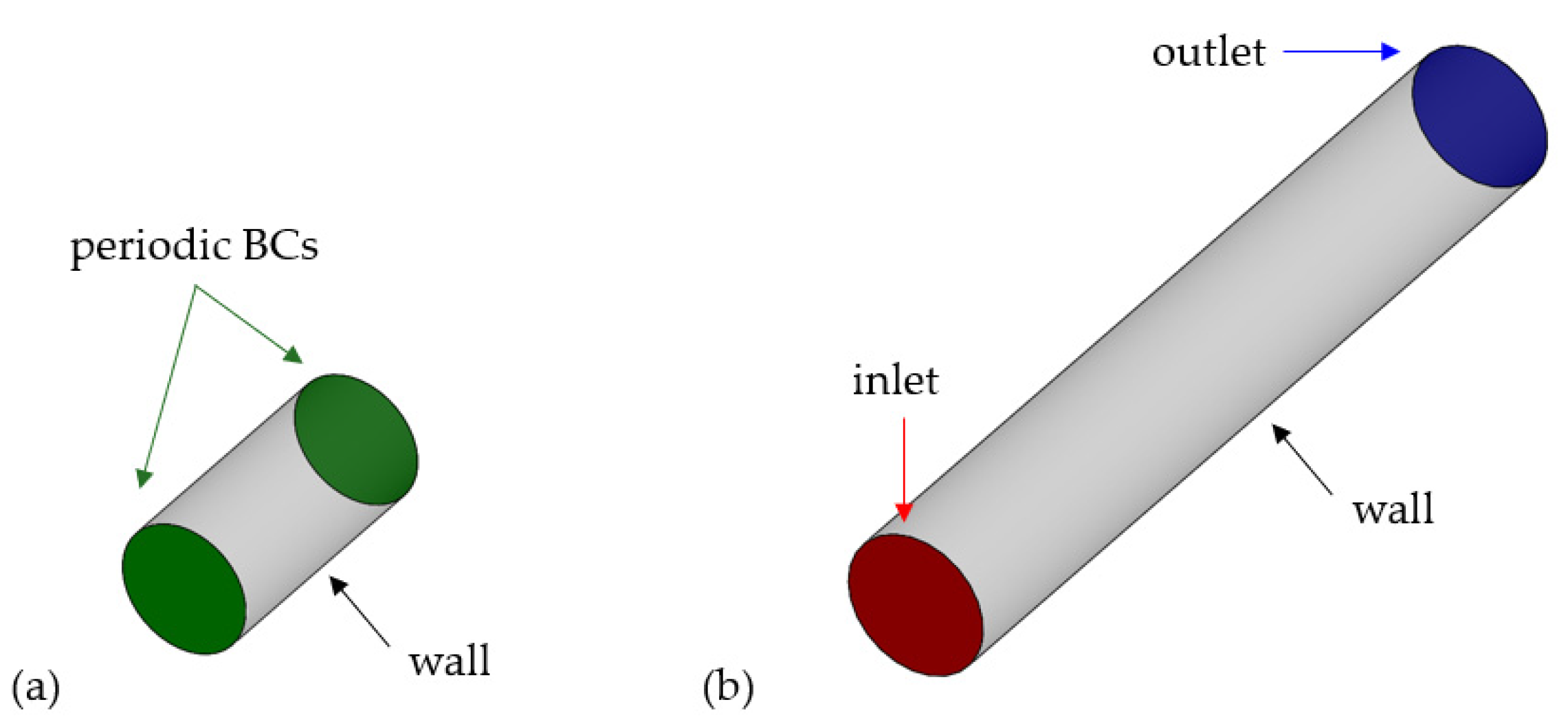
2.1.3. Boundary Conditions
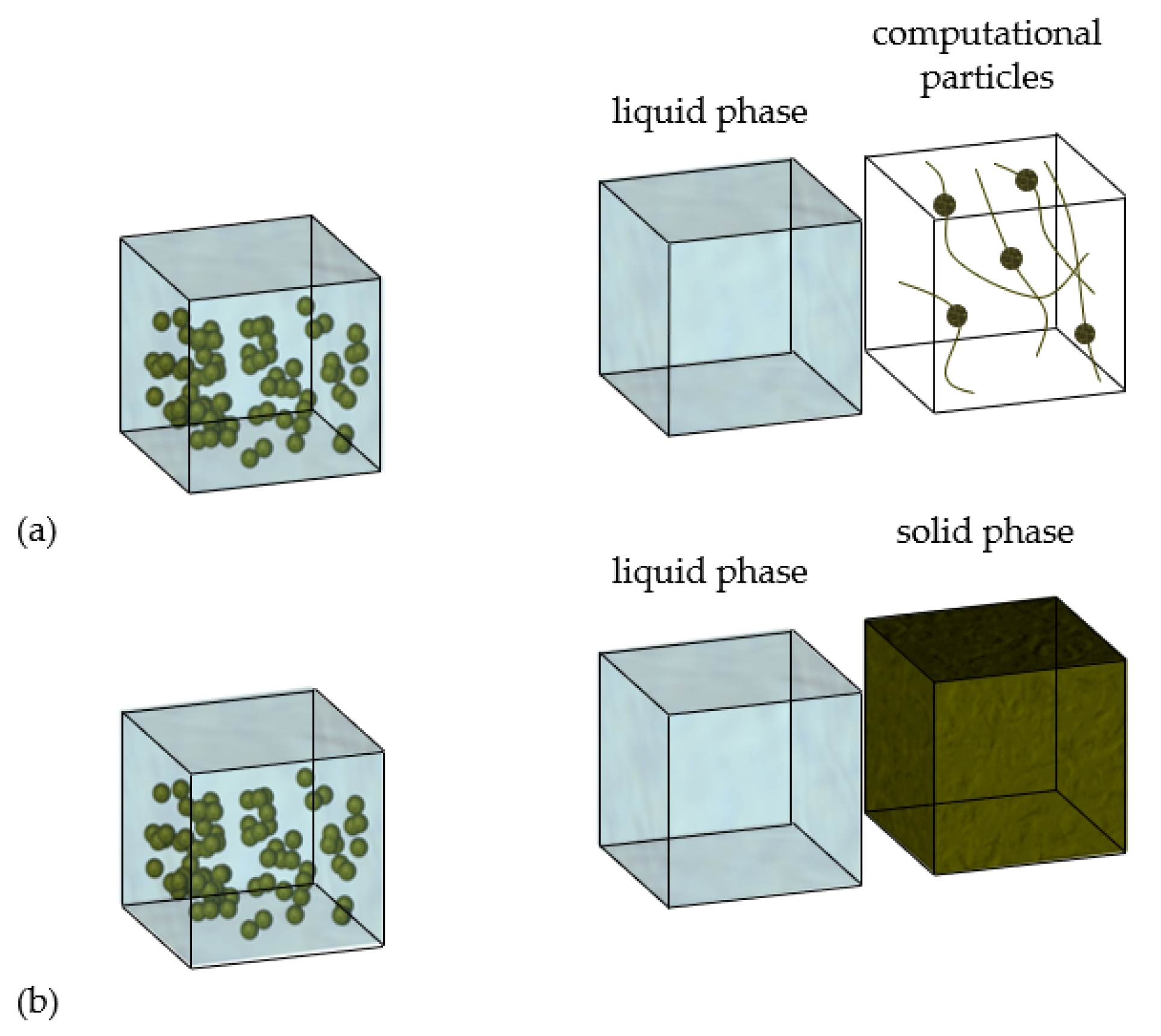
2.2. Eulerian–Eulerian Modelling (Two-Fluid Modelling)
2.2.1. Fundamental Conservation Equations
2.2.2. Constitutive Equations
2.2.3. Interfacial Momentum Transfer
2.2.4. Modelling of Turbulent Flows
2.2.5. Boundary Conditions
2.2.6. Multi-Fluid Modelling
2.3. Mixture Modelling
2.3.1. Fundamental Conservation Equations
2.3.2. Closure Equations
2.3.3. Boundary Conditions
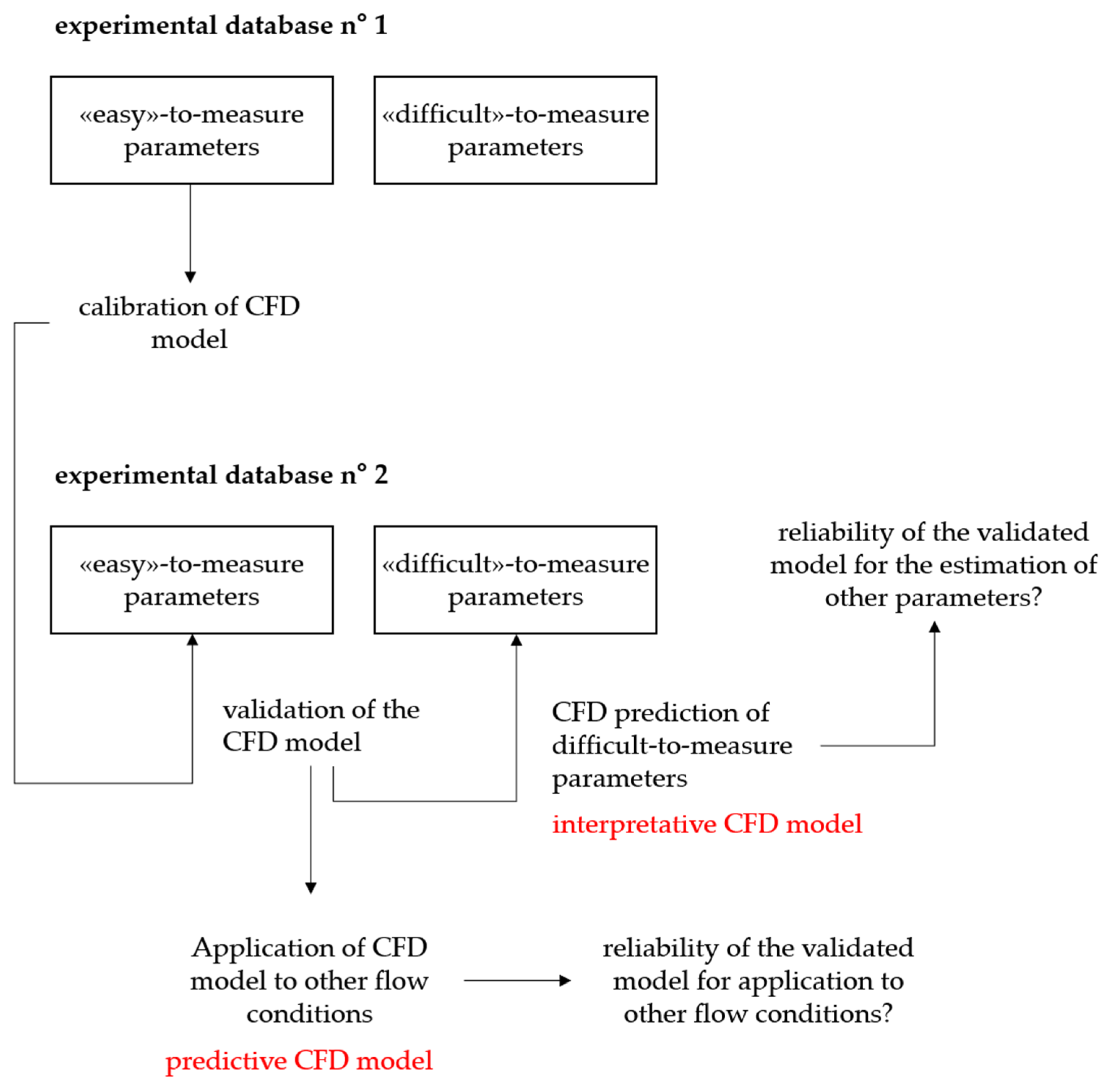
3. Sources of Uncertainty in the CFD Modelling of Slurry Flows
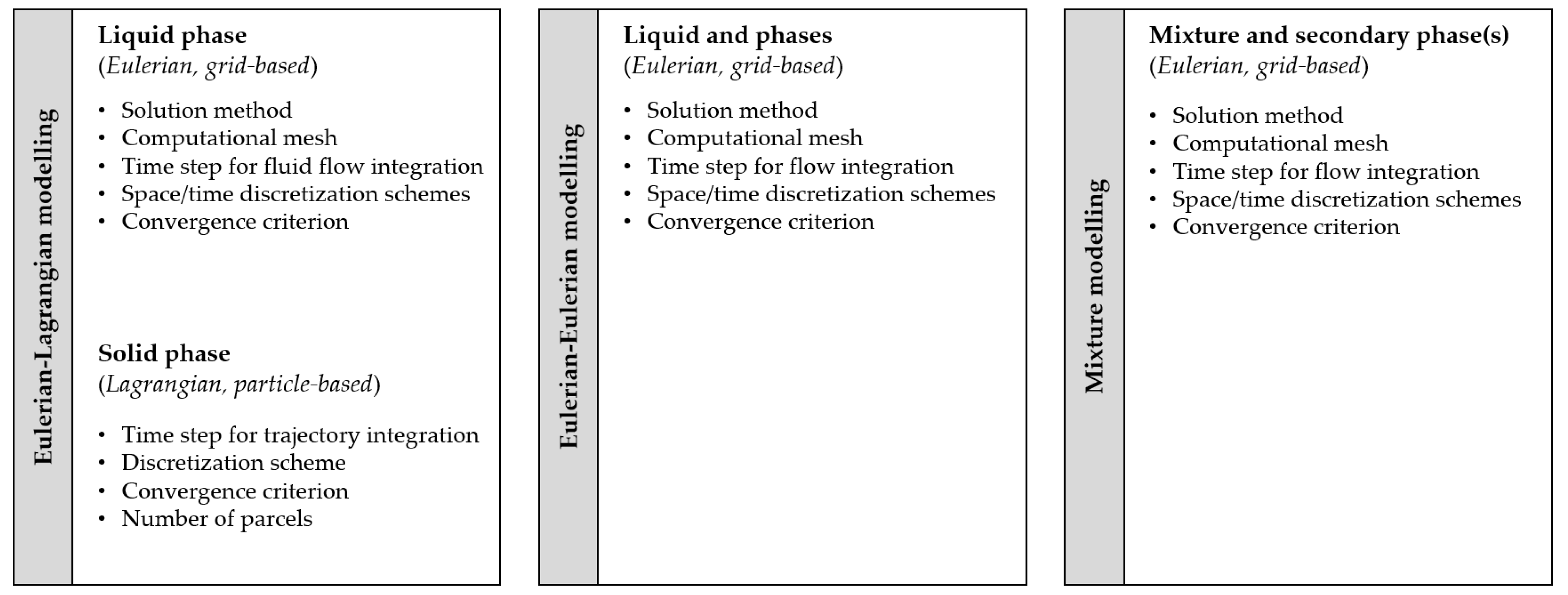
3.1. Numerical Features Producing Uncertainty
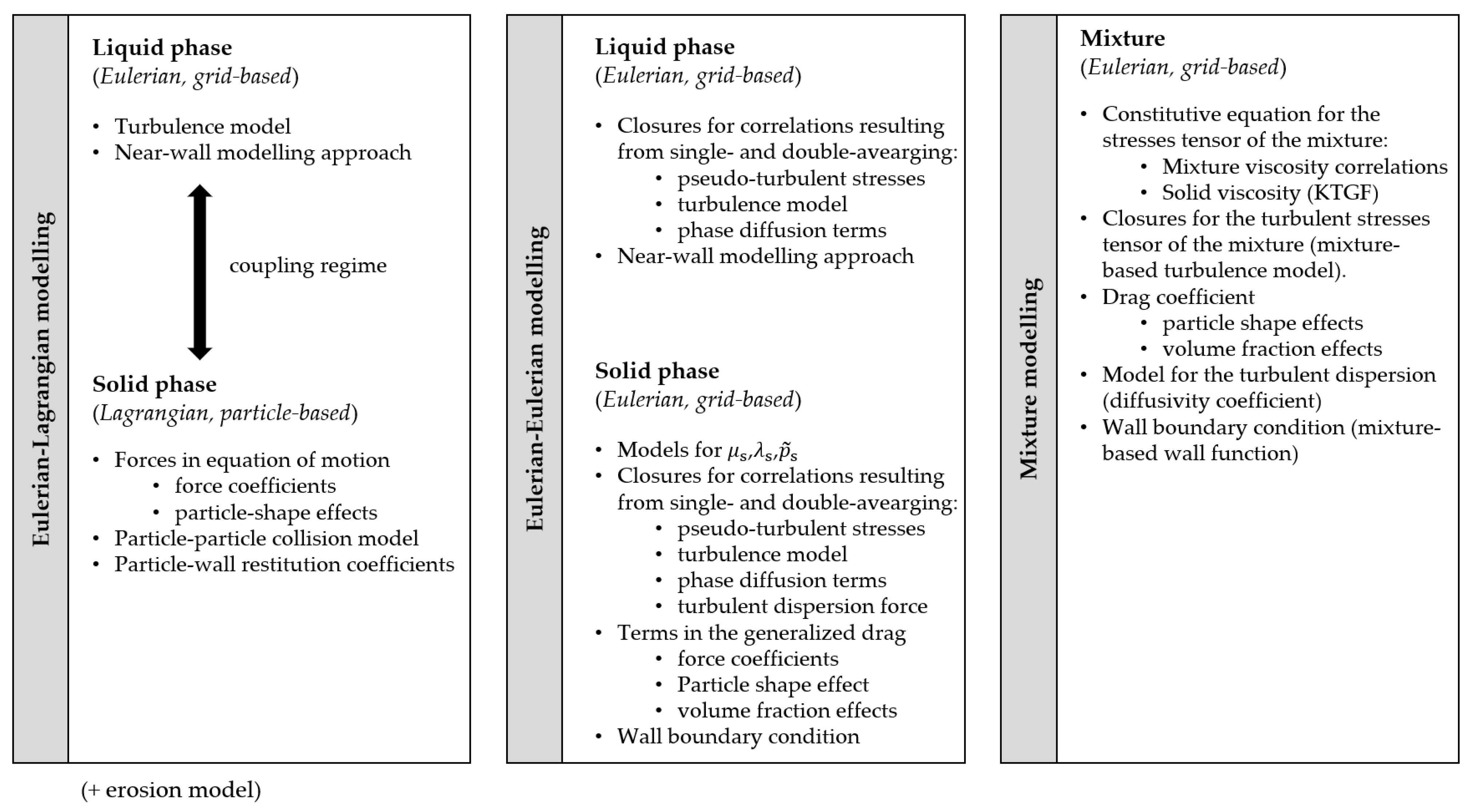
3.2. Modelling Features Producing Uncertainty
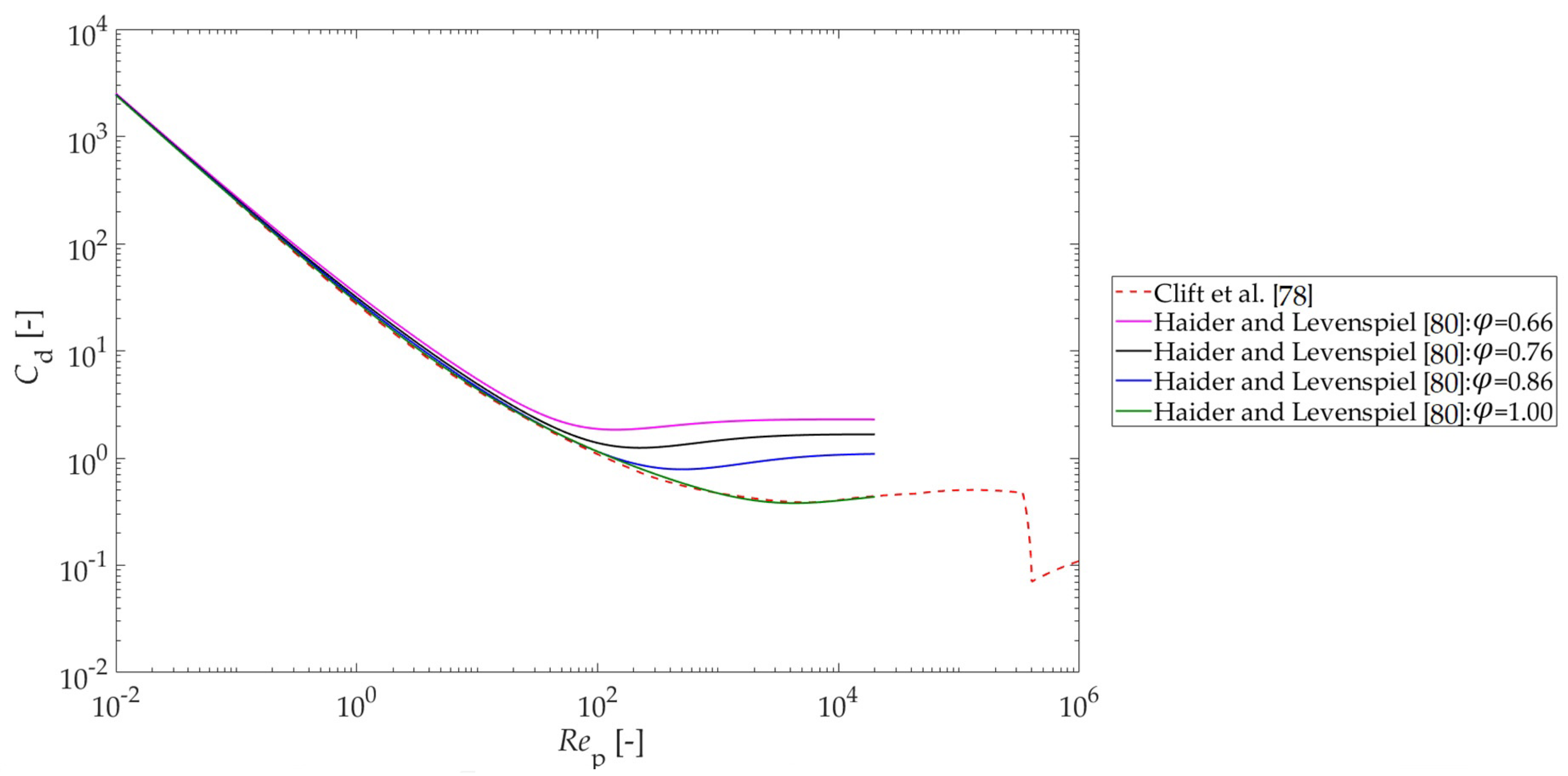
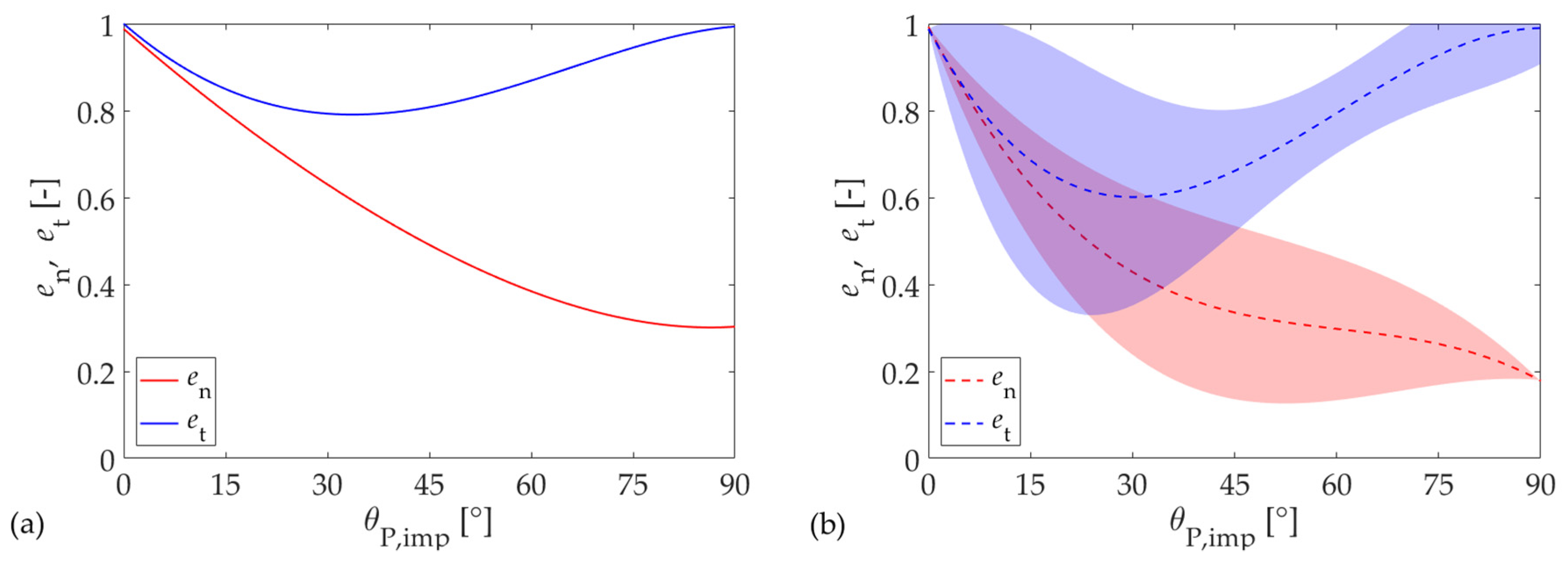
3.2.1. Modelling Sources of Uncertainty of Eulerian–Lagrangian Models
3.2.2. Modelling Sources of Uncertainty of Two- and Multi-Fluid Models
3.2.3. Modelling Sources of Uncertainty of the Mixture Model
3.2.4. Summary and Recommendations
4. Review of Previous Investigations
4.1. Overview of Published Literature
- Firstly, regarding their topic. A total of 69 articles, corresponding to about 80% out of the total 86, concern the modelling of particle transport in slurry pipelines, generally at a high solid volume fraction. Conversely, the remaining 20% are focused on slurry erosion of pipeline components, typically pipe bends, at moderate solid concentration.
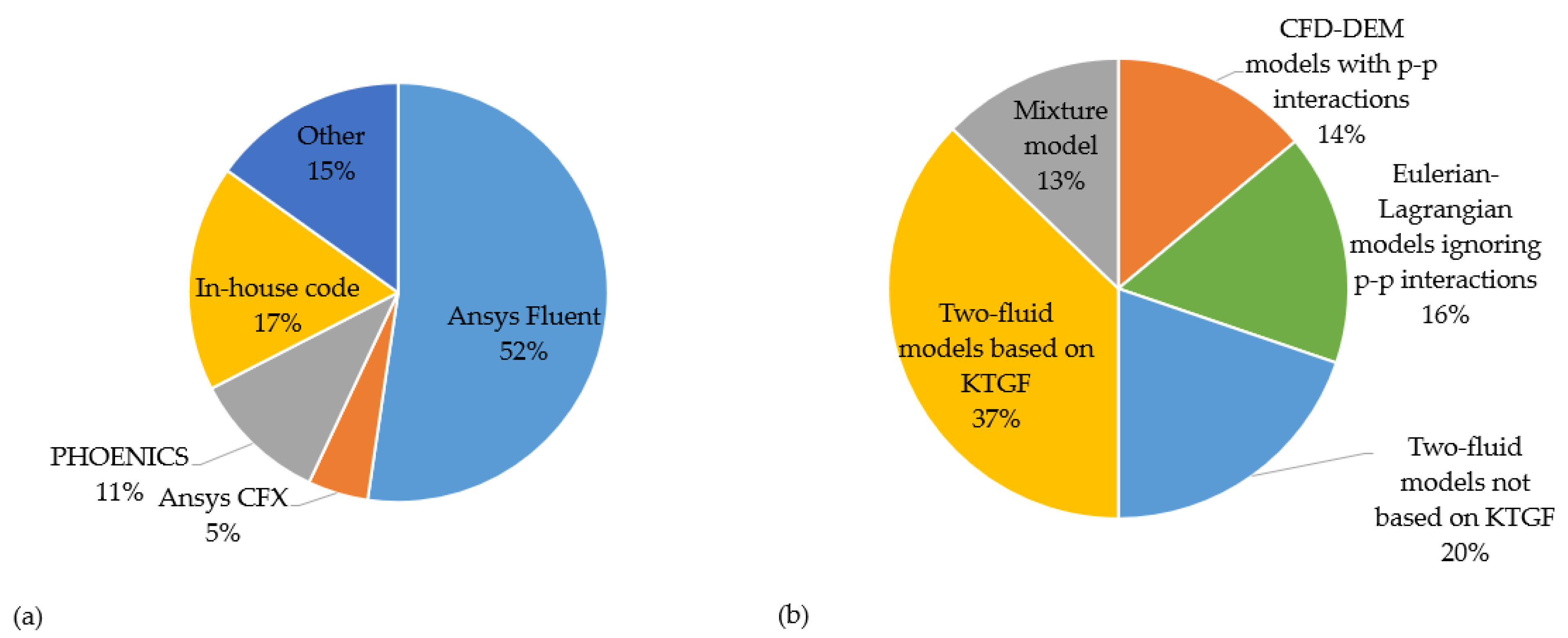
- Secondly, regarding the software used. As shown in Figure 15a, more than half of the investigations were performed using the Ansys Fluent code, which embeds all types of models described in Section 2; other commercial codes used were PHOENICS and Ansys CFX. A significant fraction (≈17%) of the numerical studies were performed using in-house codes, which mostly applies to the pioneering investigations. The category field “other” in Figure 15b include papers in which the use was made of a combination of different open source or commercial software, as well as those where no information was provided.
- Thirdly, regarding the modelling approach. As shown in Figure 15b, Eulerian–Lagrangian models, either including or ignoring particle–particle interactions, were used in around 30% of the total published articles, indicating that the Eulerian approach is the preferred one for the modelling of slurry pipe flows. However, the data must be interpreted in the light of the topic of the study: in fact, almost all papers concerning slurry erosion used the Eulerian–Lagrangian models, whereas the slurry transport at high concentrations has been rarely simulated using this approach. It is also interesting to underline the relation between the type of modelling approach and the used software: for instance, almost all investigations using two-fluid models based on KTGF and those using the Mixture Model were performed with Ansys Fluent. Conversely, although particle–particle interaction models are embedded in most commercial codes, CFD-DEM simulations have been usually run by coupling different codes, or with a single in-house package.
4.2. Studies Using Eulerian–Lagrangian Models for Predicting Particle Transport
4.3. Studies Using Eulerian–Lagrangian Models for Predicting Slurry Erosion in Pipeline Systems
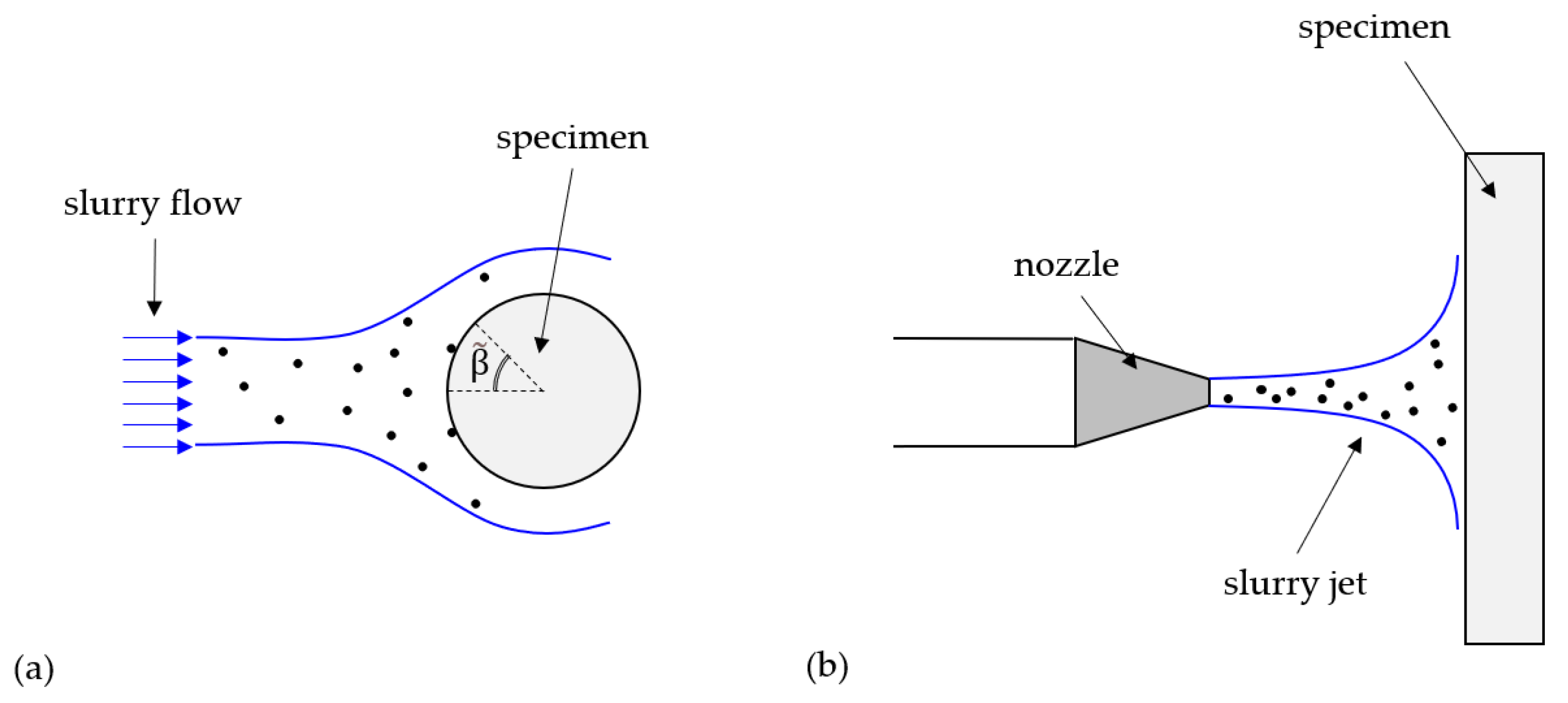
4.3.1. The Engineering Problem and Relevant Parameters
4.3.2. Challenges in the CFD Modelling of Slurry Erosion
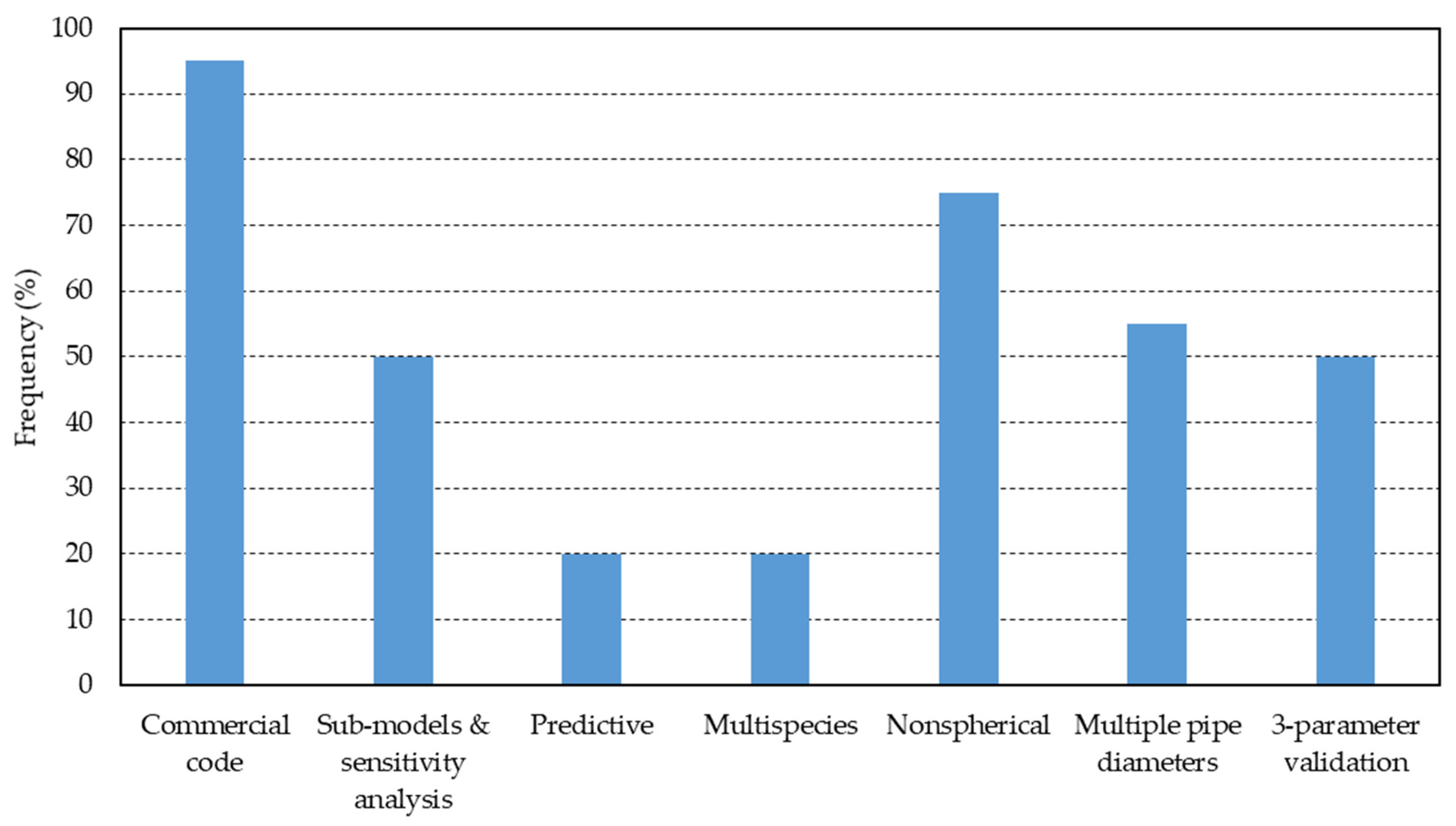
4.3.3. Critical Evaluation of Previous Investigations
4.4. Studies Using Two- and Multi-Fluid Models Based on KTGF Closures
4.4.1. KTGF Closure Equations
4.4.2. Literature Review
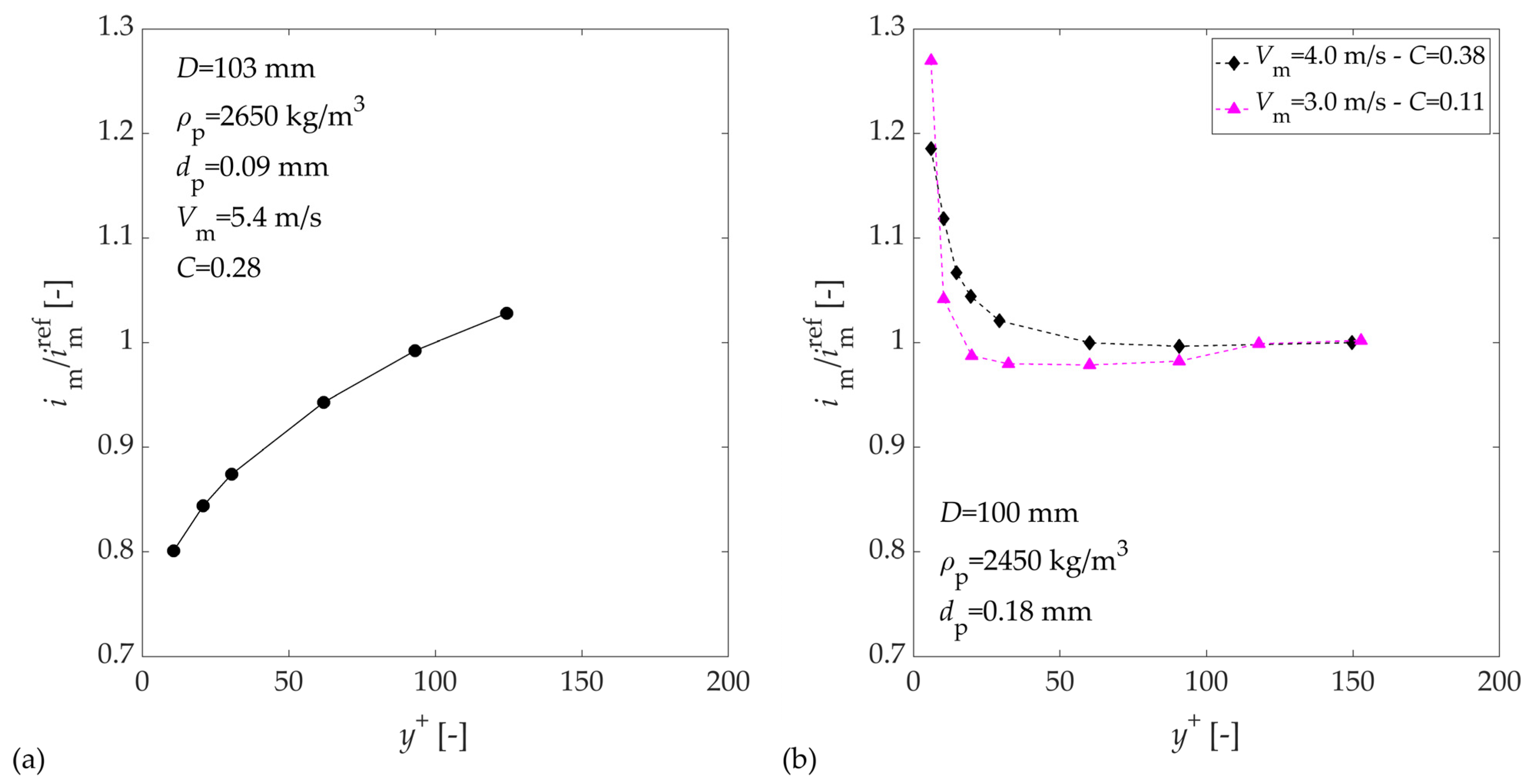
KTGF Modelling—Performance Evaluation
Verification and Validation of Eulerian KTGF Models
4.4.3. Challenges and Limitations
4.5. Studies Using Two-Fluid Models Based on Empirical Closures
4.5.1. Pioneering Studies by Roco and Co-Workers during the 1980s
4.5.2. The - Two-Fluid Model for Fully Suspended Flow
4.6. Studies Using the Mixture Model
5. Concluding Remarks and Recommendations
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Symbol | Units | Description |
| - | drag coefficient | |
| kg/(m3 s) | fluid–solid exchange coefficient | |
| - | delivered solids concentration | |
| - | average spatial volumetric concentration of solids | |
| m | particle diameter | |
| - | particle size in wall units | |
| D | m | pipe diameter |
| kg/(m3 s) | fluid–solid exchange coefficient | |
| - | normal particle(parcel)-wall restitution coefficients | |
| - | inter-particle collision restitution coefficient | |
| - | tangential particle(parcel)-wall restitution coefficients | |
| - | dimensionless wear function in Equation (81) | |
| - | particle shape related constant in Equation (86) | |
| - | radial distribution function | |
| - | hydraulic gradient | |
| Pa2 | second invariant of the deviatoric stress tensor | |
| kg m2 | moment of inertia of the particle | |
| k | m2/s2 | turbulent kinetic energy |
| - | diffusion coefficient in Equation (88) | |
| - | material related constant in Equation (86) | |
| kg/(m3 s) | fluid–solid exchange coefficient | |
| m | kg | mass of a particle |
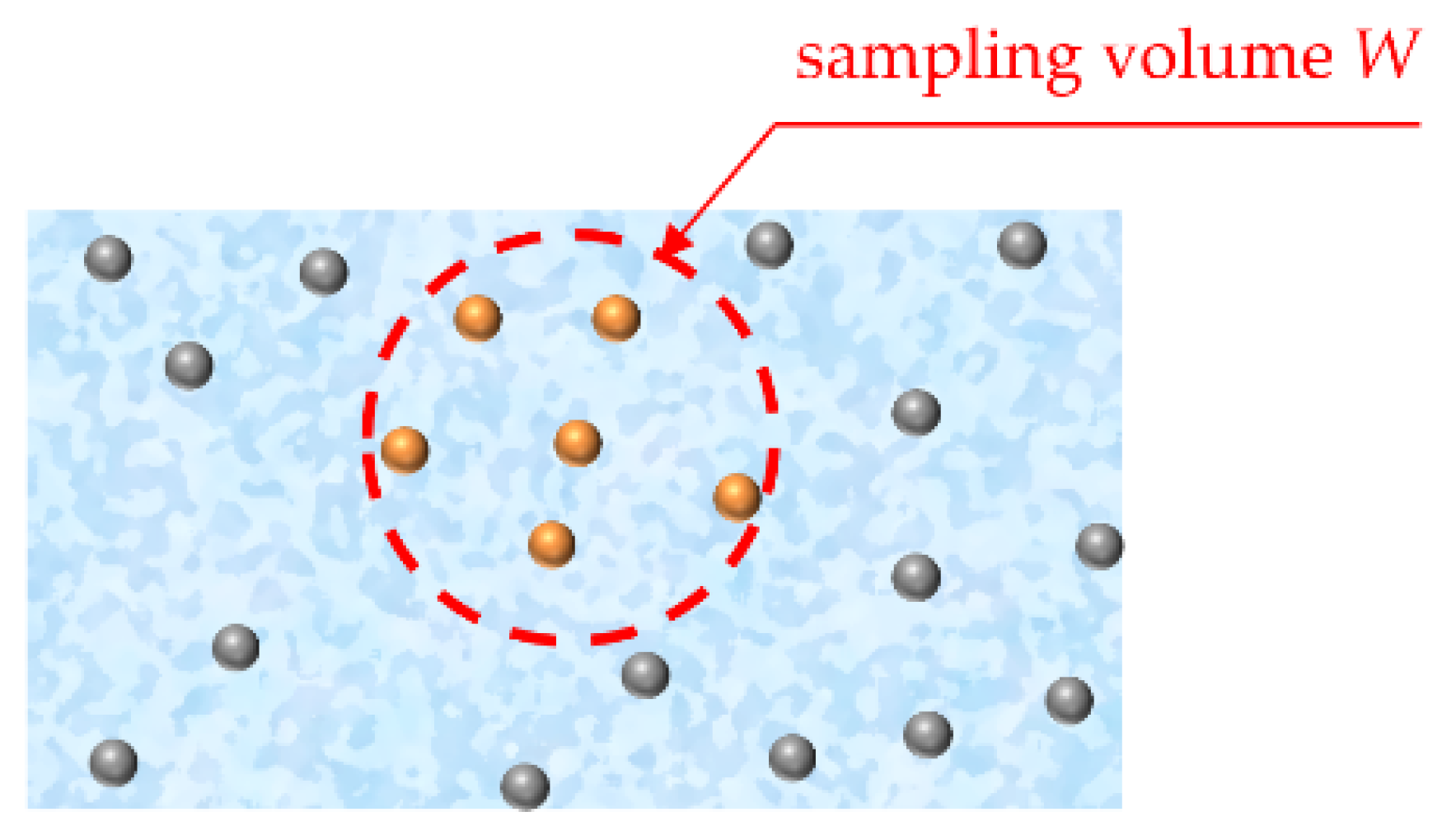
| - | number of particles in the sampling volume | |
| Rep | - | particle Reynolds number |
| p | Pa | instantaneous pressure |
| Pa | collisional solid pressure | |
| Pa | frictional solid pressure | |
| Pa | kinetic solid pressure | |
| P | Pa | locally-averaged/double-averaged pressure |
| m2/s3 | volumetric production rate of | |
| - | number of particle size classes | |
| - | velocity exponent in Equation (86) | |
| m3/s | volumetric flow rate | |
| - | relative density of particle | |
| t | s | time |
| s | time scale | |
| m/s | modulus of the impact velocity | |
| m/s | deposition-limit velocity | |
| m/s | slurry bulk-mean velocity | |
| W | m3 | sampling volume |
| y+ | - | dimensionless distance of the first grid point to the wall |
| Vectors and tensors | ||
| N | drag force | |
| N | forces exerted on the particle | |
| N | total force from liquid to solid phase in sampling volume | |
| m/s2 | gravitational acceleration vector | |
| N/m3 | momentum exchange term in Eulerian–Eulerian formulation | |
| N/m3 | generalized drag in the Eulerian–Eulerian formulation | |
| N/m3 | turbulent dispersion force | |
| m/s2 | pressure-related vector in Equation (97) | |
| m/s2 | viscosity-related vector in Equation (97) | |
| N/m3 | momentum exchange term in Eulerian–Lagrangian framework | |
| N m | torque exerted on the particle | |
| m/s | instantaneous velocity vector of the liquid phase | |
| , | m/s | fluctuating velocity vector of the liquid phase |
| m/s | the solution of Equation (73) without the last term | |
| m/s | diffusion velocities in mixture model | |
| m/s | instantaneous velocity vector of a particle/solid phase | |
| and | m/s | fluctuating velocity vector of the solid phase |
| m | position vector | |
| Pa | stresses tensor | |
| Pa | pseudo-turbulent stress tensors | |
| Pa | deviatoric part of the stresses tensor | |
| Pa | “Reynolds”-like stresses in the mixture model | |
| Pa | diffusion stresses in the mixture model | |
| s−1 | angular velocity vector of the particle | |
| Greek Symbols | ||
| - | empirical coefficient in two-fluid model of Messa et al. [37] | |
| - | numerical coefficient -σ two fluid model | |
| kg/(m3 s) | rate of energy dissipation due to collision within the solid particles | |
| ε | m2/s3 | turbulence dissipation rate |
| m | erosion depth | |
| - | empirical coefficient in two-fluid model of Messa et al. [37] | |
| ° | angle of internal friction of particle | |
| ° | impact angle | |
| m2/s2 | granular temperature | |
| Pa s | second viscosity coefficient or bulk viscosity | |
| Pa s | dynamic viscosity | |
| Pa s | effective viscosity | |
| Pa s | eddy viscosity | |
| Pa s | collisional solid viscosity | |
| Pa s | frictional solid viscosity | |
| Pa s | kinetic solid viscosity | |
| kg/m3 | density | |
| - | turbulent Schmidt number for volume fractions | |
| s | response time of a particle in the mixture | |
| - | particle spherical coefficient | |
| kg/(m3 s) | exchange term in Equation (88) | |
| kg/(m2 s) | erosion rate intensity | |
| kg/(m2 s) | local average particle impact rate | |
| - | instantaneous volume fraction of one phase | |
| - | fluctuating volume fraction of one phase | |
| s−1 | specific turbulent dissipation rate | |
| Subscripts and superscripts | ||
| before | just before a particle–wall impact occurs | |
| after | just after a particle–wall impact has occurred | |
| i | interface | |
| k | generic phase | |
| l | liquid phase | |
| m | mixture | |
| p | physical particles | |
| P | computational particles in the Lagrangian framework | |
| s | solid phase in the Eulerian framework | |
| t | target material in erosion modelling | |
| @p | at particle position in Eulerian–Lagrangian modelling | |
| @P | at parcel position in Eulerian–Lagrangian modelling | |
| normal to the wall | ||
| parallel to the wall | ||
| Operators (applied to the generic variable ψ) | ||
| + | transpose of a tensor | |
| volume-average | ||
| time-average | ||
| Favre-average | ||
| generic averaged (or double averaged) variable | ||
| Acronyms | ||
| CFD | Computational Fluid Dynamics | |
| DDPM | Dense Discrete Particle Model | |
| DEM | Discrete Element Method | |
| DNS | Direct Numerical Simulation | |
| EL | Eulerian–Lagrangian model (or approach) | |
| GCI | Grid Convergence Index | |
| IPSA | Inter-Phase Slip Algorithm | |
| KTGF | Kinetic Theory of Granular Flow | |
| LES | Large Eddy Simulation | |
| RANS | Reynolds-Averaged Navier–Stokes | |
| RSM | Reynolds Stress Model | |
| SEC | Specific Energy Consumption | |
| U-RANS | V-Unsteady Reynolds-Averaged Navier–Stokes | |
References
- Derammelaere, R.H.; Shou, G. Altamina’s Copper and Zinc Concentrate pipeline incorporates advanced technologies. In Proceedings of the 15th International Conference on Hydrotransport, Banff, AB, Canada, 3–5 June 2002. [Google Scholar]
- Paterson, A.J.C. Pipeline transport of high density slurries: A historical review of past mistakes, lessons learned and current technologies. Min. Technol. 2012, 121, 37–45. [Google Scholar] [CrossRef]
- van den Berg, C.H. IHC Merwede Handbook for Centrifugal Pumps and Slurry Transportation; MTI Holland: Kinderdijk, The Netherlands, 2013. [Google Scholar]
- van Wijk, J.M.; Talmon, A.M.; van Rhee, C. Stability of vertical hydraulic transport processes for deep ocean mining: An experimental study. Ocean Eng. 2016, 125, 203–213. [Google Scholar] [CrossRef]
- Thomas, A.D.; Cowper, N.T. The design of slurry pipelines—Historical aspects. In Proceedings of the 20th International Conference on Hydrotransport, Melbourne, Australia, 3–5 May 2017. [Google Scholar]
- Matoušek, V. Pressure drops and flow patterns in sand-mixture pipes. Exp. Therm. Fluid Sci. 2002, 26, 693–702. [Google Scholar] [CrossRef]
- Talmon, A.M. Analytical model for pipe wall friction of pseudo-homogenous sand slurries. Part. Sci. Technol. 2013, 31, 264–270. [Google Scholar] [CrossRef]
- Spelay, R.; Gillies, R.G.; Hashemi, S.A. Kinematic friction of concentrated suspensions of neutrally buoyant coarse particles. In Proceedings of the 20th International Conference on Hydrotransport, Melbourne, Australia, 3–5 May 2017. [Google Scholar]
- Wilson, K.C. Deposition-limit nomograms for particles of various densities in pipeline flow. In Proceedings of the 6th International Conference on Hydraulic Transport of Solids in Pipes, Canterbury, UK, 26–28 September 1979. [Google Scholar]
- Sanders, R.S.; Sun, R.; Gillies, R.G.; McKibbem, M.J.; Litzenberger, C.; Shook, C.A. Deposition velocities for particles of intermediate size in turbulent flow. In Proceedings of the 16th International Conference on Hydrotransport, Santiago, Chile, 26–28 April 2004. [Google Scholar]
- Hashemi, S.A.; Wilson, K.C.; Sanders, R.S. Specific Energy Consumption and optimum operating condition for coarse-particle slurries. Powder Technol. 2014, 262, 183–187. [Google Scholar] [CrossRef]
- Matoušek, V. Non-stratified flow of sand-water slurries. In Proceedings of the 15th International Conference on Hydrotransport, Banff, AB, Canada, 3–5 June 2002. [Google Scholar]
- Gillies, R.G.; Shook, C.A. Concentration distributions of sand slurries in horizontal pipe flow. Part. Sci. Technol. 1994, 12, 45–69. [Google Scholar] [CrossRef]
- Wilson, K.C.; Addie, G.R.; Sellgren, A.; Clift, R. Slurry Transport Using Centrifugal Pumps, 3rd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
- Shook, C.A.; Gillies, R.G.; Sanders, R.S.; Spelay, R.B. Saskatchewan Research Council Course Notes; SRC Publications: Saskatoon, SK, Canada, 2013. [Google Scholar]
- Durand, R. Basic Relationships of the transportation of solids in pipes—Experimental research. In Proceedings of the IAHR Minnesota International Hydraulic Convention, Minneapolis, MI, USA, 1–4 September 1953. [Google Scholar]
- Matoušek, V.; Visintainer, R.; Furlan, J.; Sellgren, A. Pipe-size scale-up of frictional head loss in settling-slurry flows using predictive models: Experimental validation. In Proceedings of the ASME FEDSM2020, Orlando, FL, USA, 13–15 July 2020. [Google Scholar]
- Wilson, K.C. A Unified physically-based analysis of solid-liquid pipeline flow. In Proceedings of the 4th International Conference on Hydrotransport, Banff, AB, Canada, 18–21 May 1976. [Google Scholar]
- Gillies, R.G.; Shook, C.A.; Wilson, K.C. An improved two layer model for horizontal slurry pipeline flow. Can. J. Chem. Eng. 1991, 69, 173–178. [Google Scholar] [CrossRef]
- Doron, P.; Barnea, D. A three-layer model for solid-liquid flow in horizontal pipes. Int. J. Multiph. Flow 1993, 19, 1029–1043. [Google Scholar] [CrossRef]
- Gillies, R.G.; Shook, C.A. Modelling high concentration slurry flows. Can. J. Chem. Eng. 2000, 78, 709–716. [Google Scholar] [CrossRef]
- Gillies, R.G.; Shook, C.A.; Xu, J. Modelling heterogeneous slurry flows at high velocities. Can. J. Chem. Eng. 2004, 82, 1060–1065. [Google Scholar] [CrossRef]
- Spelay, R.B.; Hashemi, S.A.; Gillies, R.G.; Hegde, R.; Sanders, R.S.; Gillies, R.G. Governing friction loss mechanisms and the importance of off-line characterization test in the pipeline transport of dense coarse-particle slurries. In Proceedings of the ASME 2013 Fluids Engineering Division Summer Meeting, Incline Village, NE, USA, 7–11 July 2013. [Google Scholar]
- Matoušek, V.; Krupička, J. Unified model for coarse-slurry flow with stationary and sliding Bed. In Proceedings of the 15th International Conference on Transport and Sedimentation of Solid Particles, Wroclaw, Poland, 22–25 September 2015. [Google Scholar]
- Matoušek, V.; Krupička, J.; Kesely, M. A layered model for inclined pipe flow of settling slurry. Powder Technol. 2018, 333, 317–326. [Google Scholar] [CrossRef]
- Visintainer, R.; Furlan, J.; McCall, G.; Sellgren, A.; Matoušek, V. Comprehensive loop testing of a broadly graded (4-component) slurry. In Proceedings of the 20th International Conference on Hydrotransport, Melbourne, Australia, 3–5 May 2017. [Google Scholar]
- Matoušek, V.; Visintainer, R.; Furlan, J.; Sellgren, A. Frictional head loss of various bimodal settling slurry flows in pipe. In Proceedings of the ASME-JSME-KSME 2019 Joint Fluids Engineering Conference AJKFLUIDS 2019, San Francisco, CA, USA, 28 July–1 August 2019. [Google Scholar]
- Loth, E. Particle, Drops, and Bubbles. Fluid Dynamics and Numerical Methods; Draft for Cambridge University Press: 2010. Available online: www.academia.edu (accessed on 31 August 2021).
- Elghobashi, S. On predicting particle-laden turbulent flows. Appl. Sci. Res. 1994, 52, 309–329. [Google Scholar] [CrossRef]
- Sommerfeld, M. Numerical methods for dispersed multiphase flows. In Particles in Flows; Bodnár, T., Galdi, G., Nečasová, Š., Eds.; Birkhäuser: Cham, Switzerland, 2017; pp. 327–396. [Google Scholar]
- Leguizamón, S.; Jahanbakhsh, E.; Martens, A.; Alimirzazadeh, S.; Avellan, F. A multiscale model for sediment impact erosion simulation using the finite volume particle method. Wear 2017, 392–393, 202–212. [Google Scholar] [CrossRef]
- Crowe, C.T.; Troutt, T.R.; Chung, J.N. Numerical models for two-phase turbulent flows. Annu. Rev. Fluid Mech. 1996, 28, 11–43. [Google Scholar] [CrossRef]
- van Wachem, B.G.M.; Almstedt, A.E. Methods for multiphase computational fluid dynamics. Chem. Eng. J. 2003, 96, 81–98. [Google Scholar] [CrossRef]
- Hiltunen, K.; Jäsberg, A.; Kallio, S.; Karema, H.; Kataja, M.; Koponen, A.; Manninen, M.; Taivassalo, V. Multiphase Flow Dynamics. Theory and Numerics; VTT Technical Research Centre of Finland: Espoo, Finland, 2009. [Google Scholar]
- Manninen, M.; Taivassalo, V.; Kallio, S. On the Mixture Model for Multiphase Flow; VTT Technical Research Centre of Finland: Espoo, Finland, 1996. [Google Scholar]
- Ekambara, K.; Sanders, R.S.; Nandakumar, K.; Masliyah, J.H. Hydrodynamic simulation of horizontal slurry pipeline flow using ANSYS-CFX. Ind. Eng. Chem. Res. 2009, 48, 8159–8171. [Google Scholar] [CrossRef]
- Messa, G.V.; Malin, M.; Malavasi, S. Numerical prediction of fully-suspended slurry flow in horizontal pipes. Powder Technol. 2014, 256, 61–70. [Google Scholar] [CrossRef]
- Messa, G.V.; Malin, M.; Matoušek, V. Parametric study of the β-σ two-fluid model for simulating fully-suspended slurry flow: Effect of flow conditions. Meccanica 2021, 56, 1047–1077. [Google Scholar] [CrossRef]
- Enwald, H.; Peirano, E.; Almstedt, A.T. Eulerian two-phase flow theory applied to fluidization. Int. J. Multiph. Flow 1996, 22, 21–66. [Google Scholar] [CrossRef]
- Menter, F. Two equation eddy-viscosity turbulence modeling for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
- Launder, B.E.; Spalding, D.B. Mathematical Models of Turbulence; Academic Press: London, UK, 1972. [Google Scholar]
- Prosperetti, A.; Tryggvason, G. Computational Methods for Multiphase Flow; Cambridge University Press: New York, NY, USA, 2007. [Google Scholar]
- Gosman, A.D.; Ioannides, E. Aspects of computer simulation of liquid-fueled combustors. J. Energy 1983, 7, 482–490. [Google Scholar] [CrossRef]
- Sommerfeld, M.; Kohnen, G.; Rüger, M. Some open questions and inconsistencies of Lagrangian particle dispersion models. In Proceedings of the 9th Symposium on Turbulent Shear Flows, Kyoto, Japan, 16–18 August 1993. [Google Scholar]
- Hager, A. CFD-DEM on Multiple Scales. An Extensive Investigation of Particle-Fluid Interactions. Ph.D. Thesis, Johannes Kepler University Linz, Linz, Austria, 2014. [Google Scholar]
- Rettinger, C.; Godenschwager, C.; Eibl, S.; Preclik, T.; Schruff, T.; Frings, R. Fully resolved simulations of dune formation in riverbeds. In High Performance Computing; Kunkel, J.M., Yokota, R., Balaji, P., Keyes, D., Eds.; Springer: New York, NY, USA, 2017; pp. 3–21. [Google Scholar]
- Peng, Z.; Doroodchi, E.; Luo, C.; Moghtaderi, B. Influence of void fraction calculation on fidelity of CFD-DEM simulation of gas-solid bubbling fluidized beds. AIChE J. 2014, 60, 2000–2018. [Google Scholar] [CrossRef]
- Zheng, E.; Rudman, M.; Kuang, S.; Chryss, A. Turbulent coarse-particle suspension flow: Measurement and modelling. Powder Technol. 2020, 373, 647–659. [Google Scholar] [CrossRef]
- Launder, B.E.; Spalding, D.B. The numerical computation of turbulent flows. Comput. Meth. Appl. Mech. Eng. 1974, 3, 269–289. [Google Scholar] [CrossRef]
- Huber, N.; Sommerfeld, M. Modelling and numerical calculation of dilute-phase pneumatic conveying in pipe systems. Powder Technol. 1998, 99, 90–101. [Google Scholar] [CrossRef]
- Breuer, M.; Alletto, M.; Langfeldt, F. Sandgrain roughness model for rough walls within Eulerian-Lagrangian predictions of turbulent flows. Int. J. Multiph. Flow 2012, 43, 157–175. [Google Scholar] [CrossRef]
- Messa, G.V.; Wang, Y. Importance of accounting for finite particle size in CFD-based erosion prediction. In Proceedings of the ASME 2018 Pressure Vessels and Piping Conference, Prague, Czech Republic, 15–20 July 2018. [Google Scholar]
- Cheng, N.S.; Law, A.W.K. Exponential formula for computing effective viscosity. Powder Technol. 2003, 129, 156–160. [Google Scholar] [CrossRef]
- Gomex, L.C.; Milioli, F.E. Collisional solid’s pressure impact on numerical results from a traditional two-fluid model. Powder Technol. 2005, 149, 78–83. [Google Scholar]
- Burns, A.D.; Frank, T.; Hamill, I.; Shi, J.M. The Favre averaged drag model for turbulent dispersion in Eulerian multi-phase flows. In Proceedings of the 5th International Conference on Multiphase Flow, Yokohama, Japan, 30 May–4 June 2004. [Google Scholar]
- Spalding, D.B. PHOENICS Encyclopedia. Models for Two-Phase Flows: Two-Equation k-ε Turbulence Model. Available online: http://www.cham.co.uk/phoenics/d_polis/d_enc/turmod/enc_tu74.htm (accessed on 22 July 2021).
- Messa, G.V.; Matoušek, V. Analysis and discussion of two fluid modelling of pipe flow of fully suspended slurry. Powder Technol. 2020, 30, 747–768. [Google Scholar] [CrossRef]
- Elghobashi, S.E.; Abou-Arab, T.W. A two-equation turbulence model for two-phase flows. Phys. Fluids 1983, 26, 931–938. [Google Scholar] [CrossRef]
- Crowe, C.T. On models for turbulence modulation in fluid-particle flows. Int. J. Multiph. Flow 2000, 26, 719–727. [Google Scholar] [CrossRef]
- Chen, P.E.; Wood, C.E. A turbulence closure model for dilute gas-particle flows. Can. J. Chem. Eng. 1985, 63, 349–360. [Google Scholar] [CrossRef]
- Mostafa, A.A.; Mongia, H.C. On the interaction of particles and turbulent fluid flow. Int. J. Heat Mass Transf. 1988, 31, 2066–2075. [Google Scholar] [CrossRef]
- Hadinoto, K.; Curtis, J.S. Effect of interstitial fluid on particle-particle interactions in kinetic theory approach of dilute turbulent fluid-particle flow. Ind. Eng. Chem. Res. 2004, 43, 3604–3615. [Google Scholar] [CrossRef]
- Hadinoto, K. Predicting turbulence modulation at different Reynolds numbers in dilute-phase turbulent liquid-particle flow simulations. Chem. Eng. Sci. 2010, 65, 5297–5308. [Google Scholar] [CrossRef]
- Hadinoto, K.; Chew, J.W. Modeling fluid-particle interaction in dilute-phase turbulent liquid-particle flow simulation. Particuology 2010, 8, 150–160. [Google Scholar] [CrossRef]
- Mandø, M.; Lightstone, M.F.; Rosendahl, L.; Yin, C.; Sørensen, H. Turbulence modulation in dilute particle-laden flow. Int. J. Heat Fluid Flow 2009, 30, 331–338. [Google Scholar] [CrossRef]
- Messa, G.V.; Malavasi, S. Numerical prediction of dispersed turbulent liquid–solid flows in vertical pipes. J. Hydraul. Res. 2014, 52, 684–692. [Google Scholar] [CrossRef]
- Kaushal, D.R.; Thinglas, T.; Tomita, Y.; Kuchii, S.; Tsukamoto, H. CFD modeling for pipeline flow of fine particles at high concentration. Int. J. Multiph. Flow 2012, 43, 85–100. [Google Scholar] [CrossRef]
- Melville, W.K.; Bray, K.N.C. A model of the two-phase turbulent jet. Int. J. Heat Mass Transf. 1979, 22, 647–656. [Google Scholar] [CrossRef]
- Loth, E. An Eulerian turbulent diffusion model for particles and bubbles. Int. J. Multiph. Flow 2011, 27, 1051–1063. [Google Scholar] [CrossRef]
- Mashayek, F.; Taulbee, D.B. A four-equation model for prediction of gas-solid turbulent flows. Num. Heat Transf. Part B 2002, 41, 95–116. [Google Scholar] [CrossRef]
- Johnson, P.C.; Jackson, R. Frictional-collisional constitutive relations for granular materials, with application to plane shearing. J. Fluid Mech. 1987, 176, 67–93. [Google Scholar] [CrossRef]
- Messa, G.V.; Malavasi, S. Improvements in the numerical prediction of fully-suspended slurry flow in horizontal pipes. Powder Technol. 2015, 270, 358–367. [Google Scholar] [CrossRef]
- Ferziger, J.H.; Peric, M. Computational Methods for Fluid Dynamics; Springer: Berlin/Heidelberg, Germany; New York, NY, USA, 2002. [Google Scholar]
- Roache, P.J. Perspective: A method for uniform reporting of grid refinement studies. ASME J. Fluids Eng. 1994, 116, 405–413. [Google Scholar] [CrossRef]
- Zhang, M.; Kang, Y.; Wei, W.; Li, D.; Xiong, T. CFD investigation of the flow characteristics of liquid-solid slurry in a large-diameter horizontal pipe. Part. Sci. Technol. 2020, 1–14. [Google Scholar] [CrossRef]
- Schiller, L.; Naumann, Z. A drag coefficient correlation. Z. Ver. Dtsch. Ing. 1935, 77, 318–320. [Google Scholar]
- Dellavalle, J.M. Micrometrics: The Technology of Fine Particles; Pitman: London, UK, 1948. [Google Scholar]
- Clift, R.; Grace, J.R.; Weber, M.E. Bubbles, Drops, and Particles; Academic Press: New York, NY, USA, 1978. [Google Scholar]
- Song, X.; Xu, Z.; Li, G.; Pang, Z.; Zhu, Z. A new model for predicting drag coefficient and settling velocity of spherical and non-spherical particle in Newtonian fluid. Powder Technnol. 2017, 321, 242–250. [Google Scholar] [CrossRef]
- Haider, A.; Levenspiel, O. Drag coefficient and terminal velocity of spherical and nonspherical particles. Powder Technol. 1989, 58, 63–70. [Google Scholar] [CrossRef]
- Yang, C.W. Handbook of Fluidization and Fluid-Particle Systems; Marcel Dekker Inc: New York, NY, USA, 2003. [Google Scholar]
- Forder, A.; Thew, M.; Harrison, D. A numerical investigation of solid particle erosion experienced with oilfield control valves. Wear 1998, 216, 184–193. [Google Scholar] [CrossRef]
- Grant, G.; Tabakoff, W. Erosion prediction in turbomachinery resulting from environmental solid particles. J. Aircraft 1975, 12, 471–478. [Google Scholar] [CrossRef]
- Messa, G.V.; Malavasi, S. The effect of sub-models and parameterizations in the simulation of abrasive jet impingement tests. Wear 2017, 370–371, 59–72. [Google Scholar] [CrossRef]
- Lyczkowski, R.W.; Bouillard, J.X. State-of-the-art review of erosion modeling in fluid/solids systems. Prog. Energy Combust. Sci. 2002, 28, 543–602. [Google Scholar] [CrossRef]
- Parsi, M.; Najmi, K.; Najafifard, F.; Hassani, S.; McLaury, B.S.; Shirazi, S.A. A comprehensive review of solid particle erosion modeling for oil and gas wells and pipelines applications. J. Nat. Gas Sci. Eng. 2014, 21, 850–873. [Google Scholar] [CrossRef]
- Oka, Y.I.; Okamura, K.; Yoshida, T. Practical estimation of erosion damage caused by solid particle impact: Part 1: Effects of impact parameters on a predictive equation. Wear 2005, 259, 95–101. [Google Scholar] [CrossRef]
- Oka, Y.I.; Yoshida, T. Practical estimation of erosion damage caused by solid particle impact: Part 2: Mechanical properties of materials directly associated with erosion damage. Wear 2005, 102–109. [Google Scholar] [CrossRef]
- Finnie, I. Erosion of surfaces by solid particles. Wear 1960, 3, 87–103. [Google Scholar] [CrossRef]
- Bitter, J.G.A. A study of erosion phenomena. Part I. Wear 1963, 6, 5–21. [Google Scholar] [CrossRef]
- Bitter, J.G.A. A study of erosion phenomena. Part II. Wear 1963, 6, 169–190. [Google Scholar] [CrossRef]
- Lester, D.R.; Graham, L.A.; Wu, J. High precision suspension erosion modelling. Wear 2010, 269, 449–457. [Google Scholar] [CrossRef]
- Mansouri, A. A Combined CFD-Experimental Method for Developing an Erosion Equation for Both Gas-Sand and Liquid-Sand Flows. Ph.D. Thesis, The University of Tulsa, Tulsa, OK, USA, 2016. [Google Scholar]
- Messa, G.V.; Wang, Y.; Negri, M.; Malavasi, S. An improved CFD/experimental combined methodology for the calibration of empirical erosion models. Wear 2021, 476, 203734. [Google Scholar] [CrossRef]
- Ishii, M.; Mishima, K. Two-fluid model and hydrodynamic constitutive relations. Nucl. Eng. Des. 1984, 82, 107–126. [Google Scholar] [CrossRef]
- Di Felice, R. The voidage function for fluid-particle interaction systems. Int. J. Multiph. Flow 1994, 20, 153–159. [Google Scholar] [CrossRef]
- Gidaspow, D. Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions; Academic Press: New York, NY, USA, 1994. [Google Scholar]
- Li, G.; Wang, Y.; He, R.; Cao, X.; Lin, C.; Meng, T. Numerical simulation of predicting and reducing solid particle erosion of solid-liquid two-phase flow in a choke. Pet. Sci. 2009, 6, 91–97. [Google Scholar] [CrossRef] [Green Version]
- Xu, S.L.; Sun, R.; Cai, Y.Q.; Sun, H.L. Study of sedimentation of non-cohesive particles via CFD-DEM simulations. Granul. Matter 2018, 20, 4. [Google Scholar] [CrossRef] [Green Version]
- Krampa-Morlu, F.M.; Bugg, J.D.; Bergstrom, D.J.; Sanders, R.S.; Schaan, J. Frictional pressure drop calculations for liquid-solid vertical flows using the two-fluid model. In Proceedings of the 14th Annual Conference of the Computational Fluid Dynamics Society of Canada, Kingston, ON, Canada, 16–18 July 2009. [Google Scholar]
- Messa, G.V.; Malin, M.; Malavasi, S. Numerical prediction of pressure gradient of slurry flows in horizontal pipes. In Proceedings of the ASME 2013 Pressure Vessels & Piping Division Conference, Paris, France, 14–18 July 2013. [Google Scholar]
- Zhao, Y.; Ding, T.; Zhu, L.; Zhong, Y. A specularity coefficient model and its application to dense particulate flow simulations. Ind. Eng. Chem. Res. 2016, 55, 1439–1448. [Google Scholar] [CrossRef]
- Hu, X.W.; Guo, L.J. Numerical investigations of catalyst-liquid slurry flow in the photocatalytic reactor for hydrogen production based on algebraic slip model. Int. J. Hydrogen Energy 2010, 35, 7065–7072. [Google Scholar]
- Mooney, M. The viscosity of a concentrated suspension of spherical particles. J. Colloid Sci. 1951, 6, 162–170. [Google Scholar] [CrossRef]
- Capecelatro, J.; Desjardins, O. Eulerian–Lagrangian modeling of turbulent liquid–solid slurries in horizontal pipes. Int. J. Multiph. Flow 2013, 55, 64–79. [Google Scholar] [CrossRef]
- Arolla, S.K.; Desjardins, O. Transport modeling of sedimenting particles in a turbulent pipe flow using Euler–Lagrange large eddy simulation. Int. J. Multiph. Flow 2015, 75, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Uzi, A.; Levy, A. Flow characteristics of coarse particles in horizontal hydraulic conveying. Powder Technol. 2018, 326, 302–321. [Google Scholar] [CrossRef]
- Zhou, M.; Kuang, S.; Luo, K.; Zou, R.; Wang, S.; Yu, A. Modeling and analysis of flow regimes in hydraulic conveying of coarse particles. Powder Technol. 2020, 373, 543–554. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Roco, M.; Balakrishnam, N. Multi-dimensional flow analysis of solid–liquid mixtures. J. Rheol. 1985, 29, 431–456. [Google Scholar] [CrossRef]
- Dahl, A.M.; Ladam, Y.; Unander, T.; Onsrud, G. SINTEF-IFE Sand transport 2001–2003. In SINTEF Internal Report; SINTEF: Trondheim, Norway, 2003. [Google Scholar]
- Ting, X.; Xinzhuo, Z.; Miedema, S.A.; Xiuhan, C. Study of the characteristics of the flow regimes and dynamics of coarse particles in pipeline transportation. Powder Technol. 2019, 347, 148–158. [Google Scholar] [CrossRef]
- Chen, Q.; Xiong, T.; Zhang, X.; Jiang, P. Study of the hydraulic transport of non-spherical particles in a pipeline based on the CFD-DEM. Eng. Appl. Comput. Fluid Mech. 2020, 14, 53–69. [Google Scholar] [CrossRef]
- Truscott, G.F. A literature survey on abrasive wear in hydraulic machinery. Wear 1972, 20, 29–50. [Google Scholar] [CrossRef]
- Duarte, C.A.R.; de Souza, F.J.; dos Santos, V.F. Numerical investigation of mass loading effects on elbow erosion. Powder Technol. 2015, 283, 593–606. [Google Scholar] [CrossRef]
- Duarte, C.A.R.; de Souza, F.J.; dos Santos, V.F. Mitigating elbow erosion with a vortex chamber. Powder Technol. 2016, 288, 6–25. [Google Scholar] [CrossRef]
- dos Santos, V.F.; de Souza, F.J.; Duarte, C.A.R. Reducing bend erosion with a twisted tape insert. Powder Technol. 2016, 301, 889–910. [Google Scholar] [CrossRef]
- Duarte, C.A.R.; de Souza, F.J.; de Vasconcelos Salvo, R.; dos Santos, V.F. The role of inter-particle collisions on elbow erosion. Int. J. Multiph. Flow 2017, 89, 1–22. [Google Scholar] [CrossRef]
- Duarte, C.A.R.; de Souza, F.J. Innovative pipe wall design to mitigate elbow erosion: A CFD analysis. Wear 2017, 380–381, 176–190. [Google Scholar] [CrossRef]
- Shitole, P.P.; Gawande, S.H.; Desale, G.R.; Nandre, B.D. Effect of impacting particle kinetic energy on slurry erosion wear. J. Bio-Tribo-Corros. 2015, 29, 9. [Google Scholar] [CrossRef] [Green Version]
- Javaheria, V.; Portera, D.; Kuokkalab, V.T. Slurry erosion of steel—Review of tests, mechanisms and materials. Wear 2018, 408–409, 248–273. [Google Scholar] [CrossRef]
- Messa, G.V.; Malavasi, S. A CFD-based method for slurry erosion prediction. Wear 2018, 398–399, 127–145. [Google Scholar] [CrossRef]
- Yu, W.; Fede, P.; Climent, E.; Sanders, S. Multi-fluid approach for the numerical prediction of wall erosion in an elbow. Powder Technol. 2019, 354, 561–583. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; McLaury, B.S.; Shirazi, S.A. Application and experimental validation of a CFD based erosion prediction procedure for jet impingement geometry. Wear 2018, 394–395, 11–19. [Google Scholar] [CrossRef]
- Mansouri, A.; Arabnejad, H.; Shirazi, S.A.; McLaury, B.S. A combined CFD/experimental methodology for erosion prediction. Wear 2015, 332, 1090–1097. [Google Scholar] [CrossRef]
- Zhang, J.; Kang, J.; Fan, J.; Gao, J. Research on erosion wear of high-pressure pipes during hydraulic fracturing slurry flow. J. Loss Prevent. Proc. Ind. 2016, 43, 438–448. [Google Scholar] [CrossRef]
- Yang, S.; Fan, J.; Zhang, L.; Sun, B. Performance prediction of erosion in elbows for slurry flow under high internal pressure. Tribol. Int. 2021, 157, 106879. [Google Scholar] [CrossRef]
- Gidaspow, D.; Bezburuah, R.; Ding, J. Hydrodynamics of circulating fluidized beds: Kinetic theory approach. In Proceedings of the 7th International Conference on Fluidization, Gold Coast, Australia, 3–8 May 1992. [Google Scholar]
- Schaeffer, D.G. Instability in the evolution equations describing incompressible granular flow. J. Differ. Equ. 1987, 66, 19–50. [Google Scholar] [CrossRef] [Green Version]
- Boemer, A.; Qi, H.; Renz, U.; Vasquez, S.; Boysan, F. Eulerian computation of fluidized bed hydrodynamics—A comparison of physical models. In Proceedings of the 13th International Conference on Fluidized Bed Combustion, Orlando, FL, USA, 7–10 May 1995. [Google Scholar]
- Lun, C.K.K.; Savage, S.B. The effects of an impact velocity dependent coefficient of restitution on stresses developed by sheared granular materials. Acta Mech. 1986, 63, 15–44. [Google Scholar] [CrossRef]
- Chen, L.; Duan, Y.; Pu, W.; Zhao, C. CFD simulation of coal-water slurry flowing in horizontal pipelines. Korean J. Chem. Eng. 2009, 26, 1144–1154. [Google Scholar] [CrossRef]
- Antaya, C.L.; Adane, K.F.K.; Sanders, R.S. Modelling concentrated slurry pipeline flows. In Proceedings of the ASME 2012 Fluid Engineering Division Summer Meeting, Rio Grande, PR, USA, 8–12 July 2012. [Google Scholar]
- Hashemi, S.A.; Spelay, R.B.; Adane, K.F.K.; Sanders, R.S. Solids velocity fluctuations in concentrated slurries. Can. J. Chem. Eng. 2016, 94, 1059–1065. [Google Scholar] [CrossRef]
- Krampa, F.N. Two-Fluid Modelling of Heterogeneous Coarse Particles Slurry Flow. Ph.D. Thesis, University of Saskatchewan, Saskatoon, SK, Canada, 2009. [Google Scholar]
- Kaushal, D.R.; Kumar, A.; Tomita, Y.; Kuchii, S.; Tsukamoto, H. Flow of mono-dispersed particles through horizontal bend. Int. J. Multiph. Flow 2013, 52, 71–91. [Google Scholar] [CrossRef]
- Singh, H.; Kumar, S.; Mohapatra, S.K. Modeling of solid-liquid flow inside conical diverging sections using computational fluid dynamics approach. Int. J. Mech. Sci. 2020, 186, 105909. [Google Scholar] [CrossRef]
- Jiang, Y.Y.; Zhang, P. Numerical investigation of slush nitrogen flow in a horizontal pipe. Chem. Eng. Sci. 2012, 73, 169–180. [Google Scholar] [CrossRef]
- Kumar, N.; Gopaliya, M.K.; Kaushal, D.R. Experimental investigations and CFD modeling for flow of highly concentrated iron ore slurry through horizontal pipeline. Part. Sci. Technol. 2019, 37, 232–250. [Google Scholar] [CrossRef]
- Marinos, O.R.P. Numerical Simulation of Liquid-Solid Slurry Flows Using Eulerian-Eulerian Two-Fluid Model. Master’s Thesis, University of Saskatchewan, Saskatoon, SK, Canada, 2020. [Google Scholar]
- Li, M.Z.; He, Y.P.; Liu, Y.D.; Huang, C. Effect of interaction of particles with different sizes on particle kinetics in multi-sized slurry transport by pipeline. Powder Technol. 2018, 338, 915–930. [Google Scholar] [CrossRef]
- Ting, X.; Miedema, S.A.; Xiuhan, C. Comparative analysis between CFD model and DHLLDV model in fully-suspended slurry flow. Ocean Eng. 2019, 181, 29–42. [Google Scholar] [CrossRef]
- Jamshidi, R.; Angeli, P.; Mazzei, L. On the closure problem of the effective stress in the Eulerian-Eulerian and mixture modeling approaches for the simulation of liquid-particle suspensions. Phys. Fluids 2019, 31, 013302. [Google Scholar] [CrossRef] [Green Version]
- Jiang, Y.Y.; Zhang, P. Pressure drop and flow pattern of slush nitrogen in a horizontal pipe. AIChE J. 2013, 59, 1762–1773. [Google Scholar] [CrossRef]
- Gopaliya, M.K.; Kaushal, D.R. Modeling of sand-water slurry flow through horizontal pipe using CFD. J. Hydrol. Hydromech. 2016, 64, 261–272. [Google Scholar] [CrossRef] [Green Version]
- Gopaliya, M.K.; Kaushal, D.R. Prediction correlation of solid velocity distribution for solid-liquid slurry flows through horizontal pipelines using CFD. Int. J. Fluid Mech. Res. 2020, 47, 445–459. [Google Scholar] [CrossRef]
- Sultan, R.A.; Rahman, M.A.; Rushd, S.; Zendehboudi, S.; Kelessidis, V.C. Validation of CFD model of multiphase flow through pipeline and annular geometries. Part. Sci. Technol. 2019, 37, 685–697. [Google Scholar] [CrossRef]
- Li, M.Z.; He, Y.P.; Liu, Y.D. Hydrodynamic simulation of multi-sized high concentration slurry transport in pipelines. Ocean Eng. 2018, 163, 691–705. [Google Scholar] [CrossRef]
- Roache, P.J. Verification and validation in Fluids Engineering: Some current issues. ASME J. Fluids. Eng. 2016, 138, 101205. [Google Scholar] [CrossRef]
- Roy, C.J.; Oberkampf, W.L. A comprehensive framework for verification, validation, and uncertainty quantification in scientific computing. Comput. Methods Appl. Mech. Eng. 2011, 200, 2131–2144. [Google Scholar] [CrossRef]
- Stern, F.; Wilson, R.V.; Coleman, H.W.; Paterson, E.G. Comprehensive approach to verification and validation of CFD simulations—Part 1: Methodology and procedures. ASME J. Fluids. Eng. 2001, 123, 793–802. [Google Scholar] [CrossRef]
- Brandle de Motta, J.C.; Breugem, W.P.; Gazanion, B.; Estivalezes, J.L.; Vincent, S.; Climent, E. Numerical modelling of finite-size particle collisions in a viscous fluid. Phys. Fluids 2013, 25, 083302. [Google Scholar] [CrossRef] [Green Version]
- Roco, M.C.; Shook, C.A. Modeling of slurry flow: The effect of particle size. Can. J. Chem. Eng. 1983, 61, 494–503. [Google Scholar] [CrossRef]
- Roco, M.C.; Shook, C.A. Computational method for coal slurry pipelines with heterogeneous size distribution. Powder Technol. 1984, 39, 159–176. [Google Scholar] [CrossRef]
- Roco, M.C.; Mahadevan, S. Scale-up technique of slurry pipelines—Part 1: Turbulence modeling. ASME J. Energy Resour. Technol. 1986, 108, 269–277. [Google Scholar] [CrossRef]
- Roco, M.C.; Mahadevan, S. Scale-up technique of slurry pipelines—Part 2: Numerical integration. ASME J. Energy Resour. Technol. 1986, 108, 278–284. [Google Scholar] [CrossRef]
- Spalding, D.B. PHOENICS Encyclopedia. Two-Phase Flows. Available online: http://www.cham.co.uk/phoenics/d_polis/d_lecs/ipsa/ipsa.htm (accessed on 22 July 2021).
- Ling, J.; Skudarnov, P.V.; Lin, C.X.; Ebadian, M.A. Numerical investigations of liquid-solid slurry flows in a fully developed turbulent flow region. Int. J. Heat Fluid Flow 2003, 24, 389–398. [Google Scholar] [CrossRef]
- Lin, C.X.; Ebadian, M.A. A numerical study of developing slurry flow in the entrance region of a horizontal pipe. Comput. Fluid 2013, 13, 371–388. [Google Scholar] [CrossRef]
- Pathak, M.; Khan, M.K. Inter-phase slip velocity and turbulence characteristics of micro particles in an obstructed two-phase flow. Environ. Fluid Mech. 2013, 13, 371–388. [Google Scholar] [CrossRef]
- Silva, R.; Faia, P.M.; Garcia, F.A.P.; Rasteiro, M.G. Characterization of solid-liquid settling suspensions using Electrical Impedance Tomography: A comparison between numerical, experimental and visual information. Chem. Eng. Res. Des. 2016, 111, 223–242. [Google Scholar] [CrossRef]
- Silva, R.; Garcia, F.A.P.; Faia, P.M.; Rasteiro, M.G. Settling suspensions flow modelling: A review. KONA Powder Part. J. 2015, 32, 41–56. [Google Scholar] [CrossRef] [Green Version]
- Liang, L.; Yu, X.; Bombardelli, F. A general mixture model for sediment laden flows. Adv. Water Resour. 2017, 107, 108–125. [Google Scholar] [CrossRef]
- Hossein, B.A.; Naser, J. CFD investigation of particle deposition around bends in a turbulent flow. In Proceedings of the 15th Australian Fluid Mechanics Conference, Sydney, Australia, 13–17 December 2004. [Google Scholar]
- Wood, R.J.K.; Jones, T.F.; Miles, N.J.; Ganeshalingam, J. Upstream swirl-induction for reduction of erosion damage from slurries in pipeline bends. Wear 2001, 250, 770–778. [Google Scholar] [CrossRef]
- Wood, R.J.K.; Jones, T.F.; Ganeshalingam, J.; Miles, N.J. Comparison of predicted and experimental erosion estimates in slurry ducts. Wear 2004, 256, 937–947. [Google Scholar] [CrossRef]
- Xu, J.; Rouelle, A.; Smith, K.M.; Celik, D.; Hussaini, M.Y.; Van Sciver, S.W. Two-phase flow of solid hydrogen particles and liquid helium. Cryogenics 2004, 44, 459–466. [Google Scholar] [CrossRef]
- Goeree, J.C.; Keetels, G.H.; Munts, E.A.; Bugdayci, H.H.; van Rhee, C. Concentration and velocity profiles of sediment-water mixtures using the drift flux model. Can. J. Chem. Eng. 2016, 94, 1048–1058. [Google Scholar] [CrossRef]



| Approach | Typical Application | Key Advantagesmain Strengths | Main Limitations |
|---|---|---|---|
| CFD-DEM modelling with p–p interactions | Particle transport in pipes | A lot of information at the particle and sub-particle scales Deep physical insight | High computational cost |
| EL modelling ignoring p–p interactions | Slurry erosion of pipeline components | Information at the particle scale Affordable computational cost | Low concentration only Uncertainty due to erosion model and other modelling features |
| Two-fluid modelling based on KTGF | Particle transport in pipes | Strong physical basis Affordable computational cost | Several difficult-to-set coefficients, sub-models, and parameters |
| Two-fluid modelling not based on KTGF | Particle transport in pipes | Simple mathematical structure Computationally efficient | Weak physical basis Limited applicability |
| Mixture modelling | Particle transport in pipes | Low computational cost Multiple solid phases allowed | Stringent assumptions on flow (local equilibrium approximation) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Messa, G.V.; Yang, Q.; Adedeji, O.E.; Chára, Z.; Duarte, C.A.R.; Matoušek, V.; Rasteiro, M.G.; Sanders, R.S.; Silva, R.C.; de Souza, F.J. Computational Fluid Dynamics Modelling of Liquid–Solid Slurry Flows in Pipelines: State-of-the-Art and Future Perspectives. Processes 2021, 9, 1566. https://doi.org/10.3390/pr9091566
Messa GV, Yang Q, Adedeji OE, Chára Z, Duarte CAR, Matoušek V, Rasteiro MG, Sanders RS, Silva RC, de Souza FJ. Computational Fluid Dynamics Modelling of Liquid–Solid Slurry Flows in Pipelines: State-of-the-Art and Future Perspectives. Processes. 2021; 9(9):1566. https://doi.org/10.3390/pr9091566
Chicago/Turabian StyleMessa, Gianandrea Vittorio, Qi Yang, Oluwaseun Ezekiel Adedeji, Zdeněk Chára, Carlos Antonio Ribeiro Duarte, Václav Matoušek, Maria Graça Rasteiro, R. Sean Sanders, Rui C. Silva, and Francisco José de Souza. 2021. "Computational Fluid Dynamics Modelling of Liquid–Solid Slurry Flows in Pipelines: State-of-the-Art and Future Perspectives" Processes 9, no. 9: 1566. https://doi.org/10.3390/pr9091566
APA StyleMessa, G. V., Yang, Q., Adedeji, O. E., Chára, Z., Duarte, C. A. R., Matoušek, V., Rasteiro, M. G., Sanders, R. S., Silva, R. C., & de Souza, F. J. (2021). Computational Fluid Dynamics Modelling of Liquid–Solid Slurry Flows in Pipelines: State-of-the-Art and Future Perspectives. Processes, 9(9), 1566. https://doi.org/10.3390/pr9091566








