Optimal Design of IPMSM for EV Using Subdivided Kriging Multi-Objective Optimization
Abstract
:1. Introduction
2. Proposed Algorithm
2.1. Latin Hypercube Sampling
2.2. Surrogate Model Creation
2.3. Non-Dominated Sorting
2.4. Euclidean Distance Calculation
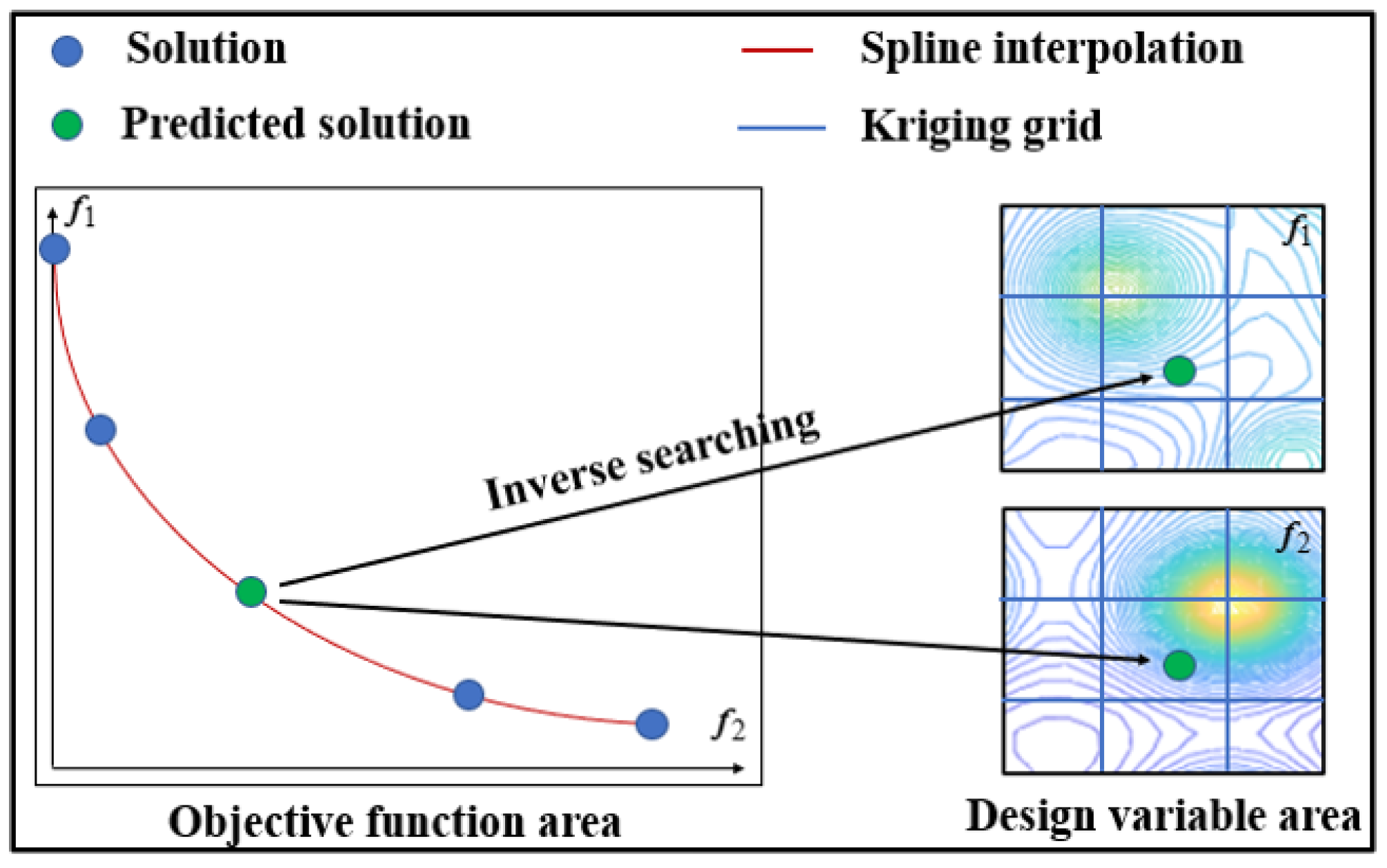
2.5. Inverse Searching
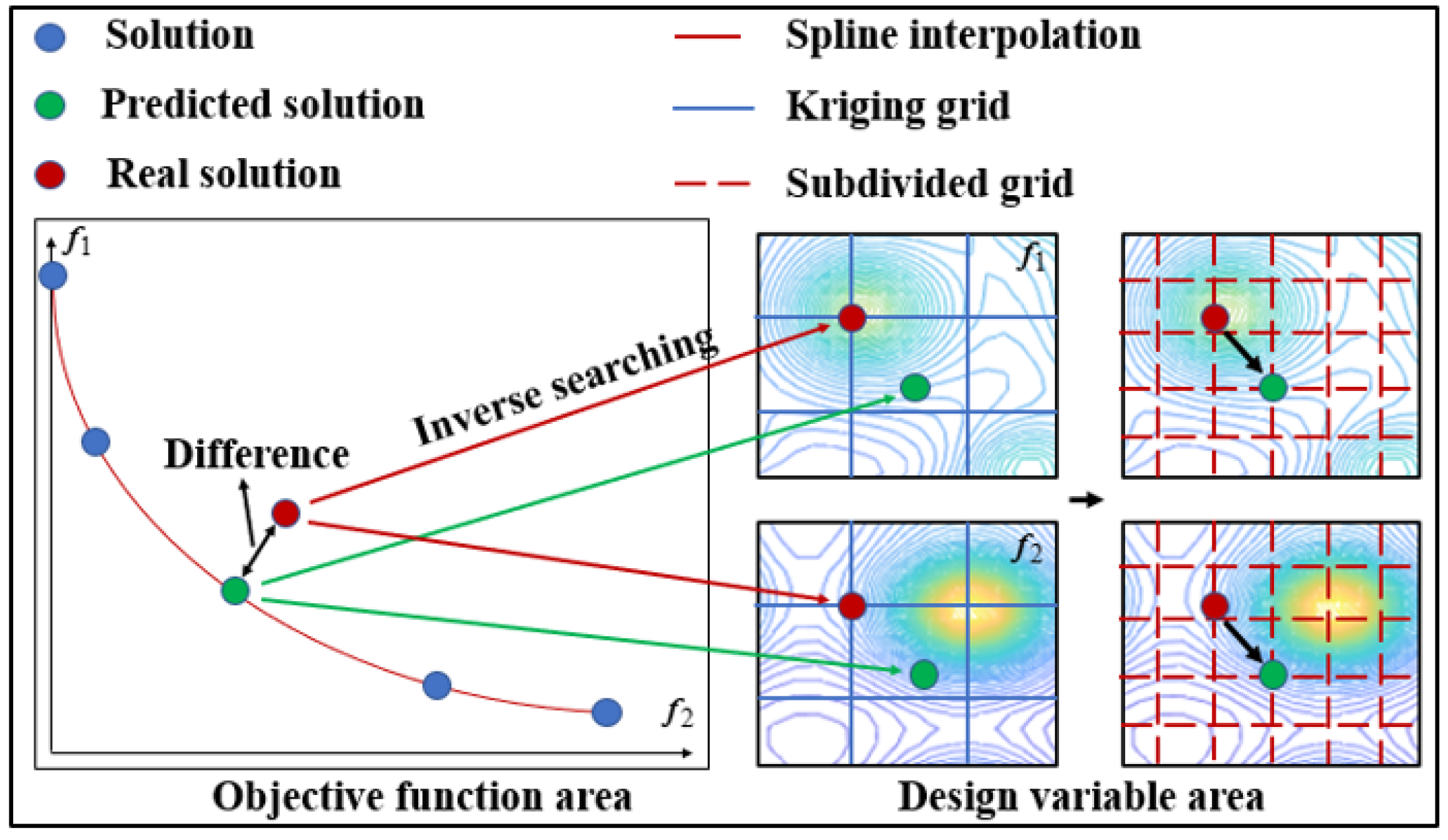
2.6. Subdivided Kriging Grid
2.7. Fill Blank Method
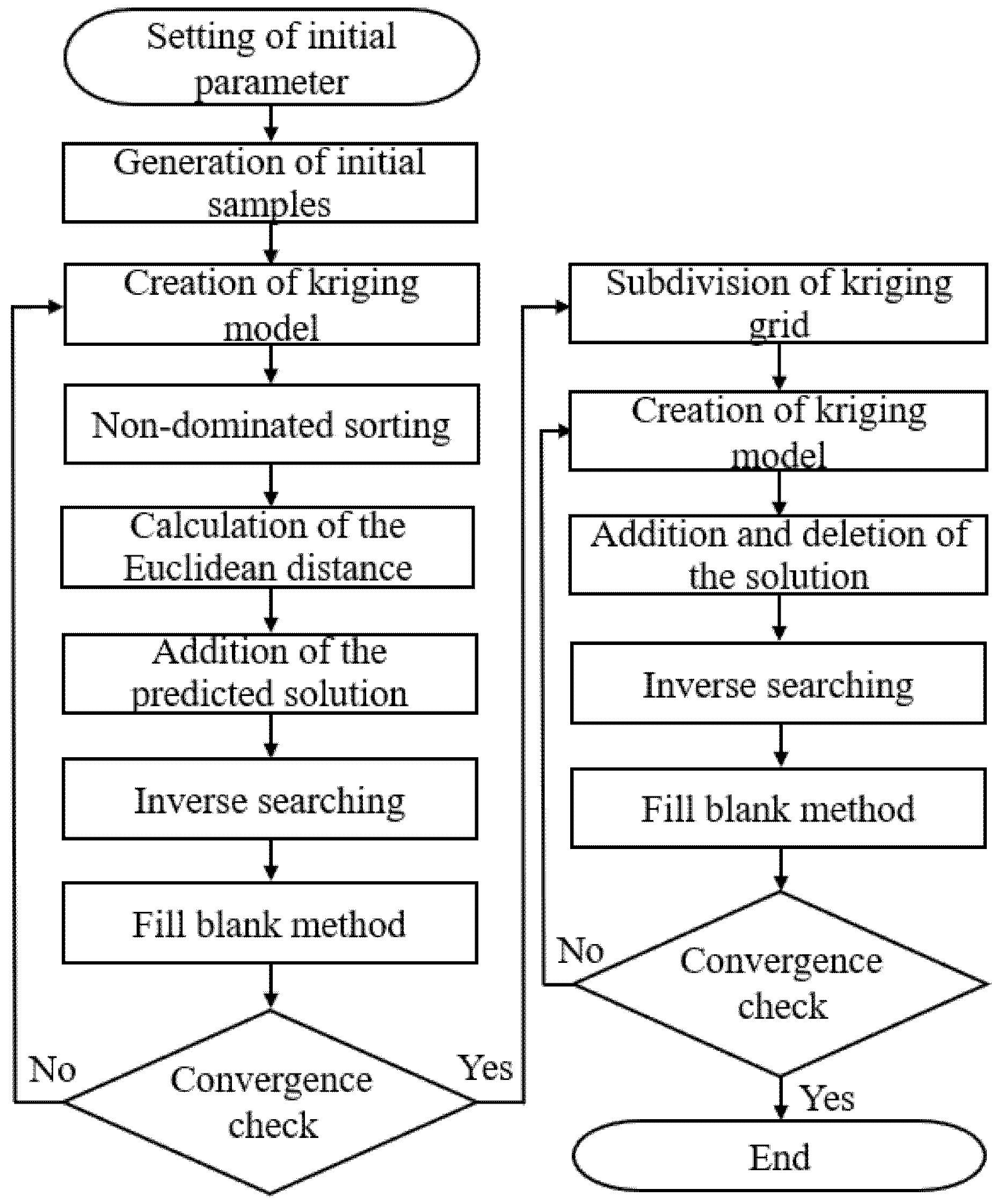
2.8. Flow Chart of the SKMOO
3. Verification of Proposed Algorithm
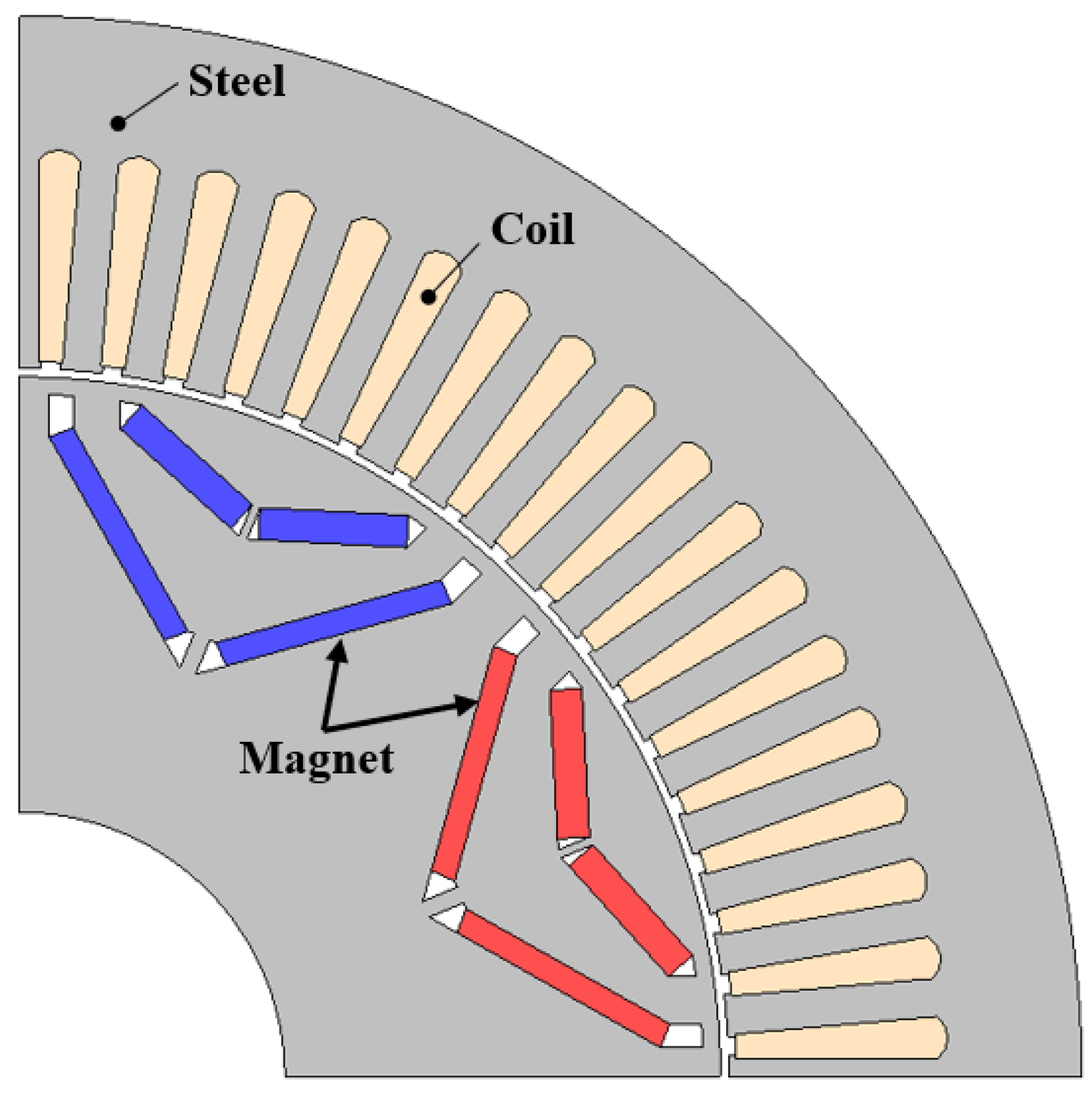
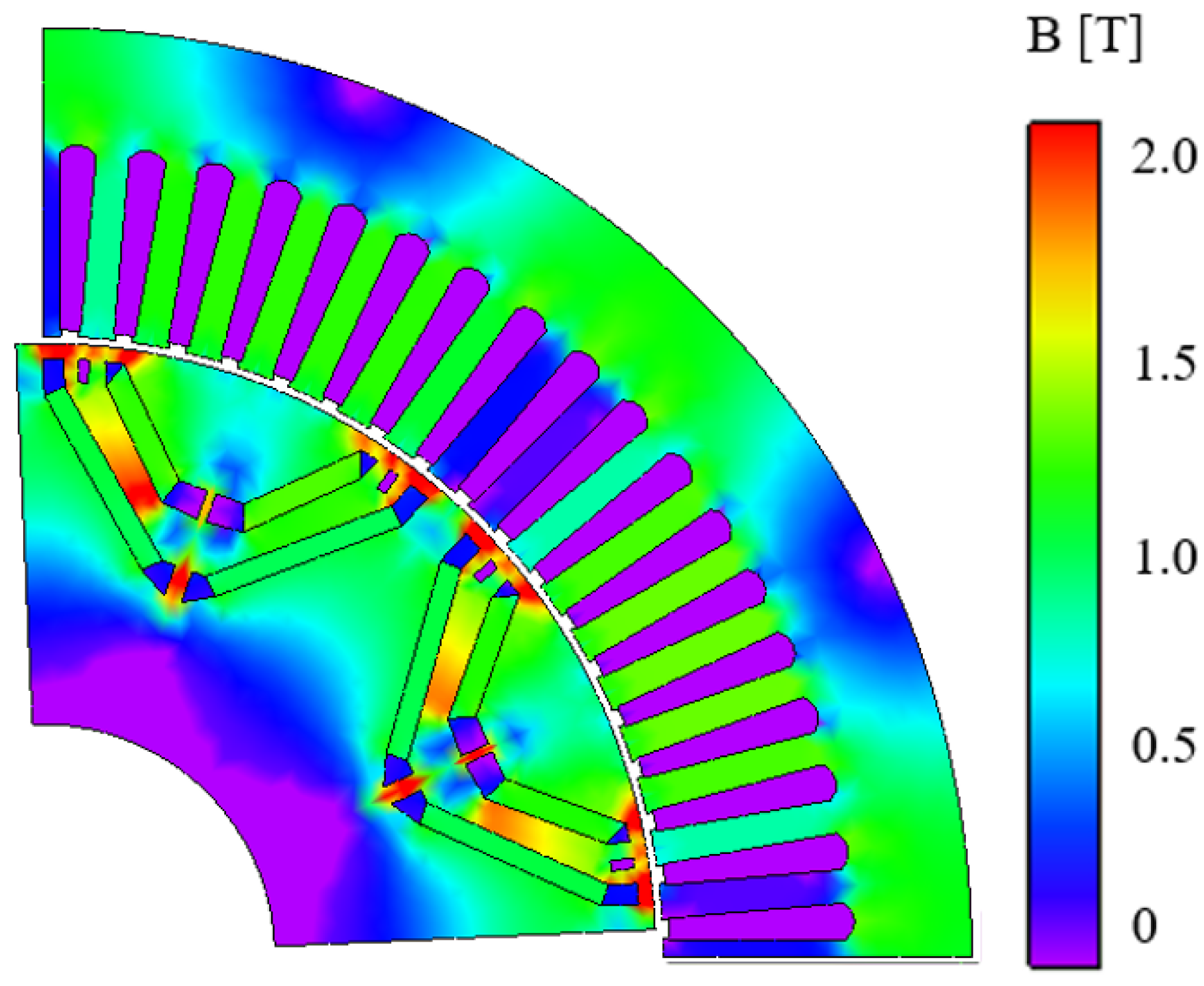
4. Optimal Design of IPMSM for EV
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhang, Z.; Liu, H.; Song, T.; Zhang, Q.; Hu, W.; Liu, W. Performance evaluation of a 60kW IPM motor for medium commercial EV traction application. CES Trans. Electr. Mach. Syst. 2019, 3, 195–203. [Google Scholar] [CrossRef]
- Sun, X.; Shi, Z.; Cai, Y.; Lei, G.; Guo, Y.; Zhu, J. Driving-Cycle-Oriented Design Optimization of a Permanent Magnet Hub Motor Drive System for a Four-Wheel-Drive Electric Vehicle. IEEE Trans. Transp. Electrif. 2020, 6, 1115–1125. [Google Scholar] [CrossRef]
- Zhang, W.; Huang, S.; Gao, J.; Li, R.; Dai, L. Electromagnetic Torque Analysis for All-Harmonic-Torque Permanent Magnet Synchronous Motor. IEEE Trans. Magn. 2018, 54, 1–5. [Google Scholar] [CrossRef]
- Liu, X.; Chen, H.; Zhao, J.; Belahcen, A. Research on the Performances and Parameters of Interior PMSM Used for Electric Vehicles. IEEE Trans. Ind. Electron. 2016, 63, 3533–3545. [Google Scholar] [CrossRef]
- Shi, Z. Torque Analysis and Dynamic Performance Improvement of a PMSM for EVs by Skew Angle Optimization. IEEE Trans. Appl. Supercond. 2019, 29, 1–5. [Google Scholar] [CrossRef]
- Chottiyanont, P.; Konghirun, M.; Lenwari, W. Genetic algorithm based speed controller design of IPMSM drive for EV. In Proceedings of the 2014 11th International Conf. Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology, Nakhon Ratchasima, Thailand, 14–17 May 2014; pp. 1–5. [Google Scholar]
- Hong, Y.; Wei, T.; Ding, X. Multi-Objective Optimal Design of Permanent Magnet Synchronous Motor for High Efficiency and High Dynamic Performance. IEEE Access 2018, 6, 23568–23581. [Google Scholar] [CrossRef]
- Kang, Y.-R.; Son, J.-C.; Lim, D.-K. Optimal Design of IPMSM for Fuel Cell Electric Vehicles Using Autotuning Elliptical Niching Genetic Algorithm. IEEE Access 2020, 8, 117405–117412. [Google Scholar] [CrossRef]
- Caruso, M.; di Tommaso, A.O.; Ferraris, L.; Miceli, R.; Viola, F. Finite-element performance comparison of IPMSMs with unsymmetrical double-layer windings. In Proceedings of the 2017 Twelfth International Conf. Ecological Vehicles and Renewable Energies (EVER), Monte Carlo, Monaco, 11–13 April 2017; pp. 11–13. [Google Scholar]
- Li, M.; Gabriel, F.; Alkadri, M. Kriging-Assisted Multi-Objective Design of Permanent Magnet Motor for Position Sensorless Control. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- An, S.; Yang, S.; Mohammed, A. A Kriging-Assisted Light Beam Search Method for Multi-Objective Electromagnetic Inverse Problems. IEEE Trans. Magn. 2018, 54, 1–4. [Google Scholar] [CrossRef]
- Alkebsi, K.; Du, W. A Fast Multi-Objective Particle Swarm Optimization Algorithm Based on a New Archive Updating Mechanism. IEEE Trans. Ind. Appl. 2020, 8, 124734–124754. [Google Scholar] [CrossRef]
- Palakonda, V.; Mallipeddi, R. An Evolutionary Algorithm for Multi and Many-Objective Optimization With Adaptive Mating and Environmental Selection. IEEE Access 2020, 8, 82781–82796. [Google Scholar] [CrossRef]
- Reddy, S. Multi-Objective Optimal Power Flow for a Thermal-Wind-Solar Power System. J. Green Eng. 2017, 7, 451–476. [Google Scholar] [CrossRef] [Green Version]
- Reddy, S.; Bijwe, P.R. Differential evolution-based efficient multi-objective optimal power flow. Neural Comput. Appl. 2019, 31, 509–522. [Google Scholar] [CrossRef]
- Reddy, S.; Abhyankar, A.R.; Bijwe, P.R. Reactive power price clearing using multi-objective optimization. Energy 2011, 36, 3579–3589. [Google Scholar] [CrossRef]
- Xu, Q.; Yang, Y.; Liu, Y.; Wang, X. An Improved Latin Hypercube Sampling Method to Enhance Numerical Stability Considering the Correlation of Input Variables. IEEE Access 2017, 5, 15197–15205. [Google Scholar] [CrossRef]
- Bidah, S.; Zakary, O.; Rachik, M. Stability and Global Sensitivity Analysis for an Agree-Disagree Model: Partial Rank Correlation Coefficient and Latin Hypercube Sampling Methods. Int. J. Differ. Equ. 2020, 2020, 14. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; Li, Y.; Liu, L.; Wang, W.; Li, Y.; Cao, Y. Latin Hypercube Sampling Method for Location Selection of Multi-Infeed HVDC System Terminal. Energies 2020, 13, 1646. [Google Scholar] [CrossRef] [Green Version]
- Ma, P.; Zhou, Y.; Shang, X.; Yang, M. Firing Accuracy Evaluation of Electromagnetic Railgun Based on Multicriteria Optimal Latin Hypercube Design. IEEE Trans. Plasma Sci. 2017, 45, 1503–1511. [Google Scholar] [CrossRef]
- Rosli, S.J.; Rahim, H.A.; Abdul Rani, K.N.; Ngadiran, R.; Ahmad, R.B.; Yahaya, N.Z.; Abdulmalek, M.; Jusoh, M.; Yasin, M.N.M.; Sabapathy, T.; et al. A Hybrid Modified Method of the Sine Cosine Algorithm Using Latin Hypercube Sampling with the Cuckoo Search Algorithm for Optimization Problems. Electronics 2020, 9, 1786. [Google Scholar] [CrossRef]
- Lu, C.; Feng, Y.; Fei, C.; Bu, S. Improved Decomposed-Coordinated Kriging Modeling Strategy for Dynamic Probabilistic Analysis of Multicomponent Structures. IEEE Trans. Reliab. 2020, 69, 440–457. [Google Scholar] [CrossRef]
- Gia Pham, T.; Kappas, M.; Van Huynh, C.; Hoang Khanh Nguyen, L. Application of Ordinary Kriging and Regression Kriging Method for Soil Properties Mapping in Hilly Region of Central Vietnam. ISPRS Int. J. Geo-Inf. 2019, 8, 147. [Google Scholar] [CrossRef] [Green Version]
- Qin, S.; Zhang, Y.; Zhou, Y.-L.; Kang, J. Dynamic Model Updating for Bridge Structures Using the Kriging Model and PSO Algorithm Ensemble with Higher Vibration Modes. Sensors 2018, 18, 1879. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Son, J.-C.; Ahn, J.-M.; Lim, J.; Lim, D.-K. Optimal Design of PMa-SynRM for Electric Vehicles Exploiting Adaptive-Sampling Kriging Algorithm. IEEE Access 2021, 9, 41174–41183. [Google Scholar] [CrossRef]
- Premkumar, M.; Jangir, P.; Sowmya, R.; Alhelou, H.H.; Heidari, A.A.; Chen, H. MOSMA: Multi-Objective Slime Mould Algorithm Based on Elitist Non-Dominated Sorting. IEEE Access 2021, 9, 3229–3248. [Google Scholar] [CrossRef]
- Gustavsson, P.; Syberfeldt, A. A New Algorithm Using the Non-Dominated Tree to Improve Non-Dominated Sorting. Evol. Comput. 2018, 26, 89–116. [Google Scholar] [CrossRef]
- Mishra, S.; Mondal, S.; Saha, S.; Coello, C.A.C. GBOS: Generalized Best Order Sort algorithm for non-dominated sorting. Swarm Evol. Comput. 2018, 43, 244–264. [Google Scholar] [CrossRef]
- Lim, D.-K.; Woo, D.-K.; Yeo, H.-K.; Jung, S.-Y.; Ro, J.-S.; Jung, H.-K. A Novel Surrogate-Assisted Multi-Objective Optimization Algorithm for an Electro-magnetic Machine Design. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar]
- Coello, C.A.C.; Pulido, G.T.; Lechuga, M.S. Handling multiple objectives with particle swarm optimization. IEEE Trans. Evol. Comput. 2004, 8, 256–279. [Google Scholar] [CrossRef]
- Kim, W.; Woo, D.K.; Lim, D.K.; Jung, S.Y.; Lee, C.G.; Ro, J.S.; Jung, H.K. Minimization of a cogging torque for an interior permanent magnet synchronous machine using a novel hybrid optimization algorithm. J. Elect. Eng. Technol. 2014, 9, 859–865. [Google Scholar] [CrossRef] [Green Version]
- Lim, D.; Yi, K.; Jung, S.; Jung, H.; Ro, J. Optimal Design of an Interior Permanent Magnet Synchronous Motor by Using a New Surrogate-Assisted Multi-Objective Optimization. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar]
- Wang, Z.; Ching, T.W.; Huang, S.; Wang, H.; Xu, T. Challenges Faced by Electric Vehicle Motors and Their Solutions. IEEE Access 2021, 9, 5228–5249. [Google Scholar]
- Dziadek, P.; Feucht, W.; Mittnacht, A.; Kula, H.; Frank, H. Eco-friendly application of EVs for home-to-work and home-to-education transports. In Proceedings of the 2013 IEEE International Conference on Industrial Technology (ICIT), Cape Town, South Africa, 25–28 February 2013; pp. 705–709. [Google Scholar]
- Jung, Y.-H.; Park, M.-R.; Kim, K.-O.; Chin, J.-W.; Hong, J.-P.; Lim, M.-S. Design of High-Speed Multilayer IPMSM Using Ferrite PM for EV Traction Considering Mechanical and Electrical Characteristics. IEEE Trans. Ind. Appl. 2021, 57, 327–339. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, W.P.; Morrow, J. Interior permanent magnet motor parameter and torque ripple analysis for EV traction. In Proceedings of the 2015 IEEE International Conference on Applied Superconductivity And Electromagnetic Devices (ASEMD), Shanghai, China, 20–23 November 2015; pp. 386–387. [Google Scholar]
- Zhang, B.; Qu, R.; Xu, W.; Li, J. A permanent magnet traction machine with wide high efficiency range for EV application. In Proceedings of the IECON 2015-41st Annual Conference of the IEEE Industrial Electronics Society, Yokohama, Japan, 9–12 November 2015; pp. 000457–000463. [Google Scholar]
- Mun, J.; Park, G.; Seo, S.; Kim, D.; Kim, Y.; Jung, S. Design Characteristics of IPMSM With Wide Constant Power Speed Range for EV Traction. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Lee, J.H.; Song, J.; Kim, D.; Kim, J.; Kim, Y.; Jung, S. Particle Swarm Optimization Algorithm With Intelligent Particle Number Control for Optimal Design of Electric Machines. IEEE Trans. Ind. Electron. 2018, 65, 1791–1798. [Google Scholar] [CrossRef]
- Wu, J.; Wang, J.; Gan, C.; Sun, Q.; Kong, W. Efficiency Optimization of PMSM Drives Using Field-Circuit Coupled FEM for EV/HEV Applications. IEEE Access 2018, 6, 15192–15201. [Google Scholar] [CrossRef]
- Xu, L.; Lin, M.; Fu, X.; Zhu, X.; Zhang, C.; Wu, W. Orthogonal Magnetic Field Analysis of a Double-Stator Linear-Rotary Permanent Magnet Motor With Orthogonally Arrayed Permanent Magnets. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Padilha, J.B.; Kuo-Peng, P.; Sadowski, N.; Batistela, N.J. Vector Hysteresis Model Associated to FEM in a Hysteresis Motor Modeling. IEEE Trans. Magn. 2017, 53, 1–4. [Google Scholar] [CrossRef]
- Zhao, W.; Lipo, T.A.; Kwon, B. Optimal Design of a Novel Asymmetrical Rotor Structure to Obtain Torque and Efficiency Improvement in Surface Inset PM Motors. IEEE Trans. Magn. 2015, 51, 1–4. [Google Scholar]
- Liu, X.; Fu, W.N. A Dynamic Dual-Response-Surface Methodology for Optimal Design of a Permanent-Magnet Motor Using Finite-Element Method. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- Cao, R.; Lu, M. Reduction of Thrust Force Ripple of High Temperature Superconducting Linear Flux-Switching Motors Using Asymmetry Mover Structure. IEEE Trans. Appl. Supercond. 2021, 31, 1–5. [Google Scholar]
- Xing, F.; Kwon, B.-I. Design of a Rotary-Linear Motor With Unipolar SPM and Voice Coil Structure. IEEE Access 2020, 8, 150291–150300. [Google Scholar] [CrossRef]








| Test Function 1 | GD | SP | Function Calls |
| NSGA-II | 0.0634 | 0.5577 | 660 |
| MOPSO | 0.0244 | 0.4297 | 680 |
| SKMOO | 0.0082 | 0.3115 | 502 |
| Test Function 2 | GD | SP | Function Calls |
| NSGA-II | 0.0130 | 1.5110 | 1266.7 |
| MOPSO | 0.0115 | 0.8913 | 1433.3 |
| SKMOO | 0.0078 | 0.2558 | 682.0 |
| Test Function 3 | GD | SP | Function Calls |
| NSGA-II | 0.0112 | 0.1713 | 1580 |
| MOPSO | 0.0077 | 0.1568 | 2130 |
| SKMOO | 0.0056 | 0.0560 | 1022 |
| Test Function 4 | GD | SP | Function Calls |
| NSGA-II | 0.0813 | 0.0800 | 2080 |
| MOPSO | 0.0664 | 0.0944 | 2500 |
| SKMOO | 0.0105 | 0.0439 | 835 |
| Specification | Value |
|---|---|
| Pole/Phase/Slot | 8/3/72 |
| Stator outer diameter | 200 [mm] |
| Stack length | 130.9 [mm] |
| Air gap | 0.8 [mm] |
| Stator and rotor core material | 27PNX1350F |
| Permanent magnet material | N46UH-G_E [Brmin: 1.31T] |
| Rated torque | 285.5 [Nm] |
| Constraint THD/Cogging torque | 5.00 [%]/4.85 [Nm] |
| Rated/Maximum speed | 2850/12,000 [rpm] |
| Model | Initial Model | Optimal Model |
|---|---|---|
| θ1 [°] | 54.17 | 49.23 |
| θ2 [°] | 45.02 | 45.35 |
| H_length [mm] | 0 | 2.44 |
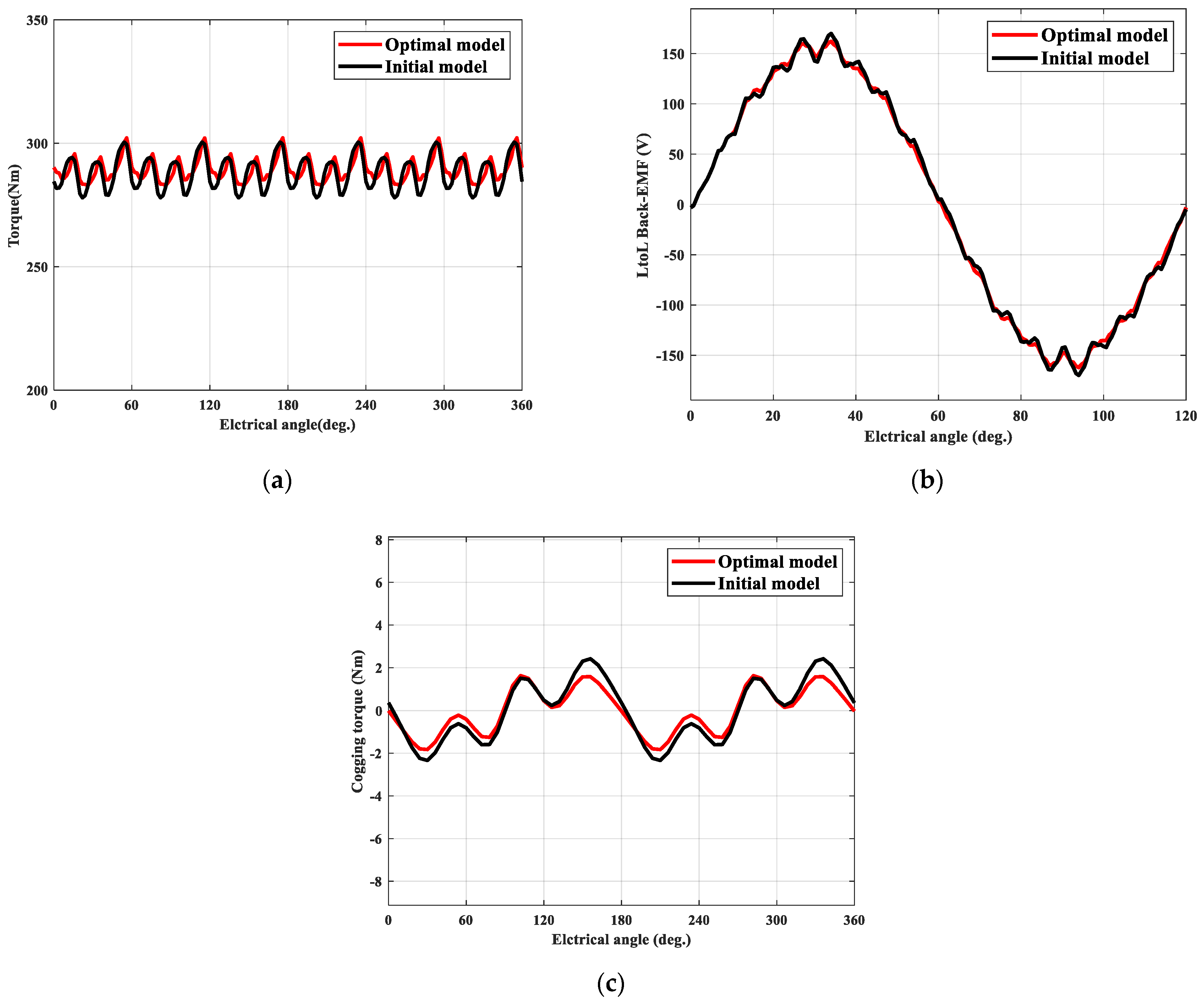
| Average torque [Nm] | 288.15 | 289.50 |
| Back EMF THD [%] | 4.96 | 2.70 |
| Cogging torque [Nm] | 4.75 | 3.45 |
| Specification | Value |
|---|---|
| Young’s modulus (Steel/Magnet) | 200/150 [GPa] |
| Friction coefficient | 0.3 |
| Density (Steel/Magnet) | 7900/7600 [kg/m3] |
| Rotation speed (Rated/Maximum) | 2850/12,000 [rpm] |
| Yield stress of the steel | 450 [MPa] |
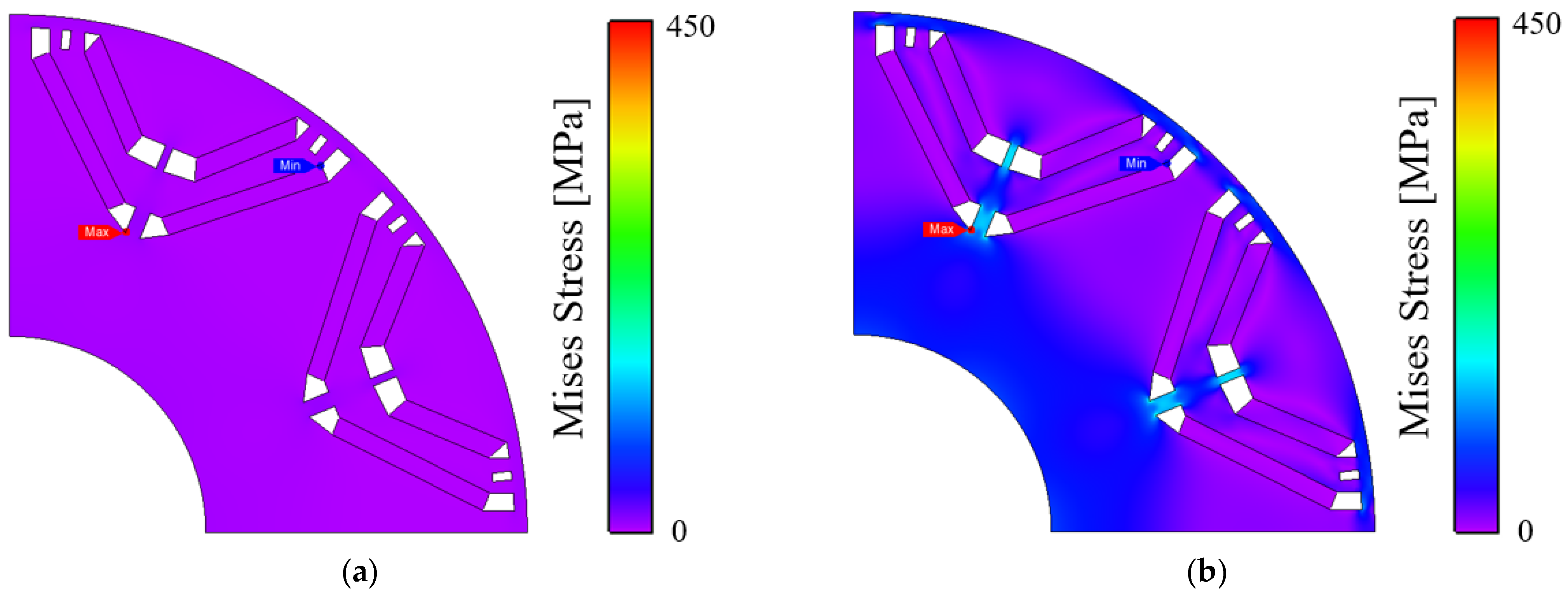
| Rotation Speed | Maximum Von Mises Stress Value |
|---|---|
| 2850 [rpm] | 14.78 [MPa] |
| 12,000 [rpm] | 262.07 [MPa] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahn, J.-M.; Baek, M.-K.; Park, S.-H.; Lim, D.-K. Optimal Design of IPMSM for EV Using Subdivided Kriging Multi-Objective Optimization. Processes 2021, 9, 1490. https://doi.org/10.3390/pr9091490
Ahn J-M, Baek M-K, Park S-H, Lim D-K. Optimal Design of IPMSM for EV Using Subdivided Kriging Multi-Objective Optimization. Processes. 2021; 9(9):1490. https://doi.org/10.3390/pr9091490
Chicago/Turabian StyleAhn, Jong-Min, Myung-Ki Baek, Sang-Hun Park, and Dong-Kuk Lim. 2021. "Optimal Design of IPMSM for EV Using Subdivided Kriging Multi-Objective Optimization" Processes 9, no. 9: 1490. https://doi.org/10.3390/pr9091490
APA StyleAhn, J.-M., Baek, M.-K., Park, S.-H., & Lim, D.-K. (2021). Optimal Design of IPMSM for EV Using Subdivided Kriging Multi-Objective Optimization. Processes, 9(9), 1490. https://doi.org/10.3390/pr9091490






