Simulation Tests of a Cow Milking Machine—Analysis of Design Parameters
Abstract
1. Introduction
2. Materials and Methods
2.1. Simplified Structure of the Vacuum Drop Model
- Linear velocity is the sum of the velocity of the milk/air mixture with coefficient characterising a turbulent flow (1.2 uM) and rise velocity of a single bubble ∞ in a quiescent liquid;
- The reduced air velocity requires the actual conditions to be lowered to normal conditions (a change in pressure causes a change in gas volume);
- The rise velocity of a single bubble in a quiescent liquid is the function of Archimedes (Ar) and Eötvös (Eo) numbers, which, due to the air density, depend on pressure p in the long milk tube;
- Volumetric air coefficient αpdpm in the long milk tube is the quotient of the reduced velocity and linear velocity (calculated relative to the tube walls);
- Pressure in the milking claw is equal to operating pressure po plus drop Δpkol.
- When analysing the value of derivative dv∞/dp for g = 9.81 ms−2, D = 0.016 m, ρm = 1030 kg m−3, T = 288 K, it was found that, for pressure variations ranging from 48,000 to 52,000 Pa, the derivative is approx. 0.5315 × 10−9 and is almost constant. A variation in diameter D does not change this relationship.
- The insensitivity of the rise velocity of a single bubble to pressure variations in the analysed task results from the values of milk and air density. Milk density is ρm = 1030 kg m−3 at 288 ÷ 293 K, whereas air density at 288 K and p = 101.3 kPa is ρp = 1.225 kg m−3 [64]. The ratio of these values is approx. 1000:1. As a result, in terms of the vacuum drops observed in the long milk tube and, thus, in terms of variations in operating pressure po, air velocity v∞ is almost constant.
2.2. Verification of a Model with a Simplified Structure of Vacuum Drops in the Claw
2.3. Sensitivity of a Model with a Simplified Structure of Vacuum Drops in the Claw
3. Results and Discussion
| ***** = [; 0.018; 1.9; 2.2; 49.3; 0.5; 0.03] Qpi = 0.2 + 0.1(i − 1) [m3 h−1], i = 1, …, 9 |
| ***** = [0.4; ; 1.9; 2.2; 49.3; 0.5; 0.03] Di = 0.014 + 0.001(i − 1) [m], i = 1, …, 9 |
| ***** = [0.4; 0.018; ; ; 49.3; 0.5; 0.03] Hi = 0.2 + 0.2(i − 1) [m], i = 1, …, 10 |
| ***** = [0.4; 0.018; 1.9; 2.2; ; 0.5; 0.03] poi = 49 + 1(i − 1) [kPa], i = 1, …, 10 |
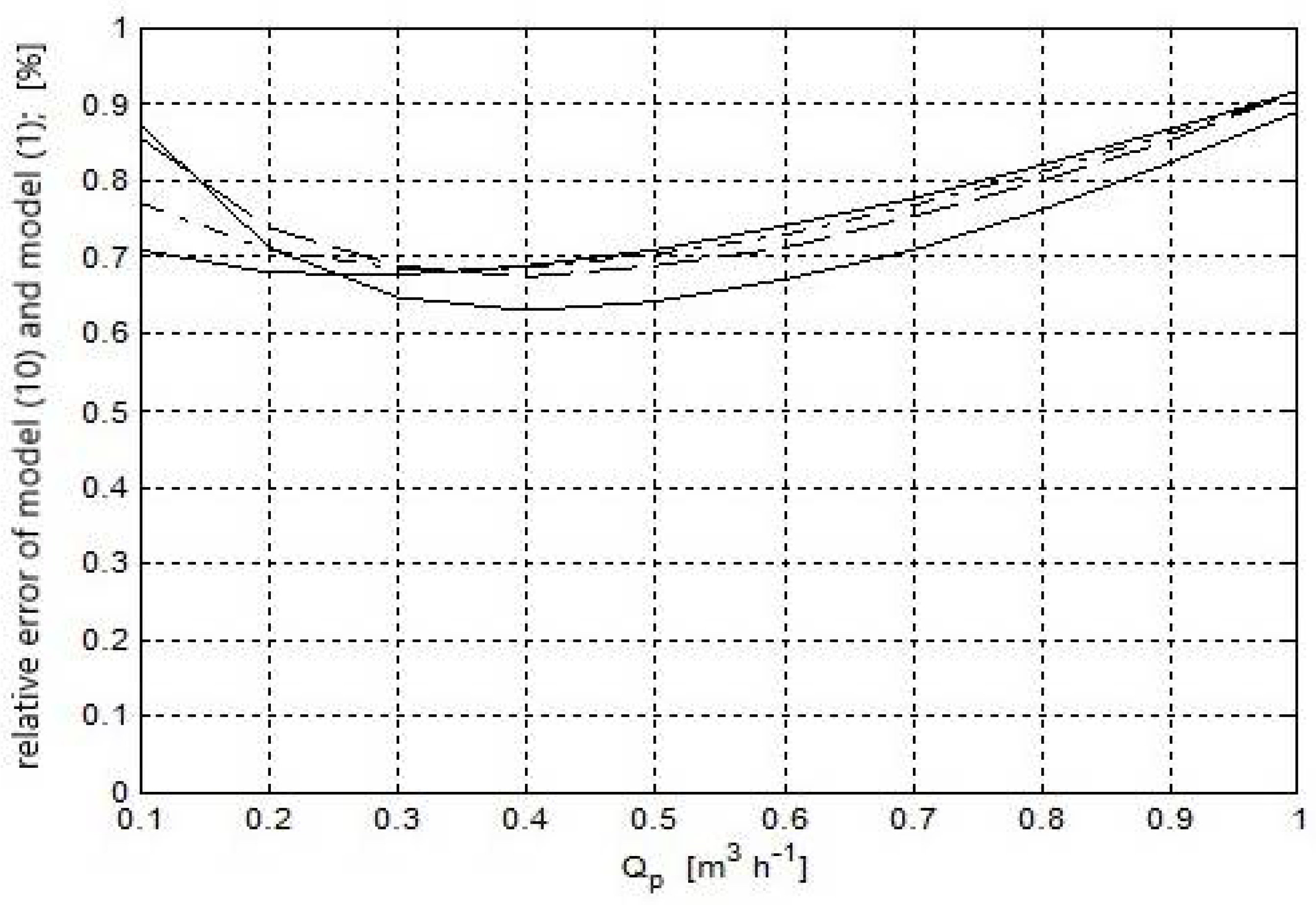
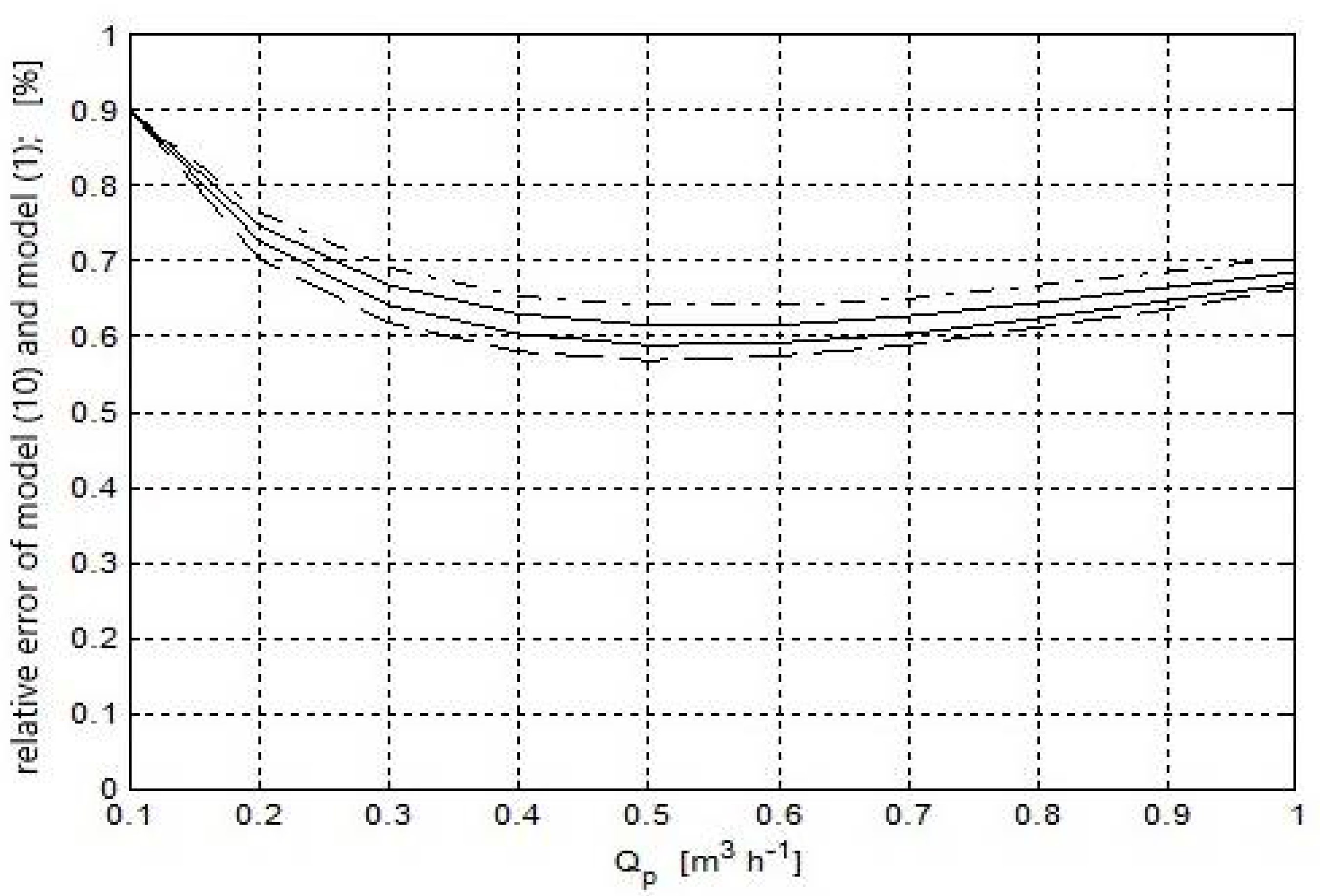
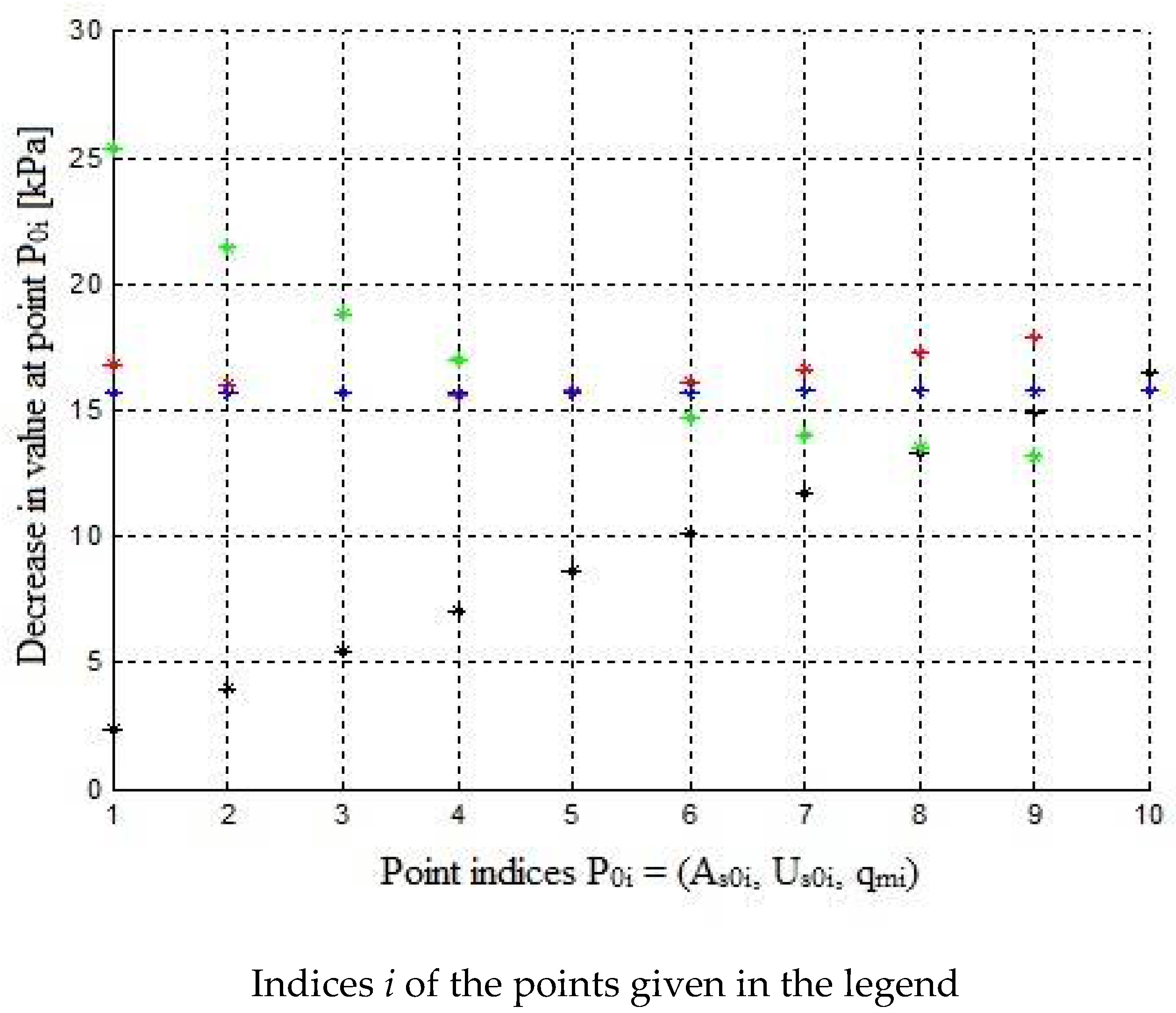
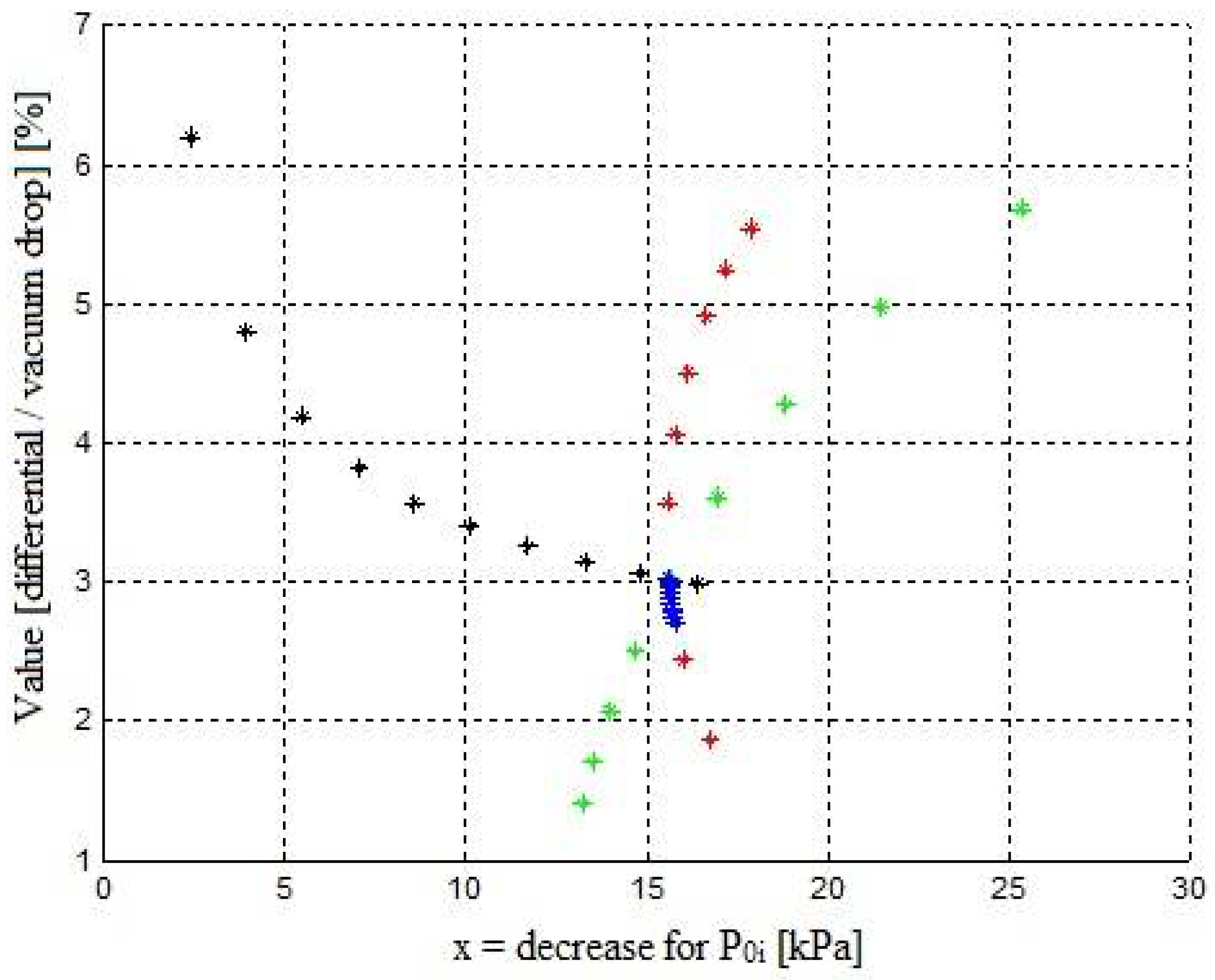
- At lower heads of the milk/air mixture, the model is more sensitive to variations in parameters ζ and λ (Figure 5, black colour).Local mechanical energy losses in the pipes are caused by various obstacles located in the tubes. The values of local loss coefficients ζ should be determined empirically based on measurements; these values are affected by, for example, pipe curvatures, kinks in tubes, an abrupt increase or decrease in the pipe cross-section, etc.Linear loss coefficient λ depends on two parameters: Reynolds number (Re) and relative roughness of a pipe (e), which is a non-dimensional parameter. Relative roughness is defined as: e = k/d, where: k—roughness (equivalent sand-grain roughness); [m], d—inside diameter of a pipe [m]. For isothermal turbulent flows with a practical importance for water supply pipelines (for Re > 4000), the flow can exist in three zones: A—hydraulically smooth piping zone, λ = f(Re), B—transition zone (with variable roughness), λ = f(Re, e), C—quadratic drag zone, λ = f(e);
- An increase in diameter D reduces the sensitivity of the system to a change in parameters (Figure 5, green colour). For the long milk tube diameter of 0.014 m, the sensitivity of the model is approx. 6%;
- A decrease in air flow reduces sensitivity (Figure 5, red colour); the course of vacuum drops as a function of inlet air flux (Figure 5, red colour), which indicates the existence of flux Ω*pi at which the drop is minimal (approx. 15 kPa in the diagram), and the sensitivity of the model around that point is approx. 3%;
- Operating pressure does not alter the sensitivity of the model to changes in parameters ς and λ (Figure 5, blue colour).The analysis presented above applies to point P0i = [0.4; 0.018; 1.9; 2.2; 49.3; 0.5; 0.03].In the entire allowable domain Ω, the nature of the relationship is similar.
4. Summary and Conclusions
- A change in local loss coefficient ς and linear drag coefficient λ in the long milk tube will have a lower impact on vacuum drops if a smaller flux of inlet air Qp, a higher head of the air/liquid mix H, and a higher diameter of the long milk tube D are used;
- Operating pressure does not affect these changes;
- The model is insensitive to changes in parameter T: ten percent changes in temperature T caused changes in the drops to be lower than one percent.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Odorčić, M.; Rasmussen, M.D.; Paulrud, C.O.; Bruckmaier, R.M. Review: Milking machine settings, teat condition and milking efficiency in dairy cows. Animals 2019, 13, S94–S99. [Google Scholar] [CrossRef]
- Gaworski, M.; Kamińska, N.; Kic, P. Evaluation and optimization of milking in some Polish dairy farms differed in milking parlours. Agron. Res. 2017, 15, 112–122. [Google Scholar]
- Chiumenti, A.; da Borso, F.; Chiumenti, R.; Kic, P. Applying a Mathematical Model to Compare, Choose, and Optimize the Management and Economics of Milking Parlors in Dairy Farms. Agriculture 2020, 10, 472. [Google Scholar] [CrossRef]
- Kic, P. Criteria for optimization of milking parlour on dairy farm. In Proceedings of the 14th International Scientific Conference on Engineering for Rural Development, Jelgava, Latvia, 20–22 May 2015; Latvia University of Agriculture: Jelgava, Latvia, 2015; pp. 106–111. [Google Scholar]
- Gaworski, M.; Kic, P. Improvement of mobile milking parlours in small dairy farms including technical and functional aspects. Conference Paper. In Proceedings of the 16th International Scientific Conference Engineering for Rural Development, Jelgava, Latvia, 24–26 May 2017. [Google Scholar] [CrossRef]
- Tremblay, M.; Hess, J.; Christenson, B.; McIntyre, K.; Smink, B.; Kamp, A.; Jong, L.; Döpfer, D. Factors associated with increased milk production for automatic milking systems. J. Dairy Sci. 2016, 99, 3824–3837. [Google Scholar] [CrossRef] [PubMed]
- Pezzuolo, A.; Cillis, D.; Marinello, F.; Sartori, L. Estimating efficiency in automatic milking systems. Eng. Rural Dev. 2017, 16, 736–741. [Google Scholar] [CrossRef]
- Costa, D.; Reinemann, D.; Billon, P. Design Considerations for Milking Machines Used in Brazil. Soc. Eng. Agric. Food Boil. Syst. 2003, 033015. [Google Scholar] [CrossRef]
- Paliy, A.; Aliiev, E.; Paliy, A.; Ishchenko, K.; Shkromada, O.; Musiienko, Y.; Plyuta, L.; Chekan, O.; Dubin, R.; Mohutova, V. Development of a device for cleansing cow udder teats and testing it under industrial conditions. East. Eur. J. Enterp. Technol. 2021, 1, 43–53. [Google Scholar] [CrossRef]
- Nielsen, N.I.; Larsen, T.; Bjerring, M.; Ingvartsen, K.L. Quarter Health, Milking Interval, and Sampling Time During Milking Affect the Concentration of Milk Constituents. J. Dairy Sci. 2005, 88, 3186–3200. [Google Scholar] [CrossRef]
- Borodin, S.A.; Andrianov, E.A.; Andrianov, A.A.; Tertychnaya, T.N. Substantiating Design Parameters of a multi functional milking machine. J. Mech. Contin. Math. Sci. 2020, 176–190. [Google Scholar] [CrossRef]
- Dmytriv, V.; Dmytriv, I.; Lavryk, Y.; Horodeckyy, I. Models of adaptation of the milking machines systems. Contemporary Contemp. Res. Trends Agric. Eng 2018, 10, 7. [Google Scholar] [CrossRef][Green Version]
- Achkevych, V.I.; Khmelevsky, V.S.; Achkevych, O.M. The influence of the design parameters of the milking machine collector on the oscillation of the vacuum pressure in the suction phase. Meh. Electrif. Agric. 2020, 117–123. [Google Scholar] [CrossRef]
- Palii, A.P.; Mihalchenko, S.A.; Chechui, H.F.; Reshetnichenko, A.P.; Rozum, Y.E.; Bredykhin, V.V.; Bogomolov, O.V.; Denicenko, S.A.; Mitiashkina, T.Y.; Sychov, A.I.; et al. Milking and udder health assessment in industrial farming. Ukr. J. Ecol. 2020, 10, 375–381. [Google Scholar]
- Nørstebø, H.; Dalen, G.; Rachah, A.; Heringstad, B.; Whist, A.C.; Nødtvedt, A.; Reksen, O. Factors associated with milking-to-milking variability in somatic cell counts from healthy cows in an automatic milking system. Prev. Vet. Med. 2019, 172, 104786. [Google Scholar] [CrossRef]
- Paliy, A.; Nanka, O.; Ishchenko, K.; Paliy, A. Research on high-yielding dairy cow treatment techniques during milking. Anim. Biol. Anim. Husb. 2019, 11, 1–11. [Google Scholar]
- Hovinen, M.; Pyörälä, S. Invited review: Udder health of dairy cows in automatic milking. J. Dairy Sci. 2011, 94, 547–562. [Google Scholar] [CrossRef]
- Vijayakumar, M.; Park, J.H.; Ki, K.S.; Lim, D.H.; Kim, S.B.; Park, S.M.; Jeong, H.Y.; Park, B.Y.; Kim, T.I. The effect of lactation number, stage, length, and milking frequency on milk yield in Korean Holstein dairy cows using automatic milking system. Asian-Australas J Anim Sci. 2017, 30, 1093–1098. [Google Scholar] [CrossRef]
- Jacobs, J.A.; Siegford, J.M. Invited review: The impact of automatic milking systems on dairy cow management, behavior, health, and welfare. J. Dairy Sci. 2012, 95, 2227–2247. [Google Scholar] [CrossRef] [PubMed]
- Dohmen, W.; Neijenhuis, F.; Hogeveen, H. Relationship between udder health and hygiene on farms with an automatic milking system. J. Dairy Sci. 2010, 93, 4019–4033. [Google Scholar] [CrossRef] [PubMed]
- Achkevych, O.; Achkevych, V.; Bratishko, V.; Potapova, S. Justification of rational design parameters of milking machine for installations with milk line system. Eng. Rural Dev. 2020, 1313–1318. [Google Scholar] [CrossRef]
- Wiercioch, M. Przepływy w Kubku Udojowym Dojarki Mechanicznej. Rozprawa Hab. Ph.D. Thesis, Akademia Rolnicza, Wrocław, Poland, 1994. [Google Scholar]
- Kupczyk, A. Improvement in Milking Conditions with Particular Emphasis on Subatmospheric Pressure in the Milking Unit. Ph.D. Thesis, Institute for Building, Mechanization and Electrification of Agriculture, Warsaw, Poland, 1999. (In Polish). [Google Scholar]
- O’Callaghan, E.J.; Gleeson, D.E. Evaluation of Milking Systems in Terms of Mastitis Risk, Teat Tissue Reactions & Milking Performance, End of Project Reports, Teagasc. 2000. Available online: https://t-stor.teagasc.ie/handle/11019/1403 (accessed on 21 April 2021).
- Pawlak, T.; Szlachta, J.; Luberański, A. The analysis of the effect of changing the volume of the under-teat chamber, rubber elasticity and pulsation type on the size of the return flow in a short milk tube. Electron. J. Pol. Agric. Univ. 2005, 8, 42. Available online: http://www.ejpau.media.pl/volume8/issue4/art-42.html (accessed on 21 April 2021).
- Abeni, F.; Terzano, M.G.; Speroni, M.; Migliorati, L.; Capelletti, M.; Calza, F.; Bianchi, L.; Pirlo, G. Evaluation of milk enzymes and electrolytes, plasma metabolites, and oxidative status in twin cows milked in an automatic milking system or twice daily in a conventional milking parlor. J Dairy Sci. 2008, 91, 3372–3384. [Google Scholar] [CrossRef]
- Besier, J.; Lind, O.; Bruckmaier, R.M. Dynamics of teat-end vacuum during machine milking: Types, causes and impacts on teat condition and udder health—A literature review. J. Appl. Anim. Res. 2015, 44, 263–272. [Google Scholar] [CrossRef]
- Gleeson, D.E.; O’Callaghan, E.J.; Rath, M.V. Effect of liner design, pulsator setting, and vacuum level on bovine teat tissue changes and milking characteristics as measured by ultrasonography. Ir. Vet. J. 2004, 57, 289. [Google Scholar] [CrossRef] [PubMed]
- Penry, J.F.; Upton, J.; Mein, G.A.; Rasmussen, M.D.; Ohnstad, I.; Thompson, P.D.; Reinemann, D.J. Estimating teat canal cross-sectional area to determine the effects of teat-end and mouthpiece chamber vacuum on teat congestion. J. Dairy Sci. 2017, 100, 821–827. [Google Scholar] [CrossRef]
- Wieland, M.; Nydam, D.V.; Virkler, P.D. A longitudinal field study investigating the association between teat-end shape and two minute milk yield, milking unit-on time, and time in low flow rate. Livest. Sci. 2017, 205, 88–97. [Google Scholar] [CrossRef]
- Hamann, J.; Mein, G.A.; Wetzel, S. Teat tissue reactions to milking: Effects of vacuum level. J Dairy Sci. 1993, 76, 1040–1046. [Google Scholar] [CrossRef]
- Enokidani, M.; Kawai, K.; Shinozuka, Y.; Watanabe, A. Milking performance evaluation and factors affecting milking claw vacuum levels with flow simulator. Anim. Sci. J. 2016, 88, 1134–1140. [Google Scholar] [CrossRef] [PubMed]
- Enokidani, M.; Kuruhara, K.; Kawai, K. Analysis of factors affecting milking claw vacuum levels using a simulated milking device. Anim. Sci. J. 2016, 87, 848–854. [Google Scholar] [CrossRef] [PubMed]
- Besier, J.; Bruckmaier, R.M. Vacuum levels and milk-flow-dependent vacuum drops affect machine milking performance and teat condition in dairy cows. J. Dairy Sci. 2016, 99, 3096–3102. [Google Scholar] [CrossRef] [PubMed]
- Stauffer, C.; Feierabend, M.; Bruckmaier, R.M. Different vacuum levels, vacuum reduction during low milk flow, and different cluster detachment levels affect milking performance and teat condition in dairy cows. J. Dairy Sci. 2020, 103, 9250–9260. [Google Scholar] [CrossRef]
- Pařilová, M.; Ježková, A.; Stádník, L.; Štolc, L. Effect of milking vacuum and overmilking on selected milking characteristics. Cattle Res. 2010, 3, 35–42. [Google Scholar]
- Ambord, S.; Bruckmaier, R.M. Milk flowdependent vacuum loss in high-line milking systems: Effects on milking characteristics and teat tissue condition. J. Dairy Sci. 2010, 93, 3588–3594. [Google Scholar] [CrossRef]
- Wiercioch, M.; Luberański, A.; Krzyś, A.; Skalska, D.; Szlachta, J. Impact of the System of Air Supply to a Milking Unit on Selected Parameters of Milking Machine Operation. Agric. Eng. 2016, 20, 195–205. [Google Scholar] [CrossRef][Green Version]
- Ströbel, U.; Rose-Meierhöfer, S.; Öz, H.; Brunsch, R. Development of a control system for the teat-end vacuum in individual quarter milking systems. Sensors 2013, 13, 7633–7651. [Google Scholar] [CrossRef] [PubMed]
- Rasmussen, M.D.; Wiking, L.; Bjerring, M.; Larsen, H.C. Influence of air intake on the concentration of free fatty acids and vacuum fluctuations during automatic milking. J. Dairy Sci. 2006, 89, 4596–4605. [Google Scholar] [CrossRef]
- Demba, S.; Ammon, C.; Rose-Meierhöfer, S. The influence of different milking settings on the measured teat load caused by a collapsing liner. Comput. Electron. Agric. 2018, 153, 54–61. [Google Scholar] [CrossRef]
- Ipema, A.H.; Hogewerf, P.H. Quarter-controlled milking in dairy cows. Comput. Electron. Agric. 2008, 62, 59–66. [Google Scholar] [CrossRef]
- Upton, J.; Reinemann, D.J.; Penry, J.F.; Thompson, P.D. A quarter milking analysis device—Development and demonstration. Biosyst. Eng. 2016, 147, 259–264. [Google Scholar] [CrossRef]
- Wiercioch, M.; Luberański, A.; Szlachta, J.; Skalska, D. Wpływ zakłóceń w instalacji próżniowej dojarki na parametry pracy wybranych pulsatorów. (Influence of disturbances in the milking machine vacuum system on the operating parameters of selected pulsators). Inżynieria Rol. 2011, 8, 285–292. [Google Scholar]
- Lisowski, A. Wpływ pojemności kolektora i średnicy przewodów mlecznych na podciśnienie w komorze podstrzykowej i kolektorze. (Influence of claw capacity and diameter of milk tubes on vacuum in the under-teat chamber and the collector). Przegląd Tech. Rol. I Leśnej 2003, 3, 12–13. [Google Scholar]
- Szlachta, J.; Krzyś, A.; Luberański, A. Modelowanie wpływu parametrów ciśnieniowych na przepływy zwrotne w krótkim przewodzie mlecznym aparatu udojowego. (Modeling the influence of pressure parameters on the return flows in the short milk tube of the milking unit). Inżynieria Rol. 2000, 2, 165–173. [Google Scholar]
- Skalska, D.; Szlachta, J.; Luberański, A. Analiza strumienia masy cieczy oraz obciążenia rurociągu mlecznego na wartość średniego podciśnienia ssania w kubku udojowym dojarki rurociągowej.(Analysis of the liquid mass flow and the load of the milk pipeline on the value of the average vacuum in the teat cup of the pipeline milking machine). Tech. Agrar. 2003, 2, 75–87. [Google Scholar]
- Juszka, H.; Tomasik, M.; Lis, S. Mikroprocesorowy system sterowania pulsacją doju maszynowego krów.( Microprocessor control system for pulsation of machine milking of cows). Inżynieria Rol. 2010, 1, 243–249. [Google Scholar]
- Juszka, H.; Lis, S. Zastosowanie programu Matlab® w modelowaniu podciśnienia w aparacie udojowym. (Application of the Matlab® program in modeling of vacuum in a milking unit). Inżynieria Rol. 2009, 13, 95–100. [Google Scholar]
- Tan, J.; Janni, K.A.; Appleman, R.D. Dynamic variations in vacuum milking systems. Presented at the Summer Meeting, Quebec City, QC, Canada, 25–28 June 1989. [Google Scholar]
- Tan, J.; Janni, K.A.; Stelson, K.A. Mathematical modeling of milking machine vacuum systems. Trans. Am. Soc. Agric. Eng. 1992, 35, 327. [Google Scholar] [CrossRef]
- Tan, J.; Janni, K.A.; Appleman, R.D. Milking system dynamics. 1. Measurement of variation. J. Dairy Sci. 1993, 76, 2195. [Google Scholar] [CrossRef]
- Skalska, D.; Nejman, M.; Wiercioch, M.; Luberański, A.; Krzyś, A. Odporność wybranych aparatów udojowych na wahania podciśnienia w instalacji dojarki rurociąg0owej. (Resistance of selected milking units to vacuum fluctuations in the pipeline milking machine installation). Inżynieria Rol. 2013, 3, 349–359. [Google Scholar]
- Juszka, H.; Lis, S.; Tomasik, M. Modelowanie matematyczne systemu sterowania aparatem udojowym. (Mathematical modeling of the milking unit control system.). Inżynieria Rol. 2006, 2006, 61–67. [Google Scholar]
- Juszka, H.; Lis, S.; Tomasik, M. Modelowanie podciśnienia w kolektorze aparatu udojowego dla krów. (Modeling of vacuum in the claw of milking apparatus for cows). Acta Tech. Agrar. 2006, 5, 81–90. [Google Scholar]
- Lis, S.; Tomasik, M.; Juszka, H. The design of a prototype system which controls the flow of milk in the collector’s column of an autonomous milking apparatus. Contemp. Res. Trends Agric. Eng. 2018, 10, 02016. [Google Scholar] [CrossRef]
- Kupczyk, A.; Gaworski, M.; Szlachta, J.; Tucki, K.; Wojdalski, J.; Luberański, A.; Dróżdż, B.; Krzywonos, M. Slug flow model in a long milk tube for designing a milking unit control system. J. Anim. Plant Sci. 2019, 29, 1238–1246. [Google Scholar]
- Juszka, H.; Tomasik, M.; Lis, S.; Haczyk, G. Sterowanie automatyczne autonomicznym aparatem udojowym. (Automatic control of an autonomous milking unit). Inżynieria Rol. 2011, 4, 99–104. [Google Scholar]
- Luberański, A.; Pruski, K.; Wiercioch, M. Metoda komputerowego wspomagania obliczeń ciśnieniowych parametrów mechanicznego doju i nacisków masujących strzyk. (A method of computer aid for calculating pressure parameters of mechanical milking and pressures that massage a teat). Inżynieria Rol. 2013, 3, 235–242. [Google Scholar]
- Chun, J. Reliability-Based Design Optimization of Structures Using theSecond-Order Reliability Method and Complex-Step Derivative Approximation. Appl. Sci. 2021, 11, 5312. [Google Scholar] [CrossRef]
- Sławik, D. Metody badania wrażliwosci cech sygnałów diagnostycznych. (Methods of studying the sensitivity of the characteristics of diagnostic signals). Politechnika Śląska 2005. Available online: https://delibra.bg.polsl.pl/Content/30996/BCPS_34767_2005_Metody-badania-wrazl_0000.pdf (accessed on 30 July 2021).
- Orzechowski, Z.; Prywer, R.; Zarzycki, R. Mechanika Płynów w Inżynierii Środowiska. (Fluid Mechanics in Environmental Engineering); Wydawnictwo Naukowe PWN: Warszawa, Poland, 2001. [Google Scholar]
- Majkowska, M. Optimization of milking unit performance in mechanical milking machines. Ph.D. Thesis, Warsaw University of Life Sciences, Warsaw, Poland, 2008. (In Polish). [Google Scholar]
- Walden, H. Mechanika Płynów. (Fluid Mechanics); PWN: Warszawa, Poland, 1978. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Golisz, E.; Kupczyk, A.; Majkowska, M.; Trajer, J. Simulation Tests of a Cow Milking Machine—Analysis of Design Parameters. Processes 2021, 9, 1358. https://doi.org/10.3390/pr9081358
Golisz E, Kupczyk A, Majkowska M, Trajer J. Simulation Tests of a Cow Milking Machine—Analysis of Design Parameters. Processes. 2021; 9(8):1358. https://doi.org/10.3390/pr9081358
Chicago/Turabian StyleGolisz, Ewa, Adam Kupczyk, Maria Majkowska, and Jędrzej Trajer. 2021. "Simulation Tests of a Cow Milking Machine—Analysis of Design Parameters" Processes 9, no. 8: 1358. https://doi.org/10.3390/pr9081358
APA StyleGolisz, E., Kupczyk, A., Majkowska, M., & Trajer, J. (2021). Simulation Tests of a Cow Milking Machine—Analysis of Design Parameters. Processes, 9(8), 1358. https://doi.org/10.3390/pr9081358





