Distributed Secondary Control of Islanded Microgrids for Fast Convergence Considering Arbitrary Sampling
Abstract
1. Introduction
- (1)
- The objectives of optimal load sharing and voltage restoration can be achieved simultaneously with a fast convergence rate due to indirect information acquisition from nodes that are multiple hops away and the exclusion of repetitive information. Further, the relevant stability issue is discussed.
- (2)
- Compared with the consensus algorithm, the proposed algorithm shows a superior robustness in cases of asynchronous execution.
- (3)
- The optimal load sharing criteria is derived based on simplifying the problem into a constrained extremum search of the objective function utilizing the Lagrange multiplier method.
2. Problem Formulation
2.1. Control Objective
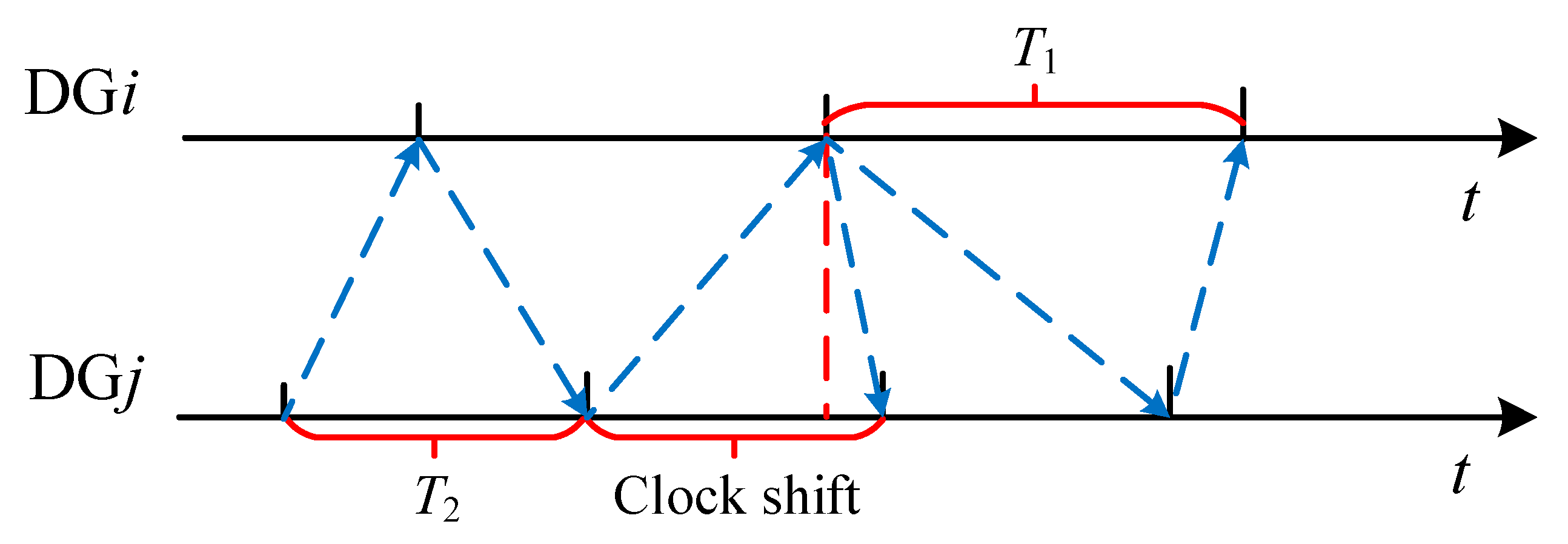
2.2. Inconsistent Information Exchange in Consensus-Based Cooperative Control
3. Fast Convergence Algorithm
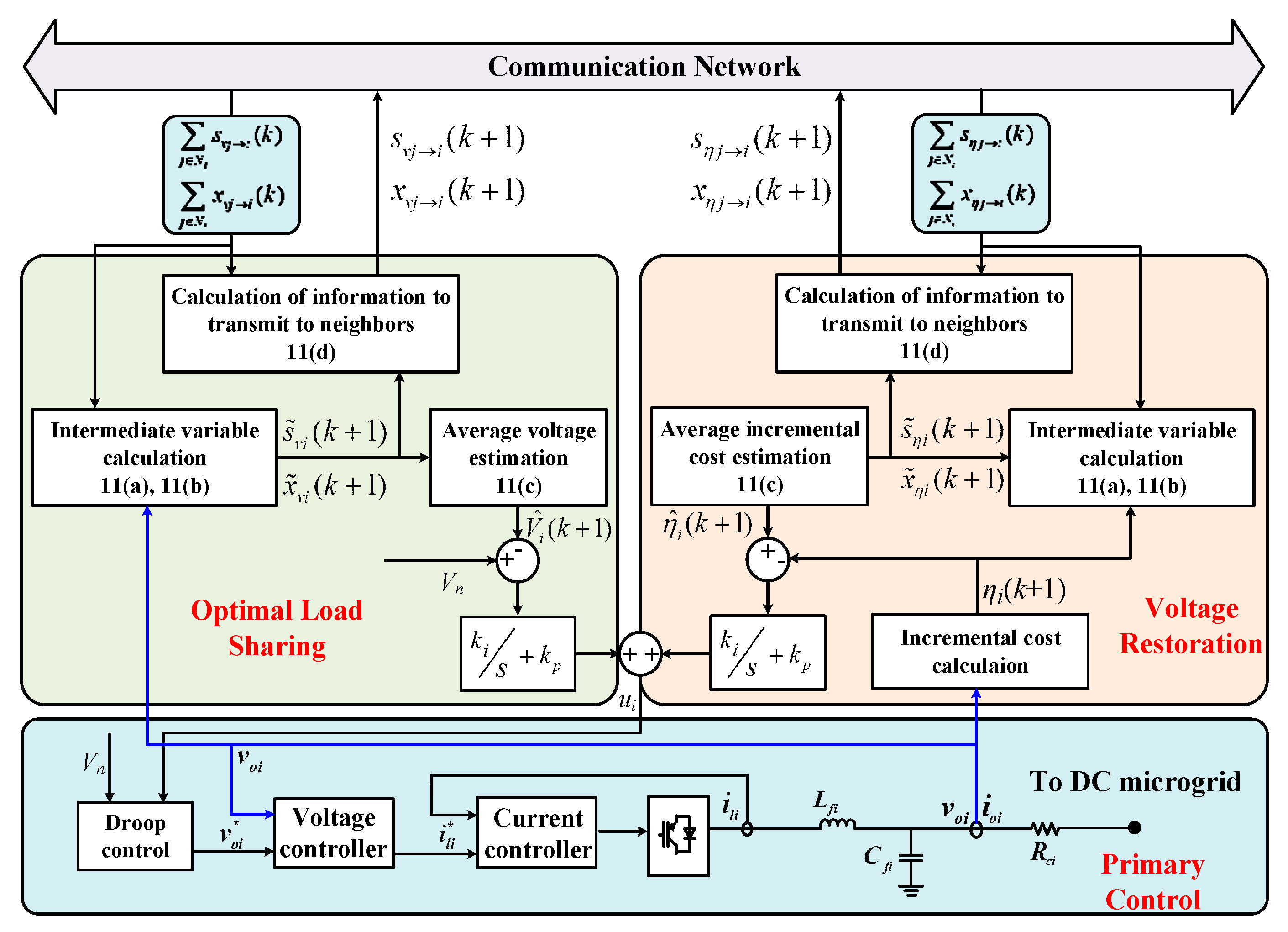
3.1. Cooperative Control Using Fast Convergence Algorithm
| Algorithm 1: Fast convergence algorithm |
| Input: yi and wi are designated as the inputs. Output: The average estimation of yi denoted as is the output. For the kth iteration of the ith DG, execute the following calculation: |
| , (12a) |
| , (12b) |
| (12c) |
| Then, for each neighbor of the ith DG, calculate the following information: |
| , (12d) |
| (12e) |
| and transmit them to the jth DG. |
3.2. Remarks of Algorithm
4. Stability Analysis
5. Simulation Results
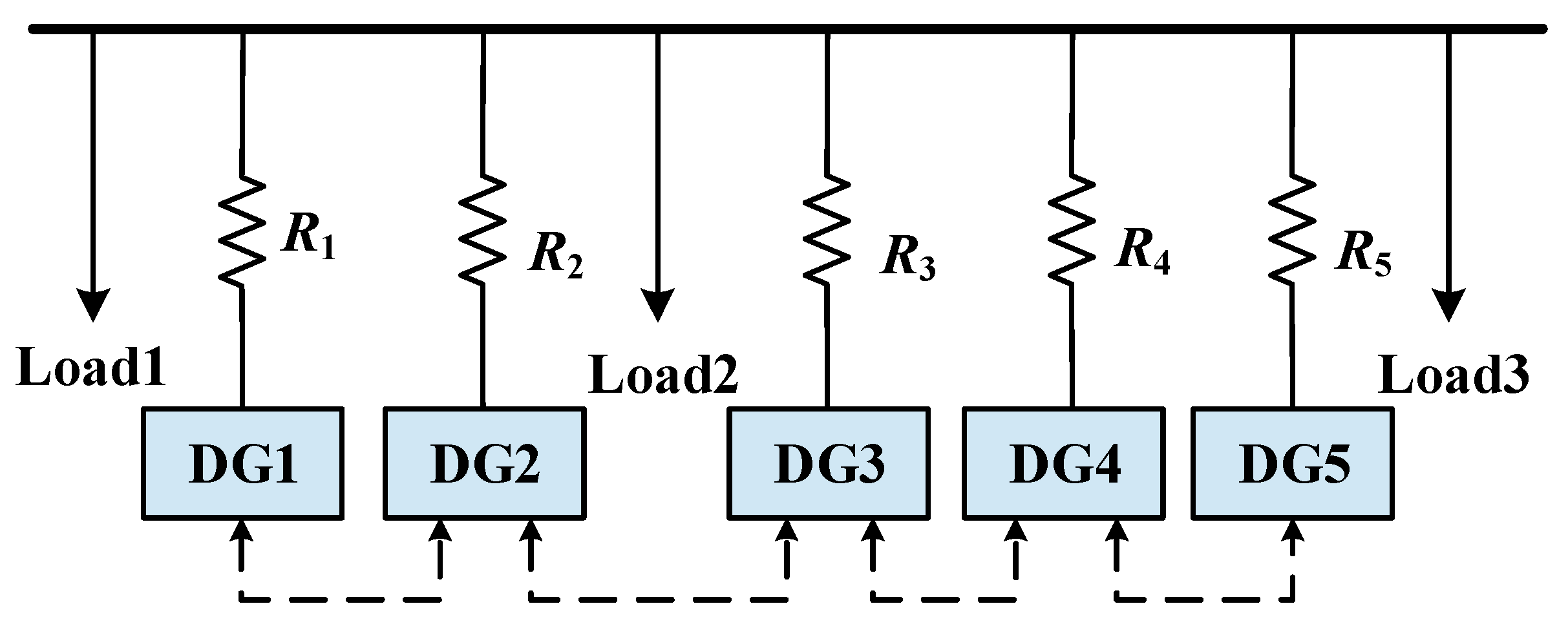
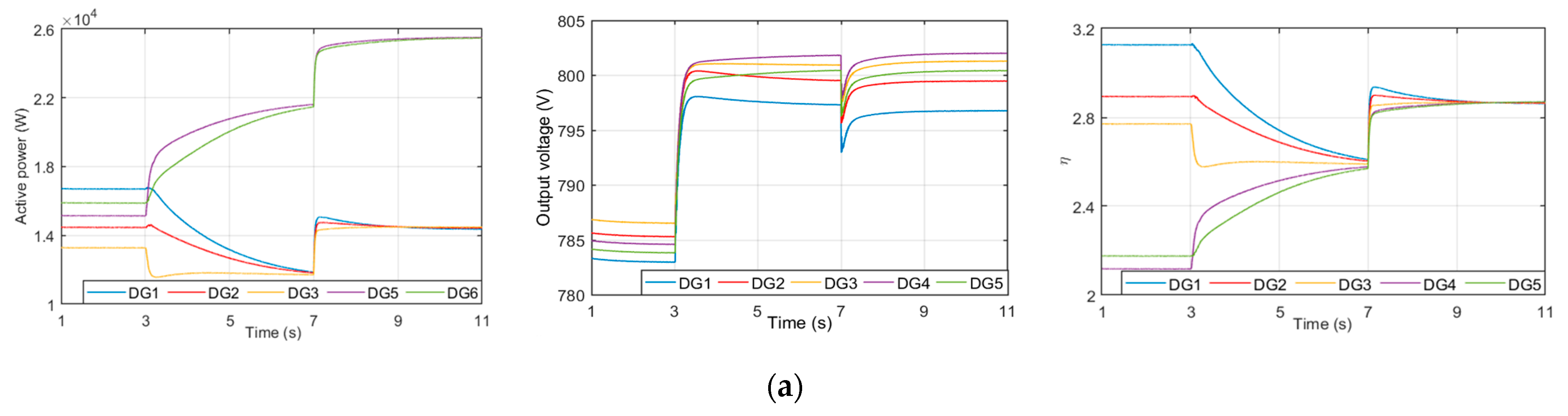
5.1. Conventional Performance
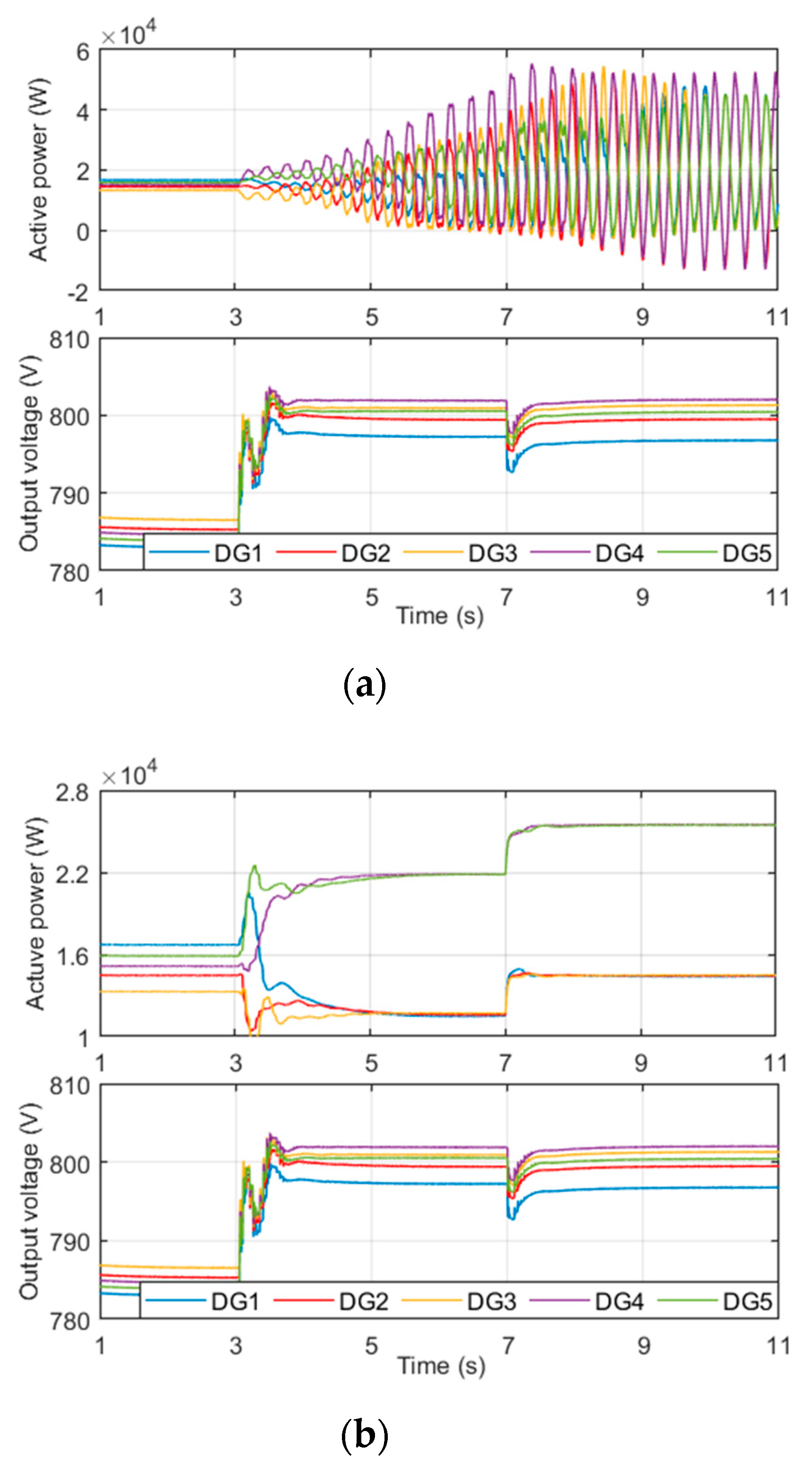
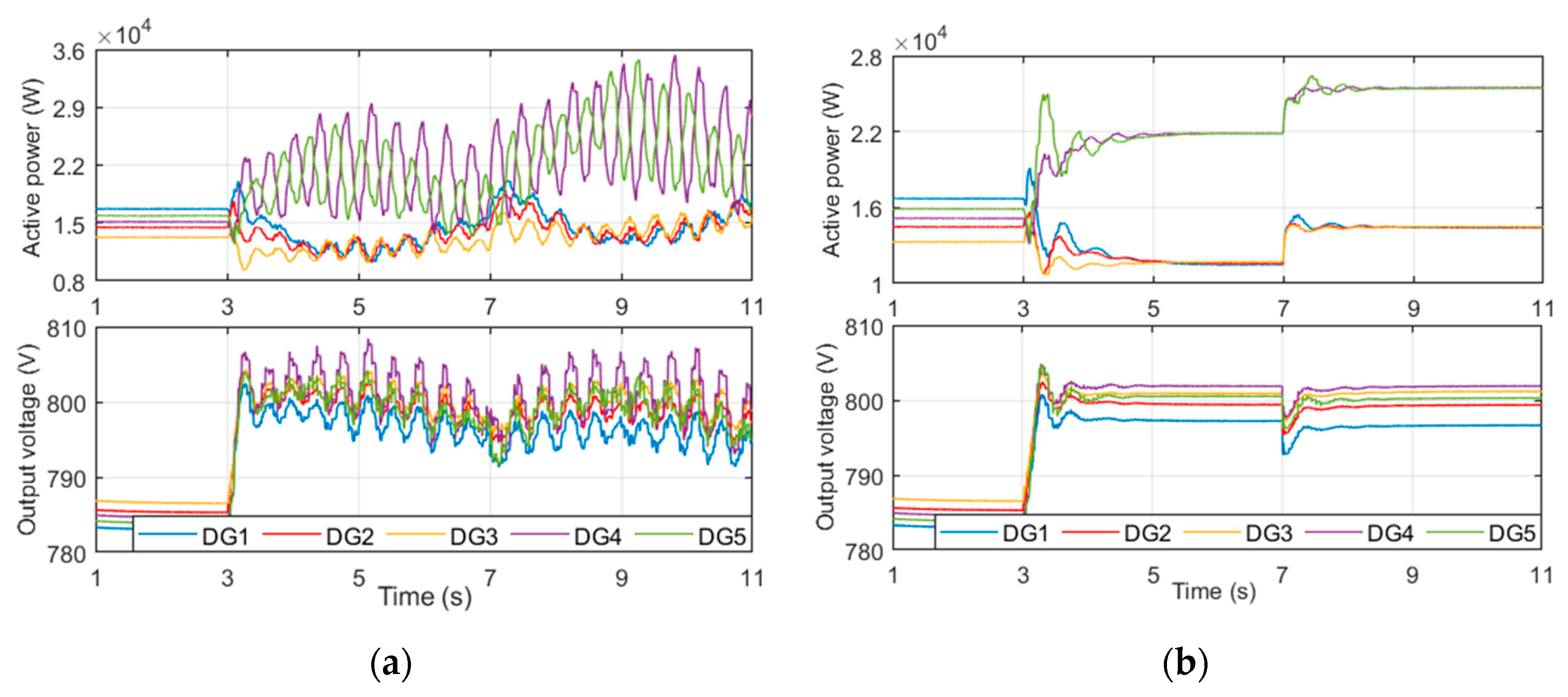
5.2. Arbitrary Sampling
5.3. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Vi | output reference voltage |
| Vrefi | nominal voltage |
| γi | droop coefficient |
| ii | output current |
| ioi | instantaneous current |
| αi, βi, ρi | related coefficients of the cost function |
| ηi | incremental cost |
| average voltage estimated by the ith DG | |
| ui | secondary control input |
| Ti | local sampling interval of the ith DG |
| ki1, ki2, ki3 | integral gains |
| iLi | the ith load current |
| iD | the total load demand |
| wi | weight in the average calculation |
| yi | dynamic state |
| weighted average incremental cost | |
| si→j | scale |
| xi→j | scaled average state estimation |
| sum of the scales | |
| sum of the scaled states | |
| estimated average value |
Abbreviations
| DG | Distributed generations |
| MG | Microgrids |
| MGCC | Microgrid centralized controller |
Appendix A
References
- Schiffer, J.; Seel, T.; Raisch, J.; Sezi, T. Voltage stability and reactive power sharing in inverter-based microgrids with consensus-based distributed voltage control. IEEE Trans. Control. Syst. Technol 2016, 24, 96–109. [Google Scholar] [CrossRef]
- Sadabadi, M.S.; Shafiee, Q.; Karimi, A. Plug-and-play voltage stabilization in inverter-interfaced microgrids via a robust control strategy. IEEE Trans. Control. Syst. Technol. 2017, 25, 781–791. [Google Scholar] [CrossRef]
- Liu, S.; Wang, X.; Liu, P.X. Impact of communication delays on secondary frequency control in an islanded microgrid. IEEE Trans. Ind. Electron. 2015, 62, 2021–2031. [Google Scholar] [CrossRef]
- Qian, T.; Liu, Y.; Zhang, W.; Tang, W.; Shahidehpour, M. Event-triggered updating method in centralized and distributed secondary controls for islanded microgrid restoration. IEEE Trans. Smart Grid 2020, 11, 1387–1395. [Google Scholar] [CrossRef]
- Colet-Subirachs, A.; Ruiz-Alvarez, A.; Gomis-Bellmunt, O.; Alvarez-Cuevas-Figuerola, F.; Sudria-Andreu, A. Centralized and distributed active and reactive power control of a utility connected microgrid using IEC61850. IEEE Syst. J. 2012, 6, 58–67. [Google Scholar] [CrossRef]
- Dou, C.; Yue, D.; Guerrero, J.M.; Xie, X.; Hu, S. Multiagent system-based distributed coordinated control for radial DC microgrid considering transmission time delays. IEEE Trans. Smart Grid 2017, 8, 2370–2381. [Google Scholar] [CrossRef]
- Nasirian, V.; Moayedi, S.; Davoudi, A.; Lewis, F.L. Distributed cooperative control of DC microgrids. IEEE Trans. Power Electron. 2015, 30, 2288–2303. [Google Scholar] [CrossRef]
- Dong, M.; Li, L.; Nie, Y.; Song, D.; Yang, J. Stability analysis of a novel distributed secondary control considering communication delay in DC microgrids. IEEE Trans. Smart Grid 2019, 10, 6690–6700. [Google Scholar] [CrossRef]
- Abdelaziz, M.M.A.; Shaaban, M.F.; Farag, H.E.; El-Saadany, E.F. A multistage centralized control scheme for islanded microgrids with PEVs. IEEE Trans. Sustain. Energy 2014, 5, 927–937. [Google Scholar] [CrossRef]
- Huang, P.; Liu, P.; Xiao, W.; Moursi, M.S.E. A novel droop-based average voltage sharing control strategy for DC microgrids. IEEE Trans. Smart Grid 2015, 6, 1096–1106. [Google Scholar] [CrossRef]
- Wu, X.; Xu, Y.; He, J.; Wang, X.; Vasquez, J.C.; Guerrero, J.M. Pinning-based hierarchical and distributed cooperative control for AC microgrid clusters. IEEE Trans. Power Electron. 2020, 35, 9865–9885. [Google Scholar] [CrossRef]
- Kumar, R.; Pathak, M.K. Distributed droop control of dc microgrid for improved voltage regulation and current sharing. Iet Renew. Power Gen. 2020, 14, 2499–2506. [Google Scholar] [CrossRef]
- Guo, F.; Wang, L.; Wen, C.; Zhang, D.; Xu, Q. Distributed voltage restoration and current sharing control in islanded DC microgrid systems without continuous communication. IEEE Trans. Ind. Electron. 2020, 67, 3043–3053. [Google Scholar] [CrossRef]
- Baranwal, M.; Askarian, A.; Salapaka, S.; Salapaka, M. A distributed architecture for robust and optimal control of DC microgrids. IEEE Trans. Ind. Electron. 2019, 66, 3082–3092. [Google Scholar] [CrossRef]
- Zhang, R.; Hredzak, B. Distributed finite-time multiagent control for DC microgrids with time delays. IEEE Trans. Smart Grid 2019, 10, 2692–2701. [Google Scholar] [CrossRef]
- Lee, G.; Ko, B.; Cho, J.; Kim, R. A distributed control method based on a voltage sensitivity matrix in DC microgrids with low-speed communication. IEEE Trans. Smart Grid 2019, 10, 3809–3817. [Google Scholar] [CrossRef]
- Zhan, J.; Li, X. Asynchronous consensus of multiple double-integrator agents with arbitrary sampling intervals and communication delays. IEEE Trans. Circuits Syst Ireg. Pap. 2015, 62, 2301–2311. [Google Scholar] [CrossRef]
- Fu, J.; Wen, G.; Yu, W.; Huang, T.; Cao, J. Exponential consensus of multiagent systems with Lipschitz nonlinearities using sampled-data information. IEEE Trans. Circuits Syst. Ireg. Pap. 2018, 65, 4363–4375. [Google Scholar] [CrossRef]
- Mattioni, M. On multiconsensus of multi-agent systems under aperiodic and asynchronous sampling. IEEE Contr. Syst. Lett. 2020, 4, 839–844. [Google Scholar]
- Li, Z.; Shahidehpour, M. Small-signal modeling and stability analysis of hybrid AC/DC microgrids. IEEE Trans. Smart Grid 2019, 10, 2080–2095. [Google Scholar] [CrossRef]
- Lou, G.; Gu, W.; Xu, Y.; Jin, W.; Du, X. Stability robustness for secondary voltage control in autonomous microgrids with consideration of communication delays. IEEE Trans. Power Syst. 2018, 33, 4164–4178. [Google Scholar] [CrossRef]
- Coelho, E.A.; Wu, D.; Guerrero, J.M.; Vasquez, J.C.; Dragičević, T.; Stefanović, C.; Popovski, P. Small-signal analysis of the microgrid secondary control considering a communication time delay. IEEE Trans. Ind. Electron. 2016, 63, 6257–6269. [Google Scholar] [CrossRef]
- Duan, J.; Chow, M. Robust consensus-based distributed energy management for microgrids with packet losses tolerance. IEEE Trans. Smart Grid 2020, 11, 281–290. [Google Scholar] [CrossRef]
- Atay, F.M. Consensus in networks under transmission delays and the normalized Laplacian. IFAC Proc. Vol. 2010, 43, 277–282. [Google Scholar] [CrossRef]
- Lai, J.; Lu, X.; Yu, X.; Monti, A.; Zhou, H. Distributed voltage regulation for cyber-physical microgrids with coupling delays and slow switching topologies. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 100–110. [Google Scholar] [CrossRef]
- Du, Y.; Tu, H.; Yu, H.; Lukic, S. Accurate consensus-based distributed averaging with variable time delay in support of distributed secondary control algorithms. IEEE Trans. Smart Grid 2020, 11, 2918–2928. [Google Scholar] [CrossRef]
- Xie, K.; Cai, Q.; Zhang, Z.; Fu, M. Distributed algorithms for average consensus of input data with fast convergence. IEEE Trans. Syst. Man Cybern. Syst. 2021, 51, 2653–2664. [Google Scholar] [CrossRef]
- Guo, G.; Ding, L.; Han, Q.L. A distributed event-triggered transmission strategy for sampled-data consensus of multi-agent systems. Automatica 2014, 50, 1489–1496. [Google Scholar] [CrossRef]
- Baghaee, H.R.; Mirsalim, M.; Gharehpetian, G.B. Real-time verification of new controller to improve small/large-signal stability and fault ride-through capability of multi-DER microgrids. IET Gener. Transm. Distrib. 2016, 10, 3068–3084. [Google Scholar] [CrossRef]
- Baghaee, H.R.; Mirsalim, M.; Gharehpetian, G.B.; Talebi, H.A. Unbalanced harmonic power sharing and voltage compensation of microgrids using radial basis function neural network-based harmonic power-flow calculations for distributed and decentralised control structures. IET Gener. Transm. Distrib. 2018, 12, 1518–1530. [Google Scholar] [CrossRef]
- Baghaee, H.R.; Mirsalim, M.; Gharehpetian, G.B. Power calculation using RBF neural networks to improve power sharing of hierarchical control scheme in multi-DER microgrids. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 1217–1225. [Google Scholar] [CrossRef]



| Parameter | Value | Parameter | Value |
|---|---|---|---|
| MG voltage | 800 V | Generation Cost Coefficient | |
| DG power ratings | α1/α2/α3/α4/α5 | 0.08/0.08/0.08/0.06/0.06 | |
| P1, P2, P3, P4, P5 | 30 kW | β1/β2/β3/β4/β5 | 1.42/1.42/1.42/0.96/0.96 |
| Voltage droop coefficient | Connection and load parameter | ||
| γ1, γ2, γ3, γ4, γ5 | 0.8 V/A | R1/R2/R3 | 0.15 Ω/0.30 Ω/0.40 Ω |
| Control parameters | R4/R5 | 0.25 Ω/ 0.20 Ω | |
| ki1/ki2/ki3 | 6/10/3 | rload1/rload2/rload3 | 25 Ω/20 Ω/30 Ω |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hong, Y.; Xie, J.; Fang, F. Distributed Secondary Control of Islanded Microgrids for Fast Convergence Considering Arbitrary Sampling. Processes 2021, 9, 971. https://doi.org/10.3390/pr9060971
Hong Y, Xie J, Fang F. Distributed Secondary Control of Islanded Microgrids for Fast Convergence Considering Arbitrary Sampling. Processes. 2021; 9(6):971. https://doi.org/10.3390/pr9060971
Chicago/Turabian StyleHong, Yinqiu, Jihua Xie, and Fang Fang. 2021. "Distributed Secondary Control of Islanded Microgrids for Fast Convergence Considering Arbitrary Sampling" Processes 9, no. 6: 971. https://doi.org/10.3390/pr9060971
APA StyleHong, Y., Xie, J., & Fang, F. (2021). Distributed Secondary Control of Islanded Microgrids for Fast Convergence Considering Arbitrary Sampling. Processes, 9(6), 971. https://doi.org/10.3390/pr9060971





