Modelling of Applied Magnetic Field and Thermal Radiations Due to the Stretching of Cylinder
Abstract
:1. Introduction
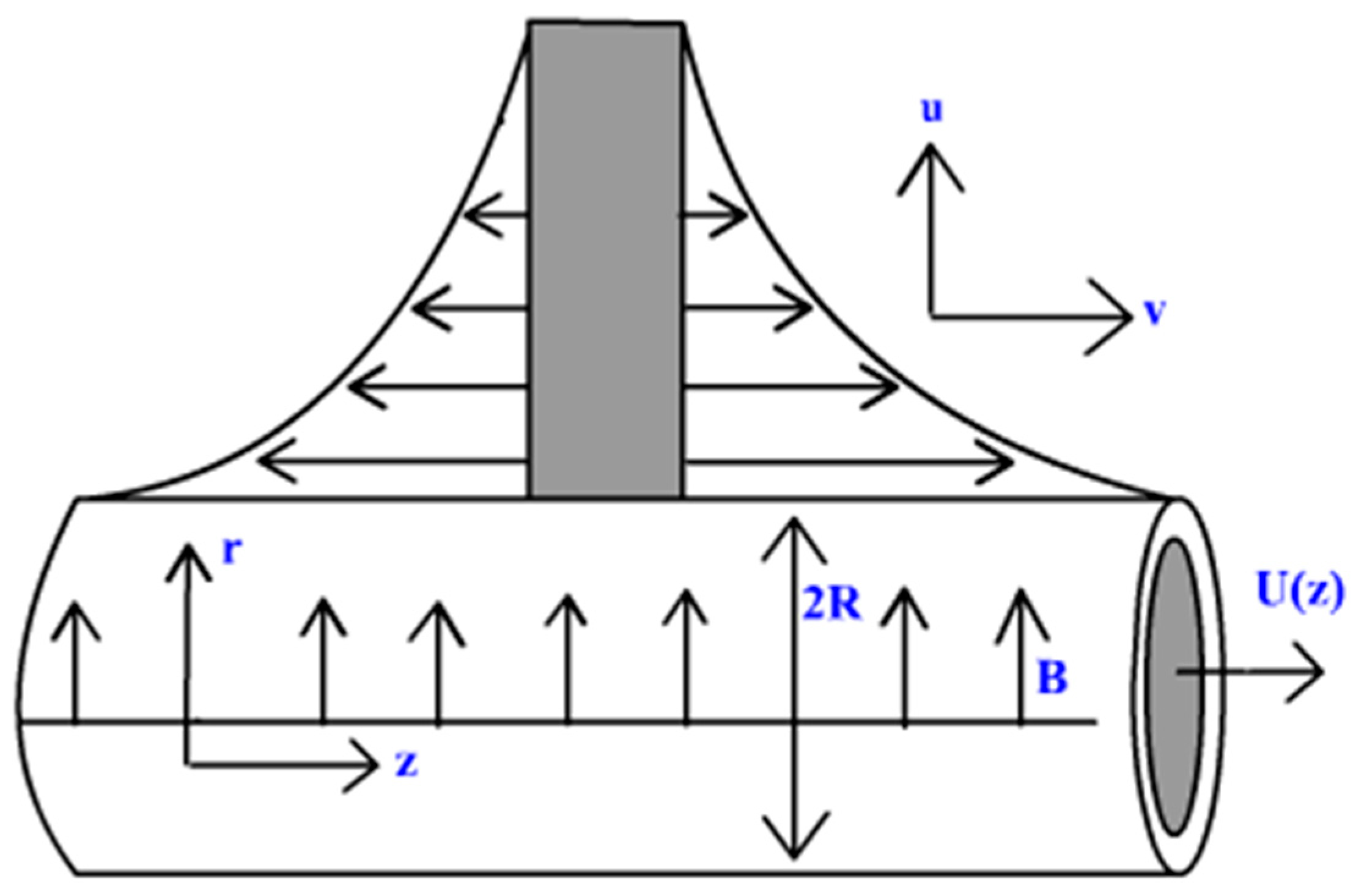
2. Mathematical Formulation
3. Numerical Method
4. Model Validity
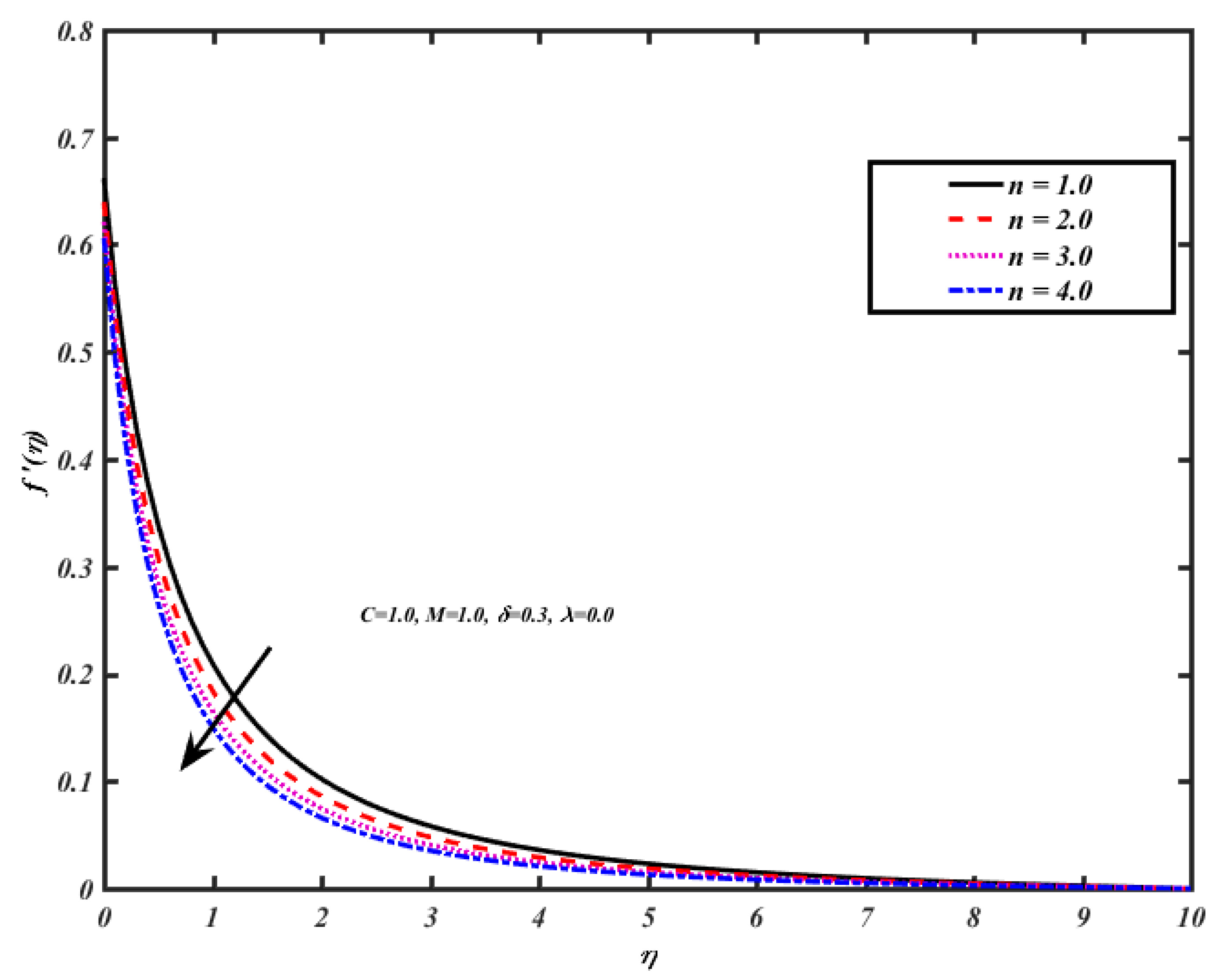
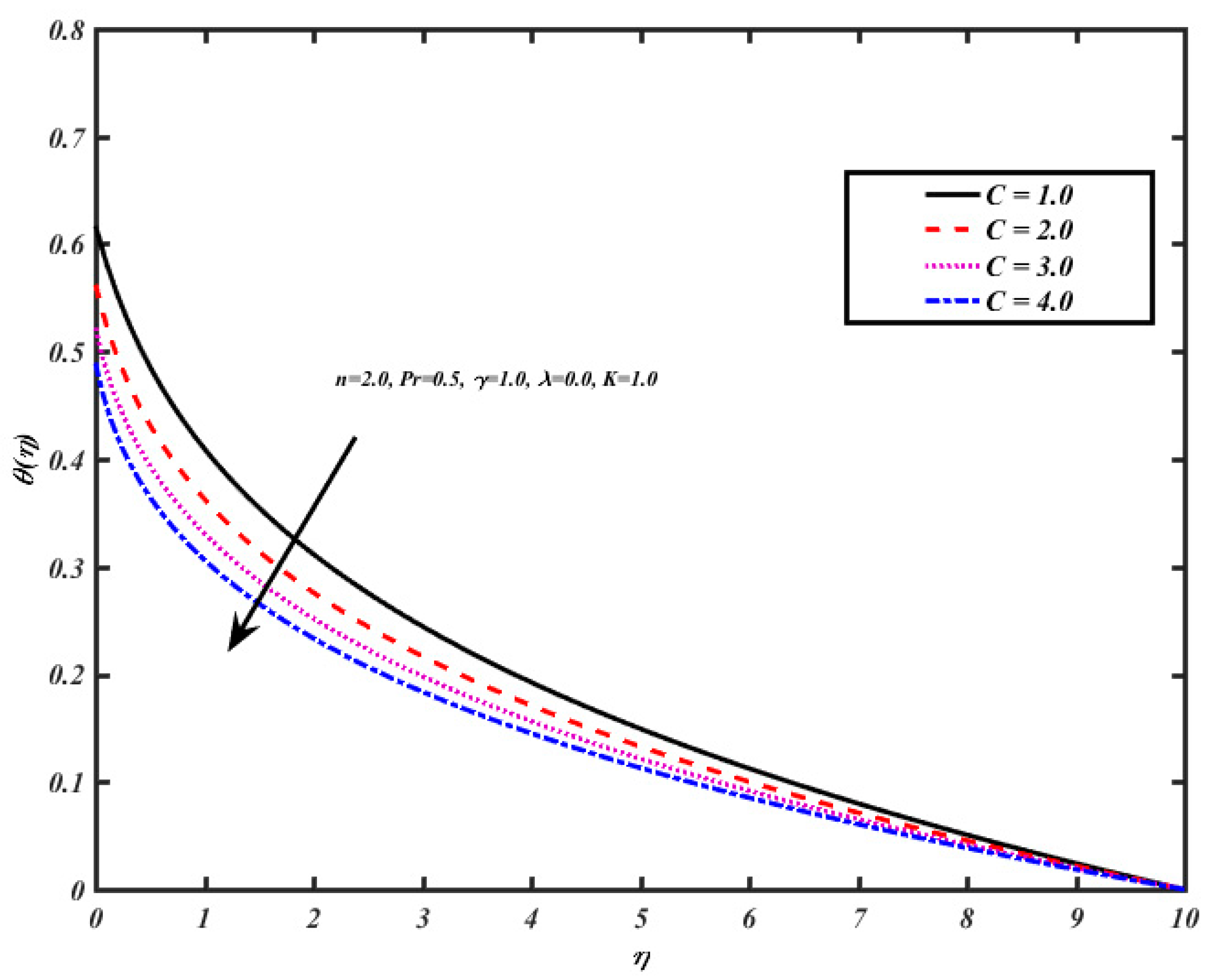
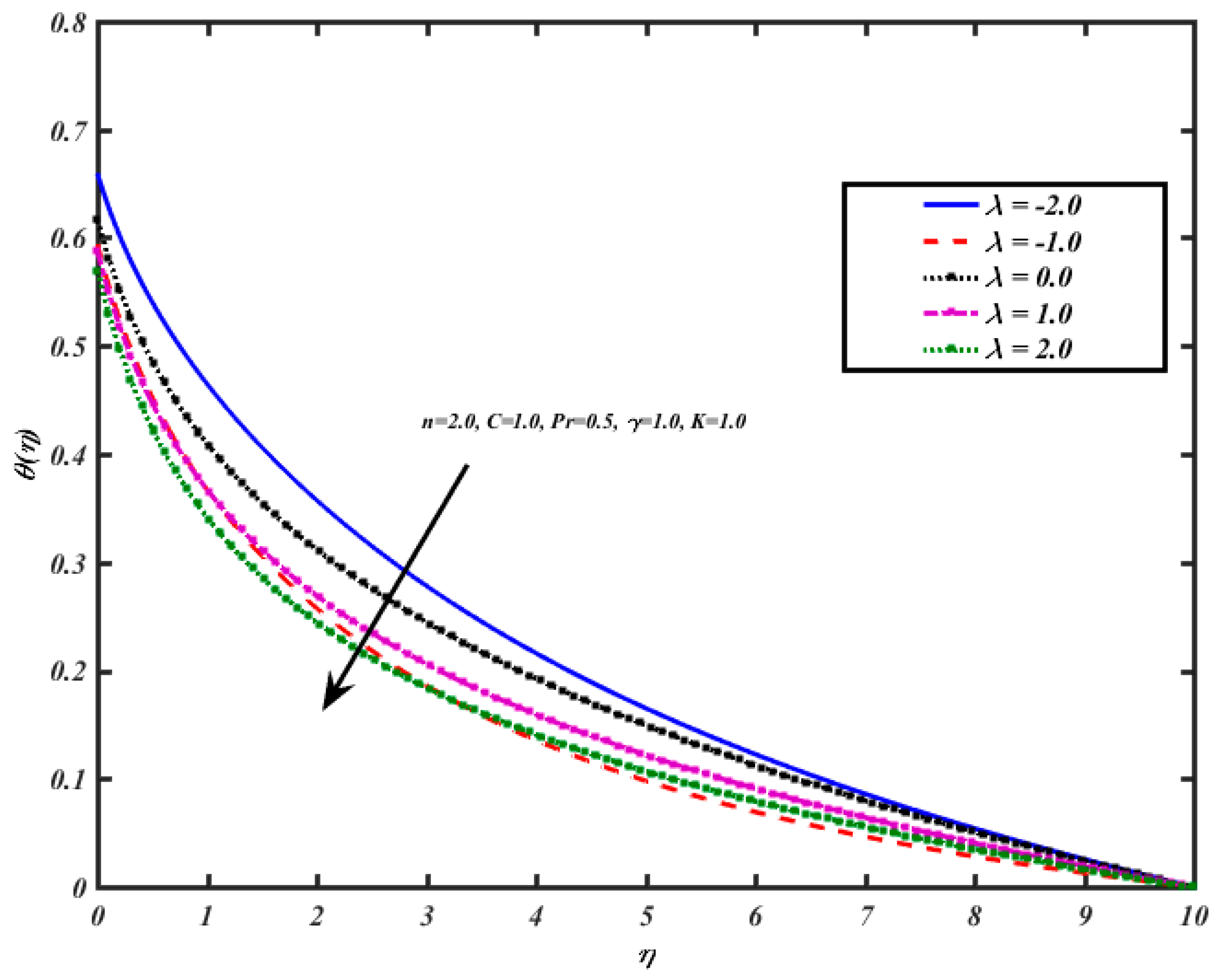
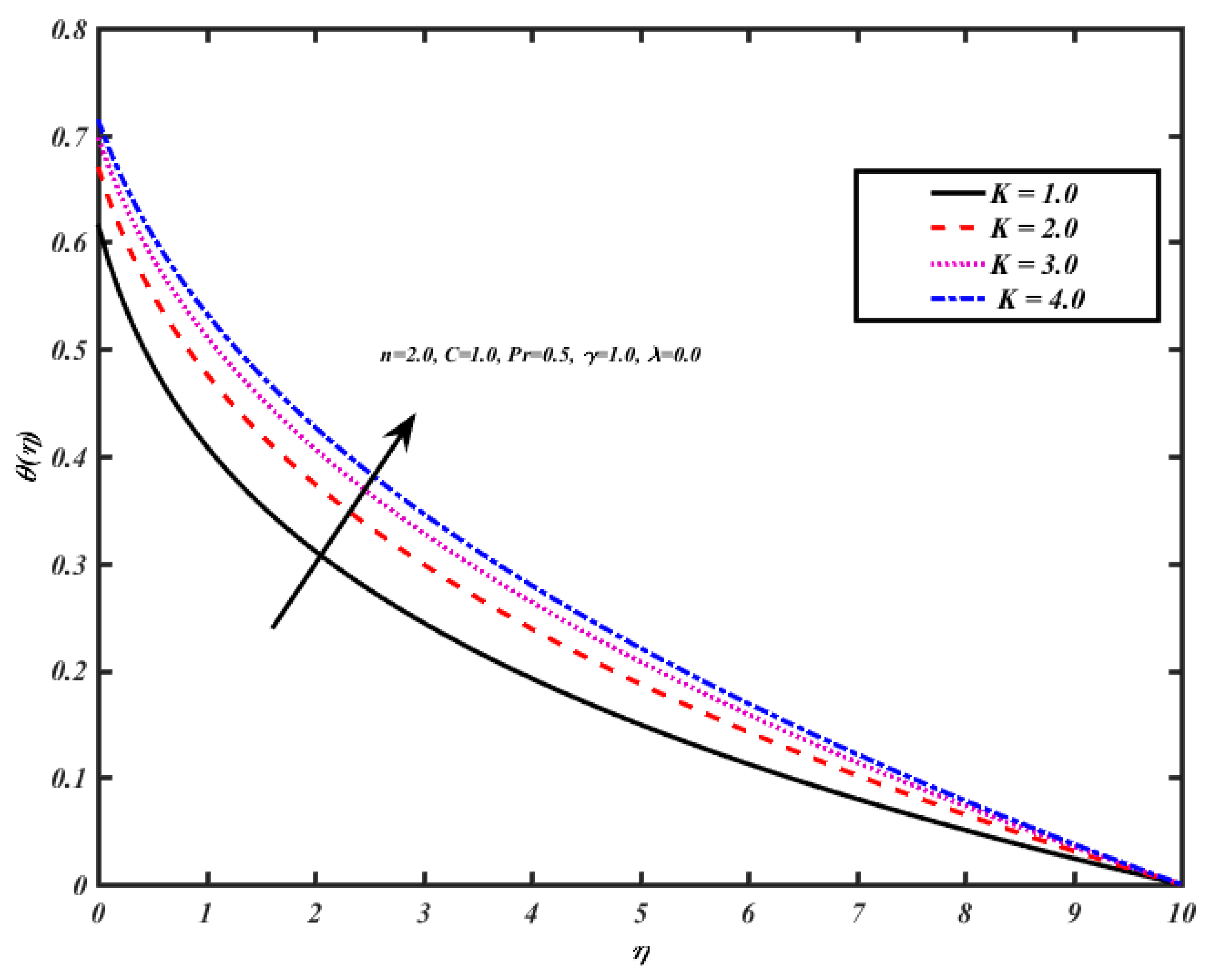
5. Results and Discussions
6. Conclusions
- The mixed convection parameter enhances the velocity profile.
- The Prandtl number reduces the temperature distribution across the flow.
- The velocity profile abruptly decreases in the presence of a velocity slip.
- The temperature profile diminishes due to the thermal slip effect.
- The skin friction was observed to increase for larger values of velocity slip and mixed convection parameter.
- The Nusselt number increased due to an increase of magnetic, velocity–temperature slip, and radiation parameters.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Ambient temperature (°C) | |
| C | Curvature parameter (m−1) |
| Cylinder temperature (°C) | |
| θ | Dimensionless temperature (-) |
| Density of fluid (kg m−3) | |
| σ | Electrical conductivity (S m−1) |
| υ | Kinematic viscosity (m2 s−1) |
| B | Magnetic field (Tesla) |
| M | Magnetic parameter (W m−2) |
| λ | Mixed convective parameter (W m−2 K−1) |
| MHD | Magnetohydrodynamic (-) |
| BLF | Boundary layer flow (-) |
| Nu | Nusselt number (-) |
| Pr | Prandtl number (-) |
| Radiative heat flux (kg s−3) | |
| K | Radiation parameter (-) |
| Re | Reynolds number (-) |
| ν | r-direction velocity (m s−1) |
| Specific heat (J kg−1 K−1) | |
| η | Self-reliant similarity variable (-) |
| ψ | Stream function (-) |
| Surface shear stress (pascal) | |
| Surface heat flux (W m−2) | |
| Skin friction coefficient (-) | |
| β | Thermal expansion coefficient (-) |
| γ | Thermal slip parameter (-) |
| L, S | Velocity and temperature slip length (m) |
| δ | Velocity slip factor (m) |
| u | z-direction velocity (m s−1) |
References
- Abbasi, A.; Mabood, F.; Farooq, W.; Hussain, Z. Non-orthogonal stagnation point flow of Maxwell nano-material over a stretching cylinder. Int. Commun. Heat Mass Transf. 2021, 120, 105043. [Google Scholar] [CrossRef]
- Abo-Eldahab, E.M.; El Aziz, M.A. Hydromagnetic three-dimensional free convective heat transfer overa stretching surface embedded in a non-Darcian porous medium inthe presence of heat generation or absorption. Can. J. Phys. 2005, 83, 739–751. [Google Scholar] [CrossRef]
- Akbar, T.; Nawaz, R.; Kamran, M.; Rasheed, A. Magnetohydrodynamic (MHD) flow analysis of second grade fluids in a porous medium with prescribed vorticity. AIP Adv. 2015, 5, 117133. [Google Scholar] [CrossRef] [Green Version]
- Ali, F.M.; Nazar, R.; Arifin, N.M.; Pop, I. Mixed convection stagnation-point flow on vertical stretching sheet with external magnetic field. Appl. Math. Mech. 2014, 35, 155–166. [Google Scholar] [CrossRef]
- Aly, E.H.; Ebaid, A. Effect of the velocity second slip boundary condition on the peristaltic flow of nanofluids in an asymmetric channel: Exact solution. Abstr. Appl. Anal. 2014, 2014, 191876. [Google Scholar] [CrossRef]
- Andersson, H.I. Slip flow past a stretching surface. Acta Mech. 2002, 158, 121–125. [Google Scholar] [CrossRef]
- Arifuzzaman, S.M.; Khan, M.; Mehedi, M.F.; Rana, B.; Ahmmed, S. Chemically reactive and naturally convective high speed MHD fluid flow through an oscillatory vertical porous plate with heat and radiation absorption effect. Eng. Sci. Technol. Int. J. 2018, 21, 215–228. [Google Scholar] [CrossRef]
- Brady, J.F.; Acrivos, A. Steady flow in a channel or tube with an accelerating surface velocity. An exact solution to the Navier—Stokes equations with reverse flow. J. Fluid Mech. 1981, 112, 127–150. [Google Scholar] [CrossRef]
- Brewster, M.Q. Thermal Radiative Transfer and Properties; John Wiley & Sons: Hoboken, NJ, USA, 1992. [Google Scholar]
- Crane, L.J. Flow past a stretching plate. Z. Angew. Math. Phys. ZAMP 1970, 21, 645–647. [Google Scholar] [CrossRef]
- Farooq, U.; Lu, D.; Munir, S.; Ramzan, M.; Suleman, M.; Hussain, S. MHD flow of Maxwell fluid with nanomaterials due to an exponentially stretching surface. Sci. Rep. 2019, 9, 7312. [Google Scholar] [CrossRef] [Green Version]
- Ferdows, M.; Khan, M.S.; Alam, M.M.; Sun, S. MHD mixed convective boundary layer flow of a nanofluid through a porous medium due to an exponentially stretching sheet. Math. Probl. Eng. 2012, 2012, 408528. [Google Scholar] [CrossRef]
- Hayat, T.; Tamoor, M.; Khan, M.I.; Alsaedi, A. Numerical simulation for nonlinear radiative flow by convective cylinder. Results Phys. 2016, 6, 1031–1035. [Google Scholar] [CrossRef] [Green Version]
- Hsiao, K.-L. Heat and mass mixed convection for MHD visco-elastic fluid past a stretching sheet with ohmic dissipation. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 1803–1812. [Google Scholar] [CrossRef]
- Ibrahim, W.; Shanker, B. MHD boundary layer flow and heat transfer of a nanofluid past a permeable stretching sheet with velocity, thermal and solutal slip boundary conditions. Comput. Fluids 2013, 75, 1–10. [Google Scholar] [CrossRef]
- Kamran, M.; Wiwatanapataphee, B.; Vajravelu, K. Hall current, Newtonian heating and second-order slip effects on convective magneto-micropolar fluid flow over a sheet. Int. J. Mod. Phys. C 2018, 29, 1850090. [Google Scholar] [CrossRef]
- Mahapatra, T.; Gupta, A. Stagnation point flow towards a stretching surface. Can. J. Chem. Eng. 2008, 81, 258–263. [Google Scholar] [CrossRef]
- Mahapatra, T.R.; Gupta, A.S. Stagnation-Point flow of a viscoelastic fluid towards a stretching surface. Int. J. Non Linear Mech. 2004, 39, 811–820. [Google Scholar] [CrossRef]
- Majeed, A.; Zeeshan, A.; Amin, N.; Ijaz, N.; Saeed, T. Thermal analysis of radiative bioconvection magnetohydrodynamic flow comprising gyrotactic microorganism with activation energy. J. Therm. Anal. Calorim. 2021, 143, 2545–2556. [Google Scholar] [CrossRef]
- Majeed, A.; Zeeshan, A.; Noori, F.M.; Masud, U. Influence of rotating magnetic field on Maxwell saturated ferrofluid flow over a heated stretching sheet with heat generation/absorption. Mech. Ind. 2019, 20, 502. [Google Scholar] [CrossRef] [Green Version]
- Maskeen, M.M.; Zeeshan, A.; Mehmood, O.U.; Hassan, M. Heat transfer enhancement in hydromagnetic alumina–copper/water hybrid nanofluid flow over a stretching cylinder. J. Therm. Anal. Calorim. 2019, 138, 1127–1136. [Google Scholar] [CrossRef]
- Mohyud-Din, S.T.; Khan, U.; Ahmed, N.; Rashidi, M.M. A study of heat and mass transfer on magnetohydrodynamic (MHD) flow of nanoparticles. Propuls. Power Res. 2018, 7, 72–77. [Google Scholar] [CrossRef]
- Mukhopadhyay, S. Effects of thermal radiation and variable fluid viscosity on stagnation point flow past a porous stretching sheet. Meccanica 2013, 48, 1717–1730. [Google Scholar] [CrossRef]
- Mukhopadhyay, S. MHD boundary layer slip flow along a stretching cylinder. Ain Shams Eng. J. 2013, 4, 317–324. [Google Scholar] [CrossRef] [Green Version]
- Mukhopadhyay, S.; De, P.R.; Bhattacharyya, K.; Layek, G.C. Casson fluid flow over an unsteady stretching surface. Ain Shams Eng. J. 2013, 4, 933–938. [Google Scholar] [CrossRef] [Green Version]
- Rasheed, H.U.; Khan, Z.; Islam, S.; Khan, I.; Guirao, J.L.G.; Khan, W. Investigation of two-dimensional viscoelastic fluid with nonuniform heat generation over permeable stretching sheet with slip condition. Complexity 2019, 2019, 3121896. [Google Scholar] [CrossRef] [Green Version]
- Reza-E-Rabbi, S.; Ahmmed, S.F.; Arifuzzaman, S.; Sarkar, T.; Khan, M.S. Computational modelling of multiphase fluid flow behaviour over a stretching sheet in the presence of nanoparticles. Eng. Sci. Technol. Int. J. 2020, 23, 605–617. [Google Scholar] [CrossRef]
- Sakiadis, B.C. Boundary-layer behavior on continuous solid surfaces: I. Boundary-layer equations for two-dimensional and axisymmetric flow. AIChE J. 1961, 7, 26–28. [Google Scholar] [CrossRef]
- Tamoor, M.; Shahzeb; Zaman, Q. Linear radiation effects on forced convective slip flow along a nonlinearly stretch cylinder in an absorptive medium. Alex. Eng. J. 2018, 57, 537–545. [Google Scholar] [CrossRef]
- Tamoor, M.; Waqas, M.; Khan, M.I.; Alsaedi, A.; Hayat, T. Magnetohydrodynamic flow of Casson fluid over a stretching cylinder. Results Phys. 2017, 7, 498–502. [Google Scholar] [CrossRef]
- Tsou, F.K.; Sparrow, E.M.; Goldstein, R.J. Flow and heat transfer in the boundary layer on a continuous moving surface. Int. J. Heat Mass Transf. 1967, 10, 219–235. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Dual and triple solutions for MHD slip flow of non-Newtonian fluid over a shrinking surface. Comput. Fluids 2012, 70, 53–58. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Heat and mass transfer of MHD second order slip flow. Comput. Fluids 2013, 71, 426–434. [Google Scholar] [CrossRef]
- Wang, C.Y. Flow due to a stretching boundary with partial slip—an exact solution of the Navier–Stokes equations. Chem. Eng. Sci. 2002, 57, 3745–3747. [Google Scholar] [CrossRef]
- Wang, M.; Fu, Y. Necking of a hyperelastic solid cylinder under axial stretching: Evaluation of the infinite-length approximation. Int. J. Eng. Sci. 2021, 159, 103432. [Google Scholar] [CrossRef]
- Waqas, M.; Farooq, M.; Khan, M.I.; Alsaedi, A.; Hayat, T.; Yasmeen, T. Magnetohydrodynamic (MHD) mixed convection flow of micropolar liquid due to nonlinear stretched sheet with convective condition. Int. J. Heat Mass Transf. 2016, 102, 766–772. [Google Scholar] [CrossRef]
- Yasmin, A.; Ali, K.; Ashraf, M. Study of heat and mass transfer in MHD flow of micropolar fluid over a curved stretching sheet. Sci. Rep. 2020, 10, 4581. [Google Scholar] [CrossRef] [Green Version]







| n | [36] | [37] | [30] | Present |
|---|---|---|---|---|
| 0 | 0.5820 | 0.5820 | 0.5821 | 0.5820 |
| 1 | 1.0000 | 1.0000 | 1.0000 | 0.9961 |
| 2 | 1.3333 | 1.3333 | 1.3332 | 1.3333 |
| M | Analytical Solution | Numerical Solution | Error |
|---|---|---|---|
| 0 | −1.00000 | −1.00001 | −0.00001 |
| 0.5 | −1.11803 | −1.11803 | −0.00000 |
| 1.0 | −1.41421 | −1.41421 | −0.00000 |
| 1.5 | −1.80277 | −1.80278 | −0.00001 |
| n | C | M | δ | λ | Pr | γ | K | −f″(0) | −θ′(0) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.12685 | 0.33489 | |||||||
| 2 | 1.20155 | 0.38309 | |||||||
| 3 | 1.26145 | 0.41789 | |||||||
| 2 | 1 | 1.20155 | 0.38309 | ||||||
| 2 | 1.33150 | 0.43739 | |||||||
| 3 | 1.44063 | 0.47790 | |||||||
| 1 | 1 | 1.20155 | 0.38309 | ||||||
| 2 | 1.48689 | 0.35397 | |||||||
| 3 | 1.73211 | 0.33479 | |||||||
| 1 | 0.1 | 1.66038 | 0.40184 | ||||||
| 0.5 | 0.94980 | 0.37065 | |||||||
| 1 | 0.63069 | 0.35164 | |||||||
| 0.3 | −2 | 1.71442 | 0.34021 | ||||||
| 0 | 1.20155 | 0.38309 | |||||||
| 2 | 0.83701 | 0.43027 | |||||||
| 0 | 0.1 | 1.20155 | 0.31291 | ||||||
| 0.5 | 0.83701 | 0.38309 | |||||||
| 1 | 1.20155 | 0.44830 | |||||||
| 0.5 | 1 | 1.20155 | 0.38309 | ||||||
| 2 | 1.20155 | 0.27698 | |||||||
| 3 | 1.20155 | 0.21691 | |||||||
| 1 | 1 | 1.20155 | 0.38309 | ||||||
| 2 | 1.20155 | 0.32934 | |||||||
| 3 | 1.20155 | 0.30183 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tamoor, M.; Kamran, M.; Rehman, S.; Farooq, A.; Khan, R.; Lee, J.R.; Shin, D.Y. Modelling of Applied Magnetic Field and Thermal Radiations Due to the Stretching of Cylinder. Processes 2021, 9, 1077. https://doi.org/10.3390/pr9061077
Tamoor M, Kamran M, Rehman S, Farooq A, Khan R, Lee JR, Shin DY. Modelling of Applied Magnetic Field and Thermal Radiations Due to the Stretching of Cylinder. Processes. 2021; 9(6):1077. https://doi.org/10.3390/pr9061077
Chicago/Turabian StyleTamoor, Muhammad, Muhammad Kamran, Sadique Rehman, Aamir Farooq, Rewayat Khan, Jung Rye Lee, and Dong Yun Shin. 2021. "Modelling of Applied Magnetic Field and Thermal Radiations Due to the Stretching of Cylinder" Processes 9, no. 6: 1077. https://doi.org/10.3390/pr9061077
APA StyleTamoor, M., Kamran, M., Rehman, S., Farooq, A., Khan, R., Lee, J. R., & Shin, D. Y. (2021). Modelling of Applied Magnetic Field and Thermal Radiations Due to the Stretching of Cylinder. Processes, 9(6), 1077. https://doi.org/10.3390/pr9061077






