Accurate Insulating Oil Breakdown Voltage Model Associated with Different Barrier Effects

Abstract

In modern power systems, power transformers are considered vital components that can ensure the grid’s continuous operation. In this regard, studying the breakdown in the transformer becomes necessary, especially its insulating system. Hence, in this study, Box–Behnken design (BBD) was used to introduce a prediction model of the breakdown voltage (VBD) for the transformer insulating oil in the presence of different barrier effects for point/plane gap arrangement with alternating current (AC) voltage. Interestingly, the BBD reduces the required number of experiments and their costs to examine the barrier parameter effect on the existing insulating oil VBD. The investigated variables were the barrier location in the gap space (a/d)%, the relative permittivity of the barrier materials (ε_r), the hole radius in the barrier (hr), the barrier thickness (th), and the barrier inclined angle (θ). Then, only 46 experiment runs are required to build the BBD model for the five barrier variables. The BBD prediction model was verified based on the statistical study and some other experiment runs. Results explained the influence of the inclined angle of the barrier and its thickness on the VBD. The obtained results indicated that the designed BBD model provides less than a 5% residual percentage between the measured and predicted VBD. The findings illustrated the high accuracy and robustness of the proposed insulating oil breakdown voltage predictive model linked with diverse barrier effects.

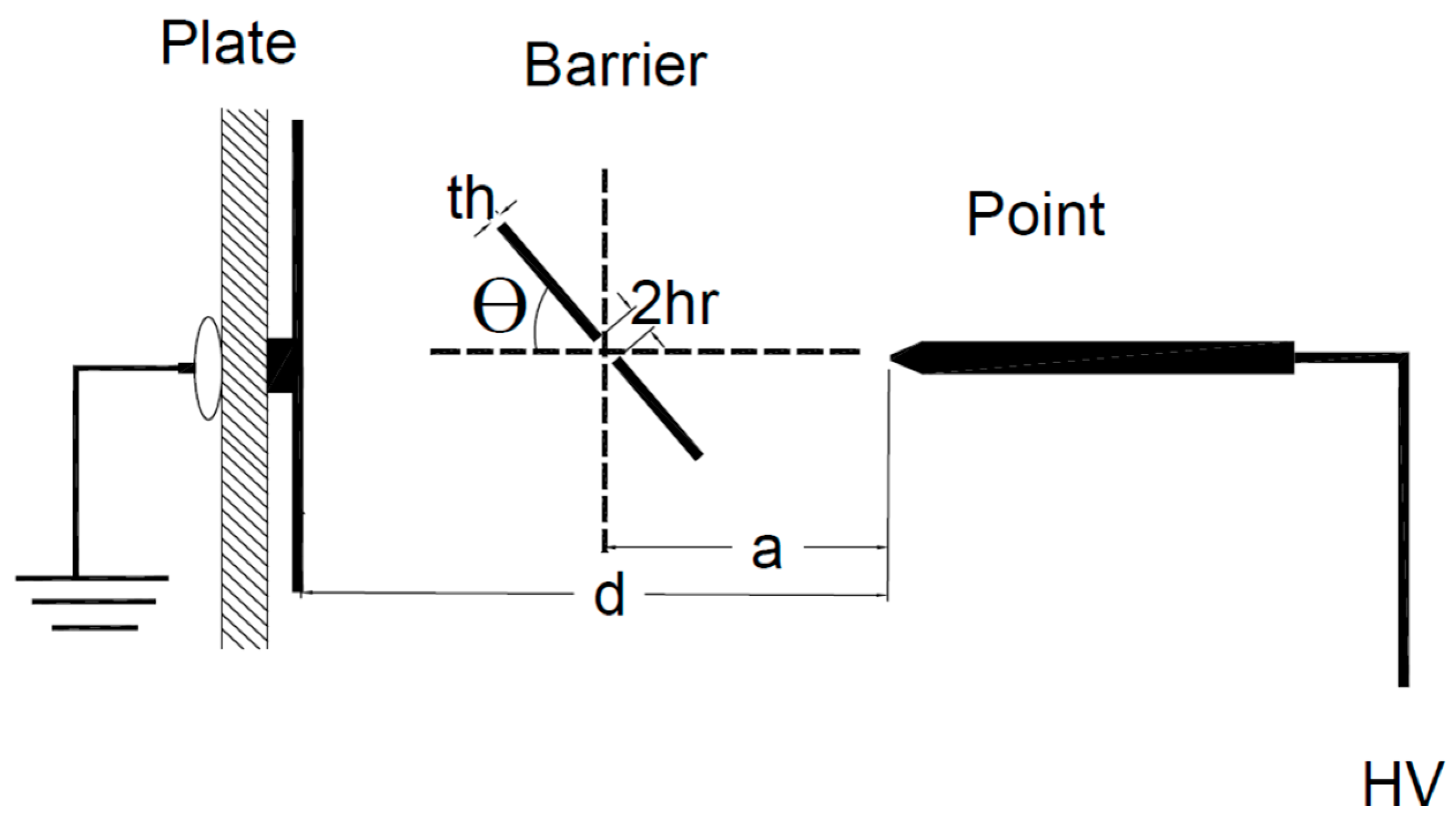
1. Introduction

A transformer is a crucial piece of equipment in the power system networks. The transformer’s primary failure comes from the insulating system’s deterioration, which consists of insulating oil and paper [1,2]. The transformer oil remains the most suitable liquid used in high-voltage apparatus as an insulating medium, but it still breaks under electrical and thermal stresses [3,4,5,6,7,8]. In the presence of a barrier in the insulating oil, the risk of the breakdown is reduced due to the stopping of the charge carriers by the barrier; then, these charge carriers accumulate on the barrier surface, constituting the barrier surface charge. Moreover, the barrier plays a significant role in impeding the discharge in the insulating oil of power transformers by encountering particle movement [9]. The breakdown voltage (VBD) of homogeneous and non-homogeneous field gaps is affected mainly by inserting thin dielectric barriers in the gaps; this phenomenon is called the barrier effect. This effect is characterized by the electric field’s uniformity between the barrier and the plane electrode, increasing the VBD. Thus, studying the influence of such barrier effect on the VBD of the transformer oil is essential [10].

The barrier effect was observed first in 1920 by C.P. Steinmetz in the point/plane air gaps [11]. Some former studies have directed to investigate the consequence of the barrier set, e.g., the location of the barrier concerning the barrier diameter (D), the space of gap (a/d)%, and the gap space among the electrodes (d) under different applied voltages and gap space configurations [11,12,13]. The influence of surface conductivity of the barrier system on the VBD was presented in [14]. A rod/plane arrangement with the 80 mm distance between the high-voltage electrode (rod) and a grounded plane electrode was used. A single barrier was placed in the arrangement, and its surface resistivity was decreased systematically. A decrease in the VBD arrangement with a reduction in surface resistivity was observed for positive, negative lightning impulse and alternating current (AC) voltage. The effect of barriers at early discharge and the failure stages for different field arrangements (homogenous and non-homogenous) was presented in [15]. The barrier location influences the failure stress, not the onset discharges. The effect of the barrier on the contaminated particle movements was investigated with the oil volume variation. The kraft paper’s influence on preventing the bridging of the pressboard fiber particles in the insulating oil through experimental works was illustrated. Three different kraft pressboard paper types under different AC and DC voltages were examined in [16]. Recently, artificial intelligence and machine learning techniques have been employed in several applications with promising performance in power system applications with renewables [17,18,19,20,21,22,23,24,25,26,27,28]. Specifically, an artificial neural network (ANN) was presented in [29] to study the barrier effect parameters on the VBD of the transformer insulating oil for the point/plane and plane/plane gaps under AC high voltage. The results showed the ANN model’s capability to predict the VBD with the barrier parameters’ variation.

A mathematical and statistical model using the response surface methodology (RSM) includes some techniques such as the center composite face (CCF) and Box–Behnken design (BBD). They have been used to model and analyze the relationship between specific experiments’ responses and their variable influence. In these techniques, a minimum number of experiment runs is required to reduce the experiment cost [30]. A second-order model was constructed using CCF and BBD in [13,31] to inspect the influence of different barrier parameters, such as barrier place in the gap spacing, the gap spacing, and the barrier diameter of point/plane electrode arrangement under AC voltage. The conclusion was that the type of RSM technique affects the constructed model’s accuracy and the cost of experimental works [31].

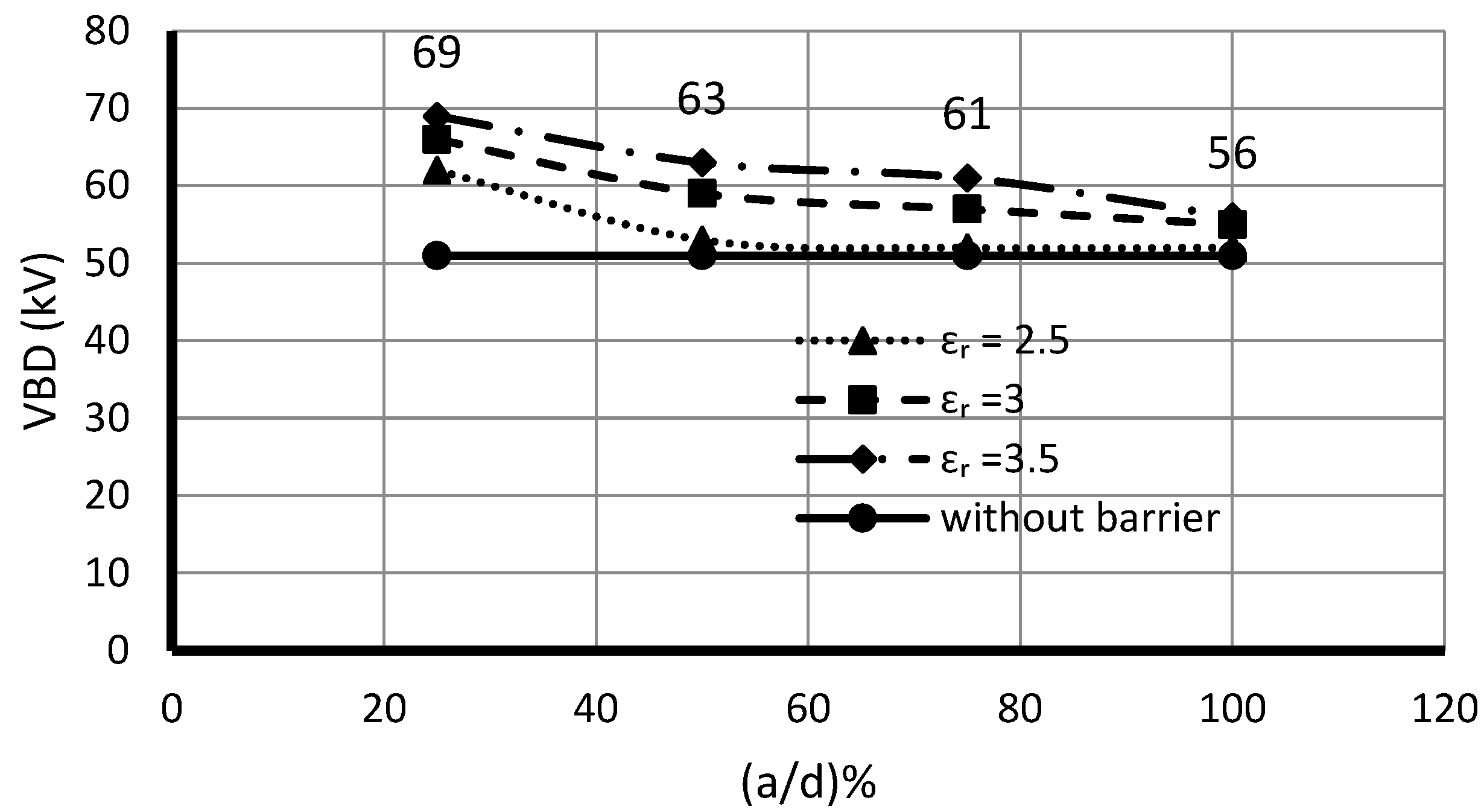
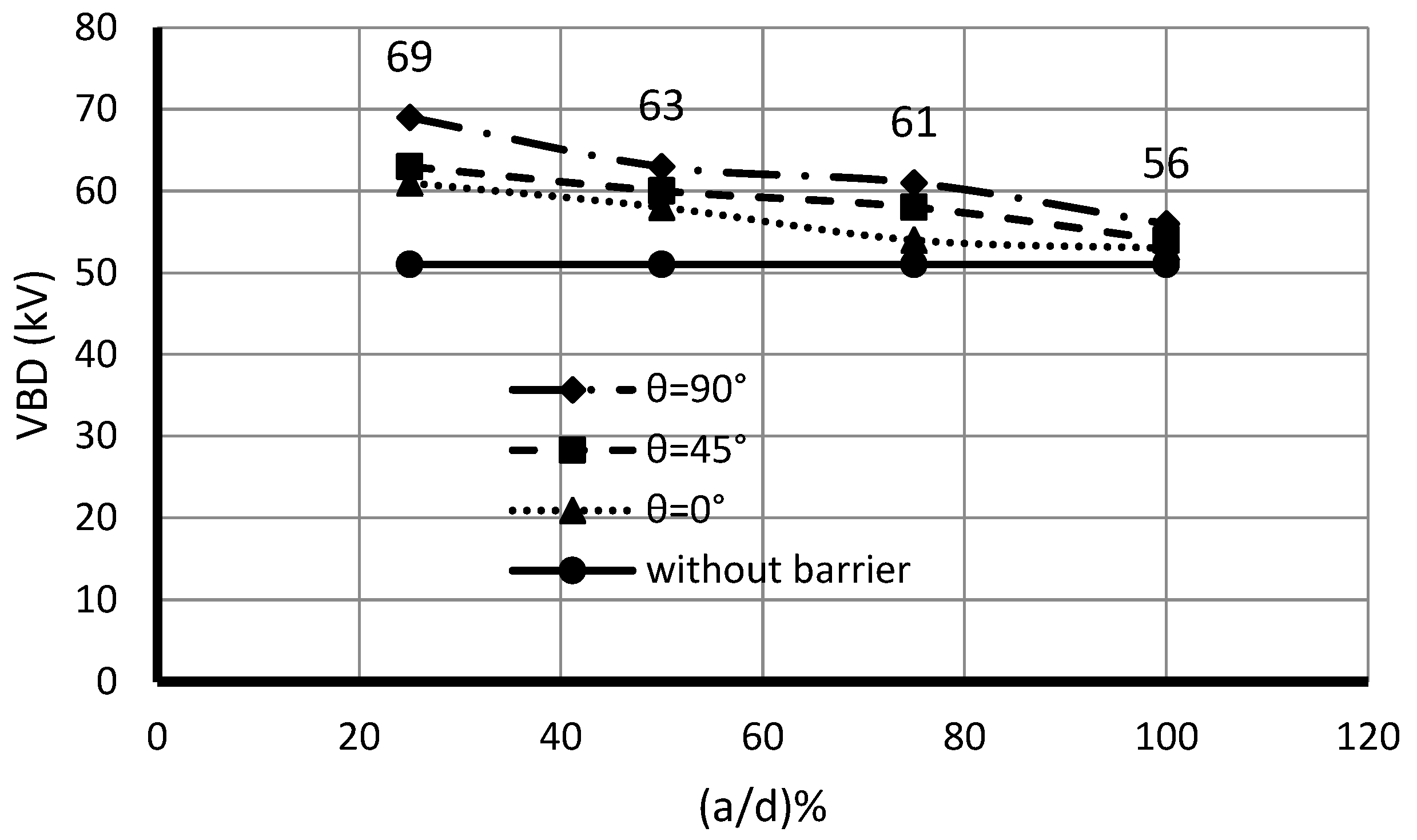
Previous works have studied the effect of some barrier variables on the strength of the insulating oil and its VBD, e.g., the barrier location and its diameter and the gap space between the electrodes [3,9,12,13,31]. In the current work, the effect of some new barrier variables is investigated. These variables are the barrier holes that may develop from the faults, whether intentional or accidental, and the barrier thickness, dielectric constant, and inclination angle. Moreover, mathematical modeling was used to construct a model linking the relation between the VBD and the barrier variables, such as a CCF design [13]. It shows a significant deviation in some cases between the measured and predicted VBD (17.17% deviation is a maximum). The proposed BBD technique was used to reduce this deviation. The number of experiments runs required for a given number of BBD factors is less than that for CCF. For five experiment factors, BBD requires 46 experiment runs, and CCF requires 52 experiment runs. In general, the greater number of variables in the model leads to many laboratory experiments. More efforts in the modeling process will be needed to create the model. All the previous reasons refer to the novelty of the current work.

Investigating the influence of more than three variables and their interaction on a particular experiment response is complicated and requires many experiments. Therefore, reducing the number of experiments with variables of more than three is a great challenge. Therefore, BBD is a technique used to reduce the number of experiments and then reduce the experiment cost. The number of experiments to build the relationship between the response based on the experiment variables depends on the number of variables; that is, 15 experiment runs are required for three experimental variables, 27 runs for four experiment variables, and 46 experiment runs for five experiments variables.

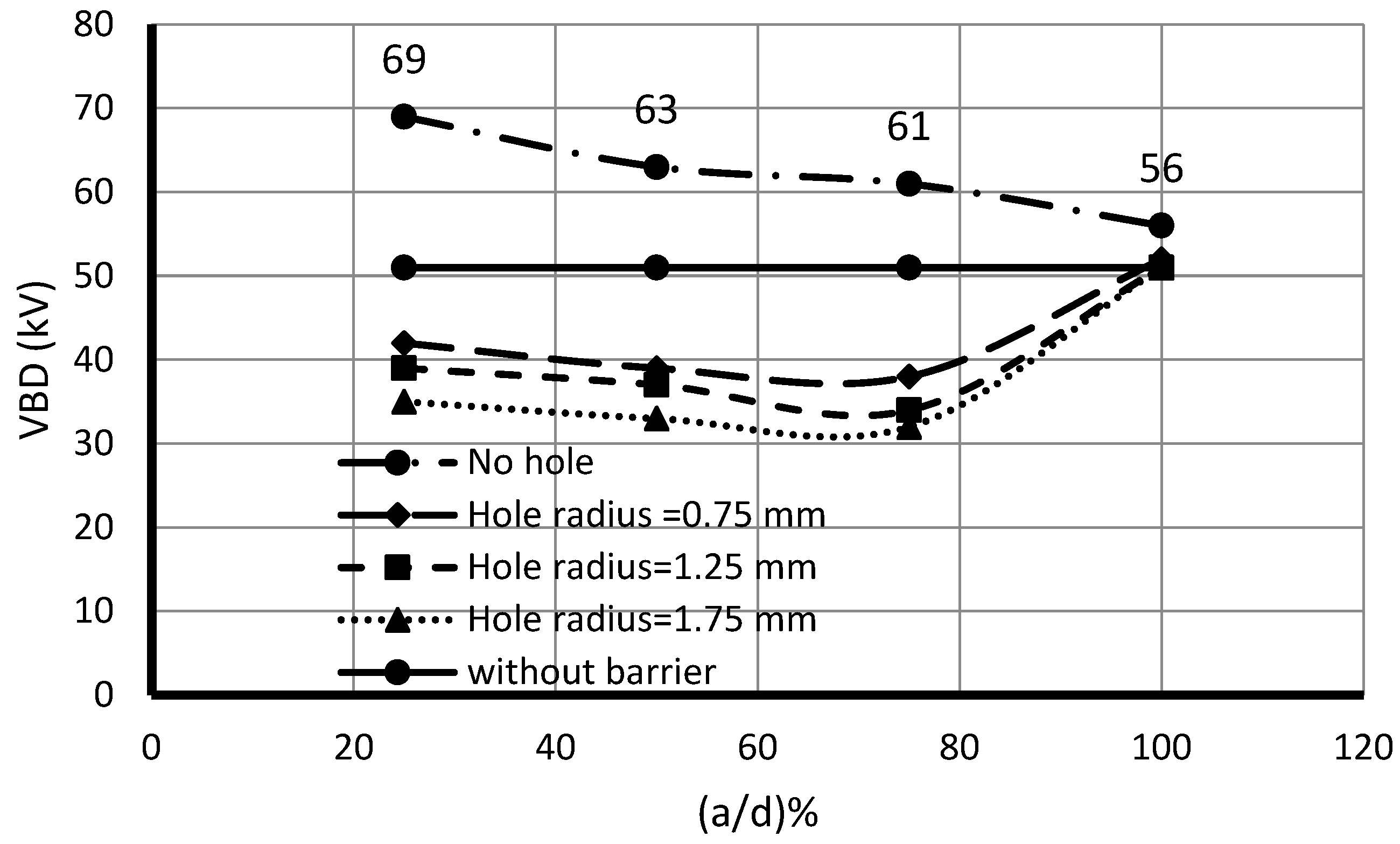
In this study, new barrier variables are considered to investigate their effects on the VBD of insulating oils with point /plane gap configuration under alternating current (AC) voltage based on BBD. These barrier variables are the barrier location in the gap space (a/d)%, the dielectric constant of barrier material (ε_r), the hole radius in the barrier (hr), the barrier thickness (th), and the inclined angle of the barrier in the gap space (θ). The advantage of using the BBD technique in treating the difficulties of practical limits is avoiding risky mixtures because the sharp edges and star points are evaded [31]. Then, altogether points nominated to build the BBD model lie on the anticipated region (i.e., studied data region). The BBD declines the chosen number of experiment runs for the constructed model. A total of 46 experiment runs are required to simulate the relation between the VBD as a response and five barrier variables. A prediction equation is developed based on BBD, and the significance of each term in this equation is investigated with the statistical study to obtain the approximated equation. The results of the predicted equation and its approximation provide minimum errors with 20 new experiment runs. In all cases, the errors are always less than 5%.

2. Experimental Works and Results

2.1. Experimental Setup

The BBD model is built based on the experimental work results established in the Extra High-Voltage Research Center of the Egyptian Electricity Holding Company. The experiments are developed using a plexiglass tank with 25 × 25 × 35 cm filled with 18.75 L of insulating oil. A 100 kV AC source is used with a capacitor divider for applying the AC high voltage on the point/plane gap configuration, as shown in Figure 1. Three types of barrier material are used (mica with a dielectric constant (ε_r) 2.5, pressboard with 3, and acrylic with 3.5). The gap space is constant at 4 cm, and the circular barrier diameter is fixed at 7 cm for all barriers. An earthed electrode is a plane with 17 cm in a diameter ring shape. The barrier is suspended in the gap space with the help of an acrylic bar. The transformer insulating oil kind is Diala D, where its dielectric strength is above 30 kV/cm (without treatment) as well as greater than 70 kV/cm (with treatment) based on both IEC 60296 and IEC 60156 [32,33]. The characteristics of the insulating oil shell Diala D are illustrated in Table 1. Note that the treatment of the original oil increases the breakdown voltage to more than 70 kV. Figure 2 explains the experimental arrangement of the point/plane gap configuration with the inclined barrier. The barrier location ((a/d)%) is varied from 25% to 100% in the gap space d. Different barrier materials are used with different dielectric constants that range from 2.5 to 3.5. The hole radius (hr) made in the barrier varies with values of 0.75, 1.25, and 1.75 mm. The holes were also made in the center of the barrier. The thickness (th) of the barrier also varies between 2 and 4 mm. The inclined angle of the barrier is considered 0°, 45°, and 90°. The barrier is in a horizontal position at 0°, and it is in a vertical one for 90°. Based on the IEC 60156, the average value of six sequences runs on the insulating oil is considered. Then, each value of breakdown voltage is the average value of the applied voltage’s six consecutive runs.

Figure 1. Schematic of the oil tank with point/plane gap configuration.

Table 1. Characteristics of insulating oil shell Diala D.

Item	Unit	IEC 60296 Requirements	Diala D
Density at 20 °C	K g/m3	<895	877
Kinematic viscosity at 20 °C	mm2/s	—	16.6
Breakdown voltage (after treatment)	kV	Min 70 kV	>30 (>70 upon treatment)
Dielectric dissipation factor at 90 °C	---	0.005 max (after treatment)	0.0005
Water content	ppm	—	<40 drams/IBC, <30 bulk
Oxidation Stability (164 h/120 °C) Total acidity	mg KOH/g	Max. 0.3	0.26

Figure 2. Arrangement of point/plane gap with an inclined barrier.

2.2. Results for Barrier Location (a/d)% and Barrier Material (ε_r)

The first barrier variable that influences the VBD is the location of the barrier in the gap space. The variation in the VBD with (a/d)% is illustrated in Figure 3, where the VBD is recorded when the barrier location varies from 25 to 100% of the gap space, and three types of barrier material are used with different dielectric constants. The maximum breakdown voltage occurs when the barrier is closing to the high voltage electrode. The breakdown voltage diminishes when the barrier is approaching the grounded electrode. When we construct the mathematical model, it is not convenient to put the variable (a/d)% equal to zero since (a/d)% minimum value is considered 25%. Figure 3 illustrated the experiments investigating the effect of barrier location were conducted at th = 2 mm, without a hole, and with a vertical barrier position. Figure 3 demonstrates that the VBD decreases with the increase in the (a/d)%. When the (a/d)% is 100%, the barrier’s effect is reduced, and the VBD reaches the gap’s VBD value without barrier. Moreover, the VBD increases with a high dielectric constant as in acrylic.

Figure 3. Effect of the barrier location on the breakdown voltage at different barrier materials.

2.3. Results for Barrier Thickness (th)

Figure 4 depicts the barrier thickness’s impact on the insulating oil VBD at diverse barrier locations in the gap space. The experiments’ parameters are acrylic material, without a hole in the barrier, and vertical barrier position (θ = 90°). An increase in the barrier thickness results in an increase in the VBD at a similar barrier position in the gap space.

Figure 4. Effect of the barrier thickness on the breakdown voltage.

2.4. Results for Barrier Hole Radius (hr)

Figure 5 shows that the barrier without any hole significantly affects VBD. With a hole in the barrier, the VBD of the point/plane oil gap decreases. In such a case, the barrier has a negative effect. Meanwhile, an increase in the hole radius leads to a reduction in the VBD at the exact barrier location. When (a/d)% is 100%, the barrier does not affect, and the VBD reaches one of the gaps without the barrier. The experiments are conducted at the barrier thickness th equal to 2 mm, acrylic barrier material, and the inclined angle (θ) equivalent to 90°.

Figure 5. Effect of barrier hole radius on the breakdown voltage.

2.5. Results for Barrier Inclined Angle (θ)

Figure 6 explains the relation between the VBD and the barrier inclined angle (θ). The vertical position (θ = 90°) of the barrier plays an imperative role in increasing the VBD of the power transformer insulating oil rather than any other inclined barrier angle or the barrier with a horizontal position. A decrease in VBD is observed when the location of the barrier increases until (a/d) reaches 100%. Then, the effect of the barrier decreases, and the VBD becomes close to that of the gap without barrier. The experiments’ parameters are an acrylic barrier made of acrylic, without a hole in the barrier, and the barrier thickness (th) of 2 mm.

Figure 6. Effect of barrier inclined angle (θ) on the breakdown voltage.

The experimental results indicated that the breakdown voltage values were of low values because there is no physical mechanism consideration. It is unclear if they can be applied to other fluids.

3. Box–Behnken Design (BBD)

The design of experiments (DOE) is considered a feature of the RSM and has numerous practices. The CCF and BBD are considered the most known DOE methods [34]. BBD is recently viewed in many applications to investigate the effect of the experimental parameters on these experiments’ responses, as in [13,31,35,36,37,38,39,40]. Further, it is lying on the division of applied statistics for analyzing, planning, and interpreting the controlled test for determining the parameters that regulate the reaction of practical experiments. Before conducting the investigation, two concepts must be considered: the experiment domain and the experiments’ mathematical model [13]. The quadratic formula of the BBD model of the designed experiment is given by Equation (1) [41]:

$$\mathrm{Y} = {\mathsf{\alpha }}_0 + {\displaystyle \sum }_{\mathrm{i}=1}^{Nv}{\mathsf{\alpha }}_{\mathrm{i}}{\mathrm{X}}_{\mathrm{i}} + {\displaystyle \sum }_{\mathrm{i}=1}^{Nv}{\displaystyle \sum }_{\mathrm{j}=1}^{Nv}{\mathsf{\alpha }}_{\mathrm{ij}}{\mathrm{X}}_{\mathrm{i}}{X}_{\mathrm{j}} + {\displaystyle \sum }_{\mathrm{i}=1}^{Nv}{\mathsf{\alpha }}_{\mathrm{ii}}{\mathrm{X}}_{\mathrm{i}}{}^2 + \epsilon$$

(1)

where Y is the response, and X_i refers to the input variables that influence the experiment response. X_iX_j is the two-way (interaction) terms; the number is calculated as k(k − 1)/2, where k is the number of input variables. The ${\mathrm{X}}_{\mathrm{i}}{}^2$ refers to the second-order of the variables. (${\mathsf{\alpha }}_0$, ${\mathsf{\alpha }}_{\mathrm{ij}}$, ${\mathsf{\alpha }}_{\mathrm{ii}}$) is the coefficient of all terms in the quadratic equation. The ε expresses the error of the equation, and N_v is the number of experiment variables.

In the BBD, the input parameters (i.e., considered factors) are categorized into three different levels for each factor. These levels involve the minimum, mean, and maximum variable values. Note that the three levels are coded by −1, 0, and 1, respectively. For example, the barrier thickness variable th is regarded as 2, 3, and 4 mm, which correspond to the coded values of −1, 0, and 1, respectively. The coding of other variables is explained in the study, as in Table 2. The coded value of the five barrier variables is described in Table 2.

Table 2. Coded and actual values of the input parameters of the barrier.

Input Variables	Coded Value
	Minimum (−1)	Mean (0)	Maximum (1)
(a/d)%	25	50	75
εr (f/m)	2.5	3	3.5
hr (mm)	0.75	1.25	1.75
th (mm)	2	3	4
θ	0°	45°	90°

BBD is considered a rotatable or nearly rotatable second-order design that needs three levels of each variable that influence a specific experiment response. It is recently widely used in many applications of the research environment [35,36,37,38,39,40]. These experiment variable levels are categorized into minimum, mean, and maximum levels, and they are coded as −1, 0, and 1, respectively. The required number of experiments runs (N_r) for BBD design is determined as follows [42]:

N_r = 2N_v(N_v − 1) + CP₀

(2)

N_v represents the counting number of factors (i.e., input parameters), and CP₀ refers to the number of repetitions tests at the center point. Note that the coded values of the input variables of the experimental are clarified in Table 2.

The authors of [42] presented only the fundamentals, advantages, and limitations of the BBD for the optimization of analytical methods. They showed an example for three parameters only with 15 experiments runs where CP₀ is three. A total of 46 experiment runs are required according to Equation (2) with six points in the center values of the five variables to apply the BBD to the designed experiments to investigate the effect of five variables on the response of these experiments (VBD). Table 3 illustrates the coded values, the values of the variables, and the response of the 46 experiments. A total of six points are repeated at the zero code of the variables to provide a CP₀-1 degree of freedom for determining the experiment errors and enhancing the response’s precision at these zero codes of the variables [43]. A total of 46 experiment runs are conducted to investigate the effect of the previous barrier variables on the VBD, as the BBD technique’s requirement is illustrated in Table 3. Each experiment run is performed to satisfy the particular need of BBD. The first experiment run in Table 3 indicates that the VBD is measured at the following conditions: the barrier location is minimum at 25% of the gap space, the dielectric strength (ε_r) is minimum at 2.5 for mica barrier material, the radius of the hole in the barrier is at the mean value of 1.25 mm, the barrier thickness is at 3 mm as a mean value of the thickness variable, and the inclined angle of the barrier is at a mean value of 45°. The remaining 46 experiment runs are conducted as illustrated in Table 3.

Table 3. Coded and actual numbers for five Box–Behnken design (BBD) input parameters.

	Coded Variables					Actual Variables
	(a/d)%	εr	hr	th	θ	(a/d)%	εr	hr (mm)	th (mm)	θ(°)	VBD (kV)
1	−1	−1	0	0	0	25	2.5	1.25	3	45	38
2	−1	1	0	0	0	25	3.5	1.25	3	45	42
3	1	−1	0	0	0	75	2.5	1.25	3	45	33
4	1	1	0	0	0	75	3.5	1.25	3	45	38
5	0	0	−1	−1	0	50	3	0.75	2	45	36
6	0	0	−1	1	0	50	3	0.75	4	45	43
7	0	0	1	−1	0	50	3	1.75	2	45	34
8	0	0	1	1	0	50	3	1.75	4	45	41
9	0	−1	0	0	−1	50	2.5	1.25	3	0	54
10	0	−1	0	0	1	50	2.5	1.25	3	90	38
11	0	1	0	0	−1	50	3.5	1.25	3	0	58
12	0	1	0	0	1	50	3.5	1.25	3	90	41
13	−1	0	−1	0	0	25	3	0.75	3	45	41
14	−1	0	1	0	0	25	3	1.75	3	45	39
15	1	0	−1	0	0	75	3	0.75	3	45	36
16	1	0	1	0	0	75	3	1.75	3	45	36
17	0	0	0	−1	−1	50	3	1.25	2	0	57
18	0	0	0	−1	1	50	3	1.25	2	90	36
19	0	0	0	1	−1	50	3	1.25	4	0	57
20	0	0	0	1	1	50	3	1.25	4	90	43
21	0	−1	−1	0	0	50	2.5	0.75	3	45	37
22	0	−1	1	0	0	50	2.5	1.75	3	45	36
23	0	1	−1	0	0	50	3.5	0.75	3	45	41
24	0	1	1	0	0	50	3.5	1.75	3	45	39
25	−1	0	0	−1	0	25	3	1.25	2	45	37
26	−1	0	0	1	0	25	3	1.25	4	45	44
27	1	0	0	−1	0	75	3	1.25	2	45	34
28	1	0	0	1	0	75	3	1.25	4	45	40
29	0	0	−1	0	−1	50	3	0.75	3	0	56
30	0	0	−1	0	1	50	3	0.75	3	90	39
31	0	0	1	0	−1	50	3	1.75	3	0	56
32	0	0	1	0	1	50	3	1.75	3	90	38
33	−1	0	0	0	−1	25	3	1.25	3	0	59
34	−1	0	0	0	1	25	3	1.25	3	90	41
35	1	0	0	0	−1	75	3	1.25	3	0	54
36	1	0	0	0	1	75	3	1.25	3	90	35
37	0	−1	0	−1	0	50	2.5	1.25	2	45	33
38	0	−1	0	1	0	50	2.5	1.25	4	45	40
39	0	1	0	−1	0	50	3.5	1.25	2	45	37
40	0	1	0	1	0	50	3.5	1.25	4	45	44
41	0	0	0	0	0	50	3	1.25	3	45	39
42	0	0	0	0	0	50	3	1.25	3	45	38.5
43	0	0	0	0	0	50	3	1.25	3	45	38
44	0	0	0	0	0	50	3	1.25	3	45	38.5
45	0	0	0	0	0	50	3	1.25	3	45	39
46	0	0	0	0	0	50	3	1.25	3	45	39.5

Equation (1) is used to build the BBD model for determining the relation between the experiment input variables and the response of the designed experiments. The number of coefficients (N_c) of Equation (1) can be computed as follows:

N_c = (N_v + 1) (N_v + 2)/2

(3)

N_c is the number of coefficients (α₀, α_i, α_ij, and α_ii), and N_v is the number of experiment variables. From Equation (3), 21 coefficients of Equation (1) are developed.

The Matlab software calculates Equation (1) coefficients, while the equivalent BBD model of the predicted formula of VBD can be explained as in Equation (4).

$$\begin{array}{cc}VBD& = 38.75 - 2.1875·\left(\raisebox{1ex}{$a$}\!\left/ \!\raisebox{-1ex}{$d$}\right.\right) + 1.9375·\left({\epsilon }_r\right) - 0.625·hr + 3·th - 8.75·\theta + 0.25·\left(\raisebox{1ex}{$a$}\!\left/ \!\raisebox{-1ex}{$d$}\right.\right)·\left({\epsilon }_r\right) + 0.5·\left(\raisebox{1ex}{$a$}\!\left/ \!\raisebox{-1ex}{$d$}\right.\right)·hr\hfill \\ & - 0.25·\left(\raisebox{1ex}{$a$}\!\left/ \!\raisebox{-1ex}{$d$}\right.\right)·\mathrm{th} - 0.25·\left(\raisebox{1ex}{$a$}\!\left/ \!\raisebox{-1ex}{$d$}\right.\right)·\mathsf{\theta } - 0.25·\left({\epsilon }_r\right)·hr - 0.25·\left({\epsilon }_r\right)·\theta - 0.25·\left(hr\right)·\theta + 1.75·th·\theta \hfill \\ & - 0.4792·{\left(\raisebox{1ex}{$a$}\!\left/ \!\raisebox{-1ex}{$d$}\right.\right)}^2 - 0.3125{\left({\epsilon }_r\right)}^2 - 0.3958·{\left(hr\right)}^2 + 0.2708·{\left(th\right)}^2 + 9.1042·{\left(\theta \right)}^2\hfill \end{array}$$

(4)

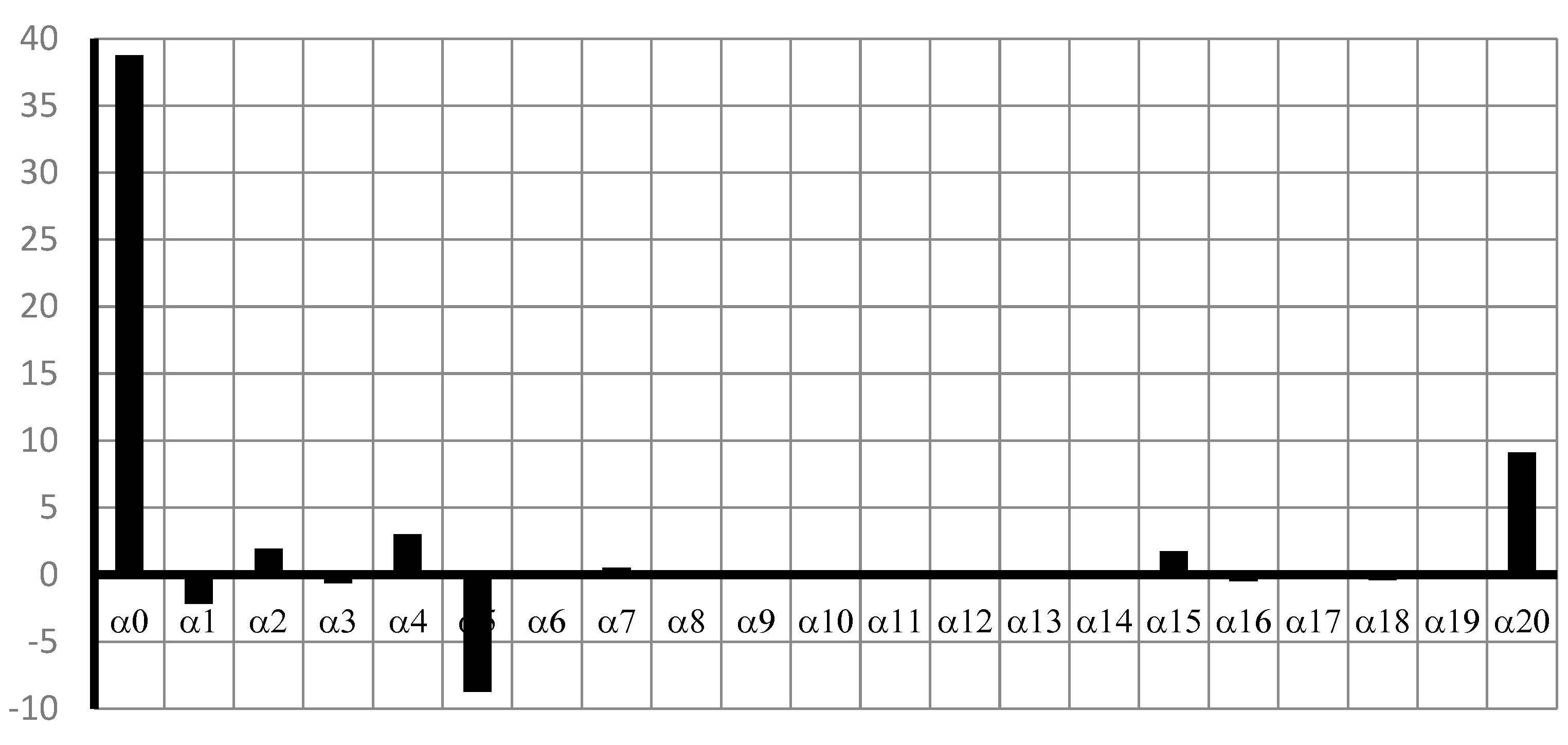
Figure 7 shows α_i magnitude of the 2-order equation (Equation (4)) for every input variable. In the statistical section, the significant terms of Equation (4) will be identified and their influence on the response value (VBD). Equation (4) is applicable only for the electrode configuration point/plane gap and not for point/point or plane/plane gap.

Figure 7. Value of α_i of the BBD model for Equation (4).

4. Statistical Analyses

The approximate solution for Equation (4) can be developed using statistical analysis to explain the significant terms. The statistical analysis provides the regression analysis to evaluate the descriptive model quality [13]. The hypothesis test (p-value) and critical value approach (t_crit) can assess the significant terms in Equation (4). The t-test (tstat) is compared with t_crit to determine the essential terms in the predicted equation. When tstat is greater than t_crit, this term is considered an effective term; otherwise, the term can be removed from the predicted equation. The p-value uses the possible probability to decide whether the null hypothesis is rejected by evaluating the p-value risk interval of β = 0.05. The tstat can be assessed using SE_i parameter. The SE_i in Table 4 denotes the modification of residue coefficients that are computed by [13]:

$$S{E}_i^2 = \frac{\left(\frac{1}{N_r - N_c}{\displaystyle \sum }{e}_i^2\right)}{N_r}$$

(5)

N_r represents the experiment number, while N_c denotes the number of used variable coefficients. Note that the variance between them, formulated by N_r − N_c, is named the number of degrees of freedom. In turn, e_i denotes the residues that rapid the alteration between the measured and forecast values of the response (VBD).

Table 4. Statistical parameters and model coefficients using coded values (see Table 1).

	Coefficient	SE	Tstat	p-Value
(Intercept)	38.75	0.33953	114.13	6.54 × 10−17
(a/d)%	−2.1875	0.20792	−10.521	9.96 × 10−7
εr	1.9375	0.20792	9.3187	3.02 × 10−6
hr	−0.625	0.20792	−3.006	0.013207
th	3	0.20792	14.429	5.07 × 10−8
θ	−8.75	0.20792	−42.084	1.38 × 10−12
(a/d)%: εr	0.25	0.41583	0.6012	0.56108
(a/d)%: hr	0.5	0.41583	1.2024	0.2569
(a/d)%: th	−0.25	0.41583	−0.6012	0.56108
(a/d)%: θ	−0.25	0.41583	−0.6012	0.56108
εr: hr	−0.25	0.41583	−0.6012	0.56108
εr: th	1.78 × 10−15	0.41583	4.27 × 10−15	1
εr: θ	−0.25	0.41583	−0.6012	0.56108
hr: th	5.32 × 10−15	0.41583	1.28 × 10−14	1
hr: θ	−0.25	0.41583	−0.6012	0.56108
th: θ	1.75	0.41583	4.2084	0.001804
(a/d)%2	−0.47917	0.28152	−1.7021	0.11957
εr2	−0.3125	0.28152	−1.11	0.29296
hr2	−0.39583	0.28152	−1.4061	0.19001
th2	0.27083	0.28152	0.96204	0.35872
θ2	9.1042	0.28152	32.339	1.88 × 10−11

The tstat represents the coefficient of t-test model. In Table 4, tstat can be assessed by the ratio of the mathematical model’s coefficients to the SE at each variable coefficient α_i, as in Equation (6).

$$tstat = \raisebox{1ex}{${\alpha }_i$}\!\left/ \!\raisebox{-1ex}{$S{E}_i$}\right.$$

(6)

The t-test is used to examine the vital result of every input variable. The critical t-test value (t_crit) can be calculated in Equation (7) as in [13].

$$t_{crit} = \left(\beta ,N_r - N_c\right)$$

(7)

Based on the parameters of Equation (7), where the risk interval β is equal to 0.05 and N_r − N_c is equal to 25, then t_crit is equal to 1.708. As shown in Table 3, the tstat values corresponding to each α coefficient indicate that the most significant terms of Equation (4) on the VBD are the shaded rows in Table 3. The value of p-value sustains this fact, where every shaded row has a p-value less than 0.005. The low p-value of each shaded row designates that the sample data can provide a productive indication to discard the null theory from the whole population of the experimental runs.

Note that the p-value (see Table 4) exemplifies which forecast variable significantly affects the response. Consequently, as for the t-test, the variables (a/d)%, ε_r, hr, th, θ, (th × θ), and θ² are significant terms of Equation (4) in the model, given that its p-value is less than 0.05.

The other statistical parameters that assess the designed model’s evocative excellence, such as the R-squared (R-sq), adjusted R-squared, and the F-statistic, can be determined in Table 5. As shown in Table 5, the R-squared is 0.993, which indicates the strong relation between the experiment variables and the experiment response. The adjusted R-squared is 0.983, which refers to the compatibility between the response’s measured and predicted value. The F-statistic is 175, which indicates the significant predictive capability of the designed model. The root means squared error of the developed model is very low (0.832), which means fewer differences between the measured and predicted response values.

Table 5. Quality coefficients for model expressive.

Observation number	46
Freedom degree	25
Root mean squared error	0.832
R-squared	0.993
Attuned R-squared	0.987
F-statistic vs. constant model	175
p-value	4.88 × 10−22

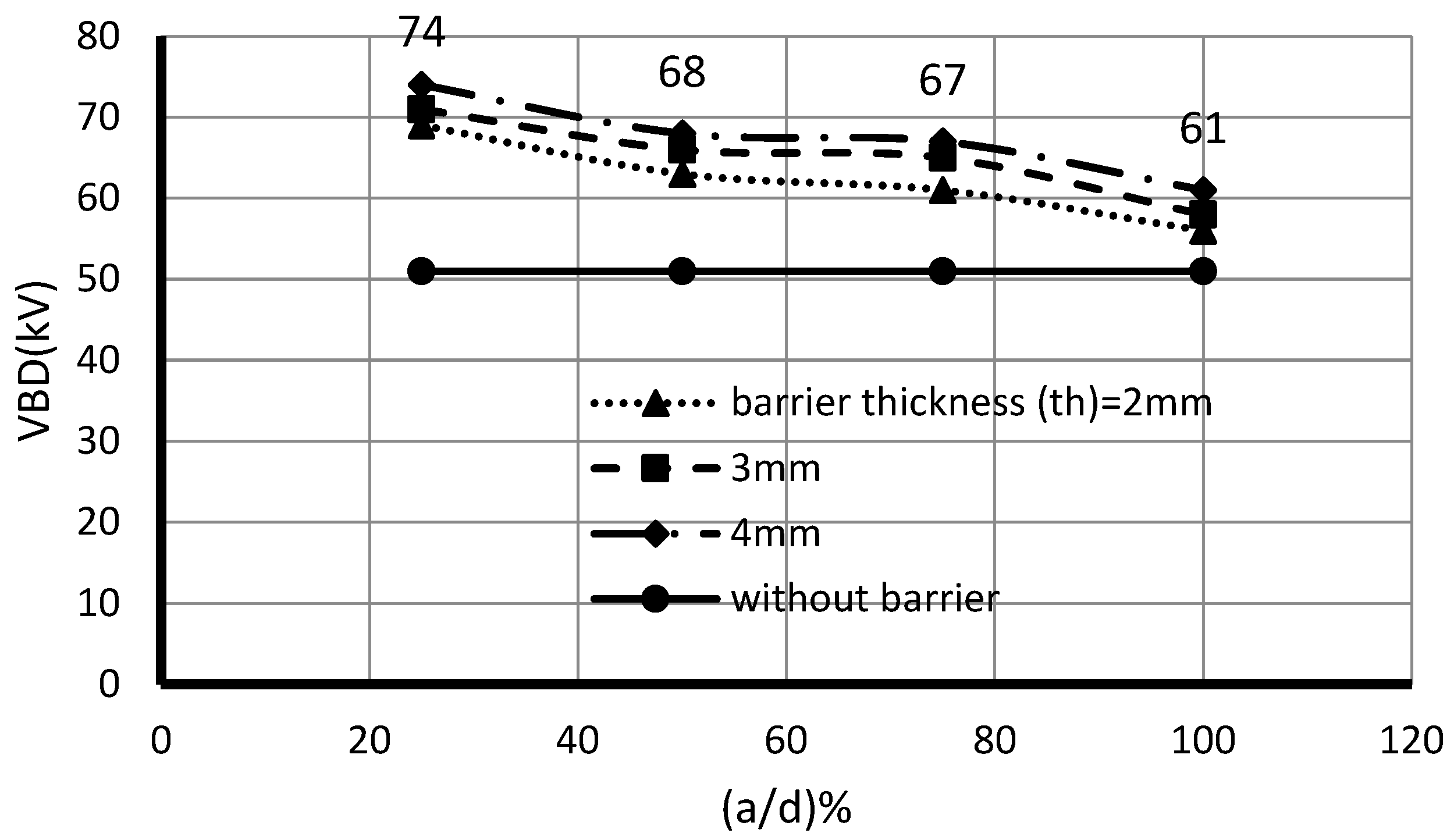
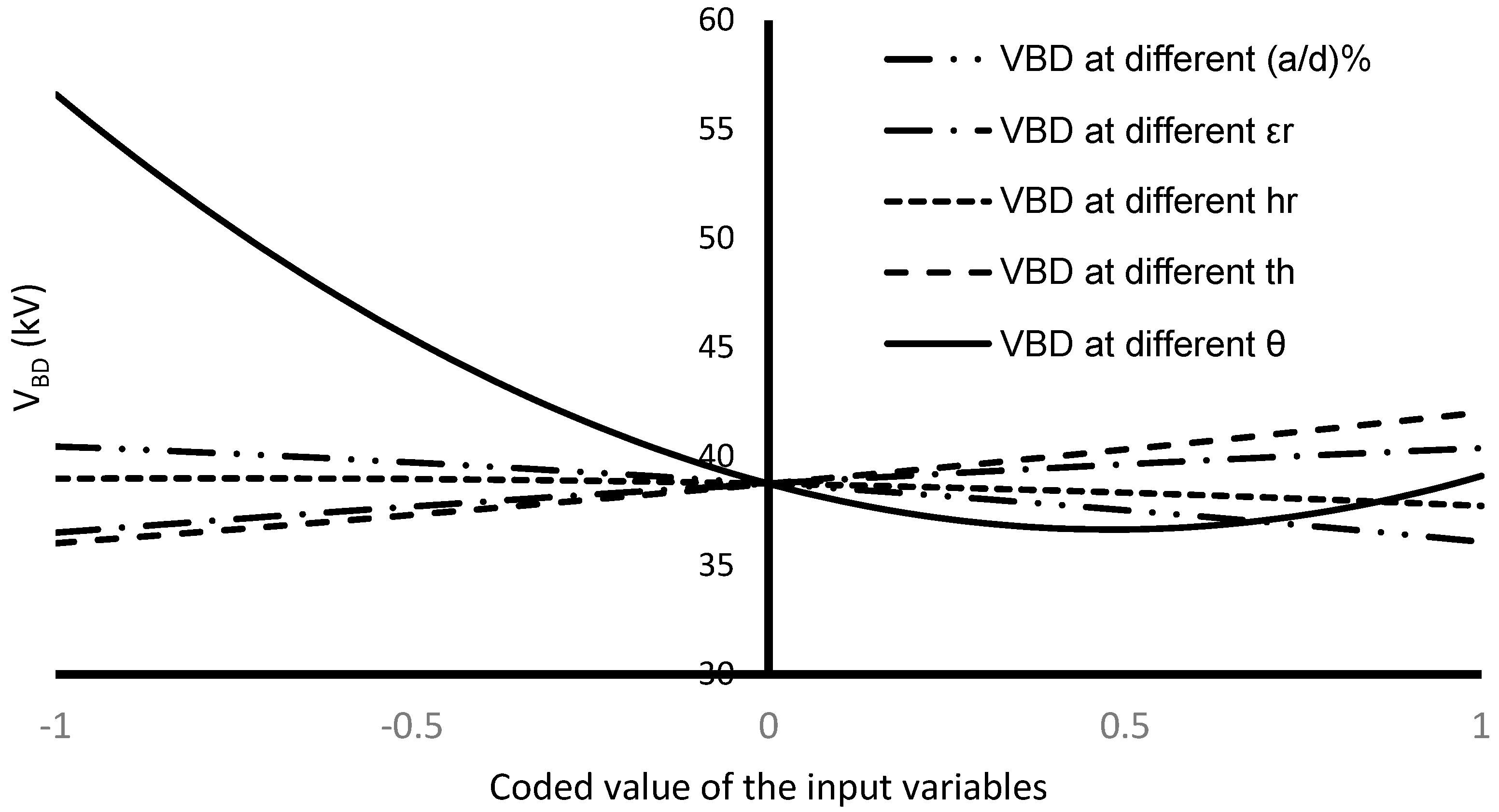
Figure 8 illustrates the variation in the experiment variables with the variation in the experiment response. As observed, the barrier thickness and the barrier’s inclined angle are essential variables that influence the magnitude of the experiment response (VBD). The absolute variation percentage of the VBD to the barrier thickness variation is ((36.0208−42.0208)/42.0208) × 100 = 14.27%, while the absolute deviation of the VBD according to the inclined angle of the barrier is ((56.6042−39.1042)/56.6042) × 100) = 30.9%.

Figure 8. Impact of the adopted variables on VBD.

Equation (4) can be approximated to Equation (8) by eliminating the variables that insignificantly affect the response, according to Table 4. The approximation equation is explained as follows:

$$VBD = 38.75 - 2.1875·\left(\raisebox{1ex}{$a$}\!\left/ \!\raisebox{-1ex}{$d$}\right.\right) + 1.9375·\left({\epsilon }_r\right) - 0.625·hr + 3·th - 8.75·\theta + 1.75·th·\theta + 9.1042·{\left(\theta \right)}^2$$

(8)

Table 6 illustrates the residual percentage between the measured value of VBD and the predicted value from Equations (4) and (8). The residual percentage refers to the percentage difference between the measured VBD (actual) and the predicted VBD using the BBD technique (simulation) at certain experiment conditions as in Table 6 and Table 7. As shown in Table 6, the maximum residual percentage from Equation (4) is 3.81% at the run number of 18, and the maximum residual percentage from Equation (8) is 5.19% at the run number of 36. All other residual percentages are within acceptable limits.

Table 6. Residual % between the measured VBD and predicted VBD based on Equations (4) and (8).

	Measured VBD	Equation (4)			Equation (8)
		Predicted VBD	Residual	Residual %	Predicted VBD	Residual	Residual %
1	38	38.4583	0.4583	1.206053	39	1	2.564103
2	42	41.8333	0.1667	0.396905	42.875	0.875	2.040816
3	33	33.5833	0.5833	1.767576	34.625	1.625	4.693141
4	38	37.9583	0.0417	0.109737	38.5	0.5	1.298701
5	36	36.25	0.25	0.694444	36.375	0.375	1.030928
6	43	42.25	0.75	1.744186	42.375	0.625	1.474926
7	34	35	1	2.941176	35.125	1.125	3.202847
8	41	41	0	0	41.125	0.125	0.303951
9	54	54.3542	0.3542	0.655926	54.6667	0.6667	1.219572
10	38	36.8542	1.1458	3.015263	37.1667	0.8333	2.242061
11	58	58.2292	0.2292	0.395172	58.5417	0.5417	0.925323
12	41	40.7292	0.2708	0.660488	41.0417	0.0417	0.101604
13	41	41.1875	0.1875	0.457317	41.5625	0.5625	1.353383
14	39	38.9375	0.0625	0.160256	40.3125	1.3125	3.255814
15	36	35.8125	0.1875	0.520833	37.1875	1.1875	3.193277
16	36	35.5625	0.4375	1.215278	35.9375	0.0625	0.173913
17	57	55.625	1.375	2.412281	55.3542	1.6458	2.973216
18	36	34.625	1.375	3.819444	34.3542	1.6458	4.790681
19	57	58.125	1.125	1.973684	57.8542	0.8542	1.47647
20	43	44.125	1.125	2.616279	43.8542	0.8542	1.947818
21	37	36.4792	0.5208	1.407568	37.4375	0.4375	1.168614
22	36	35.7292	0.2708	0.752222	36.1875	0.1875	0.518135
23	41	40.8542	0.1458	0.35561	41.3125	0.3125	0.75643
24	39	39.1042	0.1042	0.267179	40.0625	1.0625	2.652106
25	37	37.4791	0.4791	1.294865	37.9375	0.9375	2.47117
26	44	43.9791	0.0209	0.0475	43.9375	0.0625	0.142248
27	34	33.6041	0.3959	1.164412	33.5625	0.4375	1.303538
28	40	39.1041	0.8959	2.23975	39.5625	0.4375	1.105845
29	56	56.5834	0.5834	1.041786	57.2292	1.2292	2.147855
30	39	39.5834	0.5834	1.495897	39.7292	0.7292	1.835426
31	56	55.8334	0.1666	0.2975	55.9792	0.0208	0.037157
32	38	37.8334	0.1666	0.438421	38.4792	0.4792	1.245348
33	59	58.0625	0.9375	1.588983	58.7917	0.2083	0.354302
34	41	41.0625	0.0625	0.152439	41.2917	0.2917	0.706437
35	54	54.1875	0.1875	0.347222	54.4167	0.4167	0.765758
36	35	36.1875	1.1875	3.392857	36.9167	1.9167	5.191959
37	33	33.7708	0.7708	2.335758	33.8125	0.8125	2.402957
38	40	39.7708	0.2292	0.573	39.8125	0.1875	0.470958
39	37	37.6458	0.6458	1.745405	37.6875	0.6875	1.824212
40	44	43.6458	0.3542	0.805	43.6875	0.3125	0.715308
41	39	38.75	0.25	0.641026	38.75	0.25	0.645161
42	38.5	38.75	0.25	0.649351	38.75	0.25	0.645161
43	38	38.75	0.75	1.973684	38.75	0.75	1.935484
44	38.5	38.75	0.25	0.649351	38.75	0.25	0.645161
45	39	38.75	0.25	0.641026	38.75	0.25	0.645161
46	39.5	38.75	0.75	1.898734	38.75	0.75	1.935484

Table 7. Residuals % of Equations (4) and (8) according to the measured VBD for additional random experiments.

	(a/d)%	εr	hr	th	θ	Measured VBD	Predicted VBD from Equation (4)			Predicted VBD from Equation (8)
							VBD	Residual	Residual %	VBD	Residual	Residual %
1	0	1	1	1	0	44	42.375	1.625	3.693182	43.0625	0.9375	2.177068
2	0	1	−1	1	0	46	44.125	1.875	4.076087	44.3125	1.6875	3.808181
3	0	1	1	−1	0	37	36.375	0.625	1.689189	37.0625	0.0625	0.168634
4	0	−1	1	1	0	38	39	1	2.631579	39.1875	1.1875	3.030303
5	1	0	1	0	1	35	35.4167	0.4167	1.190571	36.2917	1.2917	3.559216
6	1	0	−1	0	−1	53	53.6667	0.6667	1.257925	55.0417	2.0417	3.709369
7	1	0	−1	0	1	36	36.1667	0.1667	0.463056	37.5417	1.5417	4.106633
8	−1	1	1	1	0	45	43.5833	1.4167	3.148222	45.25	0.25	0.552486
9	−1	1	−1	1	0	47	46.3333	0.6667	1.418511	46.5	0.5	1.075269
10	−1	1	−1	−1	0	40	39.8333	0.1667	0.41675	40.5	0.5	1.234568
11	−1	0	0	1	−1	59	59.8333	0.8333	1.412373	60.0417	1.0417	1.734961
12	−1	0	0	−1	−1	59	56.8333	2.1667	3.672373	57.5417	1.4583	2.534336
13	0	0	1	1	1	43	42.8542	0.1458	0.33907	43.2292	0.2292	0.530197
14	0	0	1	1	−1	57	57.3542	0.3542	0.621404	57.2292	0.2292	0.400495
15	0	0	1	−1	1	32	33.3542	1.3542	4.231875	33.7292	1.7292	5.126715
16	0	0	1	−1	−1	57	54.8542	2.1458	3.764561	54.7292	2.2708	4.149156
17	1	−1	−1	−1	−1	52	50.1875	1.8125	3.485577	51.8542	0.1458	0.281173
18	0	1	0	1	−1	58	59.75	1.75	3.017241	59.7917	1.7917	2.99657
19	1	1	−1	−1	−1	54	55.0625	1.0625	1.967593	55.7292	1.7292	3.102862
20	1	1	−1	1	1	44	43.0625	0.9375	2.130682	44.2292	0.2292	0.51821

5. Validation of the Predictive Mathematical Model

Some other random experimental works are accomplished to evaluate the robustness of the predictive model. Table 7 explains 20 random experiment results with the measured VBD and the predicted VBD based on Equations (4) and (8). The obtained results demonstrate that the designed BBD model can predict the VBD based on Equations (4) and (8). As shown in Table 7, the maximum residual percentage is 5.12% at the run number 15. All other residual results are in the acceptable range (<5%).

6. Conclusions

New barrier variables were presented to investigate their consequence on the insulating oil VBD. These new variables are barrier location (a/d)%, dielectric constant (ε_r) of the barrier material, barrier hole radius (hr), barrier thickness (th), and the barrier inclined angle (θ). The experimental work results indicated that two parameters significantly affect the VBD of the insulating oil: the first one is the thickness of the barrier (th), and the second is the barrier inclined angle (θ). BBD design was used to develop a predicted model to identify the VBD with the barrier variables’ variation. The designed DDB model is constructed for the five barrier variables with 46 experiment runs with specified forms. The BBD model results generate low residual errors between the measured VBD and predicted VBD based on Equations (4) and (8). The residual percentage of the predicted VBD from Equation (4) is less than 5% for all 46 experiment runs.

The mathematical model is constructed based on the coded values (−1, 0, 1), where –1 refers to the minimum value of the variable x, 0 refers to the mean of the variable x, and 1 refers to the maximum value of x. Therefore, the constructed model can be validated using the input parameters’ coded values (−1, 0, 1).

New 30 random experiment cases were used to measure the robustness and quality of the designed model to validate the BBD model with other experiment cases. All the residual percentages of all cases for Equation (4) are less than 5%. The approximation predicted VBD equation is developed on the basis of the statistical analysis using t-test and p-value. Then, the approximated Equation (8) is developed. The results show that only one case in the 46 experiment runs generates a residual percentage of 5.19%, and the other 20 validation experiment runs also generate one case with a residual percentage of 5.12%. Consequently, Equations (4) and (8) can predict the VBD of the insulating oil for any other new cases.

In future work, the application of nanotechnology for enhancing the breakdown voltage strength of various insulating materials [44,45,46,47,48,49,50,51,52] in the presence of different barrier effects will be investigated, specifically in the transformer insulating oil.