Numerical Analysis of a Flow over Spheres Embedded on a Flat Wall
Abstract
1. Introduction
2. Mathematical Modelling
2.1. Solution Algorithm
2.2. Spatial Discretisation
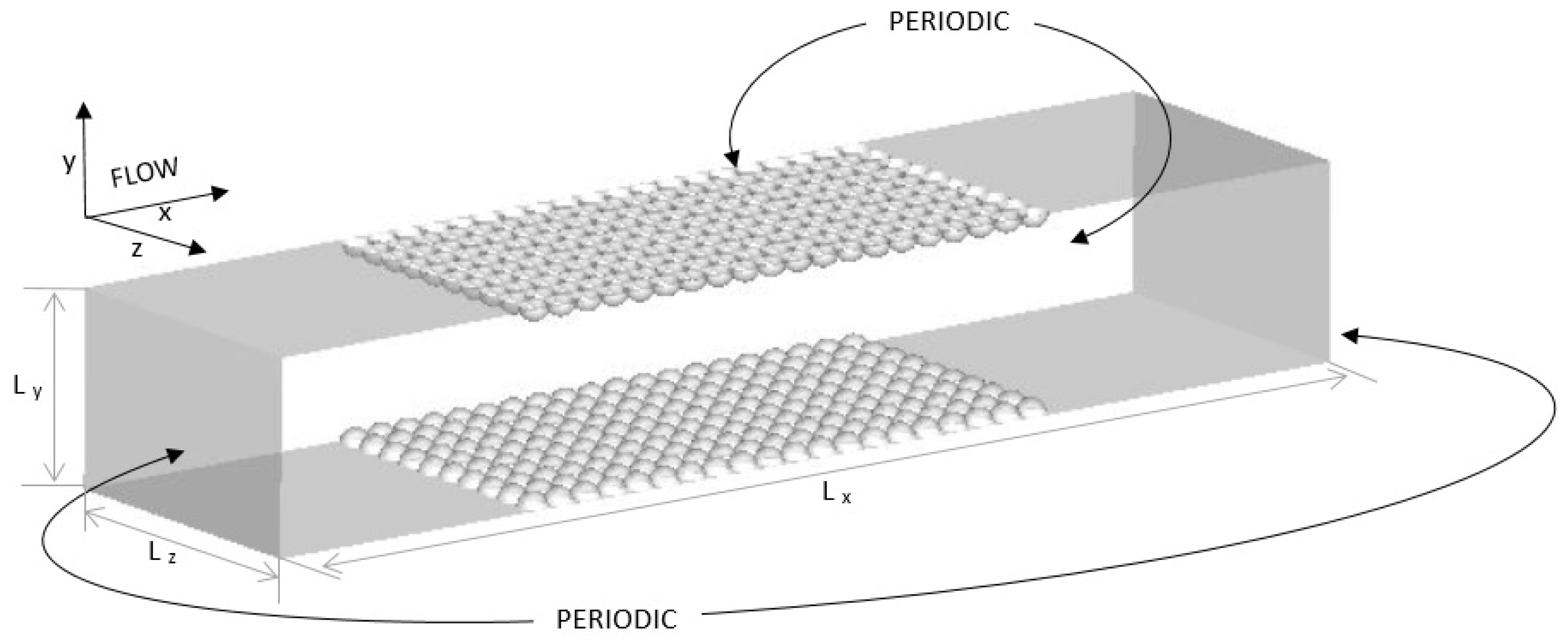
3. Computational Configuration
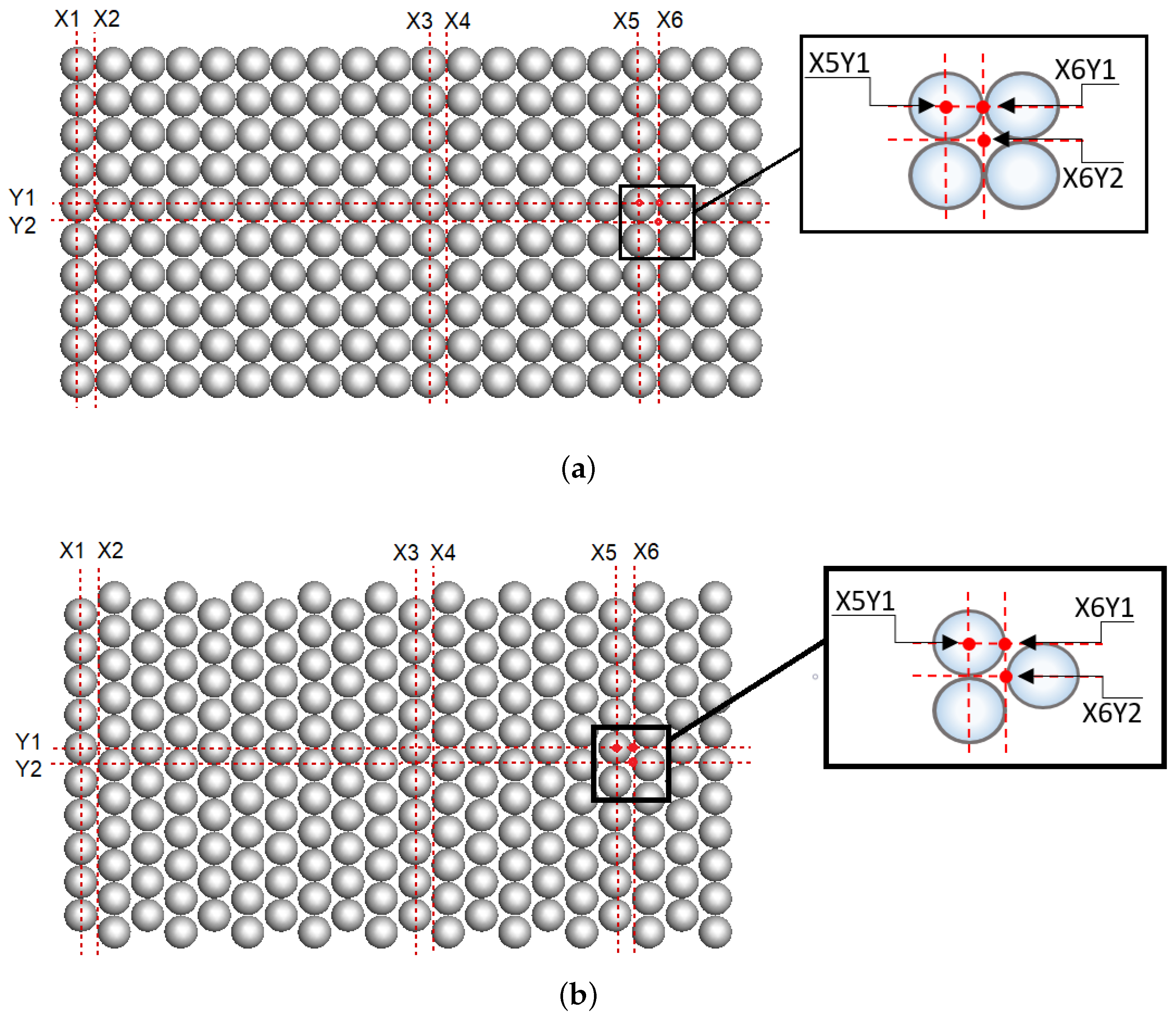
3.1. Computational Domain and Spheres Localizations
3.2. Computational Meshes
4. Results
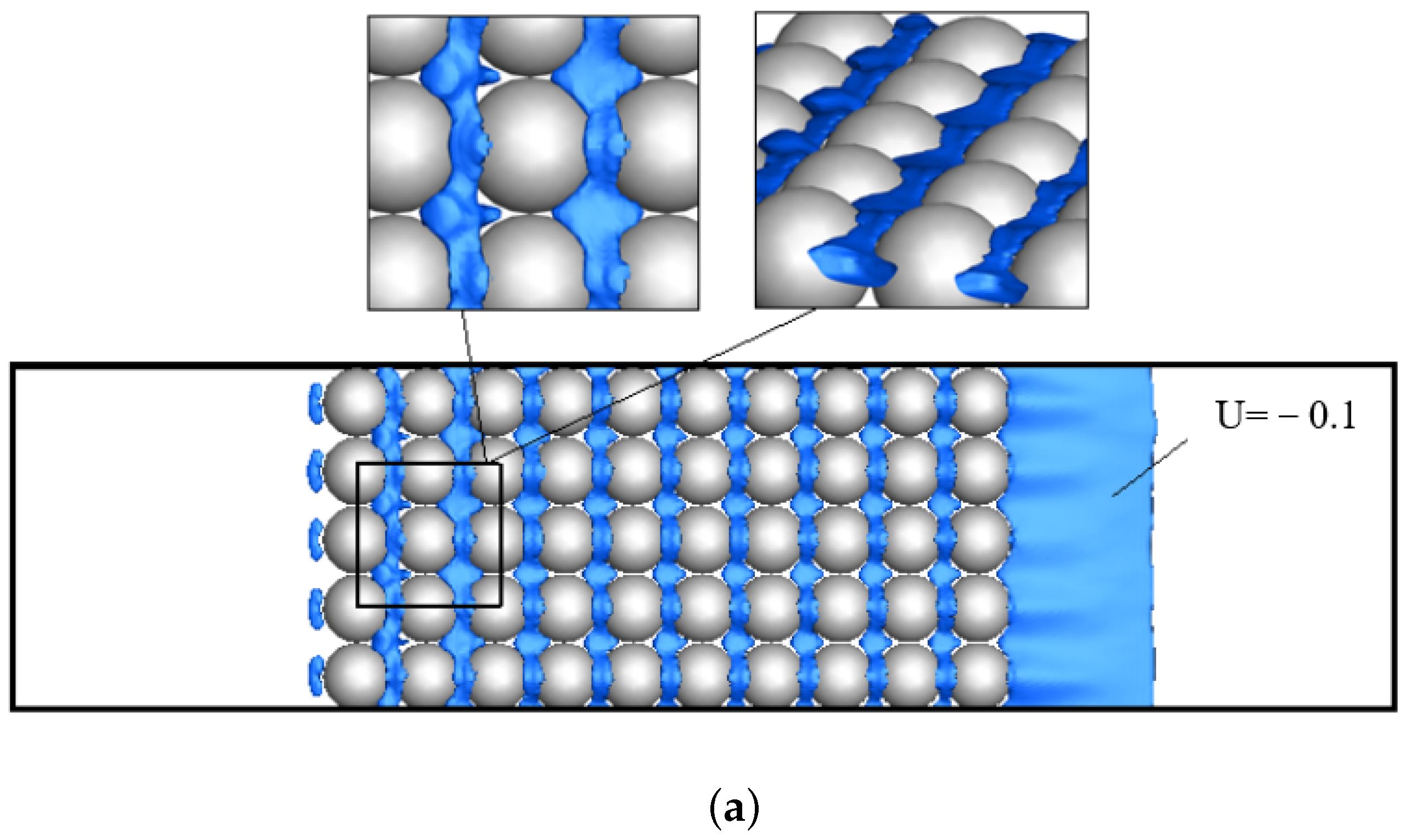
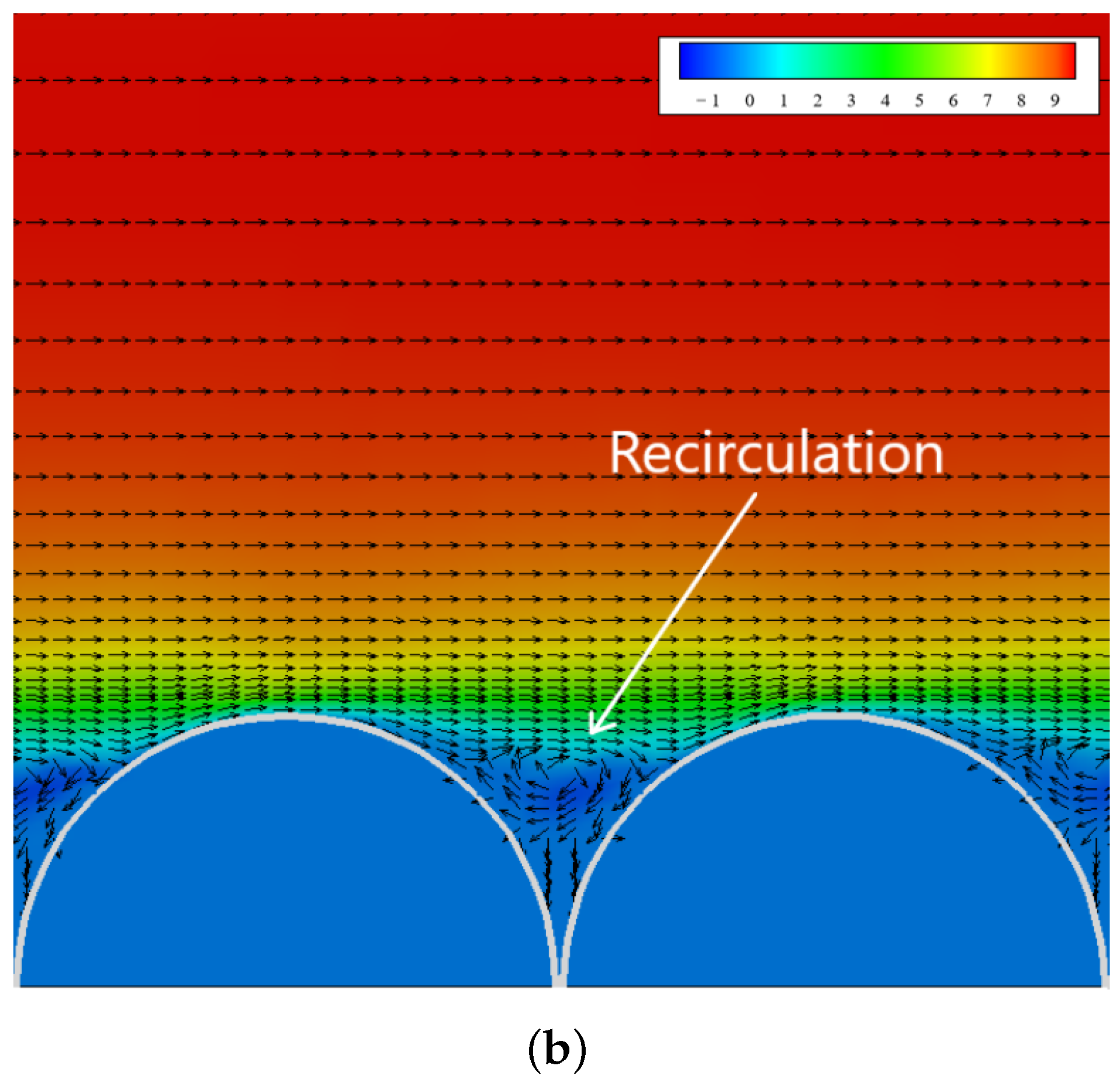
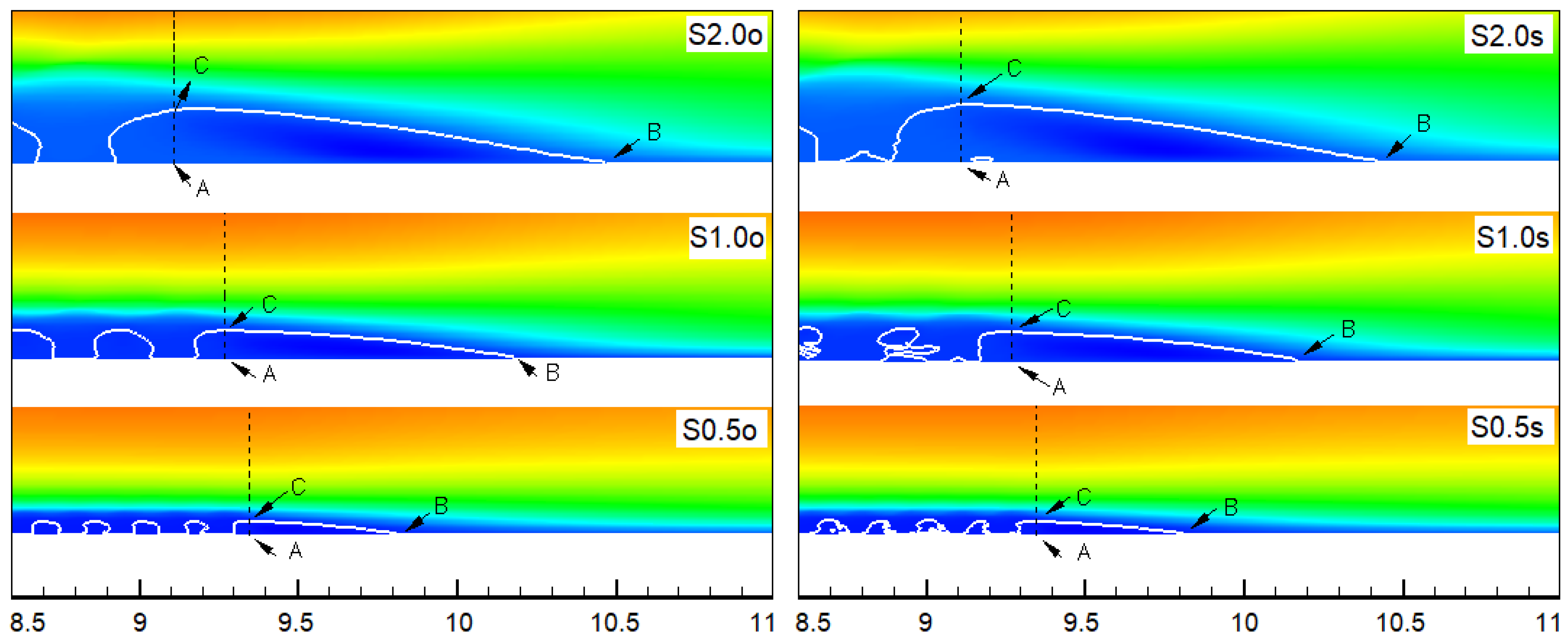
4.1. Instantaneous Flow Behavior
4.2. Time-Averaged Results
Profiles of the Mean Velocity and Its Fluctuations
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dróżdż, A.; Niegodajew, P.; Romańczyk, M.; Sokolenko, V.; Elsner, E. Effective use of the streamwise waviness in the control of turbulent separation. Exp. Therm. Fluid Sci. 2021, 121, 110291. [Google Scholar]
- Chan, L.; MacDonald, M.; Ooi, A. A systematic investigation of roughness height and wavelength in turbulent pipe flow in the transitionally rough regime. J. Fluid Mech. 2015, 771, 743–777. [Google Scholar] [CrossRef]
- Dharaiya, V.V.; Kandikar, S.G. A numerical study on the effects of 2d structured sinusoidal elements on fluid flow and heat transfer at microscale. Int. J. Heat Mass Transf. 2013, 57, 190–201. [Google Scholar] [CrossRef]
- Cherukat, P.; Na, Y.; Hanratty, T.J.; McLaughlin, J.B. Direct Numerical Simulation of a Fully Developed Turbulent Flow over a Wavy Wall. Theor. Comput. Fluid Dyn. 2018, 11, 109–134. [Google Scholar] [CrossRef]
- Kaisar, M.; Hossain, M.; Hossain, A.; Karim, A. Flow Characteristics in Convective Lid-Driven Trapezoidal Cavity with Wavy Bottom Surface. IOSR J. Mech. Civ. Eng. 2019, 16, 37–41. [Google Scholar]
- Bhaganagar, K.; Kim, J.; Coleman, G. Effect of Roughness on Wall-Bounded Turbulence. Flow Turbul. Combust. 2004, 72, 463–492. [Google Scholar] [CrossRef]
- Harikrishnan, S.; Tiwari, S. Heat transfer characteristics of sinusoidal wavy channel with secondary corrugations. Int. J. Therm. Sci. 2019, 145, 105973. [Google Scholar] [CrossRef]
- Hu, Y.D.; Werner, C.; Li, D.Q. Influence of three-dimensional roughness on pressure-driven flow through microchannels. J. Fluids Eng. ASME Digit. Collect. 2003, 125, 871–879. [Google Scholar] [CrossRef]
- Croce, G.; D’Agaro, P. Numerical analysis of roughness effect on microtube heat transfer. Superlattices Microstruct. 2004, 35, 601–616. [Google Scholar] [CrossRef]
- Guo, L.; Xu, H.; Gong, L. Influence of wall roughness models on fluid flow and heat transfer in microchannels. Appl. Therm. Eng. 2015, 84, 399–408. [Google Scholar] [CrossRef]
- Rawool, A.S.; Mitra, S.K.; Kandlikar, S.G. Numerical simulation of flow through microchannels with designed roughness. Microfluid. Nanofluids 2006, 2, 215–221. [Google Scholar] [CrossRef]
- Herwig, H.; Gloss, D.; Wenterodt, T. Flow in Channels With Rough Walls–Old and New Concepts Heat Transfer Engineering. Heat Transf. Eng. 2010, 31, 658–665. [Google Scholar] [CrossRef]
- Noorian, H.; Toghraie, D.; Azimian, A.R. The effects of surface roughness geometry of flow undergoing Poiseuille flow by molecular dynamics simulation. Heat Mass Transf. 2014, 50, 95–104. [Google Scholar] [CrossRef]
- Croce, G.; D’Agaro, P.; Nonino, C. Three-dimensional roughness effect on microchannel heat transfer and pressure drop. Int. J. Heat Mass Transf. 2007, 50, 5249–5259. [Google Scholar] [CrossRef]
- Zhang, Y.Z.; Sun, C.; Bao, Y.; Zhou, Q. How surface roughness reduces heat transport for small roughness heights in turbulent Rayleigh-Benard convection. J. Fluid Mech. 2018, 836, 045114. [Google Scholar] [CrossRef]
- Anderson, W. An immersed boundary method wall model for high-Reynolds-number channel flow over complex topography. Int. J. Numer. Methods Fluids 2012, 71, 1588–1608. [Google Scholar] [CrossRef]
- Banyassady, R.; Piomelli, U. Turbulent plane wall jets over smooth and rough surfaces. J. Turbul. 2014, 15, 186–207. [Google Scholar] [CrossRef]
- Fletcher, C.A.J. Computational Techniques for Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Tyliszczak, A. A high-order compact difference algorithm for half-staggered grids for laminar and turbulent incompressible flows. J. Comput. Phys. 2014, 276, 438–467. [Google Scholar] [CrossRef]
- Tyliszczak, A. High-order compact difference algorithm on half-staggered meshes for low Mach number flows. Comput. Fluids 2016, 127, 131–145. [Google Scholar] [CrossRef]
- Tyliszczak, A.; Szymanek, E. Modeling of heat and fluid flow in granular layers using high-order compact schemes and volume penalization method. Numer. Heat Transf. Part A Appl. 2019, 76, 737–759. [Google Scholar] [CrossRef]
- Fadlun, E.A.; Verzicco, R.; Orlandi, P.; Mohd-Yusof, J. Combined immersed-boundary finite-difference methods for three-dimensional complex flow simulations. J. Comput. Phys. 2000, 161, 35–60. [Google Scholar] [CrossRef]
- Khadra, K.; Angot, P.; Parneix, S.; Caltagirone, J.P. Fictitious domain approach for numerical modelling of Navier-Stokes equations. Int. J. Numer. Methoda Fluids 2000, 34, 651–684. [Google Scholar] [CrossRef]
- Kadoch, B.; Kolomenskiy, D.; Angot, P.; Schneider, K. A volume penalization method for incompressible flows and scalar advection diffusion with moving obstacles. J. Comput. Phys. 2012, 231, 4365–4383. [Google Scholar] [CrossRef]
- Tyliszczak, A.; Ksiezyk, M. Large eddy simulations of wall-bounded flows using a simplified immersed boundary method and high-order compact schemes. Int. J. Numer. Methods Fluids 2018, 87, 358–381. [Google Scholar] [CrossRef]
- Wang, Z.J.; Fidkowski, K.; Abgrall, R.; Bassi, F.; Caraeni, D.; Cary, A.; Deconinck Hartmann, H.; Hillewaert, R.; Huynh, K.; Kroll, H.T.; et al. High-order CFD methods: Current status and perspective. Int. J. Numer. Methods Fluids 2013, 72, 811–845. [Google Scholar] [CrossRef]
- Niegodajew, P.; Dróżdż, A.; Elsner, W. A new approach for estimation of the skin friction in turbulent boundary layer under the adverse pressure gradient conditions. Int. J. Heat Fluid Flow 2019, 79, 108456. [Google Scholar] [CrossRef]






| S0.5 | S1.0 | S2.0 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Mesh | D/Δx | D/Δy | D/Δz | D/Δx | D/Δy | D/Δz | D/Δx | D/Δy | D/Δz |
| Coarse | 5.0 | 13.81 | 5.0 | 10.0 | 27.63 | 10.0 | 20.0 | 55.26 | 20.0 |
| Dense | 7.5 | 28.11 | 7.5 | 15.0 | 56.22 | 15.0 | 30.0 | 112.44 | 30.0 |
| Case | ||||
|---|---|---|---|---|
| S2.0o | 0.19 | 1.30 | 0.146 | 0.123 |
| S1.0o | 0.10 | 0.97 | 0.103 | 0.048 |
| S0.5o | 0.04 | 0.46 | 0.087 | 0.009 |
| S2.0s | 0.17 | 1.35 | 0.126 | 0.115 |
| S1.0s | 0.09 | 0.98 | 0.092 | 0.044 |
| S0.5s | 0.04 | 0.46 | 0.087 | 0.009 |
| Case | ||||||
|---|---|---|---|---|---|---|
| S2.0o | 8.435 | 6.259 | 1.509 | 0.156 | 1.014 | 0.094 |
| S1.0o | 12.423 | 10.399 | 1.862 | 0.116 | 1.019 | 0.060 |
| S0.5o | 15.869 | 13.394 | 2.429 | 0.099 | 0.877 | 0.047 |
| S2.0s | 8.470 | 6.338 | 1.517 | 0.154 | 1.015 | 0.093 |
| S1.0s | 12.623 | 10.239 | 1.887 | 0.120 | 1.019 | 0.063 |
| S0.5s | 15.928 | 13.470 | 2.569 | 0.101 | 0.878 | 0.049 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Szymanek, E.; Tyliszczak, A. Numerical Analysis of a Flow over Spheres Embedded on a Flat Wall. Processes 2021, 9, 277. https://doi.org/10.3390/pr9020277
Szymanek E, Tyliszczak A. Numerical Analysis of a Flow over Spheres Embedded on a Flat Wall. Processes. 2021; 9(2):277. https://doi.org/10.3390/pr9020277
Chicago/Turabian StyleSzymanek, Ewa, and Artur Tyliszczak. 2021. "Numerical Analysis of a Flow over Spheres Embedded on a Flat Wall" Processes 9, no. 2: 277. https://doi.org/10.3390/pr9020277
APA StyleSzymanek, E., & Tyliszczak, A. (2021). Numerical Analysis of a Flow over Spheres Embedded on a Flat Wall. Processes, 9(2), 277. https://doi.org/10.3390/pr9020277







