Design Guideline for Hydropower Plants Using One or Multiple Archimedes Screws
Abstract
:1. Introduction
2. Methods and Materials
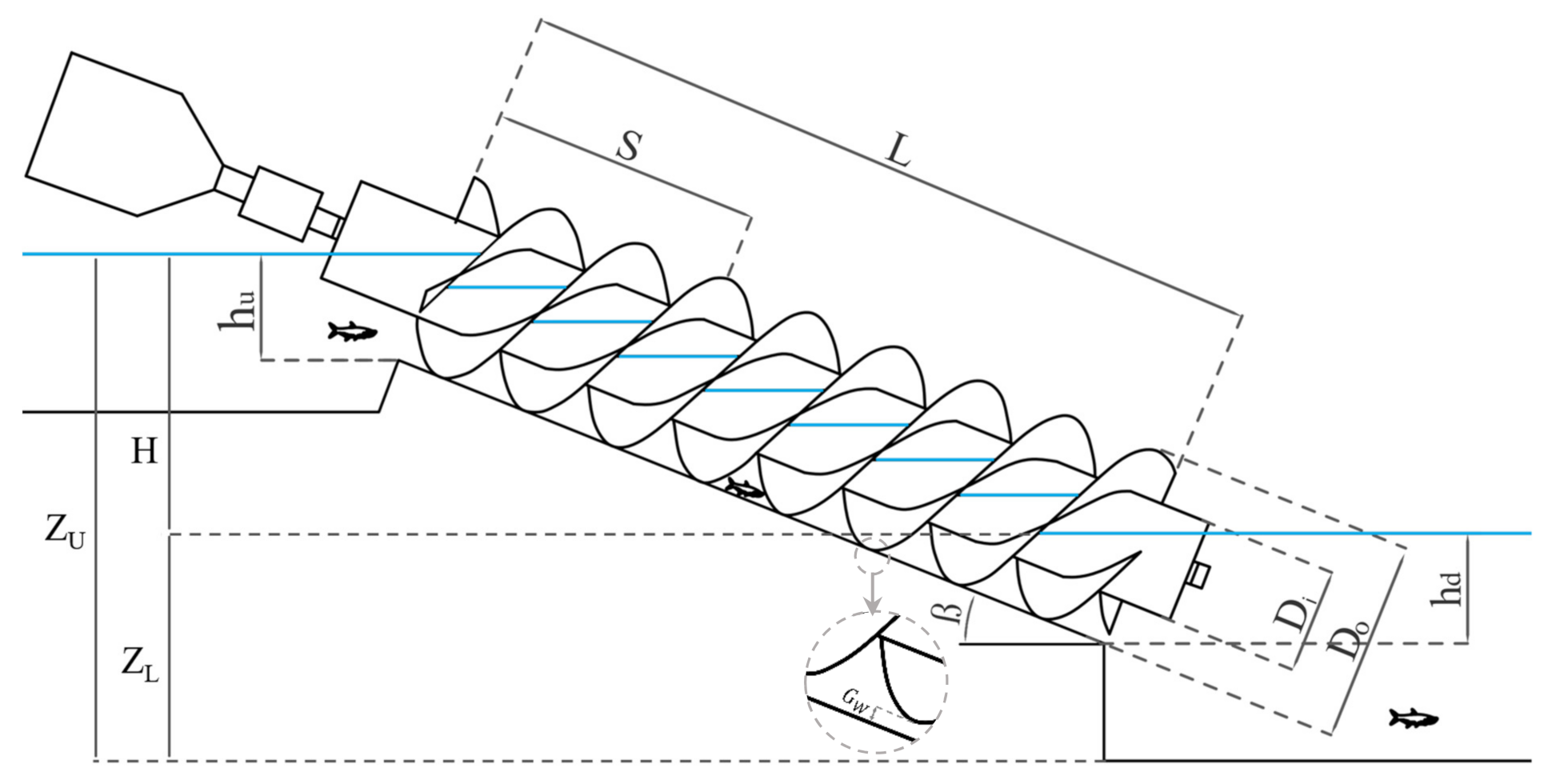
2.1. Design Parameters of Archimedes Screws
2.2. Archimedes Screws Configurations in Hydropower Plants
2.2.1. Archimedes Screws in Series Configuration
2.2.2. Archimedes Screws in Parallel Configuration
2.3. Case Studies
2.4. Evaluation Criteria
3. Results and Discussion
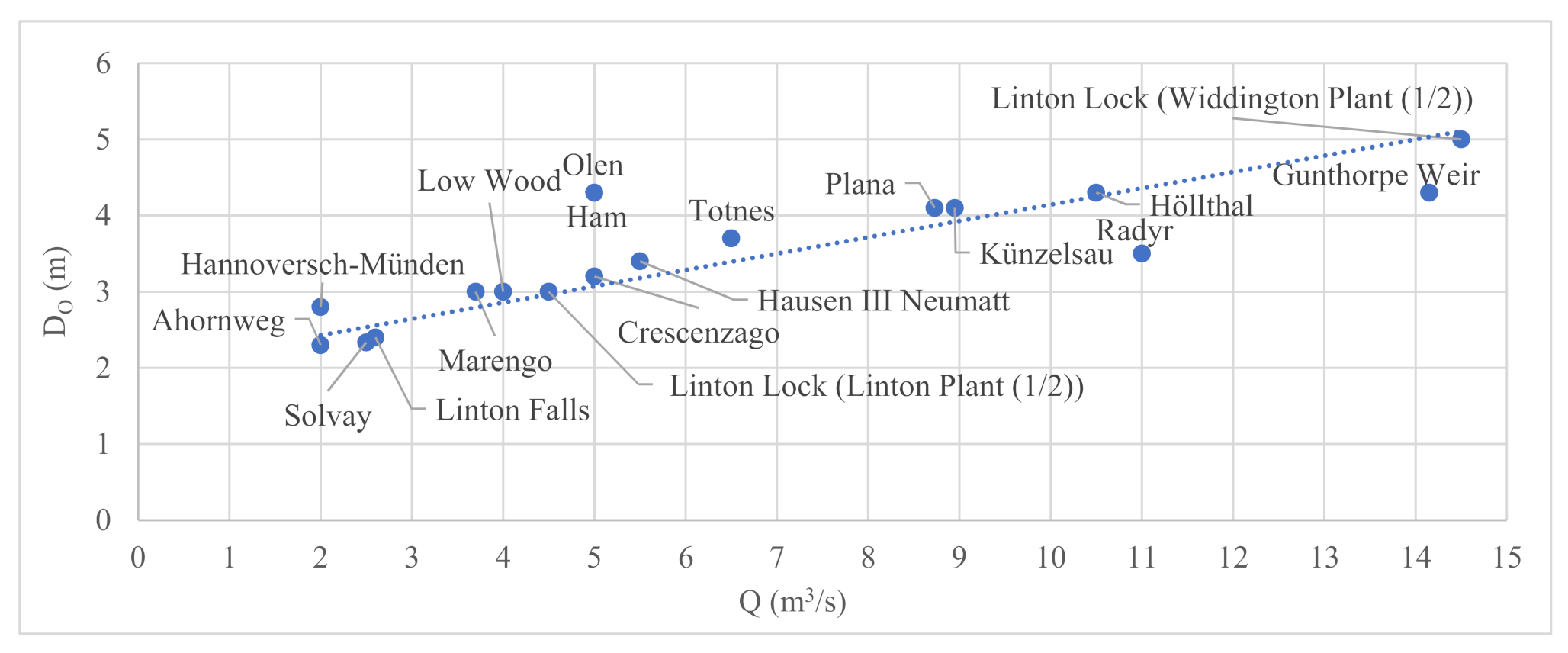
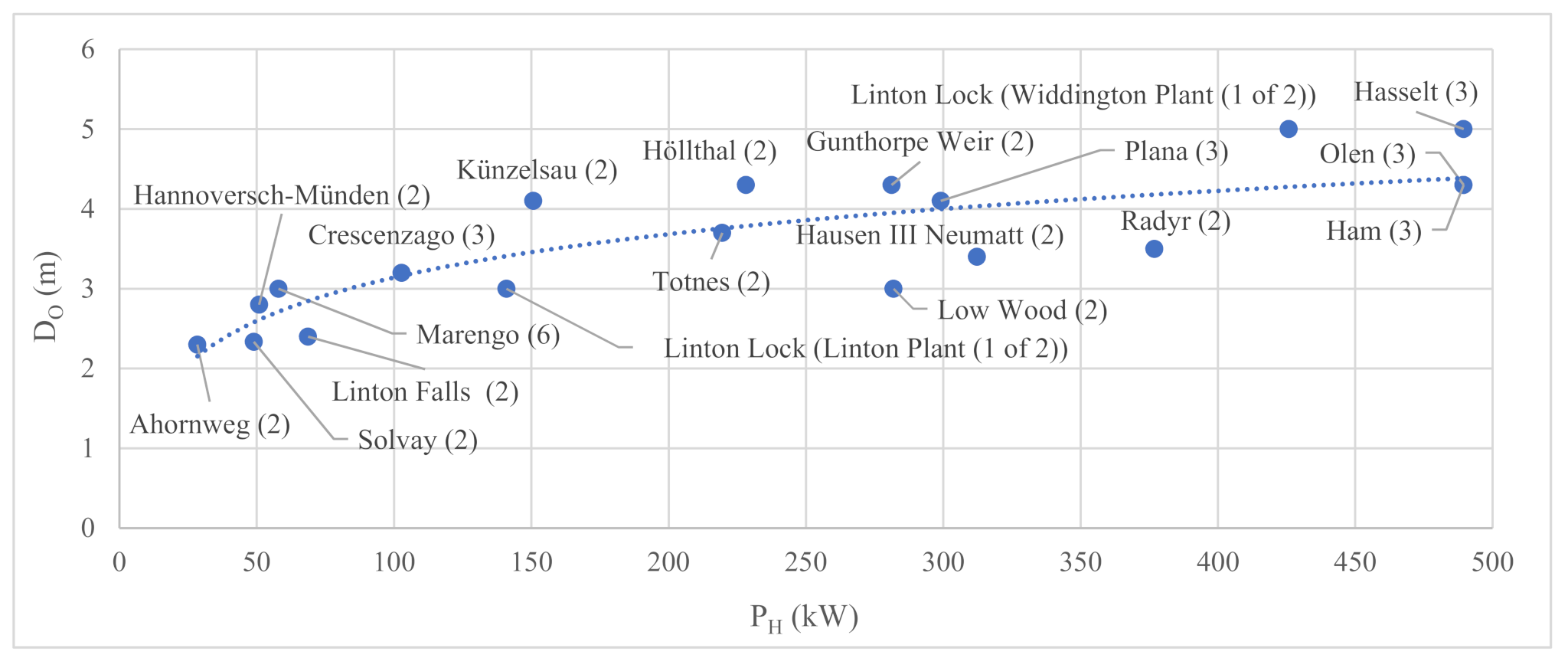
3.1. Volumetric Flow Rate and Diameter of Archimedes Screws
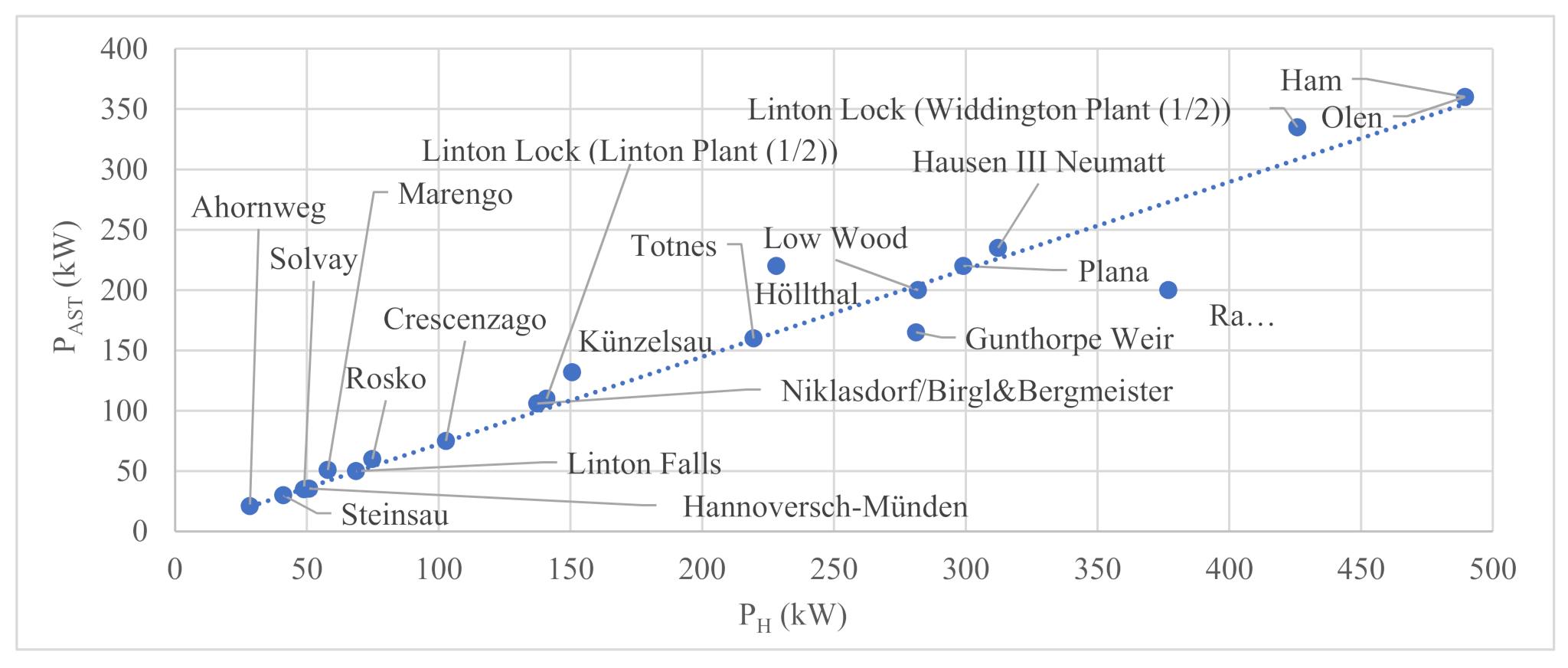
3.2. Power and Diameter of Archimedes Screws
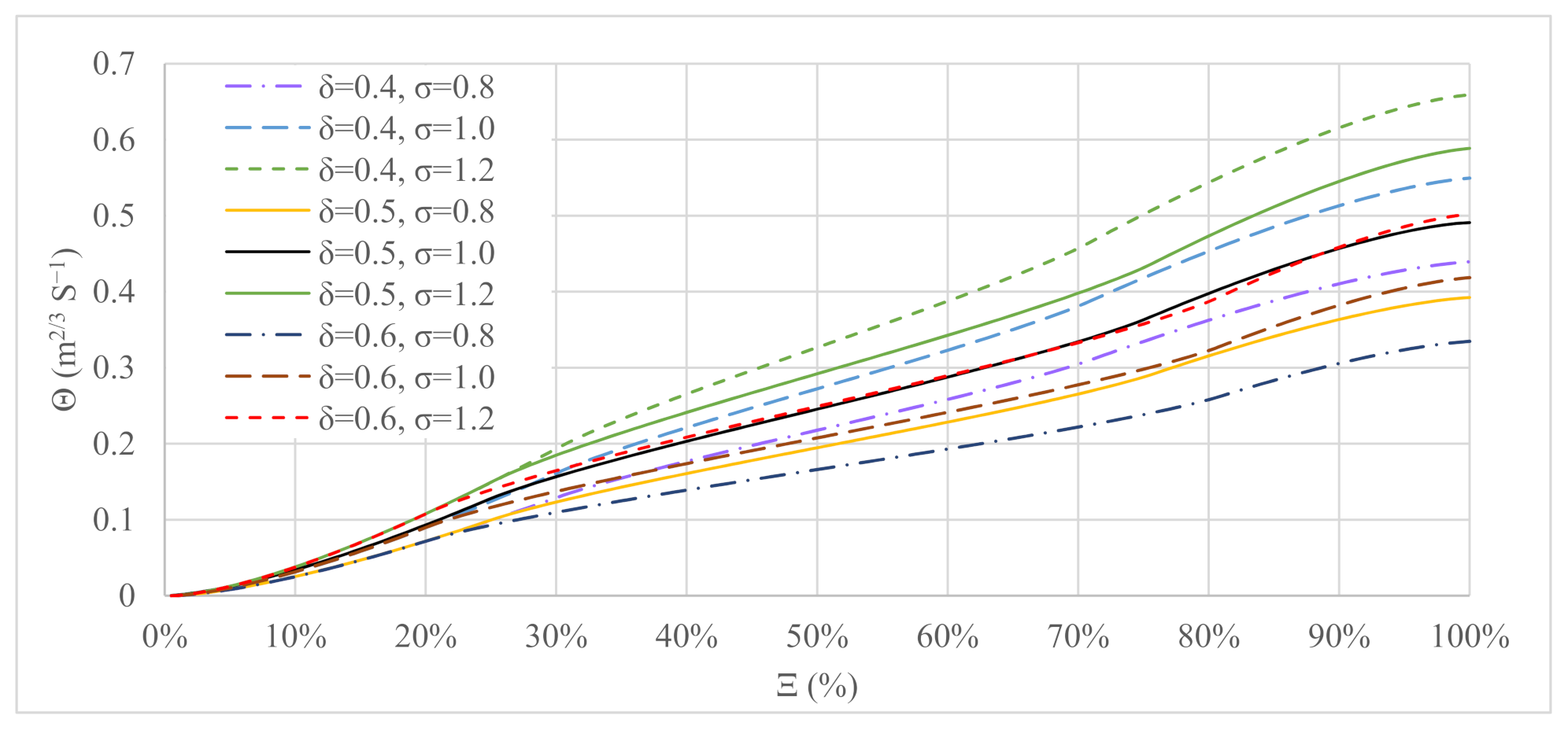
3.3. Analytical Equation
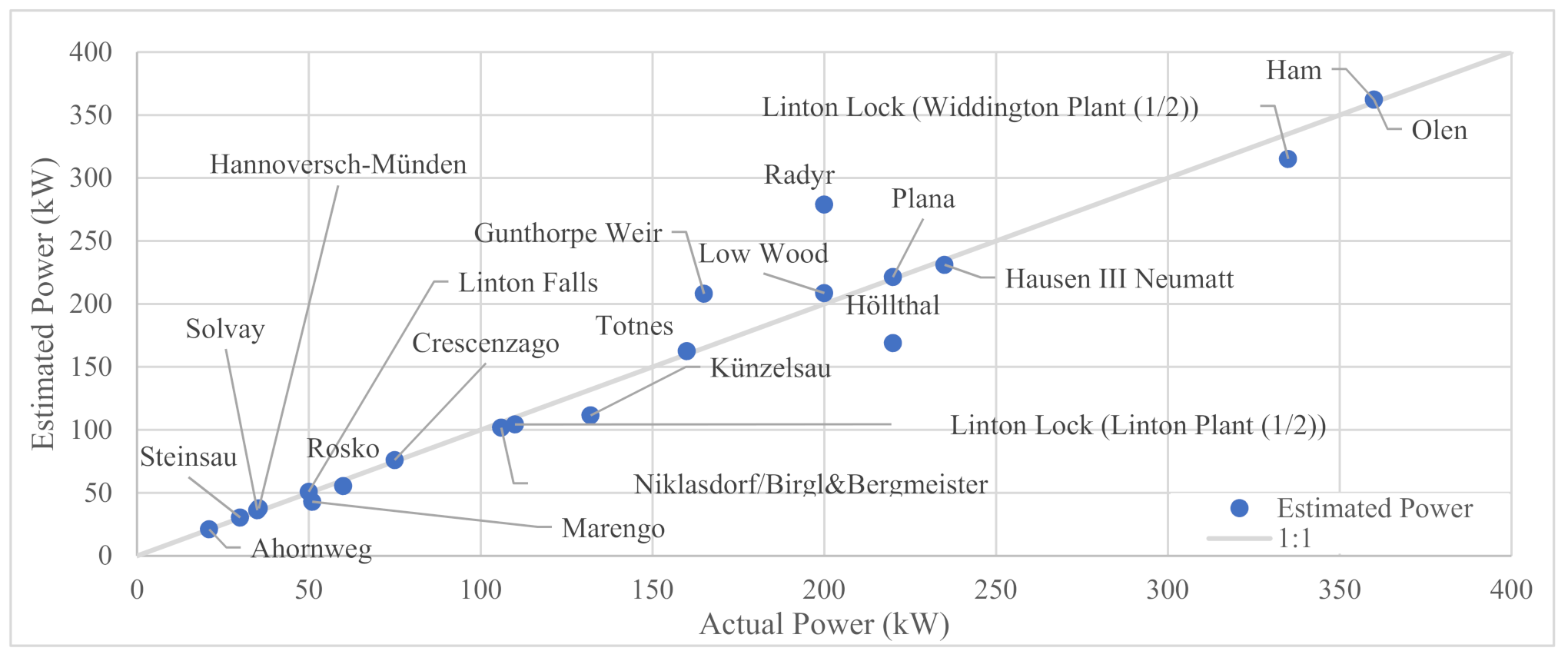
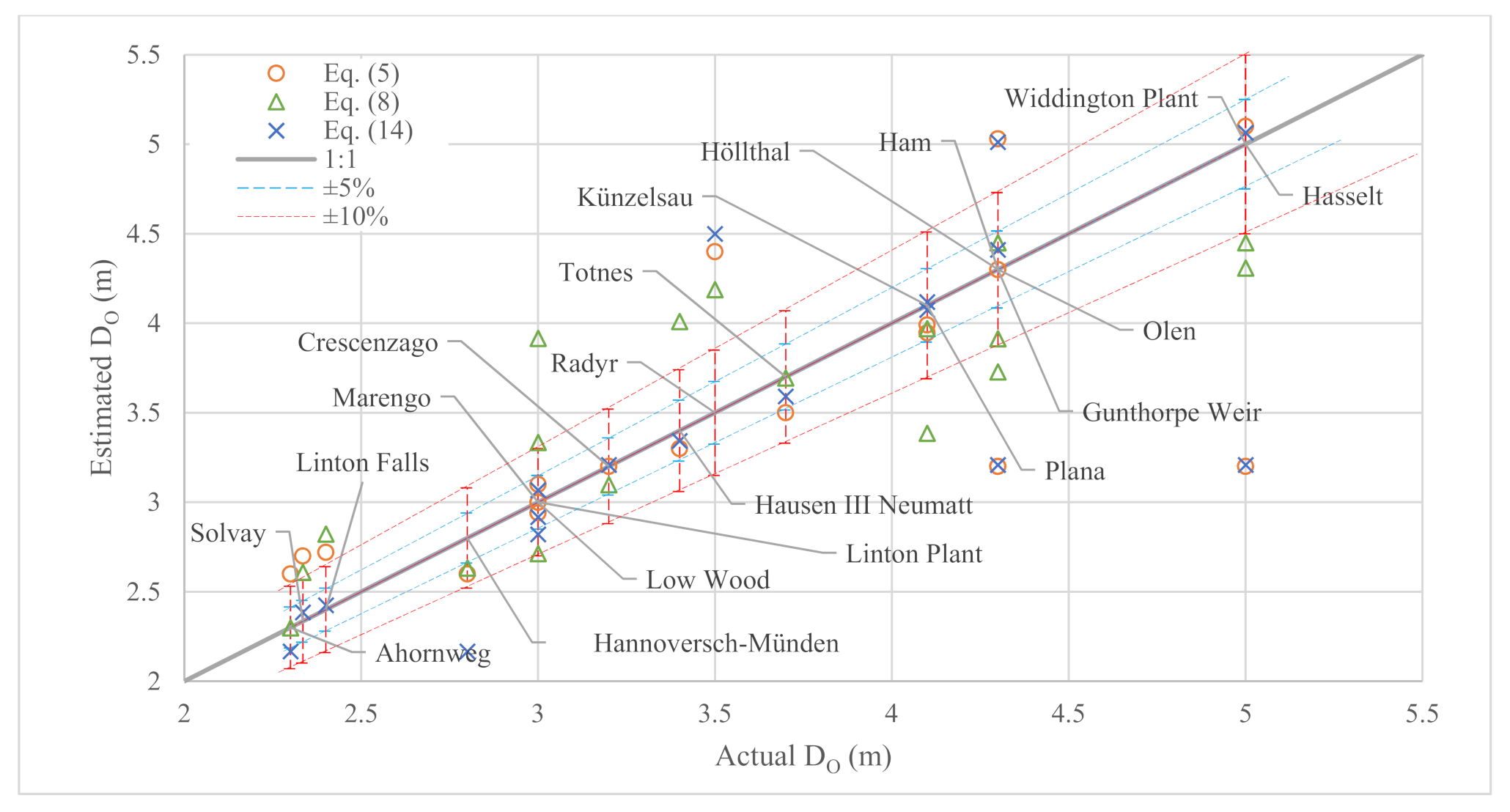
3.4. Evaluation of the Developed Equations
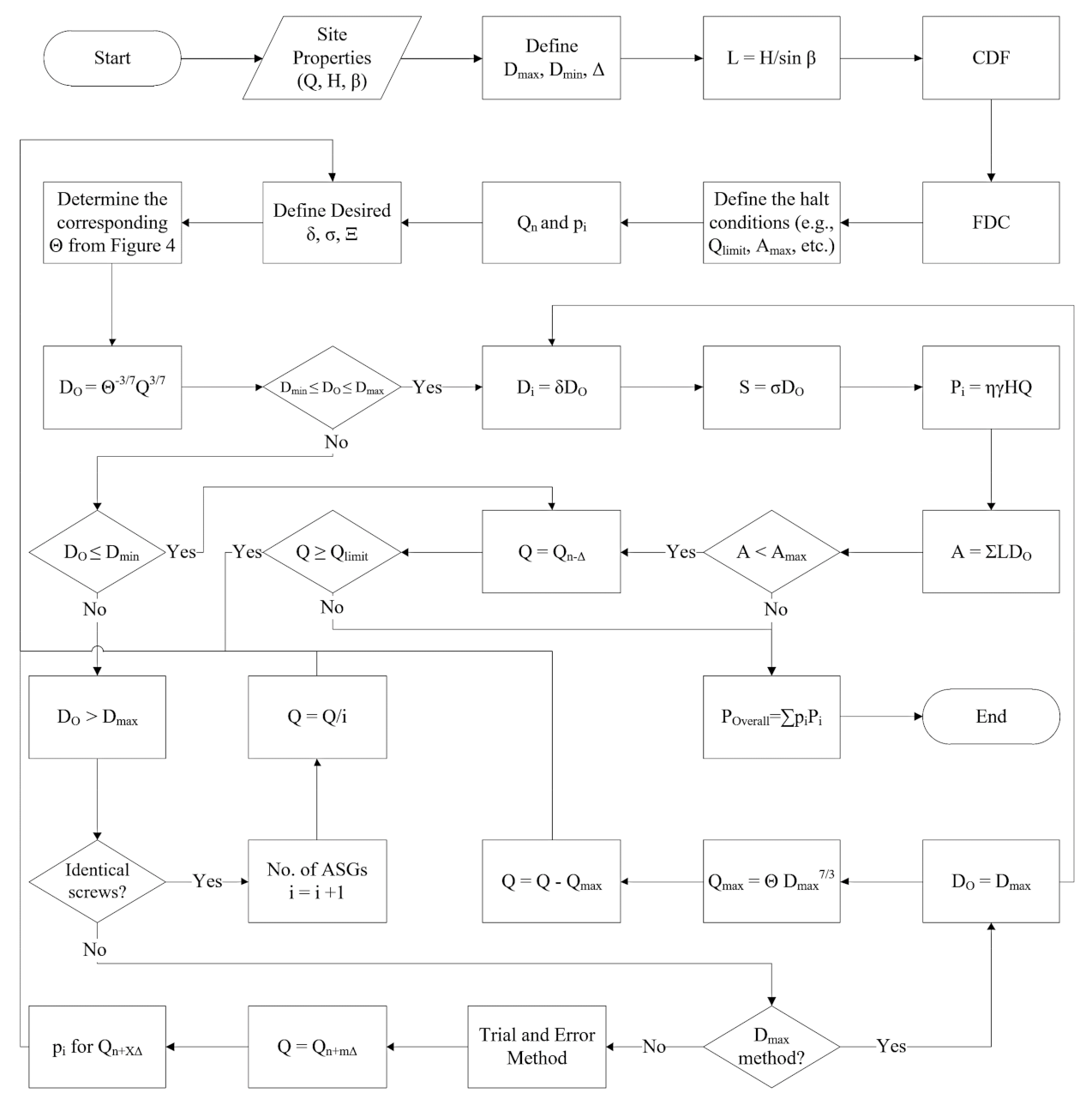
4. A Quick Design Guideline for Archimedes Screw Power Plants
4.1. Determination of the ASG Configuration
- -
- For the known available average flow rate and head, Equation (7) could be used for rough estimations about the possible amount of power that could be generated.
- -
- If the estimated power is less than the requirements, site properties could be checked to evaluate the possibilities of the series configuration of ASGs. e.g., to take advantage of low flow rates but reasonable available heads, ASGs could be installed in series to deal with technical considerations of a very long ASG.
- -
- To take advantage of high flow rates, instead of a very large (in diameter) and heavy ASG, it is possible to install ASGs in parallel. This approach could help to reduce the challenges of technical limitations and offers several advantages.
- -
- For very low flow rates and heads, using industrial pico-ASGs available in the market may facilitate the process or even save some costs. For example, currently, pico-ASGs can generate up to 500 W with a flow rate as low as 0.1 m3/s and 0.7 m of the head (more information is available in [6]). Obviously, several units of such screws could be used in parallel or in series to take advantage of higher flow rates or available heads. For higher flow rates and heads, custom ASGs designs could be more efficient options. For example, Fletcher’s Horse World Archimedes Screw can generate up to 7.2 kW using a design flow rate, head and outer diameter of 0.536 m3/s, 1.7 m [71,72] and 1.39 m [73], respectively.
4.2. Estimation of Archimedes Screws Design Properties
- Determine the site properties: the river’s historical data or hydrograph for the volumetric flow rate (Q) and the site geometry to find the appropriate head (H) and the Archimedes screw inclination angle (. Studies show that many ASGs are installed at [10].
- Determine the maximum and minimum overall diameter of the screw (Dmax, Dmin) based on the site properties and the Archimedes screw hydro power plants design assessments proposed in Section 5-1 of [6].
- Use Equation (1) to determine the screw(s) length.
- Use the historical dataset of the river’s flow rate to determine the flow duration curve (FDC). The probability that a system will take on a particular value or collection of values could be described by a mathematical expression which is known as a distribution function. The cumulative distribution function (CDF) of a variable for a value is the probability that this variable will take values less than or equal to this value [74]. Therefore, for a time series with items, for item with items equal or bigger than it:
- 5.
- Use the volume of flow rate that is provided on the flow duration curve (e.g., Q95) and use Equation (14) to estimate the corresponding diameter of the screw for this flow rate (DO).
- 6.
- Check the estimated diameter:
- -
- If , go to step 7.
- -
- If use a higher volume of flow rate (e.g., Q90) and repeat step 6.
- -
- If , several approaches could be considered:
- ○
- Identical screws: divide the volume of flow rate by i = 2 and follow the process from step 6. If it ends to again, repeat it for i = i + 1 until the condition passes. Then use the analytical Archimedes screw design method that is offered in [33] to design the screw. In this approach, “i” Archimedes screw generators with the same geometry will be designed to handle this flow rate. The advantage of this approach is that similar screws are easier to build, operate and maintain.
- ○
- Design based on the maximum diameter: design the screw for and use the analytical Archimedes screw design method that is offered in [33] to design the Archimedes screw generator. Then use Equation (15) to estimate the volumetric flow that passes through this screw and design the next Archimedes screw by following the process from step 6 for the remaining volume of flow rate. This approach could lead to reducing the number of Archimedes screws.
- ○
- Trial and error: consider a higher probability that means a lower flow rate (e.g., Q97.5 instead of Q95) and do and follow the process from step 6 and perform a trial and error. This approach could lead to an increase in the design of Archimedes screw turbines with higher reliability in generating power.
- 7.
- To utilize the remaining available volumetric flow rate, more Archimedes screws could be designed (parallel ASG power plants). The next flow rate to design the screw could be selected from the FDC based on the desired step size (Δ). For example, for the previous design flow rate of choose the next flow rate which is the flow exceeding for of the period and continue the design starting from step 5.
- 8.
- The design process should be halted based on logical constraints. For example, for economic reasons designing screws for volumetric flow rates less than the certain probability (e.g., Qlimit) is not reasonable. Or, due to site limitations, there may be some restrictions such as the total area of the power plant (the minimum required area to install the Archimedes screw generators is equal to the sum of the diameter times to the length of each screw. If it goes beyond the installation site limitations, some of the screws designed for flow rates with lower probabilities could be cancelled. In such conditions, an optimized larger screw for the flow rates with the highest probabilities or using variable speed screws could be considered as alternative solutions to utilize more flow rate).
- 9.
- Use Equation (7) to estimate the possible amount of power that each ASG can generate. Then, estimate the ideal overall power that the Archimedes screw hydropower plant could generate.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Notation | ||
| Effective cross-sectional area at the screw’s inlet | (m2) | |
| The inner diameter of the Archimedes screw | (m) | |
| The outer diameter of the Archimedes screw | (m) | |
| The estimated value | ||
| The average of the estimations | ||
| Upper (inlet) water level of the screw | (m) | |
| Lower (outlet) water level of the screw | (m) | |
| The available head | (m) | |
| Gap width (The gap between the trough and screw) | (m) | |
| The total length of the screw | (m) | |
| MAPE | The mean absolute percentage error | (%) |
| n | The number of data points in the dataset | |
| Number of helical planed surfaces | (-) | |
| The observed value | ||
| The average of the observed data | ||
| The percentage (percent) error | (%) | |
| Total flow rate passing through the screw | (m3/s) | |
| r | Radius | (m) |
| R | Pearson correlation | (%) |
| Pitch of the screw (Distance along the screw axis for one complete helical plane turn) | (m) | |
| The fill height of the inner diameter of the screw at the inlet | (m) | |
| The fill height of the screw at the inlet | (m) | |
| The free surface elevations at the upstream | (m) | |
| The free surface elevations at the downstream | (m) | |
| The inclination angle of the screw | (rad) | |
| The specific weight of water | (N/m3) | |
| The screw’s pitch to outer diameter ratio ( | (-) | |
| The average efficiency of the ASGs based on manufacturer’s specifications in Table 2 () | ||
| Step size | (%) | |
| A constant accounting for screw geometry and fill level | (m2/3s−1) | |
| θ | Angle of sector | (rad) |
| The constant value in the power function form | ||
| The screw’s inner to outer diameter ratio () | (-) | |
| The dimensionless inlet depth of the screw | (-) | |
| The value of power in the power function form of diameter equation | (-) | |
| ω | The rotation speed of the screw | (rad/s) |
| The maximum rotation speed of the screw (Muysken limit) | (rad/s) | |
| Subscripts | ||
| inner | ||
| minimum | ||
| Maximum | ||
| O | Outer | |
References
- Williamson, S.J.J.; Stark, B.H.H.; Booker, J.D.D. Low head pico hydro turbine selection using a multi-criteria analysis. RENE 2014, 61, 43–50. [Google Scholar] [CrossRef]
- Date, A.; Akbarzadeh, A. Design and cost analysis of low head simple reaction hydro turbine for remote area power supply. Renew. Energy 2009, 34, 409–415. [Google Scholar] [CrossRef]
- Casini, M. Harvesting energy from in-pipe hydro systems at urban and building scale. Int. J. Smart Grid Clean Energy 2015, 4, 316–327. [Google Scholar] [CrossRef] [Green Version]
- IRENA. Renewable Energy Techlogies: Cost Analysis Series, Hydropower; IRENA Innovation and Technology Centrer: Bonn, Germany, 2012; Volume 1. [Google Scholar]
- Suh, S.H.; Kim, K.Y.; Kim, B.H.; Kim, Y.T.; Kim, T.G.; Roh, H.W.; Yoo, Y.I.; Park, N.H.; Park, J.M.; Shin, C.S.; et al. Theory and Applications of Hydraulic Turbines, 1st ed.; Dong Myeong Publishers: Paju, Korea, 2014. [Google Scholar]
- YoosefDoost, A.; Lubitz, W.D. Archimedes screw turbines: A sustainable development solution for green and renewable energy generation-a review of potential and design procedures. Sustainability 2020, 12, 7352. [Google Scholar] [CrossRef]
- Muller, G.; Senior, J. Simplified theory of Archimedean screws. J. Hydraul. Res. 2009, 47, 666–669. [Google Scholar] [CrossRef]
- Simmons, S.; Lubitz, W. Archimedes screw generators for sustainable energy development. In Proceedings of the 2017 IEEE Canada International Humanitarian Technology Conference (IHTC), Toronto, ON, Canada, 21–22 July 2017; pp. 144–148. [Google Scholar] [CrossRef]
- Moerscher, W. Water-power system. U.S. Patent US1434138A, 31 October 1922. [Google Scholar]
- Lashofer, A.; Hawle, W.; Pelikan, B. State of technology and design guidelines for the Archimedes screw turbine. In Proceedings of the Hydro 2012—Innovative Approaches to Global Challenges, Bilbao, Spain, 29–31 October 2012. [Google Scholar]
- Vandezande BVBA. Lock of Hasselt—Hybrid hydropower screw/screw pump. Youtube. 2018. Available online: https://youtu.be/FUlYjkzAIs8 (accessed on 8 August 2021).
- Kibel, P. Fish Monitoring and Live Fish Trials. Archimedes Screw Turbine, River Dart. In Phase 1 Report: Live Fish Trials, Smolts, Leading Edge Assessment, Disorientation Study, Outflow Monitoring; Moretonhampstead: Devon, UK, 2007. [Google Scholar]
- Boys, C.A.; Pflugrath, B.D.; Mueller, M.; Pander, J.; Deng, Z.D.; Geist, J. Physical and hydraulic forces experienced by fish passing through three different low-head hydropower turbines. Mar. Freshw. Res. 2018, 69, 1934–1944. [Google Scholar] [CrossRef]
- McNabb, C.D.; Liston, C.R.; Borthwick, S.M. Passage of Juvenile Chinook Salmon and other Fish Species through Archimedes Lifts and a Hidrostal Pump at Red Bluff, California. Trans. Am. Fish. Soc. 2003, 132, 326–334. [Google Scholar] [CrossRef]
- Kibel, P.; Pike, R.; Coe, T. Archimedes Screw Turbine Fisheries Assessment. In Phase II: Eels and Kelts; Moretonhampstead: Devon, UK, 2008. [Google Scholar]
- Kibel, P.; Pike, R.; Coe, T. The Archimedes Screw Turbine: Assessment of Three Leading Edge Profiles; Fishtek Consulting Ltd.: Moretonhampstead, UK, 2009. [Google Scholar]
- United Kingdom Environment Agency. Hydropower Good Practice Guidelines Screening requirements. J. Hydraul. Res. 2012, 4, 1–16. [Google Scholar]
- Piper, A.T.; Rosewarne, P.J.; Wright, R.M.; Kemp, P.S. The impact of an Archimedes screw hydropower turbine on fish migration in a lowland river. Ecol. Eng. 2018, 118, 31–42. [Google Scholar] [CrossRef]
- Pauwels, I.S.; Baeyens, R.; Toming, G.; Schneider, M.; Buysse, D.; Coeck, J.; Tuhtan, J.A. Multi-species assessment of injury, mortality, and physical conditions during downstream passage through a large archimedes hydrodynamic screw (Albert canal, Belgium). Sustainability 2020, 12, 8722. [Google Scholar] [CrossRef]
- Durrani, A.M.; Mujahid, O.; Uzair, M. Micro Hydro Power Plant using Sewage Water of Hayatabad Peshawar. In Proceedings of the 2019 15th International Conference on Emerging Technologies (ICET), Peshawar, Pakistan, 2–3 December 2019. [Google Scholar]
- Spaans Babcock Ltd. Hydro Power Using Waste Water at Esholt WwTW. 2009. Available online: https://cms.esi.info/Media/documents/54053_1316689157666.pdf (accessed on 29 July 2020).
- Kozyn, A.; Ash, S.; Lubitz, W.D. Assessment of Archimedes Screw Power Generation Potential in Ontario. In Proceedings of the 4th Climate Change Technology Conference, Montreal, QC, Canada, 25–27 May 2015; pp. 1–11. Available online: https://www.cctc2015.ca/TECHNICALPAPERS/1570095585.pdf (accessed on 3 June 2019).
- Shahverdi, K.; Loni, R.; Maestre, J.M.; Najafi, G. CFD numerical simulation of Archimedes screw turbine with power output analysis. Ocean. Eng. 2021, 231, 108718. [Google Scholar] [CrossRef]
- UNIDO. Renewable Energy: Micro Hydraulic Power Unit (Spiral Type Pico-Hydro Unit ‘PicoPica10’, ‘PicoPica500’); United Nations Industrial Development Organization: Tokyo, Japan, 2020; Available online: http://www.unido.or.jp/en/technology_db/5276/ (accessed on 7 July 2020).
- Sumino, M. Ultra-Small Water Power Generator. 14 May 2019. Available online: https://youtu.be/XjEgFlngZ04 (accessed on 23 June 2020).
- Sumino Co. Ltd. Japan. Spiral Hydraulic Power Unit ‘PicoPica’; Ena: Gifu, Japan, 2020; Available online: http://www.unido.or.jp/files/sites/2/PICOPICA_Specification201127.pdf (accessed on 28 July 2021).
- Vandezande Diksmuide. PS/WKC Lock Hasselt. Available online: https://web.archive.org/web/20210405220637/https://www.vandezande.com/en/projects/ps-wkc-lock-hasselt (accessed on 9 August 2021).
- Rorres, C. Archimedes in the 21st Century: Proceedings of a World Conference at the Courant Institute of Mathematical Sciences; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Brada, K.; Radlik, K.-A. Wasserkraftschnecke: Eigenschaften und Verwendung. In Proceedings of the Heat Exchange and Renewable Energy Sources International Symposium, Szczecin, Poland, 17–19 June 1996; pp. 43–52. [Google Scholar]
- OMNR. Potential Waterpower Generation Sites (WPPOTSTE); Ontario Ministry of Natural Resources. 2004. Available online: https://www.ontario.ca/data/potential-waterpower-generation-sites-wppotste (accessed on 10 January 2015).
- Lubitz, W.D.; Lyons, M.; Simmons, S. Performance Model of Archimedes Screw Hydro Turbines with Variable Fill Level. J. Hydraul. Eng. 2014, 140, 04014050. [Google Scholar] [CrossRef]
- Dragomirescu, A. Design considerations for an Archimedean screw hydro turbine. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Bucharest, Romania, 21–24 October 2021; Volume 664, p. 12034. [Google Scholar] [CrossRef]
- Yoosefdoost, A.; Lubitz, W.D. Archimedes Screw Design: An Analytical Model for Rapid Estimation of Archimedes Screw Geometry. Energies 2021, 14, 7812. [Google Scholar] [CrossRef]
- Nuernbergk, D.M.; Rorres, C. Analytical Model for Water Inflow of an Archimedes Screw Used in Hydropower Generation. J. Hydraul. Eng. 2013, 139, 213–220. [Google Scholar] [CrossRef]
- Aigner, D. Current Research in Hydraulic Engineering 1993–2008; Institut für Wasserbau und Technisch Hydromechanik der TU; Association: Dresden, Germany, 2008. [Google Scholar]
- Schmalz, W. Studies on fish migration and control of possible fish loss caused by the hydrodynamic screw and hydropower plant. In Fischo—Kologische und Limnol. Untersuchungsstelle Sudthurign, Rep.; Thüringer Landesanstalt für Umwelt und Geol: Jena, Germany, 2010. [Google Scholar]
- Lashofer, A.; Kaltenberger, F.; Pelikan, B. Does the Archimedean screw turbine stand the test? (Wie gut bewährt sich die Wasserkraftschnecke in der Praxis?). WasserWirtschaft 2011, 101, 76–81. [Google Scholar] [CrossRef]
- Nuernbergk, D.M. Wasserkraftschnecken—Berechnung und Optimaler Entwurf von Archimedischen Schnecken als Wasserkraftmaschine (Hydro-Power Screws—Calculation and Design of Archimedes Screws), 2nd ed.; Verlag Moritz Schäfer: Detmold, Germany, 2020. [Google Scholar]
- Rorres, C. The Turn of the Screw: Optimal Design of an Archimedes Screw. J. Hydraul. Eng. 2000, 126, 72–80. [Google Scholar] [CrossRef] [Green Version]
- YoosefDoost, A.; Lubitz, W.D. Development of an Equation for the Volume of Flow Passing Through an Archimedes Screw Turbine. In Sustaining Tomorrow; Ting, D.S.-K., Vasel-Be-Hagh, A., Eds.; Springer: Cham, Switzerland, 2021; pp. 17–37. [Google Scholar]
- Dellinger, G.; Simmons, S.; Lubitz, W.D.; Garambois, P.A.; Dellinger, N. Effect of slope and number of blades on Archimedes screw generator power output. Renew. Energy 2019, 136, 896–908. [Google Scholar] [CrossRef]
- Simmons, S.C.; Elliott, C.; Ford, M.; Clayton, A.; Lubitz, W.D. Archimedes screw generator powerplant assessment and field measurement campaign. Energy Sustain. Dev. 2021, 65, 144–161. [Google Scholar] [CrossRef]
- Lyons, M. Lab Testing and Modeling of Archimedes Screw Turbines. Master’s Thesis, University of Guelph, Guelph, ON, Canada, 2014. [Google Scholar]
- Rosly, C.Z.; Jamaludin, U.K.; Azahari, N.S.; Mu’tasim, M.A.N.; Oumer, A.N.; Rao, N.T. Parametric study on efficiency of archimedes screw turbine. ARPN J. Eng. Appl. Sci. 2016, 11, 10904–10908. [Google Scholar]
- Songin, K. Experimental Analysis of Archimedes Screw Turbines. Master’s Thesis, University of Guelph, Guelph, Canada, 2017. [Google Scholar]
- Nagel, G. Archimedean Screw Pump Handbook; RITZ-Pumpenfabrik OHG: Schwabisch Gmund, Germany, 1968. [Google Scholar]
- Rose, R. Linton Falls and Low Wood Hydropower Schemes. No. UK Water Projects 2011. River Coast. 2011, pp. 197–202. Available online: https://web.archive.org/web/20190621110557/http://www.waterprojectsonline.com/case_studies/2011/Hydropower_Linton_Fall_2011s.pdf (accessed on 1 November 2021).
- Landustrie Sneek, B.V. Totnes Weir (UK). Landustrie Worldwide Water Technology. 2015. Available online: https://web.archive.org/web/20210803231005/https://www.landustrie.nl/fileadmin/user_upload/Totnes_Times_November_2015.pdf (accessed on 3 August 2021).
- Rehart Power. Hannoversch Münden CS. Available online: https://web.archive.org/web/20211115031954/https://www.rehart-power.de/en/reference-projects/hydropower-screw-type-cs/hannoversch-muenden-cs.html (accessed on 14 November 2021).
- RenewablesFirst. Radyr Weir Hydro Turbines. 2015. Available online: https://web.archive.org/web/20210804003006/https://www.renewablesfirst.co.uk/project-blog/radyr-weir-hydro-scheme/ (accessed on 5 July 2020).
- Ingenieurbüro Lashofer. Hydropower screws in Europe. Google Maps. Available online: Efort.info/AST-Map (accessed on 3 August 2021).
- Vandezande Diksmuide. Hydropower Screws Höllthal. Vandezande. Available online: https://web.archive.org/web/20210809061648/https://www.vandezande.com/en/projects/hydropower-screws-höllthal (accessed on 9 August 2021).
- Gratton, P.; Meadows, T.; Brook, T. Gunthorpe Weir Hydropower Scheme: Fisheries and Geomorphology Assessment; The Mill: Stroud, UK, 2019. [Google Scholar]
- SinFin. Solvay Industrial Plant; SinFin Energy: Gijón, Spain, 2019; Available online: http://www.sinfinenergy.com/en/projects/solvay/ (accessed on 8 July 2020).
- Landustrie. Linton Lock. Landustrie Sneek BV. 2017. Available online: https://web.archive.org/web/20210804020631/https://www.landustrie.nl/en/products/hydropower/projects/linton-lock.html (accessed on 29 July 2020).
- Vandezande BVBA. Vandezande Specialist in Mechanics. Vandezande.com. Zeepziederijstraat, Brugge, Belgium. Available online: https://web.archive.org/web/20210809031945/https://www.vandezande.com/sites/default/files/vandezande-folder2017-engLR04.pdf (accessed on 8 August 2021).
- Melbud, S.A. A Small Hydropower Plant–Rosko. Available online: https://web.archive.org/web/20210804011025/http://www.melbud.pl/language/pl/mala-elektrownia-wodna-rosko/ (accessed on 3 August 2021).
- Fergnani, N. Hydroelectric Plants Energy Efficiency. Hydrosmart Srl. 2020. Available online: https://www.hydrosmart.it/energia-rinnovabile (accessed on 2 August 2020).
- Sto98. Marengo Hydropower Plant-Goito [Centrale Idroelettrica Marengo—Goito]. YouTube. 2015. Available online: https://youtu.be/19px1EKa--4 (accessed on 19 July 2020).
- Rodgers, J.L.; Nicewander, W.A. Thirteen Ways to Look at the Correlation Coefficient. Am. Stat. 1988, 42, 59–66. [Google Scholar] [CrossRef]
- Yoosefdoost, A.; Yoosefdoost, I.; Asghari, H.; Sadeghian, M.S. Comparison of HadCM3, CSIRO Mk3 and GFDL CM2. 1 in Prediction the Climate Change in Taleghan River Basin. Am. J. Civ. Eng. Archit. 2018, 6, 93–100. [Google Scholar] [CrossRef] [Green Version]
- Adler, J.; Parmryd, I. Quantifying colocalization by correlation: The pearson correlation coefficient is superior to the Mander’s overlap coefficient. Cytom. Part A 2010, 77, 733–742. [Google Scholar] [CrossRef]
- Kim, S.; Kim, H. A new metric of absolute percentage error for intermittent demand forecasts. Int. J. Forecast. 2016, 32, 669–679. [Google Scholar] [CrossRef]
- Hanke, J.E.; Wichern, D. Business Forecasting, 9th ed.; Prentice Hall: London, UK, 2009. [Google Scholar]
- Bowerman, B.L.; O’Connell, R.T.; Koehler, A.B. Forecasting, Time Series, and Regression: An Applied Approach, 4th ed.; Thomson Brooks/Cole: Belmont, CA, USA, 2005. [Google Scholar]
- Hawle, W.; Lashofer, A.; Pelikan, B. Lab Testing of the Archimedean Screw. In Proceedings of the Hidroenergia Conference, Wroclaw, Poland, 23–26 May 2012. [Google Scholar]
- Lasdon, L.S.; Waren, A.D.; Jain, A.; Ratner, M. Design and Testing of a Generalized Reduced Gradient Code for Nonlinear Programming. ACM Trans. Math. Softw. 1978, 4, 34–50. [Google Scholar] [CrossRef]
- Waleed, D.; Alrabadi, H. Portfolio optimization using the generalized reduced gradient nonlinear algorithm An application to Amman Stock Exchange. Int. J. Islam. Middle East. Financ. Manag. 2016, 9, 570–582. [Google Scholar] [CrossRef]
- Muysken, J. Calculation of the Effectiveness of the Auger. De Ingenieur 1932, 21, 77–91. [Google Scholar]
- GreenBug Energy. Archimedes Screw Generators. GreenBug Energy. Available online: https://web.archive.org/web/20210128050704/https://greenbugenergy.com/how-we-do-it/archimedes-screw-generators (accessed on 6 August 2021).
- Heron, L. Fletcher’s Horse World—Nanticoke Creek—Archimedes Screw—7.2 kW. Ontario Rivers Alliance. 2014. Available online: https://web.archive.org/web/20210806171348/https://www.ontarioriversalliance.ca/fletchers-horse-world-nanticoke-creek-archimedes-screw-7-2-kw/ (accessed on 6 August 2021).
- GreenBug Energy. Fletchers Horse World; GreenBug Energy Inc.: Delhi, ON, Canada; Available online: https://greenbugenergy.com/projects/fletchers-horse-world (accessed on 6 August 2021).
- Passamonti, A. Investigation of Energy Losses in Laboratory and Full-Scale Archimedes Screw Generators Advisor; Politecnico Di Milano: Milan, Italy, 2017. [Google Scholar]
- Deisenroth, M.P.; Faisal, A.A.; Ong, C.S. Mathematics for Machine Learning; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]


| Parameter | Description | Unit | Variable | Description | Unit |
|---|---|---|---|---|---|
| L | Length of the screw | (m) | ω | Rotation speed of screw * | (rad/s) |
| DO | Outer diameter of the screw | (m) | hu | Upper (inlet) water level | (m) |
| Di | Inner diameter of the screw | (m) | hL | Lower (outlet) water level | (m) |
| S | Screw’s pitch or period [39] (The distance along the screw axis for one complete helical plane turn) | (m) | Q | Volumetric flow rate passing through the screw | (m3/s) |
| N | Number of helical planed surfaces (also called blades, flights or starts [39]) | (1) | Ratio | Description | Unit |
| δ | Inner to outer diameter ratio δ = Di/DO | (1) | |||
| β | Inclination Angle of the Screw | (rad) | σ | Pitch to outer diameter ratio σ = S/DO | (1) |
| Gw | The gap between the trough and screw. | (m) | Ξ | Dimensionless inlet depth Ξ = hu/DO cos β | (1) |
| Name | No. of ASGs | DO (m) | H (m) | Q (m3/s) | P (kW) | Location (River) | Refs. | |
|---|---|---|---|---|---|---|---|---|
| Totnes | 2 | 3.7 | 3.45 | 6.5 | 160 | Dart, UK | [48] | |
| Hannoversch-Münden | 2 | 2.8 | 2.6 | 2 | 35.455 | Werra, DE | [49] | |
| Low Wood | 2 | 3 | 7.2 | 4 | 200 | Leven, UK | [47] | |
| Radyr | 2 | 3.5 | 3.5 | 11 | 200 | Taff, UK | [50] | |
| Künzelsau | 2 | 4.1 | 1.72 | 8.95 | 132 | Kocher, DE | [51] | |
| Ahornweg | 2 | 2.3 | 1.45 | 2 | 21 | Mühlbach, DE | [51] | |
| Linton Falls | 2 | 2.4 | 2.7 | 2.6 | 50 | Trent, UK | [47] | |
| Niklasdorf/Birgl and Bergmeister | 2 | 3.9 | 3.6 | 106 | Mur, AT | [51] | ||
| Hausen III Neumatt | 2 | 3.4 | 5.8 | 5.5 | 235 | Wiese, DE | [51] | |
| Höllthal | 2 | 4.3 | 2.22 | 10.5 | 220 | Alz, DE | [52] | |
| Gunthorpe Weir | 2 | 4.3 | 2.03 | 14.15 | 165 | Trent, UK | [53] | |
| Solvay | 2 | 2.3 | 2 | 2.5 | 35 | Saja, ES | [54] | |
| Linton Lock | Linton Plant | 2 | 3 | 3.2 | 4.5 | 110 | Ouse, UK | [6,55] |
| Widdington Plant | 5 | 3 | 14.5 | 335 | ||||
| Plana | 3 | 4.1 | 3.5 | 8.73 | 220 | Vltava, CZ | [51] | |
| Crescenzago | 3 | 3.2 | 2.1 | 5 | 75 | Lambro, IT | [51] | |
| Olen | 3 | 4.3 | 10 | 5 | 360 | Albert Canal, BE | [51,56] | |
| Ham | 3 | 4.3 | 10 | 5 | 360 | Albert Canal, BE | [51,56] | |
| Hasselt | 3 | 5 | 10 | 5 | 400 | Albert Canal, BE | [11,27] | |
| Rosko | 6 | 1.7 | 4.5 | 60 | Noteć, PL | [51,57] | ||
| Steinsau | 6 | 1.4 | 3 | 30 | Ill, FR | [51] | ||
| Marengo | 6 | 3 | 1.6 | 3.7 | 51 | Goito, IT | [58,59] | |
| Equation No. | Equation | R (%) | MAPE (%) |
|---|---|---|---|
| (5) | 69.81 | 10.59 | |
| (8) | 83.28 | 10.64 | |
| (14) | 74.38 | 9.69 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
YoosefDoost, A.; Lubitz, W.D. Design Guideline for Hydropower Plants Using One or Multiple Archimedes Screws. Processes 2021, 9, 2128. https://doi.org/10.3390/pr9122128
YoosefDoost A, Lubitz WD. Design Guideline for Hydropower Plants Using One or Multiple Archimedes Screws. Processes. 2021; 9(12):2128. https://doi.org/10.3390/pr9122128
Chicago/Turabian StyleYoosefDoost, Arash, and William David Lubitz. 2021. "Design Guideline for Hydropower Plants Using One or Multiple Archimedes Screws" Processes 9, no. 12: 2128. https://doi.org/10.3390/pr9122128
APA StyleYoosefDoost, A., & Lubitz, W. D. (2021). Design Guideline for Hydropower Plants Using One or Multiple Archimedes Screws. Processes, 9(12), 2128. https://doi.org/10.3390/pr9122128