The Role of Stochastic Time-Variations in Turbulent Stresses When Predicting Drop Breakup—A Review of Modelling Approaches
Abstract
:1. Introduction
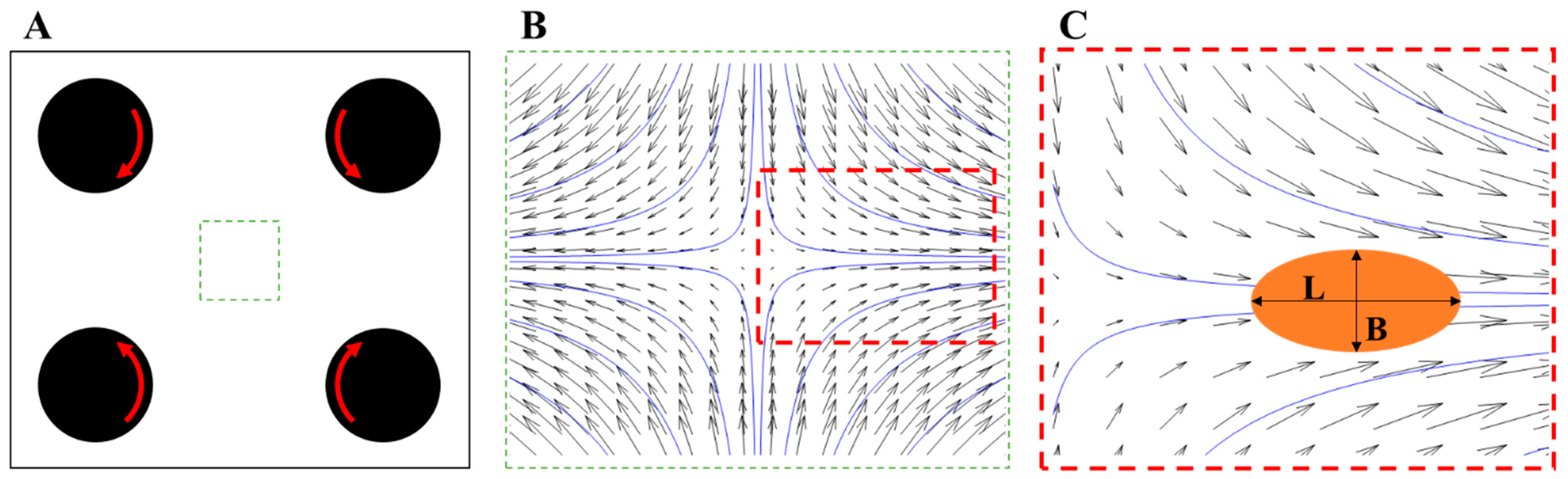
2. Laminar Viscous Breakup—A Contrasting Case
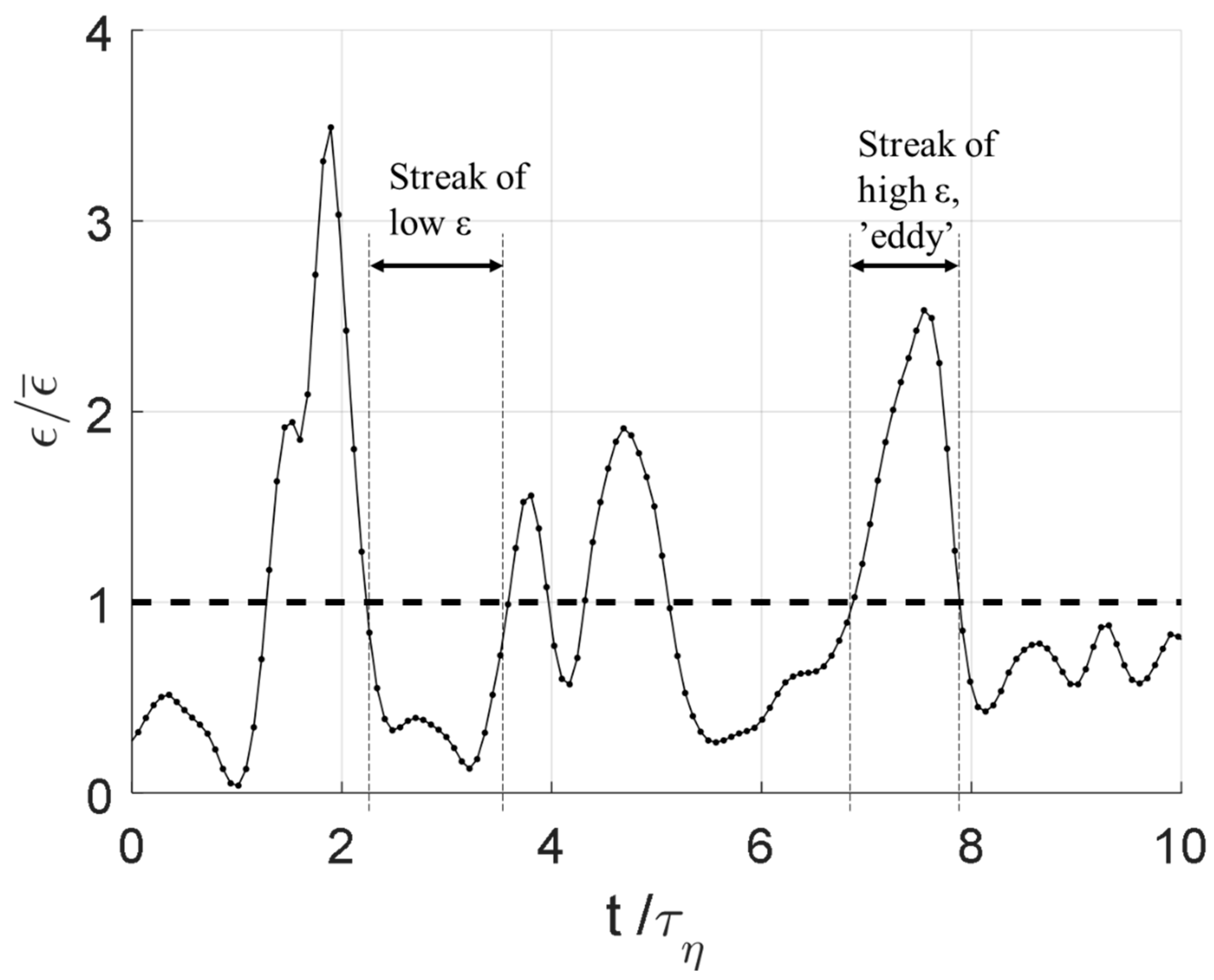
3. Stochastically Time-Varying Turbulent Quantities
4. The Kolmogorov–Hinze Framework
4.1. The Traditional Form, Neglecting Stocastic Time-Variations in Turbulent Stresses
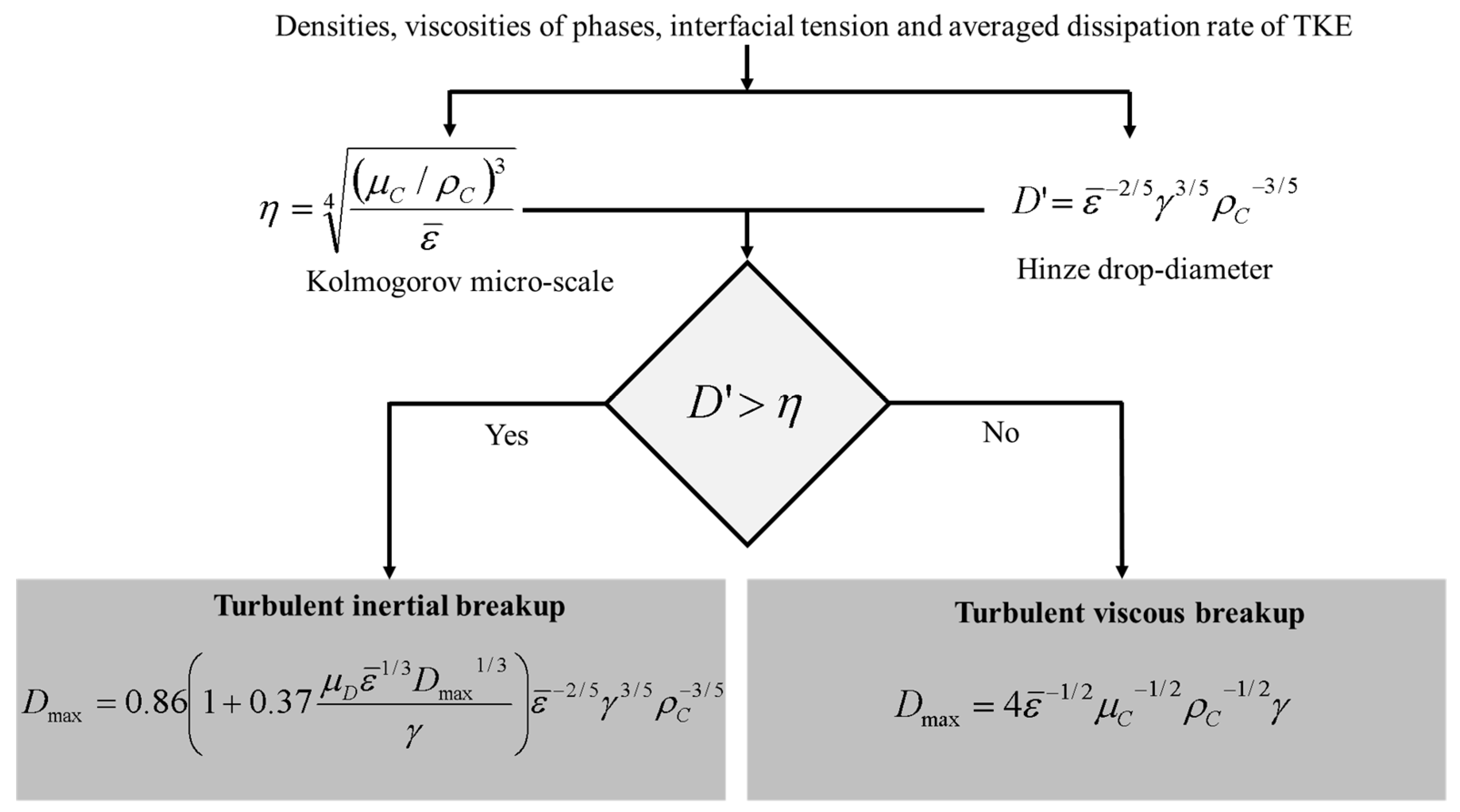
4.2. Adaptation 1. The Two-Criterion Suggestion
4.3. Adaptation 2. Multi-Fractal Theory
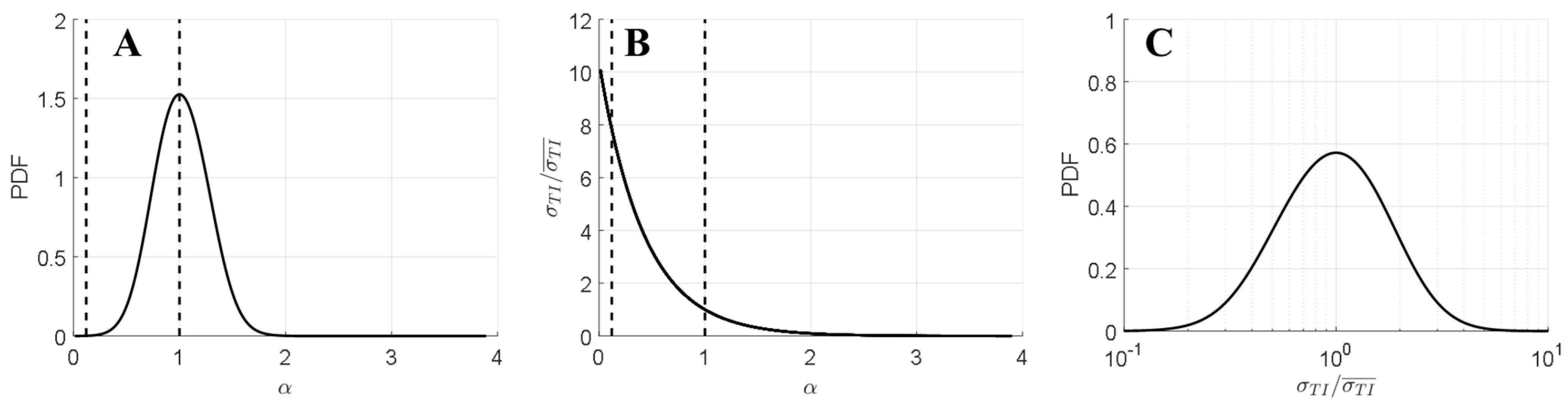
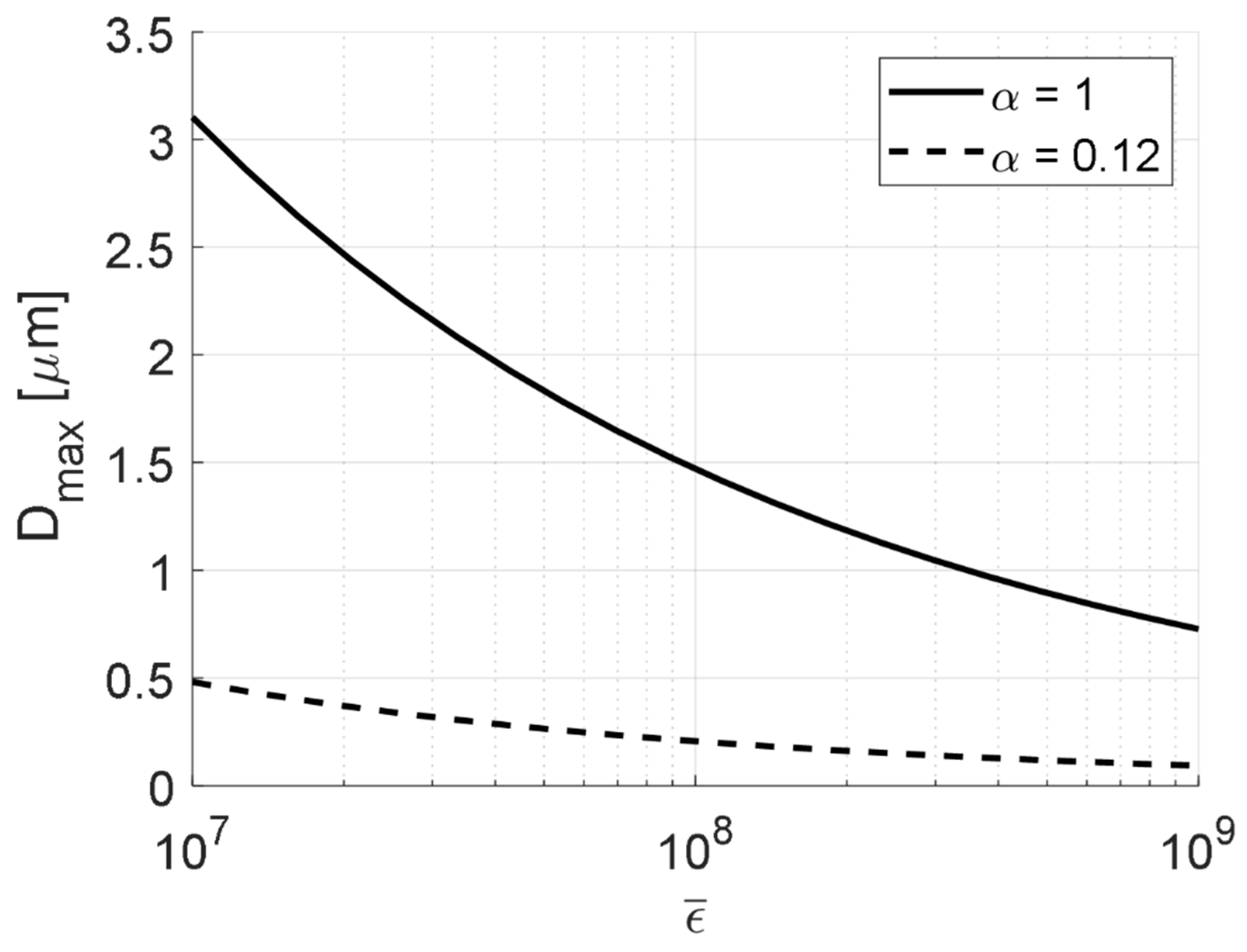
4.4. Adaptation 3. Empirical PDF Based Correction
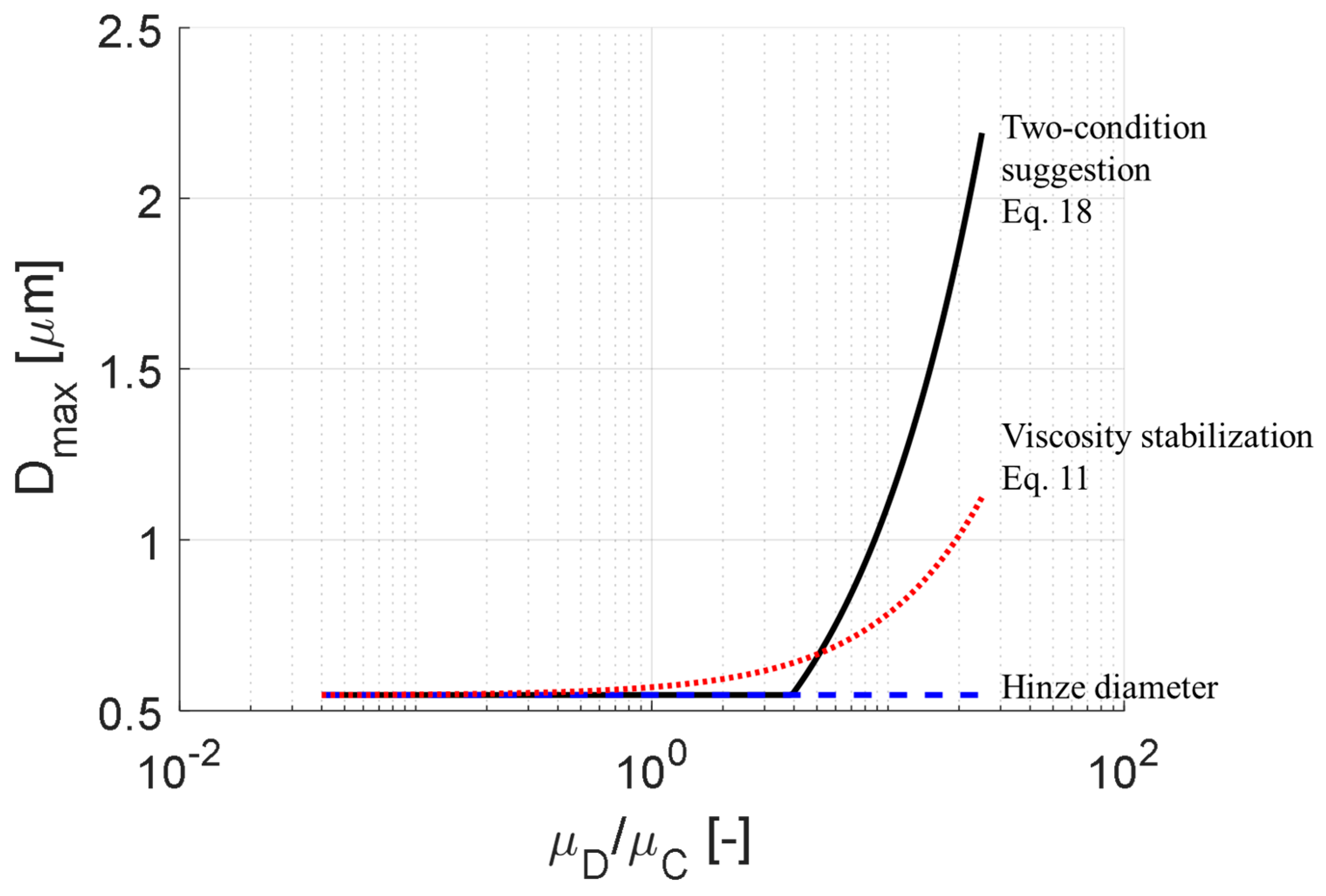
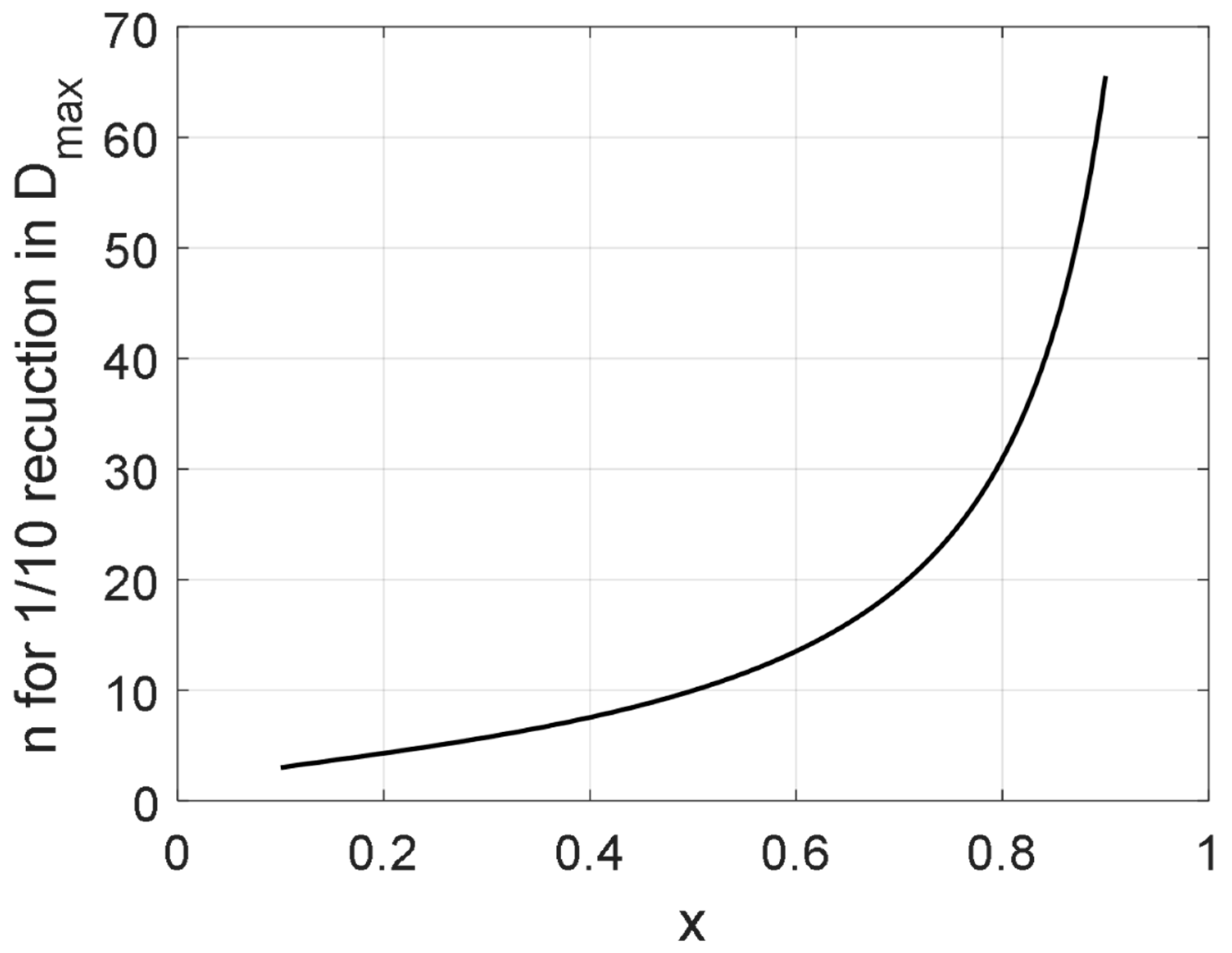
4.5. A Comparison of the Different Predictions
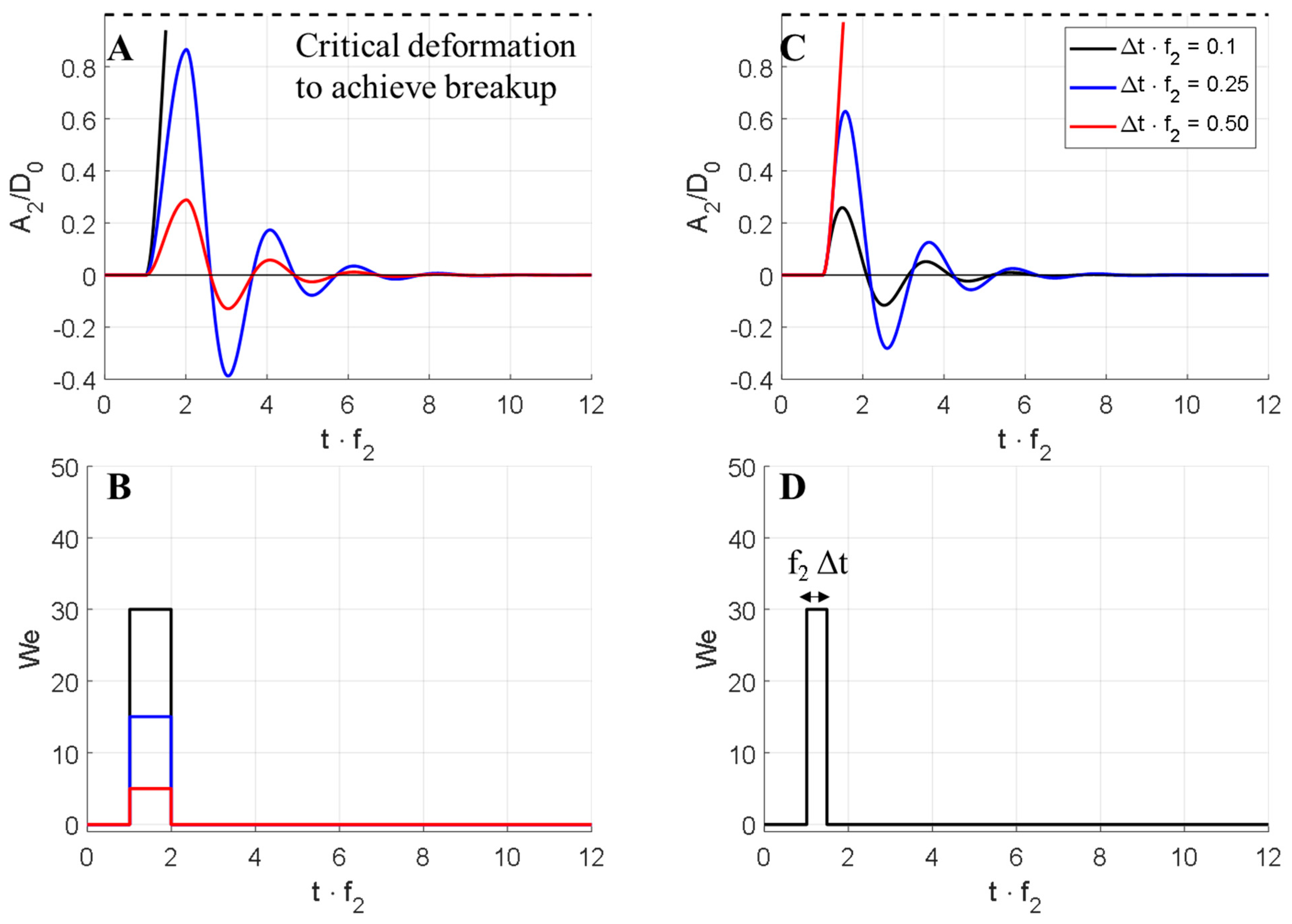
5. The Oscillatory Resonance Framework
6. Discussion, Future Perspectives and Summary
6.1. Importance of Including Stocastic Time-Variations of Stresses in Emulsification Modelling
6.2. Suggestions for Future Investigations
- Experimental characterization of emulsification devices. As discussed in Section 3, there is substantial literature in the fluid mechanics field, investigating turbulent intermittency effects in general and stochastic time-variations of turbulent stresses in particular (e.g., PDFs of dissipation rate of TKE or PDFs of velocity fluctuations) and discussing how they are best modelled [23,24,25,26,27,28]. These investigations are, however, often performed under conditions designed to be as close as possible to idealized turbulent flows (e.g., homogenous, isotropic developed turbulence at a high Reynolds number). Substantially less has been done on the less ideal turbulent flows in emulsification devices. A better understanding of, for example, the PDF of the dissipation rate of TKE in emulsification devices, and, in particular, if differences exist between designs and/or operating conditions, would help in validating proposed models. Another topic of special interest is the eddy life-time concept discussed in the influential two-condition suggestion for the Kolmogorov–Hinze framework. Direct measurements of the dissipation rate of TKE (and other suggestions for the primary fragmenting quantity) would allow for testing of the proposed expression (Equation (16)).
- Further development of multi-fractal breakup theory. In terms of theoretical consistency and connectivity to turbulence theory, the model based on multi-fractal theory stands out as especially interesting. As discussed in Section 4.3 (and further below), it provides testable predictions that are good starting points for future investigations.
- Long term statistics in emulsification devices. As discussed in Section 4.1, the Kolmogorov–Hinze framework appears to provide relatively good predictions even when neglecting stochastic time-variations altogether. However, there are indications that stochastic time-variations in turbulent stresses start to play a role when attempting to understand and predict differences between multi-pass emulsification in continuous mode of operation devices or emulsification taking place at long processing times in devices operating in the batch mode of operation (see Section 4.5). Measurements of how emulsion size distributions evolve at exceedingly long processing times, compared with the predictions provided by the adaptations reviewed in Section 4.3 and Section 4.4, would be an interesting experimental line of investigation.
- Application of the oscillatory resonance framework to emulsification devices. The oscillatory resonance framework is an interesting alternative basis for predicting size distributions resulting from emulsification. However, as it is presently formulated, it requires knowledge about the time-history of the local Weber number along the trajectory followed by the drop. This quantity can be measured under carefully controlled experimental conditions [5,18], but is inaccessible for the researcher or engineer working with designing industrial emulsification devices or optimizing processing lines. An extension and development of this framework in order to become applicable to conditions without full knowledge about time-histories (e.g., by combining the Rayleigh–Lamb model in Equation (35) with stochastic process modelling using either multi-fractal theory or purely empirical relationships, cf. Section 4.3 and Section 4.4) would be an interesting theoretical line of investigation.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Schultz, S.; Wagner, G.; Urban, K.; Ulrich, J. High-pressure homogenization as a process for emulsion formation. Chem. Eng. Technol. 2004, 27, 361–368. [Google Scholar] [CrossRef]
- Håkansson, A. Emulsion formation by homogenization: Current understanding and future perspectives. Annu. Rev. Food Sci. Technol. 2019, 10, 239–258. [Google Scholar] [CrossRef] [PubMed]
- Elghobashi, S. Direct numerical simulation of turbulent flows laden with droplets or bubbles. Annu. Rev. Fluid Mech. 2019, 51, 217–244. [Google Scholar] [CrossRef] [Green Version]
- Rivière, A.; Mostert, W.; Perrard, S.; Deike, L. Sub-Hinze scale bubble production in turbulent bubble break-up. J. Fluid Mech. 2021, 917, 40. [Google Scholar] [CrossRef]
- Risso, F.; Fabre, J. Oscillations and breakup of a bubble immersed in a turbulent field. J. Fluid Mech. 1998, 372, 323–355. [Google Scholar] [CrossRef]
- Qian, D.; McLaughlin, J.B.; Sankaranarayanan, K.; Sundaresan, S.; Kontomaris, K. Simulation of bubble breakup dynamics in homogeneous turbulence. Chem. Eng. Commun. 2006, 193, 1038–1063. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. On the breakage of drops in a turbulent flow. Dokl. Akad. Nauk. SSSR 1949, 66, 825–828. [Google Scholar]
- Hinze, J.O. Fundamentals of the hydrodynamic mechanism of splitting in dispersion processes. AIChE J. 1955, 1, 289–295. [Google Scholar] [CrossRef]
- Vankova, N.; Tcholakova, S.; Denkov, N.; Ivanov, I.B.; Vulchev, V.; Danner, T. Emulsification in turbulent flow. J. Colloid Interface Sci. 2007, 312, 363–380. [Google Scholar] [CrossRef]
- Boxall, J.A.; Koh, C.A.; Sloan, E.D.; Sum, A.; Wu, D.T. Droplet size scaling of water-in-oil emulsions under turbulent flow. Langmuir 2012, 28, 104–110. [Google Scholar] [CrossRef] [PubMed]
- Calabrese, R.V.; Chang, T.P.K.; Dang, P.T. Drop breakup in turbulent stirred-tank contactors. Part I: Effect of dispersed-phase viscosity. AIChE J. 1986, 32, 657–666. [Google Scholar] [CrossRef] [Green Version]
- Ramkrishna, D. Population Balances–Theory and Applications to Particulate Systems in Engineering; Academic Press: San Diego, CA, USA, 2000. [Google Scholar]
- Ramkrishna, D.; Singh, M.R. Population balance modeling: Current status and future prospects. Annu. Rev. Chem. Biomol. Eng. 2014, 5, 123–146. [Google Scholar] [CrossRef] [Green Version]
- Coulaloglou, C.; Tavlarides, L. Description of interaction processes in agitated liquid-liquid dispersions. Chem. Eng. Sci. 1977, 32, 1289–1297. [Google Scholar] [CrossRef]
- Solsvik, J.; Tangen, S.; Jakobsen, H.A. On the constitutive equations for fluid particle breakage. Rev. Chem. Eng. 2013, 29, 241–356. [Google Scholar] [CrossRef]
- Liao, Y.; Lucas, D. A literature review of theoretical models for drop and bubble breakup in turbulent dispersions. Chem. Eng. Sci. 2009, 64, 3389–3406. [Google Scholar] [CrossRef]
- Lalanne, B.; Masbernat, O.; Risso, F. A model for drop and bubble breakup frequency based on turbulence spectra. AIChE J. 2018, 65, 347–359. [Google Scholar] [CrossRef] [Green Version]
- Galinat, S.; Risso, F.; Masbernat, O.; Guiraud, P. Dynamics of drop breakup in inhomogeneous turbulence at various volume fractions. J. Fluid Mech. 2007, 578, 85–94. [Google Scholar] [CrossRef]
- Walstra, P. Emulsions. In Fundamentals of Interface and Colloid Science; Lyklema, J., Ed.; Elsevier: Amsterdam, The Netherlands, 2005; pp. 81–94. [Google Scholar]
- Li, Y.; Perlman, E.; Wan, M.; Yang, Y.; Meneveau, C.; Burns, R.; Chen, S.; Szalay, A.; Eyink, G. A public turbulence database cluster and applications to study Lagrangian evolution of velocity increments in turbulence. J. Turbul. 2008, 9, N31. [Google Scholar] [CrossRef] [Green Version]
- Perlman, E.; Burns, R.; Li, Y.; Meneveau, C. Data exploration of turbulence simulations using a database cluster. In Proceedings of the 2007 ACM/IEEE conference on Supercomputing-SC ’07, Reno, NV, USA, 10–16 November 2007. [Google Scholar]
- Graham, J.; Kanov, K.; Yang, X.I.A.; Lee, M.; Malaya, N.; Lalescu, C.C.; Burns, R.; Eyink, G.; Szalay, A.; Moser, R.; et al. A Web services accessible database of turbulent channel flow and its use for testing a new integral wall model for LES. J. Turbul. 2016, 17, 181–215. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. A refinement of previous hypotheses concerning the local structure of turbulence in a viscous incompressible fluid at high Reynolds number. J. Fluid Mech. 1962, 13, 82–85. [Google Scholar] [CrossRef] [Green Version]
- Obukhov, A.M. Some specific features of atmospheric turbulence. J. Geophys. Res. Space Phys. 1962, 67, 3011–3014. [Google Scholar] [CrossRef]
- Gurvich, A.S. Breakdown of Eddies and probability distributions for small-scale turbulence. Phys. Fluids 1967, 10, S59. [Google Scholar] [CrossRef]
- Jimenez, J. Small scale intermittency in turbulence. Eur. J. Mech. B Fluids 1998, 17, 405–419. [Google Scholar] [CrossRef]
- Lohse, D.; Grossmann, S. Intermittency in turbulence. Phys. A Stat. Mech. Appl. 1993, 194, 519–531. [Google Scholar] [CrossRef]
- Pope, S.B. Turbulent Flows; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Batchelor, G.K.; Townsend, A.A. The nature of turbulent motion at large wave-numbers. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1949, 199, 238–255. [Google Scholar] [CrossRef]
- Tcholakova, S.; Denkov, N.D.; Lips, A. Comparison of solid particles, globular proteins and surfactants as emulsifiers. Phys. Chem. Chem. Phys. 2008, 10, 1608–1627. [Google Scholar] [CrossRef]
- Gupta, A.; Eral, H.B.; Hatton, T.A.; Doyle, P.S. Controlling and predicting droplet size of nanoemulsions: Scaling relations with experimental validation. Soft Matter 2016, 12, 1452–1458. [Google Scholar] [CrossRef] [Green Version]
- Shinnar, R. On the behaviour of liquid dispersions in mixing vessels. J. Fluid Mech. 1961, 10, 259–275. [Google Scholar] [CrossRef]
- Taylor, G.I. The formation of emulsions in definable fields of flow. In Royal Society of London. A. Mathematical and Physical Sciences; The Royal Society: London, UK, 1934; Volume 146, pp. 501–523. [Google Scholar]
- Grace, H.P. Dispersion phenomena in high viscosity immiscible fluid systems and application of static mixers as dispersion devices in such systems. Chem. Eng. Commun. 1982, 14, 225–277. [Google Scholar] [CrossRef]
- Higdon, J.J.L. The kinematics of the four-roll mill. Phys. Fluids A Fluid Dyn. 1993, 5, 274–276. [Google Scholar] [CrossRef]
- Innings, F.; Hamberg, L.; Trägårdh, C. Dynamic modelling of the deformation of a drop in a four-roll mill. Chem. Eng. Sci. 2005, 60, 4771–4779. [Google Scholar] [CrossRef]
- Feigl, K.; Kaufmann, S.F.; Fischer, P.; Windhab, E.J. A numerical procedure for calculating droplet deformation in dispersing flows and experimental verification. Chem. Eng. Sci. 2003, 58, 2351–2363. [Google Scholar] [CrossRef]
- Windhab, E.; Dressler, M.; Feigl, K.; Fischer, P.; Megias-Alguacil, D. Emulsion processing—from single-drop deformation to design of complex processes and products. Chem. Eng. Sci. 2005, 60, 2101–2113. [Google Scholar] [CrossRef]
- Stone, H.A.; Bentley, B.J.; Leal, L.G. An experimental study of transient effects in the breakup of viscous drops. J. Fluid Mech. 1986, 173, 131–158. [Google Scholar] [CrossRef] [Green Version]
- Rallison, J.M. The deformation of small viscous drops and bubbles in shear flows. Annu. Rev. Fluid Mech. 1984, 16, 45–66. [Google Scholar] [CrossRef]
- Stone, A.H. Dynamics of drop deformation and breakup in viscous fluids. Annu. Rev. Fluid Mech. 1994, 26, 65–102. [Google Scholar] [CrossRef]
- Davidson, P. Turbulence. An Introduction for Scientists and Engineers; Oxford University Press: Oxford, UK, 2015. [Google Scholar]
- Tennekes, H.; Lumley, J.L. A First Course in Turbulence; The MIT Press: Cambridge, MA, USA, 1972. [Google Scholar]
- Batchelor, G.K. The Theory of Homogeneous Turbulence; Cambridge University Press: Cambridge, UK, 1953. [Google Scholar]
- White, F.G. Fluid Mechanics, 4th ed.; McGraw-Hill: Boston, MA, USA, 1998. [Google Scholar]
- Wang, G.; Yang, F.; Wu, K.; Ma, Y.; Peng, C.; Liu, T.; Wang, L.-P. Estimation of the dissipation rate of turbulent kinetic energy: A review. Chem. Eng. Sci. 2021, 229, 116133. [Google Scholar] [CrossRef]
- Goto, S.; Vassilicos, J.C. The dissipation rate coefficient of turbulence is not universal and depends on the internal stagnation point structure. Phys. Fluids 2009, 21, 035104. [Google Scholar] [CrossRef]
- Vassilicos, J.C. Dissipation in turbulent flows. Annu. Rev. Fluid Mech. 2015, 47, 95–114. [Google Scholar] [CrossRef] [Green Version]
- Narsimhan, G.; Gupta, J.; Ramkrishna, D. A model for transitional breakage probability of droplets in agitated lean liquid-liquid dispersions. Chem. Eng. Sci. 1979, 34, 257–265. [Google Scholar] [CrossRef]
- Perlekar, P.; Biferale, L.; Sbragaglia, M.; Srivastava, S.; Toschi, F. Droplet size distribution in homogeneous isotropic turbulence. Phys. Fluids 2012, 24, 65101. [Google Scholar] [CrossRef] [Green Version]
- Solsvik, J.; Jakobsen, H.A. A review of the statistical turbulence theory required extending the population balance closure models to the entire spectrum of turbulence. AIChE J. 2016, 62, 1795–1820. [Google Scholar] [CrossRef]
- Batchelor, G.K. Pressure fluctuations in isotropic turbulence. Math. Proc. Camb. Philos. Soc. 1951, 47, 359–374. [Google Scholar] [CrossRef]
- Karimi, M.; Andersson, R. Stochastic simulation of droplet breakup in turbulence. Chem. Eng. J. 2020, 380, 122502. [Google Scholar] [CrossRef]
- Tavoularis, S.; Corrsin, S. Experiments in nearly homogenous turbulent shear flow with a uniform mean temperature gradient. Part 1. J. Fluid Mech. 1981, 104, 311–347. [Google Scholar] [CrossRef] [Green Version]
- Vejražka, J.; Zednikova, M.; Stanovsky, P. Experiments on breakup of bubbles in a turbulent flow. AIChE J. 2017, 64, 740–757. [Google Scholar] [CrossRef]
- Jung, S.; Swinney, H.L. Velocity difference statistics in turbulence. Phys. Rev. E 2005, 72, 026304. [Google Scholar] [CrossRef] [Green Version]
- Lozovatsky, I.; Fernando, H.J.S.; Planella-Morato, J.; Liu, Z.; Lee, J.-H.; Jinadasa, S.U.P. Probability distribution of turbulent kinetic energy dissipation rate in ocean: Observations and approximations. J. Geophys. Res. Oceans 2017, 122, 8293–8308. [Google Scholar] [CrossRef]
- Lozovatsky, I.; Shearman, K.; Pirro, A.; Fernando, H.J.S. Probability distribution of turbulent kinetic energy dissipation rate in stratified turbulence: Microstructure measurements in the Southern California Bight. J. Geophys. Res. Oceans 2019, 124, 4591–4604. [Google Scholar] [CrossRef]
- Saddoughi, S.G.; Veeravalli, S.V. Local isotropy in turbulent boundary layers at high Reynolds number. J. Fluid Mech. 1994, 268, 333–372. [Google Scholar] [CrossRef]
- Davies, J. Drop sizes of emulsions related to turbulent energy dissipation rates. Chem. Eng. Sci. 1985, 40, 839–842. [Google Scholar] [CrossRef]
- Arai, K.; Konno, M.; Matunaga, Y.; Saito, S. Effect of dispersed-phase viscosity on the maximum stable drop size for breakup in turbulent flow. J. Chem. Eng. Jpn. 1977, 10, 325–330. [Google Scholar] [CrossRef] [Green Version]
- Babler, M.U.; Biferale, L.; Brandt, L.; Feudel, U.; Guseva, K.; Lanotte, A.S.; Marchioli, C.; Picano, F.; Sardina, G.; Soldati, A.; et al. Numerical simulations of aggregate breakup in bounded and unbounded turbulent flows. J. Fluid Mech. 2015, 766, 104–128. [Google Scholar] [CrossRef] [Green Version]
- Håkansson, A. Scale-down failed–Dissimilarities between high-pressure homogenizers of different scales due to failed mechanistic matching. J. Food Eng. 2017, 195, 31–39. [Google Scholar] [CrossRef]
- Walstra, P. Effect of homogenization on the fat globule size distribution in milk. Neth. Milk Dairy J. 1975, 29, 279–294. [Google Scholar]
- Walstra, P. Principles of emulsion formation. Chem. Eng. Sci. 1993, 48, 333–349. [Google Scholar] [CrossRef]
- Rayner, M. Scales and forces in emulsification. In Engineering Aspects of Food Emulsification and Homogenization; Rayner, M., Dejmek, P., Eds.; CRC Press: Boca Raton, FL, USA, 2015; pp. 3–32. [Google Scholar]
- McClements, D.J. Food Emulsions: Principles, Practices, and Techniques; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Casoli, P.; Vacca, A.; Berta, G.L. A numerical procedure for predicting the performance of high pressure homogenizing valves. Simul. Model. Pr. Theory 2010, 18, 125–138. [Google Scholar] [CrossRef]
- Baldyga, J.; Bourne, J. Some consequences for turbulent mixing of fine-scale intermittency. Chem. Eng. Sci. 1992, 47, 3943–3948. [Google Scholar] [CrossRef]
- Bałyga, J.; Bourne, J. Interpretation of turbulent mixing using fractals and multifractals. Chem. Eng. Sci. 1995, 50, 381–400. [Google Scholar] [CrossRef]
- Baldyga, J.; Podgórska, W. Drop break-up in intermittent turbulence: Maximum stable and transient sizes of drops. Can. J. Chem. Eng. 1998, 76, 456–470. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Intermittent turbulence in self-similar cascades: Divergence of high moments and dimension of the carrier. J. Fluid Mech. 1974, 62, 331–358. [Google Scholar] [CrossRef]
- Meneveau, C.; Sreenivasan, K.R. The multifractal nature of turbulent energy dissipation. J. Fluid Mech. 1991, 224, 429–484. [Google Scholar] [CrossRef]
- Håkansson, A.; Andersson, R.; Mortensen, H.-H.; Innings, F. Experimental investigations of turbulent fragmenting stresses in a rotor-stator mixer. Part 2. Probability distributions of instantaneous stresses. Chem. Eng. Sci. 2017, 171, 638–649. [Google Scholar] [CrossRef]
- Håkansson, A. An experimental investigation of the probability distribution of turbulent fragmenting stresses in a high-pressure homogenizer. Chem. Eng. Sci. 2018, 177, 139–150. [Google Scholar] [CrossRef]
- Sheng, J.; Meng, H.; Fox, R. A large eddy PIV method for turbulence dissipation rate estimation. Chem. Eng. Sci. 2000, 55, 4423–4434. [Google Scholar] [CrossRef]
- Saarenrinne, P.; Piirto, M. Turbulent kinetic energy dissipation rate estimation from PIV velocity vector fields. Exp. Fluids 2000, 29, S300–S307. [Google Scholar] [CrossRef]
- Tanaka, T.; Eaton, J.K. A correction method for measuring turbulence kinetic energy dissipation rate by PIV. Exp. Fluids 2007, 42, 893–902. [Google Scholar] [CrossRef]
- Hall, S.; Pacek, A.W.; Kowalski, A.J.; Cooke, M.; Rothman, D. The effect of scale and interfacial tension on liquid–liquid dispersion in in-line Silverson rotor–stator mixers. Chem. Eng. Res. Des. 2013, 91, 2156–2168. [Google Scholar] [CrossRef] [Green Version]
- De Hert, S.C.; Rodgers, T. Continuous, recycle and batch emulsification kinetics using a high-shear mixer. Chem. Eng. Sci. 2017, 167, 265–277. [Google Scholar] [CrossRef]
- Håkansson, A.; Chaudhry, Z.; Innings, F. Model emulsions to study the mechanism of industrial mayonnaise emulsification. Food Bioprod. Process 2016, 98, 189–195. [Google Scholar] [CrossRef]
- Lamb, H. Hydrodynamics, 6th ed.; Cambridge University Press: Cambridge, UK, 1932. [Google Scholar]
- Jafari, S.; McClements, D.J. Nanoemulsions: Formulation, Applications, and Characterization; Academic Press: Cambridge, MA, USA, 2018. [Google Scholar]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Håkansson, A. The Role of Stochastic Time-Variations in Turbulent Stresses When Predicting Drop Breakup—A Review of Modelling Approaches. Processes 2021, 9, 1904. https://doi.org/10.3390/pr9111904
Håkansson A. The Role of Stochastic Time-Variations in Turbulent Stresses When Predicting Drop Breakup—A Review of Modelling Approaches. Processes. 2021; 9(11):1904. https://doi.org/10.3390/pr9111904
Chicago/Turabian StyleHåkansson, Andreas. 2021. "The Role of Stochastic Time-Variations in Turbulent Stresses When Predicting Drop Breakup—A Review of Modelling Approaches" Processes 9, no. 11: 1904. https://doi.org/10.3390/pr9111904
APA StyleHåkansson, A. (2021). The Role of Stochastic Time-Variations in Turbulent Stresses When Predicting Drop Breakup—A Review of Modelling Approaches. Processes, 9(11), 1904. https://doi.org/10.3390/pr9111904




