Task Scheduling Problem of Double-Deep Multi-Tier Shuttle Warehousing Systems
Abstract
1. Introduction
2. Literature Review
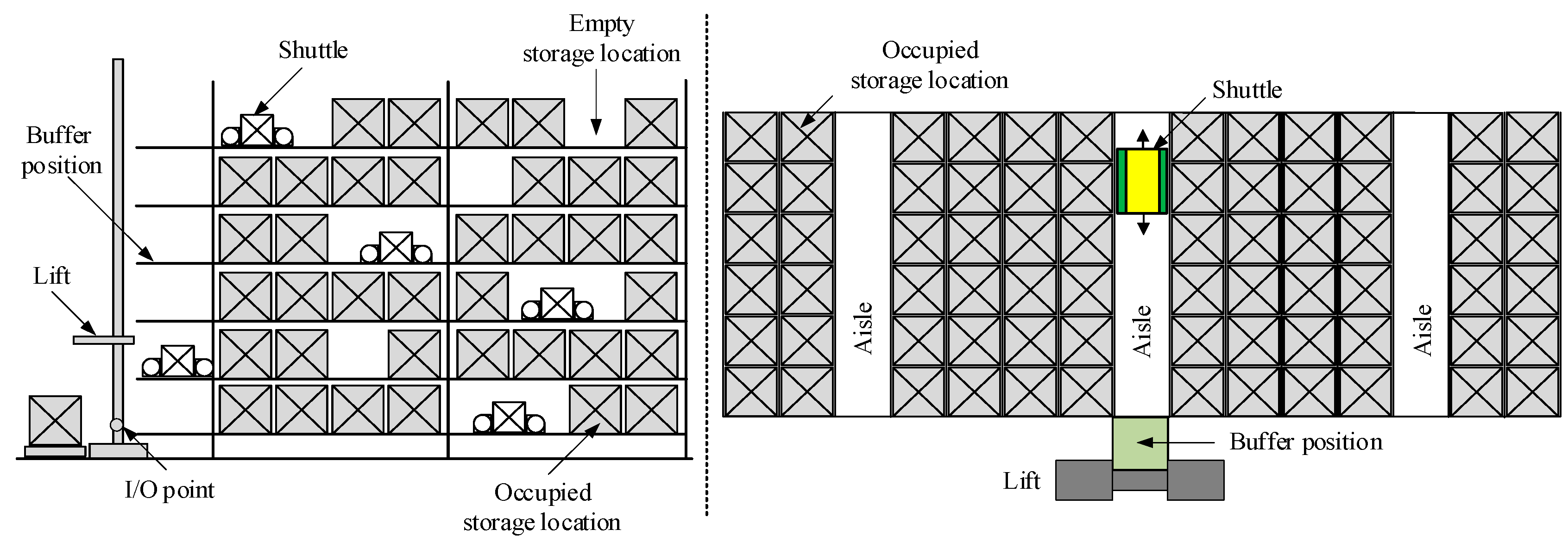
3. System Description and Modelling Preparation
- The random storage strategy is used. Under this strategy, a SKU will be placed in each empty storage location with the same probability.
- The automation equipment follow the first-come-first-served (FCFS) rule. There are no emergency orders and every retrieval task shares the same priority level.
- Shuttles and lifts abide by the dwell-point strategy of point-of-service-completion (POSC). The shuttle remain at the buffer position in each storage tier and the lift dwells at the I/O point.
- A single-command cycle is considered. The DMSWS will not accept the storage task when the system is performing a retrieval task.
4. Models of Double-Deep Multi-Tier Warehousing Systems
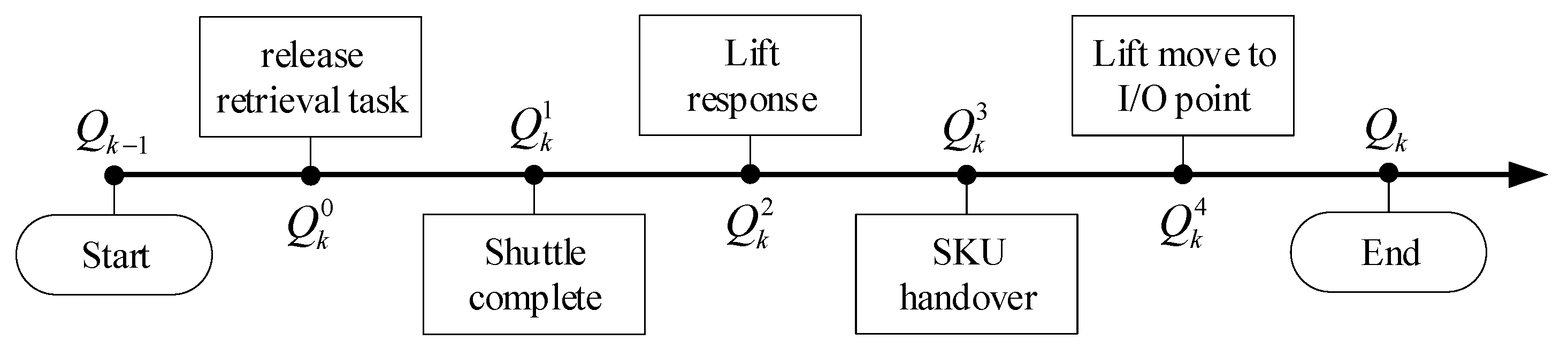
4.1. Cycle Time Model of the DMSWS
- If the lift has free time in retrieval task k, then .
- If the has shuttle waiting time in retrieval task k, then .
- Stage one. The shuttle moves to the target location to load the SKU, then returns to the buffer position and transmits a retrieval request to the lift. A rearrangement operation may be executed.
- Stage two. The lift responds to the retrieval request, moves from the I/O point to the designated tier, and completes the handover of the SKU. The shuttle is released by the control system for the next task. The lift free time is calculated in this stage.
- Stage three. The lift moves to the I/O point and unloads the SKU.
4.2. Carbon Emissions Model
4.3. Pareto Optimization
5. Solution Algorithm
- (1)
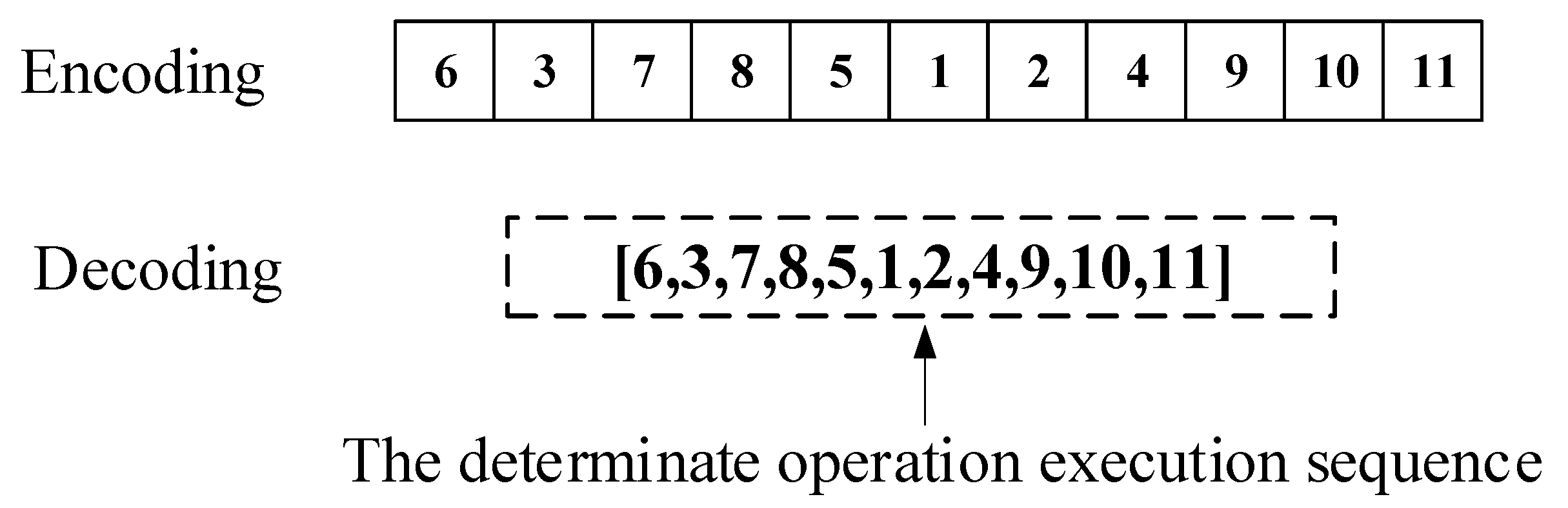
- Encoding and decoding
- (2)
- Fitness function
- (3)
- Non-dominated sort
- (4)
- Crowding distance
- (5)
- Elitism, selection, genetic operators and termination condition
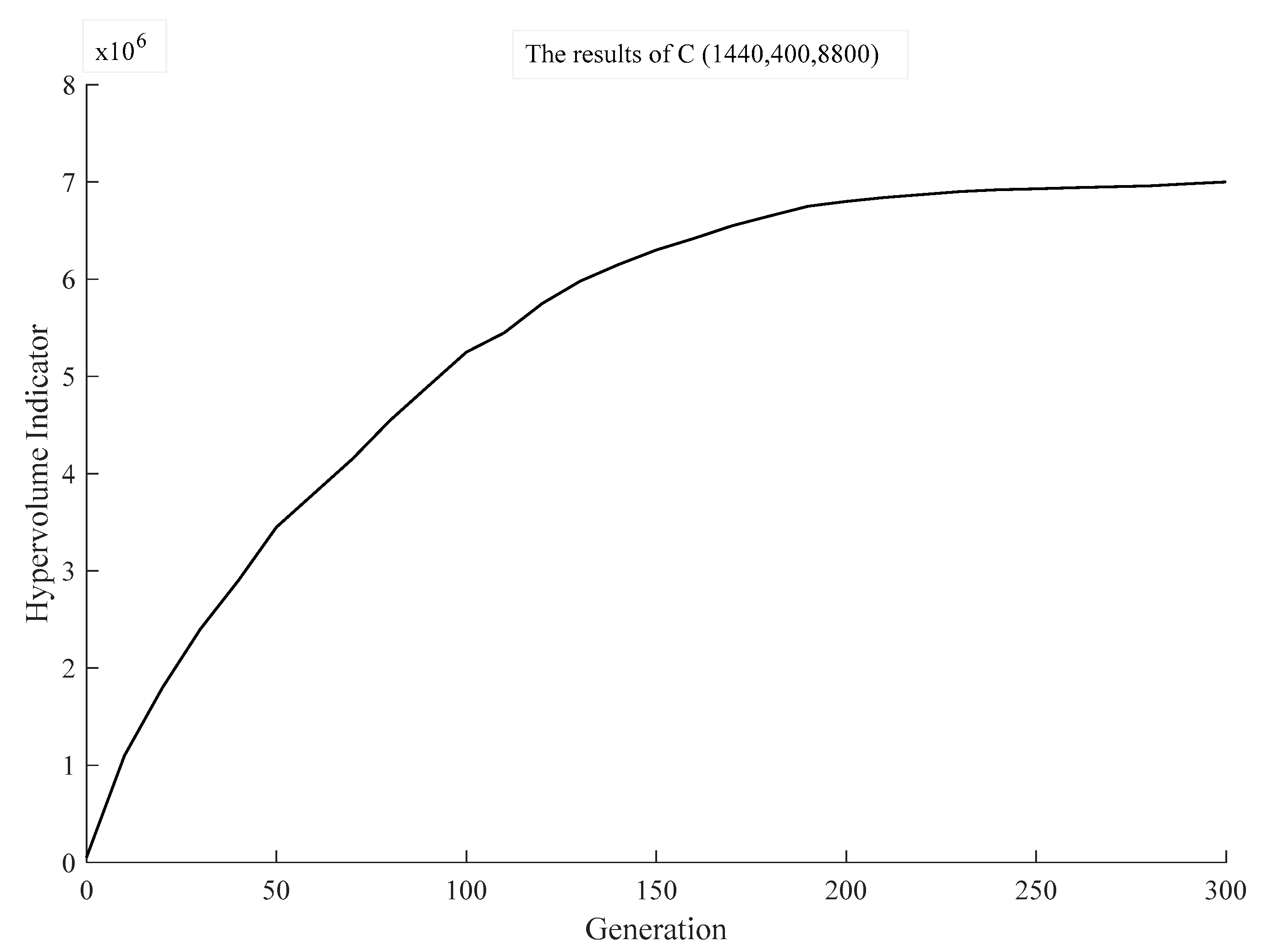
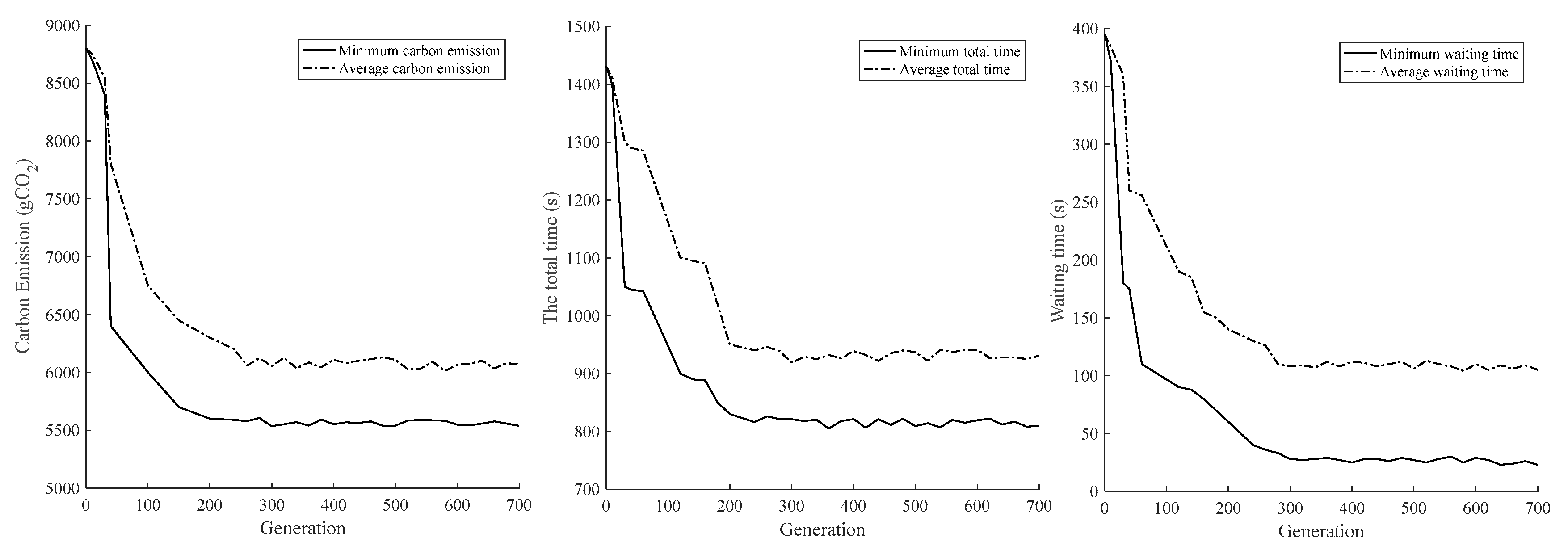
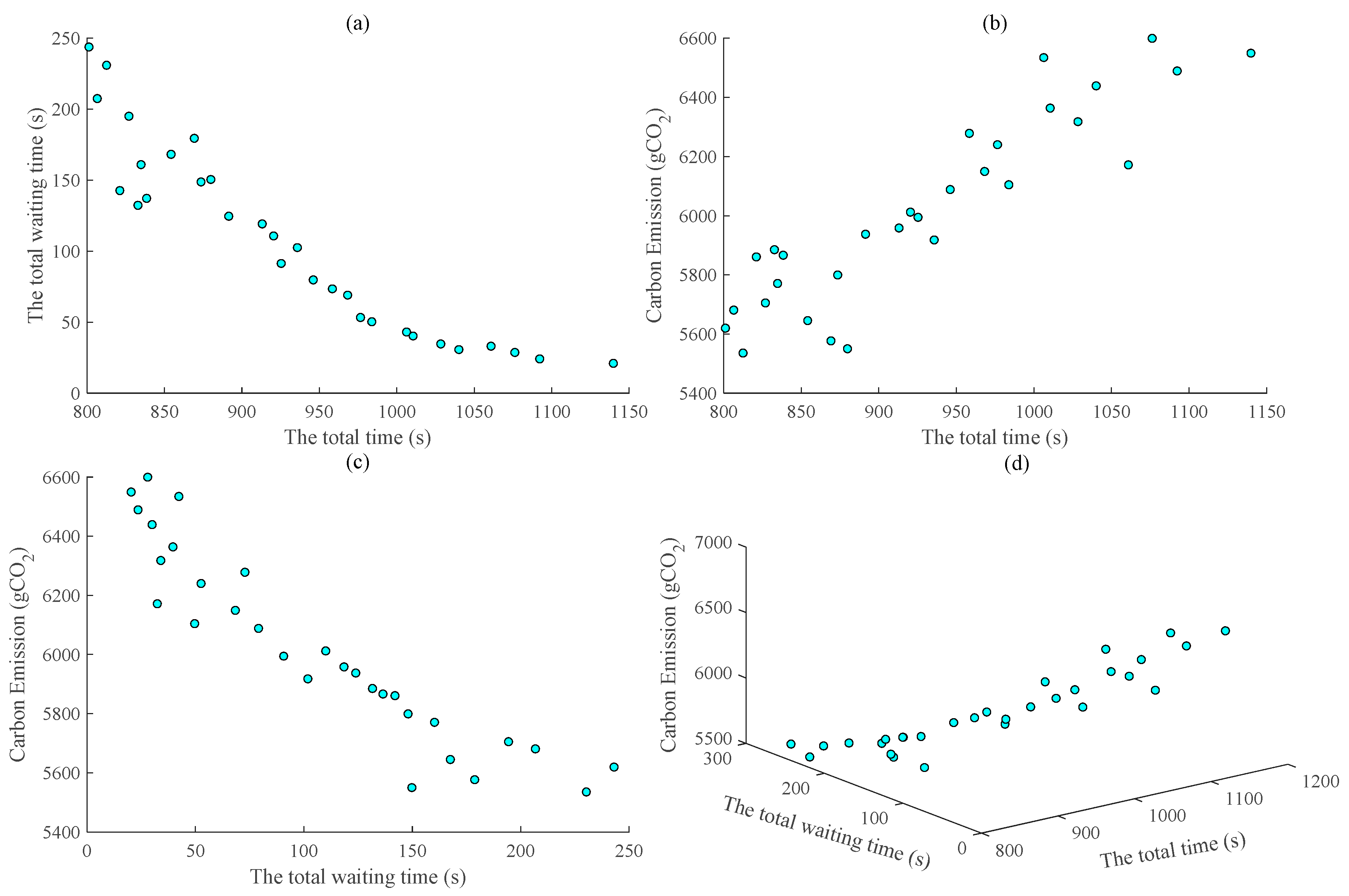
6. Case study
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tone, L.; Milan, E.; Bojan, R. Energy efficiency model for the mini-load automated storage and retrieval systems. Int. J. Adv. Manuf. Tech. 2014, 70, 97–115. [Google Scholar] [CrossRef]
- Hausman, W.H.; Schwarz, L.B.; Graves, S.C. Optimal Storage Assignment in Automatic Warehousing Systems. Manage. Sci. 1976, 22, 629–638. [Google Scholar] [CrossRef]
- Bozer, Y.A.; John, A.W. Travel-time Models for Automated Storage/Retrieval Systems. IIE Trans. 1984, 16, 329–338. [Google Scholar] [CrossRef]
- Xu, X.; Shen, G.; Yu, Y.; Huang, W. Travel Time Analysis for the Double-deep Dual-shuttle AS/RS. Int. J. Prod. Res. 2015, 53, 757–773. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, R.; Lu, H.; Zhang, X.; Liu, Z. Task scheduling model of double-deep multi-tier shuttle system. Processes 2019, 7, 604. [Google Scholar] [CrossRef]
- Hwang, H.; Seong, B.L. Travel-time Models Considering the Operating Characteristics of the Storage and Retrieval Machine. Int. J. Prod. Res. 1990, 28, 1779–1789. [Google Scholar] [CrossRef]
- Kouvelis, P.; Papanicolaou, V. Expected Travel Time and Optimal Boundary Formulas for a Two-class-based Automated Storage/Retrieval System. Int. J. Prod. Res. 1995, 33, 2889–2905. [Google Scholar] [CrossRef]
- Nia, A.; Haleh, H.; Saghaei, A. Dual command cycle dynamic sequencing method to consider GHG efficiency in unit-load multiple-rack automated storage and retrieval systems. Comput. Ind. Eng. 2017, 111, 89–108. [Google Scholar] [CrossRef][Green Version]
- Borovinsek, M.; Ekren, B.Y.; Burinskiene, A.; Lerher, T. Multi-objective optimisation model of shuttle-based storage and retrieval system. Transport 2017, 32, 120–137. [Google Scholar] [CrossRef]
- Emanuele, G.; Valeria, M.; Davide, A.; Riccardo, D.; Claudio, S.; Marco, S. Energy evalution of deep-lane autonomous vehicle storage and retrieval system. Sustainability 2019, 11, 3817. [Google Scholar] [CrossRef]
- Ene, S.; İlker, K.; Aksoy, A.; Öztürk, N. A genetic algorithm for minimizing energy consumption in warehouses. Energy 2016, 114, 973–980. [Google Scholar] [CrossRef]
- Torabizadeh, M.; Yusof, N.M.; Ma’Aram, A.; Shaharoun, A.M. Identifying sustainable warehouse management system indicators and proposing new weighting method. J. Clean. Prod. 2020, 248, 1–11. [Google Scholar] [CrossRef]
- Hao, J.; Shi, H.; Shi, V.; Yang, C. Adoption of Automatic Warehousing Systems in Logistics Firms: A Technology–Organization–Environment Framework. Sustainability 2020, 12, 5185. [Google Scholar] [CrossRef]
- Bortolini, M.; Accorsi, R.; Gamberi, M.; Manzini, R.; Regattieri, A. Optimal design of AS/RS storage systems with three-class-based assignment strategy under single and dual command operations. Int. J. Adv. Manuf. Tech. 2015, 79, 1747–1759. [Google Scholar] [CrossRef]
- Regattieri, A.; Santarelli, G.; Manzini, R.; Pareschi, A. The Impact of Dwell Point Policy in an Automated Storage/Retrieval System. Int. J. Prod. Res. 2013, 51, 4336–4348. [Google Scholar] [CrossRef]
- Hu, Y.H.; Huang, S.Y.; Chen, C.; Hsu, W.J.; Toh, A.C.; Loh, C.K.; Song, T. Travel time analysis of a new automated storage and retrieval system. Comput. Oper. Res. 2005, 32, 1515–1544. [Google Scholar] [CrossRef]
- Sari, Z.; Saygin, C.; Ghouali, N. Travel-time Models for Flow-rack Automated Storage and Retrieval Systems. Int. J. Adv. Manuf. Tech. 2005, 25, 979–987. [Google Scholar] [CrossRef]
- De Koster, M.B.M.; Le-Duc, T.; Yu, Y. Optimal Storage Rack Design for a 3-dimensional Compact AS/RS. Int. J. Prod. Res. 2008, 46, 1495–1514. [Google Scholar] [CrossRef]
- Yu, Y.; De Koster, M.B.M. Designing an Optimal Turnover-based Storage Rack for a 3D Compact Automated Storage and Retrieval System. Int. J. Prod. Res. 2009, 47, 1551–1571. [Google Scholar] [CrossRef]
- Lerher, T.; Sraml, M.; Potrc, I.; Tollazzi, T. Travel Time Models for Double-deep Automated Storage and Retrieval Systems. Int. J. Prod. Res. 2010, 48, 3151–3172. [Google Scholar] [CrossRef]
- Xu, X.; Zou, B.; Shen, G.; Yeming, G. Travel-time models and fill-grade factor analysis for double-deep multi-aisle AS/RSs. Int. J. Prod. Res. 2016, 54, 4126–4144. [Google Scholar] [CrossRef]
- Tone, L. Travel time model for double-deep shuttle-based storage and retrieval systems. Int. J. Prod. Res. 2016, 54, 2519–2540. [Google Scholar] [CrossRef]
- Roodbergen Kees, J.; Iris, F.; Vis, A. A Survey of Literature on Automated Storage and Retrieval Systems. Eur. J. Oper. Res. 2009, 194, 343–362. [Google Scholar] [CrossRef]
- Gu, J.; Marc, G.; Leon, F.M. Research on Warehouse Design and Efficiency Evaluation: A Comprehensive Review. Eur. J. Oper. Res. 2010, 203, 539–549. [Google Scholar] [CrossRef]
- Malmborg, C.J. Conceptualizing Tools for Autonomous Vehicle Storage and Retrieval Systems. Int. J. Prod. Res. 2002, 40, 1807–1822. [Google Scholar] [CrossRef]
- Fukunari, M.; Malmborg, C.J. An efficient cycle time model for autonomous vehicle storage and retrieval systems. Int. J. Prod. Res. 2008, 46, 3167–3184. [Google Scholar] [CrossRef]
- Sunderesh, S.H.; Xiao, C.; Ananth, K.; Malaborg, C.J. Analytical models for analysis of automated warehouse material handling systems. Int. J. Prod. Res. 2011, 49, 6833–6861. [Google Scholar] [CrossRef]
- Gino, M.; Marco, M.; Sara, P.; Elena, T. Analytical model to estimate efficiency of autonomous vehicle storage and retrieval systems for product totes. Int. J. Prod. Res. 2012, 50, 7134–7148. [Google Scholar] [CrossRef]
- Ekren, B.Y. Design and Analysis of Autonomous Vehicle Storage and Retrieval Systems via Queuing Network and Simulation Models. Ph.D. Thesis, University of Louisville, Louisville, KY, USA, 29 October 2009. [Google Scholar]
- Cai, X.; Heragu, S.S.; Liu, Y. Modeling and evaluating the AVS/RS with tier-to-tier vehicles using a semi-open queueing network. IIE Trans. 2014, 46, 905–927. [Google Scholar] [CrossRef]
- Zou, B.; Xu, X.; Gong, Y.; De, K.R. Modeling parallel movement of lifts and vehicles in tier-captive vehicle-based warehousing systems. Eur. J. Oper. Res. 2016, 254, 51–67. [Google Scholar] [CrossRef]
- Wang, Y.; Mou, S.; Wu, Y. Task scheduling for multi-tier shuttle warehousing systems. Int. J. Prod. Res. 2015, 53, 1–12. [Google Scholar] [CrossRef]
- Lerher, T.; Ekren, B.; Rosi, B. Travel time model for shuttle-based storage and retrieval systems. Int. J. Adv. Manuf. Techn. 2015, 78, 1705–1725. [Google Scholar] [CrossRef]
- Tappia, E.; Roy, D.; René, D.K.; Melacini, M. Modeling, analysis, and design insights for shuttle-based compact storage systems. Soc. Sci. Electron. Publ. 2017, 51, 269–295. [Google Scholar] [CrossRef]
- Marco, B.; Maurizio, F.; Emilio, F.; Mauro, G.; Francesco, P. Time and energy optimal unit-load assignment for automatic S/R warehouses. Int. J. Prod. Econ. 2017, 190, 133–145. [Google Scholar] [CrossRef]
- Bin, Y. Research on carbon emissions reduction cost of the power industry in China based on resource allocation optimization. Ph.D. Thesis, Harbin Institute of Technology, Heilongjiang, China, 13 May 2013. [Google Scholar]







| Citation | Year | Type of Cycle | Method | SR | Objective |
|---|---|---|---|---|---|
| Hausman, Schwarz, and Graves | 1976 | SC | Analytical formulae | SD | Expected travel-time |
| Bozer and White | 1984 | SC/DC | Analytical formulae | SD | Expected travel-time |
| Hwang and Lee | 1990 | SC/DC | Analytical formulae | SD | Expected travel-time |
| Kouvelis and Papanicolaou | 1995 | SC/DC | Analytical formulae | SD | Expected travel-time |
| Bortolini et al. | 2015 | SC/DC | Analytical formulae | SD | Mean travel-time |
| Regattieri et al. | 2013 | SC/DC | Simulation models | SD | Travel-time Travel distance |
| Hu et al. | 2005 | SC | Analytical formulae Simulation models | SP | Travel-time |
| Sari, Saygin, and Ghouali | 2005 | SC/DC | Analytical formulae Simulation models | 3D | Travel-time |
| De Koster, Le-Duc, and Yu | 2008 | SC/DC | Analytical formulae | 3D | Travel-time |
| Yu and De Koster | 2009 | SC | Analytical formulae | 3D | Travel-time |
| Lerher et al. | 2010 | SC/DC | Analytical formulae Simulation models | DD | Travel-time |
| Xu et al. | 2015 | SD/DC/QC | Analytical formulae | DD | Travel-time |
| Xu et al. | 2016 | SD/DC | Analytical formulae Simulation models | DD | Travel-time; Cost |
| Malmborg | 2002 | SC/DC | Probability analytical | SD | Cycle time; Capacity utilization |
| Fukunari and Malmborg | 2007 | SC/DC | Probability analytical Simulation models | SD | Cycle time; Lift utilization; Vehicle utilization |
| Heragu et al. | 2011 | SC/DC | Queuing network | SD | System throughput |
| Marchet et al. | 2012 | SC/DC | Queuing network | SD | Cycle time; Waiting time |
| Wang Y, Mou S, and Wu Y | 2015 | SC | Analytical formulae | SD | Travel-time; Waiting time Idle time |
| Lerher et al. | 2015 | SC/DC | Analytical formulae Simulation models | SD | Travel-time |
| Tappia et al. | 2017 | DC | Queuing network | SD | Travel-time |
| Lerher, Edl M, and Bojan Rosi | 2014 | DC/QC | Queuing network | SD | Throughput capacity; Energy consumption; Carbon emissions; |
| Bortolini M et al. | 2017 | SC | Analytical formulae | SD | Travel-time; Energy |
| NIA A, Haleh H, Saghaei A | 2017 | DC | Analytical formulae | SD | Cost; Carbon emissions |
| Borovinsek | 2017 | SC/DC | Analytical formulae | SD | Energy consumption; Cost |
| Wang Y et al. | 2019 | DC | Analytical formulae | DD | Travel-time |
| Parameter | Unit of Measure | Value | Parameter | Unit of Measure | Value |
|---|---|---|---|---|---|
| m | 1.5 | - | 4 | ||
| m | 1.5 | - | 8 | ||
| m | 1.0 | - | 20 | ||
| m | 1.2 | 974 | |||
| m/s | 1.5 | s | 3 | ||
| m/s | 2.0 | s | 2 | ||
| kw | 0.5 | s | 5 | ||
| kw | 1.0 | - | 0.8 | ||
| kw | 0.8 | kw | 0.1 | ||
| kw | 1.5 | kw | 0.2 |
| Sequence | Aisle | Column | Tier | Depth | Sequence | Aisle | Column | Tier | Depth |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 14 | 2 | 1 | 31 | 1 | 19 | 5 | 2 |
| 2 | 2 | 19 | 2 | 2 | 32 | 1 | 8 | 5 | 2 |
| 3 | 4 | 9 | 2 | 2 | 33 | 4 | 1 | 5 | 1 |
| 4 | 2 | 3 | 2 | 1 | 34 | 3 | 14 | 5 | 1 |
| 5 | 2 | 3 | 2 | 2 | 35 | 3 | 2 | 5 | 2 |
| 6 | 3 | 14 | 2 | 2 | 36 | 2 | 11 | 5 | 1 |
| 7 | 1 | 8 | 3 | 2 | 37 | 3 | 2 | 6 | 2 |
| 8 | 1 | 5 | 3 | 2 | 38 | 3 | 14 | 6 | 2 |
| 9 | 4 | 18 | 3 | 1 | 39 | 4 | 7 | 6 | 1 |
| 10 | 3 | 17 | 3 | 2 | 40 | 1 | 9 | 6 | 2 |
| 11 | 2 | 12 | 3 | 2 | 41 | 2 | 15 | 6 | 1 |
| 12 | 4 | 18 | 3 | 2 | 42 | 3 | 14 | 6 | 1 |
| 13 | 1 | 8 | 3 | 1 | 43 | 1 | 11 | 7 | 2 |
| 14 | 3 | 3 | 4 | 1 | 44 | 4 | 20 | 7 | 1 |
| 15 | 2 | 20 | 4 | 2 | 45 | 1 | 3 | 7 | 1 |
| 16 | 4 | 13 | 4 | 1 | 46 | 2 | 8 | 7 | 2 |
| 17 | 4 | 7 | 4 | 2 | 47 | 3 | 17 | 7 | 1 |
| 18 | 2 | 9 | 4 | 1 | 48 | 3 | 6 | 7 | 1 |
| 19 | 2 | 4 | 4 | 2 | 49 | 3 | 17 | 7 | 2 |
| 20 | 3 | 11 | 4 | 2 | 50 | 1 | 3 | 7 | 2 |
| 21 | 1 | 8 | 4 | 1 | 51 | 4 | 20 | 7 | 2 |
| 22 | 1 | 16 | 4 | 2 | 52 | 2 | 8 | 7 | 1 |
| 23 | 3 | 3 | 4 | 2 | 53 | 2 | 9 | 8 | 2 |
| 24 | 4 | 13 | 4 | 2 | 54 | 3 | 4 | 8 | 1 |
| 25 | 3 | 11 | 4 | 1 | 55 | 1 | 12 | 8 | 1 |
| 26 | 2 | 9 | 4 | 2 | 56 | 4 | 18 | 8 | 1 |
| 27 | 1 | 8 | 4 | 2 | 57 | 2 | 9 | 8 | 1 |
| 28 | 4 | 1 | 5 | 2 | 58 | 1 | 3 | 8 | 2 |
| 29 | 3 | 14 | 5 | 2 | 59 | 1 | 12 | 8 | 2 |
| 30 | 2 | 11 | 5 | 2 | 60 | 3 | 4 | 8 | 2 |
| Factor Level | Parameters | |
|---|---|---|
| Nc | Nm | |
| 1 | 0.80 | 0.10 |
| 2 | 0.85 | 0.15 |
| 3 | 0.90 | 0.20 |
| ID | ID | ||||||
|---|---|---|---|---|---|---|---|
| 1 | 801.53 * | 243.40 | 5617.71 | 16 | 925.73 | 90.95 | 5992.56 |
| 2 | 806.92 | 207.10 | 5678.98 | 17 | 936.15 | 102.10 | 5915.88 |
| 3 | 812.91 | 230.60 | 5533.45 * | 18 | 946.46 | 79.35 | 6086.46 |
| 4 | 821.47 | 142.30 | 5858.91 | 19 | 958.78 | 73.05 | 6276.44 |
| 5 | 827.35 | 194.70 | 5703.24 | 20 | 968.65 | 68.65 | 6147.46 |
| 6 | 833.18 | 131.90 | 5883.18 | 21 | 976.94 | 52.85 | 6238.18 |
| 7 | 835.16 | 160.55 | 5768.86 | 22 | 984.25 | 49.85 | 6102.57 |
| 8 | 838.81 | 136.75 | 5864.48 | 23 | 1006.76 | 42.60 | 6532.57 |
| 9 | 854.55 | 167.85 | 5643.19 | 24 | 1010.93 | 39.85 | 6361.85 |
| 10 | 869.59 | 179.10 | 5574.86 | 25 | 1028.82 | 34.25 | 6315.93 |
| 11 | 873.92 | 148.35 | 5797.45 | 26 | 1040.53 | 30.25 | 6437.27 |
| 12 | 880.25 | 150.10 | 5548.05 | 27 | 1061.29 | 32.65 | 6169.82 |
| 13 | 891.87 | 124.20 | 5935.48 | 28 | 1076.67 | 28.20 | 6597.71 |
| 14 | 913.47 | 118.80 | 5956.40 | 29 | 1092.74 | 23.75 | 6487.41 |
| 15 | 920.81 | 110.35 | 6010.21 | 30 | 1140.32 | 20.55* | 6547.53 |
| ID | Chromosome Variable Value (Operation Execution Solution) |
|---|---|
| 1 | [54,38,53,3,42,17,35,47,26,1,32,20,10,6,29,58,15,44,8,19,2,55,11,49,22,13,48,59,21,41,23,7,51,27,5,31,43,9,33,57,4,16,28,52,56,36,40,46,37,25,30,45,18,60,50,24,12,14,34,39] |
| 2 | [54,32,24,8,41,51,15,36,4,59,50,30,1,21,42,49,20,34,18,60,45,57,23,31,19,43,12,40,35,7,4,28,17,10,52,26,38,53,3,22,29,13,55,27,6,58,33,5,16,47,9,48,25,39,14,46,11,37,56,2] |
| 3 | [54,4,32,24,1,41,51,8,15,36,59,50,30,21,42,49,20,34,18,60,45,57,23,31,19,43,12,40,35,7,44,28,17,10,52,26,38,53,3,22,29,13,55,27,6,58,33,5,16,47,9,48,25,39,14,46,11,37,56,29] |
| 4 | [54,4,32,24,1,41,51,15,36,59,50,30,8,20,34,18,60,45,21,42,49,31,19,57,23,43,12,40,35,7,44,28,17,10,52,26,38,48,3,29,39,14,9,33,56,22,13,55,27,6,58,5,16,47,53,25,46,2,37,11] |
| 5 | [54,38,35,3,42,17,53,26,1,32,20,10,6,29,58,15,44,8,19,2,55,11,49,22,13,48,59,21,41,7,51,27,5,31,43,9,33,57,4,16,47,28,52,56,50,23,40,46,37,25,30,45,18,60,36,24,34,14,39,12] |
| 6 | [5,19,53,44,38,31,20,1,30,26,7,39,45,6,13,25,14,32,2,35,46,24,36,47,41,3,50,37,29,27,40,48,34,16,49,33,18,57,42,15,10,59,28,21,11,58,17,51,8,56,52,22,23,9,55,4,54,12,43,60] |
| 7 | [19,53,5,44,38,31,20,1,30,26,7,39,45,6,13,25,14,32,2,35,46,24,36,47,41,3,50,37,29,27,40,48,34,16,49,33,18,57,42,15,10,59,28,21,11,58,17,51,8,56,52,22,23,9,55,4,54,12,43,60] |
| 8 | [54,4,32,24,1,41,8,51,15,36,59,50,30,21,42,49,20,34,18,60,45,57,23,31,19,43,12,40,35,7,44,28,17,10,52,26,38,53,3,29,39,14,9,33,56,22,13,55,27,6,58,5,16,47,48,25,46,2,37,11] |
| 9 | [54,4,21,42,49,32,24,8,41,51,15,36,59,50,30,1,20,34,18,60,45,31,43,12,40,35,7,44,28,17,10,57,23,52,26,38,53,3,22,29,13,55,27,6,58,33,5,16,47,9,19,48,25,14,39,2,56,11,37,46] |
| 10 | [19,32,50,57,24,23,8,41,51,15,36,59,30,1,20,34,18,60,45,21,42,49,31,43,12,40,35,7,44,28,17,10,52,26,38,53,3,22,29,13,55,27,6,58,33,5,16,47,54,9,48,25,39,14,2,56,4,37,11,46] |
| 11 | [57,24,23,32,8,41,51,15,36,59,50,30,1,20,34,18,60,45,21,42,49,31,43,12,40,35,7,44,28,17,10,52,26,38,53,3,22,29,13,55,27,6,58,33,5,16,47,54,39,14,9,19,2,56,46,4,25,37,48,11] |
| 12 | [32,24,8,41,51,15,36,59,50,30,1,20,34,18,60,45,21,42,49,31,43,12,40,35,7,44,28,17,10,52,26,38,53,3,22,29,13,55,27,6,58,33,5,57,16,47,54,39,14,9,19,2,46,4,37,48,23,56,25,11] |
| 13 | [48,11,15,31,26,13,39,59,2,22,35,6,28,7,23,36,38,33,21,45,56,5,17,8,55,53,46,40,32,52,34,24,47,41,50,16,12,30,37,10,1,60,27,14,43,3,25,29,42,44,4,19,54,9,20,58,51,18,57,49] |
| 14 | [32,24,8,41,51,15,36,59,50,30,1,20,34,18,60,45,21,42,49,31,43,12,40,35,7,44,28,17,10,52,26,38,53,3,22,29,13,55,27,6,58,33,5,57,16,47,54,9,23,39,14,19,2,46,4,37,56,25,48,11] |
| 15 | [48,11,15,31,26,13,39,59,2,22,35,6,28,7,50,25,12,56,5,17,8,55,23,3,10,49,54,36,40,21,1,38,4,47,16,58,43,24,30,60,14,33,45,53,46,32,52,37,27,34,41,29,42,44,19,9,20,51,57,18] |
| 16 | [5,19,53,44,38,31,20,1,30,26,7,39,45,6,13,25,14,32,2,35,46,24,36,47,41,3,50,37,29,27,40,48,34,16,49,33,18,57,42,15,10,59,28,21,11,58,17,51,8,56,52,22,23,55,60,9,54,12,43,4] |
| 17 | [11,36,38,33,21,45,56,22,5,39,28,17,6,8,55,31,53,46,15,40,32,52,2,34,24,48,26,13,59,35,7,23,3,10,49,54,25,1,12,4,47,16,58,43,30,60,14,42,51,27,41,19,44,37,57,9,29,18,20,50] |
| 18 | [32,24,8,41,51,15,36,59,50,30,1,20,34,18,60,45,21,42,49,31,43,12,40,35,7,44,28,17,10,52,26,38,53,3,22,29,13,55,27,6,58,33,5,57,16,47,54,9,23,19,48,25,56,46,39,4,14,11,2,37] |
| 19 | [19,20,56,36,27,58,17,49,30,38,16,46,34,8,33,53,24,32,41,51,15,10,50,21,42,31,43,12,40,35,7,44,28,29,39,14,59,1,18,60,45,9,55,22,4,26,13,5,52,25,23,37,54,2,48,6,47,3,57,11] |
| 20 | [48,11,15,31,26,13,39,59,2,22,35,6,28,7,23,3,10,49,54,5,25,36,40,21,1,12,38,4,47,55,17,8,53,46,32,52,34,24,41,43,45,33,56,50,16,30,37,60,27,14,57,58,29,51,18,20,19,44,42,9] |
| 21 | [54,4,21,42,49,31,43,12,40,35,7,44,28,15,29,39,14,10,32,24,8,41,51,36,59,50,30,1,20,34,18,60,45,9,33,55,22,19,3,13,2,17,56,27,58,38,16,46,53,26,5,52,25,23,37,48,6,47,11,57] |
| 22 | [15,41,25,38,3,51,50,12,37,6,60,7,53,32,27,1,29,43,59,21,33,48,9,4,35,17,36,20,26,44,10,19,16,39,54,18,28,52,13,58,14,40,57,49,2,42,34,24,5,56,30,22,11,45,23,31,8,55,47,46] |
| 23 | [10,39,31,60,1,11,29,52,3,56,20,35,49,48,18,45,38,43,25,8,21,17,55,15,26,7,27,28,40,9,24,37,23,57,30,19,6,59,44,58,5,54,12,14,51,2,34,16,33,41,36,50,42,22,47,13,53,32,4,46] |
| 24 | [35,46,50,30,24,52,42,33,22,59,15,34,43,12,25,39,5,17,8,1,7,6,54,4,27,53,19,21,44,47,18,28,9,20,41,26,57,36,29,56,11,48,23,37,58,38,51,13,32,3,45,40,49,55,2,16,10,31,0,14] |
| 25 | [22,5,49,59,3,7,48,52,6,58,19,36,20,1,18,33,46,2,57,9,4,27,44,29,11,17,34,26,45,39,47,24,54,30,40,10,15,53,51,60,50,56,16,13,28,37,43,25,35,32,41,55,38,23,14,31,8,21,12,42] |
| 26 | [35,7,50,17,11,42,36,13,28,33,58,44,24,23,40,20,59,48,10,4,54,2,18,30,49,22,60,57,16,51,38,14,56,55,34,45,41,39,43,31,27,47,19,53,3,26,6,8,1,29,25,12,21,32,37,46,15,9,52,5] |
| 27 | [21,8,51,7,43,54,11,15,6,41,23,33,3,5,27,47,14,39,44,45,29,28,16,36,37,49,56,19,48,57,24,59,22,42,55,1,53,25,31,18,30,26,34,58,12,32,38,17,60,35,52,4,50,10,2,20,46,40,9,13] |
| 28 | [35,7,50,17,11,42,36,13,28,33,58,44,24,23,40,20,59,48,10,4,54,2,18,30,49,22,60,57,16,51,38,14,56,55,34,45,41,39,43,31,27,47,19,53,3,26,6,8,1,29,25,12,21,32,37,9,15,5,46,52] |
| 29 | [28,40,44,57,37,36,38,12,39,21,45,1,30,14,32,52,55,16,46,13,51,9,6,31,4,26,50,35,3,56,8,29,17,15,11,33,24,7,2,58,34,54,18,42,53,43,20,59,5,10,60,47,27,22,19,25,48,41,23,49] |
| 30 | [35,46,50,30,24,52,42,33,22,59,15,34,43,12,25,39,5,17,8,1,7,6,54,4,27,53,19,21,44,47,18,28,9,20,41,26,57,36,29,56,11,48,23,37,58,38,51,13,10,49,16,32,45,60,31,55,3,2,40,14] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhan, X.; Xu, L.; Ling, X. Task Scheduling Problem of Double-Deep Multi-Tier Shuttle Warehousing Systems. Processes 2021, 9, 41. https://doi.org/10.3390/pr9010041
Zhan X, Xu L, Ling X. Task Scheduling Problem of Double-Deep Multi-Tier Shuttle Warehousing Systems. Processes. 2021; 9(1):41. https://doi.org/10.3390/pr9010041
Chicago/Turabian StyleZhan, Xiangnan, Liyun Xu, and Xufeng Ling. 2021. "Task Scheduling Problem of Double-Deep Multi-Tier Shuttle Warehousing Systems" Processes 9, no. 1: 41. https://doi.org/10.3390/pr9010041
APA StyleZhan, X., Xu, L., & Ling, X. (2021). Task Scheduling Problem of Double-Deep Multi-Tier Shuttle Warehousing Systems. Processes, 9(1), 41. https://doi.org/10.3390/pr9010041





