A Review on Theory and Modelling of Nanomechanical Sensors for Biological Applications
Abstract
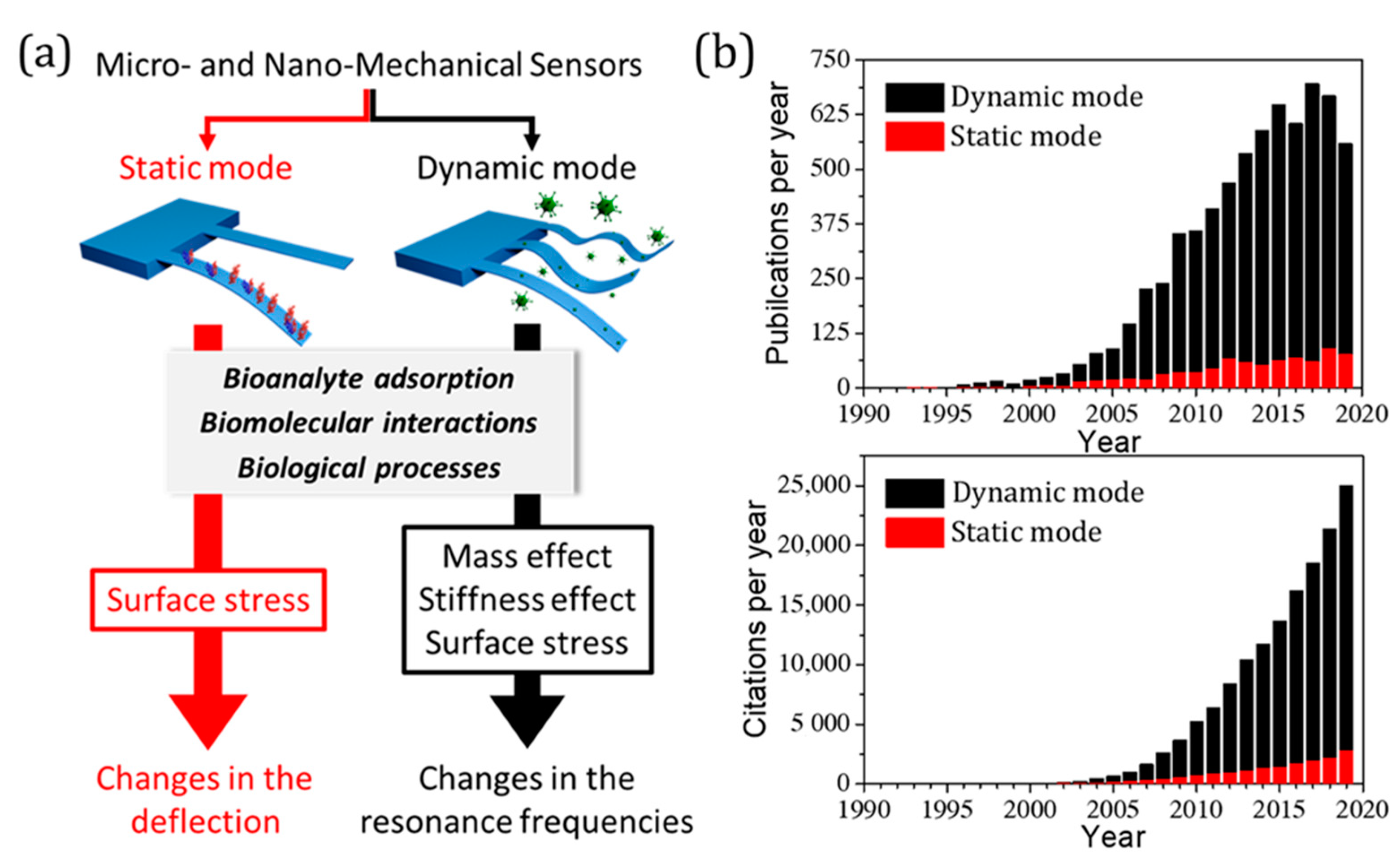
1. Introduction
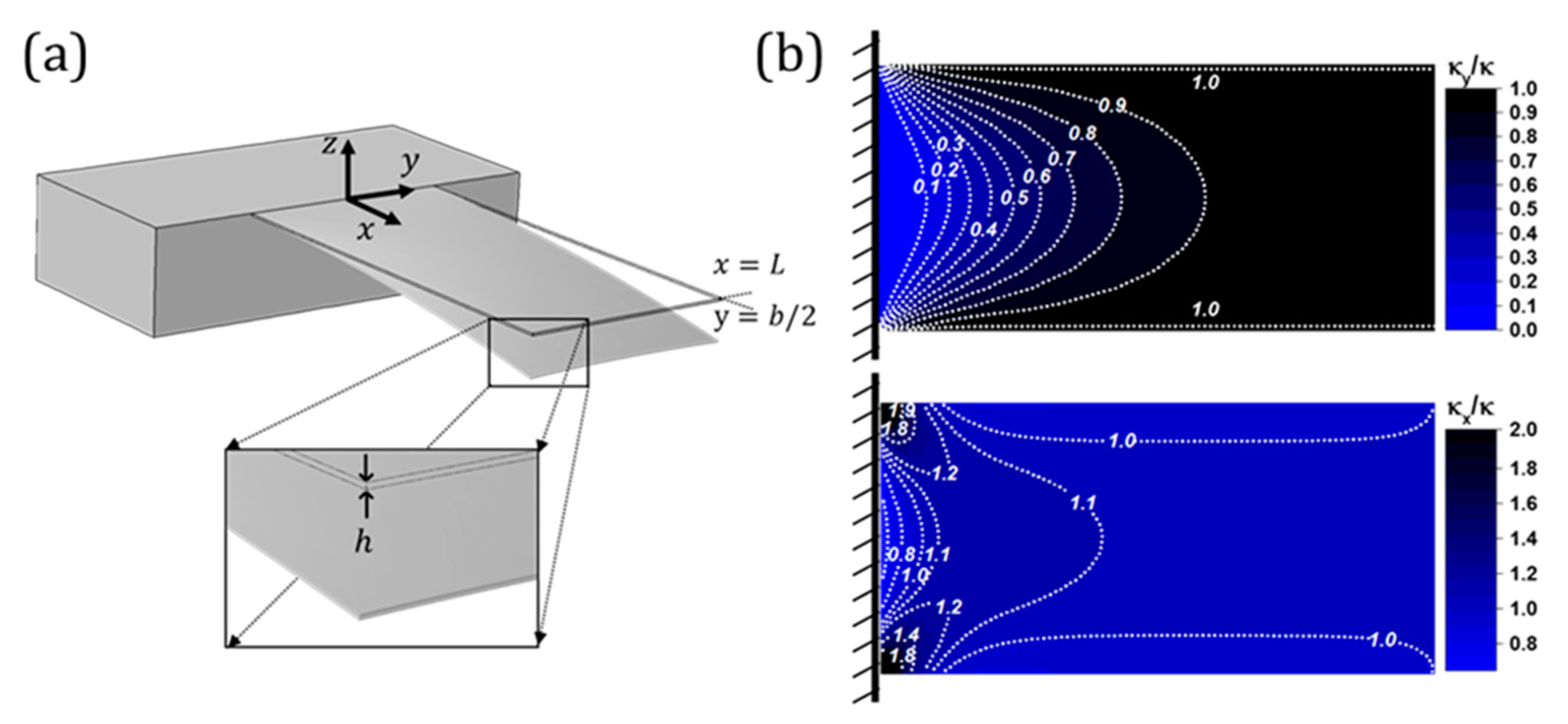
2. Nanomechanical Sensors in Static Mode: Effect of Surface Stress
3. Nanomechanical Sensors in Dynamic Mode
3.1. Effect of a Complete Layer
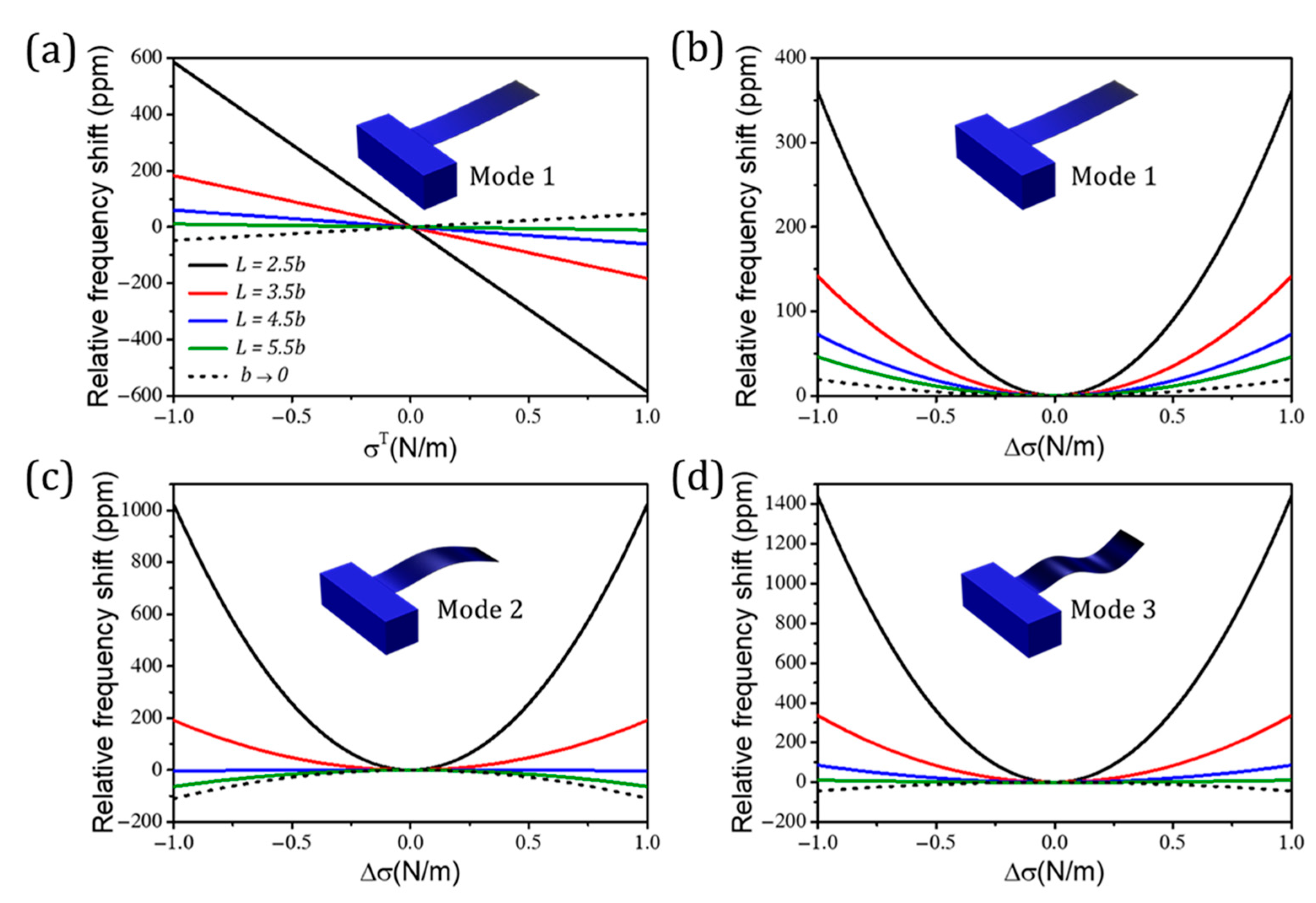
3.1.1. Effect of Surface Stress
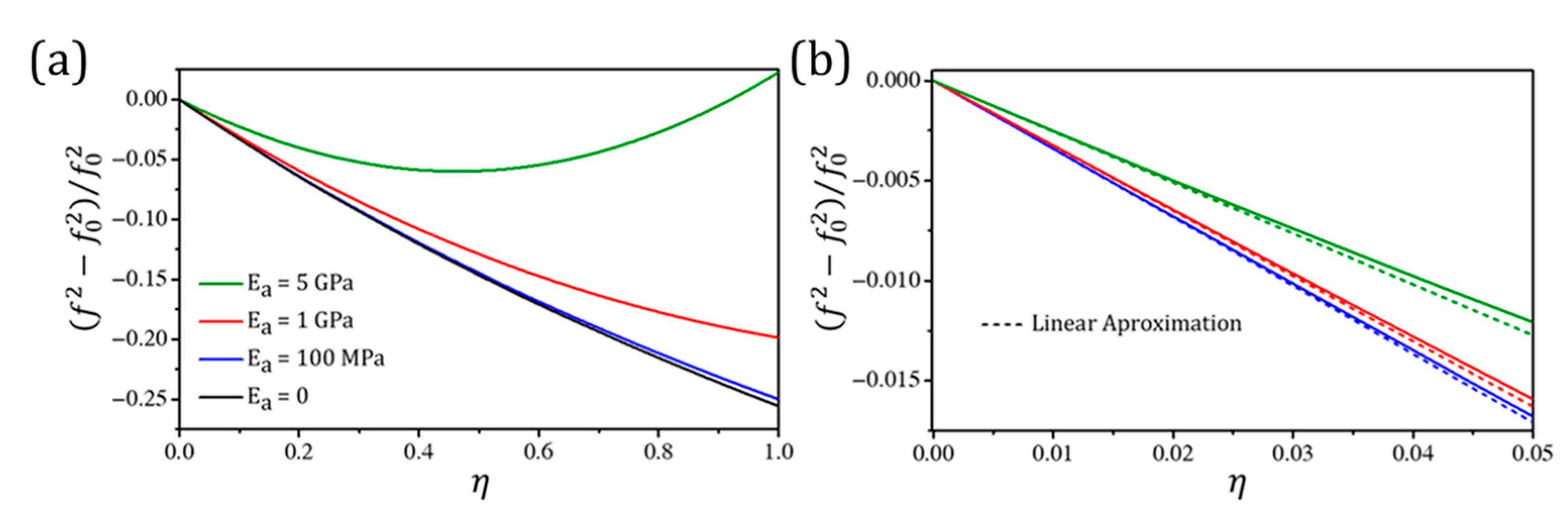
3.1.2. Mass and Stiffness Effects
3.2. Individual Particles
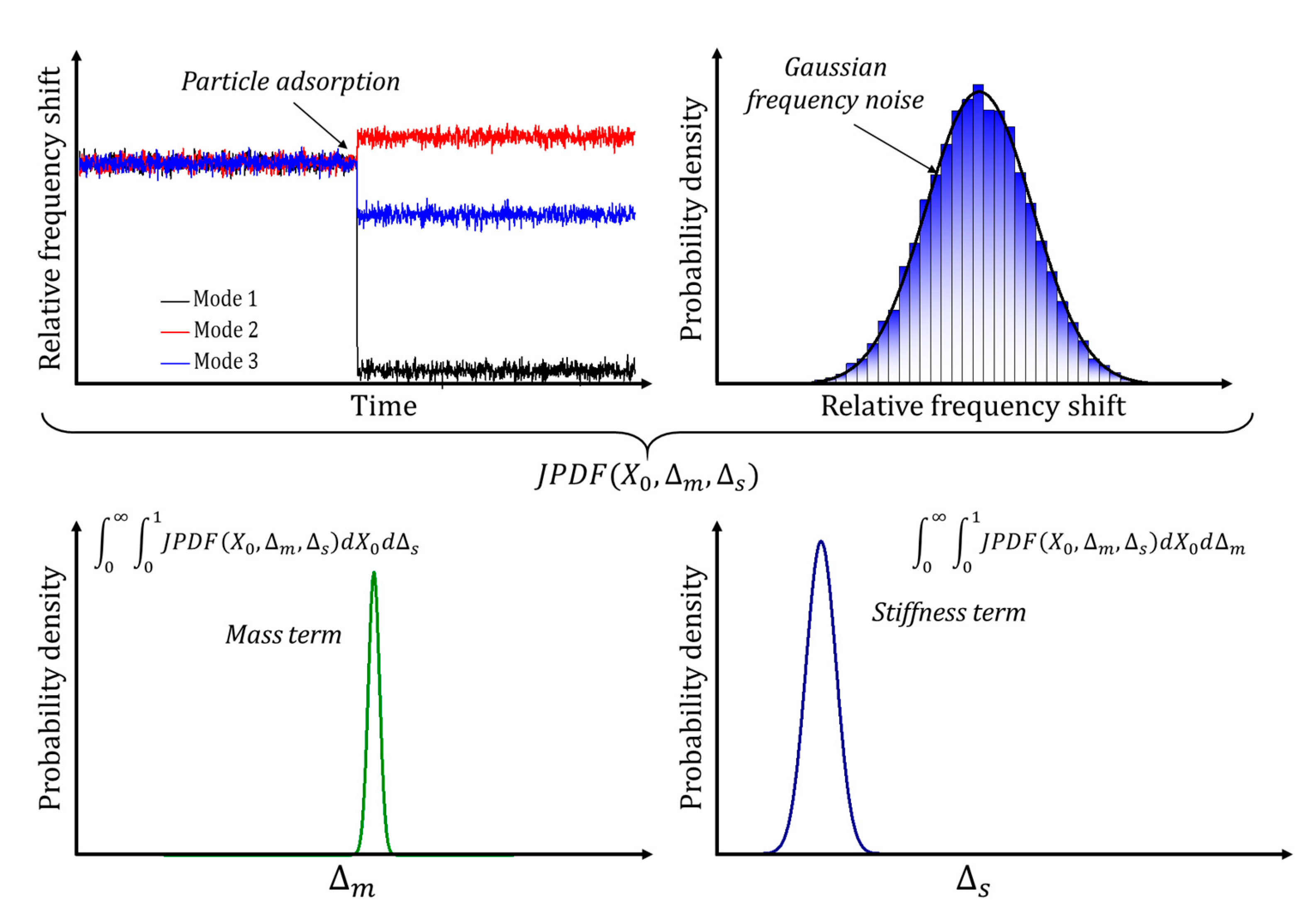
3.2.1. Multimode Measuring
3.2.2. Inertial Imaging
4. Hydrodynamic Loading
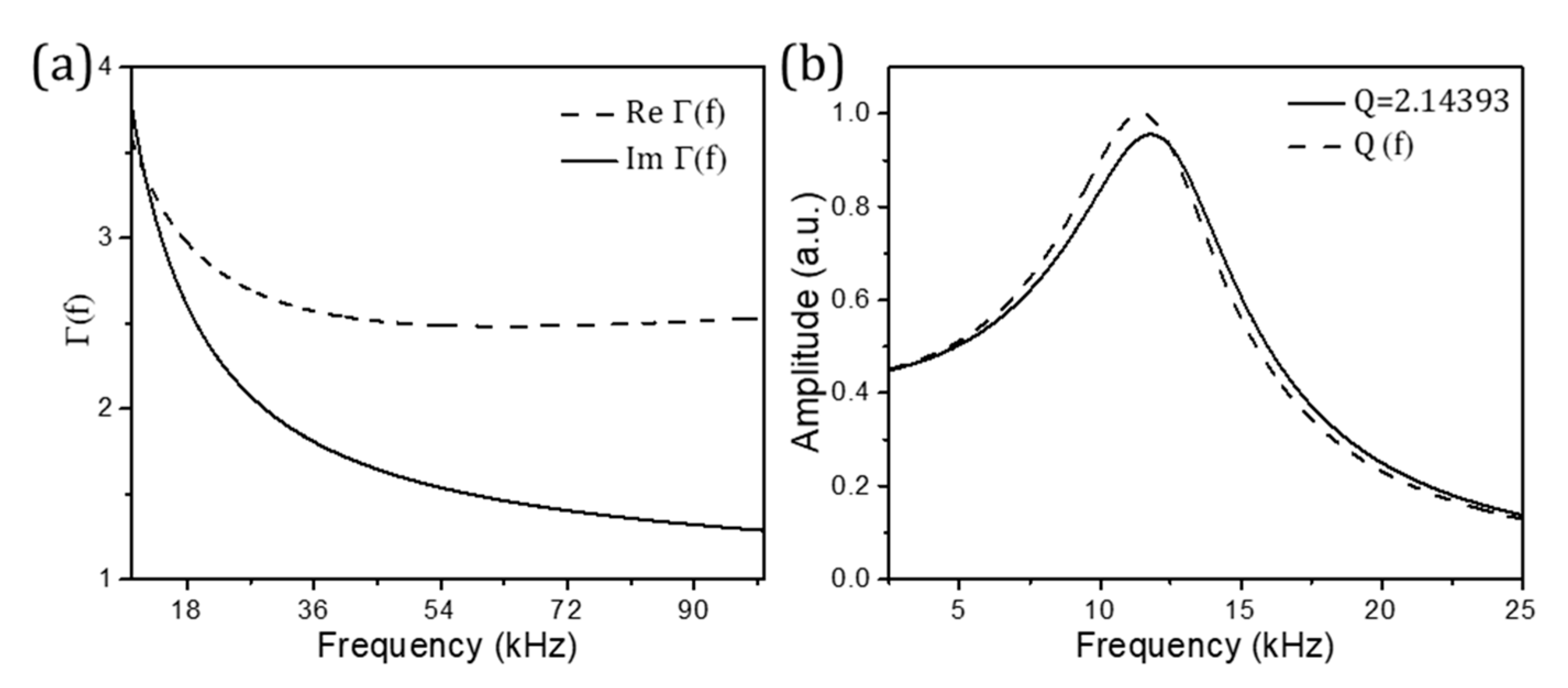
4.1. Nanomechanical Resonators Immersed in Fluid
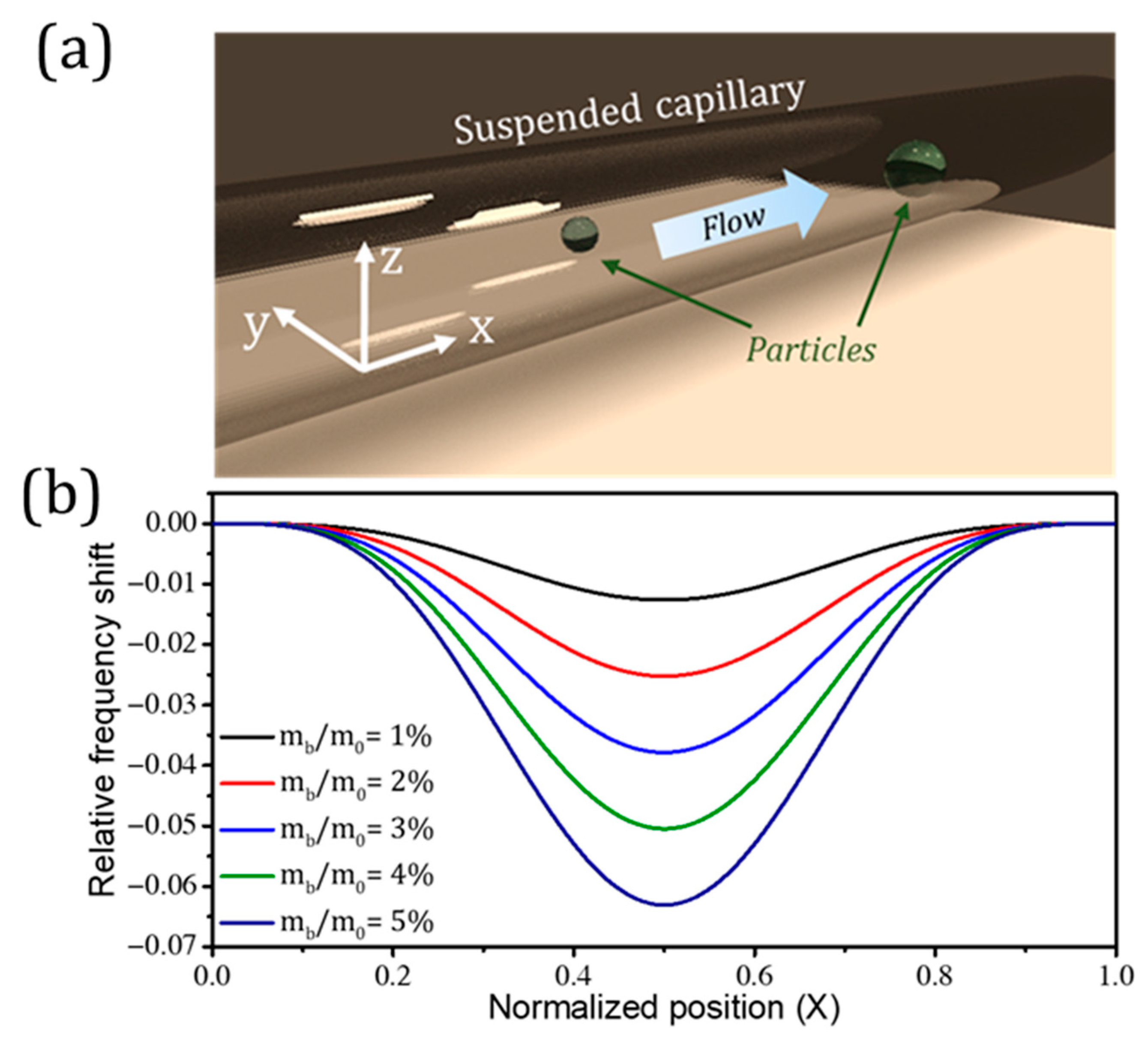
4.2. Suspended Microchannel Resonators
5. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Space coordinates | |
| Out-of-plane displacement of the plate | |
| Length of the plate | |
| Width of the plate | |
| Thickness of the plate | |
| Bending moment | |
| Young’s modulus of the resonator | |
| Poisson’s ratio | |
| Differential surface stress | |
| Stoney’s curvature | |
| Effective mass of the resonator associated with the nth mode | |
| Spring constant of the resonator associated with the nth mode | |
| Frequency | |
| Net surface stress | |
| Ratio between the thickness of the analyte and the thickness of the plate | |
| Density of the analyte | |
| Density of the cantilever | |
| Young’s modulus of the analyte | |
| Mass of the analyte | |
| Mass of the cantilever | |
| Mode shape of the nth mode | |
| Longitudinal coordinate normalized to the length of the cantilever | |
| Normalized adsorption position | |
| Volume of the analyte | |
| Volume of the cantilever | |
| Eigenvalue associated with the nth mode | |
| Stiffness coefficient of the analyte for the flexural modes of the cantilever | |
| Angle of orientation of the analyte with respect to the main axis of the cantilever | |
| Stiffness tensor of the analyte | |
| Strain component of the plate | |
| Coefficient related to the eigenvalue of the plate | |
| Mass term | |
| Stiffness term | |
| Allan deviation | |
| Covariance matrix | |
| Mass per unit length of the analyte | |
| Moment of order of the analyte mass distribution | |
| Density of the fluid | |
| Angular frequency | |
| Hydrodynamic function for circular cross section | |
| Out-of-plane displacement in the frequency domain | |
| Reynolds number | |
| Viscosity of the fluid | |
| Hydrodynamic function for rectangular cross section | |
| Correction factor for the hydrodynamic function | |
| Added mass of the surrounding fluid | |
| Damping factor | |
| Time | |
| Effective spring constant associated with the nth mode | |
| Non-correlated Langevin thermal force | |
| Buoyant mass | |
| Mass of the resonator filled with fluid | |
| Compressibility of the fluid | |
| Compressibility of the analyte |
References
- Chien, M.-H.; Brameshuber, M.; Rossboth, B.K.; Schütz, G.J.; Schmid, S. Single-molecule optical absorption imaging by nanomechanical photothermal sensing. Proc. Natl. Acad. Sci. USA 2018, 115, 11150. [Google Scholar] [CrossRef]
- Garcia, R. Nanomechanical mapping of soft materials with the atomic force microscope: Methods, theory and applications. Chem. Soc. Rev. 2020, 49, 5850–5884. [Google Scholar] [CrossRef] [PubMed]
- Barson, M.S.J.; Peddibhotla, P.; Ovartchaiyapong, P.; Ganesan, K.; Taylor, R.L.; Gebert, M.; Mielens, Z.; Koslowski, B.; Simpson, D.A.; McGuinness, L.P.; et al. Nanomechanical Sensing Using Spins in Diamond. Nano Lett. 2017, 17, 1496–1503. [Google Scholar] [CrossRef] [PubMed]
- Rugar, D.; Budakian, R.; Mamin, H.J.; Chui, B.W. Single spin detection by magnetic resonance force microscopy. Nature 2004, 430, 329–332. [Google Scholar] [CrossRef]
- Chan, J.; Alegre, T.P.M.; Safavi-Naeini, A.H.; Hill, J.T.; Krause, A.; Gröblacher, S.; Aspelmeyer, M.; Painter, O. Laser cooling of a nanomechanical oscillator into its quantum ground state. Nature 2011, 478, 89–92. [Google Scholar] [CrossRef] [PubMed]
- O’Connell, A.D.; Hofheinz, M.; Ansmann, M.; Bialczak, R.C.; Lenander, M.; Lucero, E.; Neeley, M.; Sank, D.; Wang, H.; Weides, M. Quantum ground state and single-phonon control of a mechanical resonator. Nature 2010, 464, 697–703. [Google Scholar] [CrossRef]
- Arlett, J.L.; Myers, E.B.; Roukes, M.L. Comparative advantages of mechanical biosensors. Nat. Nanotechnol. 2011, 6, 203–215. [Google Scholar] [CrossRef]
- Kosaka, P.M.; Pini, V.; Ruz, J.J.; Da Silva, R.A.; González, M.U.; Ramos, D.; Calleja, M.; Tamayo, J. Detection of cancer biomarkers in serum using a hybrid mechanical and optoplasmonic nanosensor. Nat. Nanotechnol. 2014, 9, 1047. [Google Scholar] [CrossRef]
- Hanay, M.S.; Kelber, S.; Naik, A.K.; Chi, D.; Hentz, S.; Bullard, E.C.; Colinet, E.; Duraffourg, L.; Roukes, M.L. Single-protein nanomechanical mass spectrometry in real time. Nat. Nanotechnol. 2012, 7, 602. [Google Scholar] [CrossRef] [PubMed]
- Malvar, O.; Ruz, J.J.; Kosaka, P.M.; Domínguez, C.M.; Gil-Santos, E.; Calleja, M.; Tamayo, J. Mass and stiffness spectrometry of nanoparticles and whole intact bacteria by multimode nanomechanical resonators. Nat. Commun. 2016, 7, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Domínguez, C.M.; Ramos, D.; Mendieta-Moreno, J.I.; Fierro, J.L.G.; Mendieta, J.; Tamayo, J.; Calleja, M. Effect of water-DNA interactions on elastic properties of DNA self-assembled monolayers. Sci. Rep. 2017, 7, 536. [Google Scholar] [CrossRef] [PubMed]
- Del Rey, M.; Silva, R.A.D.; Meneses, D.; Petri, D.F.S.; Tamayo, J.; Calleja, M.; Kosaka, P.M. Monitoring swelling and deswelling of thin polymer films by microcantilever sensors. Sens. Actuators B Chem. 2014, 204, 602–610. [Google Scholar] [CrossRef][Green Version]
- Domínguez, C.M.; Kosaka, P.M.; Mokry, G.; Pini, V.; Malvar, O.; del Rey, M.; Ramos, D.; San Paulo, Á.; Tamayo, J.; Calleja, M. Hydration Induced Stress on DNA Monolayers Grafted on Microcantilevers. Langmuir 2014, 30, 10962–10969. [Google Scholar] [CrossRef] [PubMed]
- Mertens, J.; Rogero, C.; Calleja, M.; Ramos, D.; Martín-Gago, J.A.; Briones, C.; Tamayo, J. Label-free detection of DNA hybridization based on hydration-induced tension in nucleic acid films. Nat. Nanotechnol. 2008, 3, 301–307. [Google Scholar] [CrossRef]
- Yubero, M.L.; Kosaka, P.M.; San Paulo, Á.; Malumbres, M.; Calleja, M.; Tamayo, J. Effects of energy metabolism on the mechanical properties of breast cancer cells. Commun. Biol. 2020, 3, 590. [Google Scholar] [CrossRef]
- Ligler, F.S.; Taitt, C.R. Optical Biosensors: Today and Tomorrow; Elsevier: Amsterdam, The Nethrelands, 2011. [Google Scholar]
- Waggoner, P.S.; Craighead, H.G. Micro-and nanomechanical sensors for environmental, chemical, and biological detection. Lab A Chip 2007, 7, 1238–1255. [Google Scholar] [CrossRef]
- Binnig, G.; Quate, C.F.; Gerber, C. Atomic Force Microscope. Phys. Rev. Lett. 1986, 56, 930–933. [Google Scholar] [CrossRef]
- Binnig, G.; Rohrer, H. Scanning tunneling microscopy. Surf. Sci. 1983, 126, 236–244. [Google Scholar] [CrossRef]
- Binnig, G.; Rohrer, H.; Salvan, F.; Gerber, C.; Baro, A. Revisiting the 7 × 7 reconstruction of Si(111). Surf. Sci. 1985, 157, L373–L378. [Google Scholar] [CrossRef]
- Eom, K.; Park, H.S.; Yoon, D.S.; Kwon, T. Nanomechanical resonators and their applications in biological/chemical detection: Nanomechanics principles. Phys. Rep. 2011, 503, 115–163. [Google Scholar] [CrossRef]
- Leng, H.; Lin, Y. A MEMS/NEMS sensor for human skin temperature measurement. Smart Struct. Syst. 2011, 8, 53–67. [Google Scholar] [CrossRef]
- Liu, P.S.; Tse, H.-F. Implantable sensors for heart failure monitoring. J. Arrhythmia 2013, 29, 314–319. [Google Scholar] [CrossRef]
- Boisen, A.; Dohn, S.; Keller, S.S.; Schmid, S.; Tenje, M. Cantilever-like micromechanical sensors. Rep. Prog. Phys. 2011, 74, 036101. [Google Scholar] [CrossRef]
- Tamayo, J.; Kosaka, P.M.; Ruz, J.J.; San Paulo, Á.; Calleja, M. Biosensors based on nanomechanical systems. Chem. Soc. Rev. 2013, 42, 1287–1311. [Google Scholar] [CrossRef]
- Barnes, J.R.; Stephenson, R.J.; Welland, M.E.; Gerber, C.; Gimzewski, J.K. Photothermal spectroscopy with femtojoule sensitivity using a micromechanical device. Nature 1994, 372, 79–81. [Google Scholar] [CrossRef]
- Thundat, T.; Chen, G.Y.; Warmack, R.J.; Allison, D.P.; Wachter, E.A. Vapor Detection Using Resonating Microcantilevers. Anal. Chem. 1995, 67, 519–521. [Google Scholar] [CrossRef]
- Thundat, T.; Wachter, E.A.; Sharp, S.L.; Warmack, R.J. Detection of mercury vapor using resonating microcantilevers. Appl. Phys. Lett. 1995, 66, 1695–1697. [Google Scholar] [CrossRef]
- Fritz, J.; Baller, M.K.; Lang, H.P.; Rothuizen, H.; Vettiger, P.; Meyer, E.J.; Güntherodt, H.; Gerber, C.; Gimzewski, J.K. Translating Biomolecular Recognition into Nanomechanics. Science 2000, 288, 316. [Google Scholar] [CrossRef]
- Ramos, D.; Tamayo, J.; Mertens, J.; Calleja, M.; Zaballos, A. Origin of the response of nanomechanical resonators to bacteria adsorption. J. Appl. Phys. 2006, 100, 106105. [Google Scholar] [CrossRef]
- Tamayo, J.; Ramos, D.; Mertens, J.; Calleja, M. Effect of the adsorbate stiffness on the resonance response of microcantilever sensors. Appl. Phys. Lett. 2006, 89, 224104. [Google Scholar] [CrossRef]
- Dominguez-Medina, S.; Fostner, S.; Defoort, M.; Sansa, M.; Stark, A.-K.; Halim, M.A.; Vernhes, E.; Gely, M.; Jourdan, G.; Alava, T.; et al. Neutral mass spectrometry of virus capsids above 100 megadaltons with nanomechanical resonators. Science 2018, 362, 918. [Google Scholar] [CrossRef] [PubMed]
- Gil-Santos, E.; Ramos, D.; Martínez, J.; Fernández-Regúlez, M.; García, R.; San Paulo, Á.; Calleja, M.; Tamayo, J. Nanomechanical mass sensing and stiffness spectrometry based on two-dimensional vibrations of resonant nanowires. Nat. Nanotechnol. 2010, 5, 641. [Google Scholar] [CrossRef] [PubMed]
- Malvar, O.; Gil-Santos, E.; Ruz, J.; Ramos, D.; Pini, V.; Fernández-Regúlez, M.; Calleja, M.; Tamayo, J.; Paulo, A. Tapered silicon nanowires for enhanced nanomechanical sensing. Appl. Phys. Lett. 2013, 103. [Google Scholar] [CrossRef]
- Yen, Y.-K.; Chiu, C.-Y. A CMOS MEMS-based Membrane-Bridge Nanomechanical Sensor for Small Molecule Detection. Sci. Rep. 2020, 10, 2931. [Google Scholar] [CrossRef] [PubMed]
- Burg, T.P.; Manalis, S.R. Suspended microchannel resonators for biomolecular detection. Appl. Phys. Lett. 2003, 83, 2698–2700. [Google Scholar] [CrossRef]
- Godin, M.; Bryan, A.K.; Burg, T.P.; Babcock, K.; Manalis, S.R. Measuring the mass, density, and size of particles and cells using a suspended microchannel resonator. Appl. Phys. Lett. 2007, 91, 123121. [Google Scholar] [CrossRef]
- Malvar, O.; Ramos, D.; Martínez, C.; Kosaka, P.; Tamayo, J.; Calleja, M. Highly sensitive measurement of liquid density in air using suspended microcapillary resonators. Sensors 2015, 15, 7650–7657. [Google Scholar] [CrossRef]
- Lee, I.; Park, K.; Lee, J. Note: Precision viscosity measurement using suspended microchannel resonators. Rev. Sci. Instrum. 2012, 83, 116106. [Google Scholar] [CrossRef]
- Linden, J.; Thyssen, A.; Oesterschulze, E. Suspended plate microresonators with high quality factor for the operation in liquids. Appl. Phys. Lett. 2014, 104, 191906. [Google Scholar] [CrossRef]
- Dohn, S.; Sandberg, R.; Svendsen, W.; Boisen, A. Enhanced functionality of cantilever based mass sensors using higher modes. Appl. Phys. Lett. 2005, 86, 233501. [Google Scholar] [CrossRef]
- Xu, W.; Choi, S.; Chae, J. A contour-mode film bulk acoustic resonator of high quality factor in a liquid environment for biosensing applications. Appl. Phys. Lett. 2010, 96, 053703. [Google Scholar] [CrossRef]
- Ramos, D.; Mertens, J.; Calleja, M.; Tamayo, J. Phototermal self-excitation of nanomechanical resonators in liquids. Appl. Phys. Lett. 2008, 92, 173108. [Google Scholar] [CrossRef]
- Burg, T.P.; Godin, M.; Knudsen, S.M.; Shen, W.; Carlson, G.; Foster, J.S.; Babcock, K.; Manalis, S.R. Weighing of biomolecules, single cells and single nanoparticles in fluid. Nature 2007, 446, 1066–1069. [Google Scholar] [CrossRef] [PubMed]
- Favero, I.; Karrai, K. Optomechanics of deformable optical cavities. Nat. Photonics 2009, 3, 201–205. [Google Scholar] [CrossRef]
- Fong, K.Y.; Poot, M.; Tang, H.X. Nano-Optomechanical Resonators in Microfluidics. Nano Lett. 2015, 15, 6116–6120. [Google Scholar] [CrossRef]
- Gil-Santos, E.; Baker, C.; Nguyen, D.T.; Hease, W.; Gomez, C.; Lemaître, A.; Ducci, S.; Leo, G.; Favero, I. High-frequency nano-optomechanical disk resonators in liquids. Nat. Nanotechnol. 2015, 10, 810. [Google Scholar] [CrossRef]
- Gil-Santos, E.; Ramos, D.; Pini, V.; Llorens, J.; Fernandez-Regulez, M.; Calleja, M.; Tamayo, J.; San Paulo, A. Optical back-action in silicon nanowire resonators: Bolometric versus radiation pressure effects. New J. Phys. 2013, 15. [Google Scholar] [CrossRef]
- Gil-Santos, E.; Ruz, J.J.; Malvar, O.; Favero, I.; Lemaître, A.; Kosaka, P.M.; García-López, S.; Calleja, M.; Tamayo, J. Optomechanical detection of vibration modes of a single bacterium. Nat. Nanotechnol. 2020, 15, 469–474. [Google Scholar] [CrossRef]
- Kosaka, P.M.; Calleja, M.; Tamayo, J. Optomechanical devices for deep plasma cancer proteomics. Semin. Cancer Biol. 2018, 52, 26–38. [Google Scholar] [CrossRef]
- Zhang, H.; Xj, Z.; Wang, Y.; Huang, Q.; Xia, J. Femtogram scale high frequency nano-optomechanical resonators in water. Opt. Express 2017, 25, 821. [Google Scholar] [CrossRef]
- Cleland, A.N.; Roukes, M.L. Noise processes in nanomechanical resonators. J. Appl. Phys. 2002, 92, 2758–2769. [Google Scholar] [CrossRef]
- Stoney, G.G. The tension of metallic films deposited by electrolysis. Proc. R. Soc. Lond. Ser. A Contain. Pap. A Math. Phys. Character 1909, 82, 172–175. [Google Scholar]
- Gruber, K.; Horlacher, T.; Castelli, R.; Mader, A.; Seeberger, P.H.; Hermann, B.A. Cantilever Array Sensors Detect Specific Carbohydrate−Protein Interactions with Picomolar Sensitivity. ACS Nano 2011, 5, 3670–3678. [Google Scholar] [CrossRef] [PubMed]
- Mader, A.; Gruber, K.; Castelli, R.; Hermann, B.A.; Seeberger, P.H.; Rädler, J.O.; Leisner, M. Discrimination of Escherichia coli Strains using Glycan Cantilever Array Sensors. Nano Lett. 2012, 12, 420–423. [Google Scholar] [CrossRef]
- McKendry, R.; Zhang, J.; Arntz, Y.; Strunz, T.; Hegner, M.; Lang, H.P.; Baller, M.K.; Certa, U.; Meyer, E.; Güntherodt, H.-J.; et al. Multiple label-free biodetection and quantitative DNA-binding assays on a nanomechanical cantilever array. Proc. Natl. Acad. Sci. USA 2002, 99, 9783. [Google Scholar] [CrossRef]
- Sader, J.E. Surface stress induced deflections of cantilever plates with applications to the atomic force microscope: Rectangular plates. J. Appl. Phys. 2001, 89, 2911–2921. [Google Scholar] [CrossRef]
- Tamayo, J.; Ruz, J.J.; Pini, V.; Kosaka, P.; Calleja, M. Quantification of the surface stress in microcantilever biosensors: Revisiting Stoney’s equation. Nanotechnology 2012, 23, 475702. [Google Scholar] [CrossRef]
- Thundat, P.I.O.; Warmack, R.J. MICROCANTILEVER SENSORS. Microscale Eng. 1997, 1, 185–199. [Google Scholar] [CrossRef]
- Ilic, B.; Czaplewski, D.; Craighead, H.G.; Neuzil, P.; Campagnolo, C.; Batt, C. Mechanical resonant immunospecific biological detector. Appl. Phys. Lett. 2000, 77, 450–452. [Google Scholar] [CrossRef]
- Ruz, J.J.; Tamayo, J.; Pini, V.; Kosaka, P.M.; Calleja, M. Physics of nanomechanical spectrometry of viruses. Sci. Rep. 2014, 4, 1–11. [Google Scholar] [CrossRef]
- Ruz, J.J.; Malvar, O.; Gil-Santos, E.; Calleja, M.; Tamayo, J. Effect of particle adsorption on the eigenfrequencies of nano-mechanical resonators. J. Appl. Phys. 2020, 128, 104503. [Google Scholar] [CrossRef]
- Ramos, D.; Mertens, J.; Calleja, M.; Tamayo, J. Study of the origin of bending induced by bimetallic effect on microcantilever. Sensors 2007, 7, 1757. [Google Scholar] [CrossRef] [PubMed]
- Ramos, D.; Tamayo, J.; Mertens, J.; Calleja, M. Photothermal excitation of microcantilevers in liquids. J. Appl. Phys. 2006, 99, 124904. [Google Scholar] [CrossRef]
- Toda, M.; Inomata, N.; Ono, T.; Voiculescu, I. Cantilever beam temperature sensors for biological applications. IEEJ Trans. Electr. Electron. Eng. 2017, 12, 153–160. [Google Scholar] [CrossRef]
- Wu, L.; Cheng, T.; Zhang, Q.-C. A bi-material microcantilever temperature sensor based on optical readout. Measurement 2012, 45, 1801–1806. [Google Scholar] [CrossRef]
- Kang, K.; Nilsen-Hamilton, M.; Shrotriya, P. Differential surface stress sensor for detection of chemical and biological species. Appl. Phys. Lett. 2008, 93, 143107. [Google Scholar] [CrossRef]
- Sang, S.; Zhao, Y.; Zhang, W.; Li, P.; Hu, J.; Li, G. Surface stress-based biosensors. Biosens. Bioelectron. 2014, 51, 124–135. [Google Scholar] [CrossRef]
- Godin, M.; Tabard-Cossa, V.; Miyahara, Y.; Monga, T.; Williams, P.J.; Beaulieu, L.Y.; Lennox, R.B.; Grutter, P. Cantilever-based sensing: The origin of surface stress and optimization strategies. Nanotechnology 2010, 21, 075501. [Google Scholar] [CrossRef]
- Haiss, W. Surface stress of clean and adsorbate-covered solids. Rep. Prog. Phys. 2001, 64, 591–648. [Google Scholar] [CrossRef]
- Ibach, H. Adsorbate-induced surface stress. J. Vac. Sci. Technol. A Vac. Surf. Film. 1994, 12, 2240–2245. [Google Scholar] [CrossRef]
- Timoshenko, S.; Woinowsky-Krieger, S. Theory of Plates and Shells; McGraw-Hill: New York, NY, USA, 1959. [Google Scholar]
- Zeng, X.; Deng, J.; Luo, X. Deflection of a cantilever rectangular plate induced by surface stress with applications to surface stress measurement. J. Appl. Phys. 2012, 111, 083531. [Google Scholar] [CrossRef]
- Timoshenko, S.P. Theory of Elasticity; McGraw-Hill Education (India) Pvt Limited: Noida, India, 2010. [Google Scholar]
- Ziegler, C. Cantilever-based biosensors. Anal. Bioanal. Chem. 2004, 379, 946–959. [Google Scholar] [CrossRef] [PubMed]
- Karabalin, R.B.; Villanueva, L.G.; Matheny, M.H.; Sader, J.E.; Roukes, M.L. Stress-induced variations in the stiffness of micro-and nanocantilever beams. Phys. Rev. Lett. 2012, 108, 236101. [Google Scholar] [CrossRef] [PubMed]
- Lachut, M.J.; Sader, J.E. Effect of surface stress on the stiffness of thin elastic plates and beams. Phys. Rev. B 2012, 85, 085440. [Google Scholar] [CrossRef]
- Chen, G.Y.; Thundat, T.; Wachter, E.A.; Warmack, R.J. Adsorption-induced surface stress and its effects on resonance frequency of microcantilevers. J. Appl. Phys. 1995, 77, 3618–3622. [Google Scholar] [CrossRef]
- Gurtin, M.E.; Markenscoff, X.; Thurston, R.N. Effect of surface stress on the natural frequency of thin crystals. Appl. Phys. Lett. 1976, 29, 529–530. [Google Scholar] [CrossRef]
- Lagowski, J.; Gatos, H.C.; Sproles, E.S. Surface stress and the normal mode of vibration of thin crystals:GaAs. Appl. Phys. Lett. 1975, 26, 493–495. [Google Scholar] [CrossRef]
- Lu, P.; Lee, H.P.; Lu, C.; O’shea, S.J. Surface stress effects on the resonance properties of cantilever sensors. Phys. Rev. B 2005, 72, 085405. [Google Scholar] [CrossRef]
- Pini, V.; Tamayo, J.; Gil-Santos, E.; Ramos, D.; Kosaka, P.; Tong, H.-D.; van Rijn, C.; Calleja, M. Shedding Light on Axial Stress Effect on Resonance Frequencies of Nanocantilevers. ACS Nano 2011, 5, 4269–4275. [Google Scholar] [CrossRef]
- Lachut, M.J.; Sader, J.E. Effect of surface stress on the stiffness of cantilever plates. Phys. Rev. Lett. 2007, 99, 206102. [Google Scholar] [CrossRef]
- Pini, V.; Ruz, J.; Kosaka, P.; Malvar, O.; Calleja, M.; Tamayo, J. How two-dimensional bending can extraordinarily stiffen thin sheets. Sci. Rep. 2016, 6. [Google Scholar] [CrossRef] [PubMed]
- Ruz, J.J.; Pini, V.; Malvar, O.; Kosaka, P.M.; Calleja, M.; Tamayo, J. Effect of surface stress induced curvature on the eigenfrequencies of microcantilever plates. AIP Adv. 2018, 8, 105213. [Google Scholar] [CrossRef]
- Ramos, D.; Tamayo, J.; Mertens, J.; Calleja, M.; Villanueva, L.G.; Zaballos, A. Detection of bacteria based on the thermomechanical noise of a nanomechanical resonator: Origin of the response and detection limits. Nanotechnology 2007, 19, 035503. [Google Scholar] [CrossRef] [PubMed]
- Hanay, M.S.; Kelber, S.I.; O’Connell, C.D.; Mulvaney, P.; Sader, J.E.; Roukes, M.L. Inertial imaging with nanomechanical systems. Nat. Nanotechnol. 2015, 10, 339–344. [Google Scholar] [CrossRef] [PubMed]
- Naik, A.K.; Hanay, M.S.; Hiebert, W.K.; Feng, X.L.; Roukes, M.L. Towards single-molecule nanomechanical mass spectrometry. Nat. Nanotechnol. 2009, 4, 445–450. [Google Scholar] [CrossRef] [PubMed]
- Ramos, D.; Malvar, O.; Davis, Z.J.; Tamayo, J.; Calleja, M. Nanomechanical Plasmon Spectroscopy of Single Gold Nanoparticles. Nano Lett. 2018, 18, 7165–7170. [Google Scholar] [CrossRef]
- Sage, E.; Brenac, A.; Alava, T.; Morel, R.; Dupré, C.; Hanay, M.S.; Roukes, M.L.; Duraffourg, L.; Masselon, C.; Hentz, S. Neutral particle mass spectrometry with nanomechanical systems. Nat. Commun. 2015, 6, 1–5. [Google Scholar] [CrossRef]
- Ekinci, K.L.; Roukes, M.L. Nanoelectromechanical systems. Rev. Sci. Instrum. 2005, 76, 061101. [Google Scholar] [CrossRef]
- Sansa, M.; Sage, E.; Bullard, E.C.; Gély, M.; Alava, T.; Colinet, E.; Naik, A.K.; Villanueva, L.G.; Duraffourg, L.; Roukes, M.L.; et al. Frequency fluctuations in silicon nanoresonators. Nat. Nanotechnol. 2016, 11, 552–558. [Google Scholar] [CrossRef]
- Kiracofe, D.; Raman, A. On eigenmodes, stiffness, and sensitivity of atomic force microscope cantilevers in air versus liquids. J. Appl. Phys. 2010, 107, 033506. [Google Scholar] [CrossRef]
- Lee, J.W.; Tung, R.; Raman, A.; Sumali, H.; Sullivan, J.P. Squeeze-film damping of flexible microcantilevers at low ambient pressures: Theory and experiment. J. Micromech. Microeng. 2009, 19, 105029. [Google Scholar] [CrossRef]
- Ricci, A.; Canavese, G.; Ferrante, I.; Marasso, S.L.; Ricciardi, C. A finite element model for the frequency spectrum estimation of a resonating microplate in a microfluidic chamber. Microfluid. Nanofluid. 2013, 15, 275–284. [Google Scholar] [CrossRef]
- Ricciardi, C.; Canavese, G.; Castagna, R.; Ferrante, I.; Ricci, A.; Marasso, S.L.; Napione, L.; Bussolino, F. Integration of microfluidic and cantilever technology for biosensing application in liquid environment. Biosens. Bioelectron. 2010, 26, 1565–1570. [Google Scholar] [CrossRef] [PubMed]
- Papi, M.; Arcovito, G.; De Spirito, M.; Vassalli, M.; Tiribilli, B. Fluid viscosity determination by means of uncalibrated atomic force microscopy cantilevers. Appl. Phys. Lett. 2006, 88, 194102. [Google Scholar] [CrossRef]
- Paul, M.R.; Clark, M.T.; Cross, M.C. The stochastic dynamics of micron and nanoscale elastic cantilevers in fluid: Fluctuations from dissipation. Nanotechnology 2006, 17, 4502–4513. [Google Scholar] [CrossRef]
- Sader, J.E. Frequency response of cantilever beams immersed in viscous fluids with applications to the atomic force microscope. J. Appl. Phys. 1998, 84, 64–76. [Google Scholar] [CrossRef]
- Van Eysden, C.A.; Sader, J.E. Frequency response of cantilever beams immersed in viscous fluids with applications to the atomic force microscope: Arbitrary mode order. J. Appl. Phys. 2007, 101, 044908. [Google Scholar] [CrossRef]
- Maali, A.; Hurth, C.; Boisgard, R.; Jai, C.; Cohen-Bouhacina, T.; Aimé, J.-P. Hydrodynamics of oscillating atomic force microscopy cantilevers in viscous fluids. J. Appl. Phys. 2005, 97, 074907. [Google Scholar] [CrossRef]
- Son, S.; Tzur, A.; Weng, Y.; Jorgensen, P.; Kim, J.; Kirschner, M.W.; Manalis, S.R. Direct observation of mammalian cell growth and size regulation. Nat. Methods 2012, 9, 910–912. [Google Scholar] [CrossRef]
- Martín-Pérez, A.; Ramos, D.; Tamayo, J.; Calleja, M. Real-Time Particle Spectrometry in Liquid Environment Using Microfluidic-Nanomechanical Resonators. In Proceedings of the 2019 20th International Conference on Solid-State Sensors, Actuators and Microsystems & Eurosensors XXXIII (TRANSDUCERS & EUROSENSORS XXXIII), Berlin, Germany, 23–27 June 2019; pp. 2146–2149. [Google Scholar]
- Olcum, S.; Cermak, N.; Wasserman, S.C.; Christine, K.S.; Atsumi, H.; Payer, K.R.; Shen, W.; Lee, J.; Belcher, A.M.; Bhatia, S.N.; et al. Weighing nanoparticles in solution at the attogram scale. Proc. Natl. Acad. Sci. USA 2014, 111, 1310. [Google Scholar] [CrossRef]
- Martín-Pérez, A.; Ramos, D.; Tamayo, J.; Calleja, M. Coherent Optical Transduction of Suspended Microcapillary Resonators for Multi-Parameter Sensing Applications. Sensors 2019, 19, 5069. [Google Scholar] [CrossRef] [PubMed]
- Pini, V.; Ramos, D.; Domínguez, C.M.; Ruz, J.; Malvar, O.; Kosaka, P.; Davis, Z.; Tamayo, J.; Calleja, M. Optimization of the readout of microdrum optomechanical resonators. Microelectron. Eng. 2017, 183, 37–41. [Google Scholar] [CrossRef]
- Martín-Pérez, A.; Ramos, D.; Gil-Santos, E.; García-López, S.; Yubero, M.L.; Kosaka, P.M.; San Paulo, Á.; Tamayo, J.; Calleja, M. Mechano-Optical Analysis of Single Cells with Transparent Microcapillary Resonators. ACS Sens. 2019, 4, 3325–3332. [Google Scholar] [CrossRef] [PubMed]
- Han, K.; Suh, J.; Bahl, G. Optomechanical non-contact measurement of microparticle compressibility in liquids. Opt. Express 2018, 26, 31908–31916. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ruz, J.J.; Malvar, O.; Gil-Santos, E.; Ramos, D.; Calleja, M.; Tamayo, J. A Review on Theory and Modelling of Nanomechanical Sensors for Biological Applications. Processes 2021, 9, 164. https://doi.org/10.3390/pr9010164
Ruz JJ, Malvar O, Gil-Santos E, Ramos D, Calleja M, Tamayo J. A Review on Theory and Modelling of Nanomechanical Sensors for Biological Applications. Processes. 2021; 9(1):164. https://doi.org/10.3390/pr9010164
Chicago/Turabian StyleRuz, Jose Jaime, Oscar Malvar, Eduardo Gil-Santos, Daniel Ramos, Montserrat Calleja, and Javier Tamayo. 2021. "A Review on Theory and Modelling of Nanomechanical Sensors for Biological Applications" Processes 9, no. 1: 164. https://doi.org/10.3390/pr9010164
APA StyleRuz, J. J., Malvar, O., Gil-Santos, E., Ramos, D., Calleja, M., & Tamayo, J. (2021). A Review on Theory and Modelling of Nanomechanical Sensors for Biological Applications. Processes, 9(1), 164. https://doi.org/10.3390/pr9010164









