Investigation of Electrochemical Processes in Solid Oxide Fuel Cells by Modified Levenberg–Marquardt Algorithm: A New Automatic Update Limit Strategy
Abstract
1. Introduction
2. Theory and Computations
2.1. EEC and Objective Function Used in EIS Study
2.2. Optimization Algorithm Used in This Study
| Algorithm 1. Pseudocode of Levenberg–Marquardt algorithm (adapted from [22,24]). Symbol references: J is the Jacobian matrix, JT(WJ) is the approximate Hessian matrix; I is the identity matrix, JT(w (yexp − ycom)) is the gradient vector, w is the vector containing weights (3), and W is the matrix with columns equal to weights (3). |
| Levenberg–Marquardt algorithm |
| a = a0; λ = λ0; ν = 2 |
| repeat |
| Solve (JT(W∘J) + λI)h = JT(w (yexp − ycom)) |
| if ρ > 0 |
| a = a + h |
| λ = λ ∗ max(1/3, 1 − (2ρ − 1)3) |
| ν = 2 |
| else |
| λ = λ ∗ ν |
| end if |
| until |
2.3. Limit Strategy in EIS Study
2.4. Ordinary Limit Strategy for Levenberg–Marquardt Algorithm
| Algorithm 2. Pseudocode of Levenberg–Marquardt algorithm, which is coupled by the ordinary limit strategy. Symbol references: J is the Jacobian matrix, JT(W∘J) is the approximate Hessian matrix; I is the identity matrix, JT(w (yexp − ycom)) is the gradient vector, w is the vector containing weights (3), and W is the matrix with columns equal to weights (3). |
| Ordinary limit strategy for the Levenberg-Marquardt algorithm |
| aext := a0; λ := λ0; ν := 2 |
| aint := k(aext) (convert to aint by (7)) |
| LUF := 1e5 (limits update factor) |
| compute limits ((7),(8),(9)) |
| repeat |
| Solve (JT(WJ) + λI)h = JT(w (yexp − ycom)) (only here use l(aint) (8) instead of aint) |
| if ρ > 0 |
| aint := aint + h |
| λ := λ ∗ max(1/3, 1 – (2ρ – 1)3) |
| ν := 2 |
| else |
| λ := λ * ν |
| ν := ν * 2 |
| end if |
| until |
| aext := l(aint) (convert to aext by (8) ) |
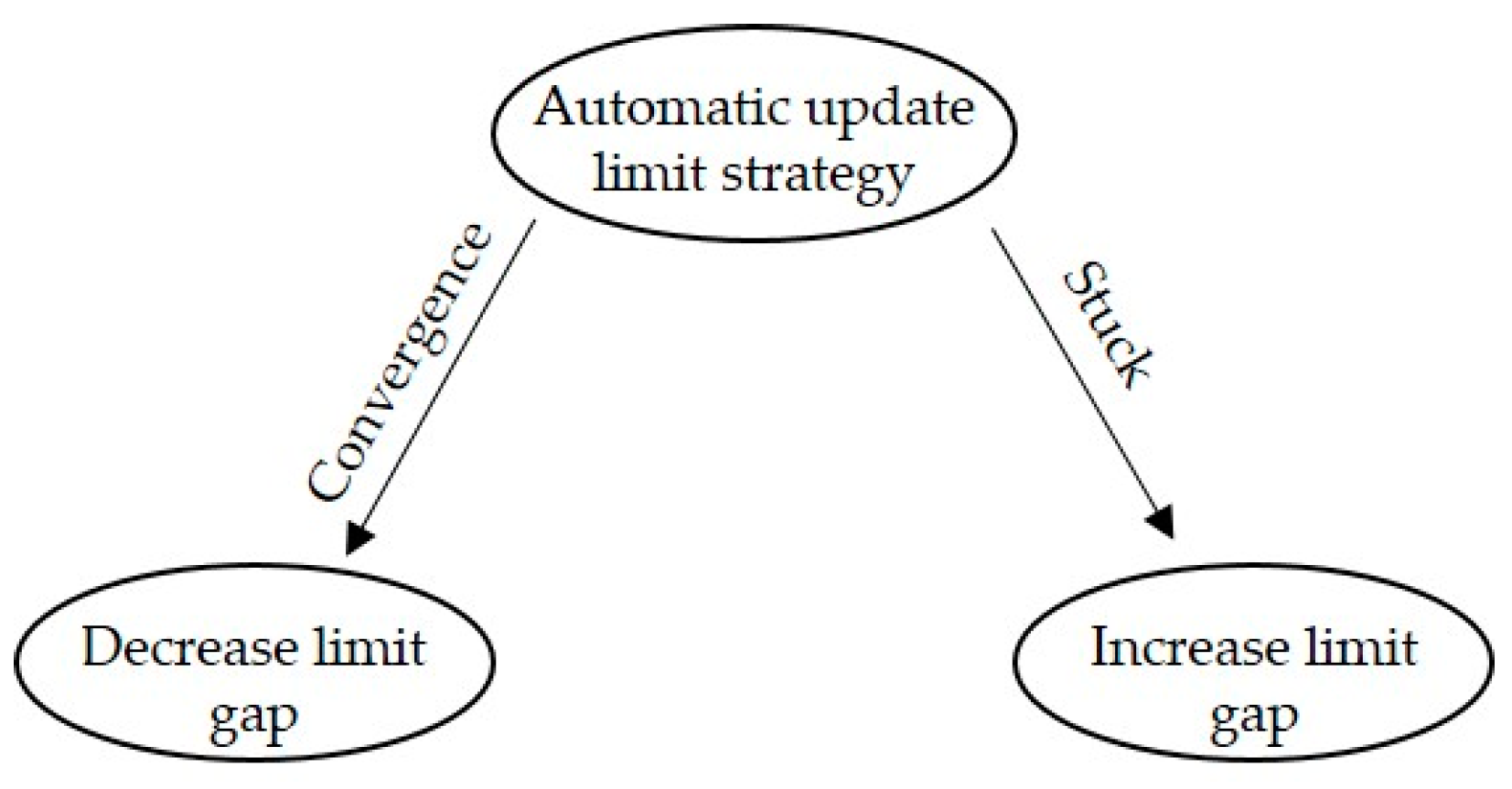
2.5. Automatic Update (i.e., Adaptive) Limit Strategy for Levenberg–Marquardt Algorithm
| Algorithm 3. Pseudocode of the Levenberg–Marquardt algorithm, which is coupled by the automatic update limit strategy (see sub procedure). Symbol references: J is the Jacobian matrix, JT(WJ) is the approximate Hessian matrix; I is the identity matrix, JT(w (yexp − ycom)) is the gradient vector, w is the vector containing weights (3), and W is the matrix with columns equal to weights (3). | |
| Automatic update limit strategy for the Levenberg-Marquardt algorithm | |
| aext := a0; λ := λ0; ν := 2 | |
| g := 0; b :=0 (g and b are number of good and bad iterations) | |
| LUF := 1e5 (limits update factor) | |
| compute limits ((7),(8),(9)) | |
| aint: = k(aext) (convert to aint by (7))) | sub update_limits |
| repeat | if g > 2 |
| Solve (JT(WJ) + λI)h = JT(w (yexp − ycom)) (use l(aint) (8) instead of aint) | LUF := LUF*0.95; 10 ≤ LUF ≤ 104 |
| if ρ > 0 (good iteration) | aext := l(aint) |
| aint := aint + h | compute lbi and ubi by aext,i |
| update_limits (using current l(aint) value) | compute aint,i:= k(aext,i) by new lbi, ubi |
| λ := λ ∗ max(1/3, 1 – (2ρ – 1)3) | end if |
| ν := 2 | if b > 2 |
| g := g+1; b := 0 | LUF := LUF*2; 10 ≤ LUF ≤ 104 |
| else (bad iteration) | aext := l(aint) |
| λ := λ * 2 | compute lbi and ubi by aext,i |
| ν := ν * 2 | compute aint,i:= k(aext,i) by new lbi,ubi |
| g := 0; b := b+1 | end if |
| end if | end sub |
| until | |
| a := l(aint) (convert to aext by (8)) | |
3. Experimental
3.1. Synthetic Noisy ZARC Data Used in This Study
3.2. Experimental SOFC Data Used in This Study
3.3. EEC Model Used in This Study
3.4. Open-Source Packages Used in This Study
4. Results and Discussion
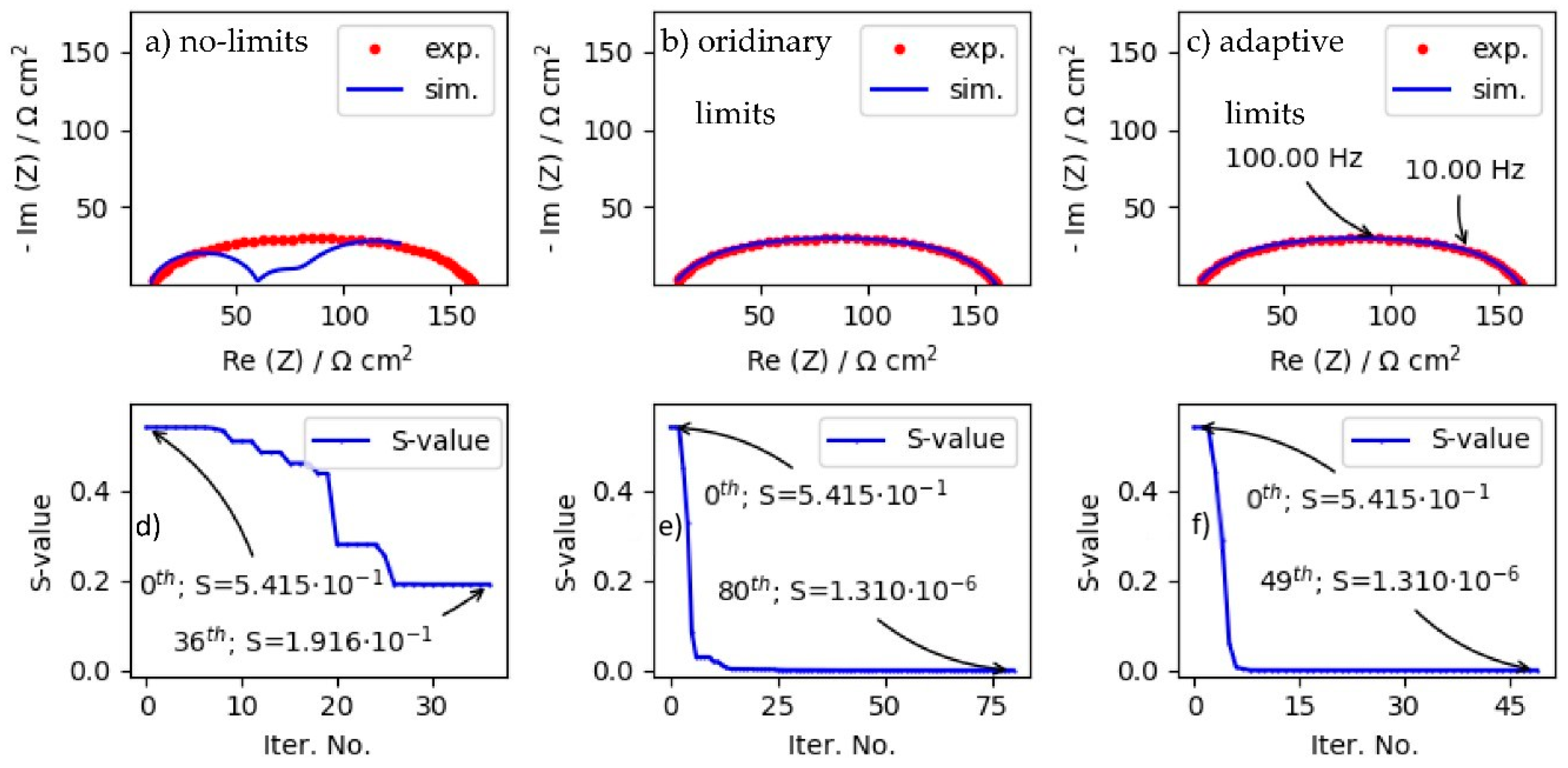
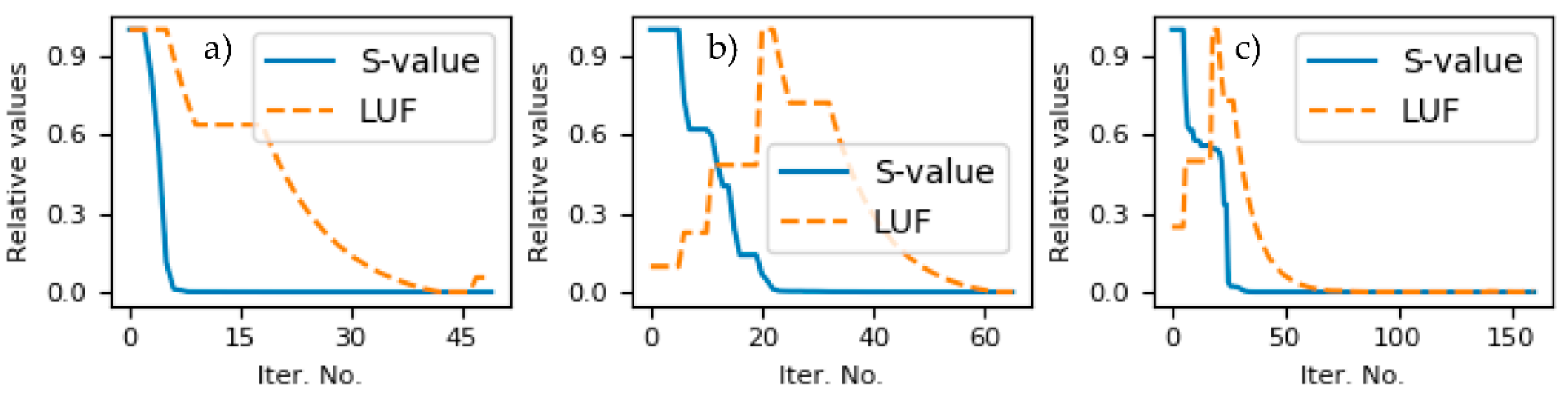
4.1. Impact of Diverse Limit Strategies on LMA Convergence Properties When Fitting ZARC Data by Using Good Starting Parameters
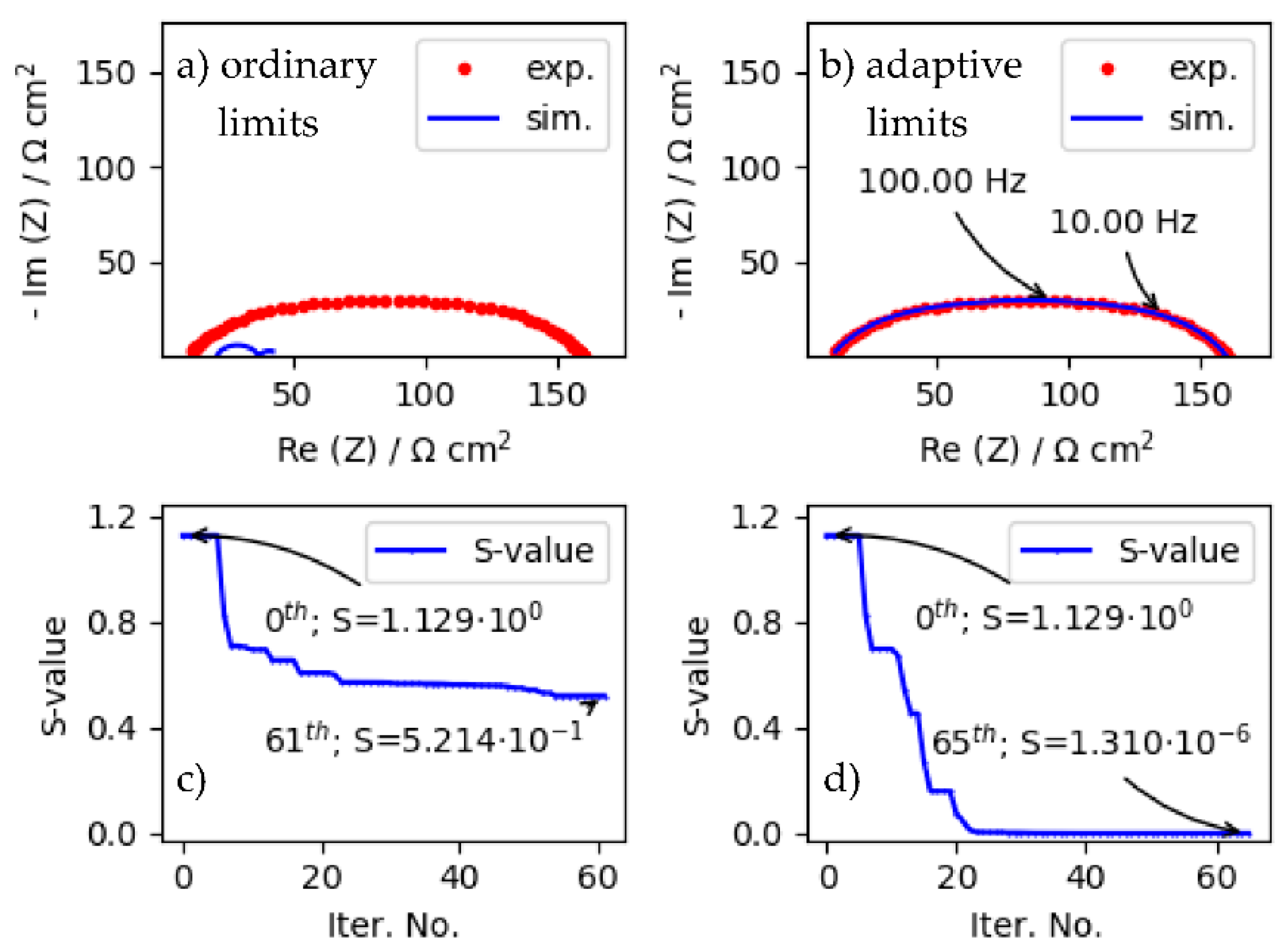
4.2. Impact of Ordinary and Automatic Update (i.e., Adaptive) Limit Strategies on LMA Convergence Properties When Fitting ZARC Data by Using Poor Starting Parameters
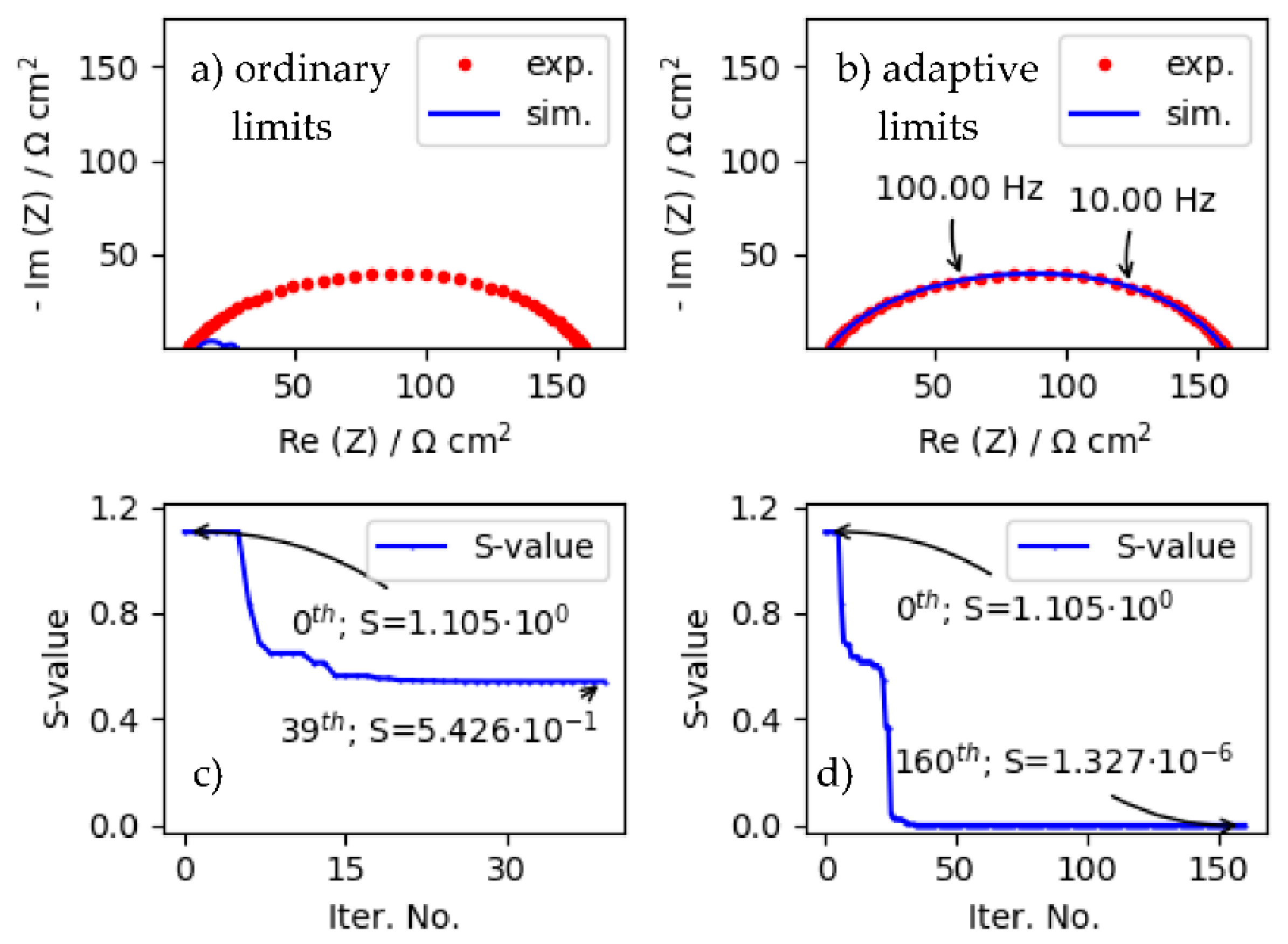
4.3. Impact of Ordinary and Automatic Update (i.e., Adaptive) Limit Strategies on LMA Convergence Properties When Fitting More Corrupted ZARC Data by Using Poor Starting Parameters
4.4. Automatic Update of LUF Value during LMA Iteration
4.5. Experimental SOFC Impedance Data
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations and Symbols
| SOFC | solid oxide fuel cells |
| EIS | electrochemical impedance spectroscopy |
| EEC | electrical equivalent circuit |
| CNLS | complex nonlinear least-square problem |
| LMA | Levenberg–Marquardt algorithm |
| LUF | limit update factor |
| g | number of good successive iterations |
| b | number of bad successive iterations |
| J | Jacobian matrix |
| C | approximated Hessian matrix (i.e.,) |
| h | vector containing computed estimates in EEC parameters |
| λ | damping parameter |
| R: | resistor |
| Q | constant phase element (impedance form: |
| QR | parallel QR circuit |
| ZZARC | ZARC data |
| S | objective function used for EIS data fitting |
| m | number of EIS data points |
| f | EEC model |
| ω | angular frequency |
| yexp | vector containing experimental EIS data |
| ycom | vector containing computed EIS data |
| w | vector containing weights (3) |
| W | matrix with columns equal to w |
| p | number of ZACR elements |
| a | vector containing EEC parameters |
| r | number of EEC parameters |
| aj | jth EEC parameter |
| aint,j | jth internal EEC parameter |
| aext,j | jth external EEC parameter |
| lbj | jth lower bound |
| ubj | jth upper bound |
References
- Subotić, V.; Baldinelli, A.; Barelli, L.; Scharler, R.; Pongratz, G.; Hochenauer, C.; Anca-Couce, A. Applicability of the SOFC technology for coupling with biomass-gasifier systems: Short- and long-term experimental study on SOFC performance and degradation behaviour. Appl. Energy 2019, 256, 113904. [Google Scholar] [CrossRef]
- Kobayashi, K.; Suzuki, T.S. Development of Impedance Analysis Software Implementing a Support Function to Find Good Initial Guess Using an Interactive Graphical User Interface. Electrochemistry 2019, 88, 39–44. [Google Scholar] [CrossRef]
- Wan, T.H.; Saccoccio, M.; Chen, C.; Ciucci, F. Influence of the Discretization Methods on the Distribution of Relaxation Times Deconvolution: Implementing Radial Basis Functions with DRTtools. Electrochim. Acta 2015, 184, 483–499. [Google Scholar] [CrossRef]
- Barsoukov, E.; Macdonald, J.R. Impedance Spectroscopy: Theory, Experiment, and Applications; Wiley: Hoboken, NJ, USA, 2005. [Google Scholar]
- Zic, M.; Pereverzyev, S., Jr.; Subotić, V.; Pereverzyev, S. Adaptive multi-parameter regularization approach to construct the distribution function of relaxation times. GEM Int. J. Geomathematics 2020, 11, 1–23. [Google Scholar] [CrossRef]
- Song, J.; Bazant, M.Z. Electrochemical Impedance Imaging via the Distribution of Diffusion Times. Phys. Rev. Lett. 2018, 120, 116001. [Google Scholar] [CrossRef]
- Pereverzyev, S.V.V.; Solodky, S.G.; Vasylyk, V.B.; Žic, M. Regularized Collocation in Distribution of Diffusion Times Applied to Electrochemical Impedance Spectroscopy. Comput. Methods Appl. Math. 2020, 20, 517–530. [Google Scholar] [CrossRef]
- Zic, M. An alternative approach to solve complex nonlinear least-squares problems. J. Electroanal. Chem. 2016, 760, 85–96. [Google Scholar] [CrossRef]
- Kelley, C.T. Iterative Methods for Optimization; SIAM: Philadelphia, PA, USA, 1999. [Google Scholar]
- Wolberg, J. Data Analysis Using the Method of Least Squares: Extracting the Most Information from Experiments; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Nocedal, J.; Wright, S.J. Numerical Optimization; Springer: New York, NY, USA, 1999. [Google Scholar]
- Levenberg, K. A method for the solution of certain non-linear problems in least squares. Q. Appl. Math. 1944, 2, 164–168. [Google Scholar] [CrossRef]
- Marquardt, D.W. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Ind. Appl. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- Moré, J.J. The Levenberg-Marquardt algorithm: Implementation and theory. In Numerical Analysis; Watson, G.A., Ed.; Springer: Berlin/Heidelberg, Germany, 1978; pp. 105–116. [Google Scholar]
- Zic, M.; Pereverzyev, S.V.V. Optimizing noisy CNLS problems by using Nelder-Mead algorithm: A new method to compute simplex step efficiency. J. Electroanal. Chem. 2019, 851, 113439. [Google Scholar] [CrossRef]
- Dellis, J.-L.; Carpentier, J.-L. Nelder and Mead algorithm in impedance spectra fitting. Solid State Ionics 1993, 62, 119–123. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Fajfar, I.; Bűrmen, Á.; Puhan, J. The Nelder–Mead simplex algorithm with perturbed centroid for high-dimensional function optimization. Optim. Lett. 2019, 13, 1011–1025. [Google Scholar] [CrossRef]
- Fajfar, I.; Puhan, J.; Árpád, B. Evolving a Nelder–Mead Algorithm for Optimization with Genetic Programming. Evol. Comput. 2017, 25, 351–373. [Google Scholar] [CrossRef] [PubMed]
- Žic, M. Solving CNLS problems by using Levenberg-Marquardt algorithm: A new approach to avoid off-limits values during a fit. J. Electroanal. Chem. 2017, 799, 242–248. [Google Scholar] [CrossRef]
- Žic, M.; Subotić, V.; Pereverzyev, S.; Fajfar, I. Solving CNLS problems using Levenberg-Marquardt algorithm: A new fitting strategy combining limits and a symbolic Jacobian matrix. J. Electroanal. Chem. 2020, 866, 114171. [Google Scholar] [CrossRef]
- Madsen, K.; Nielsen, H.B. Introduction to Optimization and Data Fitting; Technical University of Denmark: Lyngby, Denmark, 2008. [Google Scholar]
- Nielsen, H.B.; Madsen, K.; Tingleff, O. Methods for Non-Linear Least Squares Problems, 2nd ed.; Informatics and Mathematical Modelling, Technical University of Denmark (DTU): Lyngby, Denmark, 2004. [Google Scholar]
- Nielsen, H.B. Damping Parameter in Marquardt’s Method; Techcinal Report IMM-REP-1999-05; Technical University of Denmark: Lyngby, Denmark, 1999. [Google Scholar]
- James, F.; Winkler, M. Minuit User’s Guide; CERN: Geneva, Switzerland, 2004; Available online: https://inspirehep.net/files/c92c2ba4dac7c0a665cce687fb19b29c (accessed on 6 December 2020).
- James, F.; Roos, M. Minuit-A system for function minimization and analysis of the parameter errors and correlations. Comput. Phys. Commun. 1975, 10, 343–367. [Google Scholar] [CrossRef]
- Sheppard, R.J.; Jordan, B.P.; Grant, E.H. Least squares analysis of complex data with applications to permittivity measurements. J. Phys. D Appl. Phys. 1970, 3, 1759–1764. [Google Scholar] [CrossRef]
- Zoltowski, P. The error function for fitting of models to immittance data. J. Electroanal. Chem. Interfacial Electrochem. 1984, 178, 11–19. [Google Scholar] [CrossRef]
- Van Der Walt, S.; Colbert, S.C.; Varoquaux, G. The NumPy Array: A Structure for Efficient Numerical Computation. Comput. Sci. Eng. 2011, 13, 22–30. [Google Scholar] [CrossRef]
- Hunter, J.D. Matplotlib: A 2D Graphics Environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]


| Limit Strategy | Automatic Limits Update | Reported in EIS |
|---|---|---|
| No limit | No | e.g., [8] |
| Ordinary | No | [20] |
| Automatic update (i.e., adaptive) | Yes | This work |
| EEC Parameters | EEC Parameter Values | |||
|---|---|---|---|---|
| k | ||||
| 1 | 2 | 3 | ||
| Rs (Ω cm2) | 10 | - | - | - |
| Rk (Ω cm2) | - | 50 | 50 | 50 |
| τk (s) | - | 0.01 (0.01) | 0.001 (0.005) | 0.0001 (0.001) |
| nk | - | 0.7 | 0.7 | 0.7 |
| EEC Parameters | EEC Parameter Values | |||
|---|---|---|---|---|
| k | ||||
| 1 | 2 | 3 | ||
| Rs (Ω cm2) | 10 (1.1) | - | - | - |
| Y0,k (S sn cm−2) | - | 0.1 (1.2) | 0.01 (1.3) | 0.001 (1.4) |
| nk | - | 0.85 (0.85) | 0.83 (0.83) | 0.87 (0.87) |
| Rk (Ω cm2) | - | 70 (1.5) | 20 (1.6) | 50 (1.7) |
| EEC Parameters | ||||
|---|---|---|---|---|
| k | 1 | 2 | 3 | |
| Rs (Ω cm2) | 9.996 | - | - | - |
| Y0,k (S sn cm−2) | - | 6.638 × 10−4 | 1.346 × 10−4 | 3.126 × 10−5 |
| nk | - | 0.692 | 0.759 | 0.695 |
| Rk (Ω cm2) | - | 57.49 | 37.60 | 54.90 |
| * τk (s) | 8.920 × 10−3 | 9.420 × 10−4 | 1.050 × 10−4 |
| EEC Parameters | ||||
|---|---|---|---|---|
| k | 1 | 2 | 3 | |
| Rs (Ω cm2) | 9.99 | - | - | - |
| Y0,k (S sn cm−2) | - | 9.995 × 10−3 | 3.520 × 10−4 | 1.500 × 10−4 |
| n | - | 0.677 | 0.714 | 0.694 |
| R (Ω cm2) | - | 7.959 | 83.441 | 58.549 |
| aτk (s) | 2.386 × 10−2 | 7.184 × 10−3 | 1.096 × 10−3 | |
| EEC Parameters | |||
|---|---|---|---|
| k | |||
| 1 | 2 | ||
| Rs (Ω cm2) | 2.29 × 10−3(1.10) | - | - |
| Y0,k (S sn cm−2) | - | 1.038 (0.01) | 14.445 (5.00) |
| n | - | 0.767 (0.63) | 0.999 (0.73) |
| R (Ω cm2) | - | 6.427 × 10−3 (0.50) | 7.484 × 10−3 (2.50) |
| aτκ (s) | 1.459 × 10−3 | 1.078 × 10−1 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Žic, M.; Fajfar, I.; Subotić, V.; Pereverzyev, S.; Kunaver, M. Investigation of Electrochemical Processes in Solid Oxide Fuel Cells by Modified Levenberg–Marquardt Algorithm: A New Automatic Update Limit Strategy. Processes 2021, 9, 108. https://doi.org/10.3390/pr9010108
Žic M, Fajfar I, Subotić V, Pereverzyev S, Kunaver M. Investigation of Electrochemical Processes in Solid Oxide Fuel Cells by Modified Levenberg–Marquardt Algorithm: A New Automatic Update Limit Strategy. Processes. 2021; 9(1):108. https://doi.org/10.3390/pr9010108
Chicago/Turabian StyleŽic, Mark, Iztok Fajfar, Vanja Subotić, Sergei Pereverzyev, and Matevž Kunaver. 2021. "Investigation of Electrochemical Processes in Solid Oxide Fuel Cells by Modified Levenberg–Marquardt Algorithm: A New Automatic Update Limit Strategy" Processes 9, no. 1: 108. https://doi.org/10.3390/pr9010108
APA StyleŽic, M., Fajfar, I., Subotić, V., Pereverzyev, S., & Kunaver, M. (2021). Investigation of Electrochemical Processes in Solid Oxide Fuel Cells by Modified Levenberg–Marquardt Algorithm: A New Automatic Update Limit Strategy. Processes, 9(1), 108. https://doi.org/10.3390/pr9010108







