Abstract
Here, a study for MHD (magnetohydrodynamic) impacts on the rotating flow of Casson Carreau nanofluids is considered. The temperature distribution is associated with thermophoresis, Brownian motion, and heat source. The diffusion of chemically reactive specie is investigated with Arrhenius activation energy. The governing equations in the 3D form are changed into dimensionless two-dimensional form with the implementation of suitable scaling transformations. The Variational finite element procedure is harnessed and coded in Matlab script to obtain the numerical solution of the coupled non-linear partial differential problem. The variation patterns of Sherwood number, Nusselt number, skin friction coefficients, velocities, concentration, and temperature functions are computed to reveal the physical nature of this examination. It is seen that higher contributions of the magnetic force, Casson fluid, and rotational fluid parameters cause a raise in the temperature like thermophoresis and Brownian motion does but also causes a slowing down in the primary as well as secondary velocities. The FEM solutions show an excellent correlation with published results. The current study has significant applications in the biomedical, modern technologies of aerospace systems, and relevance to energy systems.
Keywords:
MHD; nanofluid; rotating Casson fluid; finite element method; heat transfer; Carreau fluid 1. Introduction
Noteworthy endeavors are made in recent years to explore nanofluids because of remarkable thermodynamic properties. Nanofluids can be utilized to cool the motors of vehicles, biomedical applications, high-transition gadgets, clothes washers machines, high-power microwaves, diode arrays of heavy-power laser, and various welding frameworks. In addition, significant advances in nano designing have opened up the chance of utilizing nanomaterials to treat various types of human body tumors, pharmacological medicines, artificial organs (lungs, heart surgery), and cancer therapy, etc. Nanofluids, presented by Choi and Eastman [1] in 1995, has gotten impressive consideration in present times. Makinde [2] examined numerically that the boundary layer flow induces in the nanofluid cause of a linear stretching surface with the influence of Brownian motion, and thermophoresis. Sarafraz et al. [3] explore the nanofluid flow as a potential coolant. Uddin et al. [4] deliberated about nanofluid through a permeable medium with thermal convective boundary conditions. Khan and Pop [5] provided nanofluids flow through the Buongiorno method, which had passed over the stretching surface. Turkyilmazoglu [6] established a closed-form arrangement for the movement of different nanomaterials through a curved vertical surface.
The flow of the boundary layer due to continuous stretching of the sheet is an important type of flow happening in chemical industries and engineering. These incorporate fluid metal, paper industry, lubricants, and fiber synthesis. The non-Newtonian liquids, including paints, colloidal and organic fluids, biopolymers, and the food industry. Many researchers utilized different geometries to investigate several aspects of non-Newtonian fluid [7,8]. Nandy et al. [9] presented a study to investigate the impacts of velocity slip on nanofluid along with extending surface.
The Darcy–Forchheimer heated law is used to allow us to add a porous medium into the fluid zone without any disbursement. The porous media engagement has significant applications in the zone of heat transfer design, geothermal, geophysics, catalytic reactors, under ground water system, insulation processes, recovery system of crude oil, and units of energy storages. The effects of Darcy–Forchheimer in a porous medium are considered to study the velocity field within the examination of the rotating frame [10]. Hayat et al. [11] investigated the movement of nanoliquids distracted in a porous medium by applying the Darcy–Forchheimer model. Darcy–Forchheimer mixed convective flow over a curved surface considered by [12]. The Hall effects in either the two-phase flow of dusty nanofluid were documented by Gireesha and co-workers [13]. Hayat et al. [14] examined the Darcy–Forchheimer 3D along with Arrhenius activation energy.
Magnetohydrodynamics (MHD) engagement has significant applications in the zone of a drug, space science, various machines, and vitality generators. Tiwana et al. [15] investigate the MHD convective flow which is portrayed in the non-newtonian liquid model. Naz et al. [16] delineated the impacts of MHD flow in channel geometry. Khan et al. [17] studied the impact of magnetohydrodynamic on Williamson fluid flow. Alarifi et al. [18] investigated the MHD impact on fluid flow with a heat source. More work on Magnetohydrodynamics is done by [19,20,21].
In recent years, the examination of liquid and problems of heat transport in the rotating frame is completely charming matter. It is an aftereffect of their titanic applications in the assembling of crystal development, biomechanics, turbomechanics, food industry, gas turbine rotors, filtration process, and cosmic fluid dynamics [22,23]. The chief undertaking toward this way was made by Wang [24]. The effect of magnetohydrodynamics (MHD) in rotating fluid is concentrated by Takhar et al. [25]. Recently, published research articles on rotating flow are mentioned in [26,27,28]. Christov [29] recommended effective speculation of Fourier law regarding thermal relaxation impact which is characterized as the time expected to develop steady-state heat transportation once the temperature gradient is introduced. Modeling of Cattaneo-Christov along with nanofluid examined by [30]. Hayat et al. [31] examined the effects of heat flux Cattaneo-Christov model on variable thermal conductivity.
The perception of current work rises up from the quest for upgraded transportation of heat, so as to elaborate the magnetohydrodynamics impacts with activation energy for time-dependent rotational flow of Casson Carreau nanofluids due to horizontally stretching surface. As far as the authors come to know, these aspects of the problem are not considered in pervious examinations. The fundamental goal of this comprehensive examination is the upgrade of heat transportation with nanofluids. Three dimensional geometrical problem is changed into two dimensional transformation. The resulting non linear partial differential formulation is solved with utilization of widely validated finite element discretization and then variational Galerkin procedure is coded and simulated in Matlab environment. The validation of the numerical outcomes is confirmed in the face of previously available data for limiting cases. Furthermore, pictorial representations of some principal findings with a detailed discussion is also been presented.
2. Statement of The Problem
The time-dependent 3D magnetohydrodynamics an incompressible Carreau and Casson nanofluid flow over an extending sheet with a rotating frame of reference are considered. Physically, we consider that the entire system is at rest in the time however for , the sheet is extended in the x-direction at with angular velocity . The framework is rotating with angular velocity () along the z-direction. The model is created through a species type that incorporates the chemical reactions and Arrhenius activation energy along with the heat flux model of Cattaneo–Christov diffusion expression. In z-direction, (magnetic field) is applied, the instigated magnetic field is overlooked due to a small magnetic Reynolds number, and also, Ohmic dissipation and Hall’s current impacts are ignored since the field of magnetic is not too much strong [32]. Moreover, we assume that the concentration and temperature at the surface are , respectively, and the ambient concentration and temperature are , respectively. The rheological model for the flow of a Casson fluid can be written as:
In the Equation (1), , , , , , and are Cauchy stress tensor, deformation rate components (i,j), yield stress of fluid, Casson fluid plastic dynamics viscosity, non-Newtonian based critical values of this product, and product of components of deformation rate with itself, respectively. The extra stress tensor for Carreau fluid is considered (see [33]). The physical and schematic setup with the coordinate system of the explained problem is sketched in Figure 1.
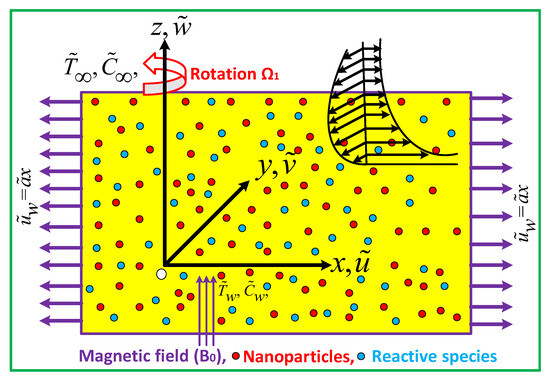
Figure 1.
Schematic configuration with coordinate system.
3. Governing Equations
Considering the above suppositions, the consistent mass, momentum, energy, and conservation of nanoparticles volume fraction equations in a Cartesian coordinate system (x, y, z) as follow [34,35,36,37,38]:
where
Here, (, ) are components of velocity in directions (), respectively, , , , , , , , , and are respectively the density, thermal diffusivity, dynamic viscosity, electrical conductivity, specific heat capacity, activation energy, thermal retardation time, power-law index, and time constant. and are the fluid temperature and nanoparticle volume concentration, and are the Brownian and thermophoretic diffusion coefficient respectively. denotes the temperature-dependent volumetric rate of heat source () and heat sink (). Further, the last term in Equation (6), shows the modified Arrhenius equation with a reaction rate of and fitted rate constant m. Furthermore, t, C, and are respectively time, concentration of nanoparticles volume fraction, and permeability of porous medium. is the non-uniform inertia coefficient and denote the drag coefficient. The current physical elaborated problem, characterized boundary conditions are [34,39]:
We offer a following set of transformation variables to proceed the analysis (see [34,40,41]):
The continuity Equation (2) is satisfied identically using above similarity transformations. In light of Equation (10), the Equations (3)–(9) reduce into following non-linear PDEs in the transformed coordinate system ().
where . The come into view parameters in Equations (11)–(14) are defined as:
where , , M, , , , , , , , , , , and are the Casson fluid parameter, rotating parameter, magnetic parameter, Prandtl number, Lewis number, temperature difference, Brownian motion, thermophoresis, heat source, chemical reaction rate, heat source, activation energy, Weissenberg number, porosity parameter, Forchheimer number, and thermal relaxation parameter, respectively. When , , then the Equations (11)–(14) become:
subject to the boundary conditions (15)
Skin friction coefficient expressions, local Nusselt number, and Sherwood number are defined as:
where the skin friction tensor at wall are (x-direction) and (y-direction), the wall heat transfer is , and the mass flux from the sheet is . By the aid of similarity transformation Equation (10), we get:
4. Finite Element Method Solutions
The transformed set of non-linear partial differential Equations (11)–(14) is solved numerically utilizing the variational finite element method along with boundary conditions (Equation (15)) because Equations (11)–(14) cannot be solved analytically due to highly non-linearity. This procedure is a great numerical computational methodology significant to solve the different types of real-word problems and problems of engineering, for example, liquids with heat transportation, Bio-materials [42], rigid body dynamics, and various regions [43]. An astounding general description of the variational finite elements method outlined by Reddy [44] and Jyothi [45] summed up the basic steps involved in the FEM. Basically the technique is included continuous piecewise function for the solution and to get the parameters of the function in an efficient way that minimizes the error [46]. The FEM solves boundary value problem adequately, rapidly, and precisely [47]. To reduce the order of nonlinear differential Equations (11)–(15), firstly we consider:
The set of Equations (11)–(15) thus reduces to
4.1. Variational Formulations
Over a typical rectangular element , the associated variational form with Equations (22)–(26) is given by
where are arbitrary weight functions or trial functions.
4.2. Finite Element Formulations
Let it divide the rectangular domain () into 4-noded (rectangular element) and () be the domain grid points (see Figure 2). The length of plate and thickness of boundary layer is fixed at , , respectively. The finite model of the element can be obtained from Equations (28)–(32) by replacing the following form of finite element approximations:
here, (j = 1,2,3,4) are the linear interpolation functions for a rectangular element (see Figure 2) and are given by:
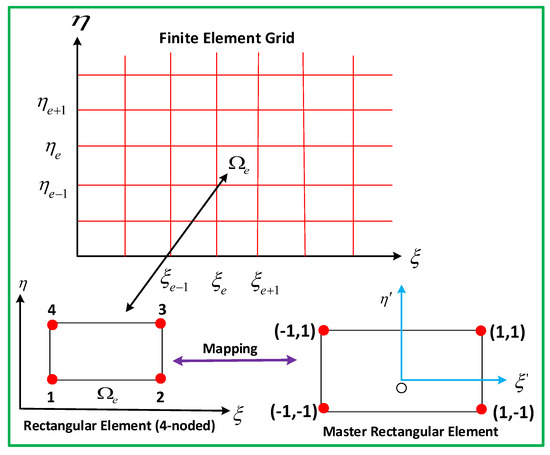
Figure 2.
Finite element grid and finite element mesh of rectangular element.
The model of finite elements of the equations thus developed is given by:
where and (m,n=1,2,3,4) are defined as:
and
where, the known values are to be considered , , , , and . The flow domain is divided into rectangular elements of similar size of grid points. Five functions can be assessed at each node, and equations are obtained after assembly of all element equations. The obtained equations are non-linear after applying boundary conditions which are solved by utilizing the Newton–Raphson method with the required precision of 0.000005.
5. Results and Discussion
This portion gives some noteworthy results of the boundary value problem as finally comprised in Equations (12) to (16). A variational Galerkin method is utilized along with finite element discretization. A broad computational continuing is performed to see the reactions of velocities , , temperature and concentration with the differing contributions of influential parameters. In addition, the outcomes for the Nusselt number as well as the coefficients of skin friction are additionally computed. Before plotting the results, we have endorsed our results with the effectively already published articles through Table 1, Table 2 and Table 3 under restricting conditions. A brilliant relationship has been accomplished which insists the validity of FEM Matlab code. The estimation of present investigation is made by putting the involved for included physical parameters: Nt = 0.2, Nb = = 0.2, , , , , , , , , , , .

Table 1.
Comparison of skin friction coefficients for different values of kp, Fr, and when , at .

Table 2.
Comparison of Nusselt number for kp, , Fr, and Pr at when M = We = 0, Nt = Nb = 0, , and .

Table 3.
Comparison of Nusselt number for and M at when other parameters are ignore.
Figure 3a–d depicted the effect of porosity boundary (kp) and Forchheimer number (Fr) on , h, and . As demonstrated in Figure 3a,b, the higher contribution of porosity boundary (kp), and Forchheimer number (Fr) decrease the and the magnitude of h. Actually, the association of permeable medium makes liquid more viscous and produces opposition force which slows . However, on as opposed to the velocity, the and show direct exceeding connection with Kp and Fr (see Figure 3c,d). The dragging of fluid the boundary layer region because of resistances forces resulted in thermal dissipation to produce extra heat in this region and hence the fluid temperature is on the rise with KP and Fr. In the same way, the rise in species concentration in the solutal boundary layer with incremented KP and Fr.
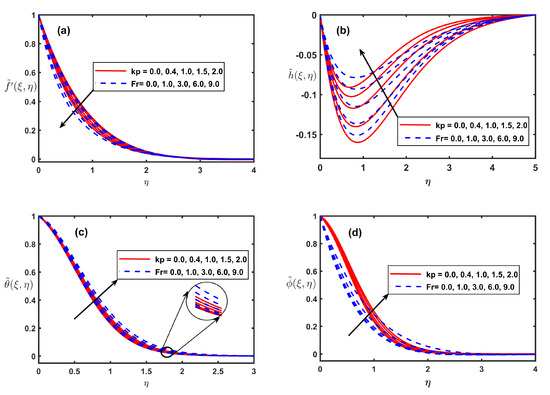
Figure 3.
Fluctuation of , , , and along with kp and Fr.
The effect of M (magnetic field) and (Casson fluid parameter) on , , and is depicted in Figure 4a–d. As demonstrated in Figure 4a,b, the advancing contribution of M subsides the primary velocity and the magnitude of secondary velocity . As a matter of fact, the interaction of M delivers an impeding force (Lorentz force) to halt the momentum of the flow in xy-plane. The perception of Figure 4b shows that h experiences reverse flow because of Lorentz resistive force, therefore a rise in the h profile is seen close to the sheet and afterward it gets zero. However, on as opposed to the velocity, the temperature and concentration display direct exceeding relation with parameter M (see Figure 4c,d).
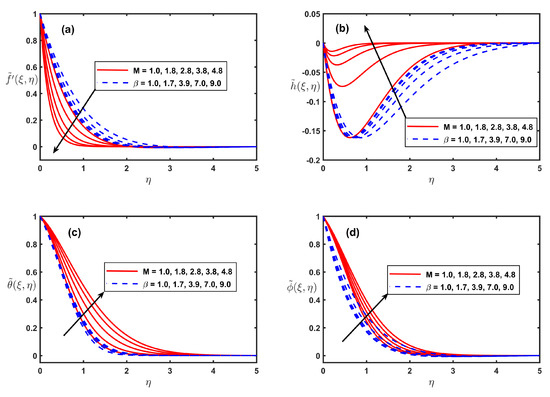
Figure 4.
Fluctuation of , , , and along with M and .
Similar dealings for progressing input of is observed. The velocities show a decline due to the resistance force created by tensile stress because of elasticity. Figure 5a,b) exhibit that both the components of velocity are diminished close to the sheet and afterward experience a variance when is incremented. The primary velocity achieves its bigger value for . It is to make reference to the extending of the sheet along the x-axis is dependable to increase momentum toward this direction but y-direction momentum is denied of any supporting element. In this way the Figure 5a,b individually show that the is switched meagerly and the h is outstandingly switched. From Figure 5c,d, it is seen that both the and are incremented with increasing of . Further, Figure 5a–d are introduced to clarify the variation of , h, , and as affected by . It is to clarify that larger exemplifies the greater lapse of time after the jerk to the stretching sheet. Thus, Figure 5a reveals that is monotonically subsided against increasing . Likewise from Figure 5b, it is seen that the is diminished with reverse flow close to the sheet and afterward it changes at some distance ways from the sheet. Both the components of velocity become smoother for larger . In opposition to velocity behavior, Figure 5c depicts that rises directly with . It is because for longer lapse to the stretch for sheet makes the flow smoother and convection currents for heat transportation are established to raise the temperature in the boundary layer regime. The increased values of set the into swaying pattern as delineated in Figure 5d. It is seen that curve of descends close to the sheet and it ascends away from the sheet.
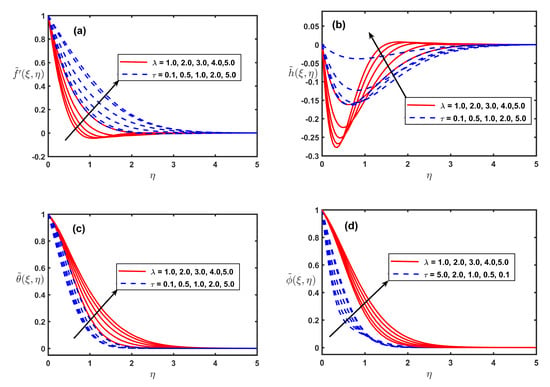
Figure 5.
Fluctuation of , , , and along with and .
Figure 6a–d represented the impact of Weissenberg number (We) and power-law index () on , h, and . As demonstrated in Figure 6a,b, the higher contribution of Weissenberg number (We)decrease the and the magnitude of h. However, on as opposed to the velocity, the and show direct exceeding connection with Weissenberg number (We) (see Figure 6c,d). Actually, the association of Weissenberg number is directly proportional to the time constant and inversely proportional to the viscosity. The time constant to viscosity ratio is higher for larger values of the Weissenberg number. Hence, a higher Weissenberg number causes to enhance the thermal boundary thickness. The higher input of Weissenberg number (We), the and h display direct exceeding relation with parameter (see Figure 6a,b) but opposite trend is observed in the temperature and concentration with direct exceeding of (see Figure 6c,d).
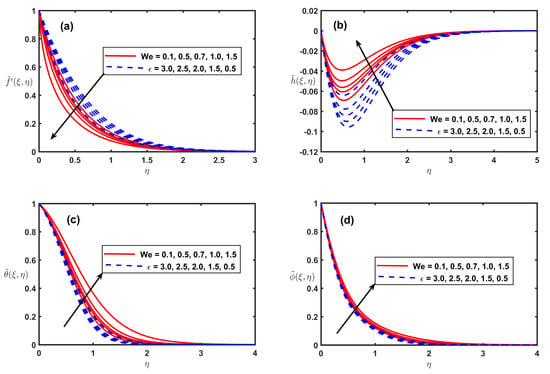
Figure 6.
Fluctuation of , , , and along with We and .
Figure 7a show the implication of Buongiorno’s model parameters on the temperature field. The thermophoretic force cause to move the nanoparticles from the hotter area to cooler area and subsequently more heat move happens in the boundary layer area. Similarly, the quicker random motion of species particles in nanofluids raised the Brownian forces to boost heat transportation. Thus the rise of and improvement in the thermal boundary layer is reported in Figure 7a respectively. Figure 7b is presented to reveal the bringing down of temperature when is apportioned higher input values. The greater values of mean lesser thermal diffusion and hence the decline in temperature field occurs. In contradiction to the impact of , the incremented boosts the temperature as displaced in Figure 7b. As proved in Figure 8a, is higher when the is augmented. Figure 8a is also demonstrated to reveal the bringing down of when is designated higher input values. Figure 8b shows the ramifications of Buongiorno’s model parameters on the . The thermophoretic force cause to move the concentration layer from lower area to higher. Thus, the quicker random movement of species particles in nano liquids raised the Brownian forces to boost up the .
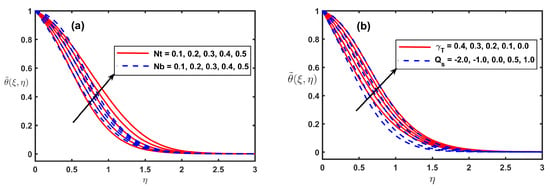
Figure 7.
Fluctuation of along with Nb, Nt, , and .
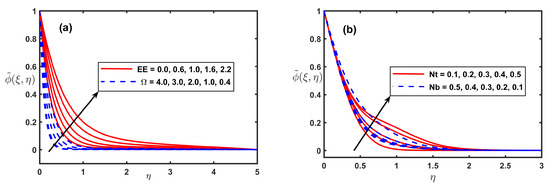
Figure 8.
Fluctuation of along with , , Nt, and Nb.
The computational outcomes for the x,y directions coefficients of skin friction, Nusselt number, and Sherwood number are showed against the in the Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 to uncover the effects of different physical quantities. The perceptions for Figure 9a,b portrays that increasing and Fr created a significant increase in the magnitudes of primary skin friction . Additionally all the negative estimations of show the reversal of primary flow at the surface. In Figure 9b, shows negatively raised magnitude with higher and Fr. Similarly, Figure 10a,b respectively show the enhancement in magnitudes of and when the M is progressed in value. The larger values of M indicate the increasing strength of the resistive force to provide resistance to the flow in both the primary and secondary directions. Furthermore, Figure 10a,b respectively exhibit similar trend for Casson fluid parameter but opposing behaviour is observed for (see Figure 10b). Figure 11a,b and Figure 12a,b respectively draw sketches of reduced Nusselt number and reduced Sherwood number against magnetic field M, rotating parameter , and Casson fluid parameter for varying values of the combine parameters Nb, Nt, and heat source . It is revealed that increments in thermophoresis and Brownian motion parameters recedes the wall heat transfer rate but they boost the wall mass transfer rate. Similar results for wall heat transfer rate and wall mass transfer rate against the are perceived (see Figure 11a,b and Figure 12a,b). Figure 11a,b and Figure 12a,b, in their respective order, demonstrate the meager reducing impacts of M and on reduced Nusselt number, and reduced Sherwood number. Further, it is seen that increments in recede the wall heat transfer rate and wall mass transfer rate. Figure 13a shows the impact of the kp, Fr, and EE on the reduced Sherwood number. It is revealed that increments in Kp, Fr. and EE parameters recedes the wall heat transfer rate. The opposite trend for wall mass transfer rate against the Lewis number (Le) and are perceived (see Figure 13b).
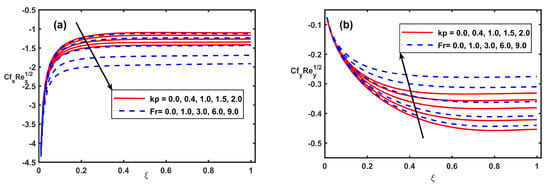
Figure 9.
Fluctuation of and along with and Fr.
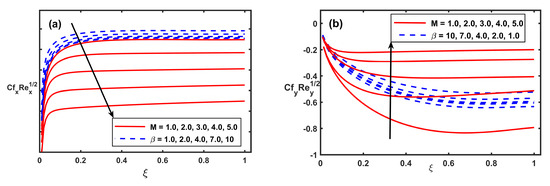
Figure 10.
Fluctuation of and along with M and .
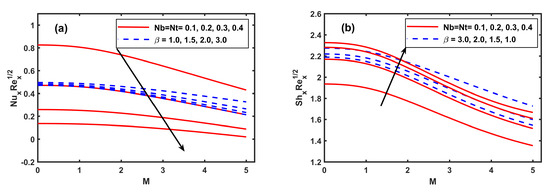
Figure 11.
Fluctuation of and along with Nb, Nt, M, and .
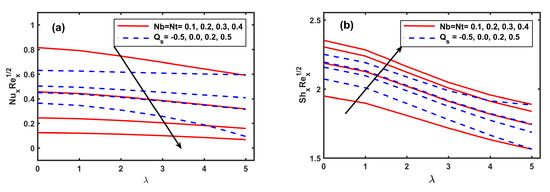
Figure 12.
Fluctuation of and along with Nb, Nt, , and .
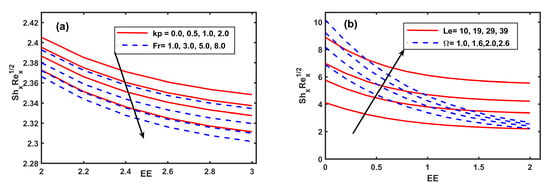
Figure 13.
Fluctuation of along with Kp, Fr, EE, Le, and .
6. Conclusions
This computational and theoretical work addresses the 3D time-dependent magnetohydrodynamics rotational flow of Casson Carreau nanofluids across an extending sheet with activation energy and heat source. The transformed 2D partial differential formulation is solved by variational Galerkin procedure. Numerical findings for velocity components, skin friction coefficients, temperature, Nusselt number, nano-particle volume fraction, and Sherwood number are computed for influential parameters. Some of the major outcomes are reported below:
- The progressing values of Casson fluid parameter , magnetic parameter M, porosity , Forchheimer number (Fr), and Weissenberg number (We) reduced the magnitude of secondary velocity and the primary velocity but concentration and temperature are incremented.
- The concentration and temperature are incremented along with rising values of . The both components of velocity diminishes near the surface when is incremented.
- Improvement in temperature is reported when Nb, Nt, and are increased but inverse behaviour is noted for power-law index ().
- The higher values of Nb, power-law index (), and chemical reaction rate parameter recede the nanoparticle concentration but it increases against higher values of Nt and EE.
- The Nusselt number attains lower values for higher values of Casson fluid parameter , Brownian (Nb), thermophoresis (Nt), magnetic (M), heat source , and rotating ().
- The Sherwood number attains higher values for higher values of Lewis number (Le), Nb, and but the reduced Sherwood number exhibits an opposite trend for magnetic, rotational, porosity , Forchheimer number (Fr), and Casson fluid parameter parameters.
Author Contributions
B.A. modeled the problem and wrote the manuscript. G.R. complete the formal analysis and revision. S.H. and D.B. thoroughly checked the mathematical modeling, English corrections, formal analysis, and revision. B.A. solved the problem using MATLAB software. G.R. and S.B.: writing—review and editing. All authors finalized the manuscript after its internal evaluation. All authors have read and agreed to the published version of the manuscript.
Funding
No funding information is available.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Technical Report; Argonne National Lab: Lemont, IL, USA, 1995. [Google Scholar]
- Makinde, O.D.; Aziz, A. Boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition. Int. J. Therm. Sci. 2011, 50, 1326–1332. [Google Scholar] [CrossRef]
- Sarafraz, M.; Arya, H.; Saeedi, M.; Ahmadi, D. Flow boiling heat transfer to MgO-therminol 66 heat transfer fluid: Experimental assessment and correlation development. Appl. Therm. Eng. 2018, 138, 552–562. [Google Scholar] [CrossRef]
- Uddin, M.J.; Khan, W.; Ismail, A.M. Free convection boundary layer flow from a heated upward facing horizontal flat plate embedded in a porous medium filled by a nanofluid with convective boundary condition. TRansport Porous Media 2012, 92, 867–881. [Google Scholar] [CrossRef]
- Khan, W.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Condensation of laminar film over curved vertical walls using single and two-phase nanofluid models. Eur. J. Mech. B Fluids 2017, 65, 184–191. [Google Scholar] [CrossRef]
- Mahanthesh, B.; Gireesha, B.J.; Thammanna, G.T.; Shehzad, S.A.; Abbasi, F.M.; Gorla, R.S.R. Nonlinear convection in nano Maxwell fluid with nonlinear thermal radiation: A three-dimensional study. Alex. Eng. J. 2018, 57, 1927–1935. [Google Scholar] [CrossRef]
- Shahzad, A.; Ali, R.; Hussain, M.; Kamran, M. Unsteady axisymmetric flow and heat transfer over time-dependent radially stretching sheet. Alex. Eng. J. 2017, 56, 35–41. [Google Scholar] [CrossRef]
- Nandy, S.K.; Mahapatra, T.R. Effects of slip and heat generation/absorption on MHD stagnation flow of nanofluid past a stretching/shrinking surface with convective boundary conditions. Int. J. Heat Mass Transf. 2013, 64, 1091–1100. [Google Scholar] [CrossRef]
- Rashid, S.; Hayat, T.; Qayyum, S.; Ayub, M.; Alsaedi, A. Three-dimensional rotating Darcy–Forchheimer flow with activation energy. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 935–948. [Google Scholar] [CrossRef]
- Hayat, T.; Ijaz, M.; Qayyum, S.; Ayub, M.; Alsaedi, A. Mixed convective stagnation point flow of nanofluid with Darcy-Fochheimer relation and partial slip. Results Phys. 2018, 9, 771–778. [Google Scholar] [CrossRef]
- Muhammad, R.; Khan, M.I.; Jameel, M.; Khan, N.B. Fully developed Darcy–Forchheimer mixed convective flow over a curved surface with activation energy and entropy generation. Comput. Methods Programs Biomed. 2020, 188, 105298. [Google Scholar] [CrossRef] [PubMed]
- Gireesha, B.; Mahanthesh, B.; Thammanna, G.; Sampathkumar, P. Hall effects on dusty nanofluid two-phase transient flow past a stretching sheet using KVL model. J. Mol. Liq. 2018, 256, 139–147. [Google Scholar] [CrossRef]
- Hayat, T.; Aziz, A.; Muhammad, T.; Alsaedi, A. Effects of binary chemical reaction and Arrhenius activation energy in Darcy–Forchheimer three-dimensional flow of nanofluid subject to rotating frame. J. Therm. Anal. Calorim. 2019, 136, 1769–1779. [Google Scholar] [CrossRef]
- Tiwana, M.H.; Mann, A.B.; Rizwan, M.; Maqbool, K.; Javeed, S.; Raza, S.; Khan, M.S. Unsteady Magnetohydrodynamic Convective Fluid Flow of Oldroyd-B Model Considering Ramped Wall Temperature and Ramped Wall Velocity. Mathematics 2019, 7, 676. [Google Scholar] [CrossRef]
- Naz, R.; Noor, M.; Hayat, T.; Javed, M.; Alsaedi, A. Dynamism of magnetohydrodynamic cross nanofluid with particulars of entropy generation and gyrotactic motile microorganisms. Int. Commun. Heat Mass Transf. 2020, 110, 104431. [Google Scholar] [CrossRef]
- Khan, M.; Salahuddin, T.; Yousaf, M.M.; Khan, F.; Hussain, A. Variable diffusion and conductivity change in 3d rotating Williamson fluid flow along with magnetic field and activation energy. Int. J. Numer. Methods Heat Fluid Flow 2019, 30, 2467–2484. [Google Scholar] [CrossRef]
- Alarifi, I.M.; Abokhalil, A.G.; Osman, M.; Lund, L.A.; Ayed, M.B.; Belmabrouk, H.; Tlili, I. MHD flow and heat transfer over vertical stretching sheet with heat sink or source effect. Symmetry 2019, 11, 297. [Google Scholar] [CrossRef]
- Thumma, T.; Wakif, A.; Animasaun, I.L. Generalized differential quadrature analysis of unsteady three-dimensional MHD radiating dissipative Casson fluid conveying tiny particles. Heat Transf. 2020, 49, 2595–2626. [Google Scholar] [CrossRef]
- Tlili, I.; Bilal, M.; Qureshi, M.Z.A.; Abdelmalek, Z. Thermal analysis of magnetized pseudoplastic nano fluid flow over 3D radiating non-linear surface with passive mass flux control and chemically responsive species. J. Mater. Res. Technol. 2020, 9, 8125–8135. [Google Scholar] [CrossRef]
- Khan, S.A.; Nie, Y.; Ali, B. Multiple slip effects on magnetohydrodynamic axisymmetric buoyant nanofluid flow above a stretching sheet with radiation and chemical reaction. Symmetry 2019, 11, 1171. [Google Scholar] [CrossRef]
- Aziz, A.; Muhammad, T.; Alsaedi, A.; Hayat, T. An optimal study for 3D rotating flow of Oldroyd-B nanofluid with convectively heated surface. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 236. [Google Scholar] [CrossRef]
- Mustafa, M.; Ahmad, R.; Hayat, T.; Alsaedi, A. Rotating flow of viscoelastic fluid with nonlinear thermal radiation: A numerical study. Neural Comput. Appl. 2018, 29, 493–499. [Google Scholar] [CrossRef]
- Wang, C. Stretching a surface in a rotating fluid. Z. Angew. Math. Phys. 1988, 39, 177–185. [Google Scholar] [CrossRef]
- Takhar, H.S.; Chamkha, A.J.; Nath, G. Flow and heat transfer on a stretching surface in a rotating fluid with a magnetic field. Int. J. Therm. Sci. 2003, 42, 23–31. [Google Scholar] [CrossRef]
- Ibrahim, W. Three dimensional rotating flow of Powell-Eyring nanofluid with non-Fourier’s heat flux and non-Fick’s mass flux theory. Results Phys. 2018, 8, 569–577. [Google Scholar] [CrossRef]
- Jusoh, R.; Nazar, R.; Pop, I. Magnetohydrodynamic rotating flow and heat transfer of ferrofluid due to an exponentially permeable stretching/shrinking sheet. J. Magn. Magn. Mater. 2018, 465, 365–374. [Google Scholar] [CrossRef]
- Jawad, M.; Shah, Z.; Islam, S.; Majdoubi, J.; Tlili, I.; Khan, W.; Khan, I. Impact of nonlinear thermal radiation and the viscous dissipation effect on the unsteady three-dimensional rotating flow of single-wall carbon nanotubes with aqueous suspensions. Symmetry 2019, 11, 207. [Google Scholar] [CrossRef]
- Christov, C. On frame indifferent formulation of the Maxwell–Cattaneo model of finite-speed heat conduction. Mech. Res. Commun. 2009, 36, 481–486. [Google Scholar] [CrossRef]
- Khan, M.I.; Alzahrani, F.; Hobiny, A.; Ali, Z. Modeling of Cattaneo-Christov double diffusions (CCDD) in Williamson nanomaterial slip flow subject to porous medium. J. Mater. Res. Technol. 2020, 9, 6172–6177. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, M.I.; Farooq, M.; Alsaedi, A.; Waqas, M.; Yasmeen, T. Impact of Cattaneo–Christov heat flux model in flow of variable thermal conductivity fluid over a variable thicked surface. Int. J. Heat Mass Transf. 2016, 99, 702–710. [Google Scholar] [CrossRef]
- Rana, P.; Bhargava, R.; Bég, O.A. Finite element simulation of unsteady magneto-hydrodynamic transport phenomena on a stretching sheet in a rotating nanofluid. Proc. Inst. Mech. Eng. Part N J. Nanoeng. Nanosyst. 2013, 227, 77–99. [Google Scholar] [CrossRef]
- Raju, C.; Sandeep, N. Unsteady three-dimensional flow of Casson–Carreau fluids past a stretching surface. Alex. Eng. J. 2016, 55, 1115–1126. [Google Scholar] [CrossRef]
- Abbas, Z.; Javed, T.; Sajid, M.; Ali, N. Unsteady MHD flow and heat transfer on a stretching sheet in a rotating fluid. J. Taiwan Inst. Chem. Eng. 2010, 41, 644–650. [Google Scholar] [CrossRef]
- Babu, M.J.; Sandeep, N. 3D MHD slip flow of a nanofluid over a slendering stretching sheet with thermophoresis and Brownian motion effects. J. Mol. Liq. 2016, 222, 1003–1009. [Google Scholar] [CrossRef]
- Hayat, T.; Muhammad, T.; Alsaedi, A. On three-dimensional flow of couple stress fluid with Cattaneo–Christov heat flux. Chin. J. Phys. 2017, 55, 930–938. [Google Scholar] [CrossRef]
- Butt, A.S.; Ali, A.; Mehmood, A. Study of flow and heat transfer on a stretching surface in a rotating Casson fluid. Proc. Natl. Acad. Sci. India Sect. Phys. Sci. 2015, 85, 421–426. [Google Scholar] [CrossRef]
- Rudraswamy, N.; Shehzad, S.; Kumar, K.G.; Gireesha, B. Numerical analysis of MHD three-dimensional Carreau nanoliquid flow over bidirectionally moving surface. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 5037–5047. [Google Scholar] [CrossRef]
- Ramaiah K, D.; Kotha, G.; Thangavelu, K. MHD rotating flow of a Maxwell fluid with Arrhenius activation energy and non-Fourier heat flux model. Heat Transf. 2020, 49, 2209–2227. [Google Scholar] [CrossRef]
- Nazar, R.; Amin, N.; Pop, I. Unsteady boundary layer flow due to a stretching surface in a rotating fluid. Mech. Res. Commun. 2004, 31, 121–128. [Google Scholar] [CrossRef]
- Shafique, Z.; Mustafa, M.; Mushtaq, A. Boundary layer flow of Maxwell fluid in rotating frame with binary chemical reaction and activation energy. Results Phys. 2016, 6, 627–633. [Google Scholar] [CrossRef]
- Uddin, M.; Rana, P.; Bég, O.A.; Ismail, A.M. Finite element simulation of magnetohydrodynamic convective nanofluid slip flow in porous media with nonlinear radiation. Alex. Eng. J. 2016, 55, 1305–1319. [Google Scholar] [CrossRef]
- Rana, P.; Bhargava, R. Numerical study of heat transfer enhancement in mixed convection flow along a vertical plate with heat source/sink utilizing nanofluids. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 4318–4334. [Google Scholar] [CrossRef]
- Reddy, J.N. Solutions Manual for an Introduction to the Finite Element Method; McGraw-Hill: New York, NY, USA, 1993; p. 41. [Google Scholar]
- Jyothi, K.; Reddy, P.S.; Reddy, M.S. Carreau nanofluid heat and mass transfer flow through wedge with slip conditions and nonlinear thermal radiation. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 415. [Google Scholar] [CrossRef]
- Reddy, G.J.; Raju, R.S.; Rao, J.A. Influence of viscous dissipation on unsteady MHD natural convective flow of Casson fluid over an oscillating vertical plate via FEM. Ain Shams Eng. J. 2018, 9, 1907–1915. [Google Scholar] [CrossRef]
- Ali, B.; Yu, X.; Sadiq, M.T.; Rehman, A.U.; Ali, L. A Finite Element Simulation of the Active and Passive Controls of the MHD Effect on an Axisymmetric Nanofluid Flow with Thermo-Diffusion over a Radially Stretched Sheet. Processes 2020, 8, 207. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).