Abstract
We applied large eddy simulation (LES) to predict the course of reactive mixing carried out in confined impinging jet reactors (CIJR). The reactive mixing process was studied in a wide range of flow rates both experimentally and numerically using computational fluid dynamics (CFD). We compared several different reactor geometries made in different sizes in terms of both reaction yields and mixing efficiency. Our LES model predictions were validated using experimental data for the tracer concentration distribution and fast parallel chemical test reactions, and compared with the k-ε model supplemented with the turbulent mixer model. We found that the mixing efficiency was not affected by the flow rate only at the highest tested Reynolds numbers. The experimental results and LES predictions were found to be in good agreement for all reactor geometries and operating conditions, while the k-ε model well predicted the trend of changes. The CFD method used, i.e., the modeling approach using closure hypothesis, was positively validated as a useful tool in reactor design. This method allowed us to distinguish the best reactors in terms of mixing efficiency (T-mixer III and V-mixer III) and could provide insights for scale-up and application in different processes.
1. Introduction
Mixing is one of the most common and important unit operations among industrial processes. The importance is particularly significant in turbulent flows with accompanying chemical reactions, because reaction time scales can be of similar or even lower orders of magnitude than those for mixing. Consequently, the mixing efficiency in the system is a crucial factor in improving the quality of a desired product. Among different reactor types, confined impinging jet reactors (referred to in this work simply as jet reactors) are often used in processes that require high mixing intensities, such as particle production through precipitation [1,2,3]. This type of reactor enables almost instantaneous mixing at the molecular level (order of milliseconds) and limits the risk of product retention (or clogging in the extreme case) [4,5,6]. Jet reactors are commonly used in industry, among others, as the reactors of choice for the production of particles [1,2,7,8] or simply as premixers [9].
In this work, large eddy simulation (LES) was used to predict the course of the reactive mixing process. Currently, LES and particularly its hybrid modes (detached eddy simulation, scale-adaptive simulation, stress-blended eddy simulation, etc.) can be regarded as useful and valuable solutions to simulate a number of complex processes. One of the reasons is the possibility of the prediction of desired processes in a wide range of Reynolds and Schmidt numbers. Another reason is the substantial increase in compute node density in recent years that happened despite a slow-down of the so-called Moore’s law (twice the transistor density increase every two years) [10,11]. Last but not least, there was a considerable effort by the scientific community over past years to develop numerical methods for unresolved processes and also for numerical meshes [12]. All of this makes LES a compelling tool in real-life engineering applications.
The main idea behind LES is that the large turbulence scales are resolved directly from the filtered transport equations, whereas for the small, subgrid scales (SGS), simple models are introduced, as it is assumed that these scales are more uniform and isotropic. LES provides more physical results in the case of systems with varying flow regimes, whereas using Reynolds-averaged Navier–Stokes (RANS) models in such cases might result in inaccurate predictions [4,13,14,15,16,17]. In jet reactors, similar behavior can be observed, i.e., the laminar and turbulent flow can coexist in different parts of the reactor. With increasing Reynolds number values above 100–125, one can observe the transition from a fully segregated flow regime to the self-sustainable chaotic flow [18]. This transition is often accompanied by noticeable increase in the mixing speed that can sometimes be misinterpreted as turbulent mixing, which tends to occur at higher Reynolds number values. Hence, the use of RANS models is limited in this case. More information regarding these phenomena can be found in [4,15,16,18,19].
Other authors [6,7,20,21,22,23] have made important contributions on the topic of computational fluid dynamics (CFD) modeling of jet reactors. However, their works were focused more on LES modeling of similarly sized reactors, or the included scale-up analysis did not cover LES modeling. Hence, this work has two aims: The first is to better explain and improve our understanding of the reactive mixing process carried out in jet reactors, i.e., the effect of mixing on the final selectivity of the chemical reaction, using two commonly available turbulence models. The second is to validate the proposed modeling approach (the turbulence, concentration variance, and closure models used) as a useful tool in reactor design.
To characterize the mixing process, a set of two competitive, parallel chemical reactions with well-known kinetics was used. The reaction system consisted of the neutralization of sodium hydroxide with hydrochloric acid and the alkaline hydrolysis of ethyl chloroacetate [24]. The LES results were validated by experimental data and compared with the k-ε model predictions that served as a good reference point. The interpretation of the CFD predictions enabled basic reactor design guidelines to be drawn up. In this contribution, we present an energetic efficiency analysis, and assessed the prediction capability for the reactive mixing of both turbulence models.
2. Jet Reactors Geometry
Several geometries of jet reactors (Figure 1, Figure 2 and Figure 3) were used to study the course of the reactive mixing process. The most typical geometry, i.e., the symmetric T-mixer (Figure 1), is characterized by inlet pipes arranged coaxially and perpendicularly to the impingement zone (outlet pipe). The vortex T-mixer (Figure 2), on the other hand, has inlet pipes that are positioned tangentially to the impingement zone. Other reactor types include the symmetric T-mixer equipped with helicoidal static mixers (Figure 3a) and the cyclone-type mixer (Figure 3b).
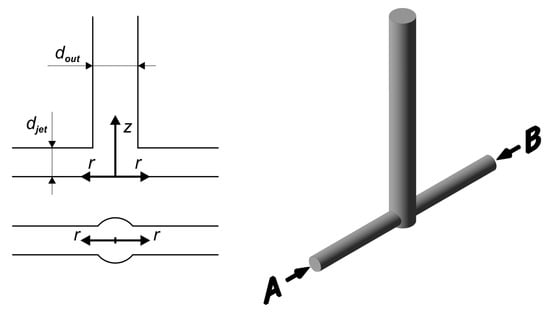
Figure 1.
Geometry of a symmetric T-mixer (T-mixer).
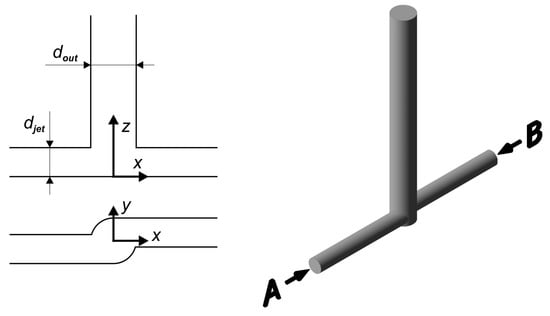
Figure 2.
Geometry of a vortex T-mixer (V-mixer).
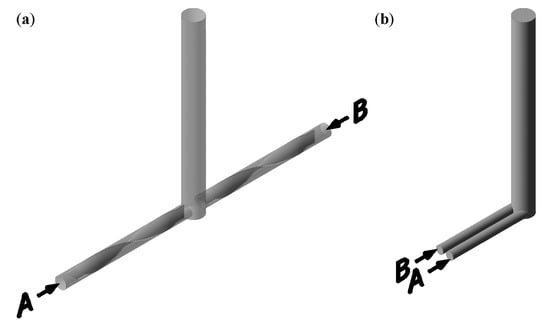
Figure 3.
Geometry of: (a) a symmetric T-mixer equipped with helicoidal static mixers (SP-mixer I); (b) a cyclone-type mixer (L-mixer II).
We investigated the mixing process using three sizes of the selected jet reactors’ geometries. This enabled us to identify the effect of the reactor shape and downsize of the geometry on the process outcome. For this reason, two reactor geometries (symmetric and vortex T-mixers) were made in three sizes, with different inlet diameters,. The largest systems were equipped with inlet pipes with = 7.0 mm (I), whereas, for the intermediate reactors, it was = 4.6 mm (II) and, for the smallest reactors, = 1.45 mm (III). The reactors were equipped with outlet pipes of diameter = 11 mm ( = 7.0 mm (I), = 4.6 mm (II)) and = 2 mm ( = 1.45 mm (III)). The cyclone-type mixer and symmetric T-mixer equipped with static mixers, however, were studied only in one variant: with equal to 7.0 mm and 4.6 mm respectively. The static mixers were of helicoidal shape, made from a flat metal bar twisted by an angle of 270 degrees, as shown in Figure 3a. The bar width was equal to 70.0 mm (5 mm from each side was flat) and its thickness was equal to 0.5 mm. One of the mixers was positioned such that its end was aligned horizontally to the outlet pipe, whereas the end of the second mixer was aligned vertically to the outlet pipe. Parametric equations of the helix can be written as follows:
where = 40/π mm and = 3.5 mm.
In order to maintain the same naming convention, the reactor names have suffixes accordingly to : = 7.0 mm—I, = 4.6 mm—II, and = 1.45 mm—III. The inlet pipes were of the same length in all studied systems (100 mm). As for the outlet pipes, the length was equal to either 300 mm ( = 7.0 mm (I) and = 4.6 mm (II)) or 200 mm ( = 1.45 mm (III)). Table 1 contains the names of the reactors with their corresponding description and characteristic size. The reactors will be further referred to with the listed names.

Table 1.
Dimensions of the studied reactors.
3. Experimental Setup
Validation experiments were conducted as a verification step of the model predictions, in which the effect of process conditions on the course of mixing and fast parallel chemical reactions was investigated. Hydrodynamics in the systems were studied in the authors’ previous works [15,16,17], in which a detailed description of the experimental system was also included. In the experiments, particle image velocimetry (PIV) and planar laser induced fluorescence (PLIF) techniques were used to measure the fluid velocity and passive tracer concentration respectively.
In this work, a well-known parallel chemical reactions system was used to investigate the course and intensity of mixing in the reactors [24] (A—sodium hydroxide, B—hydrochloric acid, and C—ethyl chloroacetate):
where = 108 m3 mol−1 s−1 [25] and = 0.0259 m3 mol−1 s−1 [26].
The experimental studies were conducted at 298 K. The reactant solutions were prepared using double distilled water and Sigma-Aldrich analytical grade reagents. The aqueous solutions were fed into the systems through inlet A (sodium hydroxide) and through inlet B (premixture of hydrochloric acid and ethyl chloroacetate), as shown in Figure 1, Figure 2 and Figure 3. The inlet reactant concentrations were equal to = = = 100 mol m−3. Postreaction samples were taken at the exit of the reactors.
To determine the effect of mixing on the course of parallel reactions, one can use a final selectivity, which is defined in this case as the ratio of the decrease in the ethyl chloroacetate concentration to the initial amount of NaOH moles [27]. As the stoichiometric coefficients of reactants were all equal to 1 and the inlet streams were equal to each other, the final selectivity can be expressed with the use of concentrations:
where the ethyl chloroacetate concentration was measured using a high-performance liquid chromatography (HPLC) technique.
In the presented reaction system, the sodium hydroxide is a limiting component. Therefore, considering the mixing process, the final selectivity takes two characteristic extremes: 0 for ideal mixing and 0.5 for full segregation. This, of course, applies to equal values of molecular diffusion coefficients of reactants.
4. Simulation Setup
Hydrodynamics in the mixers were predicted using ANSYS Fluent CFD software. Two turbulence models were employed: the realizable k-ε (RANS) model with the “enhanced wall treatment” option enabled and large eddy simulation coupled with the Smagorinsky–Lilly dynamic stress model. The RANS simulations served as a startup point and benchmark for LES.
The size of numerical grids was differentiated by the outlet pipe diameter. For = 11 mm (I, II), meshes were made of approximately 800,000 hexahedral cells, whereas for = 2 mm (III) there were approximately 300,000 hexahedral cells. The meshes were the densest in the mixing chamber region and the near-wall cell sizes were set accordingly to satisfy the y+~1 condition. The mesh independence was checked at the highest tested Reynolds numbers using two quantities: average wall shear stress value at the walls and average turbulence energy dissipation rate value in the system. The results of both of these quantities were constant (less than 3% difference), even with using denser meshes than those described.
To minimize the numerical diffusion, a bounded central differencing scheme was applied to all turbulence quantities, whereas a second-order discretization scheme was used for the pressure and scalars. The value of 10−6 or smaller for normalized residuals was considered as a fulfilled convergence condition. The averaged values predicted by large eddy simulations were obtained for a time interval equal to 10 residence times, . The residence time was defined as = /, where V is the reactor volume and is the total flow rate in the system. The time step value was set individually to meet the ≤ / condition [28], where is the time step value, is the numerical cell size (cube root of its volume), and U is the local velocity magnitude in the cell.
The transport equation for the filtered mean mixture fraction, , in LES is expressed as
where ¯ indicates a filtered value, is the molecular diffusivity, and is the subgrid diffusivity. In this work, was determined using the following formula [29]:
where is the eddy viscosity, and is the subgrid Schmidt number. In LES simulations, was calculated using an algebraic model—the Smagorinsky model with local adaptation of the Smagorinsky constant [30,31].
To predict the course of parallel chemical reactions, the probability density function (PDF) closure method using conditional moments and the probability density function (PDF), approximated in this case by the Beta function, was used [13]:
where
The PDF describes the subgrid-scale inhomogeneity based on the subgrid scale concentration variance value, . However, the subgrid concentration variance cannot be calculated directly from the conservation equation of the filtered mixture fraction (Equation (5)), and another balance equation is necessary. One possible solution was proposed by Cook and Riley [32]. This was based on the assumption that the small scale phenomena can be estimated from the slightly larger scales using the filtering operation. The proposed model [32] was based on a constant coefficient, the value of which was determined by Cook [33] for the mixing of gases, ranging from 0.54 to 1.75. In the case of liquids (high Schmidt numbers), the coefficient value increases, reaching the asymptotic value of 5 [34]. However, such model definition with a constant coefficient limits the description of the local flow characteristics, i.e., the local changes of the Reynolds and Schmidt number values. To overcome this issue, one can use the scale similarity model supplemented with the dynamic model coefficient [17]:
where indicates a test-filter (), is the Kolmogorov scale, is the Batchelor number, and is the turbulence kinetic energy dissipation rate. The main advantage of the model is that it does not require using any a priori defined coefficients and can be used for fluids with variable Schmidt numbers. The details regarding the model can be found in one of the previous works of the authors [15,17]. To predict the concentration variance distribution in the systems using the RANS model, the k-ε model was additionally supplemented with the turbulent mixer model [24,35].
A set of filtered differential balance equations for any reacting species is then solved:
The first reaction, given by Equation (2) is assumed to be instantaneous and the rate of the second reaction is expressed as
where
The physical meaning of Equation (13) is the linear interpolation between an infinitely slow and instantaneous reaction.
The closure can be applied to both LES and RANS models, where in RANS it is used for the whole spectrum of turbulent concentration fluctuations, and in LES at the subgrid level.
5. Results and Discussion
In this work, the following numerical approach was taken to predict the course of parallel chemical reactions. In the first stage, we studied the hydrodynamics in the systems. This stage consisted of predictions of velocity, tracer concentration, and tracer concentration variance profiles in the systems. In the next phase, the closure model for the chemical reaction was applied. Both of these phases were conducted using the LES and k-ε models. Such an approach enabled easy verification of each modeling phase and worked well for simulations of reactive mixing both in general and in the specific case of jet reactors [15,36].
In the case of velocity and tracer concentration distribution in jet reactors, LES generally produced more accurate results, as was shown in our previous works [15,16]. We demonstrated that, at lower jet Reynolds numbers (Rejet), the RANS results can differ significantly from the experiments, whereas, at higher jet Reynolds numbers, the discrepancy between both the LES results and experiments decreased. The results indicated that the k-ε model failed to properly predict the flow behavior, i.e., a collision of inlet streams and resulting fluid motion around the outlet pipe and impingement zone [16]. This follows from the theory of turbulence and is related to the Reynolds-averaged approach. In this approach, the variation of time-averaged quantities occurs at relatively large scales and does not necessary resolve all small-scale phenomena, both temporal and spatial [37].
Although the differences between the RANS and experimental results can be large, this may not necessarily make the RANS models unusable to qualitatively assess jet reactor performance. That is because the regions where the largest discrepancies were observed were small compared to the reactor volume, and the residence time in these regions is very short (order of milliseconds). The residence time decreases even further with the increasing Reynolds number. This applies especially to processes that are slower than mixing.
In the case of parallel chemical reactions that are fast compared to mixing, one can expect the discrepancies to increase with decreasing Reynolds numbers. This can be observed in Figure 4, Figure 5, Figure 6 and Figure 7, which show a comparison of the final selectivity predictions of both turbulence models with experimental data. The experiments and calculations were performed for = 300 ÷ 4000 for the reactors with = 4.6 or 7 mm (V-mixer I, V-mixer II, SP-mixer I, L-mixer I and T-mixer I, and T-mixer II) and = 50 ÷ 1000 for the reactors with = 1.45 mm (T-mixer III and V-mixer III). The results for the T-mixer I and T-mixer II were presented in the authors’ previous work [15], and one can observe that they are similar to those for other reactors presented in this work. is defined as:
where is the mean velocity in the jet (inlet pipe), = 997 kg m−3 is the density, and = 0.891 × 10−3 Pa s is the dynamic viscosity of the inlet solutions at 298 K.
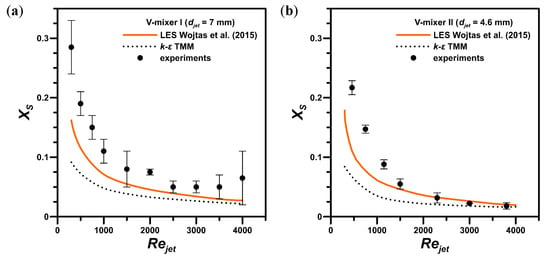
Figure 4.
The effect of the jet Reynolds number on the final selectivity of the chemical reaction: (a) V-mixer I; (b) V-mixer II.
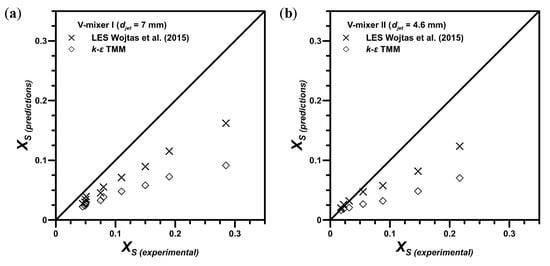
Figure 5.
Parity plot showing predictions of the large eddy simulation (LES) and Reynolds-averaged Navier–Stokes (RANS) models: (a) V-mixer I; (b) V-mixer II.
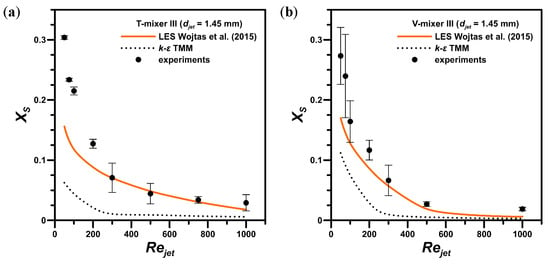
Figure 6.
The effect of the jet Reynolds number on the final selectivity of the chemical reaction: (a) T-mixer III; (b) V-mixer III.
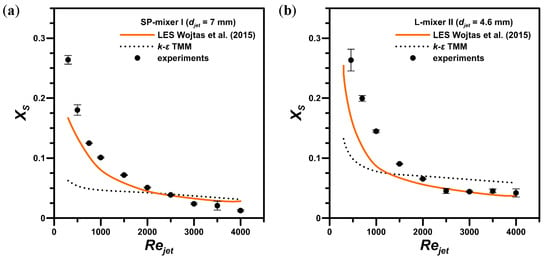
Figure 7.
The effect of the jet Reynolds number on the final selectivity of the chemical reaction in: (a) SP-mixer I; (b) L-mixer II.
The effect of on the final selectivity of the slower reaction for the V-mixer I ( = 7 mm) and V-mixer II ( = 4.6 mm) is shown in Figure 4. The LES model agreed better with the experiments for the whole tested range of , i.e., regardless of turbulence intensity that is characterized here by low and high values for high and low intensity, respectively. The k-ε model, on the other hand, gave acceptable results solely at the highest tested jet Reynolds number values, when the turbulence was more intense and the mixing mechanism was dominated by inertial convective effects. This is more clearly visible in Figure 5, which shows the differences between the LES and RANS predictions presented in a form of parity plot.
However, although advantages of using LES can be seen at both low and high turbulence intensity, the cost of using large eddy simulations is still a real concern for high Reynolds number flows, due to the mesh resolution requirements in a boundary layer [38,39]. One can estimate that, for highly turbulent flows ( > 105), calculations would be, at best, a million times more costly than for RANS models [38,40,41]. Of course, that makes it rather unrealistic that LES will become a major element of industrial CFD simulations; however, LES can still play a role in the detailed analysis of the elements of such flows. One possible solution for these extreme requirements can be LES hybrid methods, i.e., a combination of RANS in slender, near-wall regions and LES in regions away from walls. In near-wall regions, the turbulence is closer to having mature and repeatable behavior and is more likely to be accurately predicted by simpler models. Overall, pure LES for industrial flows is likely to be limited in the foreseeable future to free-shear flows or simpler geometries, such as jet reactors, preferentially at low to mid Reynolds numbers. Taking this into consideration, the k-ε model appears to be a reasonable choice for predicting of the course of a chemical reaction in a high Reynolds number regime ( > 3000) or to determine a trend of changes in the process course depending on the process parameters.
The primary reason for the RANS results underestimation lies in an overestimation of the mixing speed and concentration variance values in the reactors, where the largest differences were observed in and near the impingement zone [15,16,17,36]. These works demonstrated that the differences between the experimental and simulation data for concentration variance were present for both turbulence models. However, the shape of the variance distribution obtained by LES, which is closely related to the mixing area, was well predicted. Conversely, the residence time in this zone decreased with increasing as was already discussed in this section. Together with the fact that the k-ε model and closure method were designed to be used for fully turbulent flow simulations, this explains the improving compliance of the RANS results at high values.
The same situation occurred for the T-mixer III and V-mixer III ( = 1.45 mm), which is shown in Figure 6. The LES results were more similar to the measurements, and more importantly, the trend of changes of the final selectivity agreed better with the experimental data. At higher than 500, there was small to no improvement in the mixing quality in the systems. This was a much lower value than in the larger reactors, for which this “critical” value was around 1500–2000. The position of these points are functional dependent on the chemical concentration (speed of the reaction), hence they are not universal for a specific mixer geometry. We can conclude here that the reactors made in a smaller scale allowed better mixing at much lower flow rates (lower final selectivity values). A physical explanation for this behavior lies in Fick’s law, i.e., the diffusional mixing time is proportional to the square of the characteristic length scale, which decreases as the geometry size becomes smaller. With a decrease in the flow rates, the residence time increases, and so there is more time for the diffusion of species.
A possible reason for the discrepancy between the LES and experimental results at low values observed for all studied systems lies in the discretization schemes used in the simulations (bounded central differencing for momentum and second-order upwind for scalars). When using implicit filtering in LES as in this work (the filter corresponds to the numerical grid size), the energy content of the smallest resolved scales was underpredicted due to numerical diffusion [42]. The same underprediction applies to the concentration variance, as the model used [17] is related to the resolved scalar gradient, which is the largest on these scales. Therefore, one could argue that concentration variance models that employ algebraic relations with respect to resolved scalar or scalar gradient should be used when numerical schemes of higher-order accuracy are applied [42]. Upwind schemes or bound-preserving limiters are often used in LES as they can mitigate dispersive scalar oscillations; however, both these methods introduce artificial dissipation that can lower the accuracy of predictions [43].
The solution would be to use more complex methods, but at the time of writing this manuscript, the choice of discretization methods in ANSYS Fluent was limited. The possible options included, among others, second-order upwind, QUICK, third-order MUSCL, and bounded central differencing schemes for the momentum transport equation (with the last one as the recommended setting). As for the scalar transport equation, the choice was limited even further, without the possibility to use central differencing schemes. Given the above, the only way to surmount the problem would be to use different software or even to write custom CFD code supplemented with other numerical schemes, such as the finite-volume WENO scheme [44], which has been proven to work with minimal dissipation [43]. However, that was not within scope of this study.
The presented results so far indicate that by slightly changing the reactor geometry, better mixing in the systems could be obtained (lower values for the V-mixer III). What is more, comparing Figure 4 and Figure 6, a system scale reduction is one more method of increasing the mixing efficiency in the systems. As the scale reduction and geometry modifications are efficient methods to improve the mixing intensity, we can also consider other types of jet reactors to find a better reactor design. The results obtained for such different designs, i.e., the SP-mixer I ( = 7 mm) (Figure 3a) and L-mixer II ( = 4.6 mm) (Figure 3b), are presented in Figure 7.
By introducing static mixers into the inlet pipes, the SP-mixer I ( = 7 mm) became very similar to the V-mixer II ( = 4.6 mm) in terms of the mixing efficiency, even though it had a larger inlet pipe diameter. As for the L-mixer II ( = 4.6 mm), at low values, it quickly reached a turnover point, after which no significant improvement in the mixing intensity was observed. The experimental results also indicated that this geometry, in addition to being an interesting construction, offered mediocre mixing conditions, i.e., the final selectivity values were almost identical as in the case of the T-mixer II [15] and higher than in the V-mixer II (Figure 4b). The LES results for both reactors agreed well with the experiments at all studied jet Reynolds number values. This again shows the advantage of using large eddy simulations to predict complex chemical processes.
Given the above results, it is difficult to distinguish the most efficient reactor design from all studied jet reactors. Although the smallest mixers allow achieving the lowest values of the final selectivity, their very small dimensions create different problems. One such problem is an even distribution of solutions into the reactor in a continuous operation process, because the small inlet diameters require using syringe pumps. Furthermore, one can expect a much higher pressure drop inside the mixing chamber than in the reactors made in the larger scale. The reactors made in a larger scale also allow high mixing efficiency, but, on the other hand, require high flow rates.
For this reason an energy (economic) analysis becomes helpful. Considering a mixing zone defined as reactor volume in which the chemical reaction occurs, together with the total energy dissipation rate in this zone and total inlet stream, one can calculate the energetic unit cost of obtaining a product as follows:
where is the mean energy dissipation rate in the reaction zone, is the residence time in the reaction zone, is the reaction zone volume, and is the total flow rate through the reactor. The reaction zone volume was determined based on an area of sodium hydroxide concentration, which was a limiting component in the course of the process.
The results of this analysis are presented in Figure 8. The results are based on the k-ε model predictions, as it was shown that, despite the discrepancies, the RANS model correctly predicted the data trends and can be used in a qualitative assessment of the studied reactors. The most important assessment should be made at higher tested jet Reynolds number values, i.e., at the lowest obtained final selectivity values. These values correspond to the right-hand side of Figure 8, and, as shown in Figure 4, Figure 5, Figure 6 and Figure 7, are almost identical both for LES and the k-ε model.
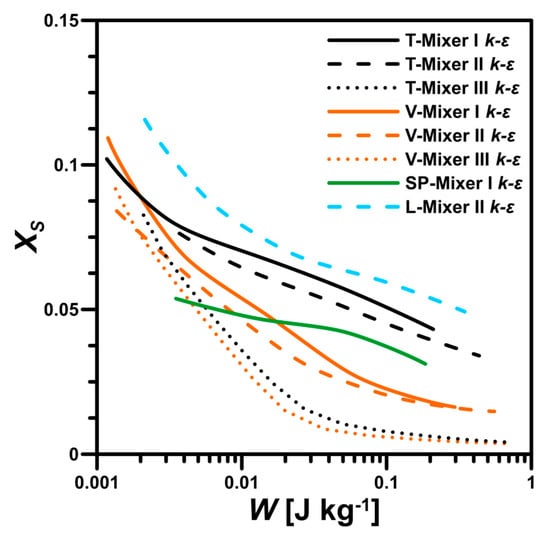
Figure 8.
The energetic unit cost of obtaining product in different reactor types. Data for T-mixer I and T-mixer II from [15].
It is clear that with the improved quality of mixing the process cost increases. More importantly, however, certain reactors were more energy-efficient than others. At almost any energy input, the T-mixer III and V-mixer III systems offered the best quality product, characterized here by low values. However, the aforementioned difficulties in the usage of such small geometries remain a concern. As for the larger scale reactors, the vortex T-mixers were the most efficient systems, with a small, but not significant advantage to the V-mixer II. Among the larger scale symmetric T-mixers, introducing static mixers into the system presented certain advantages. It can improve the mixing, as well as reduce the cost of the product.
Concluding the presented results, LES modeling provided better and more agreeable results with the experiments than those obtained using the k-ε model. This was particularly true for low jet Reynolds numbers and illustrates the importance of the effect of large scale inhomogeneities that are neglected by RANS as opposed to LES. Taking this into consideration, LES is a very promising method for obtaining accurate results, especially for processes where the flow changes from laminar to turbulent and vice versa. This is one of many reasons why LES models and the derivatives (hybrid RANS-LES) should be constantly developed, and, in particular, at the subgrid scale, to be successfully used for describing the course of chemical processes.
6. Conclusions
We used competitive, parallel chemical reactions to experimentally characterize the mixing in confined impinging jet reactors. Several systems of different geometry and size were tested. The main aims of the presented work were to validate the modeling procedure used as a useful tool in reactor design and to choose the best reactor in terms of the quality and efficiency of mixing. The methods used in this work, which involved conducting simulations and corresponding experiments (verification step), proved to provide valuable and reliable results.
The presented results showed that LES supplied with the appropriate closure models (for concentration variance and chemical reaction) can be successfully used in the reactor design stage not only for the analysis of various, not described here jet reactors, but also for more complex geometries. The results also enabled us to choose the most favorable of the studied reactor geometries in terms of product quality. The product quality in this case was the highest mixing intensity (lowest final selectivity) and efficiency. In this work, the T-mixer III and V-mixer III (both with equal to 1.45 mm) were found to be superior in this respect. The mixing characteristics, i.e., the increase of mixing quality with the increase of the jet Reynolds number, were apparent for both larger and smaller systems.
The turnover point, at which there was small to no improvement in the final selectivity, occurred at approximately = 2000 for larger reactors ( = 7 mm or 4.6 mm), whereas, for the smallest reactors ( = 1.45 mm), it was at = 500. At this point, the mixing stopped being a dominant rate controlling mechanism in the studied process. Considering these results, i.e., generally lower obtained final selectivity values and the better energetic efficiency in the smallest jet reactors, these systems should be used when the highest mixing intensity is of the highest priority, e.g., in particulate processes.
The results obtained for both the LES and k-ε models supplemented with full closure differed from each other at low Reynolds number values. This is related to the mixing being slower than the chemical reaction and the differences in the hydrodynamic predictions in the mixing chamber for both models. With increasing jet Reynolds number values, the residence time in the impingement zone decreased, making these differences insignificant. The trend of changes was predicted well by both turbulence models, thus, allowing for reactor comparison in terms of the energetic efficiency. Therefore, we conclude that LES supplemented with a PDF closure can be successfully applied to predict the course of the reactive mixing process in jet reactors, while the k-ε model can only be used for qualitative assessment or at high Reynolds numbers (fully developed turbulent flows).
Author Contributions
K.W.—Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Writing—original draft, Visualization; W.O.—Resources, Validation, Writing—review & editing, Supervision; Ł.M.—Conceptualization, Methodology, Validation, Writing—review & editing, Supervision, Project administration, Funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science Centre, Poland (Decision No. DEC-2013/09/B/ST8/02869).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lince, F.; Marchisio, D.L.; Barresi, A.A. Strategies to control the particle size distribution of poly-ε-caprolactone nanoparticles for pharmaceutical applications. J. Colloid Interface Sci. 2008, 322, 505–515. [Google Scholar] [CrossRef] [PubMed]
- Marchisio, D.L. Large eddy simulation of mixing and reaction in a confined impinging jets reactor. Comput. Chem. Eng. 2009, 33, 408–420. [Google Scholar] [CrossRef]
- Santillo, G.; Deorsola, F.A.; Bensaid, S.; Russo, N.; Fino, D. MoS2 nanoparticle precipitation in turbulent micromixers. Chem. Eng. J. 2012, 207–208, 322–328. [Google Scholar] [CrossRef]
- Icardi, M.; Gavi, E.; Marchisio, D.L.; Olsen, M.G.; Fox, R.O.; Lakehal, D. Validation of LES predictions for turbulent flow in a Confined Impinging Jets Reactor. Appl. Math. Model. 2011, 35, 1591–1602. [Google Scholar] [CrossRef][Green Version]
- Lindenberg, C.; Schöll, J.; Vicum, L.; Mazzotti, M.; Brozio, J. Experimental characterization and multi-scale modeling of mixing in static mixers. Chem. Eng. Sci. 2008, 63, 4135–4149. [Google Scholar] [CrossRef]
- Metzger, L.; Kind, M. On the mixing in confined impinging jet mixers–Time scale analysis and scale-up using CFD coarse-graining methods. Chem. Eng. Res. Des. 2016, 109, 464–476. [Google Scholar] [CrossRef]
- Johnson, B.K.; Prud’homme, R.K. Chemical processing and micromixing in confined impinging jets. AIChE J. 2003, 49, 2264–2282. [Google Scholar] [CrossRef]
- Midler, M.; Paul, E.L.; Whittington, E.F.; Futran, M.; Liu, P.D.; Hsu, J.; Pan, S.H. Crystallization Method to Improve Crystal Structure and Size. U.S. Patent 5314506, 24 May 1994. [Google Scholar]
- Raman, V.; Fox, R.O.; Harvey, A.D.; West, D.H. CFD Analysis of premixed methane chlorination reactors with detailed chemistry. Ind. Eng. Chem. Res. 2001, 40, 5170–5176. [Google Scholar] [CrossRef]
- Moore, G.E. Cramming more components onto integrated circuits. Electronics 1965, 38, 114–117. [Google Scholar] [CrossRef]
- Waldrop, M.M. The chips are down for Moore’s law. Nature 2016, 530, 144–147. [Google Scholar] [CrossRef]
- Pope, S.B. Ten questions concerning the large-eddy simulation of turbulent flows. New J. Phys. 2004, 6, 35. [Google Scholar] [CrossRef]
- Makowski, Ł.; Bałdyga, J. Large eddy simulation of mixing effects on the course of parallel chemical reactions and comparison with k–ɛ modeling. Chem. Eng. Process. Process Intensif. 2011, 50, 1035–1040. [Google Scholar] [CrossRef]
- Schwertfirm, F.; Manhart, M. A numerical approach for simulation of turbulent mixing and chemical reaction at high Schmidt numbers. In Micro and Macro Mixing; Bockhorn, H., Mewes, D., Peukert, W., Warnecke, H.-J., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 305–324. ISBN 978-3-642-04548-6. [Google Scholar]
- Wojtas, K.; Orciuch, W.; Wysocki, Ł.; Makowski, Ł. Modeling and experimental validation of subgrid scale scalar variance at high Schmidt numbers. Chem. Eng. Res. Des. 2017, 123, 141–151. [Google Scholar] [CrossRef]
- Wojtas, K.; Orciuch, W.; Makowski, Ł. Comparison of large eddy simulations and k-ε modelling of fluid velocity and tracer concentration in impinging jet mixers. Chem. Process Eng. 2015, 36. [Google Scholar] [CrossRef]
- Wojtas, K.; Makowski, Ł.; Orciuch, W.; Bałdyga, J. Comparison of subgrid closure methods for passive scalar variance at high Schmidt number. Chem. Eng. Technol. 2015, 38, 2087–2095. [Google Scholar] [CrossRef]
- Nunes, M.I.; Santos, R.J.; Dias, M.M.; Lopes, J.C.B. Micromixing assessment of confined impinging jet mixers used in RIM. Chem. Eng. Sci. 2012, 74, 276–286. [Google Scholar] [CrossRef]
- Metzger, L.; Kind, M. On the transient flow characteristics in confined impinging jet mixers—CFD simulation and experimental validation. Chem. Eng. Sci. 2015, 133, 91–105. [Google Scholar] [CrossRef]
- Lindenberg, C.; Mazzotti, M. Experimental characterization and multi-scale modeling of mixing in static mixers. Part 2. Effect of viscosity and scale-up. Chem. Eng. Sci. 2009, 64, 4286–4294. [Google Scholar] [CrossRef]
- Mahajan, A.J.; Kirwan, D.J. Micromixing effects in a two-impinging-jets precipitator. AIChE J. 1996, 42, 1801–1814. [Google Scholar] [CrossRef]
- Gillian, J.M.; Kirwan, D.J. Identification and correlation of mixing times in opposed-jet mixers. Chem. Eng. Commun. 2008, 195, 1553–1574. [Google Scholar] [CrossRef]
- Bertrand, M.; Lamarque, N.; Lebaigue, O.; Plasari, E.; Ducros, F. Micromixing characterisation in rapid mixing devices by chemical methods and LES modelling. Chem. Eng. J. 2016, 283, 462–475. [Google Scholar] [CrossRef]
- Bałdyga, J.; Bourne, J.R. Turbulent Mixing and Chemical Reactions; Wiley: New York, NY, USA, 1999; ISBN 978-0-471-98171-8. [Google Scholar]
- Crooks, J.E. Proton transfer to and from atoms other than carbon. In Comprehensive Chemical Kinetics; Elsevier: Amsterdam, The Netherlands, 1977; Volume 8, pp. 197–250. ISBN 978-0-444-41512-7. [Google Scholar]
- Kirby, A.J. Hydrolysis and formation of esters of organic acids. In Comprehensive Chemical Kinetics; Elsevier: Amsterdam, The Netherlands, 1972; Volume 10, pp. 57–207. ISBN 978-0-444-40957-7. [Google Scholar]
- Bałdyga, J.; Bourne, J.R. The effect of micromixing on parallel reactions. Chem. Eng. Sci. 1990, 45, 907–916. [Google Scholar] [CrossRef]
- Courant, R.; Friedrichs, K.; Lewy, H. On the partial difference equations of mathematical physics. IBM J. Res. Dev. 1967, 11, 215–234. [Google Scholar] [CrossRef]
- Pitsch, H.; Steiner, H. Large-eddy simulation of a turbulent piloted methane/air diffusion flame (Sandia flame D). Phys. Fluids 2000, 12, 2541. [Google Scholar] [CrossRef]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.H. A dynamic subgrid-scale eddy viscosity model. Phys. Fluids Fluid Dyn. 1991, 3, 1760–1765. [Google Scholar] [CrossRef]
- Lilly, D.K. A proposed modification of the Germano subgrid-scale closure method. Phys. Fluids Fluid Dyn. 1992, 4, 633–635. [Google Scholar] [CrossRef]
- Cook, A.W.; Riley, J.J. A subgrid model for equilibrium chemistry in turbulent flows. Phys. Fluids 1994, 6, 2868–2870. [Google Scholar] [CrossRef]
- Cook, A.W. Determination of the constant coefficient in scale similarity models of turbulence. Phys. Fluids 1997, 9, 1485–1487. [Google Scholar] [CrossRef]
- Michioka, T.; Komori, S. Large-eddy simulation of a turbulent reacting liquid flow. AIChE J. 2004, 50, 2705–2720. [Google Scholar] [CrossRef]
- Bałdyga, J. Turbulent mixer model with application to homogeneous, instantaneous chemical reactions. Chem. Eng. Sci. 1989, 44, 1175–1182. [Google Scholar] [CrossRef]
- Makowski, Ł.; Orciuch, W.; Bałdyga, J. Large eddy simulations of mixing effects on the course of precipitation process. Chem. Eng. Sci. 2012, 77, 85–94. [Google Scholar] [CrossRef]
- Ranade, V.V. Computational Flow Modeling for Chemical Reactor Engineering; Academic Press: San Diego, CA, USA, 2002; ISBN 978-0-12-576960-0. [Google Scholar]
- Spalart, P.R. Strategies for turbulence modelling and simulations. Int. J. Heat Fluid Flow 2000, 21, 252–263. [Google Scholar] [CrossRef]
- Spalart, P.R. Philosophies and fallacies in turbulence modeling. Prog. Aerosp. Sci. 2015, 74, 1–15. [Google Scholar] [CrossRef]
- Spalart, P.R.; Jou, W.; Strelets, M.; Allmaras, S. Comments of feasibility of LES for wings, and on a hybrid RANS/LES approach. In Advances in DNS/LES; Greyden Press: Ruston, LA, USA, 1997; pp. 137–148. [Google Scholar]
- Michelassi, V.; Wissink, J.G.; Rodi, W. Direct numerical simulation, large eddy simulation and unsteady Reynolds-averaged Navier-Stokes simulations of periodic unsteady flow in a low-pressure turbine cascade: A comparison. Proc. Inst. Mech. Eng. Part J. Power Energy 2003, 217, 403–411. [Google Scholar] [CrossRef]
- Pitsch, H. Large-eddy simulation of turbulent combustion. Annu. Rev. Fluid Mech. 2006, 38, 453–482. [Google Scholar] [CrossRef]
- Sharan, N.; Matheou, G.; Dimotakis, P.E. Mixing, scalar boundedness, and numerical dissipation in large-eddy simulations. J. Comput. Phys. 2018, 369, 148–172. [Google Scholar] [CrossRef]
- Dumbser, M.; Zanotti, O.; Hidalgo, A.; Balsara, D.S. ADER-WENO finite volume schemes with space–time adaptive mesh refinement. J. Comput. Phys. 2013, 248, 257–286. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).