Solid Particle Erosion Behaviour and Protective Coatings for Gas Turbine Compressor Blades—A Review
Abstract
:1. Introduction
- (1)
- Mechanical degradation: the wearing of seals and bearings, coupling problems with high levels of noise and vibration, or difficulties with the lubrication system. It is crucial to realize that on many occasions high levels of vibration will be a sign of an underlying problem, which could be aerodynamic in nature and impinge on performance; and
- (2)
- Performance degradation: this is seen in the form of component and/or performance deterioration which can be remedied by actions taken while the GTE is operating, such as compressor fouling (recoverable deterioration), by overhaul at shutdown such as surface erosion (unrecoverable deterioration), and/or cannot be fully removed and residual deterioration will remain even after major overhauls such as airfoil platform distortion (permanent deterioration).
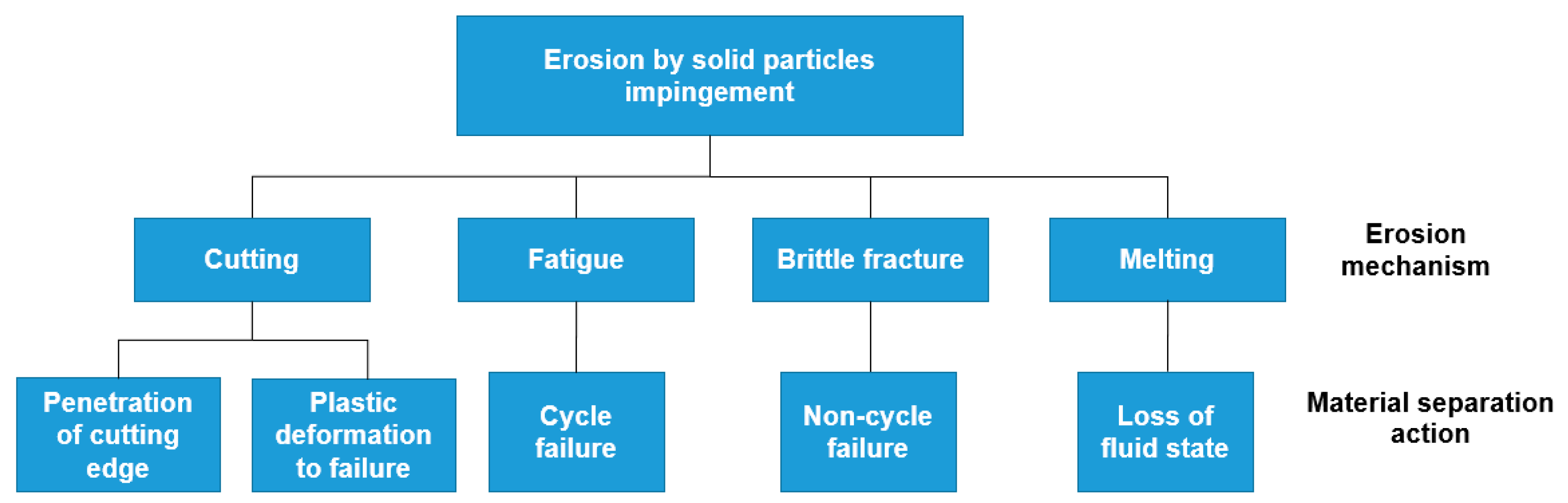
2. Solid Particle Erosion Mechanism
- (1)
- Two-thirds of the rotor blades are impacted at the leading edge, while the other one-third are hit at the trailing edge.
- (2)
- Two-thirds of the stator blades are hit at the trailing edge, while the other one-third are hit at the leading edge.
- (3)
- Cracks are equally distributed over blade height.
- (4)
- Thickening of the well-rounded leading edge and the decreased chord length caused the flow to reduce along with the isentropic compressor efficiency by 1.2% and 0.8%, respectively.
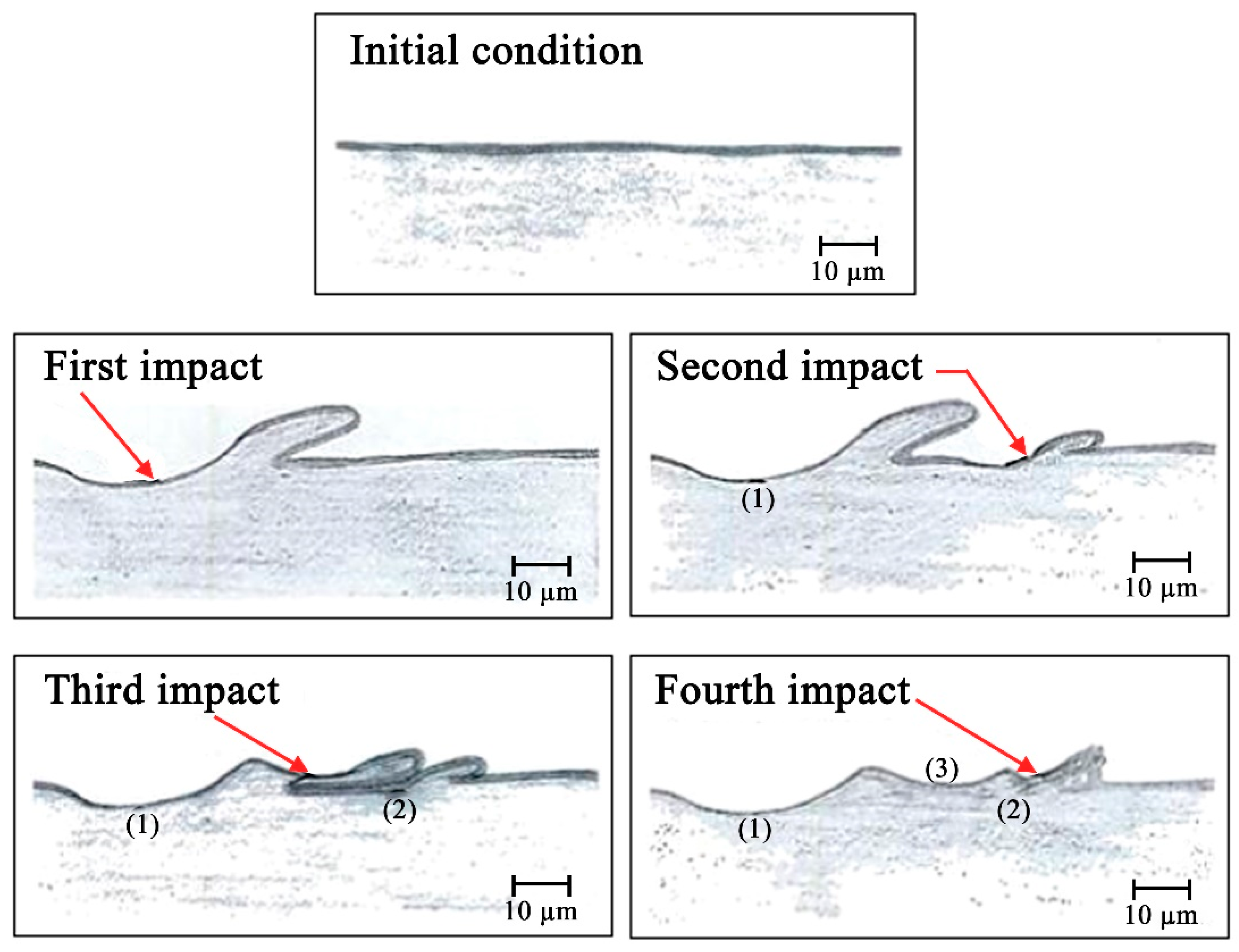
2.1. Ductile Solid Particles Erosion (SPE) Mechanism
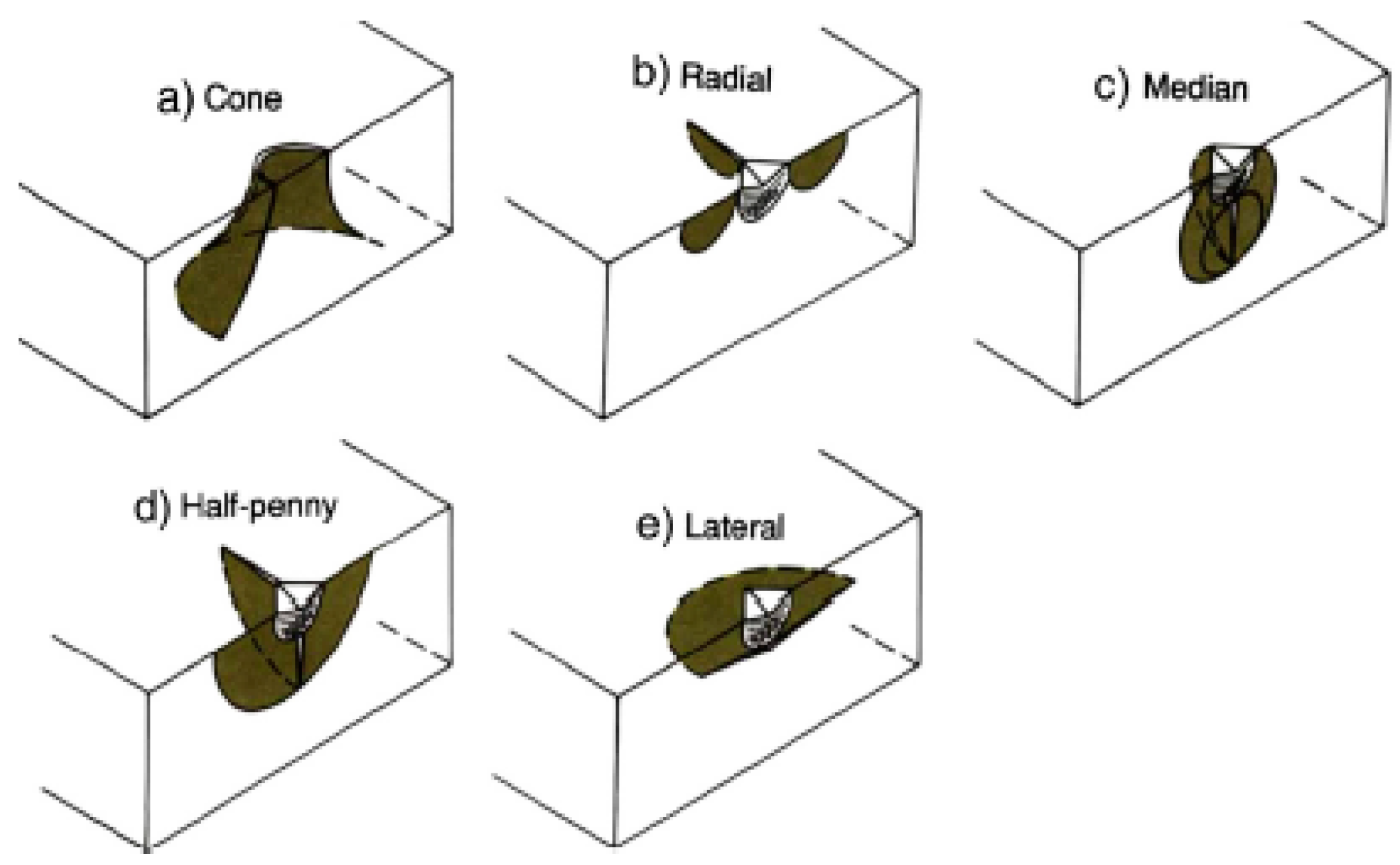
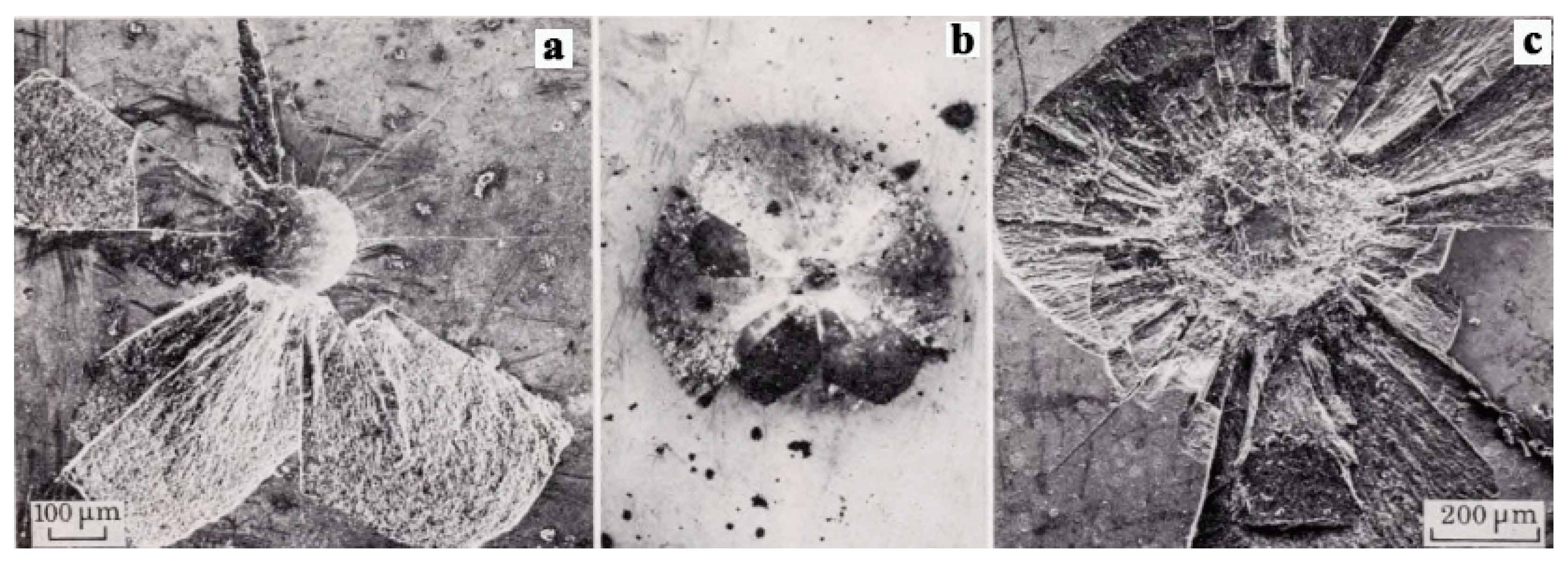
2.2. Brittle SPE Mechanism
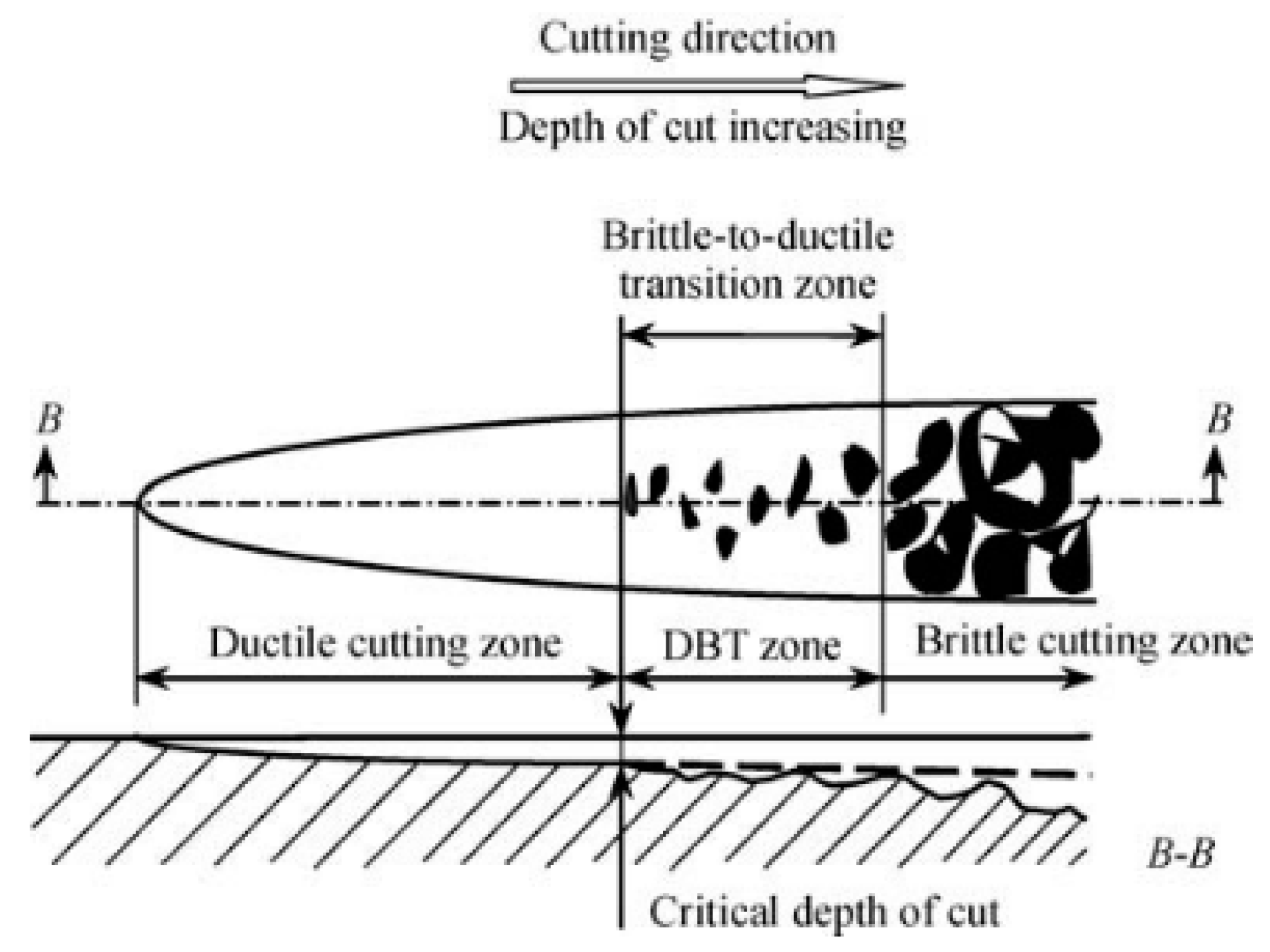
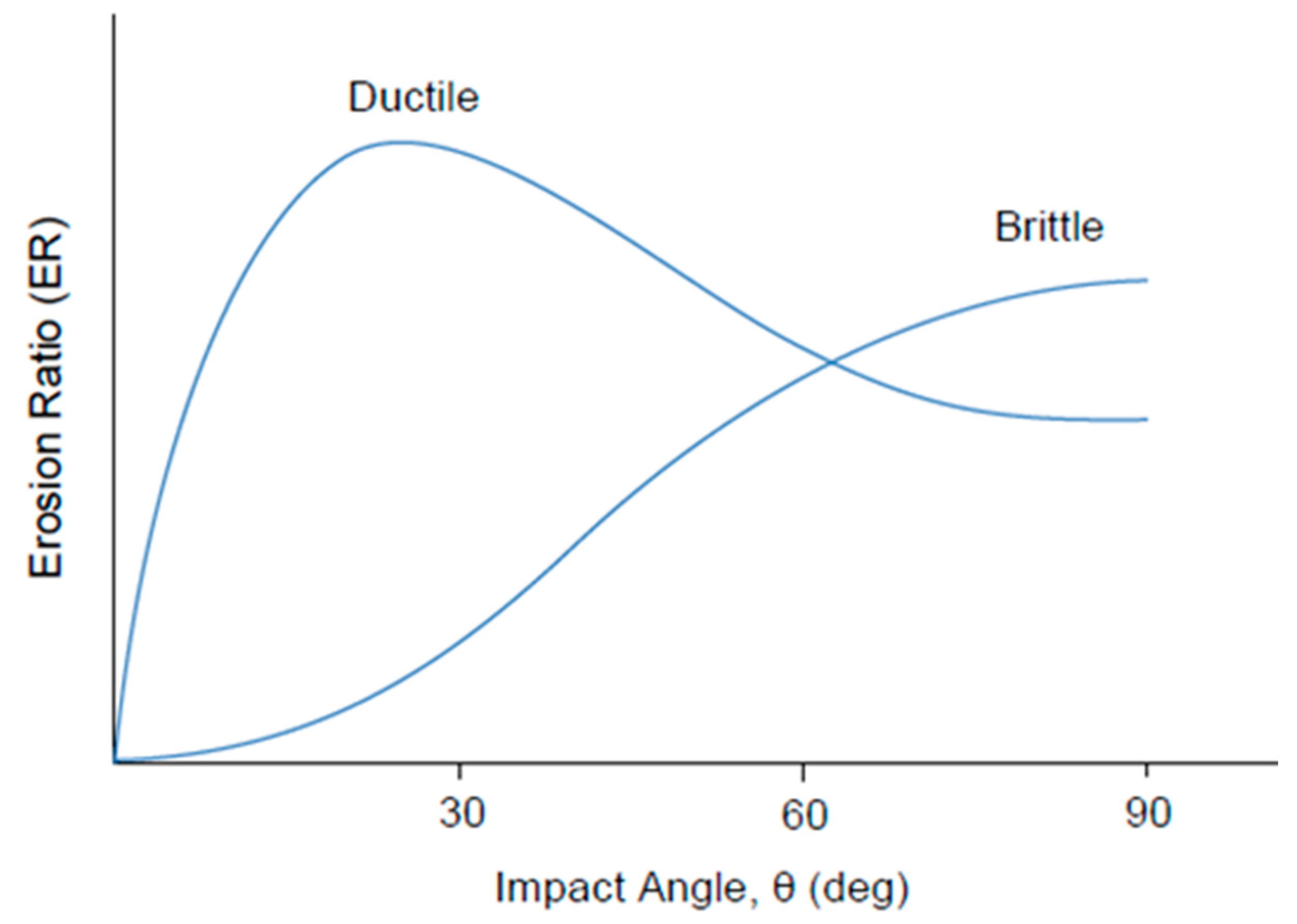
2.3. Ductile-Brittle Transition Mechanism
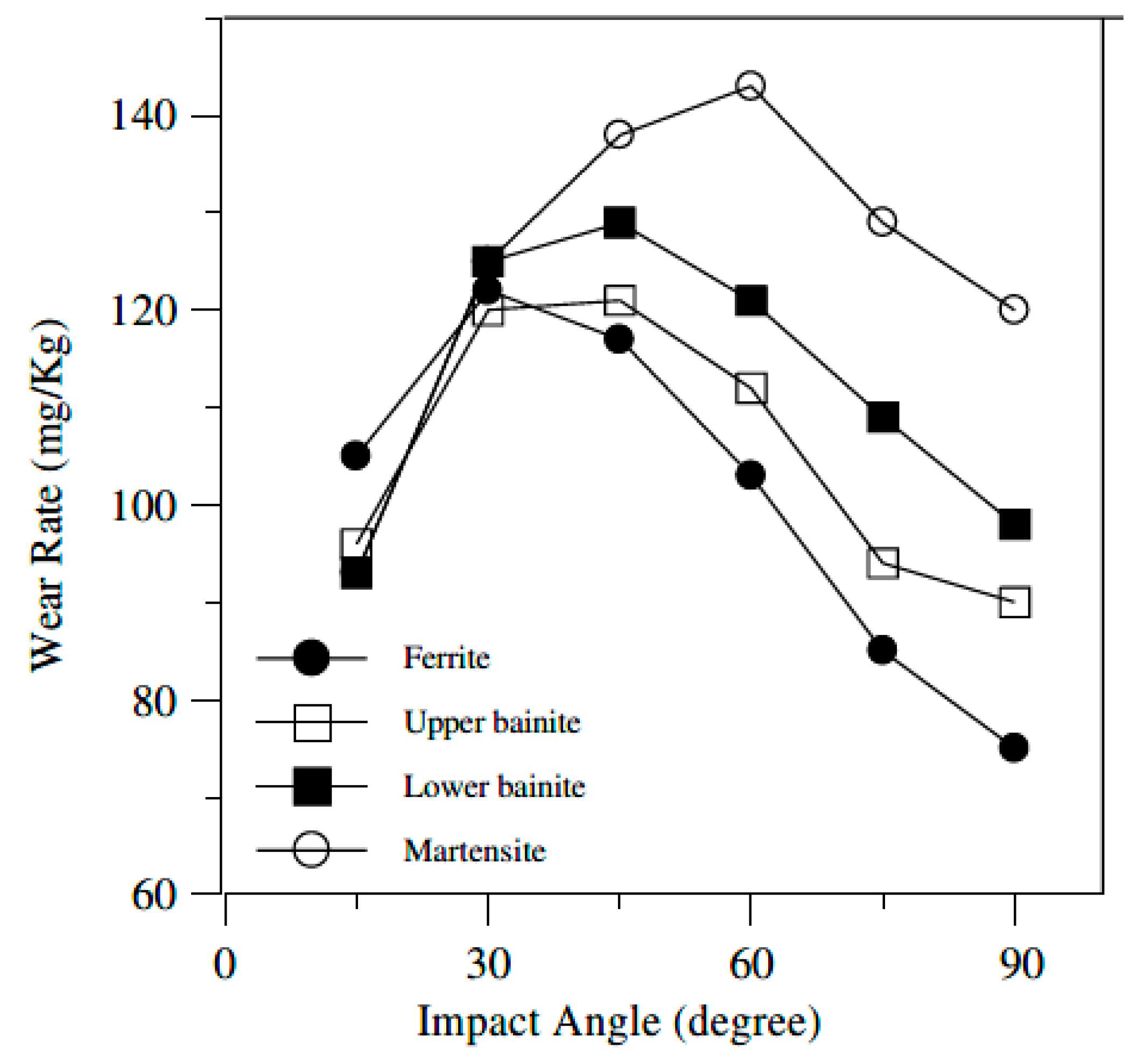
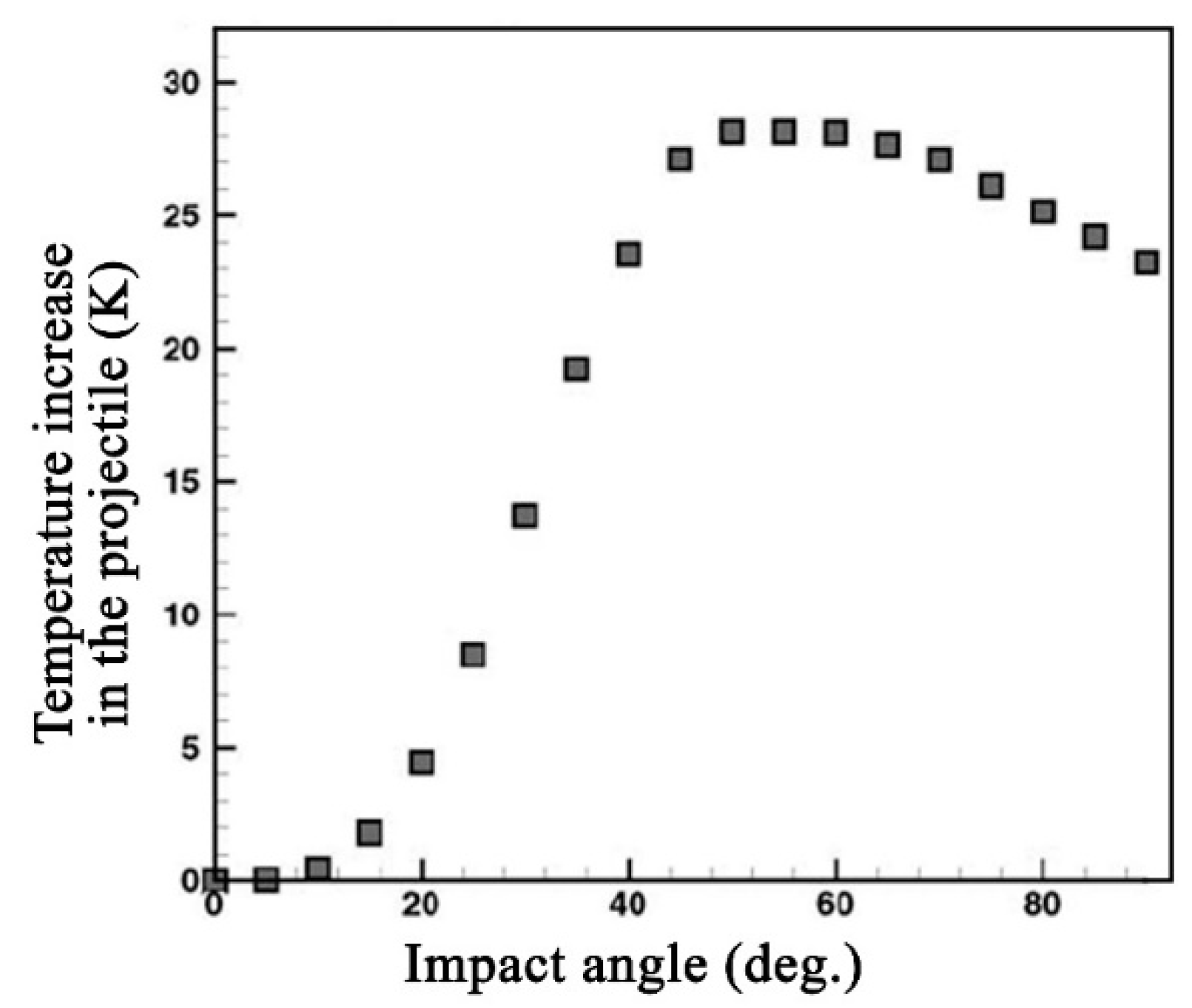
- For brittle materials, e.g., ceramics, the maximum rate of erosion rate typically takes place at an incidence angle of 90°;
- For ductile materials, e.g., metals, the maximum rate of erosion typically takes place at angles of impact between 20° and 30°.
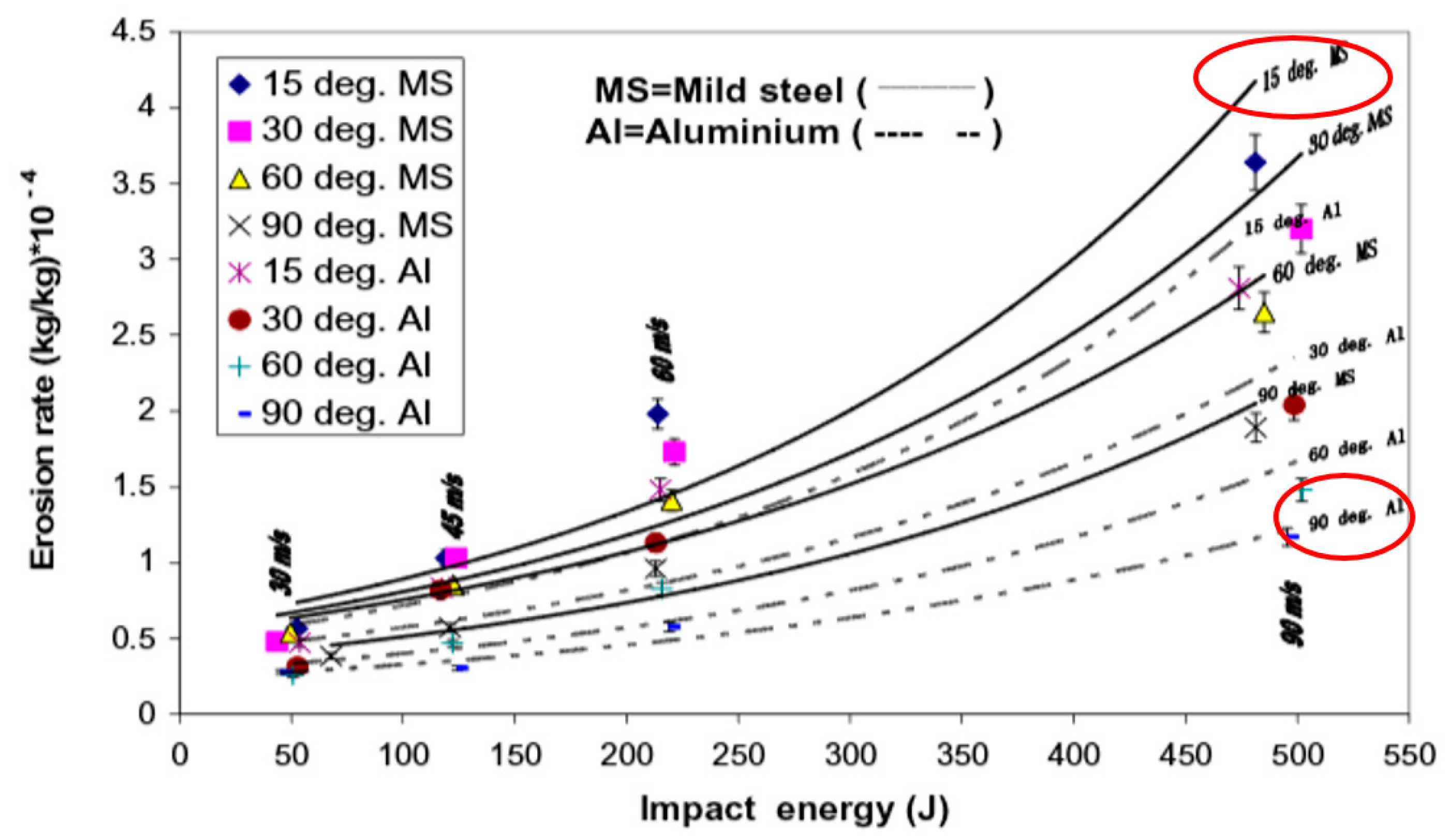
3. SPE Effective Parameters
4. Solid Particle Erosion Modelling
- Spool speed = 9170 rpm;
- Pressure ratio = 1.252;
- Mass flow = 9.475 kg/s;
- Blade tip speed = 243.9 m/s;
5. SPE Protection Coatings
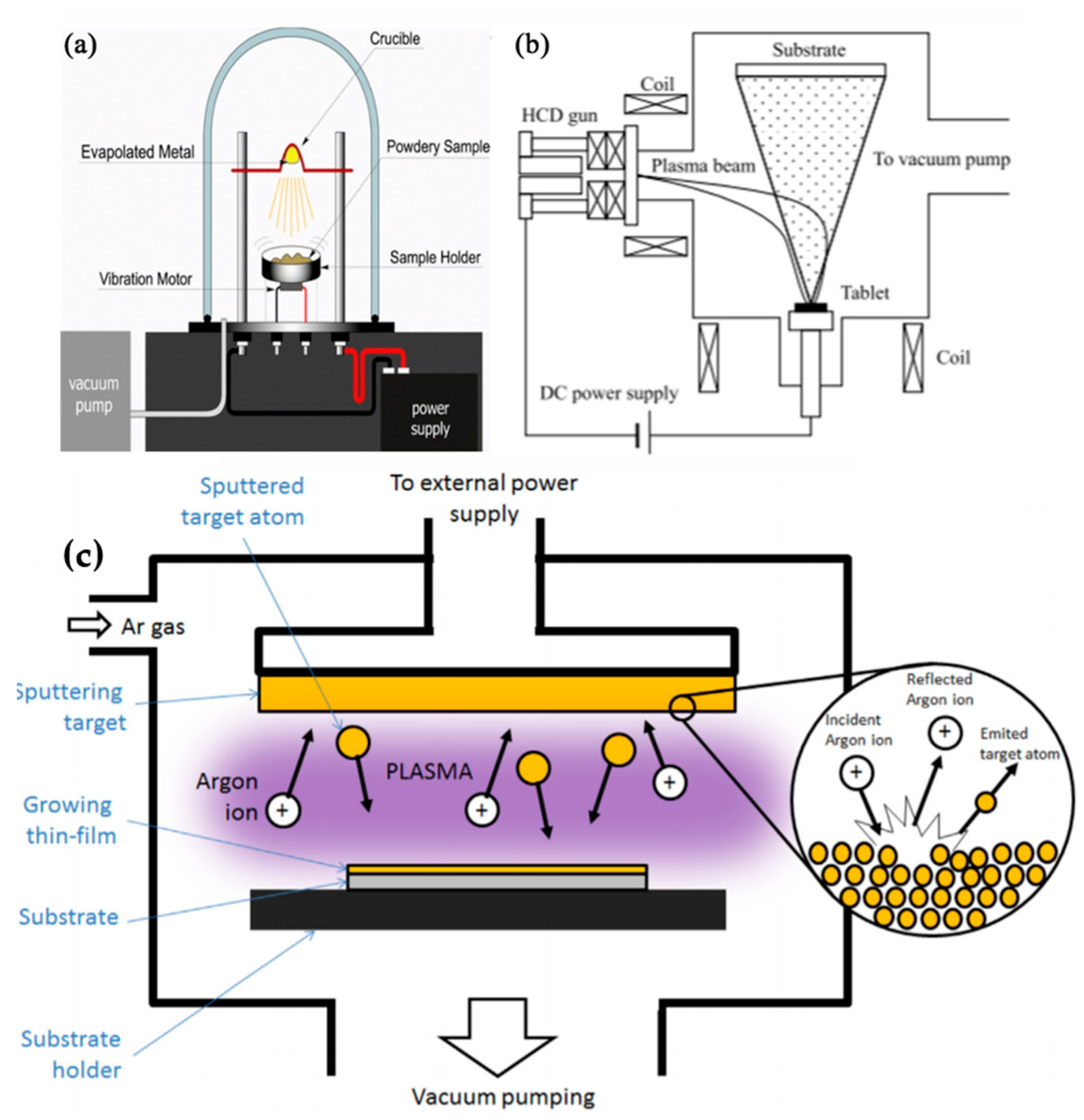
- Vapour phase: including physical and chemical vapour deposition (PVD and CVD) methods. With PVD, the material to be used for the coating is evaporated from a source (either solid or liquid) with an atomic composition that travels and condenses on the substrate exposed surface under vacuum or gaseous environments. However, the CVD is a combination process where the chemical component is introduced in the vapour phase on a heated surface to form a layer of solid deposit.
- Liquid phase or direct liquid coating technique: this approach contains any process of precursor-containing liquid deposition on an underlying layer or surface, after which there as a suitable thermal or/and chemical treatment to produce the required film layer.
- Solid phase: this process consists of solid-state deposition and unification of high-speed particles of powder entrained in a gas jet onto the substrate surface. These particles of powder experience a plastic deformation when they impact the surface and in this way adheres to the surface while simultaneously undergoing inter-particle bonding.
6. Discussion and Future Directions
- There is still a shortage in data on SPE for newly developed advanced composite materials, such as those containing graphene, carbon nanotubes, and other nano-reinforcements of carbon base.
- Simulation studies on SPE effects on composites are still not sufficient enough and need to be further explored for quantitative purposes.
- Development of new generation of thin layer coatings that are durable, of negligible weight effect, cost effective, and can easily be applied is of great importance and remains one of the main challenges to researchers.
- Producing thin films with multifunctional properties, such as anti-erosion, corrosion, de-icing, and abrasion, would be highly attractive to the GTE industry and many other sectors.
- Advancing the coatings fabrication techniques and/or standardizing existing methods in terms of deposition rate, temperature, and surrounding pressure conditions is of high importance.
- Investigating the long-life degradation of the deposited films also needs to be covered, as the majority of the available studies focuses on the short-term behaviour of the coating layer. Therefore, they do not provide the full image to the end-user.
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| A, B, C, D, , n2 | constants and exponents, which are affected by impact conditions |
| Cd | drag coefficient |
| shifting coefficient | |
| shifting exponent | |
| specific heat (J/kg °C) | |
| flow stress temperature constant | |
| Cr | heat capacity of the target (J/K) |
| blade chord (m) | |
| particles influence in an idealised manner | |
| C1 | constant |
| D | constant of material properties |
| particles density (kg/m3) | |
| material density (kg/m3) | |
| d | particle diameter (µm) |
| minimum particle diameter for erosion take place (µm) | |
| D1,2,3… | fracture constants |
| E | erosion rate (g/min) |
| young’s modulus of elasticity (N/m2) | |
| , | elastic modulus (Pa) |
| loss coefficient | |
| er | restitution coefficient |
| et | tangential restitution ratio |
| amount of solid particles cutting the target surface (particles concentration) (wt. %) | |
| threshold load for cracking (MPa (m) | |
| fragmentation for test condition | |
| Evc1,2 | volume of material removed by cutting mechanism (mm3/min) |
| Evp | volume of material removed by deformation mechanism (mm3/min) |
| F(t) | constant of several impacts |
| function of impingement angle | |
| exponents are prescribed functions of m, the flaw parameter of the Weibull fracture strength distribution | |
| G | target gram molecular weight (g/mol) |
| gp | particle gyration radius (µm) |
| Hp | hardness of particle (Pa) |
| material hardness (Pa) | |
| Hv | Vickers hardness of target (kg/mm2) |
| I | the moment of inertia of particle about its center of gravity |
| constant force component ratio of particle | |
| , | quality involving material constants |
| k | constant |
| Kc | fracture toughness (MPa M1/2) |
| km | material constant |
| equivalent sand grain roughness (µm) | |
| KT | impacting particle kinetic energy (J) |
| empirical constant | |
| velocity component normal to the surface below which no erosion takes place in certain hard materials (m/s) | |
| M | total mass of particle (Kg) |
| mass of particle (Kg) | |
| mass of an individual particle (Kg) | |
| constant of shape parameter in range of 9.5 to 12.7 | |
| n | test conditions functions values |
| normal component | |
| strain harding exponent | |
| P | pressure (Pa) |
| mean stress (Pa) | |
| R | particle roundness (µm) |
| r | particle radius (µm) |
| material volume (m3) | |
| collision velocity that reaches the material to the elastic limit (m/s) | |
| Vol | material loss volume per impacting particles mass (mg/g) |
| Vr | residual component of particle velocity (m/s) |
| Vref | standard test velocity of particle (m/s) |
| threshold velocity (m/s) | |
| rebound velocity (m/s) | |
| , | Poisson’s ratios |
| melting temperature (°C) | |
| dimensionless temperature | |
| impact velocity (m/s) | |
| plastic deformation wear rate (mm3/Nm) | |
| X | factor of cutting |
| particles horizontal velocity (m/s) | |
| Greek letters | |
| α | impact angle (deg) |
| α0 | impact angle at which the horizontal velocity component has just become zero when the particle leaves the body (deg) |
| σ | stress applied (Pa) |
| scale parameter in range of 930 to 1230 | |
| blade solidity | |
| location parameter | |
| limit of elastic load (Pa) | |
| pressure-stress ratio | |
| blade mean angle (deg) | |
| blade angle (deg) | |
| deformation factor (gf cm/c) | |
| , | velocity of maximum erosion amounts (m/s) |
| dimensionless strain rate | |
| α/εc2 | constant term = 0.7 |
| depth of contact to cut ratio | |
| friction coefficient | |
| maximum value of |
References
- Goldberg, C.; Nalianda, D.; Sethi, V.; Pilidis, P.; Singh, R.; Kyprianidis, K. Assessment of an energy-efficient aircraft concept from a techno-economic perspective. Appl. Energy 2018, 221, 229–238. [Google Scholar] [CrossRef] [Green Version]
- Ahmadi, M.H.; Nazari, M.A.; Ghasempour, R.; Pourfayaz, F.; Rahimzadeh, M.; Ming, T. A review on solar-assisted gas turbines. Energy Sci. Eng. 2018, 6, 658–674. [Google Scholar] [CrossRef]
- Bazmi, A.A.; Zahedi, G. Sustainable energy systems: Role of optimization modeling techniques in power generation and supply—A review. Renew. Sustain. Energy Rev. 2011, 15, 3480–3500. [Google Scholar] [CrossRef]
- Iakimkin, V.; Kirillov, S.; Kirillov, A.; Pecht, M. Basic Principles, Models and Algorithms for Creation of Self-Maintenance and Self-Recovery Systems for Engines, Gas Turbines and Mechanics. In Proceedings of the 2018 Prognostics and System Health Management Conference (PHM-Chongqing), Chongqing, China, 26–28 October 2018; pp. 270–275. [Google Scholar]
- Steere, R.E.; Koepnick, E.G.; Dean, R.A. Progress On The Us Air Force Approach For The Practical Management Of Engine Life Cycle Costs. AGARD Lect. Ser. 2017, 4, 1–4. [Google Scholar]
- Wollmershauser, C. American Airlines Engine Management Program; Shell Aviat News: Hague, The Netherlands, 2017; pp. 6–11. [Google Scholar]
- Wróbel, M.; Richter, M.; Zimmermann, R.; Kiewel, H.; Ullrich, A. Rotor Lifecycle Management Program. In Proceedings of the ASME Turbo Expo, Dusseldorf, Germany, 16 June 2014. [Google Scholar] [CrossRef]
- Zachos, P.; Pilidis, P.; Kalfas, A. Analysis of turbine performance degradation effects due to geometry variations between actual components and design Intent. Aeronaut. J. 2010, 114, 569–578. [Google Scholar] [CrossRef]
- DiMarco, P.C. Navy Foreign Object Damage and Its Impact on Future Gas Turbine Engine Low Pressure Compression Systems. In Agard Conference Proceedings Agard Cp; AGARD: Rotterdam, The Netherlands, 1994; p. 6. [Google Scholar]
- Isaiah, T.-G.; Dabbashi, S.; Bosak, D.; Sampath, S.; Di Lorenzo, G.; Pilidis, P. Life Analysis of Industrial Gas Turbines Used As a Back-Up to Renewable Energy Sources. Procedia CIRP 2015, 38, 239–244. [Google Scholar] [CrossRef] [Green Version]
- Hamed, A.; Tabakoff, W.C.; Wenglarz, R. Erosion and Deposition in Turbomachinery. J. Propuls. Power 2006, 22, 350–360. [Google Scholar] [CrossRef] [Green Version]
- Saravanamutto, H. Erosion, Corrosion and Foreign Object Damage in Gas Turbines. Technical Evaluator’s Report. In AGARD-CP-558; North Atlantic Treaty Organization: Rotterdam, The Netherlands, 1994; p. P.T.1. [Google Scholar]
- Akca, E.; Gürsel, A. A Review on Superalloys and IN718 Nickel-Based INCONEL Superalloy. Period. Eng. Natl. Sci. (PEN) 2015, 3, 15–27. [Google Scholar] [CrossRef]
- Klocke, F.; Zeis, M.; Klink, A.; Veselovac, D. Experimental Research on the Electrochemical Machining of Modern Titanium- and Nickel-based Alloys for Aero Engine Components. Procedia CIRP 2013, 6, 368–372. [Google Scholar] [CrossRef] [Green Version]
- Salehnasab, B.; Zateajam, H.; Mousavi, S. Failure Analysis of a C450 Stainless Steel Blade in: A Compressor. Indian J. Sci. Res. Spl. 2014, 2, 143–150. [Google Scholar]
- Jahangiri, M.R.; Fallah, A.A.; Ghiasipour, A. Cement kiln dust induced corrosion fatigue damage of gas turbine compressor blades—A failure analysis. Mater. Des. 2014, 62, 288–295. [Google Scholar] [CrossRef]
- Brun, K.; Kurz, R.; Simmons, H.R. Aerodynamic Instability and Life-Limiting Effects of Inlet and Interstage Water Injection Into Gas Turbines. J. Eng. Gas Turbines Power 2004, 128, 617–625. [Google Scholar] [CrossRef]
- Kurz, R.; Brun, K. Gas Turbine Tutorial-Maintenance and Operating Practices Effects on Degradation and Life. In Proceedings of the 36th Turbomachinery Symposium; Texas A&M University: College Station, TX, USA, 2007. [Google Scholar]
- Kurz, R.; Meher-Homji, C.; Brun, K.; Moore, J.J.; Gonzalez, F. Gas turbine performance and maintenance. In Proceedings of the 42nd Turbomachinery Symposium; Texas A&M University: College Station, TX, USA, 2013. [Google Scholar]
- Li, Y.G. Performance-analysis-based gas turbine diagnostics: A review. Proc. Inst. Mech. Eng. Part A: J. Power Energy 2002, 216, 363–377. [Google Scholar] [CrossRef] [Green Version]
- Meher-Homji, C.B.; Bromley, A. Gas Turbine Axial Compressor Fouling and Washing. In Proceedings of the 33rd Turbomachinery Symposium; Texas A&M University: College Station, TX, USA, 2004. [Google Scholar]
- Hanachi, H.; Liu, J.; Banerjee, A.; Chen, Y.; Koul, A. A Physics-Based Modeling Approach for Performance Monitoring in Gas Turbine Engines. IEEE Trans. Reliab. 2014, 64, 197–205. [Google Scholar] [CrossRef]
- Kurz, R.; Brun, K. Degradation in Gas Turbine Systems. J. Eng. Gas Turbines Power 2000, 123, 70–77. [Google Scholar] [CrossRef] [Green Version]
- Kurz, R.; Brun, K. Degradation of gas turbine performance in natural gas service. J. Nat. Gas Sci. Eng. 2009, 1, 95–102. [Google Scholar] [CrossRef]
- Meher-Homji, C.B.; Chaker, M.A.; Motiwala, H.M. Gas Turbine Performance Deterioration. In Proceedings of the 30th Turbomachinery Symposium; Texas A&M University: College Station, TX, USA, 2001. [Google Scholar]
- Kassaee, M.; Zandi, H.; Akbari, J.; Motamedi, E. An efficient and mild carboxylation of multiwall carbon nanotubes using H2O2 in the presence of heteropolyacid. Chin. Chem. Lett. 2012, 23, 470–473. [Google Scholar]
- Urban, L.A. Parameter Selection for Multiple Fault Diagnostics of Gas Turbine Engines. J. Eng. Power 1975, 97, 225–230. [Google Scholar] [CrossRef]
- Reynolds, O. XLII. On the action of a blast of sand in cutting hard material. Philos. Mag. (Fourth Ser.) 1873, 46, 337–343. [Google Scholar] [CrossRef]
- Bahramnia, H.; Semnani, H.M.; Habibolahzadeh, A.; Abdoos, H. Epoxy/polyurethane nanocomposite coatings for anti-erosion/wear applications: A review. J. Compos. Mater. 2020, 0021998320908299. [Google Scholar] [CrossRef]
- Bai, X.; Yao, Y.; Han, Z.; Zhang, J.; Zhang, S. Study of Solid Particle Erosion on Helicopter Rotor Blades Surfaces. Appl. Sci. 2020, 10, 977. [Google Scholar] [CrossRef] [Green Version]
- Finnie, I. Erosion of surfaces by solid particles. Wear 1960, 3, 87–103. [Google Scholar] [CrossRef]
- Bousser, E.; Martinu, L.; Klemberg-Sapieha, J. Solid particle erosion mechanisms of protective coatings for aerospace applications. Surf. Coat. Technol. 2014, 257, 165–181. [Google Scholar] [CrossRef] [Green Version]
- Swaminathan, V.P.; Wei, R.; Gandy, D.W. Nanotechnology Coatings for Erosion Protection of Turbine Components. J. Eng. Gas Turbines Power 2010, 132, 082104. [Google Scholar] [CrossRef]
- Shukla, K.; Rane, R.; Alphonsa, J.; Maity, P.; Mukherjee, S. Structural, mechanical and corrosion resistance properties of Ti/TiN bilayers deposited by magnetron sputtering on AISI 316L. Surf. Coat. Technol. 2017, 324, 167–174. [Google Scholar] [CrossRef]
- Lin, J.; Wei, R.; Ge, F.; Li, Y.G.; Zhang, X.; Huang, F.; Lei, M. TiSiCN and TiAlVSiCN nanocomposite coatings deposited from Ti and Ti-6Al-4V targets. Surf. Coat. Technol. 2018, 336, 106–116. [Google Scholar] [CrossRef]
- Barshilia, H.C.; Prakash, M.S.; Poojari, A.; Rajam, K. Corrosion behavior of nanolayered TiN/NbN multilayer coatings prepared by reactive direct current magnetron sputtering process. Thin Solid Films 2004, 460, 133–142. [Google Scholar] [CrossRef]
- Scopus-Database. Analysis of Scopus Search Result for the Words “Solid particle Erosion”, “Coatings”, and “Gas Urbine” from 1984 to 2019; in Elsevier. 2020. Available online: www.scopus.com (accessed on 12 April 2020).
- Chahar, B.S.; Siddhartha, A.K.P. Erosion Wear of Ductile Materials: A Review. In Proceedings of the International Conference on Advancements and Recent Innovations in Mechanical, Production and Industrial Engineering (ARIMPIE—2016), ELK Asia Pacific Journal, Gaziabad, India, 15–16 April 2016; pp. 17–22. [Google Scholar]
- Budinski, K.G. Guide to Friction, Wear and Erosion Testing; ASTM International West: Conshohocken, MA, USA, 2007. [Google Scholar]
- Zdravecká, E.; Slota, J.; Tkáčová, J. Erosive failure of steel pipeline by solid pulverized particles. Eng. Fail. Anal. 2014, 46, 18–25. [Google Scholar] [CrossRef]
- Meng, H.; Ludema, K. Wear models and predictive equations: Their form and content. Wear 1995, 181, 443–457. [Google Scholar] [CrossRef]
- Brun, K.; Nored, M.; Kurz, R. Analysis of solid particle surface impact behavior in turbomachines to assess blade erosion and fouling. In Proceedings of the Forty-First Turbomachinery Symposium, Houston, TX, USA, 24–27 September 2012. [Google Scholar]
- Schmücker, J.; Schäffler, A. Performance deterioration of axial compressors due to blade defects. In AGARD Conference Proceedings Agard CP; AGARD: Rotterdam, The Netherlands, 1994; p. 16. [Google Scholar]
- Levin, B.F.; Vecchio, K.S.; Dupont, J.N.; Marder, A.R. Modeling solid-particle erosion of ductile alloys. Met. Mater. Trans. A 1999, 30, 1763–1774. [Google Scholar] [CrossRef]
- Balan, C.; Tabakoff, W. Axial flow compressor performance deterioration. In Proceedings of the 20th Joint Propulsion Conference, Cincinnati, OH, USA, 11–13 June 1984; p. 1208. [Google Scholar]
- Balan, C.; Tabakoff, W. A Method of Predicting the Performance Deterioration of a Compressorcascade due to Sand Erosion. In Proceedings of the Aerospace Sciences Meeting, Reno, NV, USA, 10–13 January 1983; p. 178. [Google Scholar] [CrossRef]
- Hamed, A.; Tabakoff, W.; Singh, D. Modeling of Compressor Performance Deterioration Due to Erosion. Int. J. Rotating Mach. 1998, 4, 243–248. [Google Scholar] [CrossRef] [Green Version]
- Kurz, R.; Brun, K. Gas turbine performance-what makes the map? Comp. Sci. 2000, 15, 247–262. [Google Scholar]
- Hartmann, M.J. Advanced technologies for turbomachinery systems: An overview. In NASA Technical Memorandum Langley Research Center; NASA: Washington, DC, USA, 1982; Volume VI, pp. 1–80. [Google Scholar]
- Hamed, A.; Tabakoff, W. Experimental and numerical simulations of the effects of ingested particles in gas turbine engines. In AGARD Conference Proceedings AGARD CP; AGARD: Rotterdam, The Netherlands, 1994; p. 11. [Google Scholar]
- Schrade, M.; Staudacher, S. High-speed Test Rig for the Investigation of Erosion Damage of Axial Compressor Blades; Deutsche Gesellschaft für Luft-und Raumfahrt-Lilienthal-Oberth eV: Bonn, Germany, 2014. [Google Scholar]
- Lombardo, G.; Torella, G. An airborne monitoring system for FOD and erosion faults. In AGARD Conference Proceedings AGARD CP; AGARD: Rotterdam, The Netherlands, 1994; pp. 1901–1911. [Google Scholar]
- Antwi, E.K.; Liu, K.; Wang, H. A review on ductile mode cutting of brittle materials. Front. Mech. Eng. 2018, 13, 251–263. [Google Scholar] [CrossRef] [Green Version]
- Finnie, I. The Mechanism of Erosion of Ductile Metals. In Proceedings of the 3rd U.S. National Congress of Applied Mechanics, Brown University, Providence, RI, USA, 11–14 June 1958; American Society of Mechanical Engineers: New York, NY, USA, 1958; pp. 527–532. [Google Scholar]
- Biswas, S.; Cenna, A.; Williams, K.; Jones, M. Subsurface Behavior of Ductile Material by Particle Impacts and its Influence on Wear Mechanism. Procedia Eng. 2014, 90, 160–165. [Google Scholar] [CrossRef] [Green Version]
- Chang, L.; Hsui, I.; Chen, L.; Lui, T. A study on particle erosion behavior of ductile irons. Scr. Mater. 2005, 52, 609–613. [Google Scholar] [CrossRef]
- Levy, A.V. The Piatelet Mechanism of Erosion of Ductile Metals. Wear 1986, 108, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Hutchings, I.M.; Levy, A.V. Thermal effects in the erosion of ductile metals. Wear 1989, 131, 105–121. [Google Scholar] [CrossRef]
- Winter, R.E.; Hutchings, I.M. The role of adiabatic shear in solid particle erosion. Wear 1975, 34, 141–148. [Google Scholar] [CrossRef]
- Molinari, J.-F.; Ortiz, M. A study of solid-particle erosion of metallic targets. Int. J. Impact Eng. 2002, 27, 347–358. [Google Scholar] [CrossRef]
- Finnie, I. Some observations on the erosion of ductile metals. Wear 1972, 19, 81–90. [Google Scholar] [CrossRef]
- Hutchings, I.M. Ductile-brittle transitions and wear maps for the erosion and abrasion of brittle materials. J. Phys. D: Appl. Phys. 1992, 25, A212–A221. [Google Scholar] [CrossRef]
- Hutchings, I. A model for the erosion of metals by spherical particles at normal incidence. Wear 1981, 70, 269–281. [Google Scholar] [CrossRef] [Green Version]
- Sundararajan, G.; Shewmon, P. A new model for the erosion of metals at normal incidence. Wear 1983, 84, 237–258. [Google Scholar] [CrossRef]
- Laguna-Camacho, J.R.; Vite-Torres, M.; Gallardo-Hernández, E.; Vera-Cárdenas, E. Solid particle erosion on different metallic materials. Tribol. Eng. 2013, 5, 63–78. [Google Scholar]
- Gat, N.; Tabakoff, W. Effects of temperature on the behavior of metals under erosion by particulate matter. J. Test. Eval. 1980, 8, 177–186. [Google Scholar]
- ElTobgy, M.; Ng, E.; Elbestawi, M. Finite element modeling of erosive wear. Int. J. Mach. Tools Manuf. 2005, 45, 1337–1346. [Google Scholar] [CrossRef]
- Wiederhorn, S.M.; Hockey, B.J. Effect of material parameters on the erosion resistance of brittle materials. J. Mater. Sci. 1983, 18, 766–780. [Google Scholar] [CrossRef]
- Preece, C.M. Treatise on Materials Science and Technology. C.M. Preece 1979, 16, 1–67. [Google Scholar]
- Aquaro, D.; Fontani, E. Erosion of Ductile and Brittle Materials. Meccanica 2001, 36, 651–661. [Google Scholar] [CrossRef]
- Evans, A.G.; Gulden, M.E.; Rosenblatt, M.; Dewhurst, P. Impact damage in brittle materials in the elastic-plastic response régime. Proc. R. Soc. London. Ser. A. Math. Phys. Sci. 1978, 361, 343–365. [Google Scholar] [CrossRef]
- Sheldon, G.L.; Finnie, I. On the Ductile Behavior of Nominally Brittle Materials During Erosive Cutting. J. Eng. Ind. 1966, 88, 387–392. [Google Scholar] [CrossRef]
- Amaral, P.; Fernandes, J.; Rosa, L.G. Weibull statistical analysis of granite bending strength. Rock Mech. Rock Eng. 2007, 41, 917–928. [Google Scholar] [CrossRef]
- Le, J.-L.; Bazant, Z.P.; Bazant, M.Z. Unified nano-mechanics based probabilistic theory of quasibrittle and brittle structures: I. Strength, static crack growth, lifetime and scaling. J. Mech. Phys. Solids 2011, 59, 1291–1321. [Google Scholar] [CrossRef]
- Vardar, Ö.; Finnie, I. An analysis of the Brazilian disk fracture test using the Weibull probabilistic treatment of brittle strength. Int. J. Fract. 1975, 11, 495–508. [Google Scholar]
- Rodriguez, E.; Flores, M.; Perez, A.; Mercado-Solis, R.D.; González, R.; Rodriguez, J.; Valtierra, S. Erosive wear by silica sand on AISI H13 and 4140 steels. Wear 2009, 267, 2109–2115. [Google Scholar] [CrossRef]
- Wensink, H.; Elwenspoek, M.C. A closer look at the ductile–brittle transition in solid particle erosion. Wear 2002, 253, 1035–1043. [Google Scholar] [CrossRef]
- Liu, K.; Li, X.P.; Rahman, M.; Liu, X.D. A study of the cutting modes in the grooving of tungsten carbide. Int. J. Adv. Manuf. Technol. 2004, 24, 321–326. [Google Scholar] [CrossRef]
- Finnie, I. Some reflections on the past and future of erosion. Wear 1995, 186, 1–10. [Google Scholar] [CrossRef]
- Grant, G.; Tabakoff, W. Erosion Prediction in Turbomachinery Resulting from Environmental Solid Particles. J. Aircr. 1975, 12, 471–478. [Google Scholar] [CrossRef]
- Swain, M. Microfracture about scratches in brittle solids. Proc. R. Soc. London Ser. A Math. Phys. Sci. 1979, 366, 575–597. [Google Scholar] [CrossRef]
- Singh, R.; Tiwari, S.K.; Mishra, S.K. Cavitation Erosion in Hydraulic Turbine Components and Mitigation by Coatings: Current Status and Future Needs. J. Mater. Eng. Perform. 2011, 21, 1539–1551. [Google Scholar] [CrossRef]
- Chen, D.; Sarumi, M.; Al-Hassani, S.; Gan, S.; Yin, Z. A model for erosion at normal impact. Wear 1997, 205, 32–39. [Google Scholar] [CrossRef]
- Huang, C.; Chiovelli, S.; Minev, P.; Luo, J.; Nandakumar, K. A comprehensive phenomenological model for erosion of materials in jet flow. Powder Technol. 2008, 187, 273–279. [Google Scholar] [CrossRef]
- Walker, C.; Robbie, P. Comparison of some laboratory wear tests and field wear in slurry pumps. Wear 2013, 302, 1026–1034. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, S.; Mohapatra, S.K. Tribological analysis of WC–10Co–4Cr and Ni–20Cr2O3 coating on stainless steel 304. Wear 2017, 376, 1105–1111. [Google Scholar] [CrossRef]
- Neilson, J.; Gilchrist, A. Erosion by a stream of solid particles. Wear 1968, 11, 111–122. [Google Scholar] [CrossRef]
- Desale, G.R.; Gandhi, B.K.; Jain, S. Slurry erosion of ductile materials under normal impact condition. Wear 2008, 264, 322–330. [Google Scholar] [CrossRef]
- Clark, H.; Llewellyn, R. Assessment of the erosion resistance of steels used for slurry handling and transport in mineral processing applications. Wear 2001, 250, 32–44. [Google Scholar] [CrossRef]
- Arabnejad, H.; Mansouri, A.; Shirazi, S.A.; McLaury, B.S. Development of mechanistic erosion equation for solid particles. Wear 2015, 390, 1044–1050. [Google Scholar] [CrossRef]
- Vite-Torres, M.; Laguna-Camacho, J.; Baldenebro-Castillo, R.; Gallardo-Hernández, E.; Vera-Cardenas, E.J. Study of solid particle erosion on AISI 420 stainless steel using angular silicon carbide and steel round grit particles. Wear 2013, 301, 383–389. [Google Scholar] [CrossRef]
- Feng, Z.; Ball, A. The erosion of four materials using seven erodents—Towards an understanding. Wear 1999, 20, 674–684. [Google Scholar] [CrossRef]
- Chen, Q.; Li, D. Computer simulation of solid particle erosion. Wear 2003, 254, 203–210. [Google Scholar] [CrossRef]
- Winter, R.; Hutchings, I. Solid particle erosion studies using single angular particles. Wear 1974, 29, 181–194. [Google Scholar] [CrossRef]
- Levy, A.V.; Chik, P. The effects of erodent composition and shape on the erosion of steel. Wear 1983, 89, 151–162. [Google Scholar] [CrossRef] [Green Version]
- Hamed, A.; Fowler, S. Erosion Pattern of Twisted Blades by Particle Laden Flows. J. Eng. Power 1983, 105, 839–843. [Google Scholar] [CrossRef]
- Jianren, F.; Dadong, Z.; Jun, J.; Kefa, C. Numerical simulation of tube erosion by particle impaction. Wear 1991, 142, 171–184. [Google Scholar] [CrossRef]
- Ghenaiet, A. Prediction of Erosion Induced by Solid Particles in a Water Turbine. In Proceedings of the 11th European Conference on Turbomachinery Fluid dynamics & Thermodynamics, Madrid, Spain, 23–27 March 2015. [Google Scholar]
- Zheng, Z.; Zheng, Y.; Zhou, X.; He, S.; Sun, W.; Wang, J. Determination of the critical flow velocities for erosion–corrosion of passive materials under impingement by NaCl solution containing sand. Corros. Sci. 2014, 88, 187–196. [Google Scholar] [CrossRef]
- Mbabazi, J.; Sheer, T.; Shandu, R. A model to predict erosion on mild steel surfaces impacted by boiler fly ash particles. Wear 2004, 257, 612–624. [Google Scholar] [CrossRef]
- Lindsley, B.; Marder, A. The effect of velocity on the solid particle erosion rate of alloys. Wear 1999, 225, 510–516. [Google Scholar] [CrossRef]
- Bitter, J. A study of erosion phenomena part I. Wear 1963, 6, 5–21. [Google Scholar] [CrossRef]
- Oka, Y.; Ohnogi, H.; Hosokawa, T.; Matsumura, M. The impact angle dependence of erosion damage caused by solid particle impact. Wear 1997, 203, 573–579. [Google Scholar] [CrossRef]
- Tabakoff, W. Causes for Turbomachinery Performance Deterioration. In Proceedings of the ASME Gas Turbine and Aeroengine Congress; ASME, Citeseer: Amsterdam, The Netherlands, 1988. [Google Scholar] [CrossRef]
- Mansouri, A.; Khanouki, H.A.; Shirazi, S.; McLaury, B. A combined CFD/experimental methodology for erosion prediction. Wear 2015, 332-333, 1090–1097. [Google Scholar] [CrossRef]
- Bitter, J. A study of erosion phenomena. Wear 1963, 6, 169–190. [Google Scholar] [CrossRef]
- Sheldon, G.; Kanhere, A. An investigation of impingement erosion using single particles. Wear 1972, 21, 195–209. [Google Scholar] [CrossRef]
- Tilly, G. A two stage mechanism of ductile erosion. Wear 1973, 23, 87–96. [Google Scholar] [CrossRef]
- Jennings, W.; Head, W.; Manning, C. A mechanistic model for the prediction of ductile erosion. Wear 1976, 40, 93–112. [Google Scholar] [CrossRef]
- Hutchings, I.M.; Winter, R.E.; Field, J.E. Solid particle erosion of metals: The removal of surface material by spherical projectiles. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1976, 348, 379–392. [Google Scholar] [CrossRef]
- Tabakoff, W.; Kotwal, R.; Hamed, A. Erosion study of different materials affected by coal ash particles. Wear 1979, 52, 161–173. [Google Scholar] [CrossRef]
- Sundararajan, G. A comprehensive model for the solid particle erosion of ductile materials. Wear 1991, 149, 111–127. [Google Scholar] [CrossRef]
- Nsoesie, S.; Liu, R.; Chen, K.; Yao, M. Analytical modeling of solid-particle erosion of Stellite alloys in combination with experimental investigation. Wear 2014, 309, 226–232. [Google Scholar] [CrossRef]
- Parsi, M.; Najmi, K.; Najafifard, F.; Hassani, S.; McLaury, B.S.; Shirazi, S.A. A comprehensive review of solid particle erosion modeling for oil and gas wells and pipelines applications. J. Nat. Gas Sci. Eng. 2014, 21, 850–873. [Google Scholar] [CrossRef]
- Sobota, J.; Sorensen, G.; Jensen, H.; Bochnicek, Z.; Holý, V. CN/MeN nanocomposite coatings, deposition and testing of performance. Surf. Coat. Technol. 2001, 142, 590–595. [Google Scholar] [CrossRef]
- Chin, K.; Gohel, A.; Elim, H.I.; Ji, W.; Chong, G.; Lim, K.; Sow, C.; Wee, A. Optical limiting properties of amorphous SixNy and SiC coated carbon nanotubes. Chem. Phys. Lett. 2004, 383, 72–75. [Google Scholar] [CrossRef]
- Brogren, M.; Harding, G.L.; Karmhag, R.; Ribbing, C.G.; Niklasson, G.A.; Stenmark, L. Titanium–aluminum–nitride coatings for satellite temperature control. Thin Solid Films 2000, 370, 268–277. [Google Scholar] [CrossRef]
- Holleck, H. Design of nanostructured thin films for tribological applications. In TMS Conference Proceedings on Surface Engineering: Science and Technology I; Kumar, A., Chung, Y.W., Moore, J.E., Smugeresky, J.E., Eds.; Minerals, Metals, and Materials Society: Warrendale, PA, USA, 1999. [Google Scholar]
- Nicholls, J.; Lawson, K.; Rickerby, D.; Morrel, P. Advanced Processing of TBC’s for Reduced Thermal Conductivity; Rolls-Royce plc: Aslborg, Denmark, 1998. [Google Scholar]
- Ali, N.; Sebzali, M.; Bourisli, H.; Safar, A.; Ebrahem, Z.A. Nanocoating: An Energy Efficient Solution Towards Reducing Buildings Electrical Consumption in The State of Kuwait. In Proceedings of the 2020 Advances in Science and Engineering Technology International Conferences (ASET), Dubai, UAE, 4 February–9 April 2020; pp. 1–4. [Google Scholar]
- Miller, R.A. Thermal barrier coatings for aircraft engines: History and directions. J. Therm. Spray Technol. 1997, 6, 35–42. [Google Scholar] [CrossRef]
- Ünal, Ö.; Mitchell, T.E.; Heuer, A.H. Microstructures of Y2O3-Stabilized ZrO2 Electron Beam-Physical Vapor Deposition Coatings on Ni-Base Superalloys. J. Am. Ceram. Soc. 1994, 77, 984–992. [Google Scholar] [CrossRef]
- Miller, R.A. Current status of thermal barrier coatings—An overview. Surf. Coat. Technol. 1987, 30, 1–11. [Google Scholar] [CrossRef]
- Singh, J.; Wolfe, D.E.; Singh, J. Architecture of thermal barrier coatings produced by electron beam-physical vapor deposition (EB-PVD). J. Mater. Sci. 2002, 37, 3261–3267. [Google Scholar] [CrossRef]
- Goward, G. Progress in coatings for gas turbine airfoils. Surf. Coatings Technol. 1998, 108, 73–79. [Google Scholar] [CrossRef]
- Eichner, D.; Schlieter, A.; Leyens, C.; Shang, L.; Shayestehaminzadeh, S.; Schneider, J.M. Solid particle erosion behavior of nanolaminated Cr 2 AlC films. Wear 2018, 187–195. [Google Scholar] [CrossRef]
- AG, S. Advanced Compressor Coating for Siemens Gas Turbines, in, Siemens AG. Available online: https://assets.new.siemens.com/siemens/assets/api/uuid:3d6979ec63aff8183e9dc3946e330bf9297534bd/version:1541967370/acc_e50001-g520-a445-x-7600enlrfinal.pdf (accessed on 15 April 2012).
- Rajendran, R. Gas turbine coatings—An overview. Eng. Fail. Anal. 2012, 26, 355–369. [Google Scholar] [CrossRef]
- AG, S. Advanced Compressor Coating (ACC), in Siemens Energy Sector. Available online: https://new.siemens.com/global/en/products/energy/services/performance-enhancement/modernization-upgrades/gas-turbines/acc-sgt-2000e.html (accessed on 15 April 2012).
- Kablov, E.N.; Muboyadzhyan, S.A. Erosion-resistant coatings for gas turbine engine compressor blades. Russ. Met. (Metally) 2017, 2017, 494–504. [Google Scholar] [CrossRef]
- Fotovvati, B.; Namdari, N.; Dehghanghadikolaei, A. On Coating Techniques for Surface Protection: A Review. J. Manuf. Mater. Process. 2019, 3, 28. [Google Scholar] [CrossRef] [Green Version]
- Swadźba, L.; Formanek, B.; Gabriel, H.; Liberski, P.; Podolski, P. Erosion- and corrosion-resistant coatings for aircraft compressor blades. Surf. Coat. Technol. 1993, 62, 486–492. [Google Scholar] [CrossRef]
- Bonu, V.; Jeevitha, M.; Kumar, V.P.; Srinivas, G.; Barshilia, H.C. Solid particle erosion and corrosion resistance performance of nanolayered multilayered Ti/TiN and TiAl/TiAlN coatings deposited on Ti6Al4V substrates. Surf. Coat. Technol. 2020, 387, 125531. [Google Scholar] [CrossRef]
- Sun, Z.; He, G.; Meng, Q.; Li, Y.; Tian, X. Corrosion mechanism investigation of TiN/Ti coating and TC4 alloy for aircraft compressor application. Chin. J. Aeronaut. 2020, 33, 1824–1835. [Google Scholar] [CrossRef]
- Ma, K.; Bloyce, A.; Bell, T. Examination of mechanical properties and failure mechanisms of TiN and Ti−TiN multilayer coatings. Surf. Coat. Technol. 1995, 76, 297–302. [Google Scholar] [CrossRef]
- Reedy, M.W.; Eden, T.J.; Potter, J.K.; Wolfe, U.E. Erosion performance and characterization of nanolayer (Ti,Cr)N hard coatings for gas turbine engine compressor blade applications. Surf. Coat. Technol. 2011, 206, 464–472. [Google Scholar] [CrossRef]
- Ali, N.; Teixeira, J.A.; Addali, A. Effect of Water Temperature, pH Value, and Film Thickness on the Wettability Behaviour of Copper Surfaces Coated with Copper Using EB-PVD Technique. J. Nano Res. 2019, 60, 124–141. [Google Scholar] [CrossRef]
- Ali, N.; Teixeira, J.A.; Addali, A.; Saeed, M.; Al-Zubi, F.; Sedaghat, A.; Bahzad, H. Deposition of Stainless Steel Thin Films: An Electron Beam Physical Vapour Deposition Approach. Materials 2019, 12, 571. [Google Scholar] [CrossRef] [Green Version]
- Ali, N.; Teixeira, J.A.; Addali, A.; Al-Zubi, F.; Shaban, E.; Behbehani, I. The effect of aluminium nanocoating and water pH value on the wettability behavior of an aluminium surface. Appl. Surf. Sci. 2018, 443, 24–30. [Google Scholar] [CrossRef] [Green Version]
- Saeed, M.; Robson, J.D.; Kinloch, I.A.; Derby, B.; Liao, C.-D.; Al-Awadhi, S.; Al-Nasrallah, E. The formation mechanism of hexagonal Mo2C defects in CVD graphene grown on liquid copper. Phys. Chem. Chem. Phys. 2020, 22, 2176–2180. [Google Scholar] [CrossRef] [PubMed]
- Rossnagel, S.M.; Powell, R.; Ulman, A. PVD for Microelectronics: Sputter Desposition to Semiconductor Manufacturing; Elsevier: Amsterdam, The Netherlands, 1998. [Google Scholar]
- Kumar, V.; Kandasubramanian, B. Processing and design methodologies for advanced and novel thermal barrier coatings for engineering applications. Particuology 2016, 27, 1–28. [Google Scholar] [CrossRef]
- Lu, Y.; Hao, L.; Yoshi, H. Mechanical Coating Technique for Composite Films and Composite Photocatalyst Films; IntechOpen: London, UK, 2012; pp. 323–354. [Google Scholar]
- Mehran, Q.M.; Fazal, M.A.; Razak, B.A.; Rubaiee, S. A Critical Review on Physical Vapor Deposition Coatings Applied on Different Engine Components. Crit. Rev. Solid State Mater. Sci. 2017, 43, 158–175. [Google Scholar] [CrossRef]
- Xia, L.-Q.; Chang, M. Chemical vapor deposition. In Handbook of Semiconductor Manufacturing Technology; CRC Press: Boca Raton, FL, USA, 2017; pp. 13-11–13-87. [Google Scholar]
- Kelly, P.; Arnell, R. Magnetron sputtering: A review of recent developments and applications. Vacuum 2000, 56, 159–172. [Google Scholar] [CrossRef]
- Asri, R.; Harun, W.; Hassan, M.; Ghani, S.A.C.; Buyong, Z. A review of hydroxyapatite-based coating techniques: Sol–gel and electrochemical depositions on biocompatible metals. J. Mech. Behav. Biomed. Mater. 2016, 57, 95–108. [Google Scholar] [CrossRef] [Green Version]
- Moridi, A.; Hassani-Gangaraj, S.M.; Guagliano, M.; Dao, M. Cold spray coating: Review of material systems and future perspectives. Surf. Eng. 2014, 30, 369–395. [Google Scholar] [CrossRef]
- Matthews, S.; James, B. Review of Thermal Spray Coating Applications in the Steel Industry: Part 1—Hardware in Steel Making to the Continuous Annealing Process. J. Therm. Spray Technol. 2010, 19, 1267–1276. [Google Scholar] [CrossRef]
- Alsayegh, N.M.; Saeed, M.A.; Alzubi, F.G. Method for Synthesizing a Thin Film Stainless Steel Coating. U.S. Patent No. 10,392690, 27 August 2019. [Google Scholar]
- Rhys-Jones, T. The use of thermally sprayed coatings for compressor and turbine applications in aero engines. Surf. Coat. Technol. 1990, 42, 1–11. [Google Scholar] [CrossRef]
- Drexler, J.M.; Shinoda, K.; Ortiz, A.L.; Li, D.; Vasiliev, A.L.; Gledhill, A.D.; Sampath, S.; Padture, N. Air-plasma-sprayed thermal barrier coatings that are resistant to high-temperature attack by glassy deposits. Acta Mater. 2010, 58, 6835–6844. [Google Scholar] [CrossRef]
- de Almeida, D.S.; da Silva, C.R.M.; Carmo, M.D.; Nono, A.; Cairo, C.A.A. Ni Al alloy coating deposition by electron beam physical vapour deposition. In Proceedings of the 17th Brazilian Congress of Engineering and Materials Science, Paraná, Brazil, 15–19 November 2006; pp. 15–19. [Google Scholar]
- Tabakoff, W. Protection of coated superalloys from erosion in turbomachinery and other systems exposed to particulate flows. Wear 1999, 233, 200–208. [Google Scholar] [CrossRef]
- Tabakoff, W.; Simpson, G. Experimental study of deterioration and retention on coated and uncoated compressor and turbine blades. In Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit, Cincinnati, OH, USA, 14–17 January 2002. [Google Scholar] [CrossRef]
- Navinšek, B.; Panjan, P.; Milošev, I. Industrial applications of CrN (PVD) coatings, deposited at high and low temperatures. Surf. Coat. Technol. 1997, 97, 182–191. [Google Scholar] [CrossRef]
- Hetmańczyk, M.; Swadźba, L.; Mendala, B. Advanced materials and protective coatings in aero-engines application. J. Achiev. Mater. Manuf. Eng. 2007, 24, 372–381. [Google Scholar]
- LTD, J.P.P. Vacuum Deposition Apparatus for Powdery Samples: Mpvap Powder, in, Jesco Project PVT LTD. 2020. Available online: http://www.jescoprojects.com/products/vacuum-deposition-apparatus-for-powdery-samples-mpvappowder (accessed on 10 May 2020).
- Sano, H.; Ishida, R.; Kura, T.; Fujita, S.; Naka, S.; Okada, H.; Takai, T. Transparent Organic Light-Emitting Diodes with Top Electrode Using Ion-Plating Method. IEICE Trans. Electron. 2015, 98, 1035–1038. [Google Scholar] [CrossRef]
- Pessoa, R.S.; Fraga, M.A.; Santos, L.; Galvão, N.; Maciel, H.; Massi, M. Plasma-assisted techniques for growing hard nanostructured coatings. An overview. In Anti-Abrasive Nanocoatings; Aliofkhazraei, M., Ed.; Woodhead Publishing: Cambridge, UK, 2015; pp. 455–479. [Google Scholar]
- Mattox, D. Vacuum Deposition Processes, in Products Finishing. 1999. Available online: https://www.pfonline.com/articles/vacuum-deposition-processes (accessed on 10 May 2020).
- Lampert, C. Vacuum Deposition and Coating Options, in Products Finishing. 2013. Available online: https://www.pfonline.com/articles/vacuum-deposition-and-coating-options (accessed on 10 May 2020).
- European Physical Society; Institute of Physics. Thin Film and Surfaces Group; Welding Inst. Surfacing Div. (Eds.) Proceedings of the International Conference—Ion Plating and Allied Techniques (IPAT 79). In Proceedings—Micro-Delcon; CEP Consultants Ltd.: London, UK, 1979. [Google Scholar]
- Mattox, D.M. The Foundations of Vacuum Coating Technology; Noyes Publications/William Andrew Pub: New York, NY, USA, 2003. [Google Scholar]
- Taschuk, M.; Hawkeye, M.; Brett, M.; Martin, P. Handbook of Deposition Technologies for Films and Coatings. Science Applications and Technology; Elsevier: Oxford, UK, 2010. [Google Scholar]
- Carlsson, J.-O.; Martin, P.M.; Martin, P. Handbook of deposition technologies for films and coatings. Science, Applications and Technology. In Chemical Vapor Deposition; Elsevier Inc.: Oxford, UK, 2010; p. 406. [Google Scholar]
- Depla, D.; Mahieu, S.; Greene, J. Sputter deposition processes. In Handbook of Deposition Technologies for Films and Coatings; Elsevier: Oxford, UK, 2010; pp. 253–296. [Google Scholar]
- Brauer, G.; Szyszka, B.; Vergöhl, M.; Bandorf, R. Magnetron sputtering—Milestones of 30 years. Vacuum 2010, 84, 1354–1359. [Google Scholar] [CrossRef]
- Braun, M. Magnetron sputtering technique. In Handbook of Manufacturing Engineering Technology; Springer: Berlin, Germany, 2015; pp. 2929–2957. [Google Scholar]
- Frach, P.; Gottfried, C.; Fietzke, F.; Klostermann, H.; Bartzsch, H.; Gloess, D. High Power Density Pulse Magnetron Sputtering-Process and Film Properties. In Proceedings of the 13th International Conference on Plasma Surface Engineering, Garmisch-Partenkirchen, Germany, 10–14 September 2012; pp. 80–83. [Google Scholar]
- Lin, J.; Jang, J.; Park, I.-W.; Wei, R. Structure and properties of CrSiCN coatings deposited by pulsed dc magnetron sputtering for wear and erosion protection. Surf. Coat. Technol. 2016, 287, 44–54. [Google Scholar] [CrossRef]
- Bromark, M.; Larsson, M.; Hedenqvist, P.; Olsson, M.; Hogmark, S.; Bergmann, E. PVD COATINGS FOR TOOL APPLICATIONS: TRIBOLOGICAL EVALUATION. Surf. Eng. 1994, 10, 205–214. [Google Scholar] [CrossRef]
- Deng, J.; Wu, F.; Lian, Y.; Xing, Y.; Li, S. Erosion wear of CrN, TiN, CrAlN, and TiAlN PVD nitride coatings. Int. J. Refract. Met. Hard Mater. 2012, 35, 10–16. [Google Scholar] [CrossRef]
- Mitterer, C.; Holler, F.; Üstel, F.; Heim, D. Application of hard coatings in aluminium die casting—Soldering, erosion and thermal fatigue behaviour. Surf. Coat. Technol. 2000, 125, 233–239. [Google Scholar] [CrossRef]
- Alegría-Ortega, J.; Ocampo-Carmona, L.M.; Suárez-Bustamante, F.; Olaya-Florez, J. Erosion–corrosion wear of Cr/CrN multi-layer coating deposited on AISI-304 stainless steel using the unbalanced magnetron (UBM) sputtering system. Wear 2012, 290, 149–153. [Google Scholar] [CrossRef]
- Lehto, S.; Likonen, J.; Coad, J.; Ahlgren, T.; Hole, D.; Mayer, M.; Maier, H.; Kolehmainen, J. Tungsten coating on JET divertor tiles for erosion/deposition studies. Fusion Eng. Des. 2003, 66, 241–245. [Google Scholar] [CrossRef]
- Holleck, H. Material selection for hard coatings. J. Vac. Sci. Technol. A 1986, 4, 2661–2669. [Google Scholar] [CrossRef]
- Levy, A.V.; Buqian, W. Erosion of hard material coating systems. Wear 1988, 121, 325–346. [Google Scholar] [CrossRef]
- Zhao, L.; Chen, K.; Yang, Q.; Rodgers, J.; Chiou, S. Materials informatics for the design of novel coatings. Surf. Coat. Technol. 2005, 200, 1595–1599. [Google Scholar] [CrossRef]
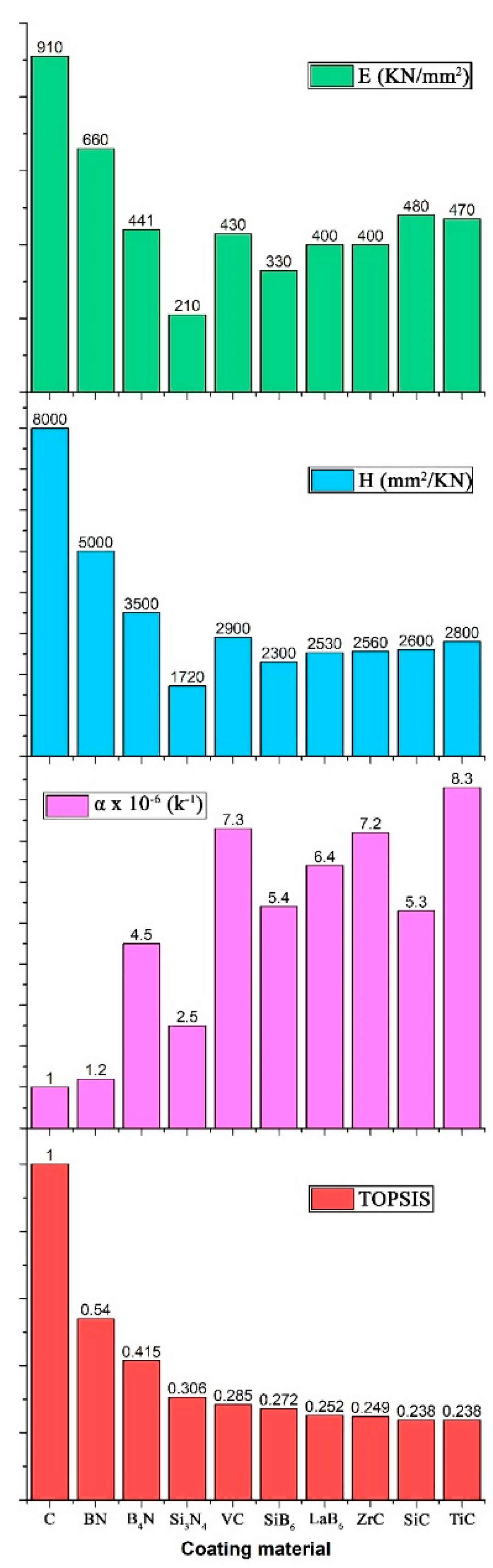
- Chauhan, A.; Vaish, R. Hard coating material selection using multi-criteria decision making. Mater. Des. 2013, 44, 240–245. [Google Scholar] [CrossRef]
- Leyland, A.; Matthews, A. On the significance of the H/E ratio in wear control: A nanocomposite coating approach to optimised tribological behaviour. Wear 2000, 246, 1–11. [Google Scholar] [CrossRef]
- Hassani, S.; Bielawski, M.; Beres, W.; Martinu, L.; Balazinski, M.; Klemberg-Sapieha, J. Predictive tools for the design of erosion resistant coatings. Surf. Coat. Technol. 2008, 203, 204–210. [Google Scholar] [CrossRef]
- Zhang, S. TiN coating of tool steels: A review. J. Mater. Process. Technol. 1993, 39, 165–177. [Google Scholar] [CrossRef]







| Material Type | Example | Application | Advantages | Disadvantages | References |
|---|---|---|---|---|---|
| Nickel based superalloys |
| Aerospace, marine, industrial and military gas turbine engines | Good mechanical properties, easy machinability, good strength properties and low material cost | High manufacturing cost | [13] |
| Titanium based superalloys |
| Aerospace and industrial gas turbine engines | Combine low densities with high strength, good weldability and high fatigue strength. | Limited by their operating temperature | [14] |
| Cobalt-based superalloys |
| Aerospace, marine and industrial gas turbine engines | The alloy retains their strength up to higher temperatures. They derive their strength greatly from a distribution of refractory metal carbides, good resistant to corrosion, not so sensitive to cracking under thermal shocks and suitable for parts that need to be rotate. | Not mechanically strong as nickel-based superalloys | [13] |
| Stainless steel |
| Aerospace, marine and industrial gas turbine engines. | Good corrosion resistance in dry environments. | Unsatisfactory corrosion resistance in wet environments (AISI 403 and 410), would suffer from thermal surface deformation in high temperatures conditions (e.g., jet turbines), can undergo pitting damages. | [15,16] |
| Degradation Mechanisms | Description |
|---|---|
| Erosion | Material removal by abrasion due to the impacts of hard, incompressible particles of, typically, a diameter greater than 10 µm on surfaces along the flow path. Modern, highly efficient, but more massive filtration systems have been introduced into industrial systems, and this problem is now predominantly one for aero-engines. |
| Corrosion | Caused by contaminants in both inlet air and fuel. Corrosion depends on the fuel used and is usually less for natural gas and increases the heavier the fuel oil, due to impurities and additives which produce aggressive deposits. Pollutants present in the inlet air can accelerate corrosion. |
| Hot corrosion | Reactive gases, mineral acids, and salts in the flow can chemically interact and cause both material deterioration and loss from exposed components in the flow path. There can also be high-temperature oxidation of the component due to chemical interaction with the surrounding hot gaseous environment. Separately, the products of these chemical processes can stick to exposed components as a film of scale. Oxide scale protection is then subjected to degradation if any surface damage (e.g., cracking) is caused during the thermal cycle. |
| Fouling | Results from particles in the flow adhering to exposed surfaces, resulting in material build up with increased roughness of the surface and even some change in aerofoil shape. Particles with the highest tendency for causing fouling are generally less than 2 µm in diameter. Typical examples are sea salts, carbon, oil or water mists, and smoke. |
| Foreign object damage | Usually generated by foreign objects in the gas and/or air streams which strike components in the flow path. These can enter via the inlet air or gas compressor, or even as a result of pieces that break off engine components. |
| Equation No. | Researchers | Model | Remarks |
|---|---|---|---|
| Equation (16) | Hamad et al. [46] | is mean angle of the compressor. | |
| Equation (17) | Finnie [30,53] | E = (sin (2α) sin2 (α)) for tan α ≤ E = () for tan α ≥ | The first cutting equation; assumes a solid particle is moving with known velocity and angle of impact striking a target surface of rigid plastic material. Where the equation parameters change according to the angle of impact α, is depth of contact to cut ratio, and k = 2 as a constant. |
| Equation (18) | Bitter [102,106] | Evp = Evc1 = . (V cos α- for α ≥ α0 Evc2 = for α ≤ α0 For the total erosion rate (cutting and deformation): E = Evp + Evc | Bitter’s equations provide better results at higher angles of impact than Finnie’s [30,53]. Four equations are presented. Where Evp and Evc1,2 are volume of surface material detached by deformation and cutting, respectively, is deformation factor, and e is the cutting wear element. |
| Equation (19) | Neilson and Gilchrist [87] | E = for α ˂ E = for α ˃ | Where Vr is residual particle velocity, X is factor of cutting, is deformation factor. |
| Equation (20) | Finnie [60] | E ( where = - | is particle’s influence in an idealised manner, and is particle horizontal velocity and is the moment of inertia of the particle about its center of gravity. |
| Equation (21) | Sheldon and Kanhere [107] | E | Where Hv is Vickers hardness of target (kg/mm2). |
| Equation (22) | Tilly [108] | E + | and is the velocity at maximum erosion rate, Vref is standard test velocity of particle, is fragmentation for test condition and is threshold velocity below which impact distortion is purely elastic and no damage takes place. |
| Equation (23) | Jennings et al. [109] | E | enthalpy of melting of target. |
| Equation (24) | Hutchings et al. [110] | E ( | This equation depend on the impact angle and particle velocity. |
| Equation (25) | Evans et al. [70] | E | is particle density, Kc is fracture toughness and Hs hardness of target material. |
| Equation (26) | Tabakoff et al. [111] | E ( sin | is the empirical constant, is a function of impact angle, et is the tangential restitution ratio, is the normal component, is the velocity of particles and is the impact angle |
| Equation (27) | Sundararajan [112] | E = ) = | Assumes that the plastic flow localisation below the particle accounts for erosion. Where represents the flow stress temperature constant, Cr is the heat capacity of the target, er is the restitution coefficient, is the strain hardening exponent, F(t) is the constant of several impacts, Hp and are particle hardness and density respectively, is the friction coefficient, is the maximum value of , and gp is radius of gyration of impacting particle. |
| Equation (28) | Chen et al. [83] | E | , is pressure-stress ratio, is dimensionless temperature and is a dimensionless strain rate. |
| Equation (29) | Nsoesiea et al. [113] | E = | Where C1 is a constant, d represents the particle diameter, Dp is particle density, Hs hardness of the target, and impacting angle correction factors (shifting coefficient) and (shifting exponent). |
| Physical Property | Equation Number | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | |
| Cutting energy | ˟ | ˟ | |||||||||||
| cutting wear element | ˟ | ||||||||||||
| Deformation factor | ˟ | ˟ | |||||||||||
| Depth of contact to cut ratio | ˟ | ||||||||||||
| Dimensionless strain rate | ˟ | ||||||||||||
| Dimensionless temperature | ˟ | ||||||||||||
| empirical constant | ˟ | ||||||||||||
| Enthalpy of melting of target | ˟ | ||||||||||||
| Erosion resistance | |||||||||||||
| Flow stress temperature | ˟ | ||||||||||||
| Fracture toughness | ˟ | ˟ | |||||||||||
| Friction coefficient | ˟ | ||||||||||||
| Impact angle | ˟ | ˟ | ˟ | ˟ | ˟ | ˟ | |||||||
| Impacting particle kinetic energy | ˟ | ||||||||||||
| Incremental strain per impact | |||||||||||||
| Main stress | ˟ | ˟ | |||||||||||
| Mass of an individual particle | |||||||||||||
| Material fragmentation limits | ˟ | ||||||||||||
| Melting temperature | ˟ | ||||||||||||
| Minimum effective particle size | ˟ | ||||||||||||
| Particle density | ˟ | ˟ | ˟ | ˟ | |||||||||
| Particle hardness | ˟ | ˟ | |||||||||||
| Particle horizontal velocity | ˟ | ||||||||||||
| Particle mass | ˟ | ˟ | |||||||||||
| Particle roundness | ˟ | ˟ | |||||||||||
| Particle size | ˟ | ˟ | ˟ | ˟ | ˟ | ||||||||
| Particle velocity | ˟ | ˟ | ˟ | ˟ | ˟ | ˟ | ˟ | ˟ | ˟ | ˟ | ˟ | ||
| Particle velocity (residual component) | ˟ | ˟ | |||||||||||
| Pressure | ˟ | ||||||||||||
| Pressure-stress ratio | ˟ | ||||||||||||
| Reparation coefficient | ˟ | ||||||||||||
| Restitution coefficient | ˟ | ||||||||||||
| shifting coefficient | ˟ | ||||||||||||
| shifting exponent | ˟ | ||||||||||||
| Strain hardening | |||||||||||||
| Strain hardening exponent | ˟ | ||||||||||||
| Target density | ˟ | ˟ | |||||||||||
| Target gram molecular weight | ˟ | ||||||||||||
| Target hardness | ˟ | ˟ | |||||||||||
| Target heat capacity | ˟ | ||||||||||||
| Thermal conductivity | |||||||||||||
| Threshold velocity | ˟ | ||||||||||||
| Total mass | |||||||||||||
| Velocity at maximum erosion rate | ˟ | ||||||||||||
| Velocity components | ˟ | ||||||||||||
| Vickers hardness of target | ˟ | ||||||||||||
| Coating Material Type | Advantages | Disadvantages | References |
|---|---|---|---|
| ZrN |
|
| [130] |
| Cr3C2 | • Erosion resistance enhances at 500 to 600 °C due to the formation of oxycarbonitrides on the surface. |
| [130] |
| WC-Co |
| • When formed using the cold spray method, the deposited layer cannot withstand extremely harsh operational environment. | [131] |
| TiN |
|
| [132,133] |
| TiN/Ti |
|
| [134,135] |
| TiN/CrN |
|
| [136] |
| Type | Process | Anti-Erosion Application |
|---|---|---|
| Thin hard films | PVD | Compressor blades, and brush seals |
| Diffusion | CVD | Protection of the turbine blades against the oxidation/corrosion |
| Dry film lubrication | Spray | Resistance to fretting wear of compressor blades |
| Thermal barrier system | Thermal spray, PVD | Coating for turbine combustor blades, cans and vanes |
| Wear resistance | Thermal spray | Coatings for turbine fans and stator blades |
| Coating Method | Advantages | Limitations |
|---|---|---|
| PVD | Thickness control; | Complicated and extensive equipment; |
| Large area coating | The coating on uniform samples | |
| CVD | Smooth coating process on a nonuniform substrate; | Complicated and extensive equipment; |
| Strong adhesion | High-temperature process | |
| Thermal spraying | Rapid coating; | High-temperature process; |
| Large specific area | Grain grows |
| Coating Method | Description | Advantages | Limitations |
|---|---|---|---|
| Vacuum deposition | The source material is vaporised and introduced to the substrate surfaces within a vacuum environment to apply the coating layer. This coating method can be employed to provide protective coatings for the following cases: (1) wear resistance; (2) corrosion; (3) electrically conducting films; (4) mirror coatings; etc. |
|
|
| Ion plating | A high energy particle flux is applied to the deposition film and substrate surface, enough to change the substrate and/or film properties. |
|
|
| Sputtering | Particle bombardment of a material results in a vapour and can be used to deposit an anti-erosion layer on a target. |
|
|
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alqallaf, J.; Ali, N.; Teixeira, J.A.; Addali, A. Solid Particle Erosion Behaviour and Protective Coatings for Gas Turbine Compressor Blades—A Review. Processes 2020, 8, 984. https://doi.org/10.3390/pr8080984
Alqallaf J, Ali N, Teixeira JA, Addali A. Solid Particle Erosion Behaviour and Protective Coatings for Gas Turbine Compressor Blades—A Review. Processes. 2020; 8(8):984. https://doi.org/10.3390/pr8080984
Chicago/Turabian StyleAlqallaf, Jasem, Naser Ali, Joao A. Teixeira, and Abdulmajid Addali. 2020. "Solid Particle Erosion Behaviour and Protective Coatings for Gas Turbine Compressor Blades—A Review" Processes 8, no. 8: 984. https://doi.org/10.3390/pr8080984
APA StyleAlqallaf, J., Ali, N., Teixeira, J. A., & Addali, A. (2020). Solid Particle Erosion Behaviour and Protective Coatings for Gas Turbine Compressor Blades—A Review. Processes, 8(8), 984. https://doi.org/10.3390/pr8080984







