Comprehensive Improvement of Mixed-Flow Pump Impeller Based on Multi-Objective Optimization
Abstract
:1. Introduction
2. Mixed-Flow Pump Model
3. Optimization Design System
3.1. CFD Analyses
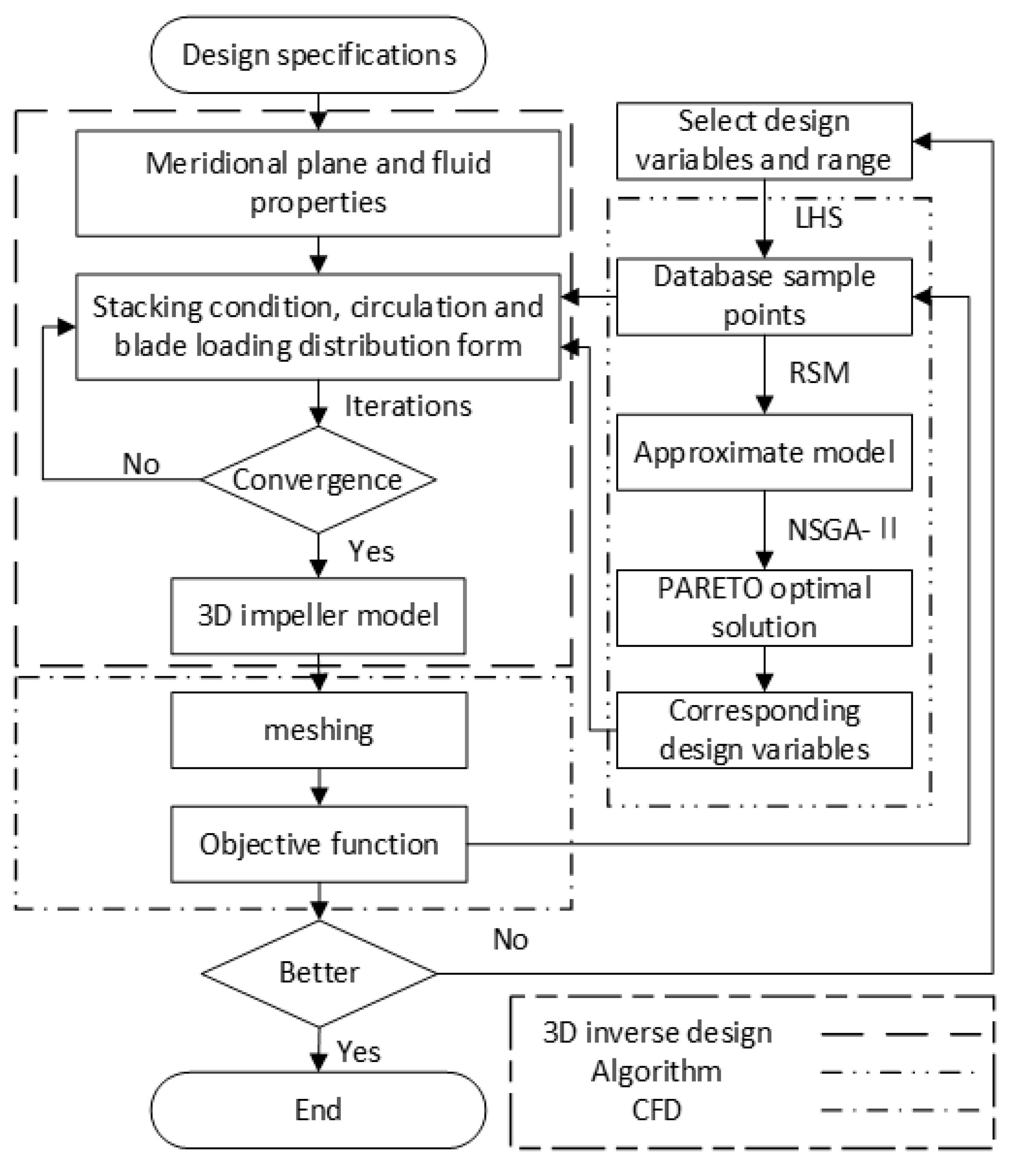
3.2. 3D Inverse Design Method
- Design specifications and fluid properties.
- Meridional shape.
- Spanwise distribution of at the impeller exit.
- The meridional derivative of the circulation (blade loading) at the hub and shroud.
- Stacking condition.
3.3. Optimization Process
4. Optimization Settings
4.1. Design Parameters
4.2. Optimization Objectives and Constraints
4.3. Algorithm Settings
5. Results and Discussions
5.1. Experimental Validation
5.2. Analysis of the Main Effect
5.3. Optimization Results
5.4. Comparisons between Original and Preferred Impellers
6. Conclusions
- (1)
- The CFD calculations accurately simulated the flow in the pump, and the performance curves agreed well with the experimental curves. The maximum efficiency and head deviations did not exceed 2% and 4% respectively.
- (2)
- The optimization results show that the non-linear SDIEC is better than the constant and linear distributions. The analysis of the main effect also shows that and have a greater impact on the performance of the mixed-flow pump impeller than other design parameters. Therefore, it is necessary to take and as design parameters in the optimization process to further improve the performance of the mixed-flow pump impeller.
- (3)
- The pump efficiency with preferred impeller at 0.8Qdes, 1.0Qdes, and 1.2Qdes are 81.11%, 88.60%, and 77.62%, respectively. Compared with the original model, these efficiencies increased by 0.63%, 3.39%, and 3.77%, respectively. At the same time, the cavitation performance of preferred impeller has been significantly improved. The area of low-pressure region further reduced by 96.92% and the pump head deviation at 1.0Qdes is less than 1.84%, which is within an acceptable range.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| specific speed | |
| H | head |
| N | rotational speed |
| Q | volume flow rate |
| tangentially velocity | |
| r | radius or radial direction |
| B | blade numbers |
| static pressure at blade work surface | |
| static pressure at blade suction surface | |
| relative velocity on the blade surface | |
| m | streamline in the meridional shape or meridional distance |
| axial components of the circumferential average absolute velocity | |
| radial components of the circumferential average absolute velocity | |
| axial component of periodic velocity | |
| radial component of periodic velocity | |
| circumferential component of periodic velocity | |
| wrap angle | |
| tangentially velocity at hub | |
| tangentially velocity at shroud | |
| normalized spanwise distance | |
| normalized tangentially velocity | |
| normalized meridional distance | |
| DRVT | blade loading at leading edge |
| NC | fore connection points |
| ND | aft fore connection points |
| K | slope of linear line |
| stacking condition | |
| pump efficiency | |
| normalized area of low-pressure area | |
| pressure at inlet or outlet | |
| torque on the impeller | |
| angular velocity of the impeller | |
| density of the fluid | |
| gravitational acceleration |
Abbreviations
| SDIEC | spanwise distribution of impeller exit circulation |
| CFD | computational fluid dynamics |
| LHS | Latin hypercube sampling |
| RSM | response surface model |
| NSGA-Ⅱ | non-dominated sorting genetic algorithm |
| DOE | design of experiment |
| CCD | central composite design |
| RANS | Reynolds average Navier–Stokes |
References
- Suh, J.-W.; Yang, H.-M.; Kim, Y.-I.; Lee, K.-Y.; Kim, J.-H.; Joo, W.-G.; Choi, Y.-S. Multi-objective optimization of a high efficiency and suction performance for mixed-flow pump impeller. Eng. Appl. Comput. Fluid Mech. 2019, 13, 744–762. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.; Jeong, U.-B.; Lee, K.-Y.; Kim, J.-H.; Yoon, J.-Y.; Choi, Y.-S. Multi-objective optimization for mixed-flow pump with blade angle of impeller exit and diffuser inlet. J. Mech. Sci. Technol. 2017, 31, 5099–5106. [Google Scholar] [CrossRef]
- Pei, J.; Wang, W.; Yuan, S. Multi-point optimization on meridional shape of a centrifugal pump impeller for performance improvement. J. Mech. Sci. Technol. 2016, 30, 4949–4960. [Google Scholar] [CrossRef]
- Shim, H.-S.; Kim, K.-Y.; Choi, Y.-S. Three-objective optimization of a centrifugal pump to reduce flow recirculation and cavitation. J. Fluids Eng. 2018, 140, 091202. [Google Scholar] [CrossRef]
- Shim, H.-S.; Afzal, A.; Kim, K.-Y.; Jeong, H.-S. Three-objective optimization of a centrifugal pump with double volute to minimize radial thrust at off-design conditions. Proc. Inst. Mech. Eng. Part A J. Power Energy. 2016, 230, 598–615. [Google Scholar] [CrossRef]
- Miao, F.; Park, H.-S.; Kim, C.; Ahn, S. Swarm intelligence based on modified PSO algorithm for the optimization of axial-flow pump impeller. J. Mech. Sci. Technol. 2015, 29, 4867–4876. [Google Scholar] [CrossRef]
- Meng, F.; Li, Y.; Yuan, S.; Wang, W.; Zheng, Y.; Osman, M.K. Multiobjective Combination Optimization of an Impeller and Diffuser in a Reversible Axial-Flow Pump Based on a Two-Layer Artificial Neural Network. Processes 2020, 8, 309. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Xiao, R. Multiobjective optimization design of a pump–turbine impeller based on an inverse design using a combination optimization strategy. J. Fluids Eng. 2014, 136, 249–256. [Google Scholar] [CrossRef]
- Zangeneh, M. A compressible 3D design method for radial and mixed flow turbomachinery blades. Int. J. Numer. Methods Fluids 1991, 13, 599–624. [Google Scholar] [CrossRef]
- Daneshkhah, K.; Zangeneh, M. Parametric design of a Francis turbine runner by means of a three-dimensional inverse design method. IOP Conf. Ser. Earth Environ. Sci. 2010, 12, 012058. [Google Scholar] [CrossRef]
- Peng, G. A practical combined computation method of mean through-flow for 3d inverse design of hydraulic turbomachinery blades. J. Fluids Eng. 2005, 127, 1183–1190. [Google Scholar] [CrossRef]
- Zangeneh, M.; Goto, A.; Harada, H. On the Design Criteria for Suppression of Secondary Flows in Centrifugal and Mixed Flow Impellers. J. Turbomach. 1998, 120, 723. [Google Scholar] [CrossRef]
- Zhu, B.; Tan, L.; Wang, X.; Ma, Z. Investigation on flow characteristics of pump-turbine runners with large blade lean. J. Fluids Eng. 2017, 140, 031101. [Google Scholar] [CrossRef]
- Yin, J.; Wang, D. Review on applications of 3D inverse design method for pump. Chin. J. Mech. Eng. 2014, 27, 520–527. [Google Scholar] [CrossRef]
- Zhu, B.; Wang, X.; Tan, L.; Zhou, D.; Zhao, Y.; Cao, S. Optimization design of a reversible pump-turbine runner with high efficiency and stability. Renew. Energy 2015, 81, 366–376. [Google Scholar] [CrossRef]
- Liu, L.; Zhu, B.; Bai, L.; Liu, X.; Zhao, Y. Parametric design of an ultrahigh-head pump-turbine runner based on multiobjective optimization. Energies 2017, 10, 1169. [Google Scholar] [CrossRef] [Green Version]
- Ma, Z.; Zhu, B.; Rao, C.; Shangguan, Y. Comprehensive hydraulic improvement and parametric analysis of a francis turbine runner. Energies 2019, 12, 307. [Google Scholar] [CrossRef] [Green Version]
- Bonaiuti, D.; Zangeneh, M. On the coupling of inverse design and optimization techniques for the multiobjective, multipoint design of turbomachinery blades. J. Turbomach. 2009, 131, 134–149. [Google Scholar] [CrossRef]
- Lee, K.-Y.; Choi, Y.-S.; Kim, Y.-L.; Yun, J.-H. Design of axial fan using inverse design method. J. Mech. Sci. Technol. 2008, 22, 1883–1888. [Google Scholar] [CrossRef]
- Lang, J. Preliminary study of the optimal distribution law of axial-flow pump impeller axial speed and circulation. Fluid Mach. 1990, 31. (In Chinese) [Google Scholar]
- Chen, L. The Optimal Design Method of Axial Flow Pump Outlet Circumference Variation Law and Geometric Parameter Integration. Hydraulic Vane Pump. 1993, 1, 27. (In Chinese) [Google Scholar]
- Zhang, D.; Li, T.; Shi, W.; Zhang, H.; Zhang, G. Experimental investigation of meridional velocity and circulation in axial-flow impeller outlet. Trans. Chin. Soc. Agric. Eng. 2012, 28, 73–77. (In Chinese) [Google Scholar]
- Zhang, D.; Shi, W.; Li, T.; Gao, X.; Guan, X. Establishment and Experiment on Nonlinear Circulation Mathematical Model of Axial Flow Pump Impeller. Trans. Chin. Soc. Agric. Mach. 2013, 44, 58–61. (In Chinese) [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.-H.; Kim, K.-Y. Analysis and optimization of a vaned diffuser in a mixed flow pump to improve hydrodynamic performance. J. Fluids Eng. 2012, 134, 071104. [Google Scholar] [CrossRef]
- Gen, M.; Cheng, R. Genetic Algorithms & Engineering Optimization; John Wiley & Sons Ltd.: New York, NY, USA, 1999. [Google Scholar]
- Lee, D.S.; Gonzalez, L.F.; Periaux, J.; Srinivas, K. Robust design optimization using multi-objective evolutionary algorithms. Comput Fluids. 2008, 37, 565–583. [Google Scholar] [CrossRef]
- Zangeneh, M.; Goto, A.; Takemura, T. Suppression of Secondary Flows in a Mixed-Flow Pump Impeller by Application of Three-Dimensional Inverse Design Method: Part 1—Design and Numerical Validation. J. Turbomach. 1996, 118, 536–543. [Google Scholar] [CrossRef]
- Goto, A.; Takemura, T.; Zangeneh, M. Suppression of Secondary Flows in a Mixed-Flow Pump Impeller by Application of Three-Dimensional Inverse Design Method: Part 2—Experimental Validation. J. Turbomach. 1996, 118, 544–551. [Google Scholar] [CrossRef]
- Miyauchi, S.; Zhu, B.; Luo, X.; Piao, B.; Matsumoto, H.; Sano, M.; Kassai, N. Optimization and Inverse Design of Pump Impeller. IOP Conf. Ser. Earth Environ. Sci. 2012, 15, 032032. [Google Scholar] [CrossRef]
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T. A fast and elitist multiobjective genetic algorithm: NSGA-Ⅱ. IEEE Trans. Evol. Comput 2002, 6, 182–197. [Google Scholar] [CrossRef] [Green Version]















| Design Flow Rate (m3/s) | 0.427 | Impeller Blade Number | 4 |
| Head on Design Points (m) | 12.66 | Impeller Diameter (mm) | 320 |
| Rotational Speed (r/min) | 1450 | Specific Speed | 511 |
| Inflow Pipe | Outflow Pipe | Impeller | Vane Diffuser | Total Mesh | Efficiency (%) | Head (m) |
|---|---|---|---|---|---|---|
| 27 | 49 | 42 | 48 | 166 | 83.828 | 12.064 |
| 58 | 67 | 84 | 92 | 301 | 84.647 | 12.146 |
| 83 | 95 | 141 | 152 | 471 | 85.208 | 12.103 |
| 129 | 142 | 211 | 268 | 750 | 85.206 | 12.096 |
| Variable | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Range | 0.3~0.34 | 0.3~0.34 | −0.2~0.2 | −0.2~0.2 | −1.5~1.5 | −1.5~1.5 | 0.1~0.9 | 0.4~0.9 | −15~15 |
| Setting | Value |
|---|---|
| Population Size | 100 |
| Number of Generations | 100 |
| Crossover Probability | 0.9 |
| Cross Distribution Index | 10 |
| Mutation Distribution Index | 20 |
| Initialization Mode | Random |
| Variable | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| I1 | 0.3363 | 0.3363 | 0.1790 | 0.1925 | −0.8935 | 1.0366 | 0.2116 | 0.6057 | −14.9394 |
| I2 | 0.3364 | 0.3363 | 0.1956 | 0.0747 | −1.1088 | 0.6562 | 0.2601 | 0.5003 | −14.7681 |
| I3 | 0.3364 | 0.3365 | 0.1363 | −0.0617 | −1.1141 | 0.3910 | 0.2937 | 0.7271 | −14.9837 |
| Performance | RSM | CFD | ||||||
|---|---|---|---|---|---|---|---|---|
| Impeller | ||||||||
| I1 | 80.58 | 80.77 | 80.40 | 80.31 | 11.92 | 88.72 | 53.97 | |
| I2 (Preferred) | 81.40 | 78.19 | 81.11 | 77.62 | 12.37 | 88.60 | 3.08 | |
| I3 | 82.00 | 74.30 | 81.31 | 74.75 | 12.44 | 87.68 | 18.22 | |
| Original model | 80.48 | 73.84 | 12.10 | 85.21 | 100 | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Li, Y.; Yuan, J.; Meng, F.; Appiah, D.; Chen, J. Comprehensive Improvement of Mixed-Flow Pump Impeller Based on Multi-Objective Optimization. Processes 2020, 8, 905. https://doi.org/10.3390/pr8080905
Wang M, Li Y, Yuan J, Meng F, Appiah D, Chen J. Comprehensive Improvement of Mixed-Flow Pump Impeller Based on Multi-Objective Optimization. Processes. 2020; 8(8):905. https://doi.org/10.3390/pr8080905
Chicago/Turabian StyleWang, Mengcheng, Yanjun Li, Jianpin Yuan, Fan Meng, Desmond Appiah, and Jiaqi Chen. 2020. "Comprehensive Improvement of Mixed-Flow Pump Impeller Based on Multi-Objective Optimization" Processes 8, no. 8: 905. https://doi.org/10.3390/pr8080905
APA StyleWang, M., Li, Y., Yuan, J., Meng, F., Appiah, D., & Chen, J. (2020). Comprehensive Improvement of Mixed-Flow Pump Impeller Based on Multi-Objective Optimization. Processes, 8(8), 905. https://doi.org/10.3390/pr8080905






