1. Introduction
Today, the issue of sustainability has been a major concern associated with palm oil production. The palm oil industry has brought a positive impact on the economic growth in Malaysia since it created jobs as well as downstream activities for national development [
1]. It has been the major contributor from the agriculture sector by 8% or over RM 80 billion of the gross national income [
2]. Nevertheless, some negative impacts caused by palm oil production have led to criticisms such as deforestation, land-use change, waste generation, greenhouse gas emissions, etc. [
3]. Furthermore, only 10% of palm oil trees can be converted into palm oil products [
4]. The remaining 90% of palm oil trees generate massive biomass residues creating environmental issues [
5], despite having the potential to be co-processed in the petroleum refinery [
6]. One of the abundant residues is empty fruit bunch (EFB), which is a waste product after the extraction of oil from the fresh fruit bunches (FFB). An estimate reveals that the EFB produced is 22% of the palm oil [
7,
8]. However, on the positive note, EFB is a potential source to be converted to value-added biochemicals due to its high content of cellulose and hemicellulose [
9]. In the current practice, waste management of EFB use from palm oil as a potential organic manure for agricultural purposes had been conducted to deal with this environmental issue [
10,
11,
12,
13,
14,
15,
16].
Efforts have been made to reduce palm oil waste by the Malaysian government through various strategies, such as renewable energy policy, the National Biomass Strategy 2020, and the 1 Malaysia Biomass Alternative Strategy (1MBAS) to encourage the utilization of biomass for value-added products and bioenergy production [
17,
18]. Previous studies had tried to improve the sustainability of the palm oil industry by valorizing the palm oil waste into several products. Yoshizaki et al. [
19] proposed a new approach for the integrated technology of biogas energy and compost production for a palm oil mill. The integrated biogas compost technology was found to be the most economically viable alternative for biomass utilization at the mill. The study by Ali et al. [
20], which extended the work of Yoshizaki et al. [
19], proposed a sustainable and integrated biorefinery concept for the palm oil mill, which showed a huge potential to enhance the economic improvement locally by generating a potential profit of RM 5.6 million and 15–20 new jobs at any given mill as well as reducing emissions. Kasivisvanathan et al. [
21] examined an integrated palm oil-based biorefinery by incorporating multiple biomass processing platforms with combined heat and power (CHP). In this case, EFB, Palm Kernel Shell (PKS), Palm Oil Mill Effluent (POME), and Mesocarp Fiber (MF) were identified as the potential biomass feedstock. These biomasses were further processed to produce valuable products (i.e., dried long fiber), pellet, briquette, charcoal, compost, etc.), and energy generated from the given palm-based biomass in CHP was integrated with palm oil-based biorefinery.
Tan et al. [
22] presented an integrated palm oil complex concept to utilize POME. Their study involved the economic, environmental, and social concerns to review the favorability of POME utilization. Three different cases in the POME utilization are biogas-biomass co-fired boiler, on-grid biogas plant, and POME evaporation. Foong et al. [
23] developed an input–output optimization approach for sustainable palm oil plantations. Their model involves determining the best management practices through optimal fertilizer application to maximize the yield of palm oil, thus minimizing the need for further land expansion. Aristizabal et al. [
24] presented an integrated palm oil biorefinery to produce different bioenergy products such as biodiesel, bioethanol, butanol, hydrogen, and electricity. Kasivisvanathan et al. [
25] developed a flexibility model to deal with the uncertain product demand towards the capacities of palm oil-based integrated biorefinery. In their work, palm oil waste was utilized to produce various bio-based products—namely, acetone, animal feed, biochar, biofuel, bio-oil, butanol, steam, and ethanol.
An interesting palm oil waste conversion to produce high-value marketable biochemicals in the form of integrated biorefinery has not been explored in the previous works. According to the International Energy Agency (IEA) Bioenergy Task 42, the concept of a biorefinery has gained critical attention to provide a sustainable process technology of biomass to a wide range of profitable chemical products; biorefineries are also seen as a sustainable waste management that can promote economic opportunities, environmental benefits, and energy security [
26]. Isikgor et al. [
27] identified around 200 potential valuable biochemicals and biopolymers derived from biomass. The department of energy (DOE) had identified the top 12 chemicals from biomass, primarily based on their market potential [
28]. Sadhukhan et al. [
29] revealed that the production of fine, specialty and platform chemicals, polymers, food and pharmaceutical ingredients, alongside biofuel and bioenergy, from palm oil waste can attain overall sustainability by the replacement of fossil resources. A wide movement to shift from non-renewable to renewable and sustainable resources to produce biochemicals is expected to reduce the dependence of fossil-based resources as well as mitigate the climate change issue [
30]. Furthermore, fluctuating oil prices and consumers’ awareness in using eco-friendly products have opened up opportunities for bio-based chemicals to replace fossil-based chemicals. Also, manufacturers see bio-based chemicals as economically attractive since they have great potential to develop bio-based building block chemicals and specialty chemicals [
31].
In the development of palm oil-based biorefinery and its sustainability aspects, there have been several works in the past. Adulrazik et al. [
32] designed an optimal EFB supply chain for the multi-products production of energy and chemicals considering economic aspects. Lim et al. [
3] assessed the sustainability of the crude palm oil supply chain in Malaysia, taking into account economic, environmental, and social aspects. Following Abdulrazik et al. [
32], Rubinsin et al. [
33] developed an optimal supply chain that integrated availability, locations, processing technologies, capacities, bioproducts, and power production by simultaneously considering economic and environmental aspects as an expansion approach for the palm oil industry. Kasivisvanathan et al. [
21] adapted fuzzy optimization for designing the retrofitted palm oil-based integrated biorefinery considering economic performance and environmental impact. Andiappan et al. [
34] presented an integrated approach of the palm oil industry by determining the optimal allocation of incremental profits and corresponding sustainability and economic viability. Munasinghe et al. [
35] addressed the optimal planning of the supply chain of crude palm oil production considering economic, environmental, and social aspects. Vaskan et al. [
36] presented an economic and environmental impact evaluation for the valorization of EFB to produce bioethanol, C5 syrup as cattle feed, power, and heat. Foo et al. [
37] proposed a linear programming (LP) model to address the optimum allocation of palm oil biomass taking into account profit maximization and cost/CO
2 minimization. Foong et al. [
38] addressed the optimal palm oil milling process considering economic evaluation using a hybrid combined mathematical programming and graphical approach. Tan et al. [
39] proposed an LP cooperative game model to allocate benefits that accrue from inter-plant integration in an eco-industrial park (EIP).
In this study, the abundant and underutilized EFB has been selected as a feedstock to produce various high value chemical building blocks, which have not been considered in the previous papers. Bhullar [
40] had identified sugars-based and lignin-based chemicals that have high economic potential; they are xylitol, levulinic acid, succinic acid, guaiacol, and vanillin, which are considered in this work. The growing concern of sustainability has increased the importance of taking economic, environment, and safety aspects into consideration as the criteria for the integrated sustainable biorefinery. Yet, most of the previous studies on palm oil-based biorefinery have focused on economic and environmental performance, and/or limited to individual chemicals such as levulinic and succinic acids [
41,
42]. Safety assessment is infrequently conducted at the early design stage, and it is commonly performed in the detailed design phase due to the nature of process safety methodologies, e.g., HAZOP. It is expected that, by simultaneously incorporating economic, environmental, and safety aspects, the conceptual design of an integrated biorefinery will lead to sustainable and optimal processes and consequently biorefinery establishment, as demonstrated for other cases in our previous works [
43,
44,
45].
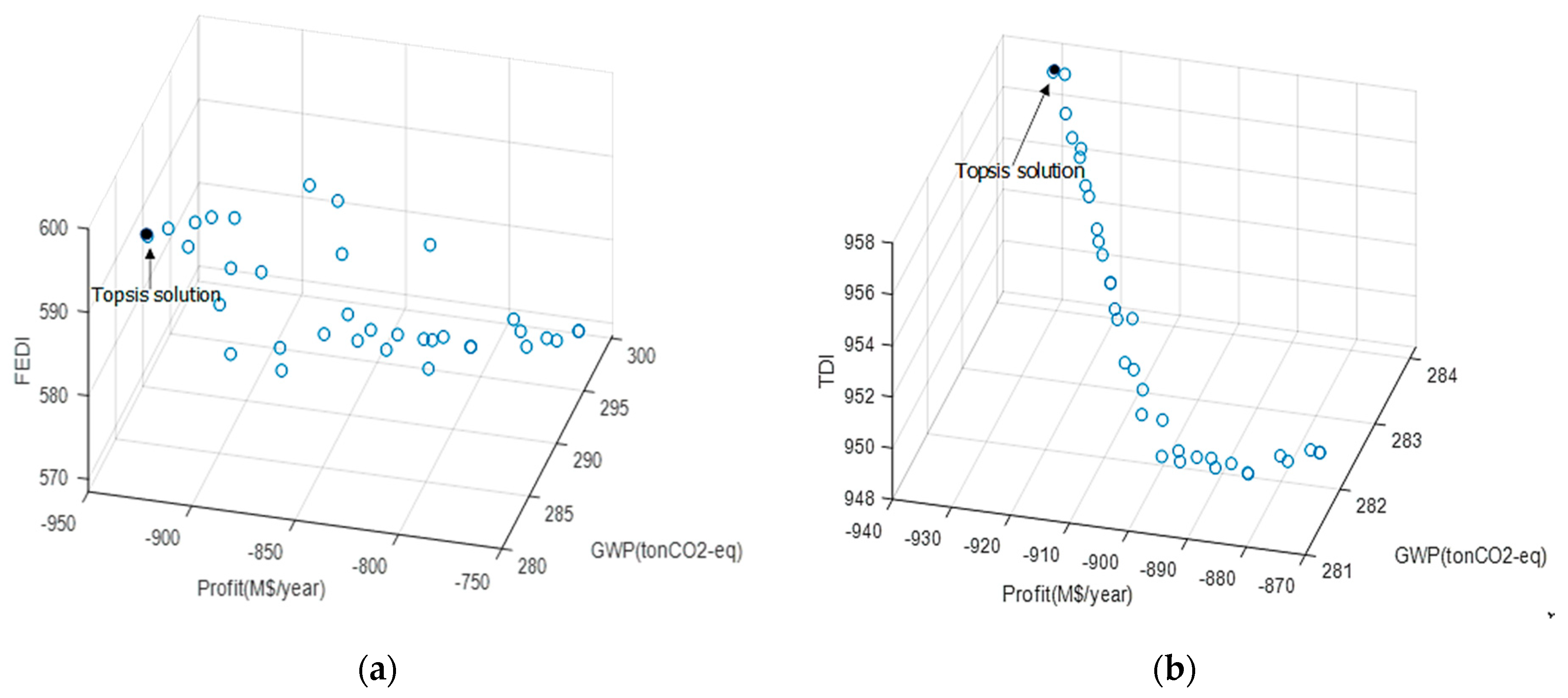
In this work, annual profit is estimated by Techno-Economic Analysis (TEA), Global Warming Potential (GWP) is quantified using Life Cycle Assessment (LCA), and Fire and Explosion Damage Index (FEDI) and Toxicity Damage Index (TDI), categorized as hazard potential, are performed using Hazard Identification and Ranking Assessment (HIRA) from Khan et al. [
46]. The goal is to find an optimal EFB-based biorefinery configuration, simultaneously considering economic, environmental, and safety aspects. The design problem is presented as a multi-objective optimization (MOO) problem, which is solved by a multi-objective genetic algorithm to determine optimal capacities, yield and biomass allocation lead to maximum profit, the minimum of both global warming potential and hazard level. The obtained results (the so-called Pareto-optimal solutions) reveal the trade-off among the objectives. In the subsequent step, a combined approach of Fuzzy Analytical Hierarchy Process (FAHP) and Technique for Order Preference by Similarity to Ideal Solution (TOPSIS) is applied to select one of the Pareto-optimal solutions.
2. Methodology
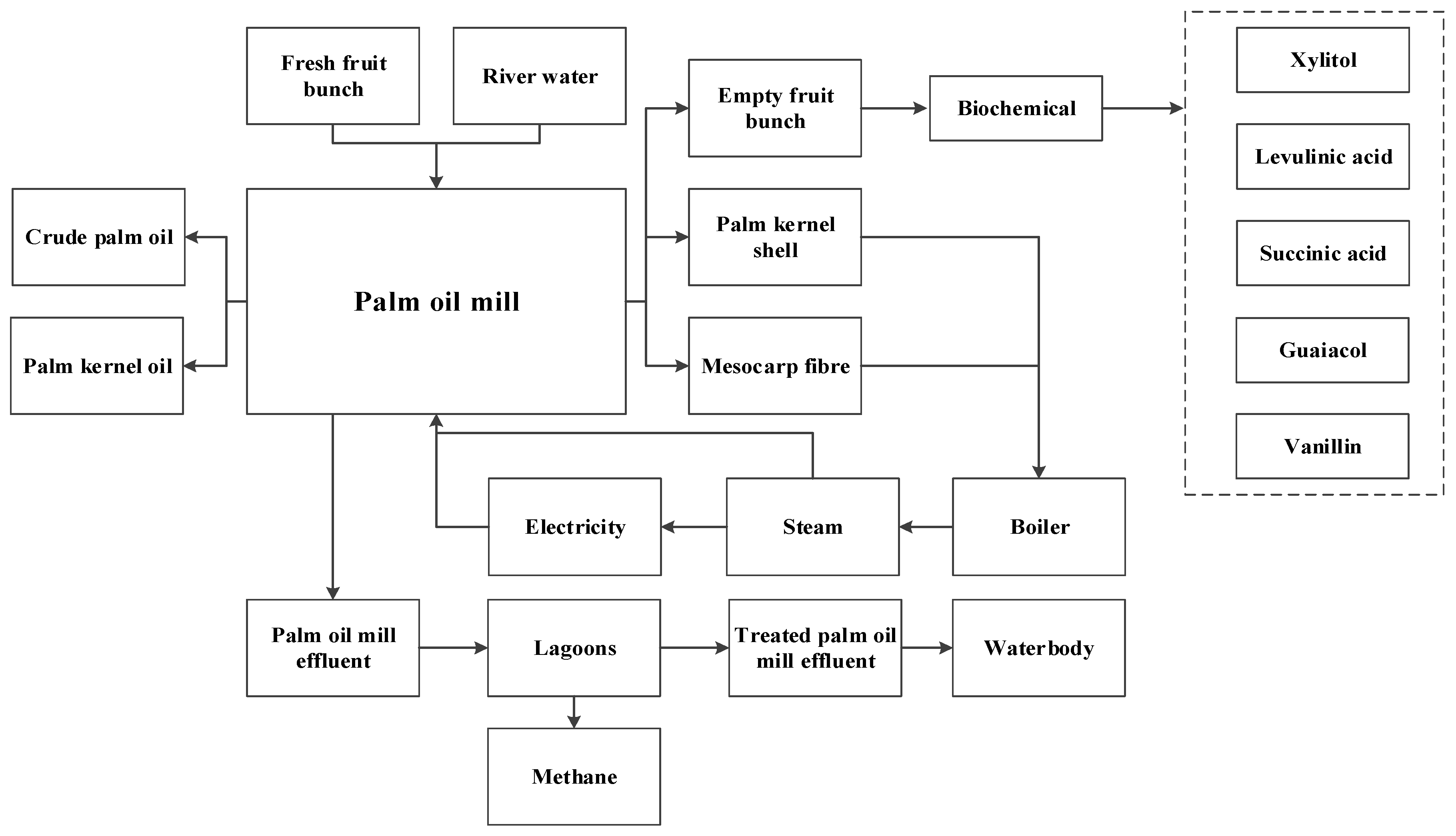
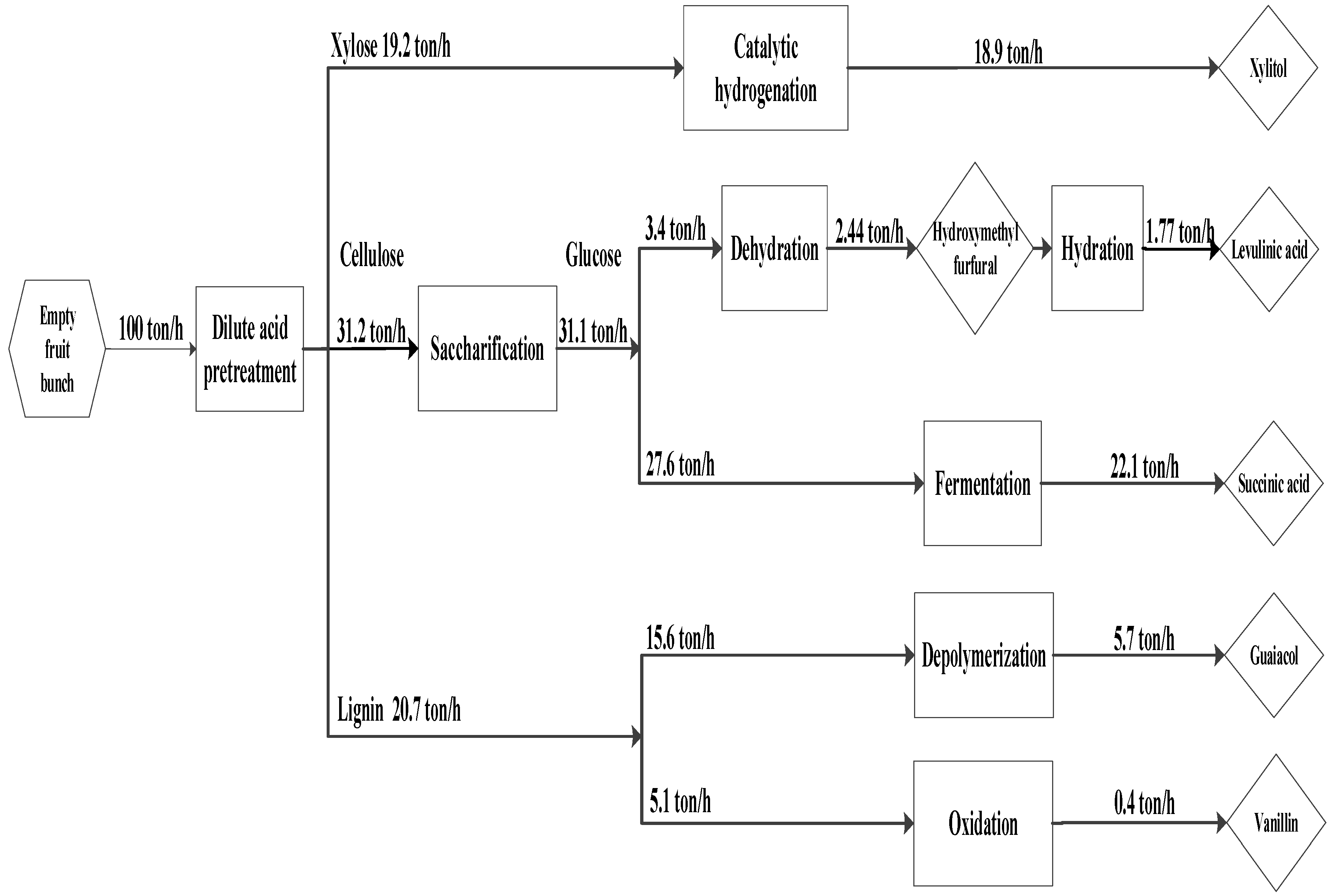
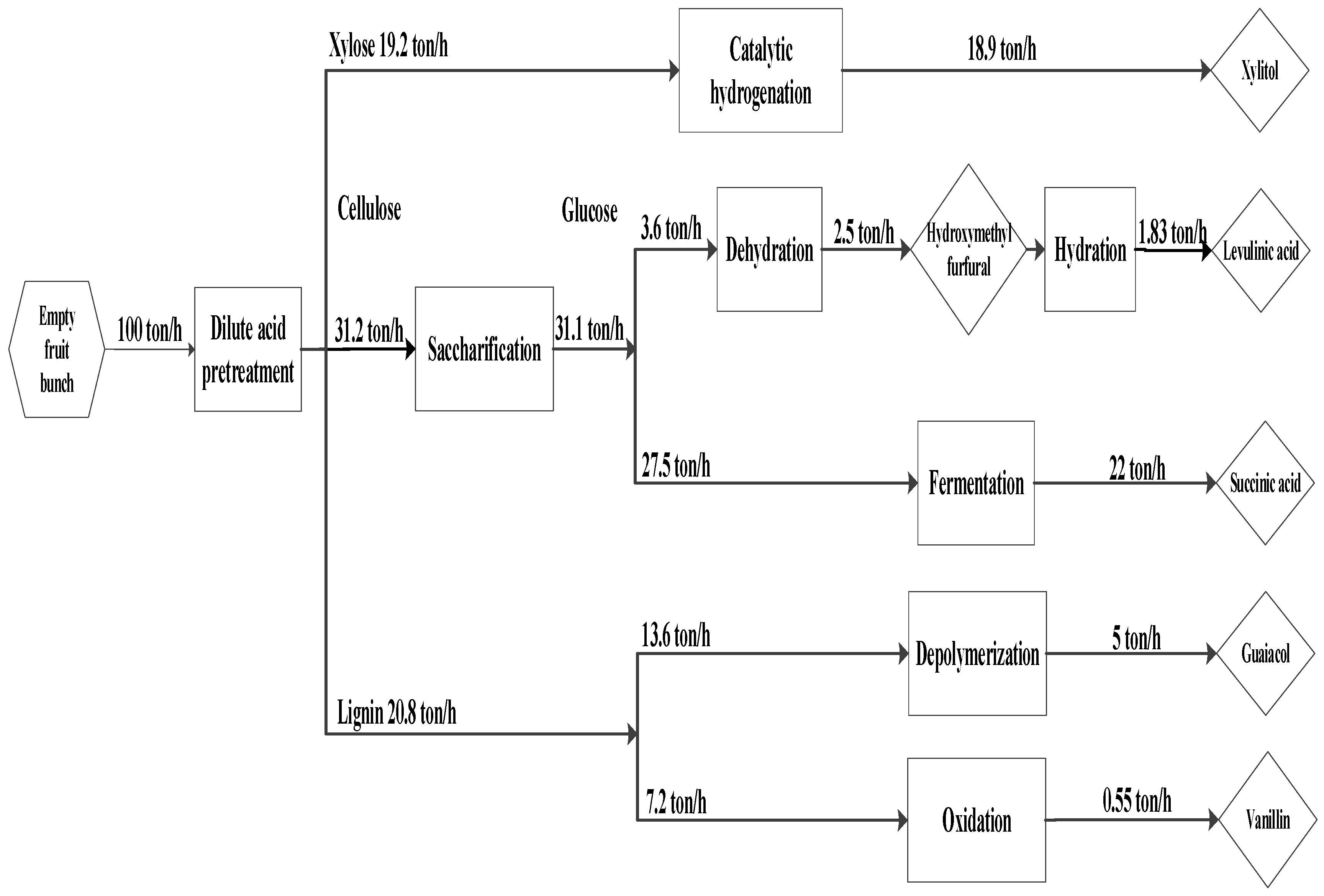
The proposed integrated biorefinery model is depicted in
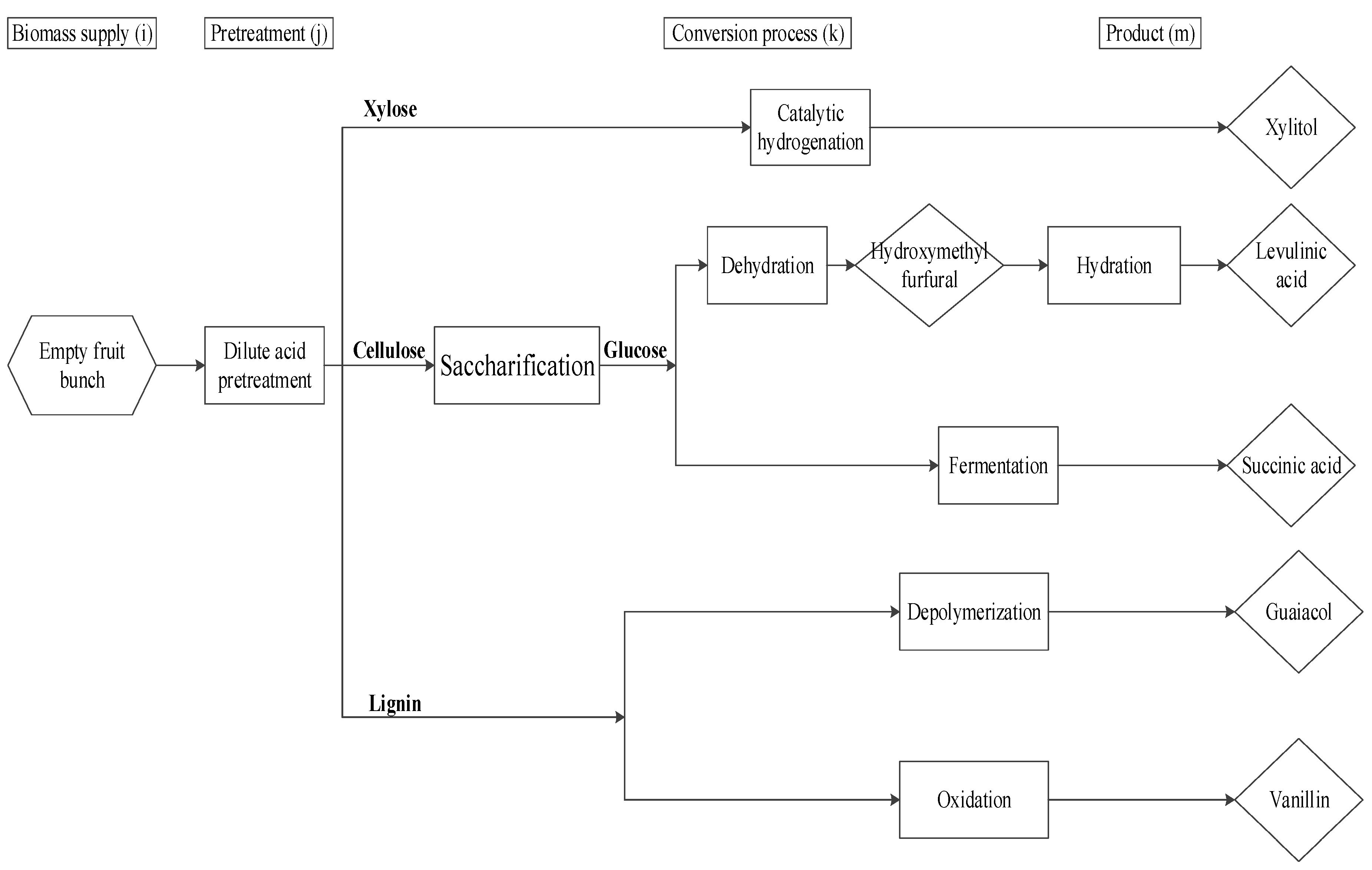
Figure 1, where EFB generated from palm oil mill activity is collected and sent to a centralized integrated biorefinery area. The potential of converting other palm oil wastes to valuable products is not considered in this work. A flowchart of the methodology of the present study is outlined in
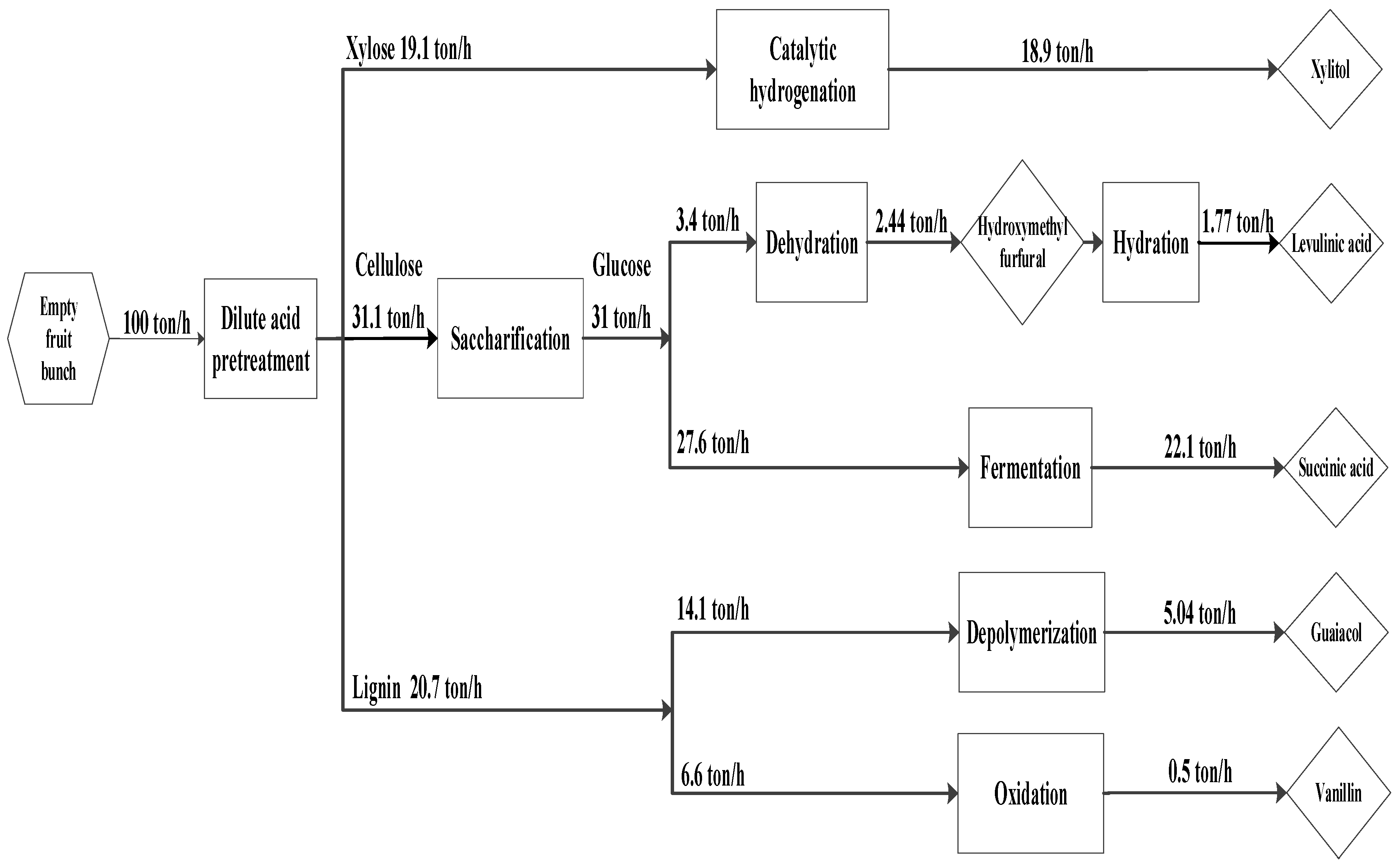
Figure 2. EFB composition is taken from Chiesa et al. [
47]. Dilute acid pretreatment, enzyme production, and saccharification processes are selected and simulated in Aspen Plus V10 according to Humbird et al. [
48]. The number of conversion steps for this work is limited to five biochemical products according to the potential revenues, and they are xylitol [
49,
50], levulinic acid [
51], succinic acid [
52], guaiacol [
53], and vanillin [
54]. The process simulation results are then used for equipment sizing and sustainability assessment.
For sustainability assessment of the integrated biorefinery, TEA is used to estimate the annual profit, LCA to quantify GWP, and HIRA to measure the hazard potential at initial design in terms of FEDI and TDI. These multiple criteria lead to a MOO problem to simultaneously maximize annual profit and minimize GWP, FEDI, and HIRA. The decision variables involved are biomass availability and product yields, and the constraints are related to mass and energy balances and global products demand. Prior to solving MOO problems, the developed process simulation models are simplified as surrogate models relating decision variables with the objectives [
56]. The surrogate (regression) models are developed from rigorous simulation results obtained through a central composite design (CCD) for later use in solving the MOO problem. The solution of MOO problems produces Pareto-optimal solutions, which reveal the trade-off among the objectives. To choose one of these solutions, FAHP and TOPSIS are used; FAHP takes into account the subjective inputs of experts with profound knowledge [
57].
The proposed superstructure for biorefinery based on EFB is shown in
Figure 3. The underutilized EFB supply is collected and transported to a central processing facility. Transportation costs and supply chain issues are not considered in this work. The EFB then undergoes a pre-treatment process to break down its major components into cellulose, hemicellulose, and lignin, which will be used as the feedstock to subsequent processes to produce xylitol, levulinic acid, succinic acid, guaiacol, and vanillin.
2.1. Techno-Economic Analysys
TEA of the processes is estimated using Aspen Process Economic Analyzer (APEA) V.10. The basis for this estimation is the simulated results and equipment sizing. Investment factors to calculate project capital expenditure are taken from Peters and Timmerhaus [
58], as tabulated in
Table S1 in the Supplementary Materials. The estimation of annual operating cost is based on Turton et al. [
59], and details of this estimations are reported in
Table S2 in the Supplementary Materials. The annual profit is calculated as the difference between the product annual sales and total cost, which is the sum of annualized capital expenditure (CAPEX) and annual operating expenditure (OPEX). The economic objective is to maximize annual profit (
$/year), as shown in Equations (1)–(3).
Here, (kg/h) is the mass production rate of products (xylitol, levulinic acid, succinic acid, guaiacol, and vanillin) and ($/kg) is the product price. ($/year) is annualized CAPEX of the pretreatment and final processes. The CAPEX is the sum of total direct plant cost, total indirect plant cost, contractor’s fee, contingency and fixed capital investment. ($/year) is equal to sum of direct manufacturing cost, fixed manufacturing cost and general manufacturing cost.
2.2. Life Cycle Assessment
The environmental impact assessment of the integrated biorefinery adopts the LCA technique using the ISO standard [
60]. All emissions are taken from the developed process simulation such as direct emissions of the process, electricity and heat consumption. The emission data related to electricity and heat consumption are acquired from commercial LCA databases such as Ecoinvent 3.5 [
61] and Simapro 8.5.3 [
62]. Then, the total Life Cycle Inventory (LCI) can be formulated as a function of the direct emission, electricity and heat consumption, as stated in Equation (4).
The
LCI is then translated into the corresponding environmental impact (GWP). The emissions considered are carbon dioxide (CO
2), methane (CH
4), and nitrous oxide (N
2O). The GWP is calculated as the total of GWP from each of these emissions as shown in Equations (5) and (6).
In this equation,
mi is the damage factor that accounts for each greenhouse emission, which is retrieved from Guinee [
63].
GWPj denotes the GWP in the pretreatment process while
GWPk indicates that of the chemical production process.
2.3. Inherent Safety
Two hazards potential, quantified in this work, are FEDI and TDI [
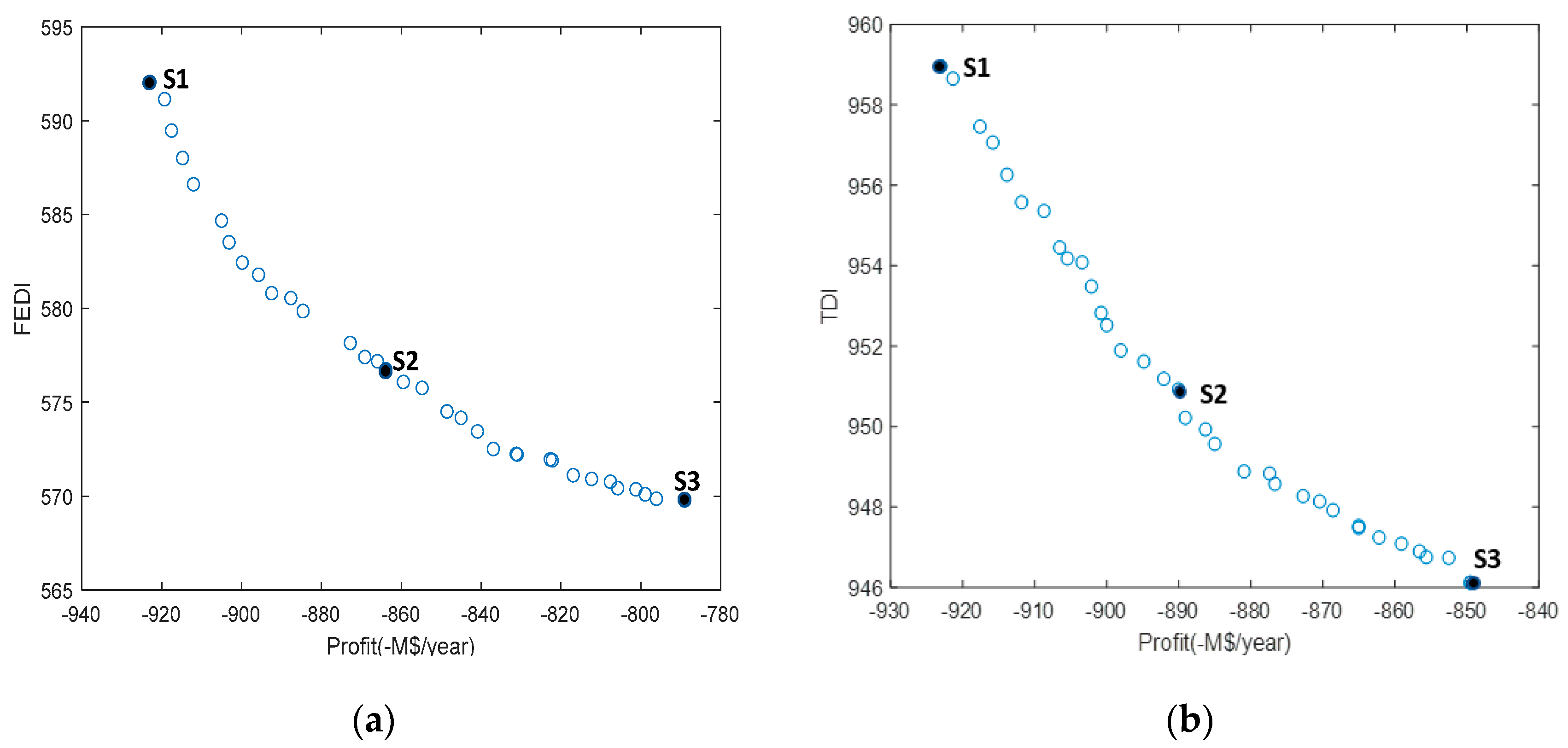
46]. FEDI is based on thermodynamic data, where the energy factor is the main aspect of the calculation. Another aspect is penalty, which is given based on the operating range of the process. The penalties involve five categories—namely, storage units, units involving physical operations, units involving chemical reactions, transportation units, and other hazardous units. Finally, the damage potential of FEDI is found by the multiplication of the penalties and the energy factors. For TDI calculation, toxic load contained in the processing unit is the major factor. Physical and chemical reaction units are considered. Penalties typically assigned for the location of the nearest hazardous unit and space occupied by the unit are neglected because of lack of required data during this conceptual design phase. The formulation of FEDI and TDI is stated in Equations (7)–(16)
Here, F1, F2, F3, and F4 are chemical, physical, and reaction energy, respectively. M is the mass flow rate of the chemical (kg/s), Hc is the heat of combustion of the chemical (kJ/kg), and K is a constant (3.148). In Equations (8) and (9), Pp (kPa) and Vp (kPa) are the process pressure and vapor pressure of the chemical at process temperature. V is the volumetric flow rate of chemical (m3/h). TDI involves a G factor and several penalties. G factor is obtained from A (phase condition), and m is the anticipated release rate in kg/s.
2.4. Constraints
Biomass availability constraint is shown in Equation (17).
This shows that EFB consumed in the production process is within a minimum and maximum range of EFB supplied. EFB is delivered to plant using a truck with a capacity of 25 ton/truck [
64]. The maximum allowable number of trucks to transport EFB is taken to vary from 2 trucks/h to 4 trucks/h. This range is set based on the assumed biomass unloading time of 15–30 min/truck and only one unloading facility within the plant. The assumption of 15 min/truck is based on about 5–10 min of unloading time, and the remaining time is for traveling in and out of the plant. This number becomes the logistic limit within the plant, which in turn limits the maximum production to 4 trucks/h. The same reasoning applies to 2 trucks/h.
Chemical mass yield information is gathered from the experimental data of references and they are modelled in min and max scenarios, which are used in the process simulation, as stated in Equation (18).
The mass yield of each process
Xk is set within the range of
Xkmin and
Xkmax, which are determined from the experimental data of xylitol [
49,
50], levulinic acid [
51], succinic acid [
53], guaiacol [
53], and vanillin [
54]. The yield information is modelled in min and max scenarios which are used in the process simulation. The data are tabulated in
Table 1.
The biochemical products are expected to fulfill the global demand for each product, as shown in Equation (19) and tabulated in
Table 2.
The products obtained from the integrated biorefinery Pm must be equal to or greater than the global demand.
2.5. Genetic Algorithm
Genetic algorithm (GA) is a directed random search technique that is modeled on the natural evolution/selection process toward the survival of the fittest [
70]. In briefly, this algorithm begins with an initial population of chromosomes or trial solutions or individuals, each characterized by a set of values of decision variables in MOO problem. The individuals are generated randomly within the lower and upper bounds of decision variables, and are supplied to calculate objective functions (annual profit, GWP, FEDI, and TDI). Individuals from one generation are used to create a new population, based on selection and reproduction by crossover and mutation. The crossover is carried out on randomly selected parent individuals and generates offspring by swapping parts of the parent chromosomes. Afterward, mutation occurs by randomly altering the offspring created by crossover. This drastic change helps to prevent solutions from being stuck near a local optimum. Thus, the algorithm generates different individuals for the next generation (i.e., new population) from the previous population. These steps are repeated until some termination criterion (e.g., maximum number of generations or improvement of the best solution) is satisfied.
One adaptation of GA for MOO is gamultobj code in MATALAB, which was used in this study.
Table 3 lists the values of GA parameters used in the present study. Bounds on the decision variables are tabulated in
Table 4. The developed model equations used in multi-objective genetic algorithm are given in Section B in the
Supplementary Materials.
2.6. Multi-Criteria Decision Making
To choose one preferred solution from the Pareto-optimal frontier, FAHP and TOPSIS are applied. Both these are outlined in this section.
2.6.1. Fuzzy Analytical Hierarchy Process
FAHP is a combination of fuzzy logic and linguistic variables [
71]. In this work, such a method is applied to overcome the uncertainty in the judgment of decision makers in their selection of the best optimum solution [
72]. The steps involved in the computation of criterion weights using FAHP are described in this sub-section.
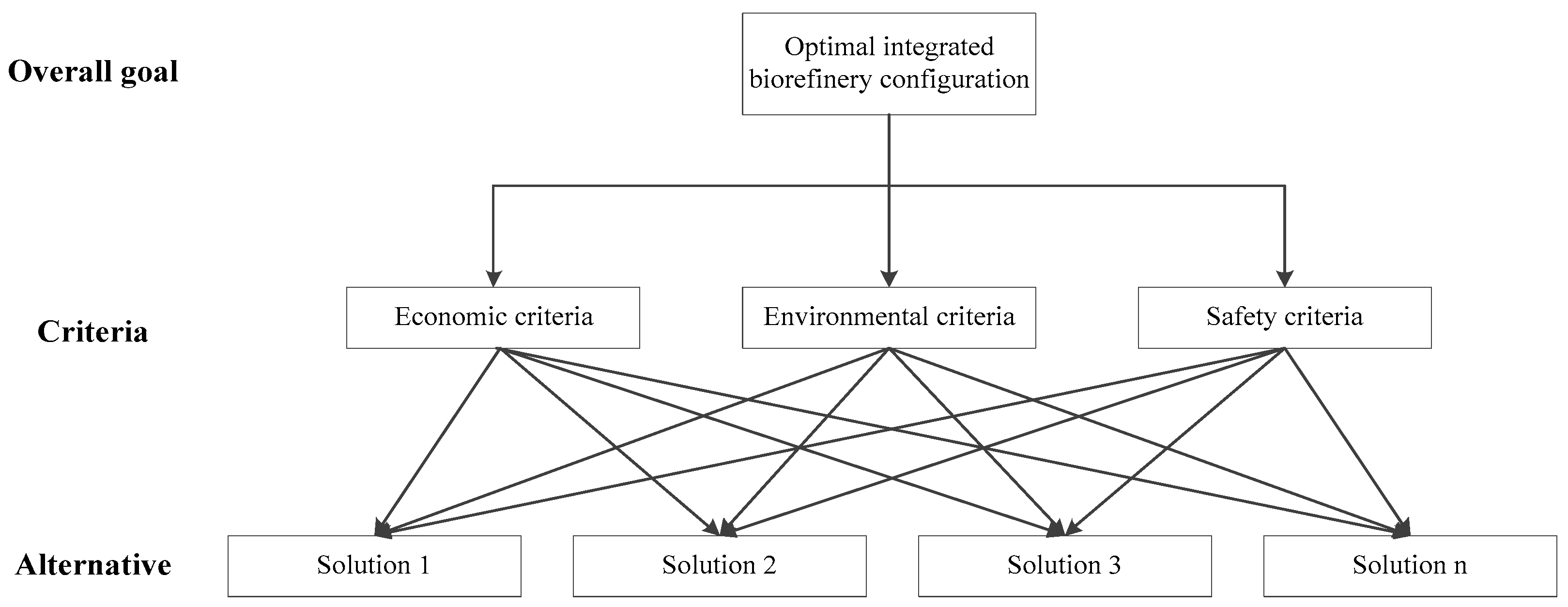
1. Generating a hierarchy system evaluation
This work is to find the best optimal biorefinery superstructure configuration incorporating the sustainability criteria, which are comprised of economic, environment and safety aspects. The Pareto-optimal solutions generated by solving the MOO problem are the alternatives. The detailed decision model is presented in
Figure 4.
2. Create a fuzzified pairwise comparison matrix
In this work, the decision maker’s judgment is gathered according to the questionnaire, which was taken from Yan [
73] and is summarized in
Table S6 in the Supplementary Materials. Afterward, the pairwise comparison of the evaluation criteria is made based on a linguistic scale. The calibrated linguistic fuzzy scale suggested by Promentilla et al. [
74] is implemented in this work, as shown in
Table 5. The result of fuzzy pairwise comparison judgments can be expressed in the form of a matrix. The matrix A is an m x m real matrix, where
m is the number of evaluation criteria. Each entry
ajk of a matrix A represents the importance of the criterion. If
ajk > 1, the
jth criterion is more important than the
kth criterion; if
ajk < 1, the
jth criterion is less important than the
kth criterion. Then, the weight of the criteria and the rating of alternatives concerning can be calculated using Equation (20).
3. Aggregation of DM’s judgment
Then, fuzzy judgments of all DMs are aggregated using Equation (21):
4. Computation of criteria weights
The criteria weights are then deduced through the non-linear programming model proposed by Tan et al. [
75], as stated in Equations (22) and (23). This model approximates the criteria weights by constraining the consistency index (
) within the fuzzy bound. A positive
indicates a consistent fuzzy pairwise judgment given by the expert; hence, the criteria weights elicited are acceptable and can be applied for further computation. Note that
= 1 suggests perfect consistency in preserving the order of preference intensities.
Maximize
Subject to
, where
2.6.2. Technique for Order Preference by Similarity to Ideal Solution
The methodology of TOPSIS is briefly explained below. Application and assessment of TOPSIS to many problems are available in Wang et al. [
76].
1. Calculate a normalized matrix
The decision matrix of
Xij is normalized using the following Equation (24):
2. Calculate weighted normalized matrix
The normalized decision matrix is multiplied by the weight,
wi, obtained from Equations (22) and (23). Calculation is performed by the following Equation (25):
3. Calculate the ideal best and ideal worst value
The positive ideal solution
A* and the negative ideal solution
A− are determined using the following Equations (26) and (27):
4. Calculate Euclidean distance from the positive/negative ideal
The distance from the positive and negative ideal for each alternative can be computed by the Euclidean distance as given in Equations (28) and (29).
5. Calculate performance score
The relative closeness of the
ith alternative is defined as
The ranking priority of alternatives is determined based on the higher score of .