Optimization of Magnetic Properties of Magnetic Microwires by Post-Processing
Abstract
:1. Introduction
2. Experimental Methods and Materials
3. Results and Discussion
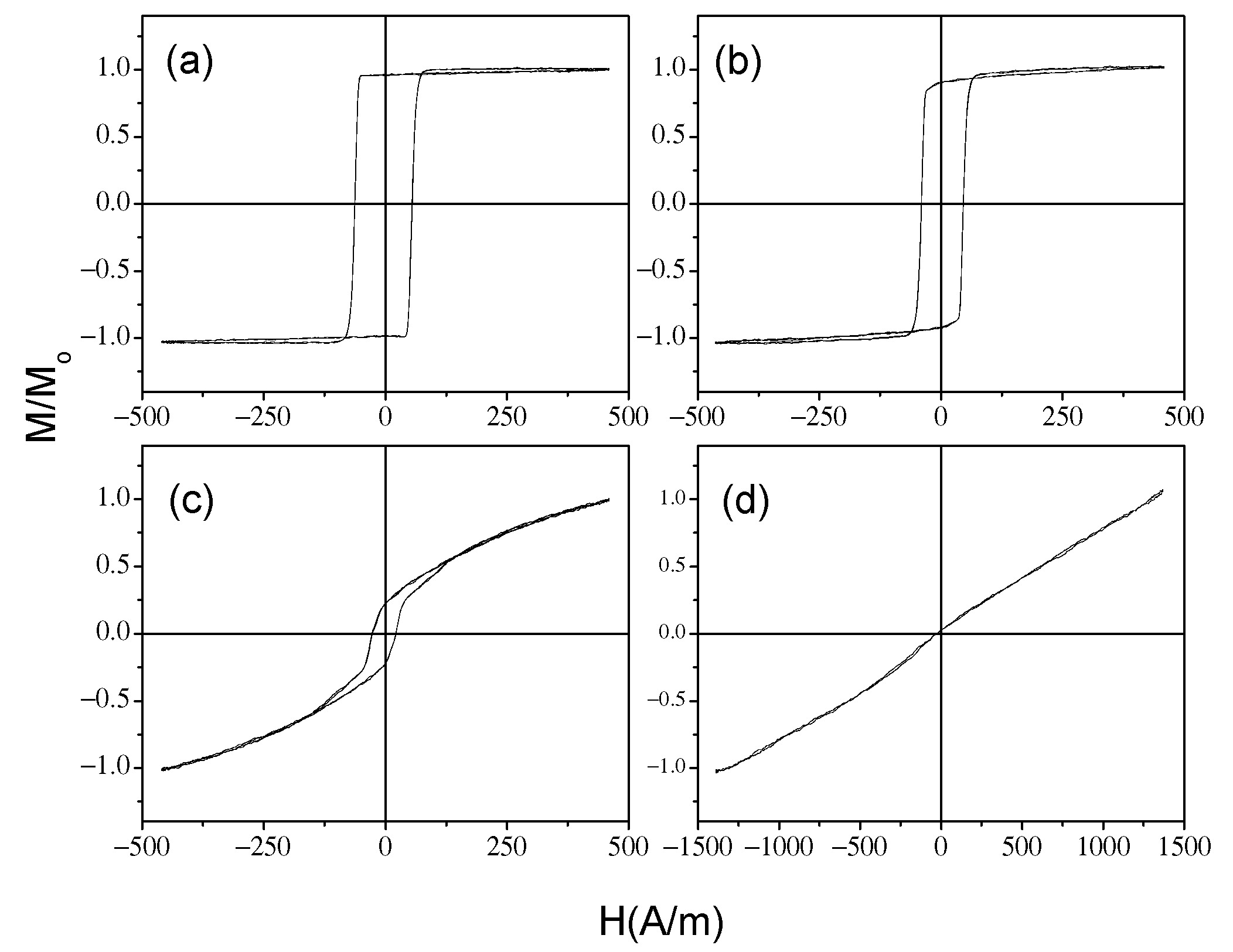
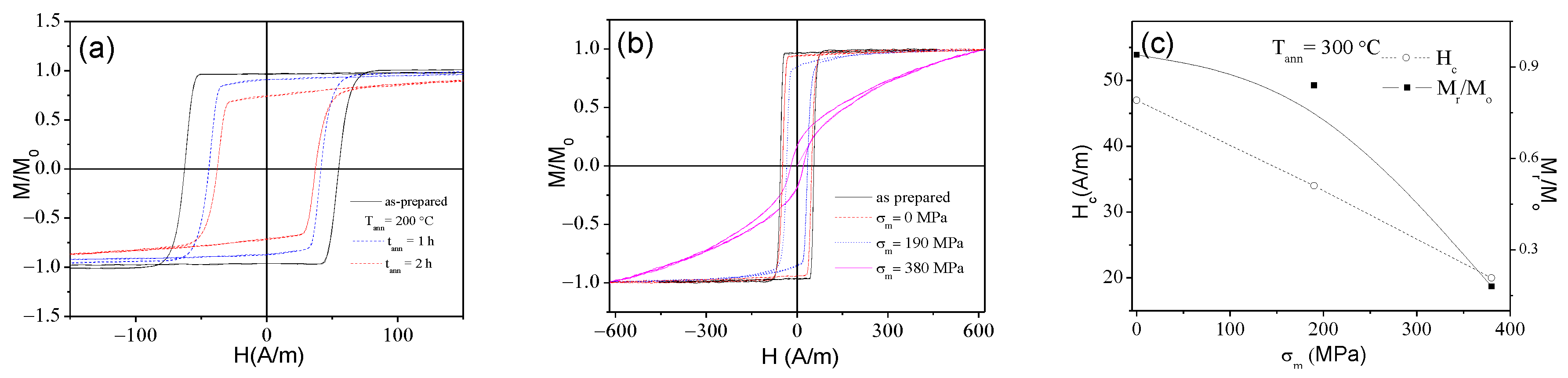
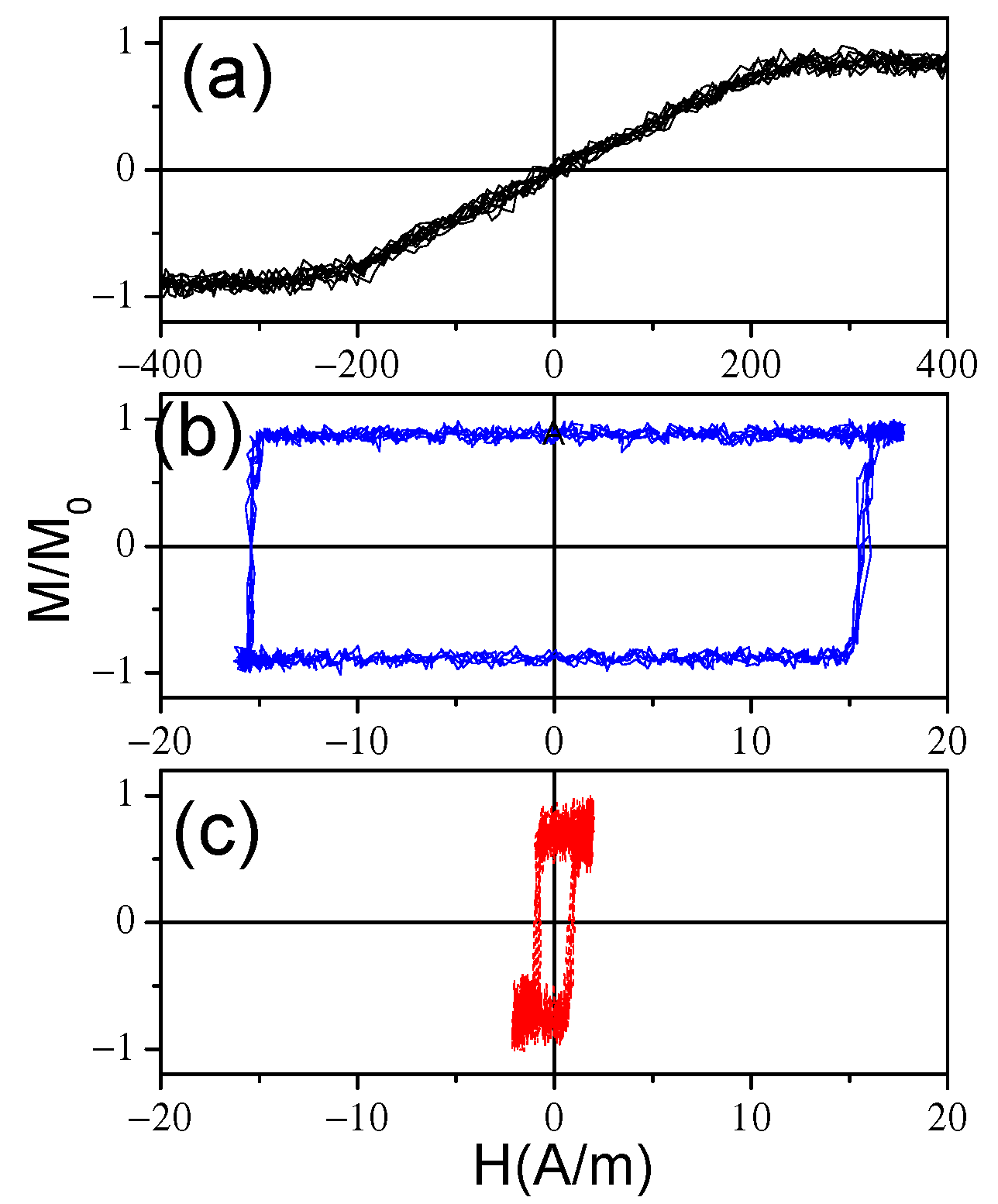
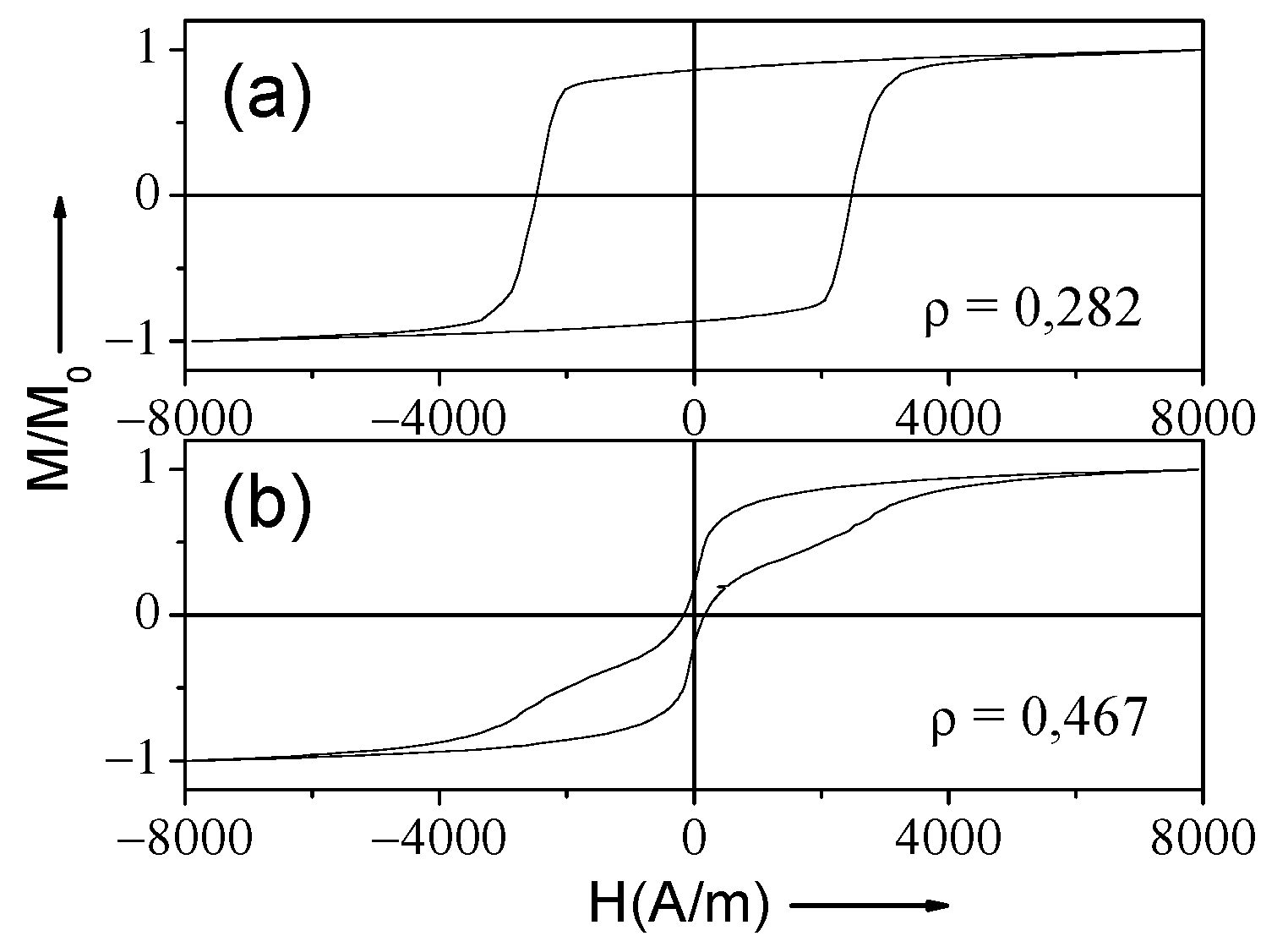
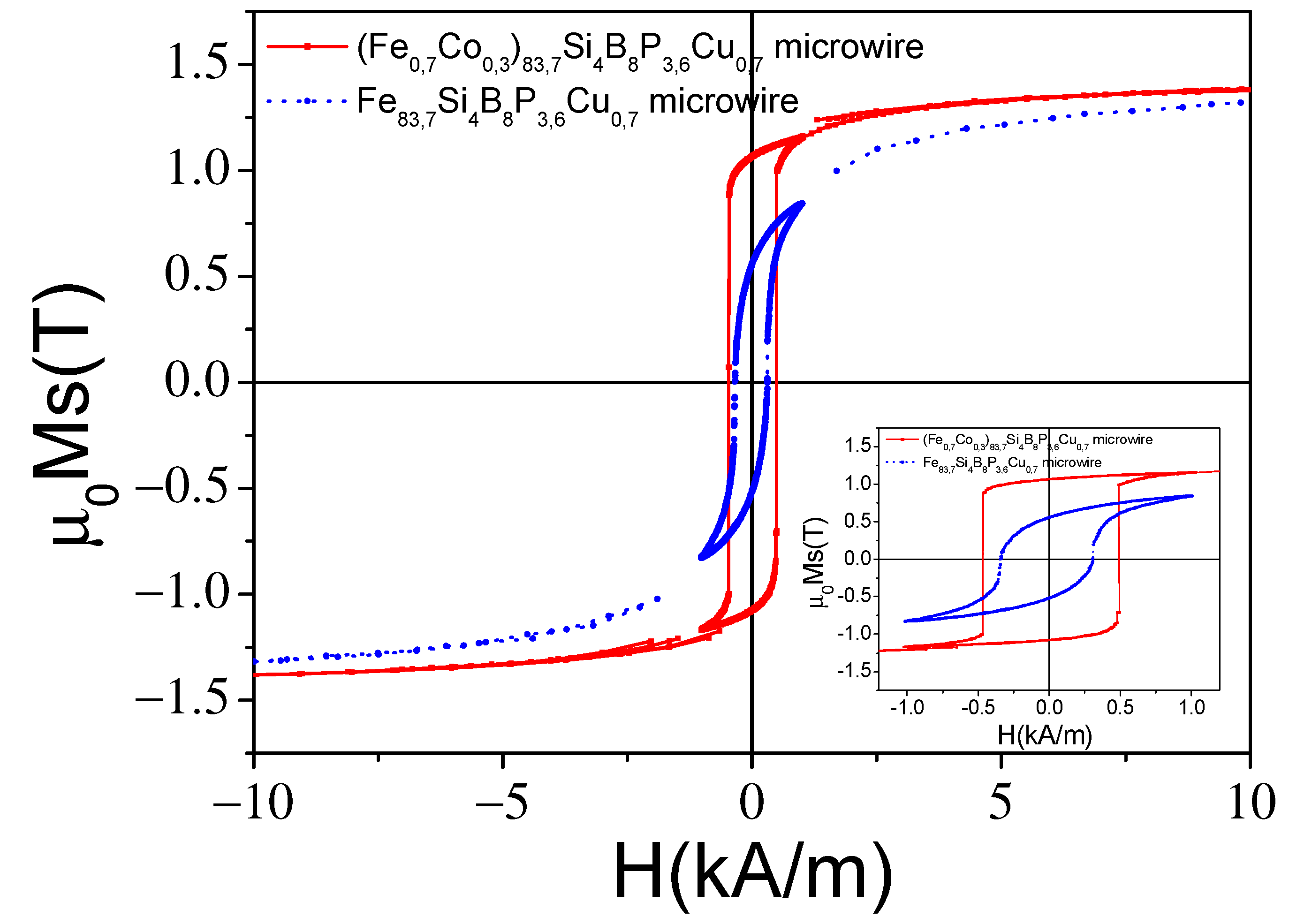
3.1. Effect of Magnetoelastic Anisotropy on Magnetic Properties of Amorphous Glass-Coated Microwires
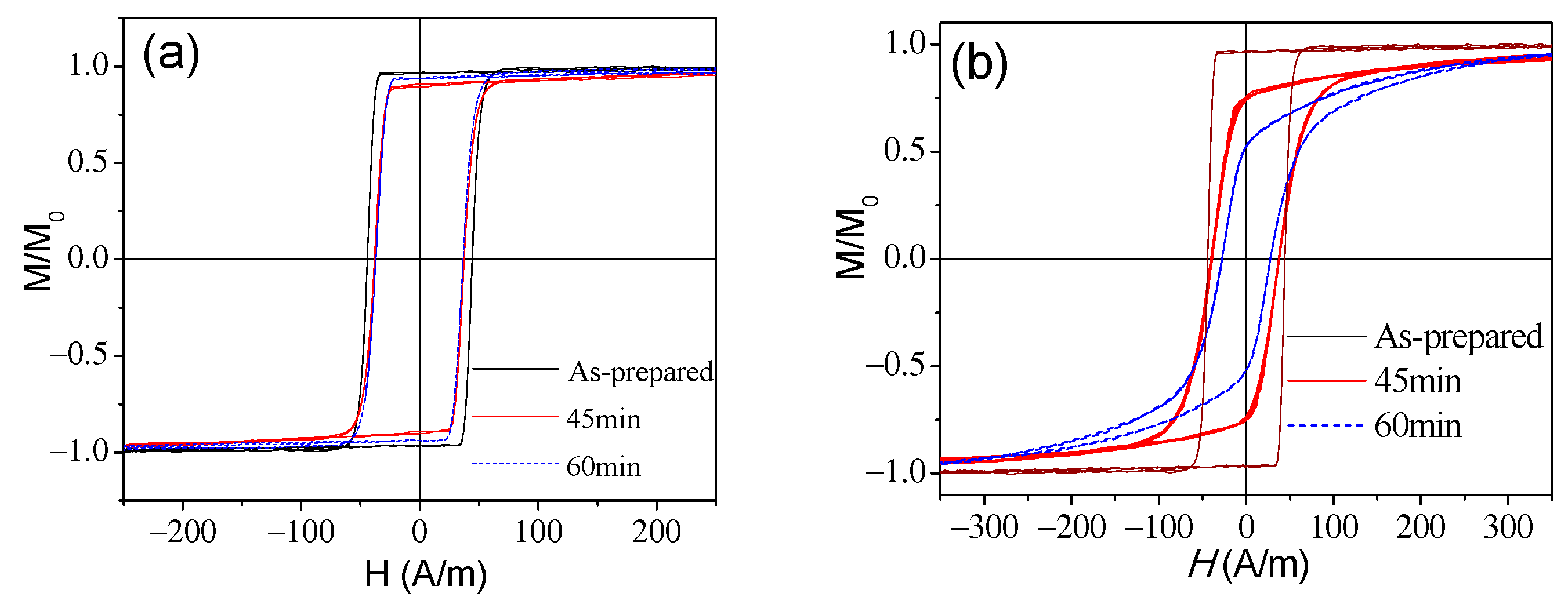
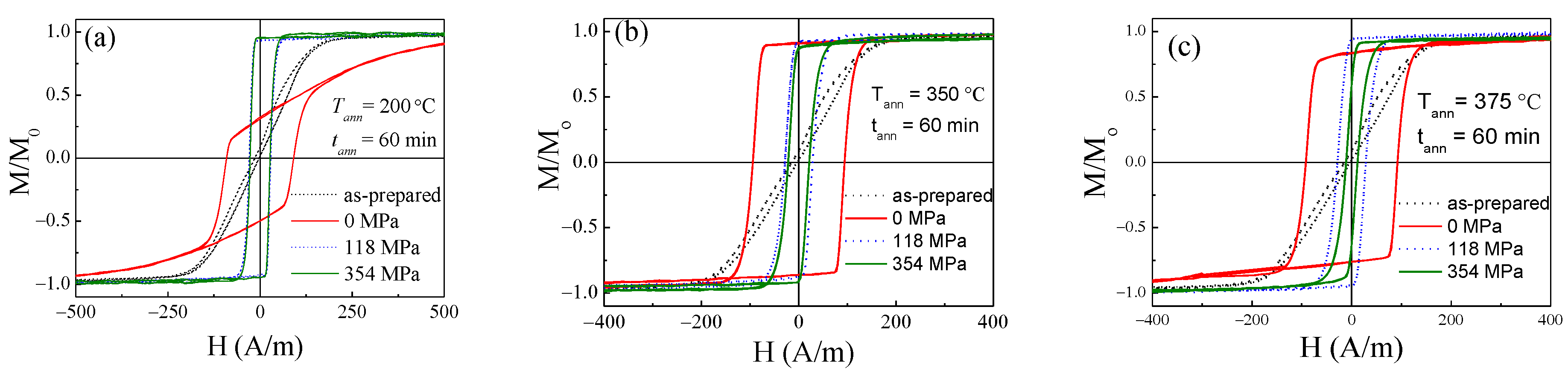
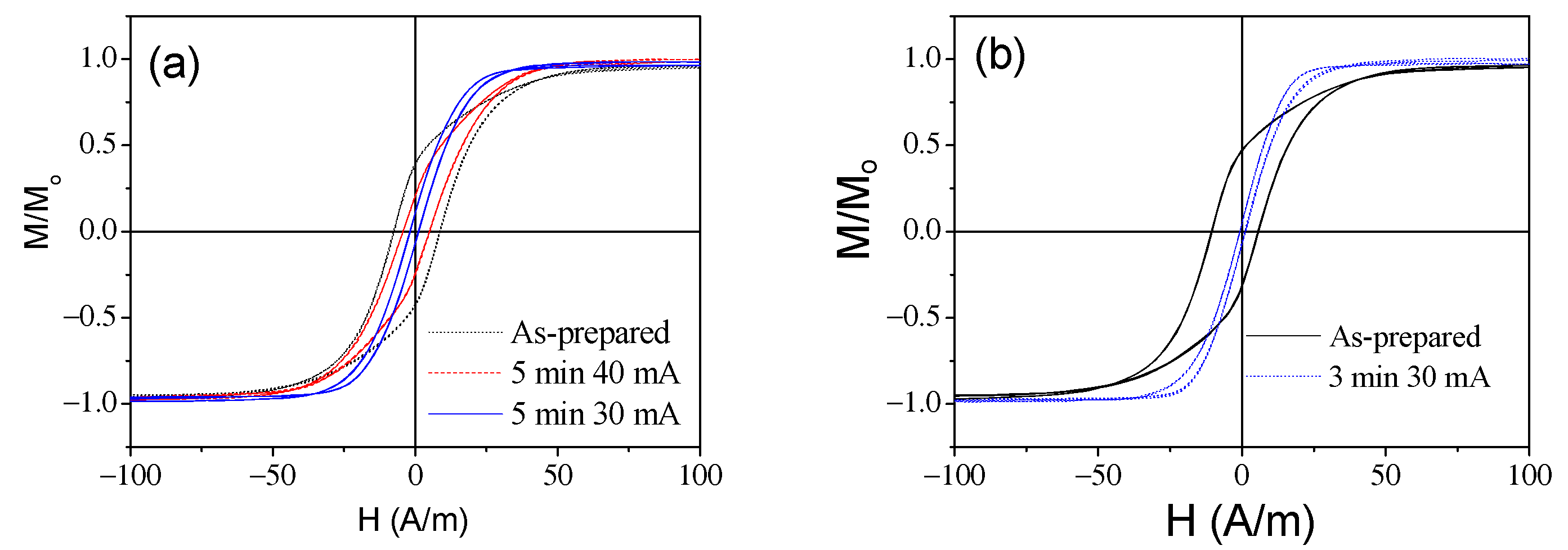
3.2. Effect of Induced Magnetic Anisotropy on Hysteretic Magnetic Properties of Amorphous Glass-Coated Microwires
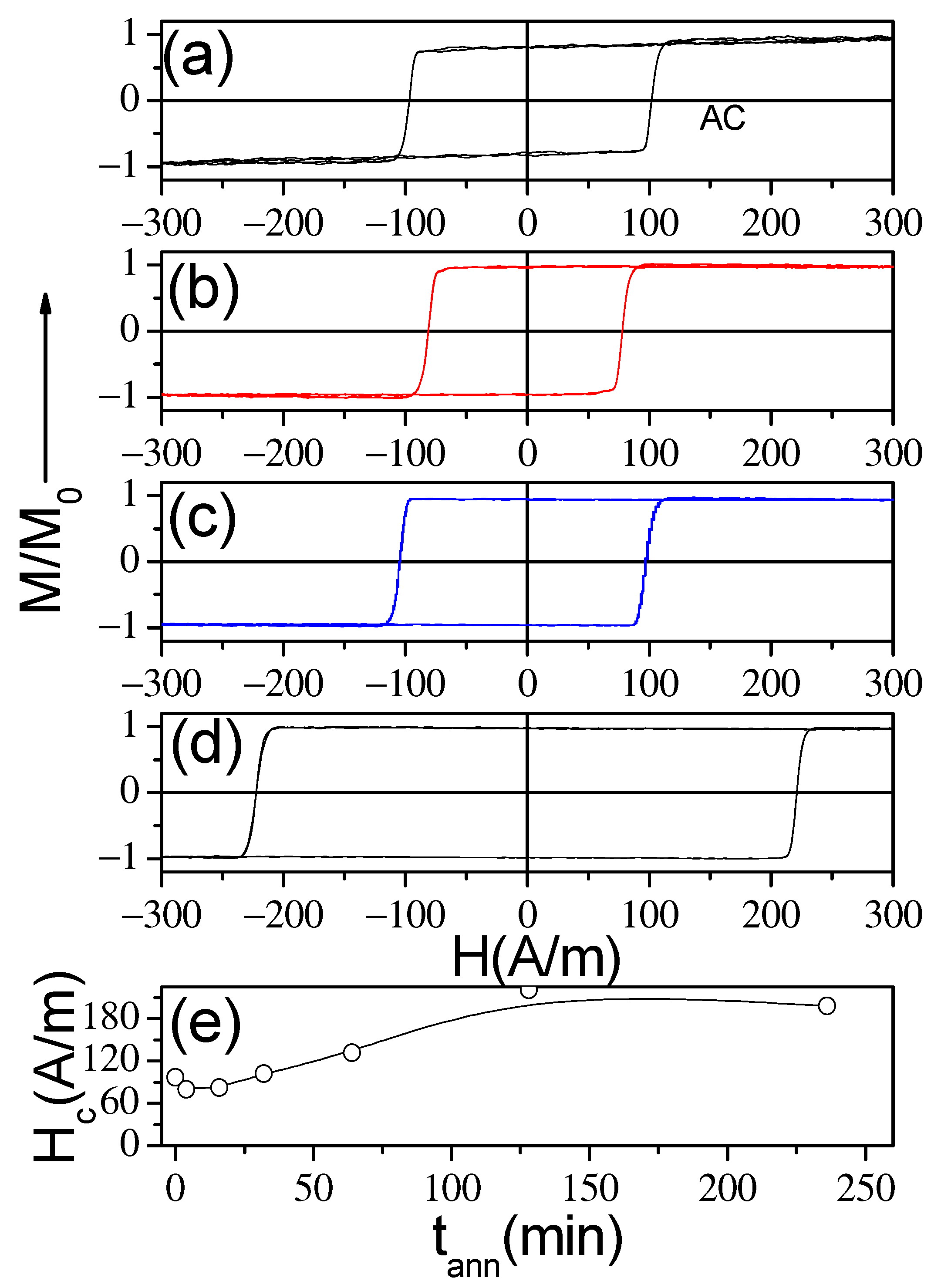
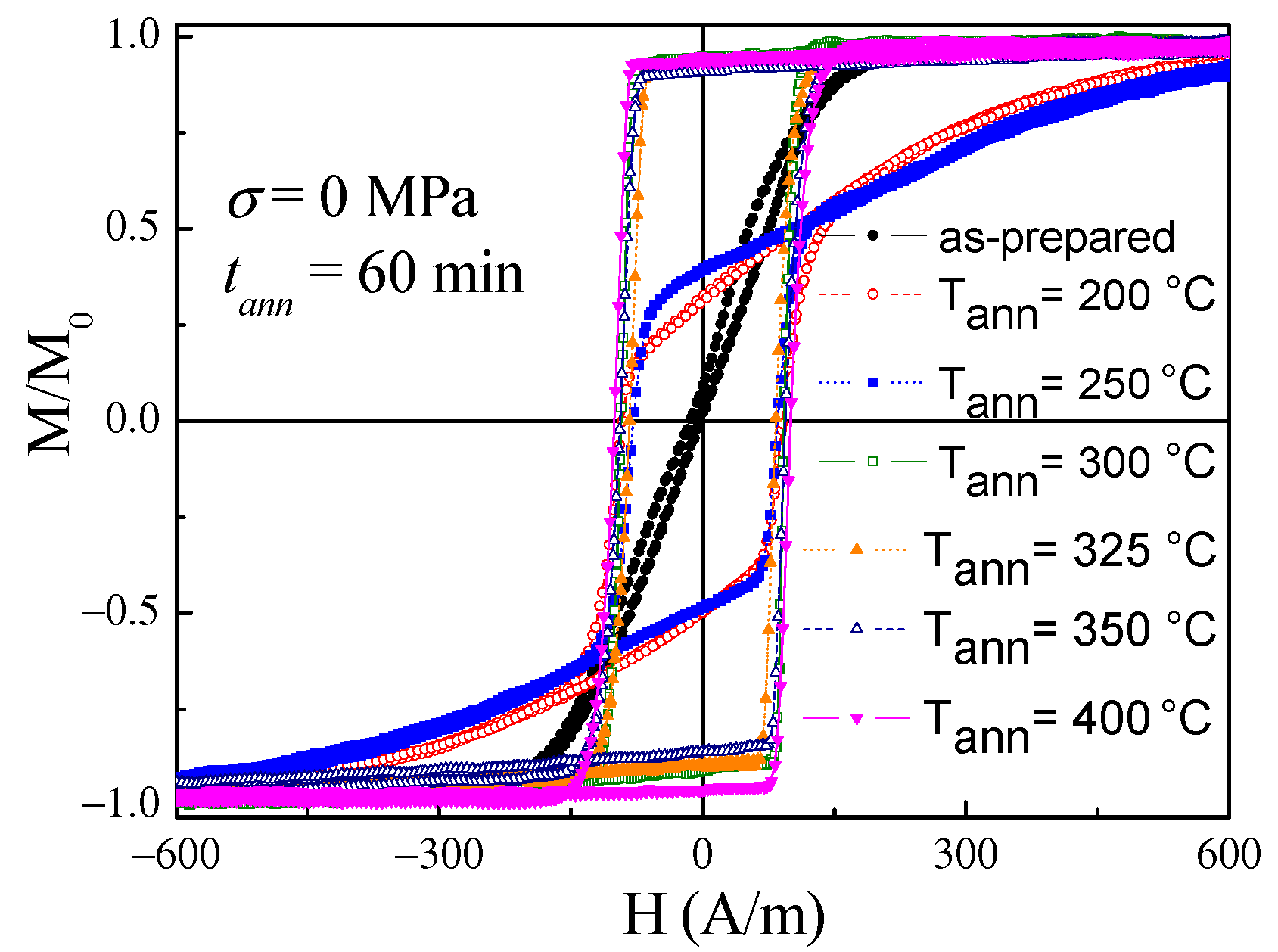
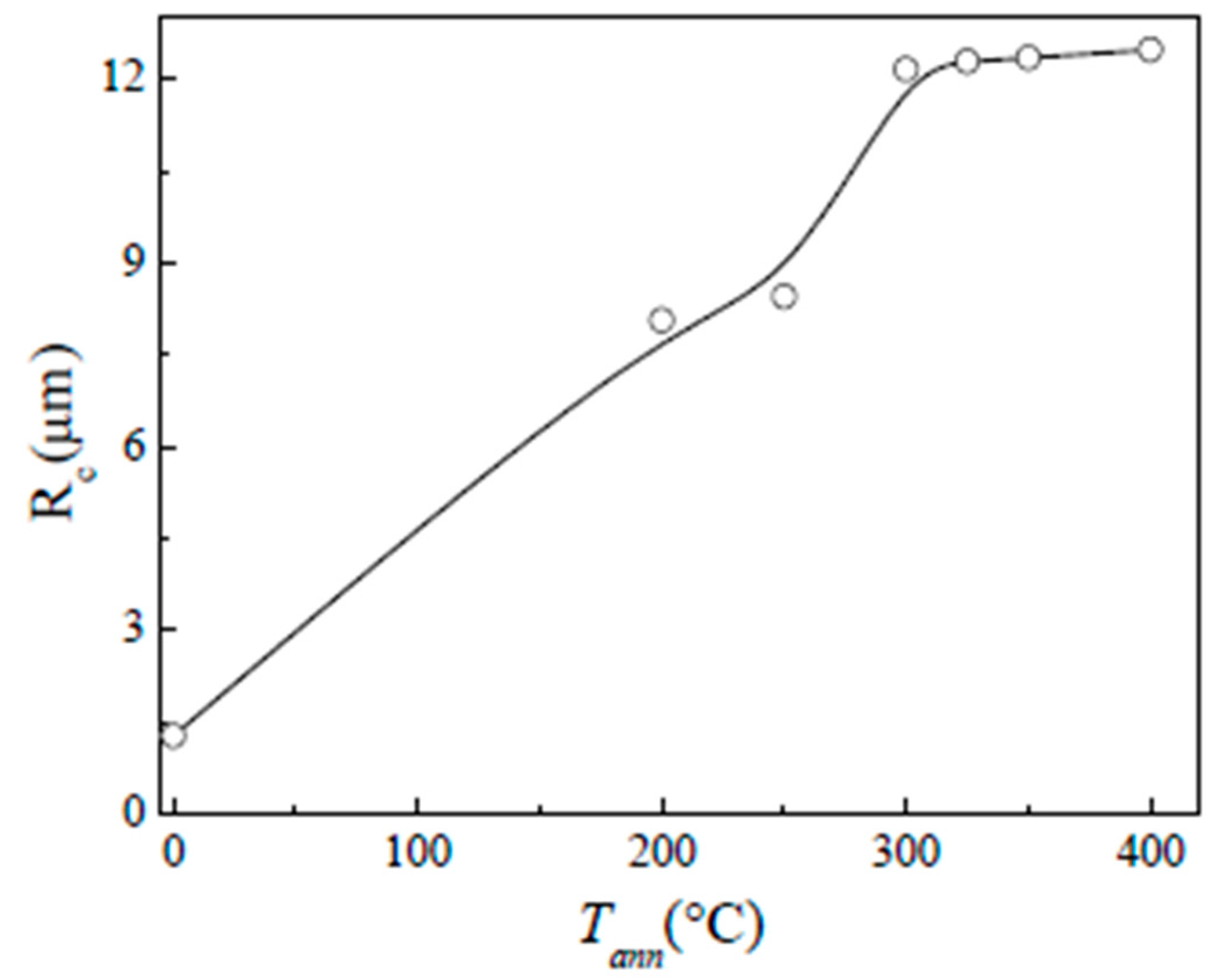
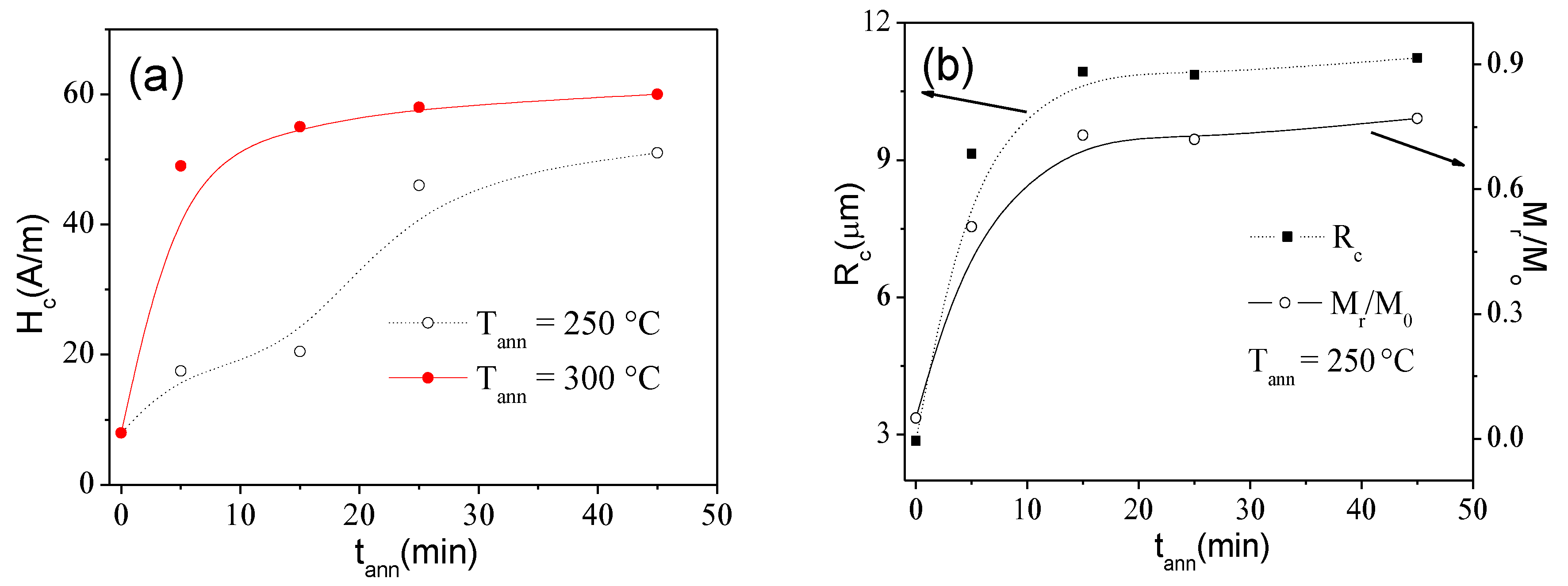
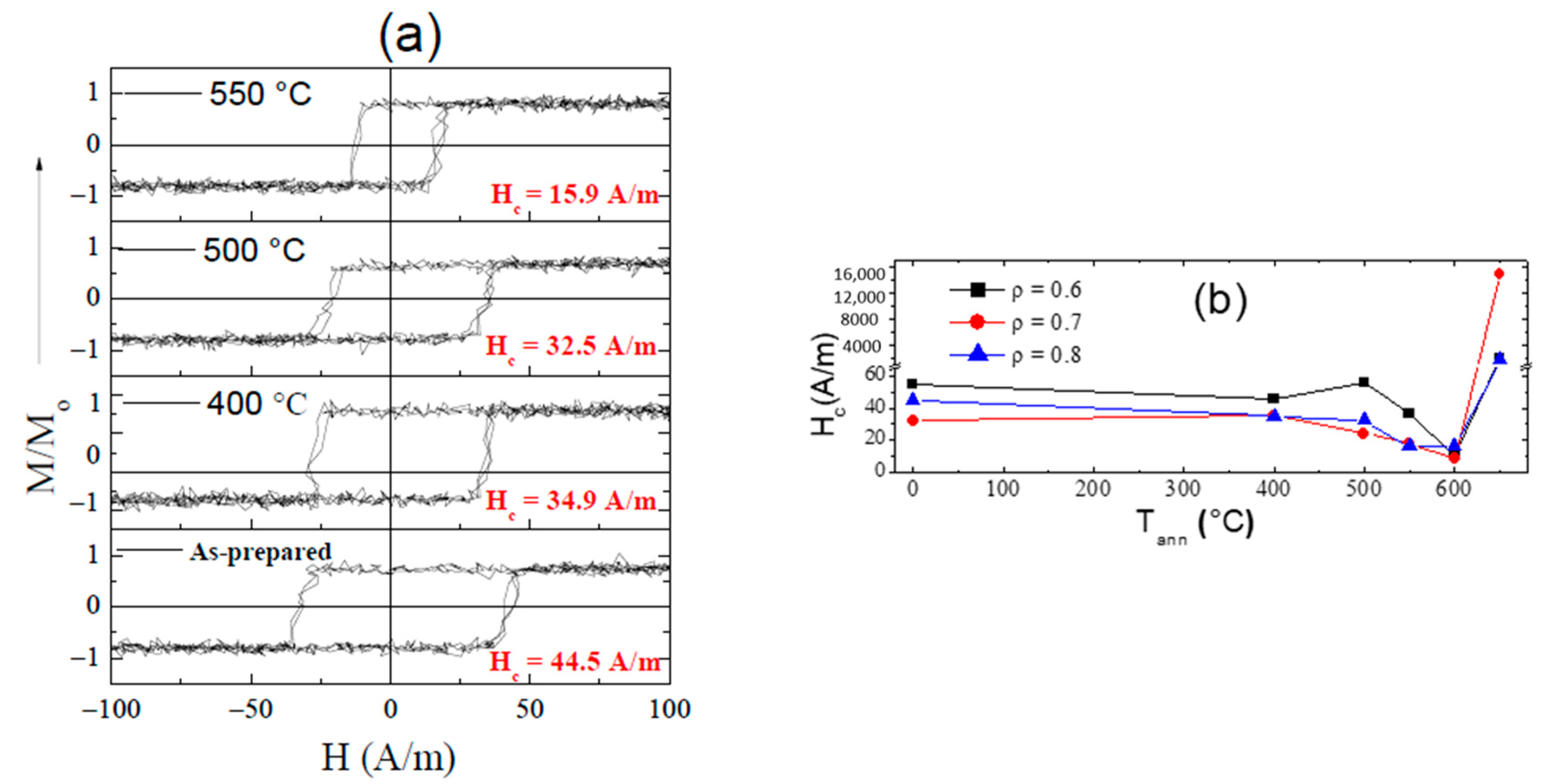
3.3. Tuning of Hysteretic Magnetic Properties in Crystalline and Devitrified Glass-Coated Microwires
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Lenz, J.; Edelstein, S. Magnetic sensors and their applications. IEEE Sens. J. 2006, 6, 631–649. [Google Scholar] [CrossRef]
- Díaz-Michelena, M. Small Magnetic Sensors for Space Applications. Sensors 2009, 9, 2271–2288. [Google Scholar] [CrossRef] [PubMed]
- Ripka, P.; Vértesy, G. Sensors based on soft magnetic materials Panel discussion. J. Magn. Magn. Mater. 2000, 215, 795–799. [Google Scholar] [CrossRef]
- Fiorillo, F.; Bertotti, G.; Appino, C.; Pasquale, M. Soft Magnetic Materials. In Wiley Encyclopedia of Electrical and Electronics Engineering; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2016; pp. 1–42. [Google Scholar]
- Jiles, D.C. Recent advances and future directions in magnetic materials. Acta Mater. 2003, 51, 5907–5939. [Google Scholar] [CrossRef]
- Zhukov, A. (Ed.) High Performance Soft Magnetic Materials; Springer Series in Materials Science; Springer International Publishing: Cham, Switzerland, 2017; p. 216. ISBN 978-3-319-49705-1. [Google Scholar]
- Mohri, K.; Humphrey, F.B.; Kawashima, K.; Kimura, K.; Mizutani, M. Large Barkhausen and Matteucci effects in FeCoSiB, FeCrSiB, and FeNiSiB amorphous wires. IEEE Trans. Magn. 1990, 26, 1789–1791. [Google Scholar] [CrossRef]
- Ogasawara, I.; Ueno, S. Preparation and properties of amorphous wires. IEEE Trans. Magn. 1995, 31, 1219–1223. [Google Scholar] [CrossRef]
- Vazquez, M.; Chen, D.-X. The magnetization reversal process in amorphous wires. IEEE Trans. Magn. 1995, 31, 1229–1238. [Google Scholar] [CrossRef]
- Panina, L.V.; Mohri, K. Magneto-impedance effect in amorphous wires. Appl. Phys. Lett. 1994, 65, 1189–1191. [Google Scholar] [CrossRef]
- Beach, R.S.; Berkowitz, A.E. Giant magnetic field dependent impedance of amorphous FeCoSiB wire. Appl. Phys. Lett. 1994, 64, 3652–3654. [Google Scholar] [CrossRef]
- Zhukov, A.; Ipatov, M.; Zhukova, V. Chapter 2—Advances in Giant Magnetoimpedance of Materials. In Handbook of Magnetic Materials; Buschow, K.H.J., Ed.; Elsevier: Amsterdam, The Netherlands, 2015; Volume 24, pp. 139–236. [Google Scholar]
- Knobel, M.; Vázquez, M.; Kraus, L. Giant Magnetoimpedance. In Handbook of Magnetic Materials; Elsevier: Amsterdam, The Netherlands, 2003; Volume 15, pp. 497–563. [Google Scholar]
- Harrison, E.P.; Turney, G.L.; Rowe, H. Electrical Properties of Wires of High Permeability. Nature 1935, 135, 961. [Google Scholar] [CrossRef]
- Sixtus, K.J.; Tonks, L. Propagation of Large Barkhausen Discontinuities. II. Phys. Rev. 1932, 42, 419–435. [Google Scholar] [CrossRef]
- Zhukov, A.P. The remagnetization process of bistable amorphous alloys. Mater. Des. 1993, 14, 299–306. [Google Scholar] [CrossRef]
- Phan, M.-H.; Peng, H.-X.; Yu, S.-C.; Vázquez, M. Optimized giant magnetoimpedance effect in amorphous and nanocrystalline materials. J. Appl. Phys. 2006, 99, 08C505. [Google Scholar] [CrossRef] [Green Version]
- Zhukov, A.; Zhukova, V.; Blanco, J.M.; Gonzalez, J. Recent research on magnetic properties of glass-coated microwires. J. Magn. Magn. Mater. 2005, 294, 182–192. [Google Scholar] [CrossRef]
- Varga, R.; Richter, K.; Zhukov, A.; Larin, V. Domain Wall Propagation in Thin Magnetic Wires. IEEE Trans. Magn. 2008, 44, 3925–3930. [Google Scholar] [CrossRef]
- Corodeanu, S.; Chiriac, H.; Óvári, T.-A. Accurate measurement of domain wall velocity in amorphous microwires, submicron wires, and nanowires. Rev. Sci. Instrum. 2011, 82, 094701. [Google Scholar] [CrossRef]
- Biziere, N.; Gatel, C.; Lassalle-Balier, R.; Clochard, M.C.; Wegrowe, J.E.; Snoeck, E. Imaging the Fine Structure of a Magnetic Domain Wall in a Ni Nanocylinder. Nano Lett. 2013, 13, 2053–2057. [Google Scholar] [CrossRef]
- Da Col, S.; Jamet, S.; Staňo, M.; Trapp, B.; Le Denmat, S.; Cagnon, L.; Toussaint, J.C.; Fruchart, O. Nucleation, imaging, and motion of magnetic domain walls in cylindrical nanowires. Appl. Phys. Lett. 2016, 109, 062406. [Google Scholar] [CrossRef] [Green Version]
- Blanco, J.M.; Zhukova, V.; Ipatov, M.; Zhukov, A. Magnetic Properties and Domain Wall Propagation in Micrometric Amorphous Microwires. Sens. Lett. 2013, 11, 187–190. [Google Scholar] [CrossRef]
- Óvári, T.-A.; Corodeanu, S.; Chiriac, H. Domain wall velocity in submicron amorphous wires. J. Appl. Phys. 2011, 109, 07D502. [Google Scholar] [CrossRef]
- Pirota, K.R.; Kraus, L.; Chiriac, H.; Knobel, M. Magnetic properties and giant magnetoimpedance in a CoFeSiB glass-covered microwire. J. Magn. Magn. Mater. 2000, 221, L243–L247. [Google Scholar] [CrossRef]
- Corte-León, P.; Zhukova, V.; Ipatov, M.; Blanco, J.M.; Gonzalez, J.; Zhukov, A. Engineering of magnetic properties of Co-rich microwires by joule heating. Intermetallics 2019, 105, 92–98. [Google Scholar] [CrossRef]
- Mohri, K.; Uchiyama, T.; Panina, L.V.; Yamamoto, M.; Bushida, K. Recent Advances of Amorphous Wire CMOS IC Magneto-Impedance Sensors: Innovative High-Performance Micromagnetic Sensor Chip. Available online: https://www.hindawi.com/journals/js/2015/718069/abs/ (accessed on 18 January 2019).
- Honkura, Y.; Honkura, S. The Development of ASIC Type GSR Sensor Driven by GHz Pulse Current. Sensors 2020, 20, 1023. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sandacci, S.; Makhnovskiy, D.; Panina, L.; Mohri, K.; Honkura, Y. Off-diagonal impedance in amorphous wires and its application to linear magnetic sensors. IEEE Trans. Magn. 2004, 40, 3505–3511. [Google Scholar] [CrossRef] [Green Version]
- Dufay, B.; Saez, S.; Dolabdjian, C.; Yelon, A.; Menard, D. Development of a High Sensitivity Giant Magneto-Impedance Magnetometer: Comparison with a Commercial Flux-Gate. IEEE Trans. Magn. 2013, 49, 85–88. [Google Scholar] [CrossRef]
- Uchiyama, T.; Mohri, K.; Nakayama, S. Measurement of Spontaneous Oscillatory Magnetic Field of Guinea-Pig Smooth Muscle Preparation Using Pico-Tesla Resolution Amorphous Wire Magneto-Impedance Sensor. IEEE Trans. Magn. 2011, 47, 3070–3073. [Google Scholar] [CrossRef]
- Cobeño, A.F.; Zhukov, A.; Blanco, J.M.; Larin, V.; Gonzalez, J. Magnetoelastic sensor based on GMI of amorphous microwire. Sens. Actuators Phys. 2001, 91, 95–98. [Google Scholar] [CrossRef]
- Zhukova, V.; Blanco, J.M.; Ipatov, M.; Zhukov, A.; García, C.; Gonzalez, J.; Varga, R.; Torcunov, A. Development of thin microwires with low Curie temperature for temperature sensors applications. Sens. Actuators B Chem. 2007, 126, 318–323. [Google Scholar] [CrossRef]
- Ulitovsky, A.V.; Maianski, I.M.; Avramenco, A.I. Method of Continuous Casting of Glass Coated Microwire. USSR Patent No. 128427, 15 May 1960. Bulletin 1960, 10, 14. [Google Scholar]
- Kraus, L.; Schneider, J.; Wiesner, H. Ferromagnetic resonance in amorphous alloys prepared by rapid quenching from the melt. Czech. J. Phys. B 1976, 26, 601–602. [Google Scholar] [CrossRef]
- Zhukov, A.; Ipatov, M.; Talaat, A.; Blanco, J.M.; Hernando, B.; Gonzalez-Legarreta, L.; Suñol, J.J.; Zhukova, V. Correlation of Crystalline Structure with Magnetic and Transport Properties of Glass-Coated Microwires. Crystals 2017, 7, 41. [Google Scholar] [CrossRef]
- Baranov, S.A.; Larin, V.S.; Torcunov, A.V. Technology, Preparation and Properties of the Cast Glass-Coated Magnetic Microwires. Crystals 2017, 7, 136. [Google Scholar] [CrossRef]
- Zhukova, V.; Blanco, J.M.; Ipatov, M.; Zhukov, A. Magnetoelastic Contribution in Domain-Wall Dynamics of Magnetically Bistable Microwires. IEEE Trans. Magn. 2011, 47, 3783–3787. [Google Scholar] [CrossRef]
- Zhukov, A.; Gonzalez, J.; Zhukova, V. Magnetoresistance in thin wires with granular structure. J. Magn. Magn. Mater. 2005, 294, 165–173. [Google Scholar] [CrossRef]
- Zhukov, A.; Rodionova, V.; Ilyn, M.; Aliev, A.M.; Varga, R.; Michalik, S.; Aronin, A.; Abrosimova, G.; Kiselev, A.; Ipatov, M.; et al. Magnetic properties and magnetocaloric effect in Heusler-type glass-coated NiMnGa microwires. J. Alloys Compd. 2013, 575, 73–79. [Google Scholar] [CrossRef]
- Zhukova, V.; Talaat, A.; del Val, J.J.; Ipatov, M.; Zhukov, A. Preparation and Characterization of Fe-Pt and Fe-Pt-(B, Si) Microwires. IEEE Magn. Lett. 2016, 7, 5200704. [Google Scholar] [CrossRef]
- Zhukova, V.; Corte-Leon, P.; Ipatov, M.; Blanco, J.M.; Gonzalez-Legarreta, L.; Zhukov, A. Development of Magnetic Microwires for Magnetic Sensor Applications. Sensors 2019, 19, 4767. [Google Scholar] [CrossRef] [Green Version]
- Zhukov, A.; Ipatov, M.; Corte-León, P.; Gonzalez-Legarreta, L.; Blanco, J.M.; Zhukova, V. Soft magnetic microwires for sensor applications. J. Magn. Magn. Mater. 2020, 498, 166180. [Google Scholar] [CrossRef]
- Antonov, A.S.; Borisov, V.T.; Borisov, O.V.; Prokoshin, A.F.; Usov, N.A. Residual quenching stresses in glass-coated amorphous ferromagnetic microwires. J. Phys. Appl. Phys. 2000, 33, 1161. [Google Scholar] [CrossRef]
- Zhukova, V.; Blanco, J.M.; Ipatov, M.; Zhukov, A. Magnetoelastic contribution in domain wall dynamics of amorphous microwires. Phys. B Condens. Matter 2012, 407, 1450–1454. [Google Scholar] [CrossRef]
- Zhukov, A.; Cobeño, A.F.; Gonzalez, J.; Torcunov, A.; Pina, E.; Prieto, M.J.; Blanco, J.M.; Larin, V.; Baranov, S. Ferromagnetic resonance, magnetic behaviour and structure of Fe-based glass-coated microwires. J. Magn. Magn. Mater. 1999, 203, 238–240. [Google Scholar] [CrossRef]
- Velázquez, J.; Vázquez, M.; Hernando, A.; Savage, H.T.; Wun-Fogle, M. Magnetoelastic anisotropy in amorphous wires due to quenching. J. Appl. Phys. 1991, 70, 6525–6527. [Google Scholar] [CrossRef]
- Talaat, A.; Zhukova, V.; Ipatov, M.; del Val, J.J.; Blanco, J.M.; Gonzalez-Legarreta, L.; Hernando, B.; Churyukanova, M.; Zhukov, A. Engineering of Magnetic Softness and Magnetoimpedance in Fe-Rich Microwires by Nanocrystallization. JOM 2016, 68, 1563–1571. [Google Scholar] [CrossRef]
- Gonzalez-Legarreta, L.; Corte-León, P.; Zhukova, V.; Ipatov, M.; Blanco, J.M.; Churyukanova, M.; Taskaev, S.; Zhukov, A. Route of magnetoimpedance and domain walls dynamics optimization in Co-based microwires. J. Alloys Compd. 2020, 830, 154576. [Google Scholar] [CrossRef]
- Goto, T.; Nagano, M.; Wehara, N. Mechanical Properties of Amorphous Fe80P16C3B1 Filament Produced by Glass-Coated Melt Spinning. Trans. Jpn. Inst. Met. 1977, 18, 759–764. [Google Scholar] [CrossRef] [Green Version]
- Zhukova, V.; Cobeño, A.F.; Zhukov, A.; de Arellano Lopez, A.R.; Blanco, J.M.; Larin, V.; Gonzalez, J.; López-Pombero, S. Correlation between magnetic and mechanical properties of devitrified glass-coated Fe71.8Cu1Nb3.1Si15B9.1 microwires. J. Magn. Magn. Mater. 2002, 249, 79–84. [Google Scholar] [CrossRef]
- Corte-León, P.; Gonzalez-Legarreta, L.; Zhukova, V.; Ipatov, M.; Blanco, J.M.; Churyukanova, M.; Taskaev, S.; Zhukov, A. Controlling the domain wall dynamics in Fe-, Ni- and Co-based magnetic microwires. J. Alloys Compd. 2020, 834, 155170. [Google Scholar] [CrossRef]
- Zhukov, A.; Talaat, A.; Ipatov, M.; Zhukova, V. Tailoring the High-Frequency Giant Magnetoimpedance Effect of Amorphous Co-Rich Microwires. IEEE Magn. Lett. 2015, 6, 1–4. [Google Scholar] [CrossRef]
- Zhukov, A.; Churyukanova, M.; Kaloshkin, S.; Sudarchikova, V.; Gudoshnikov, S.; Ipatov, M.; Talaat, A.; Blanco, J.M.; Zhukova, V. Magnetostriction of Co–Fe-Based Amorphous Soft Magnetic Microwires. J. Electron. Mater. 2016, 45, 226–234. [Google Scholar] [CrossRef]
- Churyukanova, M.; Semenkova, V.; Kaloshkin, S.; Shuvaeva, E.; Gudoshnikov, S.; Zhukova, V.; Shchetinin, I.; Zhukov, A. Magnetostriction investigation of soft magnetic microwires. Phys. Status Solidi A 2016, 213, 363–367. [Google Scholar] [CrossRef]
- Konno, Y.; Mohri, K. Magnetostriction measurements for amorphous wires. IEEE Trans. Magn. 1989, 25, 3623–3625. [Google Scholar] [CrossRef]
- Herzer, G. Amorphous and nanocrystalline soft magnets. In Magnetic Hysteresis in Novel Magnetic Materials; NATO ASI Series (Series E: Applied Sciences); Hadjipanayis, G.C., Ed.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1997; Volume 338, pp. 711–730. [Google Scholar]
- Cobeño, A.F.; Zhukov, A.; Blanco, J.M.; Gonzalez, J. Giant magneto-impedance effect in CoMnSiB amorphous microwires. J. Magn. Magn. Mater. 2001, 234, L359–L365. [Google Scholar] [CrossRef]
- Corte-Leon, P.; Zhukova, V.; Blanco, J.M.; González-Legarreta, L.; Ipatov, M.; Zhukov, A. Stress-induced Magnetic Anisotropy Enabling Engineering of Magnetic Softness of Fe-rich Amorphous Microwires. J. Magn. Magn. Mater. 2020, 510, 166939. [Google Scholar] [CrossRef]
- Zhukova, V.; Blanco, J.M.; Chizhik, A.; Ipatov, M.; Zhukov, A. AC-current-induced magnetization switching in amorphous microwires. Front. Phys. 2018, 13, 137501. [Google Scholar] [CrossRef]
- Zhukova, V.; Zhukov, A.; Blanco, J.M.; Gonzalez, J.; Ponomarev, B.K. Switching field fluctuations in a glass-coated Fe-rich amorphous microwire. J. Magn. Magn. Mater. 2002, 249, 131–135. [Google Scholar] [CrossRef]
- Chiriac, H.; Óvári, T.-A.; Corodeanu, S.; Ababei, G. Interdomain wall in amorphous glass-coated microwires. Phys. Rev. B 2007, 76, 214433. [Google Scholar] [CrossRef]
- Astefanoaei, I.; Radu, D.; Chiriac, H. Internal stress distribution in DC joule-heated amorphous glass-covered microwires. J. Phys. Condens. Matter 2006, 18, 2689–2716. [Google Scholar] [CrossRef]
- Chiriac, H.; Óvári, T.A.; Pop, G. Internal stress distribution in glass-covered amorphous magnetic wires. Phys. Rev. B 1995, 52, 10104–10113. [Google Scholar] [CrossRef]
- García-Prieto, M.J.; Pina, E.; Zhukov, A.; Larin, V.; Marín, P.; Vázquez, M.; Hernando, A. Glass-coated Co-rich amorphous microwires with enhanced permeability. Sens. Actuators A Phys. 2000, 81, 227–231. [Google Scholar] [CrossRef]
- Catalan, C.F.; Prida, V.M.; Alonso, J.; Vázquez, M.; Zhukov, A.; Hernando, B.; Velázquez, J. Effect of glass coating on magnetic properties of amorphous microwires, Rapidly Quenched & Metastable Materials. Mater. Sci. Eng. A Suppl. 1997, 438–441. [Google Scholar]
- Takajo, M.; Yamasaki, J.; Humphrey, F.B. Domain structure of chemically thinned Fe-Si-B amorphous wires. IEEE Trans. Magn. 1999, 35, 3904–3906. [Google Scholar] [CrossRef]
- Kabanov, Y.; Zhukov, A.; Zhukova, V.; Gonzalez, J. Magnetic domain structure of wires studied by using the magneto-optical indicator film method. Appl. Phys. Lett. 2005, 87, 142507. [Google Scholar] [CrossRef]
- Usov, N.; Antonov, A.; Dykhne, A.; Lagar’kov, A. Possible origin for the bamboo domain structure in Co-rich amorphous wire. J. Magn. Magn. Mater. 1997, 174, 127–132. [Google Scholar] [CrossRef]
- Nderu, J.N.; Takajo, M.; Yamasaki, J.; Humphrey, F.B. Effect of stress on the bamboo domains and magnetization process of CoSiB amorphous wire. IEEE Trans. Magn. 1998, 34, 1312–1314. [Google Scholar] [CrossRef]
- Corte-Leon, P.; Zhukova, V.; Ipatov, M.; Blanco, J.M.; Gonzalez, J.; Churyukanova, M.; Baraibar, J.M.; Taskaev, S.; Zhukov, A. Stress dependence of the magnetic properties of glass-coated amorphous microwires. J. Alloys Compd. 2019, 789, 201–208. [Google Scholar] [CrossRef]
- Barandiarán, J.M.; Hernando, A.; Madurga, V.; Nielsen, O.V.; Vázquez, M.; Vázquez-López, M. Temperature, stress, and structural-relaxation dependence of the magnetostriction in (Co0.94Fe0.06)75Si15B10 glasses. Phys. Rev. B 1987, 35, 5066–5071. [Google Scholar] [CrossRef] [Green Version]
- Zhukov, A.; Ipatov, M.; Gonzalez, J.; Blanco, J.M.; Zhukova, V. Recent advances in studies of magnetically soft amorphous microwires. J. Magn. Magn. Mater. 2009, 321, 822–825. [Google Scholar] [CrossRef]
- Zhukov, A.; Ipatov, M.; Corte-León, P.; Legarreta, L.G.; Churyukanova, M.; Blanco, J.M.; Gonzalez, J.; Taskaev, S.; Hernando, B.; Zhukova, V. Giant magnetoimpedance in rapidly quenched materials. J. Alloys Compd. 2020, 814, 152225. [Google Scholar] [CrossRef]
- Zhukov, A.; González, J.; Blanco, J.M.; Vázquez, M.; Larin, V. Microwires coated by glass: A new family of soft and hard magnetic materials. J. Mater. Res. 2000, 15, 2107–2113. [Google Scholar] [CrossRef]
- Allwood, D.A.; Xiong, G.; Faulkner, C.C.; Atkinson, D.; Petit, D.; Cowburn, R.P. Magnetic Domain-Wall Logic. Science 2005, 309, 1688–1692. [Google Scholar] [CrossRef]
- Moriya, R.; Hayashi, M.; Thomas, L.; Rettner, C.; Parkin, S.S.P. Dependence of field driven domain wall velocity on cross-sectional area in Ni65Fe20Co15 nanowires. Appl. Phys. Lett. 2010, 97, 142506. [Google Scholar] [CrossRef]
- Zhukova, V.; Blanco, J.M.; Rodionova, V.; Ipatov, M.; Zhukov, A. Domain wall propagation in micrometric wires: Limits of single domain wall regime. J. Appl. Phys. 2012, 111, 07E311. [Google Scholar] [CrossRef]
- Zhukova, V.; Blanco, J.M.; Rodionova, V.; Ipatov, M.; Zhukov, A. Fast magnetization switching in Fe-rich amorphous microwires: Effect of magnetoelastic anisotropy and role of defects. J. Alloys Compd. 2014, 586, S287–S290. [Google Scholar] [CrossRef]
- Aragoneses, P.; Blanco, J.M.; Dominguez, L.; González, J.; Zhukov, A.; Vázquez, M. The Stress dependence of the switching field in glass-coated amorphous microwires. J. Phys. D Appl. Phys. 1998, 31, 3040–3045. [Google Scholar] [CrossRef]
- Zhukova, V.; Talaat, A.; Corte-Leon, P.; Blanco, J.M.; Ipatov, M.; Zhukov, A. Engineering of magnetic properties and domain wall dynamics in Fe-Ni-based amorphous microwires by annealing. Aip Adv. 2020, 10, 015130. [Google Scholar] [CrossRef] [Green Version]
- Zhukov, A.; Churyukanova, M.; Kaloshkin, S.; Semenkova, V.; Gudoshnikov, S.; Ipatov, M.; Talaat, A.; Blanco, J.M.; Zhukova, V. Effect of annealing on magnetic properties and magnetostriction coefficient of Fe–Ni-based amorphous microwires. J. Alloys Compd. 2015, 651, 718–723. [Google Scholar] [CrossRef]
- Luborsky, F.; Walter, J. Magnetic anneal anisotropy in amorphous alloys. IEEE Trans. Magn. 1977, 13, 953–956. [Google Scholar] [CrossRef]
- Haimovich, J.; Jagielinski, T.; Egami, T. Magnetic and structural effects of anelastic deformation of an amorphous alloy. J. Appl. Phys. 1985, 57, 3581–3583. [Google Scholar] [CrossRef]
- Zhukova, V.; Korchuganova, O.A.; Aleev, A.A.; Tcherdyntsev, V.V.; Churyukanova, M.; Medvedeva, E.V.; Seils, S.; Wagner, J.; Ipatov, M.; Blanco, J.M.; et al. Effect of annealing on magnetic properties and structure of Fe-Ni based magnetic microwires. J. Magn. Magn. Mater. 2017, 433, 278–284. [Google Scholar] [CrossRef]
- Zhukova, V.; Blanco, J.M.; Ipatov, M.; Gonzalez, J.; Churyukanova, M.; Zhukov, A. Engineering of magnetic softness and giant magnetoimpedance effect in Fe-rich microwires by stress-annealing. Scr. Mater. 2018, 142, 10–14. [Google Scholar] [CrossRef]
- Zhukova, V.; Blanco, J.M.; Ipatov, M.; Churyukanova, M.; Taskaev, S.; Zhukov, A. Tailoring of magnetoimpedance effect and magnetic softness of Fe-rich glass-coated microwires by stress- annealing. Sci. Rep. 2018, 8, 1–14. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yamasaki, J.; Mohri, K.; Watari, K.; Narita, K. Domain wall induced anisotropy during annealing in amorphous ribbons. IEEE Trans. Magn. 1984, 20, 1855–1857. [Google Scholar] [CrossRef]
- Kohmoto, O.; Ohya, K. Amorphous FeCo-SiB alloys with zero magnetostriction. J. Appl. Phys. 1981, 52, 928–932. [Google Scholar] [CrossRef]
- Becker, J.; Luborsky, F.; Walter, J. Magnetic moments and Curie temperatures of (Fe,Ni)80(P,B)20 amorphous alloys. IEEE Trans. Magn. 1977, 13, 988–991. [Google Scholar] [CrossRef]
- Rancourt, D.G.; Dang, M.-Z. Relation between anomalous magnetovolume behavior and magnetic frustration in Invar alloys. Phys. Rev. B 1996, 54, 12225–12231. [Google Scholar] [CrossRef]
- Gaskell, P.H. On the structure of simple inorganic amorphous solids. J. Phys. C Solid State Phys. 1979, 12, 4337–4368. [Google Scholar] [CrossRef]
- Zhukov, A.; Chichay, K.; Talaat, A.; Rodionova, V.; Blanco, J.M.; Ipatov, M.; Zhukova, V. Manipulation of magnetic properties of glass-coated microwires by annealing. J. Magn. Magn. Mater. 2015, 383, 232–236. [Google Scholar] [CrossRef]
- Zhukov, A.; Talaat, A.; Churyukanova, M.; Kaloshkin, S.; Semenkova, V.; Ipatov, M.; Blanco, J.M.; Zhukova, V. Engineering of magnetic properties and GMI effect in Co-rich amorphous microwires. J. Alloys Compd. 2016, 664, 235–241. [Google Scholar] [CrossRef]
- Corte-León, P.; Talaat, A.; Zhukova, V.; Ipatov, M.; Blanco, J.M.; Gonzalez, J.; Zhukov, A. Stress-Induced Magnetic Anisotropy Enabling Engineering of Magnetic Softness and GMI Effect of Amorphous Microwires. Appl. Sci. 2020, 10, 981. [Google Scholar] [CrossRef] [Green Version]
- Zhukov, A.; Talaat, A.; Blanco, J.M.; Ipatov, M.; Zhukova, V. Tuning of Magnetic Properties and GMI Effect of Co-Based Amorphous Microwires by Annealing. J. Electron. Mater. 2014, 43, 4532–4539. [Google Scholar] [CrossRef]
- Aragoneses, P.; Blanco, J.M.; Cobeño, A.F.; Dominguez, L.; Gonzalez, J.; Zhukov, A.; Larin, V. Stress Dependence of the Switching Field in Co-rich Amorphous Microwires. J. Magn. Magn. Mater. 1999, 196, 248–250. [Google Scholar] [CrossRef]
- Corte-León, P.; Blanco, J.M.; Zhukova, V.; Ipatov, M.; Gonzalez, J.; Churyukanova, M.; Taskaev, S.; Zhukov, A. Engineering of Magnetic Softness and Domain Wall Dynamics of Fe-rich Amorphous Microwires by Stress-induced Magnetic Anisotropy. Sci. Rep. 2019, 9, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Larin, V.S.; Zhukova, V.; Zhukov, A.; Torcunov, A.V.; Vazquez, M. Tailoring of magnetic anisotropy in Fe-rich glass-coated magnetic microwires by thermo-mechanical annealing. Sens. Actuators A Phys. 2003, 106, 96–100. [Google Scholar] [CrossRef]
- Zhukov, A.; Zhukova, V.; Larin, V.; Gonzalez, J. Tailoring of magnetic anisotropy of Fe-rich microwires by stress induced anisotropy. Phys. B Condens. Matter 2006, 384, 1–4. [Google Scholar] [CrossRef]
- Gonzalez-Legarreta, L.; Corte-Leon, P.; Zhukova, V.; Ipatov, M.; Blanco, J.M.; Gonzalez, J.; Zhukov, A. Optimization of magnetic properties and GMI effect of Thin Co-rich Microwires for GMI Microsensors. Sensors 2020, 20, 1558. [Google Scholar] [CrossRef] [Green Version]
- Chichay, K.; Rodionova, V.; Ipatov, M.; Zhukova, V.; Zhukov, A. Effect of Temperature and Time of Stress Annealing on Magnetic Properties of Amorphous Microwires. Acta Phys. Pol. A 2015, 127, 600–602. [Google Scholar] [CrossRef]
- Corte-León, P.; Zhukova, V.; Ipatov, M.; Blanco, J.M.; González, J.; Zhukov, A. Optimization of GMI Effect and Magnetic Properties of Co-Rich Microwires by Joule Heating. IEEE Trans. Magn. 2019, 55, 1–4. [Google Scholar] [CrossRef]
- Zhukova, V.; Cobeño, A.F.; Zhukov, A.; Blanco, J.M.; Puerta, S.; Gonzalez, J.; Vázquez, M. Tailoring of magnetic properties of glass-coated microwires by current annealing. J. Non-Cryst. Solids 2001, 287, 31–36. [Google Scholar] [CrossRef]
- Becker, J. A new mechanism for magnetic annealing in amorphous metals. IEEE Trans. Magn. 1978, 14, 938–940. [Google Scholar] [CrossRef]
- Zhukov, A.P.; Talaat, A.; Ipatov, M.; Blanco, J.M.; Gonzalez-Legarreta, L.; Hernando, B.; Zhukova, V. Effect of Nanocrystallization on Magnetic Properties and GMI Effect of Microwires. IEEE Trans. Magn. 2014, 50, 1–5. [Google Scholar] [CrossRef]
- Zhukova, V.; Cobeño, A.F.; Zhukov, A.; Blanco, J.M.; Larin, V.; Gonzalez, J. Coercivity of glass-coated Fe73.4-xCu1Nb3.1Si13.4+xB9.1 (0 ≤ x ≤ 1.6) microwires. Nanostruct. Mater. 1999, 11, 1319–1327. [Google Scholar] [CrossRef]
- Rodionova, V.; Ipatov, M.; Ilyn, M.; Zhukova, V.; Perov, N.; Gonzalez, J.; Zhukov, A. Tailoring of Magnetic Properties of Magnetostatically-Coupled Glass-Covered Magnetic Microwires. J. Supercond. Nov. Magn. 2011, 24, 541–547. [Google Scholar] [CrossRef]
- Zhukova, V.; Ipatov, M.; Corte-Leon, P.; Blanco, J.M.; Zanaeva, E.; Bazlov, A.I.; Jiang, J.; Louzguine-Luzgin, D.V.; Olivera, J.; Zhukov, A. Excellent magnetic properties of (Fe0.7Co0.3)83.7Si4B8P3.6Cu0.7 ribbons and microwires. Intermetallics 2020, 117, 106660. [Google Scholar] [CrossRef]
- Talaat, A.; Del Val, J.J.; Zhukova, V.; Ipatov, M.; Klein, P.; Varga, R.; Gonzalez, J.; Zhdanova, M.; Churyukanova, M.; Zhukov, A. Effect of annealing on magnetic properties of nanocrystalline Hitperm-type glass-coated microwires. J. Alloys Compd. 2016, 660, 297–303. [Google Scholar] [CrossRef]
- Zhang, Y.; Sharma, P.; Makino, A. Effects of minor precipitation of large size crystals on magnetic properties of Fe-Co-Si-B-P-Cu alloy. J. Alloys Compd. 2017, 709, 663–667. [Google Scholar] [CrossRef]
- Cordery, R.A.; Murphy, C.F.M., III. Deactivatable Electronic Article Surveillance Markers Using Short Semi-Hard Magnetic Wires. U.S. Patent 5,191,315, 2 March 1993. [Google Scholar]
- Ferri, A.F.A.; Pereira-da-Silva, M.A.; Marega, E., Jr. Magnetic Force Microscopy: Basic Principles and Applications, Atomic Force Microscopy-Imaging, Measuring and Manipulating Surfaces at the Atomic Scale; Bellitto, V., Ed.; InTech: Rijeka, Croatia, 2012. [Google Scholar]
- Zhukov, A.; Ipatov, M.; Talaat, A.; Aronin, A.; Abrosimova, G.; del Val, J.J.; Zhukova, V. Magnetic hardening of Fe-Pt and Fe-Pt-M (M=B, Si) microwires. J. Alloys Compd. 2018, 735, 1071–1078. [Google Scholar] [CrossRef]
- Zhukov, A.; Ipatov, M.; del Val, J.J.; Churyukanova, M.; Zhukova, V. Tailoring of magnetic properties of Heusler-type glass-coated microwires by annealing. J. Alloys Compd. 2018, 732, 561–566. [Google Scholar] [CrossRef]
- Evstigneeva, S.A.; Nematov, M.G.; Omelyanchik, A.; Yudanov, N.A.; Rodionova, V.V.; Panina, L.V. Hard Magnetic Properties of Co-Rich Microwires Crystallized by Current Annealing. IEEE Magn. Lett. 2020, 11, 1–5. [Google Scholar] [CrossRef]

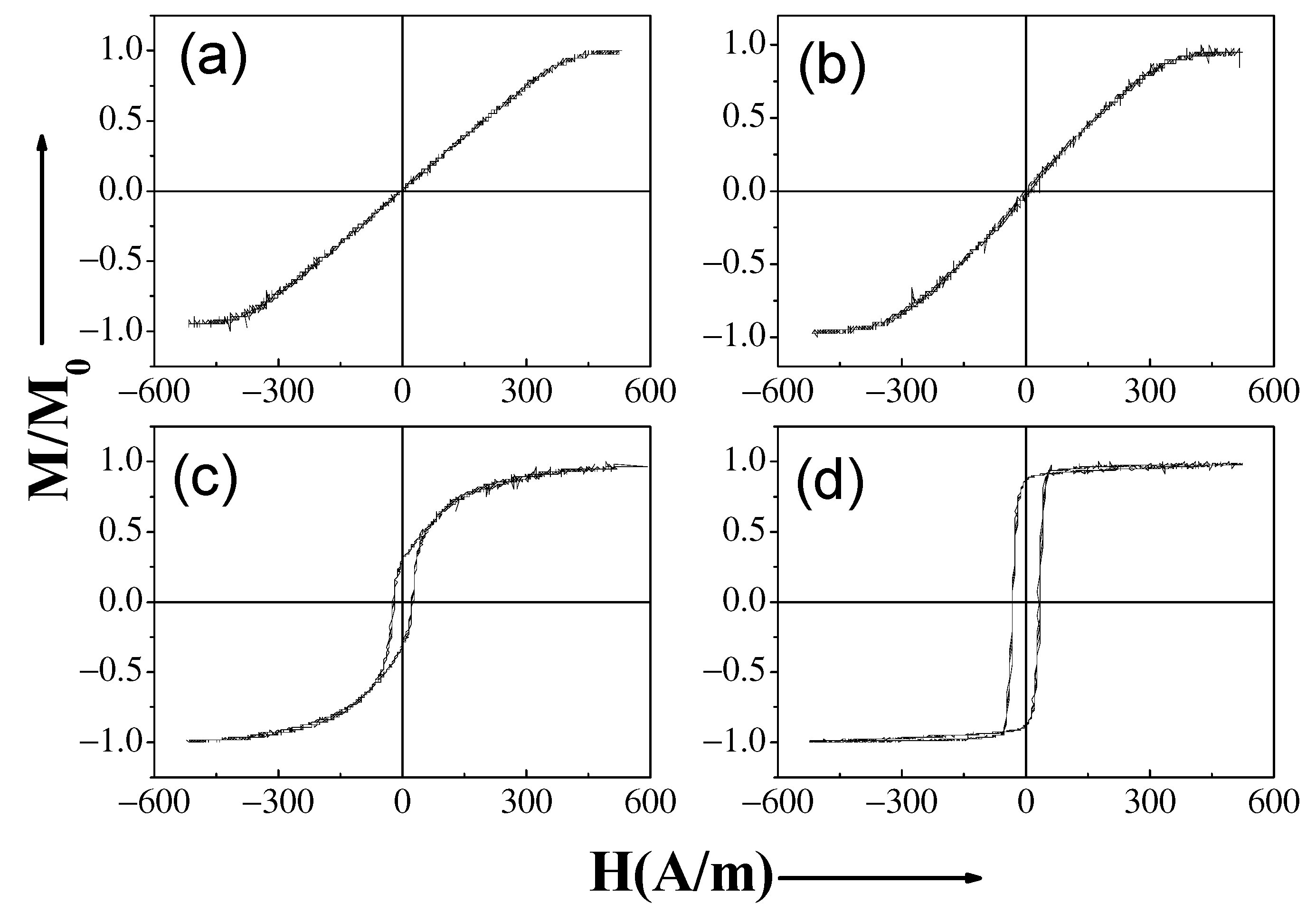
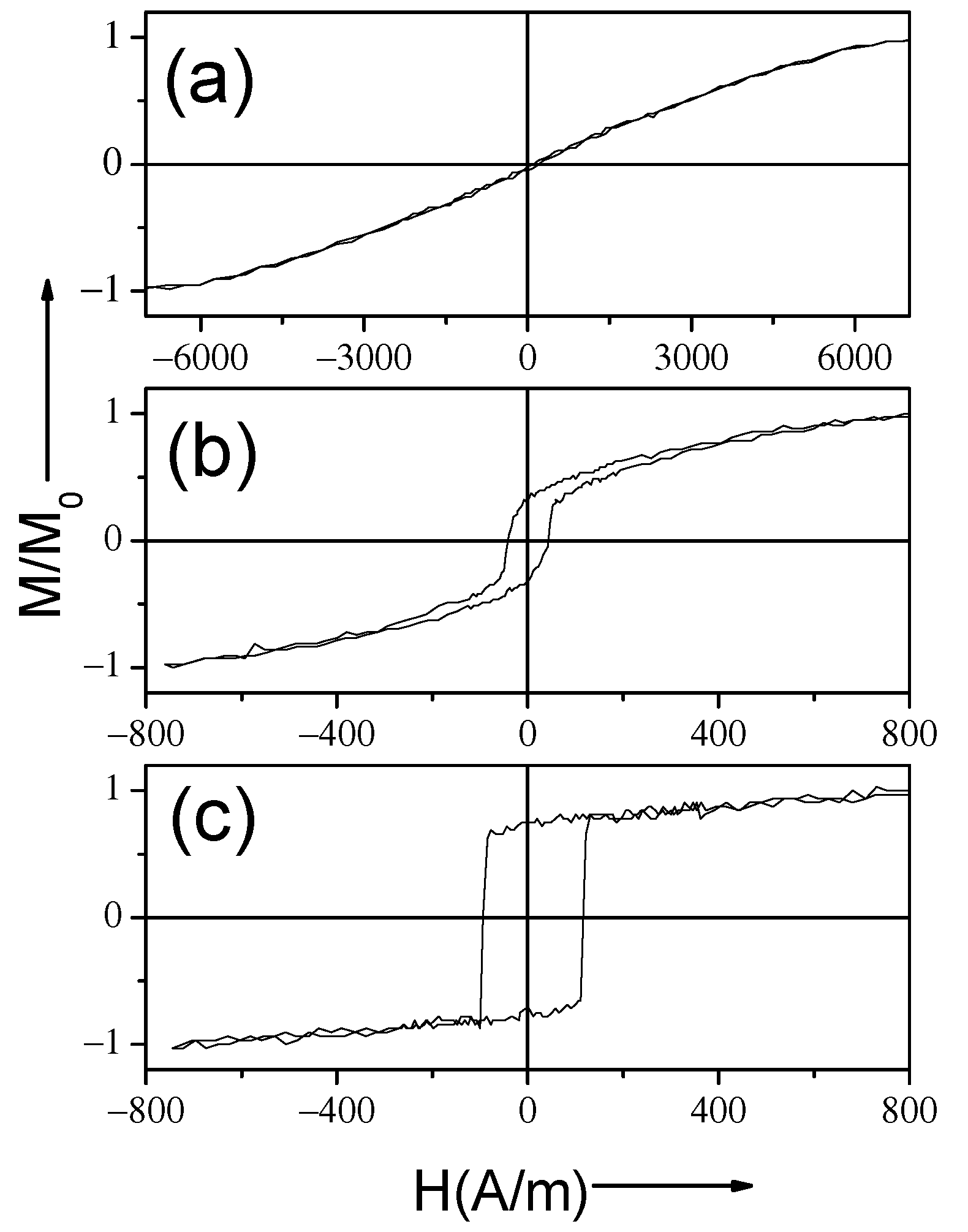
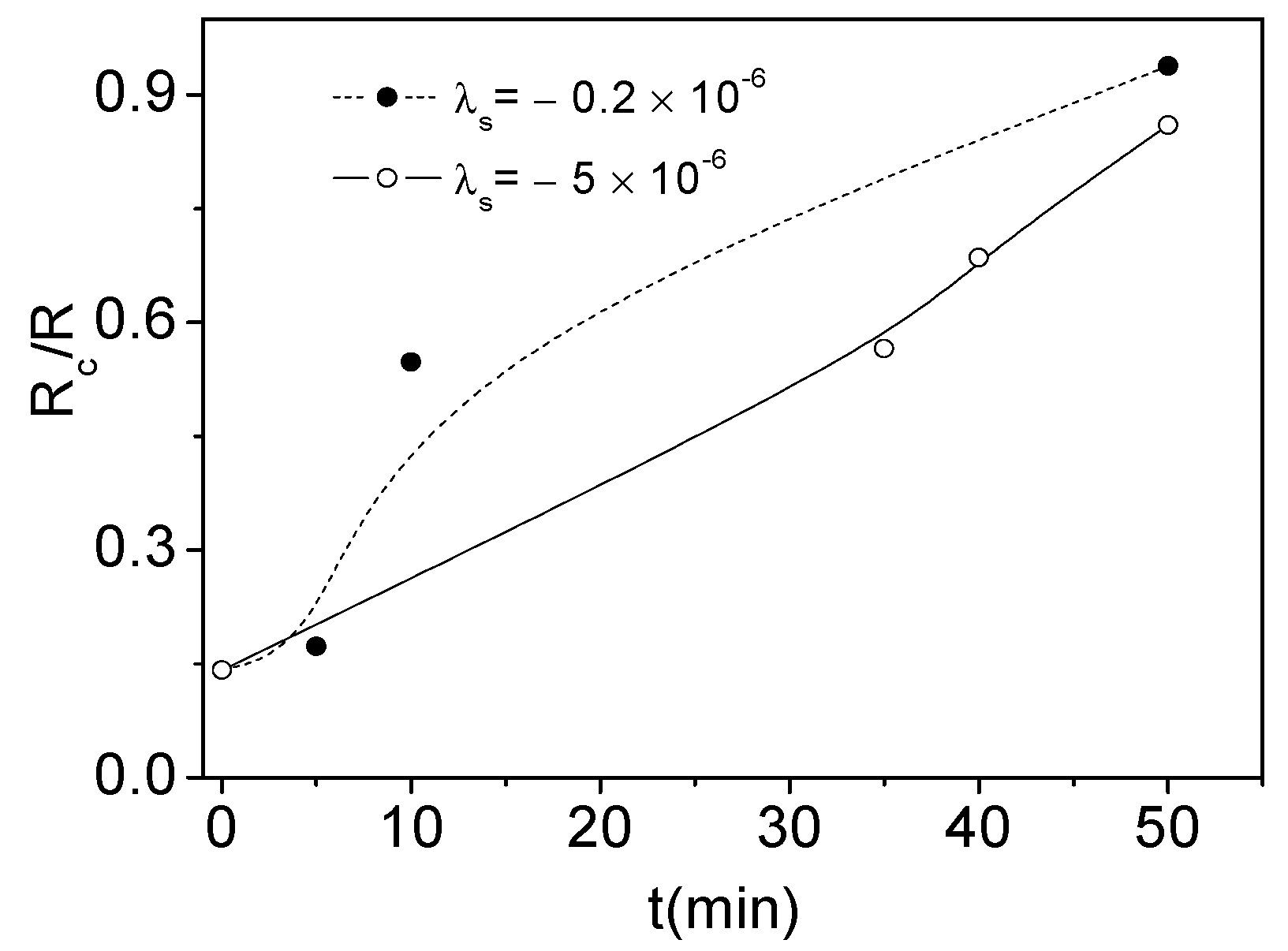
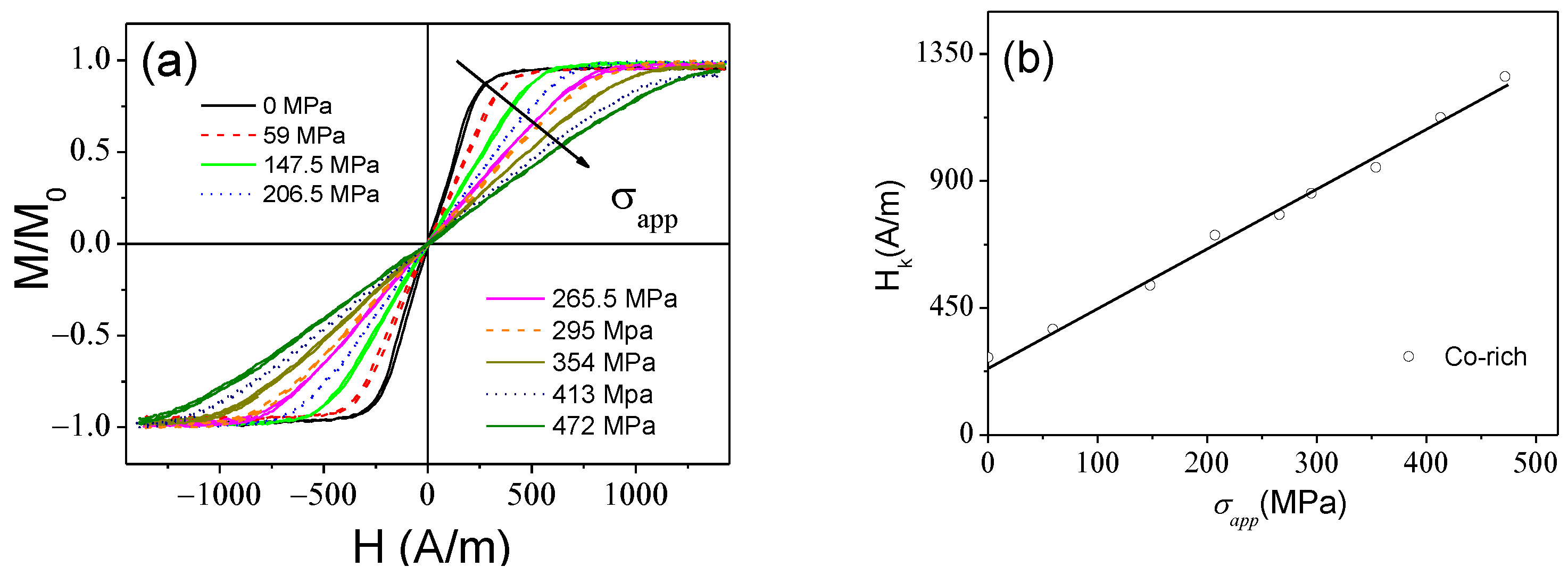
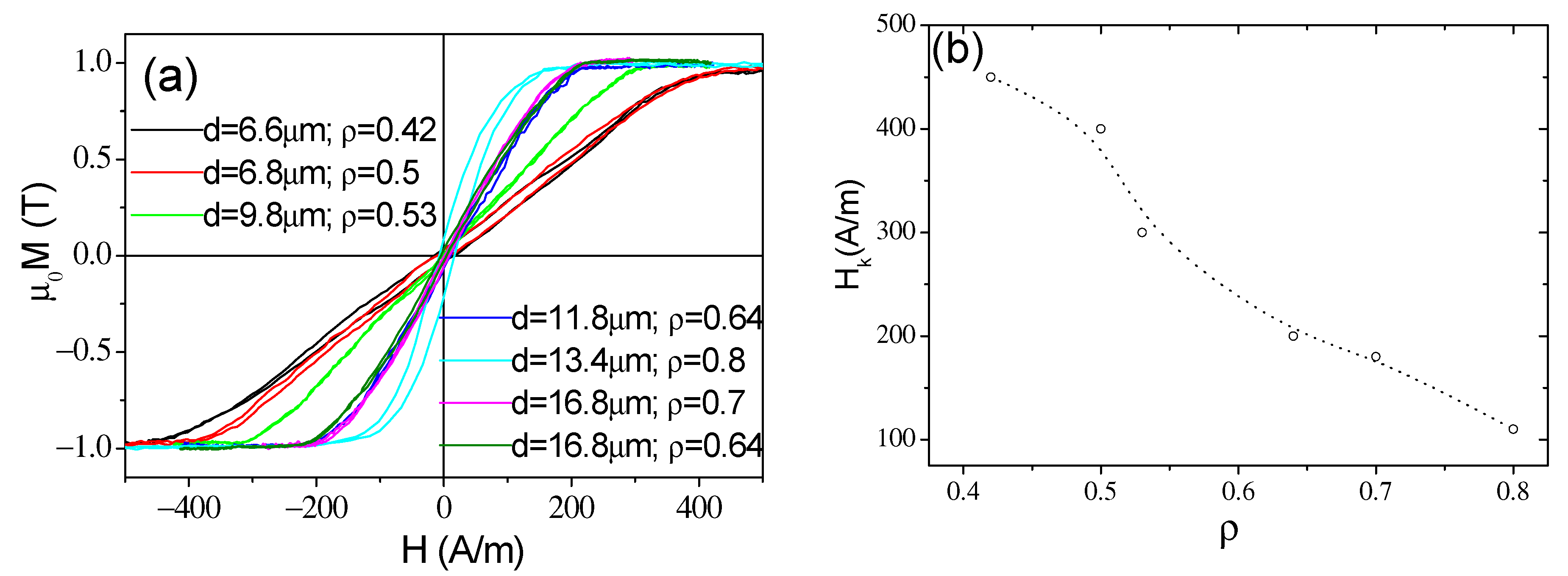
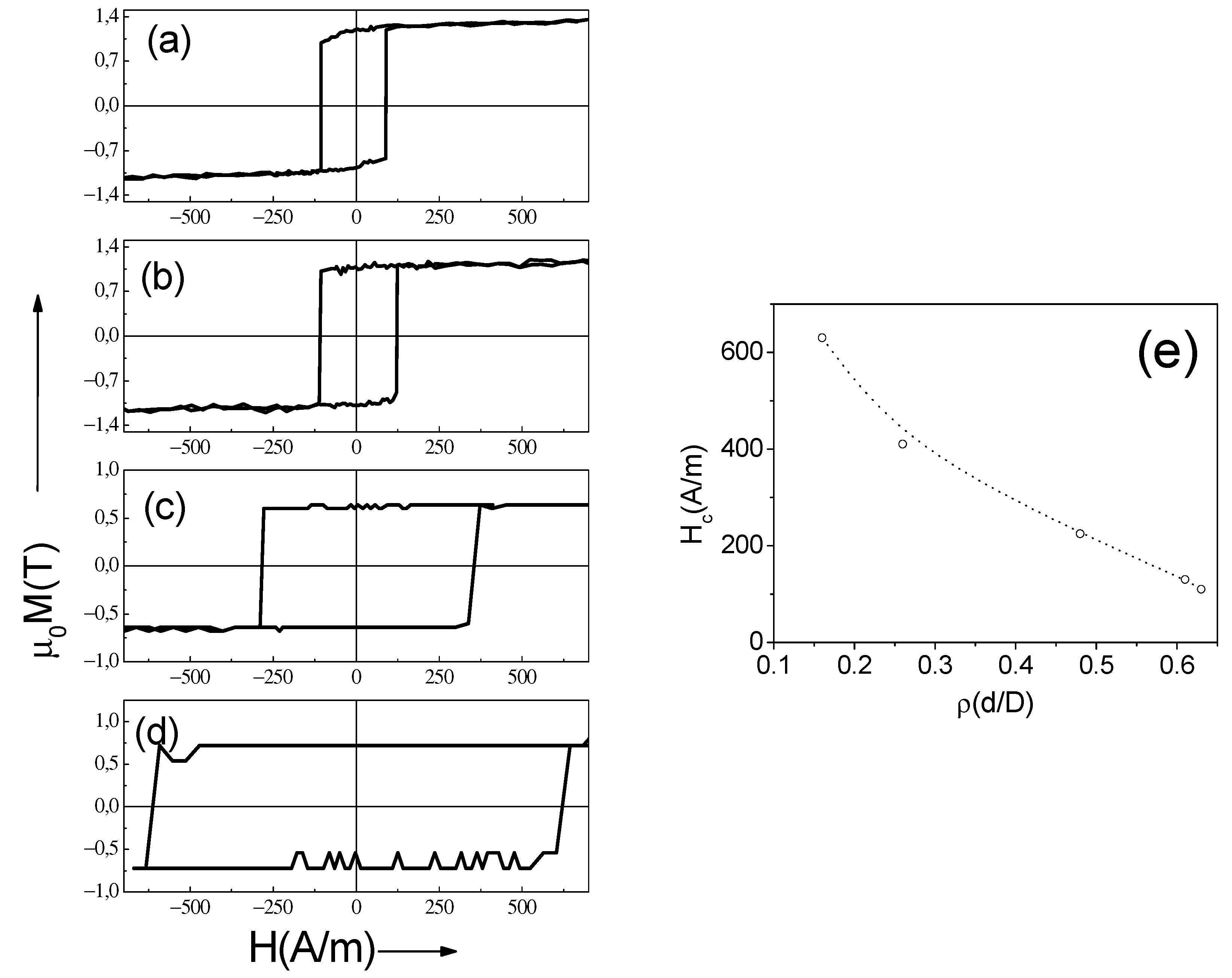

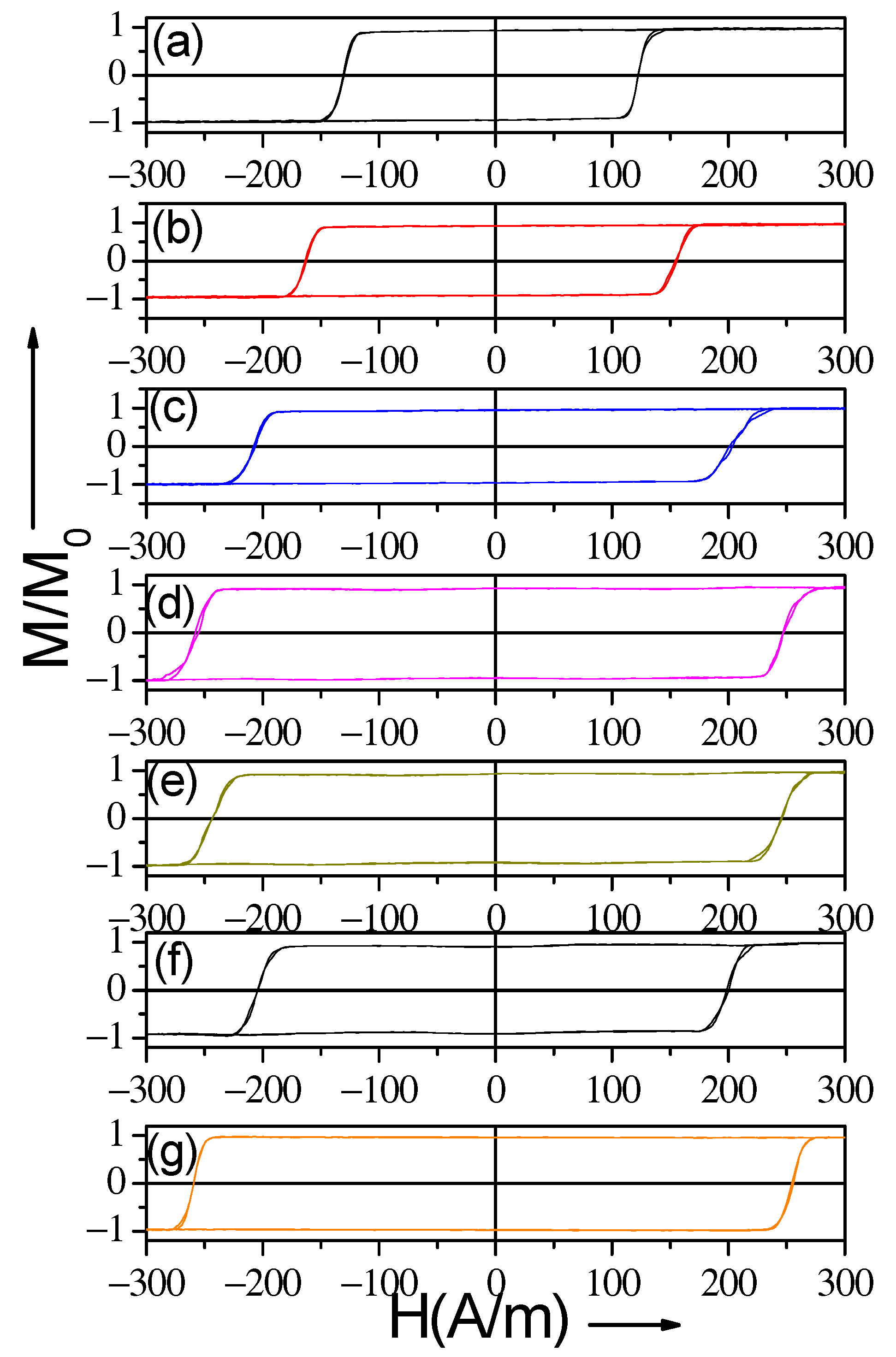
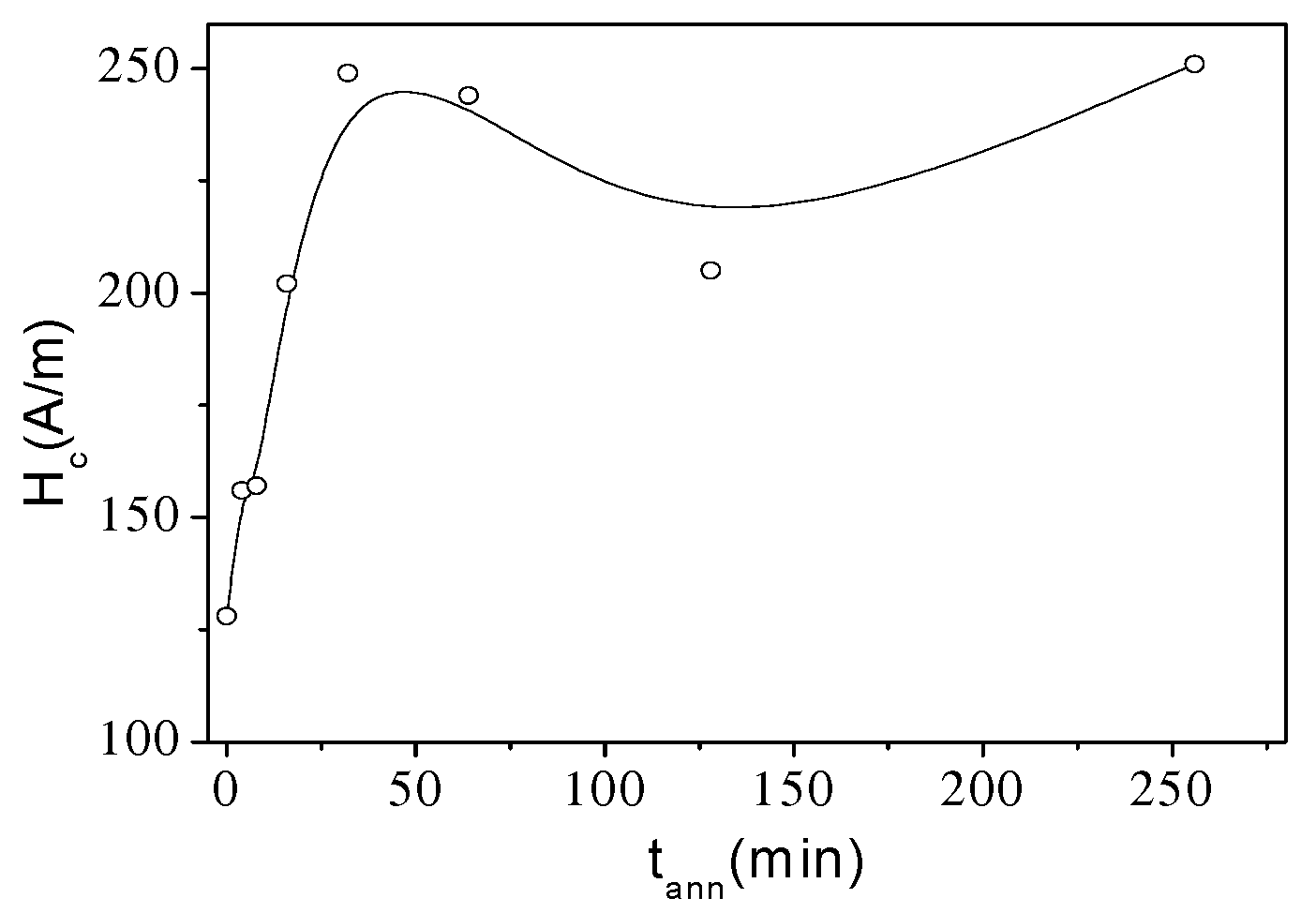




| Composition | Metallic Nucleus Diameter, d (μm) | Total Diameter, D (μm) | Ratio = d/D | Magnetostriction Coefficient, λs × 10−6 |
|---|---|---|---|---|
| Fe62Ni15.5Si7.5B15 | 14.35 | 33.25 | 0.43 | 27 |
| Fe49.6Ni27.9Si7.5B15 | 14.2 | 33.85 | 0.42 | 20 |
| Co70.5Mn4.5Si10B15 | 10 | 26 | 0.38 | −0.2 |
| Co77.5Si15B7.5 | 13.1 | 18 | 0.73 | −5 |
| Co69.2Fe3.6Ni1B12.5Si11C1.2Mo1.5 | 22.8 | 23.2 | 0.98 | −1 |
| Co68.5Si14.5B14.5Y2.5 | 5 | 22 | 0.23 | −5 |
| Co65.4Fe3.8Ni1B13.8Si13C1.65Mo1.35 | 18.8 | 22.2 | 0.85 | −1 |
| Co67Fe3.85Ni1.45B11.5Si14.5Mo1.7 | 6.6 | 15.7 | 0.42 | −3 |
| Co67Fe3.85Ni1.45B11.5Si14.5Mo1.7 | 6.8 | 13.6 | 0.5 | −3 |
| Co67Fe3.85Ni1.45B11.5Si14.5Mo1.7 | 9.8 | 18.5 | 0.53 | −3 |
| Co67Fe3.85Ni1.45B11.5Si14.5Mo1.7 | 11.8 | 18.4 | 0.64 | −3 |
| Co67Fe3.85Ni1.45B11.5Si14.5Mo1.7 | 13.4 | 20.9 | 0.64 | −3 |
| Co67Fe3.85Ni1.45B11.5Si14.5Mo1.7 | 16.8 | 24 | 0.7 | −3 |
| Co67Fe3.85Ni1.45B11.5Si14.5Mo1.7 | 16.8 | 21 | 0.8 | −3 |
| Co69.2Fe4.1B11.8Si13.8C1.1 | 25.6 | 30.2 | 0.85 | −0.03 |
| Fe71,8Cu1Nb3,1Si15B9,1 | 7.0 | 24.8 | 0.282 | 30 |
| Fe71,8Cu1Nb3,1Si15B9,1 | 18.2 | 39 | 0.467 | 30 |
| Fe70.8Cu1Nb3.1Si14.5B10.6 | 11.8 | 14.4 | 0.8 | 30 |
| Co67Fe3.9Ni1.5B11.5Si14.5Mo1.6 | 25.6 | 26.6 | 0.96 | −0.29 |
| Co68.7Fe4Ni1B13Si11Mo2.3 | 17 | 23.6 | 0.72 | −1.06 |
| Fe38.5Co38.5B18Mo4Cu1 | 9.4 | 22.5 | 0.41 | |
| Fe38.5Co38.5B18Mo4Cu1 | 10 | 16.6 | 0.6 | |
| Fe50Pt40Si10 | 8 | 21 | 0.38 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhukova, V.; Corte-Leon, P.; González-Legarreta, L.; Talaat, A.; Blanco, J.M.; Ipatov, M.; Olivera, J.; Zhukov, A. Optimization of Magnetic Properties of Magnetic Microwires by Post-Processing. Processes 2020, 8, 1006. https://doi.org/10.3390/pr8081006
Zhukova V, Corte-Leon P, González-Legarreta L, Talaat A, Blanco JM, Ipatov M, Olivera J, Zhukov A. Optimization of Magnetic Properties of Magnetic Microwires by Post-Processing. Processes. 2020; 8(8):1006. https://doi.org/10.3390/pr8081006
Chicago/Turabian StyleZhukova, Valentina, Paula Corte-Leon, Lorena González-Legarreta, Ahmed Talaat, Juan Maria Blanco, Mihail Ipatov, Jesus Olivera, and Arcady Zhukov. 2020. "Optimization of Magnetic Properties of Magnetic Microwires by Post-Processing" Processes 8, no. 8: 1006. https://doi.org/10.3390/pr8081006
APA StyleZhukova, V., Corte-Leon, P., González-Legarreta, L., Talaat, A., Blanco, J. M., Ipatov, M., Olivera, J., & Zhukov, A. (2020). Optimization of Magnetic Properties of Magnetic Microwires by Post-Processing. Processes, 8(8), 1006. https://doi.org/10.3390/pr8081006








