Kinetic Parameter Determination for Depolymerization of Biomass by Inverse Modeling and Metaheuristics
Abstract
1. Introduction
2. Materials and Methods
2.1. Experimental Data Collection
2.2. Inverse Modeling
2.3. Metaheuristics
| Algorithm 1 General Estimation of Distribution Algorithm | |
| 1: | Generate an initial population of candidate solutions: at iteration , uniformly |
| 2: | WHILE (stopping criteria are not met) // = 100 in this work |
| 3: | Compute the quality measure of each candidate solution // in this work |
| 4: | Select a subset of the best solutions, from // in this work |
| 5: | Build a probabilistic model based on |
| 6: | Sample to generate new solutions |
| 7: | Substitute/Incorporate into |
| 8: | Update |
| 9: | END WHILE |
| 10: | Output the best solution found, , as a result |
2.4. Experimental Methodology
| Algorithm 2 Experimental Methodology for Kinetic Model Evaluation | ||||||
| INPUT: A set of experimental data files (D), a set of kinetic models (K), a set of optimizers (O), user-defined search ranges for parameters and . Number of folds for data partition and performance metrics OUTPUT: Optimal optimizer, kinetic models, kinetic parameters , and Performance Indexes on train () and test () data. | ||||||
| 1: | FOR EACH experimental data file d in D: | // 14 data files | ||||
| 2: | Partition into | // 4-fold cross-validation | ||||
| 3: | FOR EACH pair of train and test data folds (f_tr, f_te) in F: | // f_tr = 75% of experimental data | ||||
| 4: | FOR EACH kinetic model mod in K: | // Described in Equations (2)–(5) | ||||
| 5: | FOR EACH optimizer opt in O: | // IPA, PSO and UMDA | ||||
| 6: | // Calibrate and evaluate kinetic models | |||||
| 7: | // Compute prediction error (MSE_test) | |||||
| 8: | END FOR | |||||
| 9: | END FOR | |||||
| 10: | Save_file( | // Store partial results | ||||
| 11: | END FOR | |||||
| 12: | Compute Average and Standard deviation on PI | //Compute Statistics and plots | ||||
| 13: | END FOR | |||||
| 14: | Output the best optimizer, kinetic model, and corresponding optimal parameters as a result | |||||
3. Results
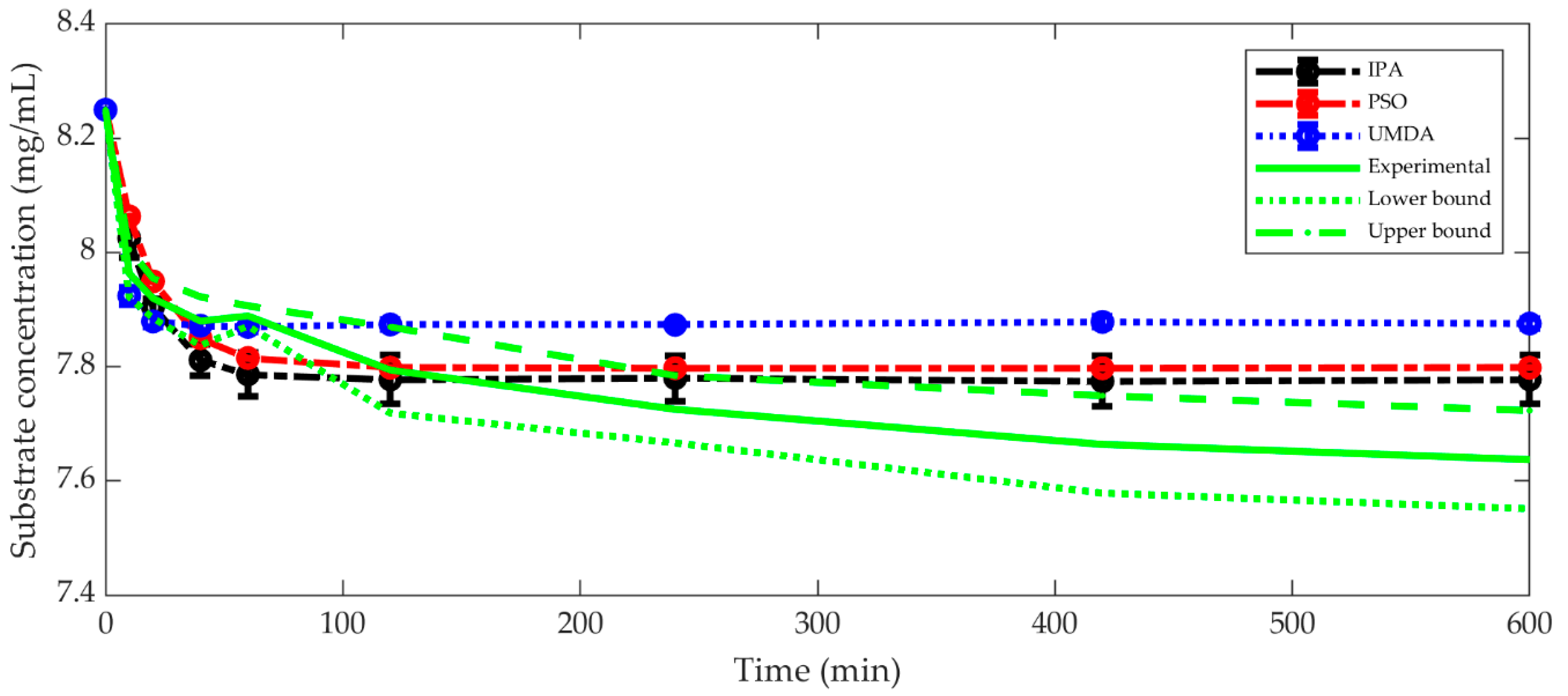
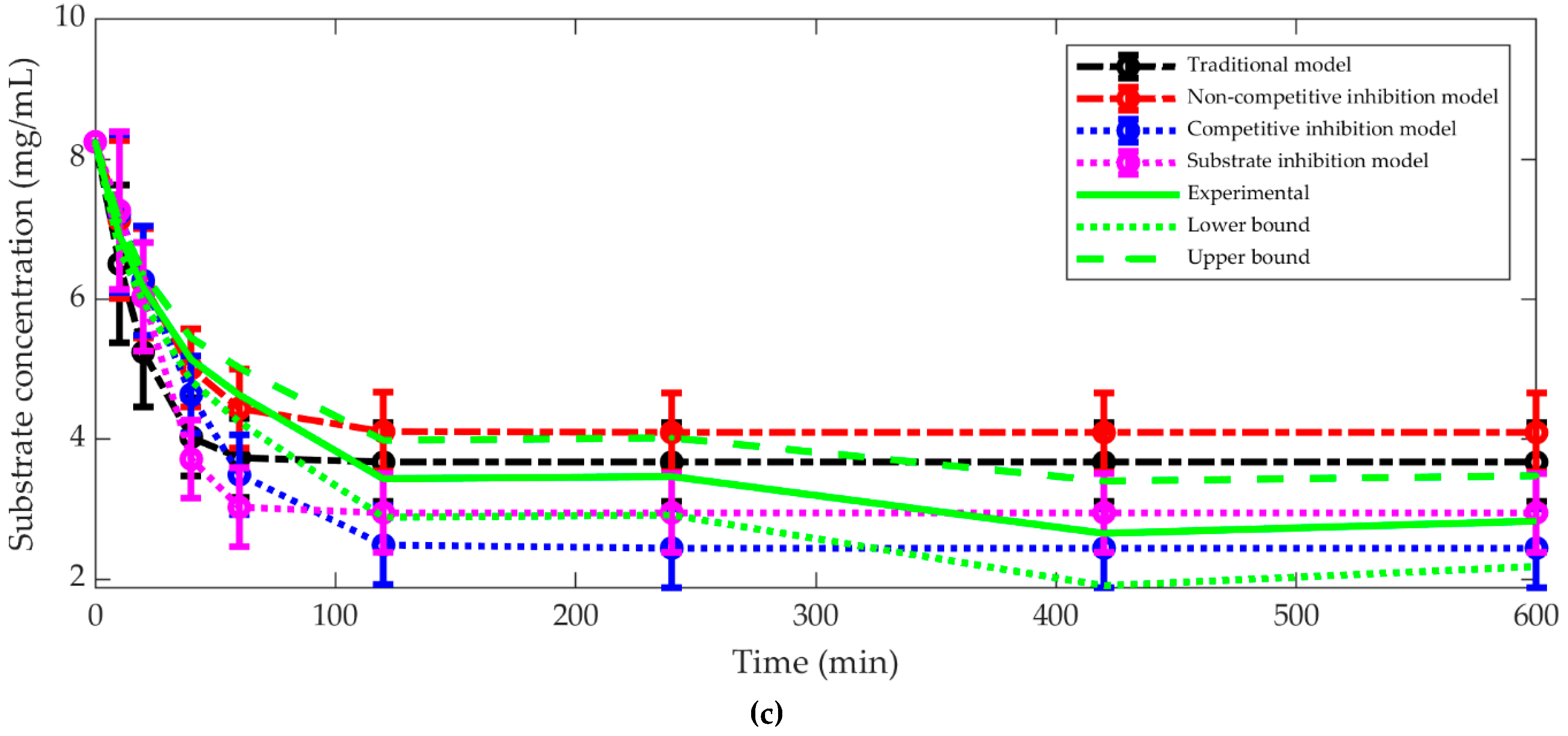
3.1. The Best Kinetic Model
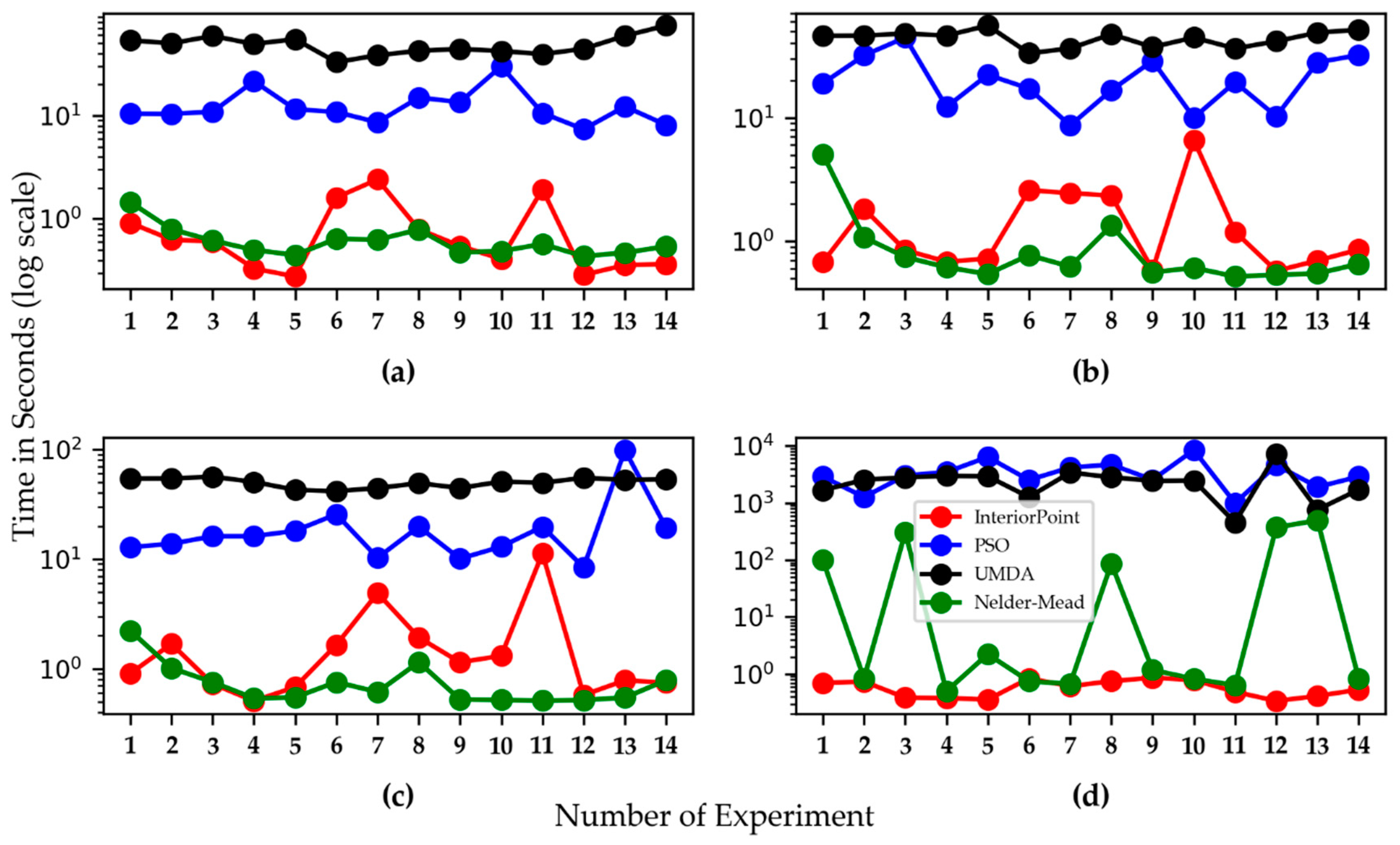
3.2. Computation Time for Kinetic Parameter Optimization
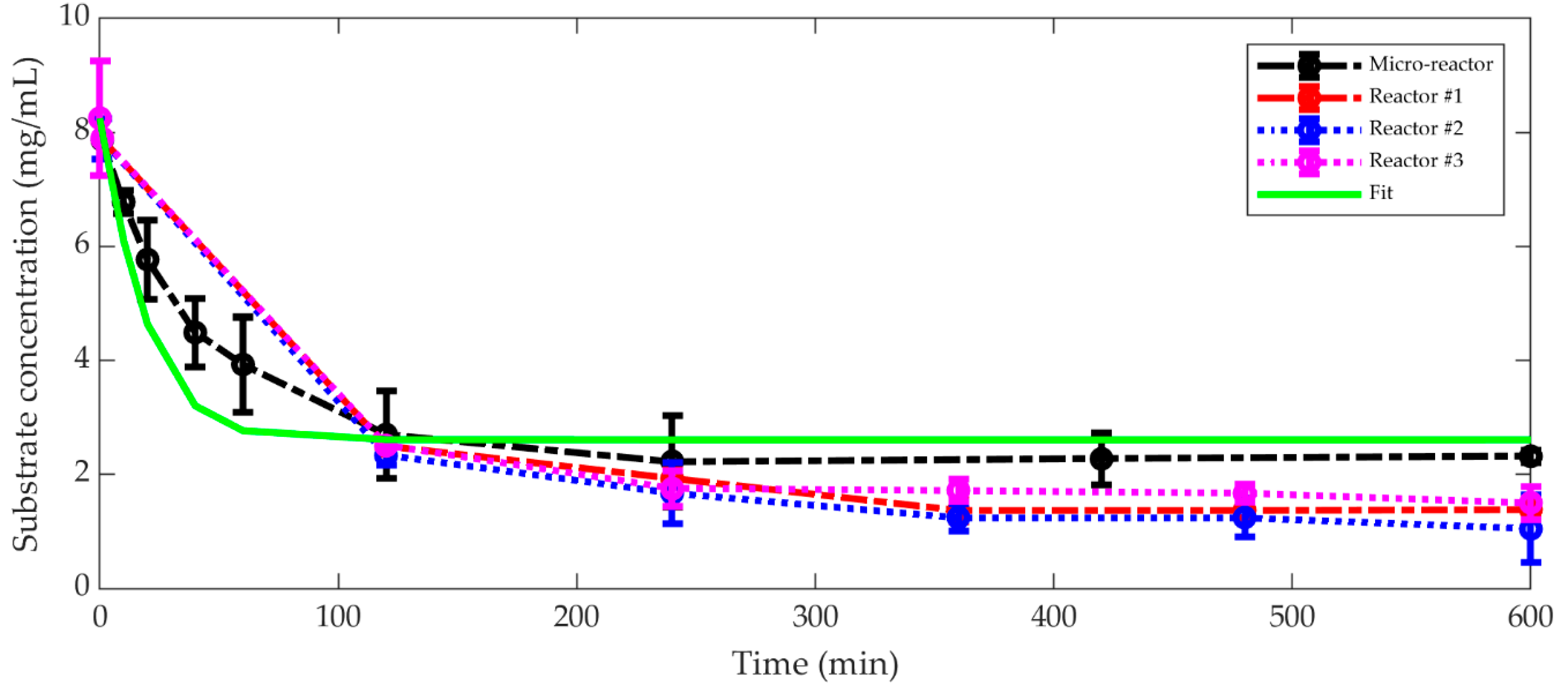
3.3. Comparison between Micro-Reaction and Bench Scale Reactor
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Molina-Guerrero, C.E.; de la Rosa, G.; Castillo-Michel, H.; Sánchez, A.; García-Castañeda, C.; Hernández-Rayas, A.; Valdez-Vazquez, I.; Suarez-Vázquez, S. Physicochemical Characterization of Wheat Straw during a Continuous Pretreatment Process. Chem. Eng. Technol. 2018, 41, 1350. [Google Scholar] [CrossRef]
- Sakimoto, K.; Kanna, M.; Matsumura, Y. Kinetic model of cellulose degradation using simultaneous saccharification and fermentation. Biomass. Bioenergy 2017, 99, 116–121. [Google Scholar] [CrossRef]
- Cho, Y.S.; Lim, H.S. Comparison of various estimation methods for the parameters of Michaelis–Menten equation based on in vitro elimination kinetic simulation data. Transl. Clin. Pharmacol. 2018, 26, 39–47. [Google Scholar] [CrossRef] [PubMed]
- Valencia, P.; Cornejo, I.; Almonacid, S.; Teixeira, A.A.; Simpson, R. Kinetic Parameter Determination for Enzyme Hydrolysis of Fish Protein Residue Using D-optimal Design. Food Bioprocess. Tech. 2013, 6, 290–296. [Google Scholar] [CrossRef]
- Pernice, S.; Follia, L.; Balbo, G.; Milanesi, L.; Sartini, G.; Totis, N.; Lió, P.; Merelli, I.; Cordero, F.; Beccuti, M. Integrating Petri Nets and Flux Balance Methods in Computational Biology Models: A Methodological and Computational Practice. Fundamenta Informaticae 2019, 171, 367–392. [Google Scholar]
- Chou, I.C.; Voit, E.O. Recent developments in parameter estimation and structure identification of biochemical and genomic systems. Math. Biosci. 2009, 219, 57–83. [Google Scholar] [CrossRef] [PubMed]
- Kruse, R.; Borgelt, C.; Braune, C.; Mostaghim, S.; Steinbrecher, M. Introduction to computational intelligence. In Computational Intelligence; Springer: London, UK, 2014; Volume 62, pp. 3–17. ISBN 9781447172963. [Google Scholar]
- Quaranta, G.; Lacarbonara, W.; Masri, S.F. A Review on Computational Intelligence for Identification of Nonlinear Dynamical Systems; Springer: Amsterdam, The Netherlands, 2020; Volume 99, ISBN 1107101905. [Google Scholar]
- Tangherloni, A.; Spolaor, S.; Cazzaniga, P.; Besozzi, D.; Rundo, L.; Mauri, G.; Nobile, M.S. Biochemical parameter estimation vs. benchmark functions: A comparative study of optimization performance and representation design. Appl. Soft Comput. 2019, 81, 105494. [Google Scholar] [CrossRef]
- Rojas-Dominguez, A.; Padierna, L.C.; Carpio Valadez, J.M.; Puga-Soberanes, H.J.; Fraire, H.J. Optimal Hyper-Parameter Tuning of SVM Classifiers with Application to Medical Diagnosis. IEEE Access 2017, 6, 7164–7176. [Google Scholar] [CrossRef]
- Berlin, A.; Maximenko, V.; Bura, R.; Kang, K.Y.; Gilkes, N.; Saddler, J. A rapid microassay to evaluate enzymatic hydrolysis of lignocellulosic substrates. Biotechnol. Bioeng. 2006, 93, 880–886. [Google Scholar] [CrossRef] [PubMed]
- Molina, C.; Sánchez, A.; Serafín-Muñoz, A.; Folch-Mallol, J. Optimization of Enzymatic Saccharification of Wheat Straw in a Micro-Scale System By Response Surface Methodology. Rev. Mex. Ing. Quím. 2014, 13, 765–778. [Google Scholar]
- Molina Guerrero, C.E.; De la Rosa, G.; Gonzalez Castañeda, J.; Sánchez, Y.; Castillo-Michel, H.; Valdez-Vazquez, I.; Balcazar, E.; Salmerón, I. Optimization of Culture Conditions for Production of Cellulase by Stenotrophomonas maltophilia. BioResources 2018, 13, 8358–8372. [Google Scholar] [CrossRef]
- Fogler, S. Elements of Chemical Reaction Enginnering, 5th ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2020. [Google Scholar]
- Strutz, T. Data Ftitting and Uncertainity, 1st ed.; Springer Fachmedien: Heidelberg, Germany, 2011; ISBN 9783834810229. [Google Scholar]
- Talbi, E.-G. Metaheuristics: From Design to Implementation, 1st ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009; ISBN 9780470278581. [Google Scholar]
- Aztatzi-Pluma, D.; Figueroa-Gerstenmaier, S.; Padierna, L.C.; Vazquez-Nuñez, E.; Molina-Guerrero, C.E. Análisis paramétrico de la depolimerización de paja de trigo en un sistema en microescala. In Proceedings of the XLI Encuentro Nacional de la AMIDIQ, Ixtapa, Mexico, 27–30 October 2020. (In Spanish). [Google Scholar]
- Larrañaga, P. A Review on Estimation of Distribution Algorithms. In Estimation of Distribution Algorithms, 1st ed.; Springer: Boston, MA, USA, 2002. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle Swarm Optimization. In Proceedings of the Proceedings of ICNN’95—International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Byrd, R.; Hribar, M.; Nocedal, J. An Interior Point Algorithm for large-scale Nonlinear Programming. Ind. Eng. Manag. Sci. 1999, 9, 877–900. [Google Scholar] [CrossRef]
- Hauschild, M.; Pelikan, M. An introduction and survey of estimation of distribution algorithms. Swarm. Evol. Comput. 2011, 1, 111–128. [Google Scholar] [CrossRef]
- Zhang, Q.; Mühlenbein, H. On the Convergence of a Class of Estimation of Distribution Algorithms. IEEE T. Evolut. Comput. 2004, 8, 127–136. [Google Scholar] [CrossRef]
- Poli, R.; Kennedy, J.; Blackwell, T. Particle swarm optimization: An overview. Swarm. Intell. 2007, 1, 33–57. [Google Scholar] [CrossRef]
- Rao, S.S.; Mulkay, E. Using Interior-Point Algorithms. AIAA J. 2000, 38, 2127–2132. [Google Scholar] [CrossRef]
- Vanderbei, R. Linear Programming: Foundations and Extensions, 5th ed.; Springer: New York, NY, USA, 2020; ISBN 9783030394141. [Google Scholar]
- Lustig, I.J.; Marsten, R.E.; Shanno, D.F. Feature Article—Interior Point Methods for Linear Programming: Computational State of the Art. ORSA J. Comput. Publ. 1994, 6, 1–14. [Google Scholar] [CrossRef]
- Hofstee, B.H.J. On the Evaluation of the Constants Vm and KM in Enzyme Reactions. Science 1952, 116, 329–331. [Google Scholar] [CrossRef]
- Murphy, A. The Coefficients of Correlation and Determination as Measures of Performance in Forecast Verification. Weather Forecast. 1995, 10, 681–688. [Google Scholar] [CrossRef]
- Dutta, K.; Dasu, V.V.; Mahanty, B.; Prabhu, A.A. Substrate Inhibition Growth Kinetics for Cutinase Producing Pseudomonas Substrate Inhibition. Chem. Biochem. Eng. Q. 2015, 3, 437–445. [Google Scholar] [CrossRef]



| Experiment | pH | °C | µL/mg | Experiment | pH | °C | µL/mg |
|---|---|---|---|---|---|---|---|
| 1 | 4.3 | 48 | 1.4656 | 8 | 4.0 | 55 | 0.9000 |
| 2 | 4.3 | 62 | 0.3343 | 9 | 6.0 | 55 | 0.9000 |
| 3 | 4.3 | 62 | 1.4656 | 10 | 5.0 | 45 | 0.9000 |
| 4 | 5.7 | 48 | 0.3343 | 11 | 5.0 | 65 | 0.9000 |
| 5 | 5.7 | 48 | 1.4656 | 12 | 5.0 | 55 | 0.1000 |
| 6 | 5.7 | 62 | 0.3343 | 13 | 5.0 | 55 | 1.8000 |
| 7 | 5.7 | 62 | 1.4656 | 14 | 5.0 | 55 | 0.9000 |
| Experiment | Optimizer | Best-Fitting Kinetic Model | R2 Train | AIC Mean ± Std | VMax* | Km* | K* | MSE Train | MSE Test | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | IPA | Traditional | 0.98 ± 0.03 | −15.29 ± 11.52 | 2.77 ± 5.0 | 1.43 | 0.58 | 1.25 | 0.02 ± 0.03 | 0.01 ± 0.02 | |
| PSO | Traditional | 0.88 ± 0.10 | −2.01 ± 5.80 | 15.76 ± 3.59 | 0.83 | 8.25 | 0.32 | 0.19 ± 0.19 | 1.05 ± 1.38 | ||
| UMDA | Non-Competitive I. | 0.81 ± 0.12 | 2.88 ± 5.11 | 23.55 ± 14.6 | 2.19 | 3.29 | 0.80 | 4.33 | 0.31 ± 0.23 | 0.76 ± 0.57 | |
| 2 | IPA | Traditional | 0.86 ± 0.21 | −11.08 ± 5.45 | 12.72 ± 19.33 | 1.05 | 8.25 | 0.44 | 0.06 ± 0.06 | 0.08 ± 0.07 | |
| PSO | Non-Competitive I. | 0.82 ± 0.25 | −8.92 ± 6.32 | 31.17 ± 55.71 | 3.21 | 8.25 | 0.73 | 4.02 | 0.06 ± 0.05 | 0.09 ± 0.06 | |
| UMDA | Non-Competitive I. | 0.82 ± 0.14 | −6.33 ± 5.81 | 16.19 ± 19.77 | 3.47 | 4.21 | 1.04 | 6.66 | 0.09 ± 0.07 | 0.1 ± 0.09 | |
| 3 | IPA | Traditional | 0.90 ± 0.16 | −4.63 ± 8.43 | 6.32 ± 8.78 | 0.55 | 8.25 | 0.17 | 0.17 ± 0.22 | 0.39 ± 0.02 | |
| PSO | Competitive I. | 0.90 ± 0.14 | −2.51 ± 6.85 | 7.3 ± 9.95 | 1.15 | 7.84 | 0.15 | 8.11 | 0.16 ± 0.15 | 0.18 ± 0.11 | |
| UMDA | Substrate I. | 0.81 ± 0.10 | 1.63 ± 4.06 | 22.12 ± 14.81 | 4.96 | 7.74 | 1.23 | 0.39 ± 0.17 | 0.81 ± 0.63 | ||
| 4 | IPA | Traditional | 0.98 ± 0.01 | −7.79 ± 3.66 | 43.98 ± 58.02 | 0.17 | 8.25 | 0.04 | 0.07 ± 0.05 | 0.73 ± 1.14 | |
| PSO | Non-Competitive I. | 0.80 ± 0.33 | 6.67 ± 9.17 | 144.2 ± 188.17 | 8.04 | 0.10 | 2.62 | 8.25 | 0.57 ± 0.87 | 0.85 ± 1.25 | |
| UMDA | Substrate I. | 0.86 ± 0.07 | 3.73 ± 3.13 | 227.62 ± 121.3 | 4.80 | 6.40 | 1.26 | 0.49 ± 0.21 | 1.12 ± 0.91 | ||
| 5 | IPA | Non-Competitive I. | 0.87 ± 0.06 | 3.97 ± 2.1 | 37.01 ± 65.49 | 0.38 | 8.25 | 0.12 | 0.001 | 0.37 ± 0.13 | 0.65 ± 0.62 |
| PSO | Non-Competitive I. | 0.84 ± 0.08 | 5.06 ± 2.55 | 37.19 ± 65.92 | 2.16 | 2.31 | 0.6 | 7.97 | 0.44 ± 0.20 | 1.03 ± 1.01 | |
| UMDA | Non-Competitive I. | 0.78 ± 0.14 | 6.48 ± 1.85 | 38.14 ± 66.29 | 1.52 | 5.78 | 0.34 | 7.94 | 0.56 ± 0.16 | 0.75 ± 0.60 | |
| 6 | IPA | Non-Competitive I. | 0.72 ± 0.15 | −20.73 ± 6.98 | 12.86 ± 4.66 | 2.06 | 8.25 | 0.99 | 5.58 | 0.01 ± 0.01 | 0.01 ± 0.00 |
| PSO | Traditional | 0.81 ± 0.09 | −20.64 ± 4.58 | 8.89 ± 3.07 | 5.37 | 0.66 | 4.90 | 0.01 ± 0.01 | 0.01 ± 0.01 | ||
| UMDA | Traditional | 0.64 ± 0.04 | −21.18 ± 1.99 | 15.48 ± 1.56 | 6.36 | 6.35 | 3.50 | 0.01 ± 0.00 | 0.02 ± 0.01 | ||
| 7 | IPA | Competitive I. | 0.76 ± 0.33 | −22.2 ± 3.87 | 47.33 ± 83.02 | 2.13 | 1.50 | 1.44 | 5.58 | 0.01 ± 0.00 | 0.02 ± 0.01 |
| PSO | Traditional | 0.77 ± 0.16 | −22.35 ± 2.68 | 50.41 ± 78.26 | 3.81 | 8.25 | 1.80 | 0.01 ± 0.00 | 0.02 ± 0.02 | ||
| UMDA | Non-Competitive I. | 0.82 ± 0.17 | −23.27 ± 3.49 | 48.61 ± 78.27 | 6.12 | 5.15 | 2.06 | 5.22 | 0.01 ± 0.00 | 0.02 ± 0.01 | |
| 8 | IPA | Traditional | 0.89 ± 0.16 | −8.22 ± 6.91 | 396.46 ± 784.32 | 0.97 | 8.25 | 0.38 | 0.09 ± 0.11 | 0.06 ± 0.05 | |
| PSO | Traditional | 0.89 ± 0.14 | −7.5 ± 6.02 | 398.22 ± 782.66 | 0.88 | 3.82 | 0.5 | 0.10 ± 0.10 | 0.10 ± 0.07 | ||
| UMDA | Non-Competitive I. | 0.75 ± 0.12 | 1.12 ± 1.54 | 428.95 ± 764.32 | 2.57 | 3.61 | 1.40 | 0.97 | 0.27 ± 0.07 | 0.38 ± 0.71 | |
| 9 | IPA | Traditional | 0.87 ± 0.15 | −6.75 ± 4.9 | 237.31 ± 444.35 | 0.58 | 8.25 | 0.22 | 0.11 ± 0.10 | 0.25 ± 0.36 | |
| PSO | Non-Competitive I. | 0.86 ± 0.12 | −3.38 ± 2.71 | 243.96 ± 441.48 | 7.21 | 0.18 | 6.86 | 0.0001 | 0.14 ± 0.07 | 0.11 ± 0.12 | |
| UMDA | Non-Competitive I. | 0.8 ± 0.09 | −0.3 ± 3.58 | 259.85 ± 419.39 | 4.58 | 4.53 | 1.30 | 7.01 | 0.22 ± 0.10 | 0.23 ± 0.13 | |
| 10 | IPA | Traditional | 0.88 ± 0.2 | −9.58 ± 6.29 | 57.97 ± 83.54 | 0.83 | 8.25 | 0.33 | 0.07 ± 0.09 | 0.08 ± 0.03 | |
| PSO | Competitive I. | 0.9 ± 0.07 | −7.79 ± 6.27 | 88.4 ± 132.63 | 1.28 | 2.47 | 0.85 | 0.23 | 0.07 ± 0.05 | 0.11 ± 0.08 | |
| UMDA | Non-Competitive I. | 0.86 ± 0.06 | −3.85 ± 5.28 | 91.28 ± 70.49 | 5.05 | 4.26 | 1.39 | 7.60 | 0.13 ± 0.09 | 0.13 ± 0.13 | |
| 11 | IPA | Traditional | 0.86 ± 0.24 | −18.82 ± 7.1 | 57.15 ± 102.38 | 3.83 | 7.26 | 1.83 | 0.01 ± 0.00 | 0.07 ± 0.09 | |
| PSO | Traditional | 0.86 ± 0.23 | −16.58 ± 2.91 | 63.04 ± 103.31 | 3.92 | 8.20 | 1.78 | 0.01 ± 0.00 | 0.01 ± 0.00 | ||
| UMDA | Traditional | 0.86 ± 0.22 | −16.31 ± 2.64 | 62.35 ± 98.77 | 5.32 | 5.06 | 3.04 | 0.01 ± 0.00 | 0.02 ± 0.01 | ||
| 12 | IPA | Traditional | 0.89 ± 0.07 | 1.44 ± 7.89 | 28.75 ± 27.83 | 0.19 | 8.25 | 0.05 | 0.38 ± 0.24 | 0.73 ± 0.51 | |
| PSO | Substrate I. | 0.87 ± 0.08 | 2.5 ± 3.77 | 68.16 ± 41.92 | 0.53 | 8.25 | 0.09 | 0.43 ± 0.22 | 1.09 ± 1.02 | ||
| UMDA | Substrate I. | 0.76 ± 0.18 | 5.99 ± 2.27 | 104.04 ± 69.11 | 5.15 | 8.21 | 1.27 | 0.76 ± 0.28 | 0.75 ± 0.29 | ||
| 13 | IPA | Traditional | 0.93 ± 0.07 | −3.06 ± 6.19 | 15.03 ± 23.47 | 0.55 | 8.25 | 0.16 | 0.20 ± 0.19 | 0.24 ± 0.15 | |
| PSO | Competitive I. | 0.93 ± 0.1 | −1.24 ± 6.89 | 15.11 ± 25.02 | 0.42 | 3.99 | 0.14 | 1.91 | 0.19 ± 0.23 | 0.14 ± 0.08 | |
| UMDA | Substrate I. | 0.86 ± 0.13 | 1.02 ± 4.87 | 29.65 ± 35.81 | 3.64 | 7.61 | 0.84 | 0.35 ± 0.23 | 0.73 ± 0.70 | ||
| 14 | IPA | Traditional | 0.95 ± 0.02 | −7.72 ± 1.46 | 164.65 ± 309.48 | 0.78 | 8.25 | 0.24 | 0.10 ± 0.03 | 0.15 ± 0.10 | |
| PSO | Traditional | 0.85 ± 0.19 | −4.17 ± 4.47 | 138.93 ± 249.87 | 1.07 | 7.15 | 0.38 | 0.17 ± 0.09 | 0.18 ± 0.11 | ||
| UMDA | Non-Competitive I. | 0.81 ± 0.23 | −0.38 ± 2.95 | 144.33 ± 247.4 | 3.94 | 2.83 | 1.14 | 6.80 | 0.22 ± 0.08 | 0.26 ± 0.23 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aztatzi-Pluma, D.; Figueroa-Gerstenmaier, S.; Padierna, L.C.; Vázquez-Núñez, E.; Molina-Guerrero, C.E. Kinetic Parameter Determination for Depolymerization of Biomass by Inverse Modeling and Metaheuristics. Processes 2020, 8, 836. https://doi.org/10.3390/pr8070836
Aztatzi-Pluma D, Figueroa-Gerstenmaier S, Padierna LC, Vázquez-Núñez E, Molina-Guerrero CE. Kinetic Parameter Determination for Depolymerization of Biomass by Inverse Modeling and Metaheuristics. Processes. 2020; 8(7):836. https://doi.org/10.3390/pr8070836
Chicago/Turabian StyleAztatzi-Pluma, Dalyndha, Susana Figueroa-Gerstenmaier, Luis Carlos Padierna, Edgar Vázquez-Núñez, and Carlos E. Molina-Guerrero. 2020. "Kinetic Parameter Determination for Depolymerization of Biomass by Inverse Modeling and Metaheuristics" Processes 8, no. 7: 836. https://doi.org/10.3390/pr8070836
APA StyleAztatzi-Pluma, D., Figueroa-Gerstenmaier, S., Padierna, L. C., Vázquez-Núñez, E., & Molina-Guerrero, C. E. (2020). Kinetic Parameter Determination for Depolymerization of Biomass by Inverse Modeling and Metaheuristics. Processes, 8(7), 836. https://doi.org/10.3390/pr8070836






