A Fractal-Based Correlation for Time-Dependent Surface Diffusivity in Porous Adsorbents
Abstract
1. Introduction
2. Surface Transport and Variable Surface Diffusivity Models
3. Results and Discussion
3.1. Formulation of a Time-Dependent Correlation for Surface Diffusivity
- In the case of anomalous transport (such as single-file diffusion in zeolites), for which the mean square displacement of the diffusing entity exhibits a nonlinear growth with time, the time variation of the diffusion coefficient can be expressed via a power-law scaling equation, and the diffusivity decreases or increases with time for sub-diffusion and super-diffusion, respectively, as discussed in the works by Kärger and colleagues [37,38], Metzler and Klafter [39], de Gauw et al. [40], Lutz et al. [41], Wu and Berland [42];
- Kopelman [43] applied fractal-like kinetics to describe the dynamics of diffusion-limited heterogeneous processes, for which the time-decrease of rate coefficients derives from the non-re-randomization of the reactants position in the diffusion space due to dimensional or topological constraints. Fractal-like kinetic models have been successfully applied to interpret kinetic data for gas–solid reactive systems and fluid–solid adsorption processes, as in Haerifar and Azizian [44] and in the works by Balsamo and Montagnaro [45,46,47,48].
3.2. Analysis of the Time-Dependent Equation for Surface Diffusivity
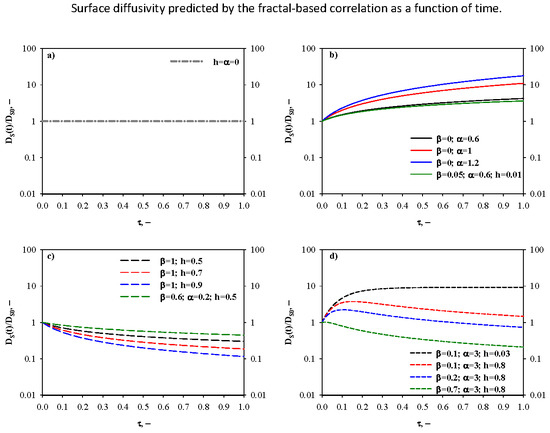
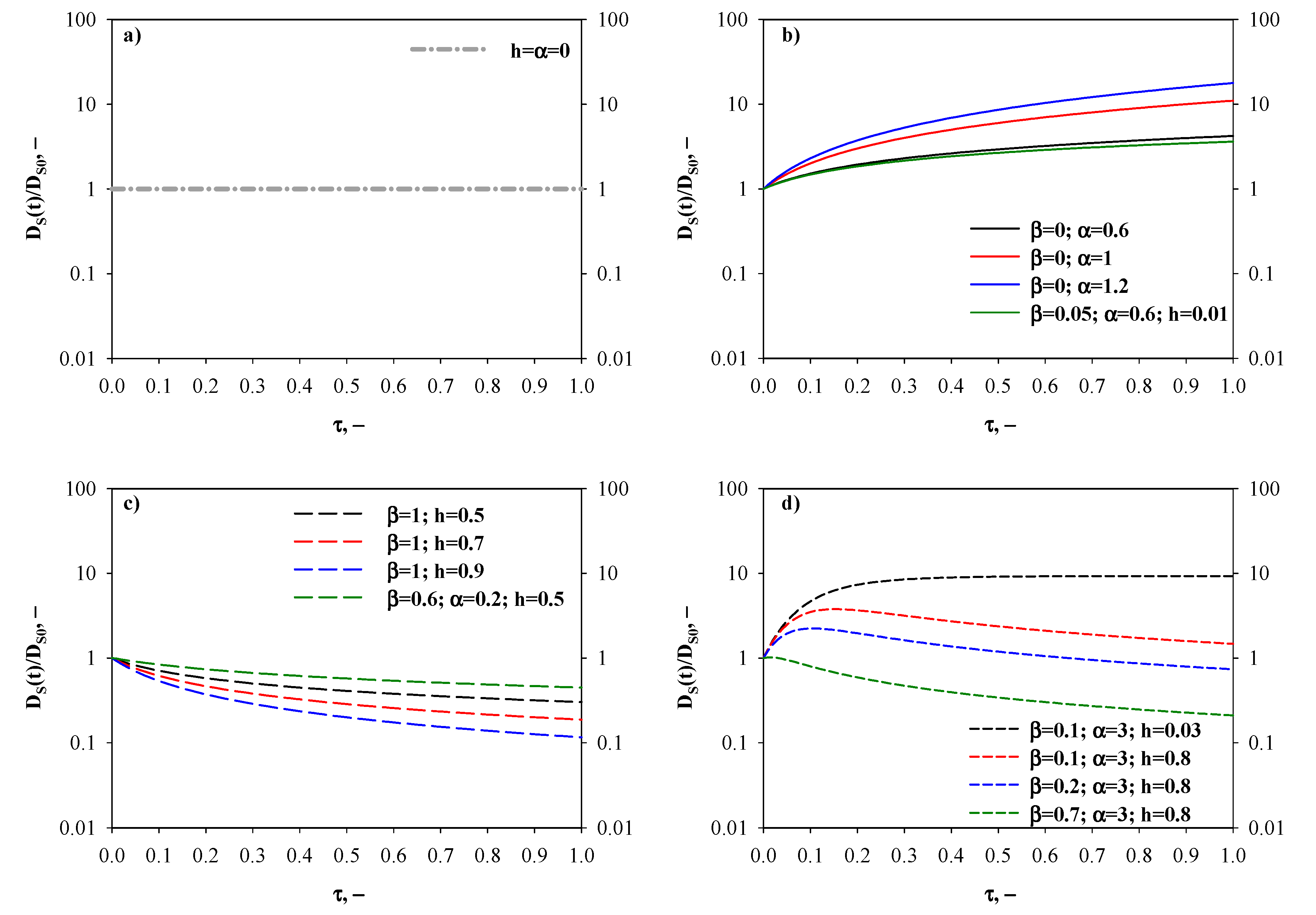
- Time-invariant diffusivity ratio—Figure 2a. The simplest case, for which DS(t) = DS0, occurs when both the fractal and hopping exponents are zero (i.e., h = α = 0). This indicates a memoryless transport process, that is to say the adsorbate surface diffusion is not affected by alterations of the porous diffusion environment taking place along the adsorption process.
- Monotonically increasing diffusivity ratio—Figure 2b. In this scenario, the surface transport of the diffusing species is continuously enhanced as new adsorbate molecules/ions are captured by the adsorbent. First of all, this pattern can be established when there is no contribution of the fractal diffusion resistance to the overall one, i.e., β = 0 and therefore the surface diffusivity is equal to its time-increasing hopping term only (). The time-increase of the diffusivity ratio is more marked at greater values of the hopping exponent α, and the differences in DS(t)/DS0 values become augmented as the adsorption time proceeds. For instance, at τ = 0.5 the surface diffusivity ratio is 2.93 and 8.58 for α = 0.6 and 1.2, respectively. Under equilibrium conditions, DS(t)/DS0 is 4.21 and 17.77 for α = 0.6 and 1.2, respectively. Furthermore, a time-increasing surface diffusivity ratio can be also obtained for a non-zero value of β. In this case, the constraint ≥ teq+1 (i.e., t* ≥ teq) needs to be satisfied, because otherwise the maximum for the surface diffusivity ratio would fall in the existence domain for τ.
- Monotonically decreasing diffusivity ratio—Figure 2c. This is the case of a hindered diffusion process, for which the surface diffusivity decreases with time, and it is common for diffusion in zeolites. A monotonically decreasing DS(t)/DS0 pattern can be predicted by setting β = 1, therefore the surface diffusivity is equal to its time-decreasing fractal term only (). In this context, the fractal exponent h regulates the time-decay of the surface diffusivity. For h = 0.5, a slight decrease of the surface diffusivity with time can be observed: DS(t)/DS0 is 0.41 and 0.30 for τ = 0.5 and 1, respectively. An increase of h produces a more relevant reduction of the surface diffusivity. In fact, for h = 0.9 the surface diffusivity diminishes by about one order of magnitude when comparing the initial value with respect to the one retrieved at τ = 1. In addition, a time-decreasing trend for surface diffusivity can be also derived for a non-negligible contribution of the hopping transport resistance when the condition ≤ 1 is fulfilled (i.e., t* ≤ 0).
- Diffusivity ratio exhibiting a maximum—Figure 2d. In this scenario, factors determining an increase of surface diffusivity prevail for short adsorption times, whereas hindered transport rules thereafter. From a mathematical standpoint, the constraint 1 < < teq+1 needs to be satisfied to obtain a maximum value for DS(t). The effects of β, α and h on the time evolution of the surface diffusivity are shown in Figure 2d. In particular, when fixing α and h, an increase of the fractional contribution of the fractal diffusion resistance (i.e., greater values of β) determines a shift of the maximum towards shorter adsorption times and an associated reduction of the maximum value of the surface diffusivity (i.e., the diffusion process is negatively affected by increases in β). As an example, when α = 3 and h = 0.8, τ* equals to 0.15 (maximum diffusivity ratio = 3.76) and 0.10 (maximum diffusivity ratio = 2.23) for β = 0.1 and 0.2, respectively. Very interestingly, sufficiently high values of β also allow to predict surface diffusivity values smaller than DS0. Finally, it is worth observing that when the α/h ratio is very high (example in the figure: α = 3 and h = 0.03), the surface diffusivity decreases very weakly with time after having reached its maximum value.
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| C | concentration of adsorbate in fluid phase | (M/L3) |
| DS | adsorbate surface diffusivity | (L2/t) |
| DS0 | zero-loading adsorbate surface diffusivity | (L2/t) |
| coefficient introduced in Equation (9) | (L2/t(1−h)) | |
| coefficient introduced in Equation (12) | (L2/t(1+α)) | |
| DSS | adsorbate self-diffusivity | (L2/t) |
| f | fugacity | (–) |
| g | function defined in Equation (4) | (–) |
| H | Heaviside function | (–) |
| h | fractal exponent | (–) |
| J | mass flux (with respect to density) | (L/t) |
| m | exponent in Equation (8) | (–) |
| q | concentration of adsorbate in solid phase | (M/M) |
| r | radial coordinate of the adsorbent particle | (L) |
| T | temperature | (T) |
| t | time | (t) |
| t1 | unitary value of time (t1 = 1) | (t) |
| Greek letters: | ||
| α | hopping exponent | (–) |
| β | fractional contribution defined in MBI Equation (15) | (–) |
| θ | surface coverage degree | (–) |
| λ | blockage parameter | (–) |
| τ | dimensionless time | (–) |
| Superscripts: | ||
| * | point of maximum | |
| fr | fractal | |
| hop | hopping | |
| Subscripts: | ||
| eq | equilibrium value | |
| m | saturation (monolayer) conditions | |
| max | maximum value | |
| L | length | |
| M | quantity | |
| T | temperature | |
| t | time |
References
- Zagorodni, A.A. Ion Exchange Materials: Properties and Applications, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2006; ISBN 9780080445526. [Google Scholar]
- Schwaab, M.; Steffani, E.; Barbosa-Coutinho, E.; Severo Júnior, J.B. Critical analysis of adsorption/diffusion modelling as a function of time square root. Chem. Eng. Sci. 2017, 173, 179–186. [Google Scholar] [CrossRef]
- Sen Gupta, S.; Bhattacharyya, K.G. Kinetics of adsorption of metal ions on inorganic materials: A review. Adv. Colloid Interface Sci. 2011, 162, 39–58. [Google Scholar] [CrossRef] [PubMed]
- Inglezakis, V.J.; Fyrillas, M.M.; Stylianou, M.A. Two-phase homogeneous diffusion model for the fixed bed sorption of heavy metals on natural zeolites. Micropor. Mesopor. Mater. 2018, 266, 164–176. [Google Scholar] [CrossRef]
- Suzuki, M. Adsorption Engineering; Elsevier: Amsterdam, The Netherlands, 1990; p. 8025. ISBN 044498. [Google Scholar]
- Crank, J. The Mathematics of Diffusion; Oxford University Press: Oxford, UK, 1986; p. 4116. ISBN 019853. [Google Scholar]
- Boyd, G.E.; Schubert, J.; Adamson, A.W. The exchange adsorption of ions from aqueous solutions by organic zeolites. 1. Ion-exchange equilibria. J. Am. Chem. Soc. 1947, 69, 2818–2829. [Google Scholar] [CrossRef]
- Paterson, S. The heating or cooling of a solid sphere in a well-stirred fluid. Proc. Phys. Soc. 1947, 59, 50–58. [Google Scholar] [CrossRef]
- Helfferich, F. Ion Exchange; Dover Publications: New York, NY, USA, 1995; ISBN 0486687848. [Google Scholar]
- Inglezakis, V.J.; Fyrillas, M.M. Adsorption fixed beds modeling revisited: Generalized solutions for S-shaped isotherms. Chem. Eng. Commun. 2017, 204, 1299–1317. [Google Scholar] [CrossRef]
- Inglezakis, V.J.; Fyrillas, M.M.; Park, J. Variable diffusivity homogeneous surface diffusion model and analysis of merits and fallacies of simplified adsorption kinetics equations. J. Hazard. Mater. 2019, 367, 224–245. [Google Scholar] [CrossRef]
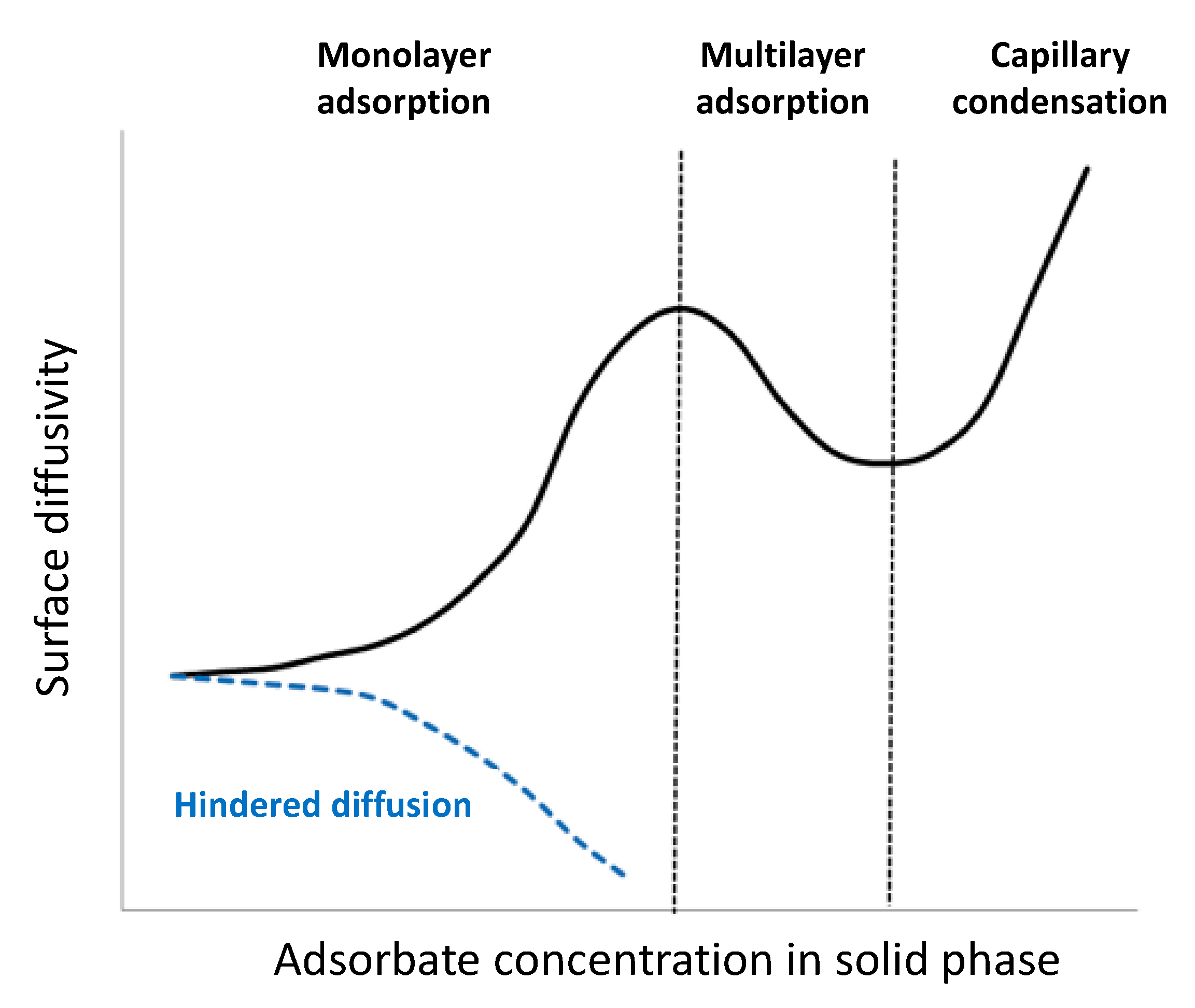
- Choi, J.G.; Do, D.D.; Do, H.D. Surface diffusion of adsorbed molecules in porous media: Monolayer, multilayer, and capillary condensation regimes. Ind. Eng. Chem. Res. 2001, 40, 4005–4031. [Google Scholar] [CrossRef]
- Valiullin, R.; Kortunov, P.; Kärger, J.; Timoshenko, V. Concentration-dependent self-diffusion of liquids in nanopores: A nuclear magnetic resonance study. J. Chem. Phys. 2004, 120, 11804–11814. [Google Scholar] [CrossRef] [PubMed]
- Ruthven, D.M. Principles of Adsorption and Adsorption Processes; John Wiley & Sons: Hoboken, NJ, USA, 1984; ISBN 9780471866060. [Google Scholar]
- Jia, B.; Tsau, J.S.; Barati, R. Different flow behaviors of low-pressure and high-pressure carbon dioxide in shales. SPE J. 2018, 23, SPE–191121–PA. [Google Scholar] [CrossRef]
- Kärger, J.; Ruthven, D.M. Diffusion in zeolites. Comparison of sorption and nuclear magnetic resonance diffusivities. J. Cemical Soc. Faraday Trans. I 1981, 77, 1485–1496. [Google Scholar] [CrossRef]
- Skoulidas, A.I.; Sholl, D.S. Molecular dynamics simulations of self-diffusivities, corrected diffusivities, and transport diffusivities of light gases in four silica zeolites to assess influences of pore shape and connectivity. J. Phys. Chem. A 2003, 107, 10132–10141. [Google Scholar] [CrossRef]
- Do, D.D. Adsorption Analysis: Equilibria and Kinetics; Imperial College Press: London, UK, 1998; Volume 2, ISBN 9781783262243. [Google Scholar]
- Ruthven, D.M. Sorption kinetics for diffusion-controlled systems with a strongly concentration-dependent diffusivity. Chem. Eng. Sci. 2004, 59, 4531–4545. [Google Scholar] [CrossRef]
- Do, D.D.; Do, H.D. Surface diffusion of hydrocarbons in activated carbon: Comparison between constant molar flow, differential permeation and differential adsorption bed methods. Adsorption 2001, 7, 189–209. [Google Scholar] [CrossRef]
- Kärger, J.; Ruthven, D.M. Diffusion in nanoporous materials: Fundamental principles, insights and challenges. New J. Chem. 2016, 40, 4027–4048. [Google Scholar] [CrossRef]
- Kärger, J. Measurement of diffusion in zeolites—A never ending challenge? Adsorption 2003, 9, 29–35. [Google Scholar] [CrossRef]
- Carman, P.C.; Rideal, E.K. Diffusion and flow of gases and vapours through micropores. IV. Flow of capillary condensate. Proc. R. Soc. A Math. Phys. Eng. Sci. 1951, 209, 38–58. [Google Scholar] [CrossRef]
- Gilliland, E.R.; Baddour, R.F.; Perkinson, G.P.; Sladek, K.J.; Perkinson, G.P.; Sladek, K.J. Diffusion on surfaces. I. Effect of concentration on the diffusivity of physically adsorbed gases. Ind. Eng. Chem. Fundam. 1974, 13, 95–100. [Google Scholar] [CrossRef]
- Okazaki, M.; Tamon, H.; Toei, R. Interpretation of surface flow phenomenon of adsorbed gases by hopping model. AlChE J. 1981, 27, 262–270. [Google Scholar] [CrossRef]
- Hu, X.; Do, D.D.; Rao, G.N. Experimental concentration dependence of surface diffusivity of hydrocarbons in activated carbon. Chem. Eng. Sci. 1994, 49, 2145–2152. [Google Scholar] [CrossRef]
- Karge, H.G.; Weitkamp, J. Molecular Sieves Science and Technology. Adsorption and Diffusion; Springer: Berlin/Heidelberg, Germany, 2008; Volume 7, ISBN 9783540739654. [Google Scholar]
- Ocampo-Perez, R.; Leyva-Ramos, R.; Alonso-Davila, P.; Rivera-Utrilla, J.; Sanchez-Polo, M. Modeling adsorption rate of pyridine onto granular activated carbon. Chem. Eng. J. 2010, 165, 133–141. [Google Scholar] [CrossRef]
- Chen, Y.D.; Yang, R.T. Concentration dependence of surface diffusion and zeolitic diffusion. AIChE J. 1991, 37, 1579–1582. [Google Scholar] [CrossRef]
- Chen, Y.D.; Yang, R.T. Surface and mesoporous diffusion with multilayer adsorption. Carbon 1998, 36, 1525–1537. [Google Scholar] [CrossRef]
- Liu, Z.; Fujita, N.; Miyasaka, K.; Han, L.; Stevens, S.M.; Suga, M.; Asahina, S.; Slater, B.; Xiao, C.; Sakamoto, Y.; et al. A review of fine structures of nanoporous materials as evidenced by microscopic methods. Microscopy 2013, 62, 109–146. [Google Scholar] [CrossRef]
- Higashi, K.; Ito, H.; Oishi, J. Surface diffusion phenomena in gaseous diffusion, (II). J. Nucl. Sci. Technol. 1964, 1, 298–304. [Google Scholar] [CrossRef]
- Marbán, G.; Ramírez-Montoya, L.A.; García, H.; Menéndez, J.Á.; Arenillas, A.; Montes-Morán, M.A. Load-dependent surface diffusion model for analyzing the kinetics of protein adsorption onto mesoporous materials. J. Colloid Interface Sci. 2018, 511, 27–38. [Google Scholar] [CrossRef]
- Murch, G.E.; Thorn, R.J. Interstitial solute diffusion in metals. J. Phys. Chem. Solids 1977, 38, 789–793. [Google Scholar] [CrossRef]
- Smit, B.; Maesen, T.L.M. Molecular simulations of zeolites: Adsorption, diffusion, and shape selectivity. Chem. Rev. 2008, 108, 4125–4184. [Google Scholar] [CrossRef]
- Jia, B.; Tsau, J.S.; Barati, R. Measurement of CO2 diffusion coefficient in the oil-saturated porous media. J. Petrol. Sci. Eng. 2019, 181, 106189. [Google Scholar] [CrossRef]
- Kärger, J.; Petzold, M.; Pfeifer, H.; Ernst, S.; Weitkamp, J. Single-file diffusion and reaction in zeolites. J. Cat. 1992, 136, 283–299. [Google Scholar] [CrossRef]
- Hahn, K.; Kärger, J.; Kukla, V.V. Single-file diffusion observation. Phys. Rev. Lett. 1996, 76, 2762–2765. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. The random walk’s guide to anomalous diffusion: A fractional dynamics approach. Phys. Rep. 2000, 339, 1–77. [Google Scholar] [CrossRef]
- De Gauw, F.J.M.M.; van Grondelle, J.; van Santen, R.A. Effect of single-file diffusion on the kinetics of hydroisomerization catalyzed by Pt/H-mordenite. J. Cat. 2001, 204, 53–63. [Google Scholar] [CrossRef]
- Lutz, C.; Kollmann, M.; Leiderer, P.; Bechinger, C. Diffusion of colloids in one-dimensional light channels. J. Condens. Matter Phys. 2004, 16, S4075. [Google Scholar] [CrossRef]
- Wu, J.; Berland, K.M. Propagators and time-dependent diffusion coefficients for anomalous diffusion. Biophys. J. 2008, 95, 2049–2052. [Google Scholar] [CrossRef] [PubMed]
- Kopelman, R. Fractal reaction kinetics. Science 1988, 241, 1620–1626. [Google Scholar] [CrossRef] [PubMed]
- Haerifar, M.; Azizian, S. Fractal-like adsorption kinetics at the solid/solution interface. J. Phys. Chem. C 2012, 116, 13111–13119. [Google Scholar] [CrossRef]
- Montagnaro, F.; Balsamo, M. Deeper insights into fractal concepts applied to liquid-phase adsorption dynamics. Fuel Process. Technol. 2014, 128, 412–416. [Google Scholar] [CrossRef]
- Balsamo, M.; Montagnaro, F. Fractal-like Vermeulen kinetic equation for the description of diffusion-controlled adsorption dynamics. J. Phys. Chem. C 2015, 119, 8781–8785. [Google Scholar] [CrossRef]
- Montagnaro, F.; Balsamo, M.; Salatino, P. A single particle model of lime sulphation with a fractal formulation of product layer diffusion. Chem. Eng. Sci. 2016, 156, 115–120. [Google Scholar] [CrossRef]
- Montagnaro, F.; Balsamo, M. Modelling CO2 adsorption dynamics onto amine-functionalised sorbents: A fractal-like kinetic perspective. Chem. Eng. Sci. 2018, 192, 603–612. [Google Scholar] [CrossRef]
- Havlin, S.; Ben-Avraham, D. Diffusion in disordered media. Adv. Phys. 1987, 36, 695–798. [Google Scholar] [CrossRef]
- Kapoor, A.; Yang, R.T. Surface diffusion on energetically heterogeneous surfaces-an effective medium approximation approach. Chem. Eng. Sci. 1990, 45, 3261–3270. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Inglezakis, V.J.; Balsamo, M.; Montagnaro, F. A Fractal-Based Correlation for Time-Dependent Surface Diffusivity in Porous Adsorbents. Processes 2020, 8, 689. https://doi.org/10.3390/pr8060689
Inglezakis VJ, Balsamo M, Montagnaro F. A Fractal-Based Correlation for Time-Dependent Surface Diffusivity in Porous Adsorbents. Processes. 2020; 8(6):689. https://doi.org/10.3390/pr8060689
Chicago/Turabian StyleInglezakis, Vassilis J., Marco Balsamo, and Fabio Montagnaro. 2020. "A Fractal-Based Correlation for Time-Dependent Surface Diffusivity in Porous Adsorbents" Processes 8, no. 6: 689. https://doi.org/10.3390/pr8060689
APA StyleInglezakis, V. J., Balsamo, M., & Montagnaro, F. (2020). A Fractal-Based Correlation for Time-Dependent Surface Diffusivity in Porous Adsorbents. Processes, 8(6), 689. https://doi.org/10.3390/pr8060689