Abstract
Measurements of pressure drop during experiments with fan-induced air flow in the open-cathode proton exchange membrane fuel cells (PEMFCs) show that flow friction in its open-cathode side follows logarithmic law similar to Colebrook’s model for flow through pipes. The stable symbolic regression model for both laminar and turbulent flow presented in this article correlates air flow and pressure drop as a function of the variable flow friction factor which further depends on the Reynolds number and the virtual roughness. To follow the measured data, virtual inner roughness related to the mesh of conduits of fuel cell used in the mentioned experiment is 0.03086, whereas for pipes, real physical roughness of their inner pipe surface goes practically from 0 to 0.05. Numerical experiments indicate that the novel approximation of the Wright-ω function reduced the computational time from half of a minute to fragments of a second. The relative error of the estimated friction flow factor is less than 0.5%.
1. Introduction
Flow friction is a complicated physical phenomenon and it is not constant but depends on flow rate and pressure drop. Because of its complexity, equations which describe the flow friction are mostly empirical []. The most used empirical formulation for turbulent pipe flow is given by Colebrook’s equation []. Here we will evaluate flow friction factor caused by air flow in the cathodic side of the observed PEMFCsand we will provide accurate and consistent solution.
1.1. Colebrook Equation for Pipe Flow Friction
The standard Colebrook’s friction equation for turbulent pipe flow []; Equation (1), follows logarithmic law and is based on an experiment performed by Colebrook and White in the 1930s [], while its graphical interpretation was given by Moody in 1944 [].
where:
—turbulent Darcy flow friction factor for pipes (dimensionless)
—Reynolds number (dimensionless)—the same definition as for fuel cells
—relative roughness of inner pipe surface (dimensionless)
—logarithmic function with base 10
—index related to pipes
In Moody’s diagram, for the turbulent regime the Reynolds number goes from around 2320 to 108 while the relative roughness of inner pipe surface from 0 for smooth surfaces to about 0.05 for very rough surfaces (on the other hand, flow friction for laminar regime for pipe flow does not depend of roughness while the Reynolds number goes from 0 to around 2320; the formula for laminar Darcy flow friction factor for pipe flow, is not empirical but theoretically founded).
Colebrook and White experimented with airflow through pipes of different roughness of inner surface []. They used a set of pipes from which one left with a smooth inner surface, while others were covered with sand of different size of grains. For each pipe, one uniform grain size with glue as adhesive material was used. Thus, the pipes in the experiment were gradually smooth to the fully rough. The experiment revealed that the turbulent flow friction depends on the Reynolds number and on the relative roughness of inner pipe surface . As can be seen from the Moody diagram [], for the same values of the Reynolds number the turbulent flow friction factor is higher in the pipes with higher relative roughness , where subsequently for the same flow, the corresponding pressure drop is higher, too.
The Colebrook equation is implicitly given in respect to the unknown turbulent flow friction factor and it can be rearranged in explicit form only in terms of Lambert W-function [] or its cognate Wright ω-function, and even then further evaluation can be only approximated. Very accurate approximate formulas for the Colebrook equation for pipe flow based on the Wright ω-function are available [,].
1.2. Modified Colebrook Equation for Flow Friction
The Colebrook equation is empirical [] and therefore possible modifications based on different conditions of flow can be done. We will evaluate here a modification for fuel cells [,]. Further, for example, US Bureau of Mines published a report in 1956 [] that introduced a modified form of the Colebrook equation for gas flow where coefficient 2.51 was replaced with 2.825. Also, very recent modifications of a variety of empirical equations for pipe flow are available []. Here we analyze one modification for air flow friction in the open-cathode side of the observed type of PEMFCs [], and subsequently, we give a stable and computationally efficient explicit solution which is valid in this case. Analogous analyses can be done for air flow for cooling of electronic products from hand-held devices to supercomputers [,]. Here we discuss the only influence of hydraulic effects of flow through the open-cathode conduits of fuel cells while available literature [,,,,,,,] should be consulted for thermodynamic aspects.
The Colebrook equation can be rearranged following data obtained from the experiment by Barreras et al. with fuel cells []. Based on this data and following analogy with pipe flow, it is estimated that virtual roughness is fixed by value . Therefore, the Colebrook equation can be rewritten for the observed fuel cell as Equation (2). We will further analyze this equation to provide its stable numerical solution. The value of virtual roughness is from [].
where:
—turbulent Darcy flow friction factor for fuel cells (dimensionless)
—Reynolds number (dimensionless)—the same definition as for pipes
—virtual relative roughness of fuel cell (dimensionless)
—logarithmic function with base 10
—index related to Fuel Cells
2. Proposed Model
Proton exchange membrane fuel cells (PEMFCs) transform chemical energy from electrochemical reaction of hydrogen and oxygen to electrical energy [,,,]. Here we analyze fan-induced air-forced flow, based on data from the experiment with pressure drop in the cathode side of air-forced open-cathode PEMFCs by Barreras et al. []. Their experiment with fuel cells can be compared with the experiment performed by Colebrook and White with air flow through pipes []. Barreras et al. [] use three different cathode configurations with aspect ratios from 0.83 to 2.5 to form a mesh of cathodic channels to supply the fuel cell with enough air for cooling and with oxygen for a chemical reaction (roughness is real physical characteristic of pipe surface [], but not of cathodic channels of fuel cells in terms of hydraulic performances).
Value of the Reynolds number during the experiment was from 45 to 4000, while as a difference from pipes, during flow through the observed fuel cell, the transition from laminar to turbulent flow occurred around . In our numerical experiments, we use between 50 and 4100.
As already mentioned, the original Colebrook equation is valid for turbulent flow of air, water, or natural gas through pipes. On the other hand, for laminar flow, is used whereas the transition from laminar to turbulent flow is around . This transitional border at the Moody’s plot [] is sharp where the equivalent sharp transition from laminar to turbulent flow for the observed fuel cell starts at around , as explained in []. Therefore, for airflow through the cathode side of the observed fuel cells, the flow friction factor consists of two clearly defined types of flow:
- laminar flow that depends both on the Reynolds number and on the geometry of conduits; height and width of the mesh of conduits that forms a mesh of cathodic air channels, and
- turbulent flow is solely the function of the Reynolds number for the case from the experiment of Barreras et al. [] (in general also on virtual roughness [], which is in this case ).
For solving implicitly given equations, instead of iterative procedures [,], appropriate explicit approximations which are accurate but also computationally efficient can be used (review of appropriate explicit approximations for pipe flow friction is available in []). A computationally efficient and stabile unified equation for the observed type of fuel cells which is valid both for laminar and turbulent regime will be given in this article [].
2.1. Turbulent Flow
In case of turbulent airflow during experiments with open-cathode PEMFCs, measurements show that pressure drop during turbulent flow at its cathode side follows logarithmic law, which form is comparable to the Colebrook’s flow friction equation for pipe flow, but with different numerical values []. The flow friction related to air flow is given by Equation (3):
where:
—turbulent Darcy flow friction factor for fuel cells (dimensionless)
—Reynolds number (dimensionless) – the same definition as for pipes
—logarithmic function with base 10
—index related to Fuel Cells
During turbulent flow, numerical values for the flow friction factor in pipe and fuel cells are different and that difference can go up to 60%. To make a direct connection between Equation (1) for pipe flow and Equation (3) for the observed fuel cell, Equation (4) can be used []:
where:
—turbulent Darcy flow friction factor for fuel cells (dimensionless)
—Reynolds number (dimensionless)—the same definition as for pipes
—virtual relative roughness of fuel cell (dimensionless)
—logarithmic function with base 10
—index related to Fuel Cells
For Equation (4), virtual roughness can be recalculated based on the Colebrook equation as for the observed fuel cell in the experiment []. This fuel cell was tested with three different cathode configurations []. As noted in [], this roughness is not a real measurable physical characteristic of the surface of the used material for conduits (on the contrary for pipes can be measured or at least estimated accurately [,,,,,]).
Both, Equations (3) and (4) are numerically unstable for , which can be a critical problem knowing that turbulent zone starts for . However, the novel solution proposed in this article is numerically stable.
Generally, implicitly given equations can be transformed in explicit form through the Lambert W-function [,]. The Lambert W-function [] is defined as the multivalued function W that satisfies . However, such transformation for the Colebrook equation for pipes contains a fast-growing term and because of that, overflow error in computers is possible [,]. Happily, results with fuel cells show that the solution is not in the zone where is too big to be stored in registers of computers. The model for fuel cells is given in Equation (5), while the related model for pipe flow friction model can be seen in [].
where:
—turbulent Darcy flow friction factor for fuel cells (dimensionless)
—Reynolds number (dimensionless)—the same definition as for pipes
—virtual relative roughness of fuel cell (dimensionless)
, , —constants
—variable
—logarithmic function with base 10
—natural logarithm
—exponential function
—Lambert function
—index related to Fuel Cells
The parameter for fuel cell is .
After procedures from [,,], the following form for fuel cells expressed through the Lambert W-function and its cognate Wright ω-function is given in Equation (6):
where:
—turbulent Darcy flow friction factor for fuel cells (dimensionless)
—Reynolds number (dimensionless)—the same definition as for pipes
—constant
, , —variable
—natural logarithm
—Lambert function
—Wright function
—index related to Fuel Cells
However, symbolic regression applied on the explicit formulation, Equation (6), which involves gives very simple, but still accurate results in case of pipe flow [,] ([,] confirm these results), but unfortunately these analytical formulas, which are optimized for pipes, cannot be directly applied on the fuel cell equation. Fortunately, symbolic regression gives also very promising results for fuel cells as given in Equation (7):
where:
—Reynolds number (dimensionless)—the same definition as for pipes
—variable
—natural logarithm
—Lambert function
—Wright function
—index related to Fuel Cells
To avoid repetitive computations, parameters and are introduced, in Equation (8). Both symbolic regression analyses were performed in Eureqa, a commercial software tool, which automates the process of model building and interpretation [,].
where:
—turbulent Darcy flow friction factor for fuel cells (dimensionless)
—Reynolds number (dimensionless)—the same definition as for pipes
, —variable
—natural logarithm
—index related to Fuel Cells
2.2. Unified Model
Although the expression for laminar flow through pipes is , for fuel cells it is different, as given in Equation (9) []:
where:
—laminar Darcy flow friction factor for fuel cells (dimensionless)
—channel depth/channel width used only in laminar flow (dimensionless)
—exponential function
—index related to Fuel Cells
Values of are from 0.83 to 2.5.
The experiment [] shows that air flow through the cathode side of air-forced open-cathode PEMFCs are (1) laminar for the lower values of the Reynolds number, and (2) turbulent for the higher values, 500 < < 4000, where the Reynolds number is in hydraulics a very well-known dimensionless parameter that is used as a criterion for foreseeing flow patterns in a fluid’s behavior (defined in the same way for air flow through pipes and here discussed air flow through fuel cells). The dimensionless Darcy’s unified flow friction factor , is the function of the switching function , the laminar flow friction , and the turbulent flow friction . The unified coherent flow friction model that covers both laminar and turbulent zones is set by Equation (10) []:
where:
—unified Darcy flow friction factor for fuel cells (dimensionless)
—turbulent Darcy flow friction factor for fuel cells (dimensionless)
—laminar Darcy flow friction factor for fuel cells (dimensionless)
—switching function
—index related to Fuel Cells
The novel switching function is given in Equation (11):
where:
—Reynolds number (dimensionless)—the same definition as for pipes
—switching function
—exponential function
—index related to Fuel Cells
The switching function was obtained by symbolic regression using HeuristicLab [] and it is given in Figure 1.
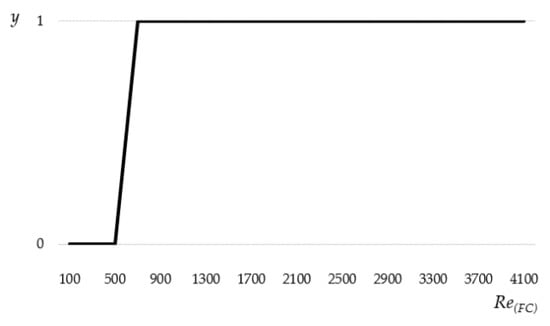
Figure 1.
Switching function given in Equation (11).
The laminar flow friction depends on the Reynolds number , but also on geometry of conduits, while the turbulent flow friction depends only on the Reynolds number . In the case of fuel cells, both coefficients are empirical. In addition, the switching function contains the exponential function, (the similar situation is for calculation of as already explained).
To avoid numerical instability, it is recommended to use the explicit approximation which gives the following unified formula in Equation (12).
where:
—unified Darcy flow friction factor for fuel cells (dimensionless)
—turbulent Darcy flow friction factor for fuel cells (dimensionless)
—laminar Darcy flow friction factor for fuel cells (dimensionless)
—Reynolds number (dimensionless)—the same definition as for pipes
—channel depth/channel width used only in laminar flow (dimensionless)
, , —variables
—switching function
—exponential function
—natural logarithm
—index related to Fuel Cells
For 216 = 65536 Sobol Quasi Monte-Carlo pairs [], which cover = 50–4100 and for from 0.83 to 2.45, the maximal relative error of the final calculated flow friction factor using Equation (12) is 0.46% compared with the original Equation (2). The accuracy and speed of execution are tested through the code given in the next section.
3. Software Code and Measurement of Execution Speed
The unified equation for laminar and turbulent fan-induced air flow through open-cathode side of the observed PEMFCs is given in Equation (12), where the algorithm from Figure 2 should be followed.
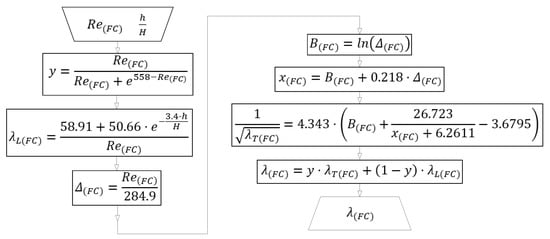
Figure 2.
Algorithm for solving Equation (12).
The turbulent flow friction (with the intermediate step through ) can be expressed using “wrightOmega“ function as , but it can be executed faster using approximation as given in Equation (8), as The MATLAB code also works in GNU Octave, but it can be easily translated in any programming language. The final unified fuel cell model given by Equation (12) is coded in MATLAB as:
in this code:
Output parameters of the function:
-flow friction factor is given as
Input parameters of the function:
-Reynolds number is given as (from the interval 50 < < 4100)
-channel depth/channel width is given as (from 0.83 to 2.5)
In MATLAB, symbol log() denotes the natural logarithm.
Implicitly given equations can be solved using iterative procedures [,], but also using appropriate accurate but also computationally efficient explicit approximations especially developed for the observed purpose. Our numerical results show that the computationally efficient approximation does not contain the time-consuming evaluation of the Wright ω-function [,], but simple polynomials found by symbolic regression [], which can be easily evaluated on computers. It is because simple functions such as +, −, ∗ and / are executed directly in the CPU and hence they are very fast [].
Using 216 = 65536 Sobol Quasi Monte-Carlo pairs [], which cover = 50–4100 and for from 0.83 to 2.45, the evaluation of the MATLAB built-in “wrightOmega“ function required 30.9 s, while our novel approximation required only 0.0022 s (our approximation is around fourteen thousand times faster). Consequently, numerical tests show that the novel approximation presented here is very suitable for modeling of fan-induced flow friction in a mesh with virtual roughness for air-forced flow in the open-cathode PEMFCs, as it is very fast and still very accurate.
4. Conclusions
This paper gives a novel numerically stable explicit solution for flow friction during airflow in cathode side of open-cathode PEMFCs. Symbolic regression is successfully used for obtaining a cheap but still accurate approximation of the Wright-ω function for fuel cells-based explicit friction model and also for approximations of the switching function, which is needed for the unified formulation of fuel cell friction model. Numerical experiments indicate that the novel approximation of the Wright-ω function reduced the computational time from half of a minute to fragments of a second. The relative error of the estimated friction flow factor is less than 0.5%.
In future research, further analyses and experiments are foreseen to show if and how this value of the virtual roughness of fan-induced friction in a mesh of conduits for air-forced flow in the open-cathode PEMFCs can be changed and how it depends on fuel cells parameters (type of fuel cells, size, geometry of channels, etc.). The study should be extended to cover other types of fuel cell, to include water and heat management, etc. [,,,,,,,,].
Author Contributions
D.B. had the initial idea for this article and he dealt with physical interpretation of the problem. P.P. conducted detailed numerical experiments (included symbolic regression) following initial inputs of D.B. D.B. wrote a draft of this article. Both authors contributed equally to this article. All authors have read and agreed to the published version of the manuscript.
Funding
The work of D.B. has been supported by the Ministry of Education, Youth and Sports of the Czech Republic through the National Programme of Sustainability (NPS II) project “IT4Innovations excellence in science-LQ1602”, while the work of P.P. has been partially supported by the Technology Agency of the Czech Republic under the project “Energy System for Grids” TK02030039. Additionally, the work of D.B. has been partially supported by the Ministry of Education, Science, and Technological Development of the Republic of Serbia.
Conflicts of Interest
The authors declare no conflict of interest.
Notations
The following symbols are used in this article:
| For pipes: | |
| turbulent Darcy flow friction factor for pipes (dimensionless) | |
| turbulent Darcy flow friction factor for pipes (dimensionless) | |
| Reynolds number (dimensionless)—the same definition as for fuel cells | |
| relative roughness of inner pipe surface (dimensionless) | |
| index related to pipes | |
| For Fuel Cells: | |
| unified Darcy flow friction factor for fuel cells (dimensionless) | |
| turbulent Darcy flow friction factor for fuel cells (dimensionless) | |
| laminar Darcy flow friction factor for fuel cells (dimensionless) | |
| Reynolds number (dimensionless)—the same definition as for pipes | |
| virtual relative roughness of fuel cell (dimensionless) | |
| channel depth/channel width used only in laminar flow (dimensionless) | |
| , , | variables |
| , , | constants |
| index related to Fuel Cells | |
| Functions: | |
| logarithmic function with base 10 | |
| natural logarithm | |
| exponential function | |
| Lambert function | |
| Wright function | |
| switching function |
References
- Díaz-Curiel, J.; Miguel, M.J.; Caparrini, N.; Biosca, B.; Arévalo-Lomas, L. Improving basic relationships of pipe hydraulics. Flow Meas. Instrum. 2020, 72, 101698. [Google Scholar] [CrossRef]
- Colebrook, C.F. Turbulent flow in pipes with particular reference to the transition region between the smooth and rough pipe laws. J. Inst. Civ. Eng. 1939, 11, 133–156. [Google Scholar] [CrossRef]
- Colebrook, C.F.; White, C. Experiments with fluid friction in roughened pipes. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1937, 161, 367–381. [Google Scholar] [CrossRef]
- Moody, L.F. Friction factors for pipe flow. Trans. ASME 1944, 66, 671–684. [Google Scholar]
- Hayes, B. Why W? On the Lambert W function, a candidate for a new elementary function in mathematics. Am. Sci. 2005, 93, 104–108. [Google Scholar] [CrossRef]
- Brkić, D.; Praks, P. Accurate and efficient explicit approximations of the Colebrook flow friction equation based on the Wright ω-function. Mathematics 2019, 7, 34. [Google Scholar] [CrossRef]
- Praks, P.; Brkić, D. Review of new flow friction equations: Constructing Colebrook’s explicit correlations accurately. Rev. Int. Métodos Numér. Cálc. Diseño Ing. 2020, 36. in press. [Google Scholar]
- Barreras, F.; López, A.M.; Lozano, A.; Barranco, J.E. Experimental study of the pressure drop in the cathode side of air-forced open-cathode proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2011, 36, 7612–7620. [Google Scholar] [CrossRef]
- Brkić, D. Comments on “Experimental study of the pressure drop in the cathode side of air-forced open-cathode proton exchange membrane fuel cells” by Barreras et al. Int. J. Hydrogen Energy 2012, 37, 10963–10964. [Google Scholar] [CrossRef]
- Smith, R.; Miller, J.; Ferguson, J. Flow of Natural Gas through Experimental Pipelines and Transmission Lines; US Bureau of Mines American Gas Association AGA: New York, NY, USA, 1956; p. 89. [Google Scholar]
- Plascencia, G.; Díaz-Damacillo, L.; Robles-Agudo, M. On the estimation of the friction factor: A review of recent approaches. SN Appl. Sci. 2020, 2, 163. [Google Scholar] [CrossRef]
- Kheirabadi, A.C.; Groulx, D. Cooling of server electronics: A design review of existing technology. Appl. Therm. Eng. 2016, 105, 622–638. [Google Scholar] [CrossRef]
- Khalaj, A.H.; Halgamuge, S.K. A Review on efficient thermal management of air-and liquid-cooled data centers: From chip to the cooling system. Appl. Energy 2017, 205, 1165–1188. [Google Scholar] [CrossRef]
- Soupremanien, U.; Le Person, S.; Favre-Marinet, M.; Bultel, Y. Tools for designing the cooling system of a proton exchange membrane fuel cell. Appl. Therm. Eng. 2012, 40, 161–173. [Google Scholar] [CrossRef]
- Guo, H.; Wang, M.H.; Ye, F.; Ma, C.F. Experimental study of temperature distribution on anodic surface of MEA inside a PEMFC with parallel channels flow bed. Int. J. Hydrogen Energy 2012, 37, 13155–13160. [Google Scholar] [CrossRef]
- Henriques, T.; César, B.; Branco, P.C. Increasing the efficiency of a portable PEM fuel cell by altering the cathode channel geometry: A numerical and experimental study. Appl. Energy 2010, 87, 1400–1409. [Google Scholar] [CrossRef]
- Zhao, C.; Xing, S.; Chen, M.; Liu, W.; Wang, H. Optimal design of cathode flow channel for air-cooled PEMFC with open cathode. Int. J. Hydrogen Energy 2020. [CrossRef]
- Li, C.; Liu, Y.; Xu, B.; Ma, Z. Finite Time thermodynamic optimization of an irreversible Proton Exchange Membrane Fuel Cell for vehicle use. Processes 2019, 7, 419. [Google Scholar] [CrossRef]
- De Lorenzo, G.; Andaloro, L.; Sergi, F.; Napoli, G.; Ferraro, M.; Antonucci, V. Numerical simulation model for the preliminary design of hybrid electric city bus power train with polymer electrolyte fuel cell. Int. J. Hydrogen Energy 2014, 39, 12934–12947. [Google Scholar] [CrossRef]
- Darjat; Sulistyo; Triwiyatno, A.; Sudjadi; Kurniahadi, A. Designing hydrogen and oxygen flow rate control on a solid oxide fuel cell simulator using the fuzzy logic control method. Processes 2020, 8, 154. [Google Scholar] [CrossRef]
- Taner, T. A Flow Channel with Nafion Membrane Material Design of Pem Fuel Cell. J. Therm. Eng. 2019, 5, 456–468. [Google Scholar] [CrossRef]
- Majlan, E.H.; Rohendi, D.; Daud, W.R.W.; Husaini, T.; Haque, M.A. Electrode for proton exchange membrane fuel cells: A review. Renew. Sustain. Energy Rev. 2018, 89, 117–134. [Google Scholar] [CrossRef]
- Fly, A.; Thring, R.H. A comparison of evaporative and liquid cooling methods for fuel cell vehicles. Int. J. Hydrogen Energy 2016, 41, 14217–14229. [Google Scholar] [CrossRef]
- Rahgoshay, S.M.; Ranjbar, A.A.; Ramiar, A.; Alizadeh, E. Thermal investigation of a PEM fuel cell with cooling flow field. Energy 2017, 134, 61–73. [Google Scholar] [CrossRef]
- Topal, H.; Taner, T.; Naqvi, S.A.; Altınsoy, Y.; Amirabedin, E.; Ozkaymak, M. Exergy Analysis of a circulating fluidized bed power plant co-firing with olive pits: A case study of power plant in Turkey. Energy 2017, 140, 40–46. [Google Scholar] [CrossRef]
- Brkić, D. Can pipes be actually really that smooth? Int. J. Refrig. 2012, 35, 209–215. [Google Scholar] [CrossRef]
- Praks, P.; Brkić, D. Choosing the optimal multi-point iterative method for the Colebrook flow friction equation. Processes 2018, 6, 130. [Google Scholar] [CrossRef]
- Praks, P.; Brkić, D. Advanced iterative procedures for solving the implicit Colebrook equation for fluid flow friction. Adv. Civ. Eng. 2018, 2018, 5451034. [Google Scholar] [CrossRef]
- Brkić, D. Review of explicit approximations to the Colebrook relation for flow friction. J. Pet. Sci. Eng. 2011, 77, 34–48. [Google Scholar] [CrossRef]
- Brkić, D.; Praks, P. Unified friction formulation from laminar to fully rough turbulent flow. Appl. Sci. 2018, 8, 2036. [Google Scholar] [CrossRef]
- Barreras, F.; Lozano, A.; Barranco, J.E. Response to the comments on “Experimental study of the pressure drop in the cathode side of air-forced open-cathode proton exchange membrane fuel cells” by Dejan Brkić. Int. J. Hydrogen Energy 2012, 37, 10965. [Google Scholar] [CrossRef][Green Version]
- Sharp, W.W.; Walski, T.M. Predicting internal roughness in water mains. J. AWWA 1988, 80, 34–40. [Google Scholar] [CrossRef]
- Guo, X.; Wang, T.; Yang, K.; Fu, H.; Guo, Y.; Li, J. Estimation of equivalent sand–grain roughness for coated water supply pipes. J. Pipeline Syst. Eng. Pract. 2020, 11, 04019054. [Google Scholar] [CrossRef]
- Bhui, A.S.; Singh, G.; Sidhu, S.S.; Bains, P.S. Experimental investigation of optimal ED machining parameters for Ti-6Al-4V biomaterial. Facta Univ. Ser. Mech. Eng. 2018, 16, 337–345. [Google Scholar] [CrossRef]
- Niazkar, M.; Talebbeydokhti, N.; Afzali, S.H. Novel grain and form roughness estimator scheme incorporating artificial intelligence models. Water Resour. Manag. 2019, 33, 757–773. [Google Scholar] [CrossRef]
- Niazkar, M.; Talebbeydokhti, N.; Afzali, S.H. Development of a new flow-dependent scheme for calculating grain and form roughness coefficients. KSCE J. Civ. Eng. 2019, 23, 2108–2116. [Google Scholar] [CrossRef]
- Andersson, J.; Oliveira, D.R.; Yeginbayeva, I.; Leer-Andersen, M.; Bensow, R.E. Review and comparison of methods to model ship hull roughness. Appl. Ocean Res. 2020, 99, 102119. [Google Scholar] [CrossRef]
- Keady, G. Colebrook-White formula for pipe flows. J. Hydraul. Eng. 1998, 124, 96–97. [Google Scholar] [CrossRef]
- Brkić, D. Lambert W function in hydraulic problems. Math. Balk. 2012, 26, 285–292. Available online: http://www.math.bas.bg/infres/MathBalk/MB-26/MB-26-285-292.pdf (accessed on 21 May 2020).
- Sonnad, J.R.; Goudar, C.T. Constraints for using Lambert W function-based explicit Colebrook–White equation. J. Hydraul. Eng. 2004, 130, 929–931. [Google Scholar] [CrossRef]
- Brkić, D. Comparison of the Lambert W-function based solutions to the Colebrook equation. Eng. Comput. 2012, 29, 617–630. [Google Scholar] [CrossRef]
- Sonnad, J.R.; Goudar, C.T. Turbulent flow friction factor calculation using a mathematically exact alternative to the Colebrook–White equation. J. Hydraul. Eng. 2006, 132, 863–867. [Google Scholar] [CrossRef]
- Biberg, D. Fast and accurate approximations for the Colebrook equation. J. Fluids Eng. Trans. ASME 2017, 139, 031401. [Google Scholar] [CrossRef]
- Muzzo, L.E.; Pinho, D.; Lima, L.E.; Ribeiro, L.F. Accuracy/speed analysis of pipe friction factor correlations. In Proceedings of the International Congress on Engineering and Sustainability in the XXI Century 2019, Faro, Portugal, 9–11 October 2019; pp. 664–679. [Google Scholar] [CrossRef]
- Zeyu, Z.; Junrui, C.; Zhanbin, L.; Zengguang, X.; Peng, L. Approximations of the Darcy–Weisbach friction factor in a vertical pipe with full flow regime. Water Supply 2020. [Google Scholar] [CrossRef]
- Dubčáková, R. Eureqa: Software review. Genet. Program. Evol. M. 2011, 12, 173–178. [Google Scholar] [CrossRef]
- Schmidt, M.; Lipson, H. Distilling free-form natural laws from experimental data. Science 2009, 324, 81–85. [Google Scholar] [CrossRef]
- Wagner, S.; Kronberger, G.; Beham, A.; Kommenda, M.; Scheibenpflug, A.; Pitzer, E.; Vonolfen, S.; Kofler, M.; Winkler, S.; Dorfer, V.; et al. Architecture and design of the HeuristicLab optimization environment. Top. Intell. Eng. Inform. 2014, 6, 197–261. [Google Scholar] [CrossRef]
- Sobol, I.M.; Turchaninov, V.I.; Levitan, Y.L.; Shukhman, B.V. Quasi-Random Sequence Generators; Distributed by OECD/NEA Data Bank; Keldysh Institute of Applied Mathematics; Russian Academy of Sciences: Moscow, Russia, 1992; Available online: https://ec.europa.eu/jrc/sites/jrcsh/files/LPTAU51.rar (accessed on 20 May 2020).
- Winning, H.K.; Coole, T. Explicit friction factor accuracy and computational efficiency for turbulent flow in pipes. Flow Turbul. Combust. 2013, 90, 1–27. [Google Scholar] [CrossRef]
- Winning, H.K.; Coole, T. Improved method of determining friction factor in pipes. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 941–949. [Google Scholar] [CrossRef]
- Praks, P.; Brkić, D. Rational Approximation for Solving an Implicitly Given Colebrook Flow Friction Equation. Mathematics 2020, 8, 26. [Google Scholar] [CrossRef]
- Taner, T. Energy and Exergy Analyze of PEM fuel cell: A case study of modeling and simulations. Energy 2018, 143, 284–294. [Google Scholar] [CrossRef]
- Andaloro, L.; Napoli, G.; Sergi, F.; Dispenza, G.; Antonucci, V. Design of a hybrid electric fuel cell power train for an urban bus. Int. J. Hydrogen Energy 2013, 38, 7725–7732. [Google Scholar] [CrossRef]
- Taner, T. Alternative energy of the future: A technical note of PEM fuel cell water management. J. Fundam. Renew. Energy Appl. 2015, 5, 1000163. [Google Scholar]
- Andaloro, L.; Arista, A.; Agnello, G.; Napoli, G.; Sergi, F.; Antonucci, V. Study and design of a hybrid electric vehicle (Lithium Batteries-PEM FC). Int. J. Hydrogen Energy 2017, 42, 3166–3184. [Google Scholar] [CrossRef]
- Taner, T. The micro-scale modeling by experimental study in PEM fuel cell. J. Therm. Eng. 2017, 3, 1515–1526. [Google Scholar] [CrossRef]
- Napoli, G.; Micari, S.; Dispenza, G.; Di Novo, S.; Antonucci, V.; Andaloro, L. Development of a fuel cell hybrid electric powertrain: A real case study on a Minibus application. Int. J. Hydrogen Energy 2017, 42, 28034–28047. [Google Scholar] [CrossRef]
- Taner, T.; Naqvi, S.A.; Ozkaymak, M. Techno-Economic Analysis of a more efficient hydrogen generation system prototype: A case study of PEM electrolyzer with Cr-C coated Ss304 bipolar plates. Fuel Cells 2019, 19, 19–26. [Google Scholar] [CrossRef]
- Mendicino, G.; Colosimo, F. Reply to Comment by J. Qin and T. Wu on “Analysis of flow resistance equations in gravel bed rivers with intermittent regimes: Calabrian fiumare data set”. Water Resour. Res. 2020, 56, e2019WR027003. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).