Abstract
The dynamics of the 3-dimensional flow of magnetized Carreau fluid past a paraboloid surface of revolution is studied through thermal radiation and mass transfer analysis. The impacts of Brownian motion and chemical reaction rate are considered on the flow dynamics. The system of nonlinear PDEs are converted to coupled ODEs by employing suitable transformation relations. The developed ODEs are solved by applying the standard procedure of homotopy analysis method (HAM). The impacts of various interesting parameters on the state variables of the Carreau fluid (velocity components, temperature, concentration, and shear stress) are explained through various graphs and tables. It is found that the horizontal velocity components augment with the rising magnetic parameter and Grashof number values. The fluid temperature augments with the higher values of the pertinent parameters except Prandtl number. The Nusselet number and fluid concentration enhance with the augmenting Brownian motion parameter. The shear stress augments with the rising Grashof number. The agreement of the obtained and published results validate the accuracy of the employed technique.
1. Introduction
Fluids (liquids and gases) are characterized by their ability to flow, as contrasted to solids which possess definite shapes. For decades, the investigators of fluid mechanics have focused on the flow characteristics of Newtonian and power-law fluids. The main impetus behind this is the fact that in many fluids, the stresses developed during the flow are directly proportional to the local strain. On the other hand, a lot of research groups are working on the generalized Newtonian fluids flow. In such type of fluids, the shear stress depends on the shear rate at a given time. In 1972, Pierre J. Carreau [1,2] presented a model capable of describing the Newtonian fluids (power-law fluids) flow at low (and high) shear rate. A few years later, Bush and Phan-Thien [3] used the Carreau viscosity relation to find the drag force effect of a sphere in a fluid exhibiting shear-thinning as well as elastic properties. Khellaf and Lauriat [4] explained the heat energy transfer flow between two cylinders, in which the inside cylinder was rotatory while the other cylinder was static. The authors employed the Carreau constitutive relation to examine the non-Newtonian shear-thinning model of viscosity. It was concluded that the fluid motion becomes oscillatory with the decreasing flow index or with augmenting Weissenberg number. The motion of the Carreau fluid at an extending wall and at free-stream was analyzed by Khan et al. [5]. In this study, the fluid flow was characterized as shear-thickening , Newtonian , and shear-thinning . The analysis implied that the Carreau fluid shows the Newtonian fluid characteristics at low and power-law fluid characteristics at high shear rates. Olajuwon [6] pointed out that Carreau fluid constitutive equation can describe fluids whose viscosity varies with the increasing deformation rate. The Carreau fluid model gives a finite fluid viscosity in the limit when the shear rate tends to zero in contrast to Ostwald-De Waele or power-law models. Hsu et al. [7] calculated the drag coefficient of a rigid and isolated particle of cylindrical shape flowing in a Carreau fluid. The analysis confirmed that the drag coefficient in this case is smaller due to the Carreau fluid shear-thinning nature as compared to the Newtonian fluid. The study further reveals the direct dependence of the index parameter in the drag coefficient on the relaxation time constant.
It is to be mentioned that the 3-dimensional Carreau fluid flow on complex surfaces like over an upper portion of the aircraft, rocket upper surface, and on car bonnet, etc., has not been undertaken. This may be due to the unavailability of suitable 3D flow solving techniques. The non-Newtonian fluids, for example, structured as well as genetic liquid organisms, human blood, polymeric solutions, and exotic liquids are ubiquitous in this industrialized world. A lot of research has been executed in this direction. The peristaltic flow through a nonsymmetrical channel of a Carreau fluid was explained by Ali and Hayat [8]. The induced magnetic field impact on the transport of Carreau fluid was explained by Hayat et al. [9]. The Carreau fluid motion through an inclined and free surface was analyzed by Tshehla [10]. Elahi et al. [11] discussed the 3D flow of Carreau fluid in a rectangular duct. The investigation of fluid flow in the magnetic field presence to measure its various macroscopic properties is called Magneto Hydro Dynamics (MHD). MHD flow finds its applications in different disciplines like plasma and astrophysics, cooling of nuclear reactors, engineering and technology, and so on. The transfer of heat energy during the MHD fluid flow over a vertical stretching surface was examined by Nazar et al. [12]. He concluded that the rising magnetic field strength results in the reduction of the heat energy loss and coefficient of local skin friction. Ishak et al. [13] discussed the stagnation-point motion in the magnetic field presence towards a stretchable surface. Xu et al. [14] examined analytically the 3D flow of magnetized fluid along with heat energy transfer on a stretchable plate by using a series solution technique. Vajravelu et al. [15] analyzed the convective heat energy transformation over a stretchable surface by applying field. Pop and Na [16] investigated the MHD flow on a stretching and porous surface. Gnaneswara Reddy et al. [17] analyzed the magnetic field and Ohmic heating effects on the viscous nanofluid flow over a nonlinear permeable and extending surface.
The existence of gradients in physical quantities is necessary for the development of various fluxes, which then results in different kinds of flow. The heat energy transfer is mainly associated with the gradients in temperature, this effect is called the Soret effect. The gradients in concentration cause mass transfer flow which gives rise to Dufour effect. These effects play an important role when density differences exist in a system. The phenomena in which heat energy transport takes place, for example, heat energy exchangers, manufacturing of steel, and other cooling processes, the convective heat energy transformation plays a dominant role. The impact due to convective thermal energy transfer flow over a three-dimensional exponential stretching surface was discussed by Liu et al. [18]. Hayat et al. [19] discussed the Carreau fluid flow of a boundary layer and showed that the rising suction parameter augments (drops) the thickness range (velocity) of the fluid boundary layer. The analysis of thermal energy radiations is of basic importance in solar energy systems, nuclear power reactors, combustion engines and chambers, propulsion engines for high-velocity aircraft, and chemical activities at high operating temperatures. The thermal radiation boundary layer MHD nanofluid flow over an extending surface was examined by Gnaneswara Reddy [20]. Emad [21] examined the effects produced due to the presence of radiation on the electrically conducting fluid motion on an extendable surface. Gnaneswara Reddy [22] investigated the mixed convective magnetized layer slip flow through a permeable surface in the existence of heat energy source and Ohmic effect by taking into account the impacts of radiation energy and chemical reaction. The radiation impact on the convective heat energy transformation in a current carrying fluid over an extendable surface having varying viscosity was investigated by Abo-Eldahab and Elgendy [23]. Gnaneswara Reddy [24] examined the collective impact of Joule heating, thermophoresis and dissipation on a steady magnetized fluid flow on an inclined isothermal surface. The impact of thermal radiations on magnetized fluid motion is numerically investigated in the references [25,26,27] by taking into account the presence of suction/injection. The mixed convective MHD flow by considering the impacts of joule heating, temperature jump, slip, and viscous dissipation was studied in the references [28,29]. The impact of varying viscosity on a porous plate heated convectively in the presence of thermophoresis effect was considered by Makinde et al. [30]. The study of nanofluid stagnation flow on a stretchable sheet by considering the varying viscosity effect was performed by Khan et al.. Ibrahim and Makinde [31] further expanded their previous work to examine the convective boundary value flow of Casson fluid. The mass and heat energy transformation properties of Newtonian as well as non-Newtonian fluids by considering the thermal radiation impact are discussed in the references [32,33,34]. The impact of chemical reaction and thermal radiations on the MHD flow was considered by Hayat et al. [35]. Shehzad et al. [36] numerically examined the 3D Casson fluid motion within a permeable medium by considering the effect of internal heat energy. The impacts of radiation and chemically reactive components on a magnetized convection flow near a vertical moving wall was examined by Gnaneswara Reddy [37]. The mass and heat energy transformation properties of Newtonian as well as non-Newtonian fluids were investigated by Raju et al. [38,39] in the existence of thermal radiation.
Motivated by the above studies, we want to analytically examine the 3D Carreau fluid MHD flow over a horizontal paraboloid surface of revolution through thermal radiation and mass transfer analysis by considering the chemical reaction and Brownian motion effects. The geometry and mathematical modeling of the problem is given in Section 2. The solution methodology used is explained in Section 3. The impacts of pertinent parameters on the various aspects of the Carreau fluid flow are explained through graphs in Section 4. The comparison and calculations of Sherwood and Nuselt numbers as well as the shear stresses are explained through different tables in Section 5. The work is concluded in Section 6.
2. Formulation of the Problem
We analyze the nonlinear and magnetized mixed convective Carreau fluid flow. The geometry of the problem is selected such that the axis lies parallel to the surface. The -field is applied normal to the sheet, i.e., along the axis as shown Figure 1. The basic relation that governs the Carreau fluid flow is [40,41]
where denotes the extra stress tensor, () is the infinity shear rate (zero shear rate) viscosity, is the time constant, n is the index of power-law, and is given by [4]
where ∏ is the second invariant of the strain-rate tensor. Assuming , we have from Equation (1),
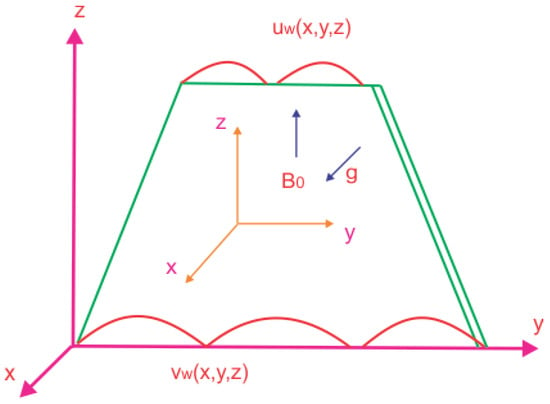
Figure 1.
Geoemtrical demonstrarion of the physical problem.
We assume that , , , , where and b are constants. The model equations that govern the dynamics of the magnetized Carreua fluid are
The boundary restrictions on the system are given by
Here, and w are the velocity Cartesian components, is the time constant, (k) is the kinematic fluid viscosity (thermal conductivity), is the dimensional parameter of the chemical reaction, is the mass diffusivity, C () is the fluid concentration (ambient fluid concentration), and is the heat capacity. The nonuniform heat source () is given by [42]
where and show the reflection, whereas and show the heat absorption inside the system. The radiation flux is defined as [6,42]
where is the Stefan–Boltzmann constant and is the average absorption coefficient. Taylor expanding about the fixed temperature and ignoring and higher order terms in Equation (11), we get
Assume the following transformations [42,43]:
Using Equations (10) and (12) together with Equations (17) and (18) in Equations (4)–(8), we get
where Equation (4) is satisfied identically.
Here, denotes the Prandtl number, is the Weissenberg number, is the Grashof number, demonstrates the internal heat source, is the Schmidt number, is the parameter of chemical reaction, is the thermoporesis parameter, is the Brownian motion parameter, and is the radiation parameter. The boundary restrictions of the system are nondimensional, as discussed in the references [44,45]. The boundary restrictions on the system must be set at because the exceeding of the , but it is impossible in practice that all the restrictions be set at at the parabolic upper horizontal surface. As a result, it is impossible to use in the similarity variables. Choosing at the slot starting point gives the minimum value of the similarity variable and is given by
It is to be noted here that the boundary restrictions in Equation (22) depend on , while Equations (17)–(20) depend on the independent variable . For this, the domain is transformed to as discussed by Abegunrin [45]. Therefore, assume that , then , , , and . From these assumptions, Equations (17)–(20) and Equation (22) are given by
The engineering quantities of interest are given by
where,
From above, we can write
3. Analytical Solution
The basic mechanism of HAM is explained by Liao in his PhD thesis [46]. The advantages and comparison of HAM are discussed in reference [47]. Liao used a topological concept known as “Homotopy”. He used two different continuous functions and defined over the two spaces and . The basic theory of the transformation is based on linking the closed unit interval with the topological spaces defined, as given below:
where and holds . The transformation given in Equation (31) is called homotopic transformation. The set of Equations (23)–(26), together with the boundary restrictions (27) are solved with HAM [48], by choosing suitable initial guesses , , , and with the corresponding liner operators defined as
that satisfies
4. Results and Discussion
Here, we explain graphically the impacts due to the varying values of the associated parameters in the state variables (velocity, shear stress, temperature, and concentration). We also explain the variation of Sherwood and Nusselet numbers as well as the skin friction, respectively. Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16 and Figure 17 show the variation in the state variables, whereas Figure 18, Figure 19 and Figure 20 represent the variation in the Sherwood number, Nusselt number, and the skin friction with the changing associated parameters values.
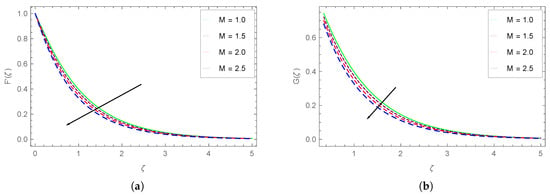
Figure 2.
Impact of M on (a) and (b) .
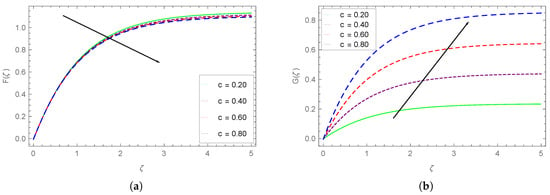
Figure 3.
(a) Impact of c on and (b) .
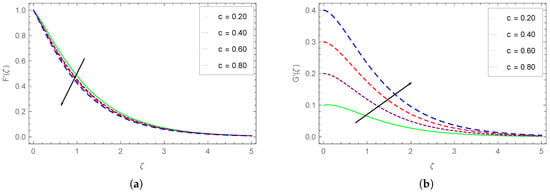
Figure 4.
(a) Impact of c on and (b) .
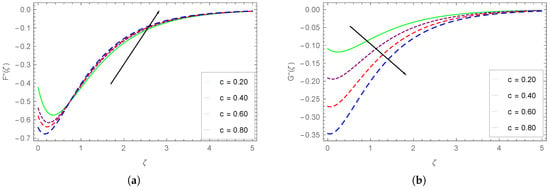
Figure 5.
Impact of c on the shear stresses (a) and (b) .
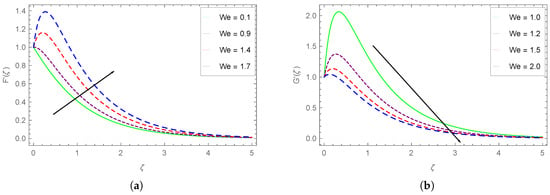
Figure 6.
Impact of on the horizontal velocity components (a) and (b) .
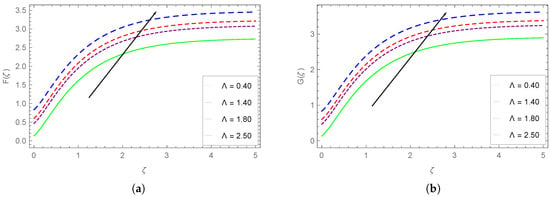
Figure 7.
Impact of on (a) and (b) .
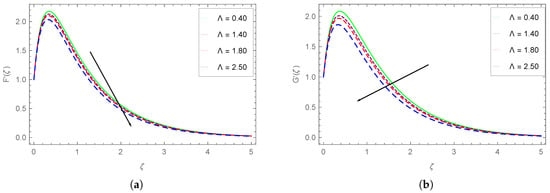
Figure 8.
Impact of on (a) and (b) .
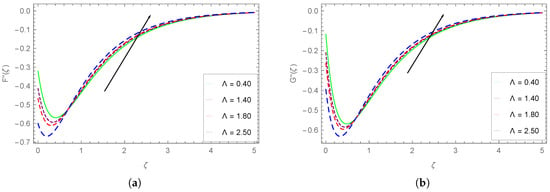
Figure 9.
Impact of on the shear stress profiles (a) and (b) .
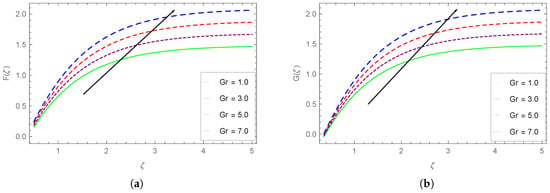
Figure 10.
Impact of on (a) and (b) .
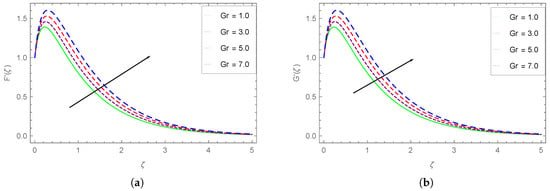
Figure 11.
Impact of on (a) and (b) .
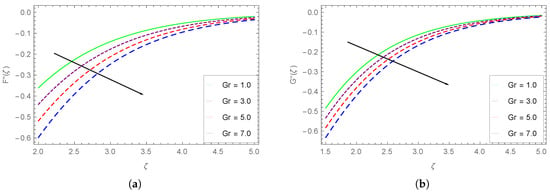
Figure 12.
Impact of on (a) and (b) .
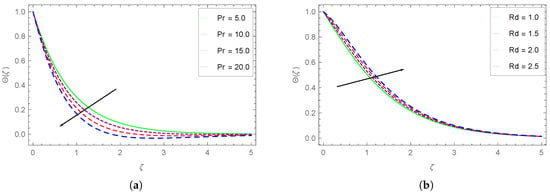
Figure 13.
(a) Impact of on and (b) influence of on .
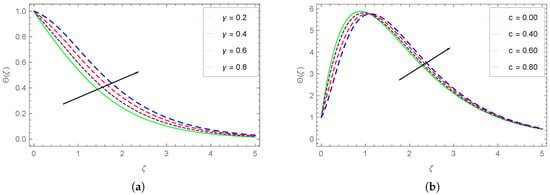
Figure 14.
Dependence of on (a) and (b) c.
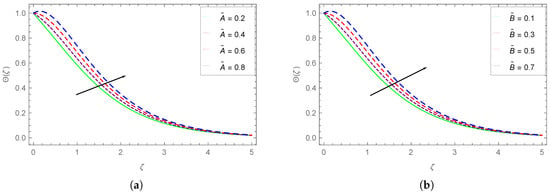
Figure 15.
(a) Effect of on () and (b) influence of on .
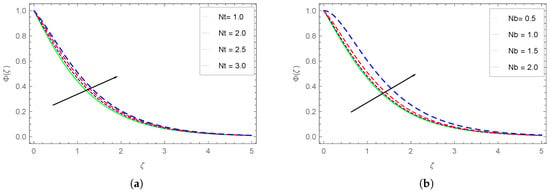
Figure 16.
(a) dependence on . (b) dependence on .
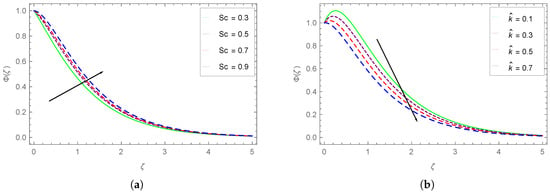
Figure 17.
Impact of (a) on and (b) on .
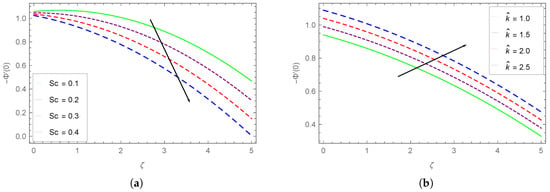
Figure 18.
Dependence of Sherwood number on (a) and (b) .
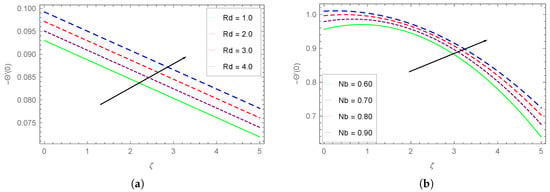
Figure 19.
Dependence of Nusselt number on (a) and (b) .
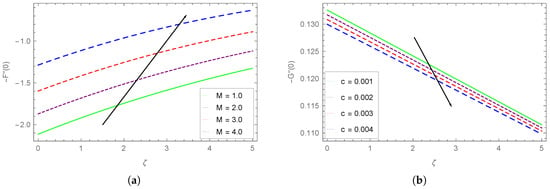
Figure 20.
(a) The dependence of skin friction () on M. (b) The dependence of skin friction () on c.
We plotted the impact of the changing magnetic parameter (M) values over and (horizontal velocity profiles), respectively, in Figure 2a,b. It is found that at a given M, both velocity components vary inversely with higher values of almost at the same manner. It is clear that the increasing M drops the profiles of both these components. The drop in the profiles is prominent at the smaller values of . The increasing magnetic field produces higher Lorentz force which results in the reduction of velocities.
The dependence of the vertical components of velocity ( and ) on the stretching rate ratio (c) is plotted in Figure 3a,b. It is clear that the component drops while the other component rises with the increasing c values. The drop in is very minute and is visible beyond . The rising behavior of with the higher stretching rate ratio is more prominent, as can be seen in Figure 3b.
The dependence of and on the stretching rate ratio c is depicted in Figure 4a,b. We observe that the component drops while the other horizontal component rises with the augmenting c values. These dropping and enhancing behaviors are more obvious for the smaller values of , i.e., close to the wall.
The variation of the shear stress profiles and with the varying values of stretching rate ratio is explained in Figure 5a,b. We see from Figure 5a that up to about , the shear stress drops; while beyond it rises with larger c values. The shear stress drops with higher values of c, as is clear from Figure 5b. The rate at which drops is larger for smaller values of . As c is the ratio between two stretching velocities, if one component enhances, then the other must drop with higher c values, as observed in all cases in which c is changing.
The influence of (Weissenberg number) on the horizontal components of velocity is sketched respectively in Figure 6a,b. It is seen from Figure 6a that the component augments with the increasing Weissenberg number values. This increase in with is dominant up to . The rate at which enhances is larger for higher . A decreasing trend is observed for the horizontal component with increasing We, as can be seen from Figure 6b. Here, the rate at which drops is larger for smaller values.
The influence of upon and (the vertical velocity profiles) is portrayed in Figure 7. We observe that both the vertical components show almost similar increasing dependence with the augmenting values of .
The influence of upon and profiles is portrayed in Figure 8. We observe that both these velocity components show decreasing behavior with the augmenting values. The spacing among the curves is larger for higher values as compared to the spacing between curves.
The dependence of the shear stress profiles and on is portrayed in Figure 9. It is obvious from the figures that both the shear stress components show almost the same rising behavior. Initially, up to about , the shear stress profiles drop with higher , while up to , both these shear stress components augment with higher rate. Beyond , the profiles remain almost constant.
The impact of the Grashof number () on and profiles is plotted in Figure 10. These graphs show that the velocity components display a similar rising trend with the larger values of the Grashof number. The spacing between the curves for augmenting values is almost constant. This physically means that lager buoyancy forces (associated with higher Gr values) augment the velocity components of the magnetic Carreau fluid.
The impact of the varying values of Grashof number on the horizontal velocity profiles are depicted in Figure 11. These graphs show that the velocity components follow similar increasing tendency with the augmenting Grashof number. The augmenting trend in these components is more obvious for the intermediate values of . This again means that the larger buoyancy forces (high Gr values) augment the Carreau fluid velocity components.
The variation of the shear stress components and with varying values of is shown in Figure 12. Both these components show a decreasing trend with higher . The decreasing tendency is more obvious for smaller values of . The spacing between different curves is larger compared to spacing between curves for varying values. Thus, the increasing buoyancy forces with the higher values of Gr result in depreciating the shear stresses.
The temperature distributions of the magnetized Carreau fluid with the changing Prandtl number () and radiation parameter () are plotted in Figure 13a,b, respectively. From Figure 13a, we see that at a given value of , the Carreau fluid temperature reduces with the larger . The rate at which temperature drops decreases for larger . The fluid temperature drops with the augmenting values. The drop in is dominant for the intermediate values. The reason for the temperature drop of the Carreau fluid with the ascending is due to the decreasing values of the Carreau fluid thermal diffusivity. Figure 13b displays that the temperature enhances with higher radiation parameter values. The increase in the profiles of the Carreau fluid with larger is more obvious for the smaller values of .
The impacts of the internal heat source parameter and stretching rate ratio c on the temperature distribution of the Carreau fluid are depicted in Figure 14a,b, respectively. It is obvious from Figure 14a that the fluid temperature drops as we go away from the wall (at larger ). Furthermore, the temperature rises with the rising values. The temperature of the fluid first rises, reaches maximum value, then drops with increasing at constant stretching rate ratio (c). The augmenting values of the stretching rate ratio first drop the fluid temperature up to about and then enhance it beyond .
The influence of the internal source reflection terms and on the Carreau fluid temperature are respectively displayed in Figure 15a,b. Both figures show that the increasing values of the reflection terms and cause an enhancement in the temperature. Both these terms have approximately the same influence over the enhancement in . Thus, the positive values of the reflection terms augment the Carreau fluid temperature.
Figure 16a,b respectively show the impact of the variation of the thermoporesis and Brownian motion parameters over the Carreau fluid concentration . We observe that at a given value of , the fluid concentration drops as increases. The rising values cause an enhancement of the fluid concentration. This increase in concentration is more dominant at the smaller values of . The increase in fluid concentration due to higher may be associated with the existence of larger concentration gradients. We also observe an increase in the fluid concentration with the ascending values. The increase in the fluid concentration is more drastic for the highest . This enhancement of fluid concentration may be due to the higher rate of random collisions between fluid particles.
The dependence of the Carreau fluid concentration on the changing Schmidt number is shown in Figure 17a, and (chemical reaction rate parameter) is pictured in Figure 17b. We can see from Figure 17a that the ascending values of raise the fluid concentration. The enhancement in is more prominent for smaller values. This physically means that the higher momentum diffusivity causes enhancement in the fluid concentration. Figure 17b displays that the rising values drop the fluid concentration. The reduction in the fluid concentration is more dominant at small values.
The dependence of Sherwood number on Schmidt number () and reaction rate parameter () is respectively displayed in Figure 18a,b. We see from Figure 18a that at a given , the Sherwood number drops with higher . As the values of are enhanced, the Sherwood number profiles drop. This drop in Sherwood number is more drastic at higher values of . Figure 18b depicts that Sherwood number enhances with increasing values of thermal reaction rate parameter .
The impact of increasing values of radiation and Brownian motion parameters ( and ) on Nusselt number is plotted respectively in Figure 19a,b. It is clear from Figure 19a that the Nusselet number varies inversely with higher values of at a given value of . The Nusselet number enhances with higher values of almost at the same rate. Figure 19b shows that the Nusselt number enhances with rising values. The spacing between different curves for varying values decreases at the intermediate values of .
The impact of M (magnetic parameter) on the skin friction () along x-axis is shown in Figure 20a. We observe that the augments with rising values of at fixed M. By increasing the magnetic field strength, enhances with an almost uniform amount. Figure 20b is the graphical representation of the skin friction along y-axis with varying values of stretching rate ratio c. We see that drops with the augmenting values of c almost at the same rate.
5. Tables Discussion
The engineering quantities of interest are explained in this section. Table 1, Table 2 and Table 3 show the impact of varying values of various parameters over the Nusselt number, skin frictions, and Sherwood number, respectively.

Table 1.
Impact of the variation of on Nusselt number for the nonzero values of the Schmidth number and the Brownian motion parameter.

Table 2.
Different values of and for varying , , and .

Table 3.
Calculation of and for varying , , , and Pr by keeping the remaining parameters fixed.
The comparison between the results achieved in this study and the already published results for the computation of Nusselt number for the nonzero Schmidt number and Brownian motion parameter is displayed in Table 1. We see an excellent agreement in both results.
The skin frictions along the x-axis () and y-axis () are computed for varying values of , , and in Table 2.
The Nusselt and Sherwood numbers are computed for various values of , , , and in Table 3.
6. Conclusions
We examined the impact of chemical reaction rate and Brownian motion parameters on the MHD Carreau fluid 3-dimensional flow by using thermal radiation and mass transfer analysis. A simplified set of coupled second order ODEs is obtained through suitable transformation relations. These coupled ODEs are solved by using the homotopy analysis method (HAM). The influence of magnetic filed, stretching rate ratio, Weissenberg number, Grashof number, chemical reaction rate and Brownian motion parameters, Schmidt number, and other parameters are explained through various graphs. The agreement of achieved and published results confirms the accuracy of the employed procedure. We concluded the following main points:
- The horizontal velocity components ( and ) drop with the ascending M.
- The enhancement in the stretching rate ratio drops the shear stress horizontal and vertical velocity profiles (, , ) and enhances the (, , ) profiles.
- The horizontal and vertical velocity profiles (, , , ) augment, while the shear stress profiles () drop with the ascending Grashof number values.
- The fluid temperature augments with the higher values of all pertinent parameters except Prandtl number.
- The fluid concentration augments with the higher values of thermoporesis and Brownian motion parameters, and Schmidt number, while drops with the higher values of the parameter of chemical reaction rate.
- The Nusselt number augments with the increasing radiation and Brownian motion parameters.
- The skin friction along x-axis augments with the augmenting magnetic parameter values, and along the y-axis drops with the rising stretching rate ratio.
- The agreement between obtained and published results confirms the accuracy of our employed analytical technique.
Author Contributions
Conceptualization, A.U. and Ikramullah; Software, W.K. and T.A.; Writing—Original Draft Preparation, W.K. and M.A.; Writing—Review and Editing, H.U.K., M.A., T.A. and Ikramullah; Formal Analysis, H.A., H.U.K. and M.A.; Validation, A.U. and W.K.; Methodology, A.U., W.K. and H.A.; Investigation, Ikramullah, I.K. and A.U.; Resources, I.K. and H.A.; Project Administration, T.A. and H.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors are thankful to anonymous reviewers for their fruitful suggestion which improved the quality of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Abbrevations
The below mentioned parameters and abbreviations with their possible dimensions are used in this article:
| Electrical conductivity | |
| B | Uniform magnetic parameter strength T |
| Nusslet number along x-axis and y-axis | |
| Local Reynolds number | |
| Skin friction along the x-axis | |
| Skin friction along the y-axis | |
| Sherwood number | |
| Mass diffusivity parameter | |
| Prandtl number | |
| Constant Fluid velocity () | |
| T | Fluid temperature |
| Kinematic viscosity | |
| Density | |
| Dynamic viscosity | |
| Specific heat | |
| Schmidt number | |
| Dimensionless velocities | |
| Dimensionless temperature | |
| Dimensionless concentration | |
| ∞ | Condition at infinity |
| 0 | Reference condition |
| x, y, and z | Coordinates |
| Similarity variable | |
| Stream function | |
| Brownian motion parameter | |
| Thermophoresis parameter | |
| t | Time |
| n | Power law index |
| M | Magnetic field interaction parameter |
| Extra stress tensor | |
| Stefan Boltzmann constant | |
| Restricted dimensionless velocity components along x and y-axis respectively. | |
| Restricted dimensionless temperature | |
| Restricted dimensionless concentration | |
| Surface heat transfer | |
| Chemical reaction parameter | |
| Time constant | |
| Average absorption coefficient | |
| Weissenberg number | |
| Grashof number | |
| Internal heat generation parameters | |
| Internal heat source and sink |
References
- Carreau, P.J. Rheological equations from molecular network theories. Trans. Soc. Rheol. 1972, 16, 99–127. [Google Scholar] [CrossRef]
- Carreau, P.; Kee, D.D.; Daroux, M. An analysis of the viscous behaviour of polymeric solutions. Can. J. Chem. Eng. 1979, 57, 135–140. [Google Scholar] [CrossRef]
- Bush, M.; Phan-Thien, N. Drag force on a sphere in creeping motion throug a carreau model fluid. J. Non-Newton. Fluid Mech. 1984, 16, 303–313. [Google Scholar] [CrossRef]
- Khellaf, K.; Lauriat, G. Numerical study of heat transfer in a non-Newtonian Carreau-fluid between rotating concentric vertical cylinders. J. Non-Newton. Fluid Mech. 2000, 89, 45–61. [Google Scholar] [CrossRef]
- Khan, M.; Sardar, H.; Gulzar, M.M.; Alshomrani, A.S. On multiple solutions of non-Newtonian Carreau fluid flow over an inclined shrinking sheet. Results Phys. 2018, 8, 926–932. [Google Scholar] [CrossRef]
- Olajuwon, I.B. Convection heat and mass transfer in a hydromagnetic Carreau fluid past a vertical porous plate in presence of thermal radiation and thermal diffusion. Thermal Sci. 2011, 15, 241–252. [Google Scholar] [CrossRef]
- Hsu, J.P.; Shie, C.F.; Tseng, S. Sedimentation of a cylindrical particle in a Carreau fluid. J. Colloid Interface Sci. 2005, 286, 392–399. [Google Scholar] [CrossRef]
- Ali, N.; Hayat, T. Peristaltic motion of a Carreau fluid in an asymmetric channel. Appl. Math. Comput. 2007, 193, 535–552. [Google Scholar] [CrossRef]
- Hayat, T.; Saleem, N.; Ali, N. Effect of induced magnetic field on peristaltic transport of a Carreau fluid. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 2407–2423. [Google Scholar] [CrossRef]
- Tshehla, M. The flow of Carreau fluid down an incline with a free surface. Int. J. Phys. Sci 2011, 6, 3896–3910. [Google Scholar]
- Ellahi, R.; Riaz, A.; Nadeem, S.; Ali, M. Peristaltic flow of Carreau fluid in a rectangular duct through a porous medium. Math. Probl. Eng. 2012, 2012. [Google Scholar] [CrossRef]
- Ishak, A.; Nazar, R.; Pop, I. Hydromagnetic flow and heat transfer adjacent to a stretching vertical sheet. Heat Mass Transf. 2008, 44, 921. [Google Scholar] [CrossRef]
- Ishak, A.; Jafar, K.; Nazar, R.; Pop, I. MHD stagnation point flow towards a stretching sheet. Physica A 2009, 388, 3377–3383. [Google Scholar] [CrossRef]
- Xu, H.; Liao, S.J.; Pop, I. Series solutions of unsteady three-dimensional MHD flow and heat transfer in the boundary layer over an impulsively stretching plate. Eur. J. Mech.-B/Fluids 2007, 26, 15–27. [Google Scholar] [CrossRef]
- Vajravelu, K.; Hadjinicolaou, A. Convective heat transfer in an electrically conducting fluid at a stretching surface with uniform free stream. Int. J. Eng. Sci. 1997, 35, 1237–1244. [Google Scholar] [CrossRef]
- Pop, I.; Na, T.Y. A note on MHD flow over a stretching permeable surface. Mech. Res. Commun. 1998, 25, 263–269. [Google Scholar] [CrossRef]
- Machireddy, G.R.; Polarapu, P.; Bandari, S. Effects of magnetic field and Ohmic heating on viscous flow of a nanofluid towards a nonlinear permeable stretching sheet. J. Nanofluids 2016, 5, 459–470. [Google Scholar] [CrossRef]
- Liu, I.C.; Wang, H.H.; Peng, Y.F. Flow and heat transfer for three-dimensional flow over an exponentially stretching surface. Chem. Eng. Commun. 2013, 200, 253–268. [Google Scholar] [CrossRef]
- Hayat, T.; Asad, S.; Mustafa, M.; Alsaedi, A. Boundary layer flow of Carreau fluid over a convectively heated stretching sheet. Appl. Math. Comput. 2014, 246, 12–22. [Google Scholar] [CrossRef]
- Reddy, M.G. Influence of magnetohydrodynamic and thermal radiation boundary layer flow of a nanofluid past a stretching sheet. J. Sci. Res. 2014, 6, 257–272. [Google Scholar] [CrossRef]
- AboEldahab, E.M. Radiation effect on heat transfer in an electrically conducting fluid at a stretching surface with a uniform free stream. J. Phys. D Appl. Phys. 2000, 33, 3180. [Google Scholar] [CrossRef]
- Gnaneswara Reddy, M. Thermal radiation and chemical reaction effects on MHD mixed convective boundary layer slip flow in a porous medium with heat source and Ohmic heating. EPJP 2014, 129, 41. [Google Scholar] [CrossRef]
- Abo-Eldahab, E.M.; El Gendy, M.S. Radiation effect on convective heat transfer in an electrically conducting fluid at a stretching surface with variable viscosity and uniform free stream. Phys. Scr. 2000, 62, 321. [Google Scholar] [CrossRef]
- Reddy, M.G. Effects of Thermophoresis, Viscous Dissipation and Joule Heating on Steady MHD Flow over an Inclined Radiative Isothermal Permeable Surface with Variable Thermal Conductivity. J. Appl. Fluid Mech. 2014, 7, 51–61. [Google Scholar]
- KRISNA, P.M.; SANDEEP, N.; SUGUNAMMA, V. Effects of radiation and chemical reaction on MHD convective flow over a permeable stretching surface with suction and heat generation. Walailak J. Sci. Technol. (WJST) 2015, 12, 831–847. [Google Scholar]
- Sandeep, N.; Sulochana, C.; Sugunamma, V. Radiation and magnetic field effects on unsteady mixed convection flow over a vertical stretching/shrinking surface with suction/injection. Ind. Eng. Lett. 2015, 5, 127–136. [Google Scholar]
- Jonnadula, M.; Polarapu, P.; Reddy, G. Influence of thermal radiation and chemical reaction on MHD flow, heat and mass transfer over a stretching surface. Procedia Eng. 2015, 127, 1315–1322. [Google Scholar] [CrossRef]
- Das, S.; Jana, R.; Makinde, O. Magnetohydrodynamic mixed convective slip flow over an inclined porous plate with viscous dissipation and Joule heating. Alexandria Eng. J. 2015, 54, 251–261. [Google Scholar] [CrossRef]
- Singh, G.; Makinde, O.D. Mixed convection slip flow with temperature jump along a moving plate in presence of free stream. Thermal Sci. 2015, 19, 119–128. [Google Scholar] [CrossRef]
- Makinde, O.; Khan, W.; Culham, J. MHD variable viscosity reacting flow over a convectively heated plate in a porous medium with thermophoresis and radiative heat transfer. Int. J. Heat Mass Transf. 2016, 93, 595–604. [Google Scholar] [CrossRef]
- Ibrahim, W.; Makinde, O. Magnetohydrodynamic stagnation point flow and heat transfer of Casson nanofluid past a stretching sheet with slip and convective boundary condition. J. Aerosp. Eng. 2016, 29, 04015037. [Google Scholar] [CrossRef]
- Hayat, T.; Muhammad, T.; Shehzad, S.A.; Alsaedi, A. Simultaneous effects of magnetic field and convective condition in three-dimensional flow of couple stress nanofluid with heat generation/absorption. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 1165–1176. [Google Scholar] [CrossRef]
- Abbasi, F.; Shehzad, S.; Hayat, T.; Ahmad, B. Doubly stratified mixed convection flow of Maxwell nanofluid with heat generation/absorption. J. Magn. Magn. Mater. 2016, 404, 159–165. [Google Scholar] [CrossRef]
- Shehzad, S.; Abdullah, Z.; Alsaedi, A.; Abbasi, F.; Hayat, T. Thermally radiative three-dimensional flow of Jeffrey nanofluid with internal heat generation and magnetic field. J. Magn. Magn. Mater. 2016, 397, 108–114. [Google Scholar] [CrossRef]
- Hayat, T.; Muhammad, T.; Shehzad, S.A.; Alsaedi, A.; Al-Solamy, F. Radiative three-dimensional flow with chemical reaction. Int. J. Chem. React. Eng. 2016, 14, 79–91. [Google Scholar] [CrossRef]
- Shehzad, S.; Hayat, T.; Alsaedi, A. Three-dimensional MHD flow of Casson fluid in porous medium with heat generation. J. Appl. Fluid Mech. 2016, 9, 215–223. [Google Scholar] [CrossRef]
- Machireddy, G.R. Chemically reactive species and radiation effects on MHD convective flow past a moving vertical cylinder. Ain Shams Eng. J. 2013, 4, 879–888. [Google Scholar] [CrossRef][Green Version]
- Raju, C.; Ibrahim, S.; Anuradha, S.; Priyadharshini, P. Bio-convection on the nonlinear radiative flow of a Carreau fluid over a moving wedge with suction or injection. Eur. Phys. J. Plus 2016, 131, 1–16. [Google Scholar] [CrossRef]
- Raju, C.; Sandeep, N. Opposing and assisting flow characteristics of radiative Casson fluid due to cone in the presence of induced magnetic field. Int. J. Adv. Sci. Technol. 2016, 88, 43–62. [Google Scholar] [CrossRef]
- Akbar, N.S.; Nadeem, S. Carreau fluid model for blood flow through a tapered artery with a stenosis. Ain Shams Eng. J. 2014, 5, 1307–1316. [Google Scholar] [CrossRef]
- Suneetha, S.; Gangadhar, K. Thermal radiation effect on MHD stagnation point flow of a Carreau fluid with convective boundary condition. Open Sci. J. Math. Appl. 2015, 3, 121. [Google Scholar]
- Durga Prasad, P.; Varma, S.; Raju, C.; Shehzad, S.A.; Meraj, M. 3D flow of Carreau polymer fluid over variable thickness sheet in a suspension of microorganisms with Cattaneo-Christov heat flux. Revista Mexicana de Física 2018, 64, 519–529. [Google Scholar] [CrossRef]
- Ibrahim, W.; Gizewu, T. Nonlinear mixed convection flow of a tangent hyperbolic fluid with activation energy. Heat Transf. 2020. [Google Scholar] [CrossRef]
- Kumaran, G.; Sandeep, N. Thermophoresis and Brownian moment effects on parabolic flow of MHD Casson and Williamson fluids with cross diffusion. J. Mol. Liq. 2017, 233, 262–269. [Google Scholar] [CrossRef]
- Abegunrin, O.; Okhuevbie, S.; Animasaun, I. Comparison between the flow of two non-Newtonian fluids over an upper horizontal surface of paraboloid of revolution: Boundary layer analysis. Alex. Eng. J. 2016, 55, 1915–1929. [Google Scholar] [CrossRef]
- Liao, S.J. The Proposed Homotopy Analysis Technique for the Solution of Nonlinear Problems. Ph.D. Thesis, Shanghai Jiao Tong University Shanghai, Shanghai, China, 1992. [Google Scholar]
- Sajid, M.; Hayat, T. Comparison of HAM and HPM methods in nonlinear heat conduction and convection equations. Nonlinear Anal. Real World Appl. 2008, 9, 2296–2301. [Google Scholar] [CrossRef]
- Zhu, J.; Zheng, L.; Zheng, L.; Zhang, X. Second-order slip MHD flow and heat transfer of nanofluids with thermal radiation and chemical reaction. Appl. Math. Mech. 2015, 36, 1131–1146. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).