1. Introduction
Modern solar thermal systems have the potential to achieve very high energy conversion efficiency, even at average solar radiation values, and thus achieve high output temperatures [
1,
2,
3]. This effect is multiplied by the way the panels are connected [
4]. On one hand, the serial connection of the panels enables the required temperatures of the panels to be reached even at times with reduced energy input or energy consumption (allows for an increase in the dynamics of the system). On the other hand, it is sensitive to the way heat is being consumed. As stated by [
5,
6], current technologies make it possible to maximize the thermal performance of collectors of various absorber designs. This performance is ensured mainly by improving the material properties of the absorbers as well as by using new selective materials applied in multiple layers. Technical practice points to the use of multilayer applications in up to thirteen layers.
In the case of a decrease in power consumption due to a short-term change in system load—or in the case of a drop in the fluid flow or during interruption of the energy supply to the circulator or during routine shutdowns—the average temperature of the medium of flat collectors may reach values in excess of 170 °C [
7]. These temperatures mean a sharp increase in operating pressure. Moreover, phase changes also occur in critical situations, and the resulting vapor causes a further increase in pressure, thus leading to permanent damage to the components. Energy-saturation of the system also causes serious problems. As stated by [
8], the energy-saturation of the system occurs when the system reaches its energy capacity and begins to overheat and approach stagnation by further energy intake. When a saturation temperature of 100 °C is reached, steam begins to form in the collector and enters the system. The saturation temperature and system pressure increase only slightly. When the stagnation temperature is reached, this condition lasts approximately 10 minutes. These issues occur mainly due to oversizing of the solar thermal system during the summer season [
8]. In these conditions, referred to as stagnation, significant damage to the solar thermal system as a whole or to its individual parts (mainly collectors) may occur [
9,
10]. At the same time, stagnation greatly accelerates the degradation of materials and heat-transfer fluid. The heat-transfer fluid can act highly corrosive, resulting in accelerated clogging of the collectors and other system components [
7,
11]. Research results [
10,
12] show that stagnation also has a negative effect on the resulting heat loss of the collectors due to the degradation of the insulating materials and thus their characteristic coefficients.
However, the stagnation process is difficult to control and difficult to manage. In principle, there are two ways to control collector stagnation temperature: reduce solar energy input into the collector or remove excess heat from the collector [
7].
Stagnation processes according to [
8,
9,
13] can be divided into five basic phases. In the first phase, the heat transfer medium is heated until the evaporation temperature is reached. The temperature of the medium rises below the boiling point, causing it to expand and increase the pressure. In the second phase, when the boiling point is reached, the heat transfer medium is evaporated. A smaller part of the medium evaporates and pushes a larger part of the liquid medium in the collector until the inlet and outlet pipes are immersed in saturated steam. A large amount of liquid medium is pushed into the expansion vessel, causing the pressure to rise rapidly. In simple hydraulic systems (horizontal or rising pipes), a larger proportion of the medium flows through the outlet pipe and a smaller proportion flows through the inlet pipe. With more complex collector hydraulic systems (a combination of horizontal, rising and falling pipe sections), the behavior of the medium is more complicated. The pressure in the system rises sharply and the boiling point rises in the saturated steam area. The second phase lasts only a few minutes. If there is only steam in the area from the inlet to the outlet pipe, this phase ends. In the third phase, the pressure growth slows. The remaining liquid in the collector also evaporates and the steam reaches other parts of the system. The energy transferred from the collector is released into the components (e.g., heat exchanger) and the surrounding environment through the formation of condensate. At the end of the third phase, the steam volume and system pressure will reach maximum values. In the next phase, the steam in the collector becomes overheated and cooling becomes more difficult. The amount of steam in the collector is constantly decreasing and the collector gradually becomes drier. The efficiency of the collectors decreases and the amount of energy to be removed by steam is lower. This fourth phase may take several hours on a cloudless day and only ends when irradiance diminishes. The fifth phase occurs only after the fall of the incident energy on the collector, then the temperature drops below the boiling point and gradual condensation of the heat transfer medium begins.
In the case of fixed installation of panels, this process is dependent on the change of the position of the sun and usually the last phase is reached only in the evening, when the angle of incident solar radiation on the collector is significantly unfavorable. In this case, however, there may occur permanent mechanical damage to the collectors or other technological parts [
14,
15].
According to [
16] one of the technical options is the application of thermochromic absorber coatings which enables a significant reduction in collector and solar circuit temperature during stagnation. However, this principle of elimination of stagnation could be used only with new technological equipment. Another way to avoid overheating is to apply new smart coatings as described by [
17].
As shown by the results of [
7], stagnation conditions were evaluated in relation to parameters such as temperature dependence on the input and output of thermal panels, flow opening size, module tilt angle from 0° to 90° and operating conditions, with particular emphasis on emissivity. The research has focused on plate-type air-cooled panels, which significantly change the possibilities for conventional panel systems.
Another option is to use butane as the heat transfer medium as described by [
18]. The results showed that butane as a heat transfer medium can limit the maximum temperature in the solar circuit of the system to 120 °C or lower, allowing high collector performance. The disadvantage is that the heat transfer capacity with butane in the operating range for a typical heat pipe geometry is lower compared to other organic media, like, e.g., acetone. This is mainly caused by butanes’ comparatively low values for thermal conductance and enthalpy of vaporization. Thus, optimization of butane heat-pipes is essential to reach a high thermal conductance. Experimental investigations show that the thermal conductance of butane heat pipes with collector-typical dimensions (l
cond = 80 mm) is significantly lower, compared to acetone heat pipes. By increasing the condenser area five-fold the butane hat pipe exhibits a thermal conductance, which is in the same range to that of an acetone heat pipe with the same dimensions [
18].
As stated by [
19], the solution in terms of overheating of the solar thermal system is to insert an aluminum layer between the absorption plate and the glass cover. This protection can be complete or partial and the overheating problem is eliminated even at 50% overlap.
The prototype presented [
20] represents a new technology of aluminum heat pipes with minimal use of copper. With this new type of pipe, stagnation temperature is lower at a maximum stagnation temperature reaches 140 °C.
According to [
21], the use of thermotropic glazing is effective in lowering stagnation temperature. Glass and absorber temperatures during stagnation revealed that the developed thermotropic glazing is a powerful component that prevents overheating in solar collectors and decreased the absorber temperatures by 29 K when compared to the reference collector.
As reported by [
9], although various approaches are currently being applied in the research and practice to minimize the effects of a stagnation state, some proposed methods are not suitable for all system designs and applications. Factors such as storage and system capacity, load, distribution requirements, temperature and frost protection affect the choice of stagnation control.
When tilting the collectors, it is possible to significantly increase the efficiency of obtaining thermal energy from solar radiation [
22]. A tracker construction with different designs can be used to tilt the collectors [
23]. Control algorithm is important for the best use of tracker construction [
24,
25]. These systems can also be optimized and improved, as reported by [
26,
27,
28]. As a result, a series of experiments and simulations was conducted to investigate the possibilities of eliminating the stagnation state using the collector field rotation system with the tracker construction.
The thermal risks of the process represent the achievement of working medium temperatures above the phase transition values of the working substance. Directly with increasing temperature, the pressure of the working medium increases sharply. The generated vapors continue to increase the working pressure, which in many cases leads to unavoidable damage to components. Safety elements in the form of safety valves are installed in the system, but these will only ensure a pressure drop in the system but will eliminate the problem of temperature rise. At the same time, further circulation of the liquid is disabled due to its lack in the system by its evaporation and i tis still thermally significantly stressed. During further vapors generation, the circulation pump is unable to ensure its operation with the generated vapors. Such thermal stress leads to permanent degradation of the components as well as the solar thermal panels themselves. In the proposed method of eliminating stagnation in iterations proportional to the time constant, the value of temperature of medium in the storage tank as well as at the outlet and inlet to the solar thermal system is evaluated. By changing the position of the panels using the tracker construction and the control system, there is a decrease in the irradiated area as well as a significant increase of angle towards the incident sunlight. The result is a significant decrease in the efficiency of the panels and thus another significant increase in temperature. Subsequently, this effect is manifested only by a slight increase in temperature in the system. Synergically, the temperature at the outlet of the collectors decreases due to the natural balancing of the energy balance of surrounding environment and panels.
2. Materials and Methods
To eliminate thermal stagnation, the collector tilting system was used. Verification of the operation of the system took place using a laboratory thermal system consisting of a panel array consisting of four flat solar panels HERZ CS 100F located at the workplace of the Department of Process Engineering. The total area of the collectors is 8.28 m
2 and the absorption area of the collector is 7.56 m
2, which means that 91.3% of the total area is actively used. A maximum of seven panels can be placed in one collector array as stated by (Hafez et al., 2018). The collector frame features a double-chamber made of anodized aluminum with insulation consisting of mineral wool with a temperature resistance up to 300 °C mounted in the lower part of the frame. In order to obtain the best possible conditions and the most ideal angle between the incident solar radiation and the absorption surface of the collectors, the collectors were placed on a structure that allows the entire surface to be automatically tilted according to the current position of the sun controlled by the Siemens Desigo Insight system.
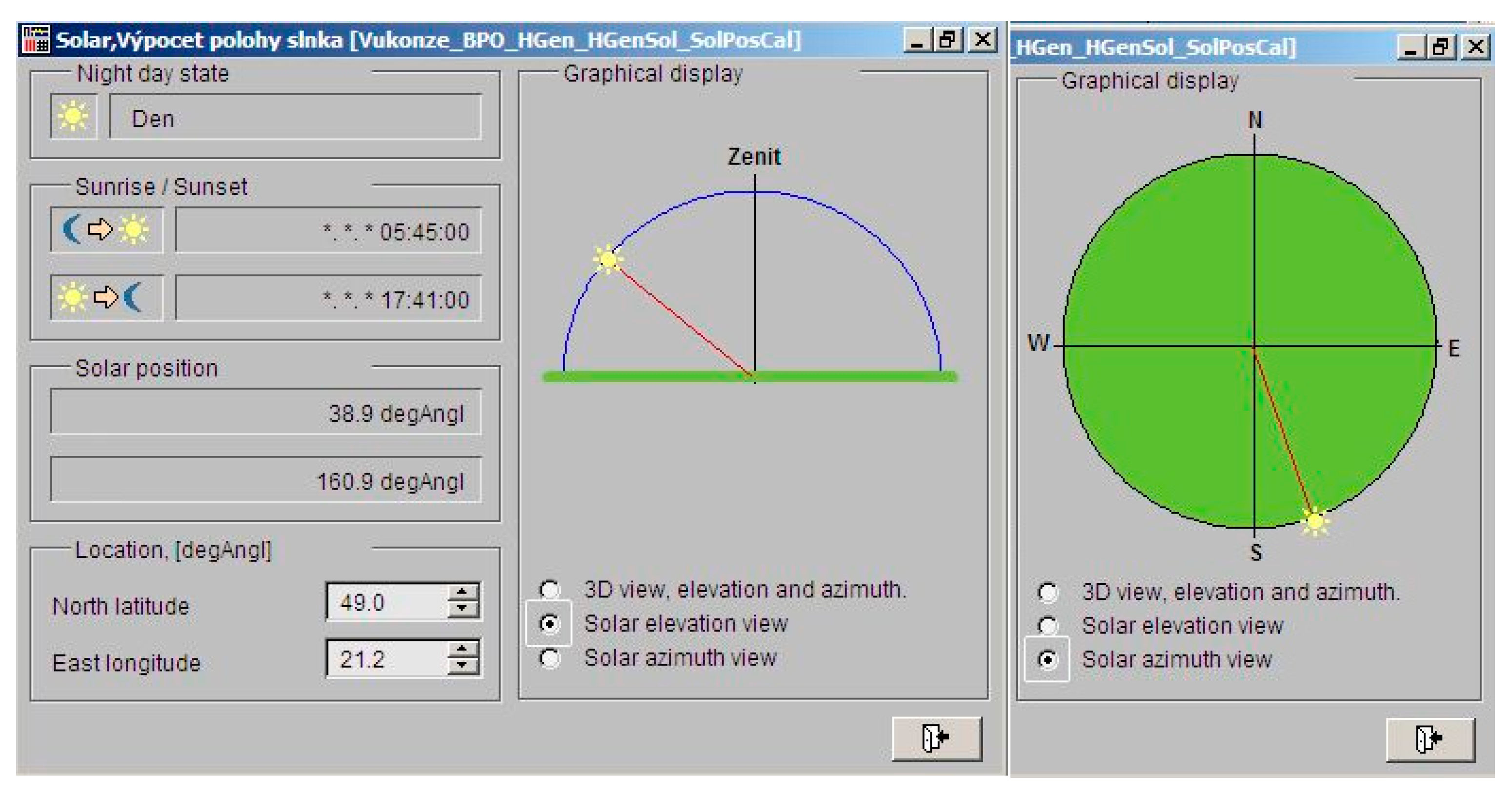
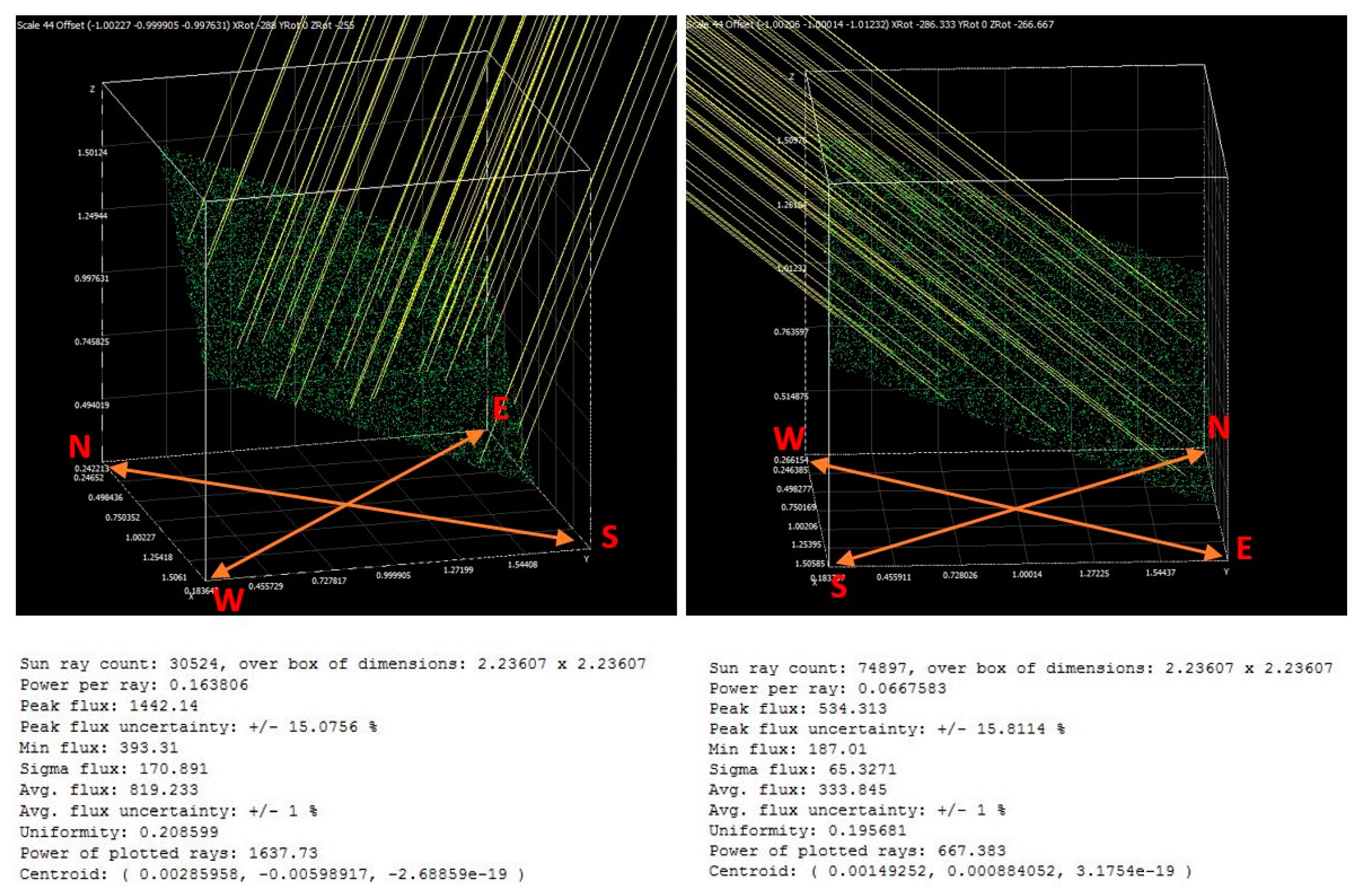
Figure 1 shows the tracker construction enabling the collector tilting.. The Siemens Desigo Insight control system (
Figure 2) is used for correct and automatic collector tilting.
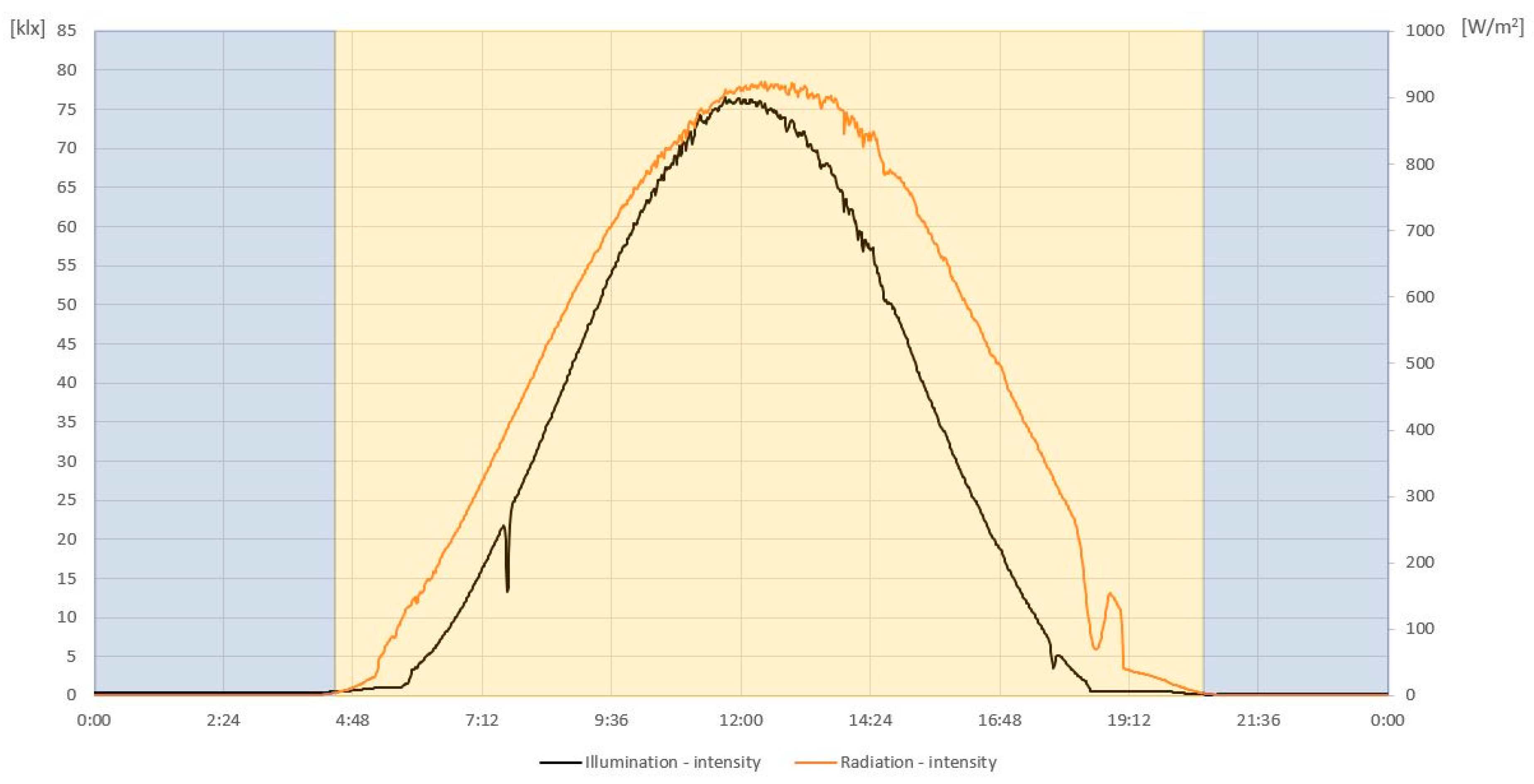
2.1. Sun Radiation
For the most effective heat recovery in terms of incident solar radiation, it is necessary to calculate the optimal angle of incidence of solar radiation. Calculations of the optimum angle of incidence of solar radiation on an inclined surface are described by a number of studies [
29,
30,
31,
32,
33,
34,
35,
36,
37,
38] According to [
39], the global solar irradiation (G) incident on an inclined surface is composed of direct (Gb), diffuse (Gd) and reflected (Gr) radiation:
The radiation incident on the illuminated part of the surface is inversely proportional to the area illuminated by the beam, and the illuminated surface depends on the angle of incidence of the beam. Irradiation above the tilted surface (Gbt) at an angle of incidence θ is:
G
bn—normal irradiation (perpendicular to surface.
On a horizontal surface, the angle of incidence is equal to that of the solar zenith and the horizontal irradiance is:
Irradiation above the tilted surface (Gbt) can be expressed by a combination of Equations (2) and (3):
Assuming that the diffuse radiation is the same at all times and in all directions from the half-space above the horizontal surface, we can conclude that it is isotropic. Irradiation on an inclined surface, due to only diffuse radiation, can then be defined as:
β—tilt angle.
The reflected radiation depends on the global radiation (G) and the reflectance of the surfaces (R). The reflected radiation is isotropic at the given place and time, the same in all directions from the half-space below the horizontal surface. Irradiation on an inclined surface due to reflected radiation is calculated as:
The calculation of the position of the sun relative to the panel is based on DIN 5034-2 [
40] The particular parameters are shown in
Figure 3, which shows solar radiation incident on a titled plane. The first step is to define the variable J’ that represents the average angular movement of the earth around the sun. With the variable J’, the height and position of the sun can be calculated.
The declination δ is determined by the equation:
To calculate the position of the sun for a specific place, it is necessary to know the altitude γ
s and the sun azimuth α
s as those depend on the day and the season. The height of the sun is calculated as follows:
The solar azimuth is given by the equation:
or
RLT—real local time, φ = latitude.
The solar radiation on an inclined south-facing surface with a tracker structure is described in [
23] as follows. Declination is the angular position of the sun at noon with respect to the equator and is expressed by the equation:
The solar hour angle (ω) is the angle of the sun east or west of the local meridian. The hour angle is positive in the morning, zero at noon and negative in the afternoon. Hourly angle is calculated as:
The altitude angle (γ
s) is the angle between the sun rays and the horizontal surface, which is calculated as:
The solar azimuth angle is the horizontal angle measured from north to the horizontal projection of the sun’s rays. The azimuth angle is given as:
The angle of the sun zenith is the angular distance of the sun from the local vertical and depends directly on the angle of the sun:
The surface azimuth angle γ is the angle between the normal surface of the panel and the local meridian:
γ = 0 for south-facing surfaces
γ = 180−αs for surfaces with a biaxial tracker system.
The angle of incidence of solar radiation θ is the angle between the normal of the panel and solar radiation. This angle can be expressed by the equation:
For a south-facing surface, γ = 0 and for the tracker system, the angle of incidence of solar radiation is θ = 0. The angle of the inclined plane of the tracker system (β) is given by the equation:
2.2. Solar Collector Efficiency and Causes of Stagnation
Harrison et al. [
9] describe stagnation conditions as any situation in which a solar collector must receive heat from solar radiation and pass it on to the heat-transfer fluid, causing the solar collector and its components to rise in temperature above the maximum allowable level. Stagnation conditions may arise during the exposure to solar radiation when the flow of heat-transfer fluid in the system is interrupted due to technical faults such as power outages, component failures, system maintenance and repair and pump controller interventions due to capacity storage limitations or any other reason for temporary low heat consumption.
Stagnation behavior is crucial for long-term, reliable and low level of maintenance operation of solar thermal systems. This is particularly important in industrial applications where the entire installed thermal capacity of a solar system cannot be fully utilized. This may be due to technical failures (e.g., circulator pump failure), lack of heat consumption (e.g., weekends, holidays, maintenance, repairs) or power outages. This operating state causes all components in the solar system to be under high stress, which is different from normal operating conditions [
41].
When the stagnation temperature is reached, the thermal output of the Q
coll solar thermal collector drops to zero. The heat output of a solar thermal collector can be approximated by the following equation:
Qcoll—thermal output of the collector [W]
A—area of the collector [m2]
η0—peak efficiency (conversion factor) [−]
a1—heat transfer coefficient at (Tm − Ta) = 0 [Wm−2 K−1]
a2—temperature-dependent heat transfer coefficient [Wm−2 K−2]
Tm,f—mean liquid temperature in the collector [°C]
Ta—ambient temperature [°C]
G—hemispherical solar radiation on the collector [Wm−2]
A temperature that reaches η
coll = 0 gives a stagnant temperature T
stag each collector and can be calculated from the efficiency curve equation (T
m,f = T
stag):
T
stag equilibrium (stagnant) temperature [°C].
The efficiency of a solar collector under steady conditions is defined as the ratio of the heat output dissipated by the heat transfer medium from the collector field to the incident solar radiation.
η—efficiency of solar collector, Qk—heat output, G—amount of solar radiation [W/m2], Ak—reference surface of the collector [m2].
The reference surface for evaluating the efficacy may be the absorber area, the aperture area or the thick area. The efficiency of the solar collector is evaluated and reported as a curve depending on the climatic and operating conditions.
G—amount of solar radiation [W/m2], Ak—reference surface of the collector [m2], η0—solar collector efficiency at zero heat loss (optical collector efficiency), a1—linear heat loss coefficient [W/(m2.K)], a2—quadratic coefficient of heat loss of collector (expresses temperature dependence).
2.3. Experimental Details
Heat-transfer fluid with a volume of 5.2 L flows through the collector with a flow rate of 4.6 L.min
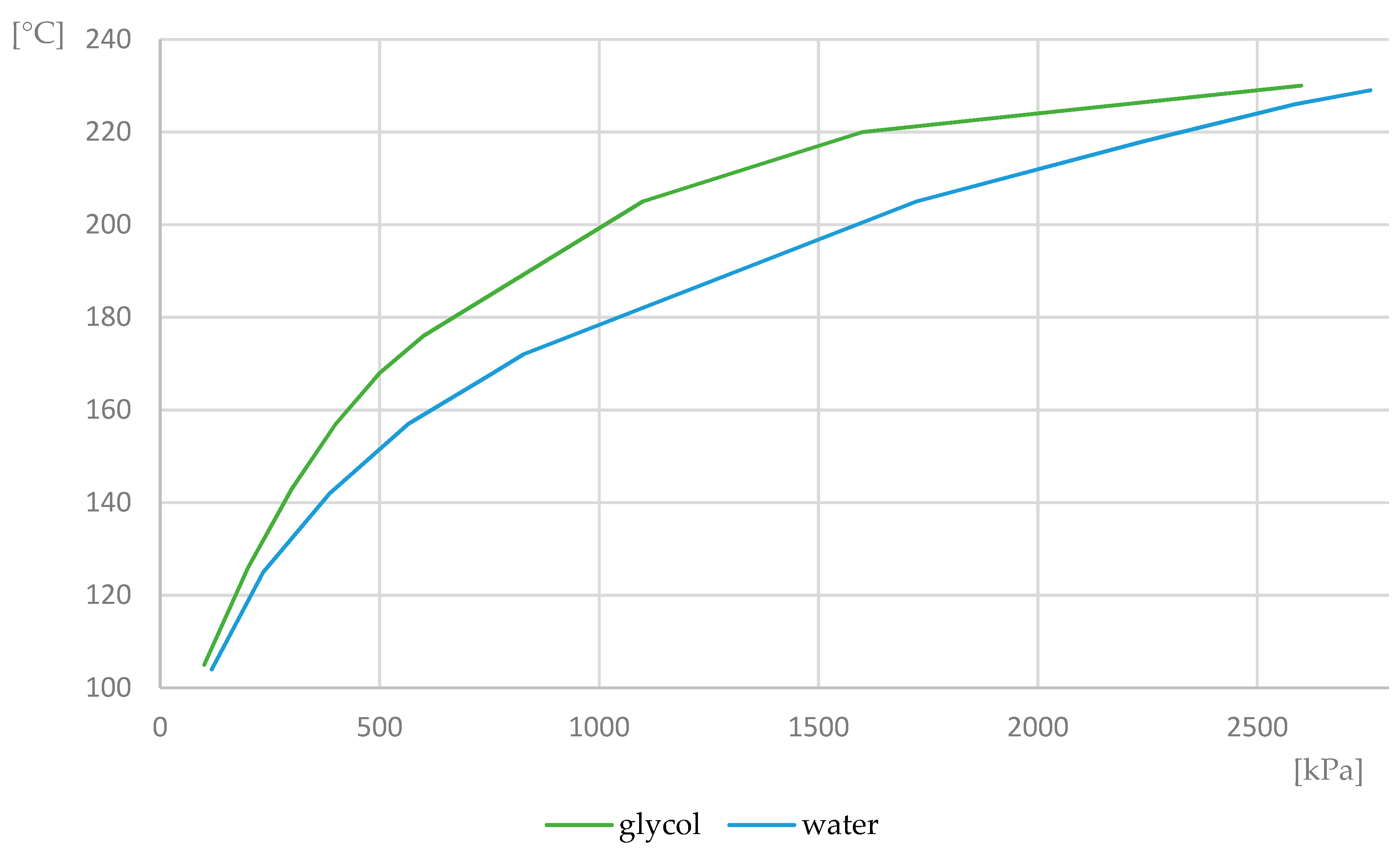
−1. It is a heat-transfer fluid Agrimex Collector P super with a low pour point suitable for all types of collectors. The liquid is based on monopropylene glycol (1,2-propanediol) with the addition of non-toxic corrosion inhibitors and stabilizer to achieve increased thermal stability and extended life. The heat-transfer fluid has a freezing temperature of −30 °C, which is necessary for local climatic conditions. The fluid can be short-term overheated up to 300 °C and has constant heat conductivity and pH. In addition, the heat capacity and density of the fluid are only slightly variable at different temperatures. The temperature pressure diagram is shown in
Figure 4. These properties have a high stability and are suitable for performing experiments and measurements. The heat-transfer fluid is described in
Table 1.
Fluid life expectancy in professionally operated systems is 10 years. The manufacturer recommends checking the fluid for freezing temperature and pH once every 2 years.
Table 2 shows the parameters of the heat-transfer fluid in temperature regimes of −30 °C to 100 °C.
2.4. Tilting of Collectors
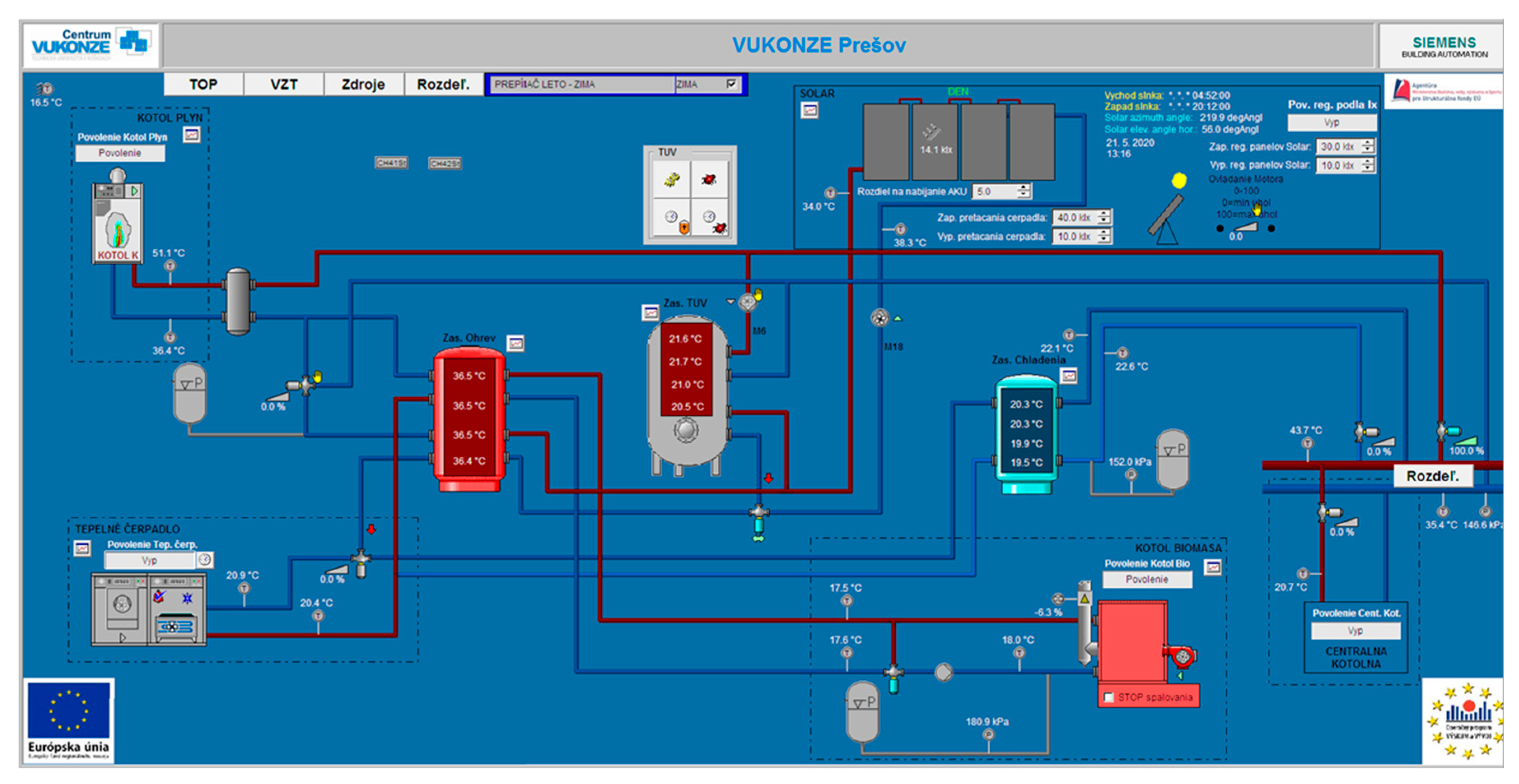
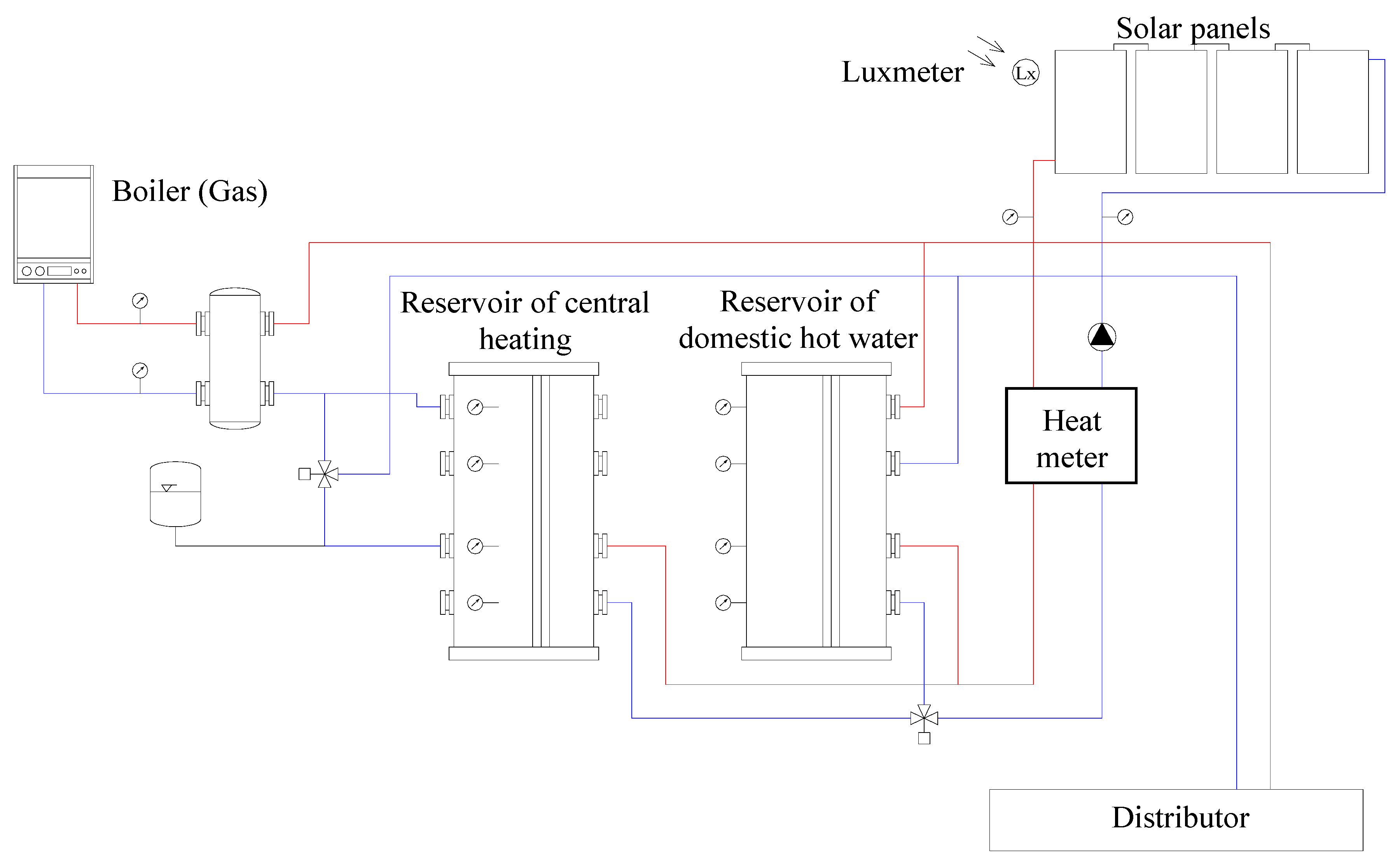
Tilting of collectors is carried out thanks to the construction solution that tilts around one axis. Azimuth extrapolation is used to determine the correct position of the collector. Due to the size of the whole multivalence system of the experimental laboratory, a part with a gas boiler and thermal panels was used and the resulting scheme of the part of the system used in the experiments is shown in
Figure 5. This system consists of the control system, a three-way changeover valve with actuator and a fluid flowmeter with calorimetric counter. The thermal energy that is obtained from the panels is transmitted in the DHW cylinder VT-S 1000 FRMR with a capacity of 970 L and then in the PSR 800 with the capacity of 800 L.
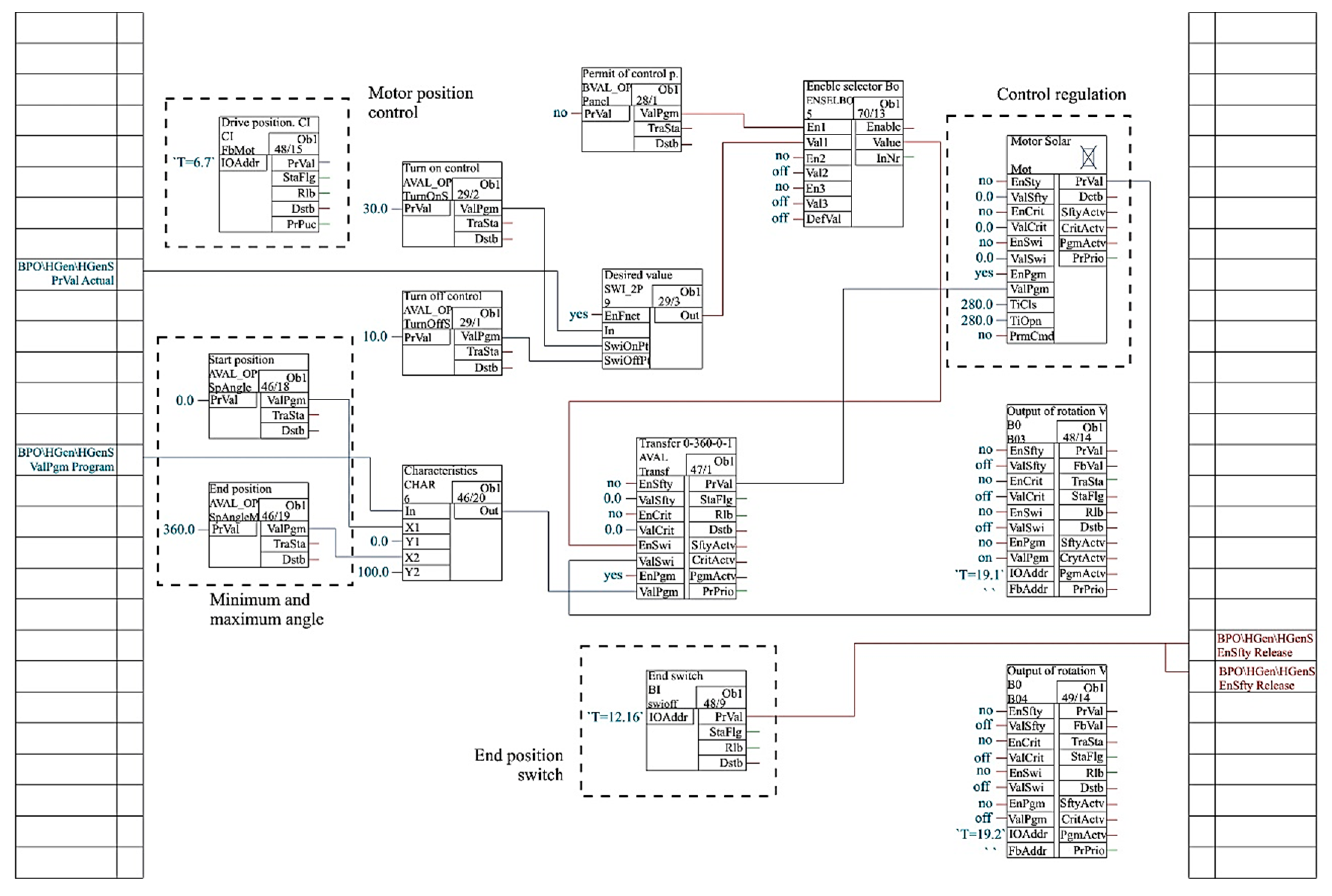
Position control (
Figure 6) transfers the signal to two binary outputs with three degrees: open–close–stop; in this case it is a right–left–stop. This signal is determined by evaluating the solar radiation intensity. In case of sufficient solar radiation intensity, the structure is tilted according to the current recalculated position of the sun. If the intensity falls below the critical solar radiation intensity, the engine stops. Subsequent triggering occurs only after the solar radiation intensity has increased again. To ensure the rotation of the structure, the end position sensors are located in the end positions (
Figure 7), which also serve as zero points for the calculation of end positions in the interval 0–100.
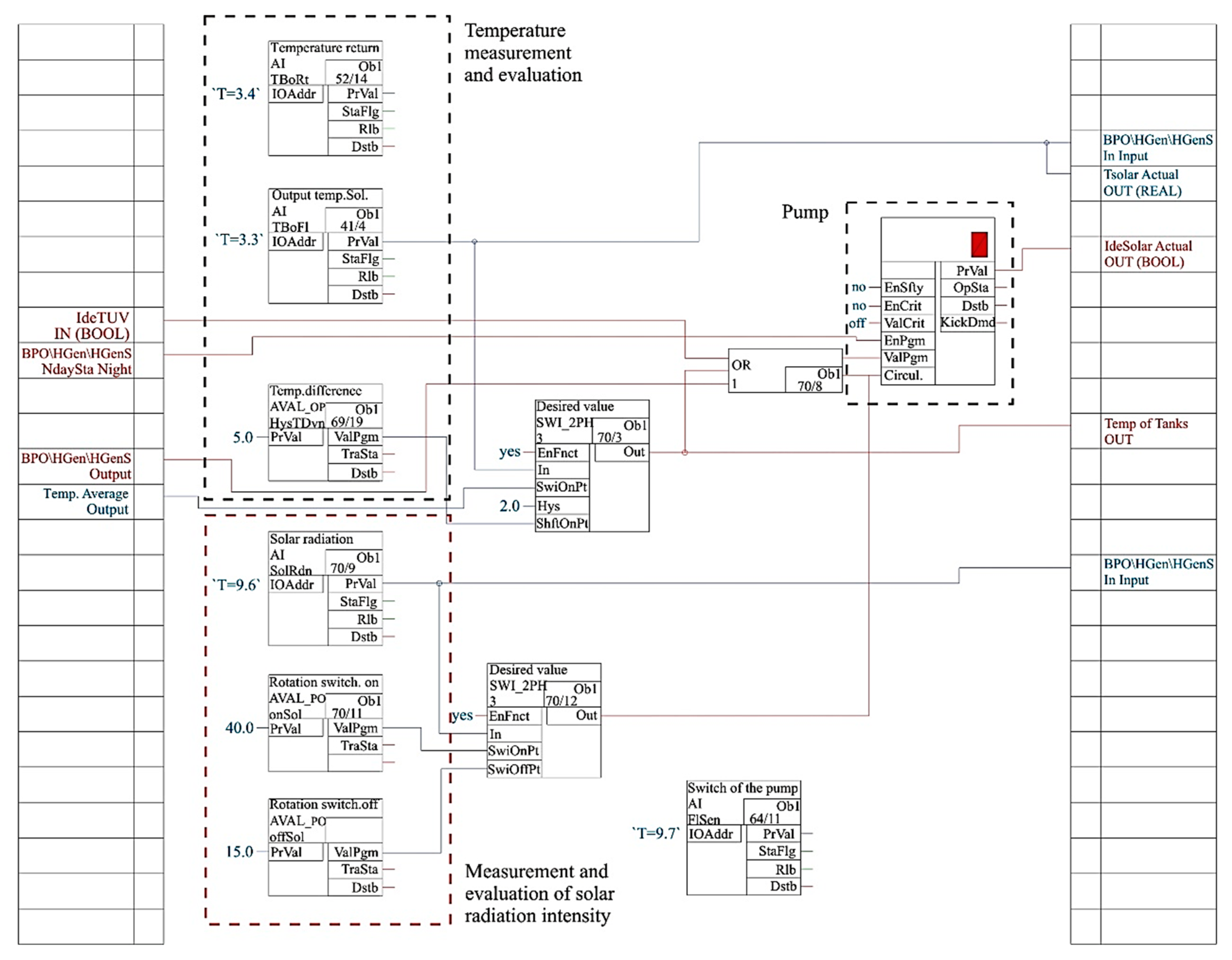
The pump operation (
Figure 8) is conditional upon the achievement of the defined difference of the measured temperature values at the output of the solar panels and the temperature values in the accumulation tanks.
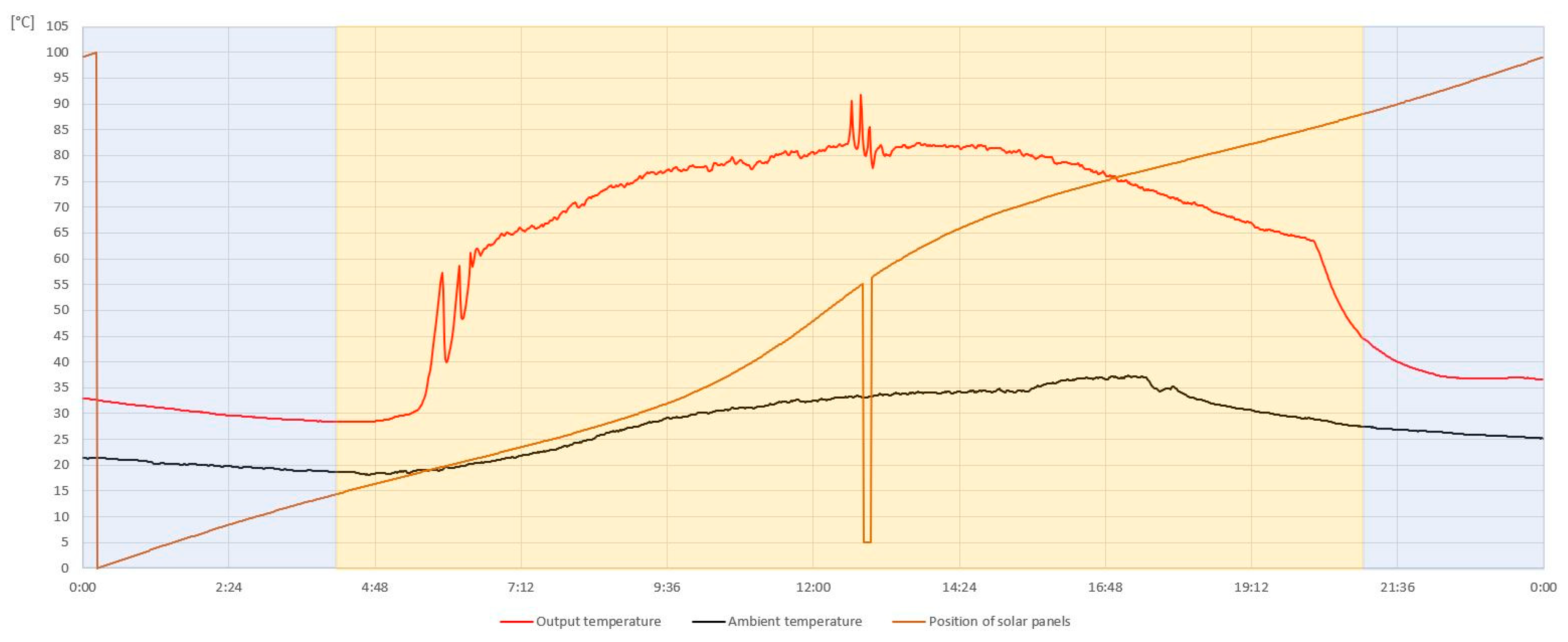
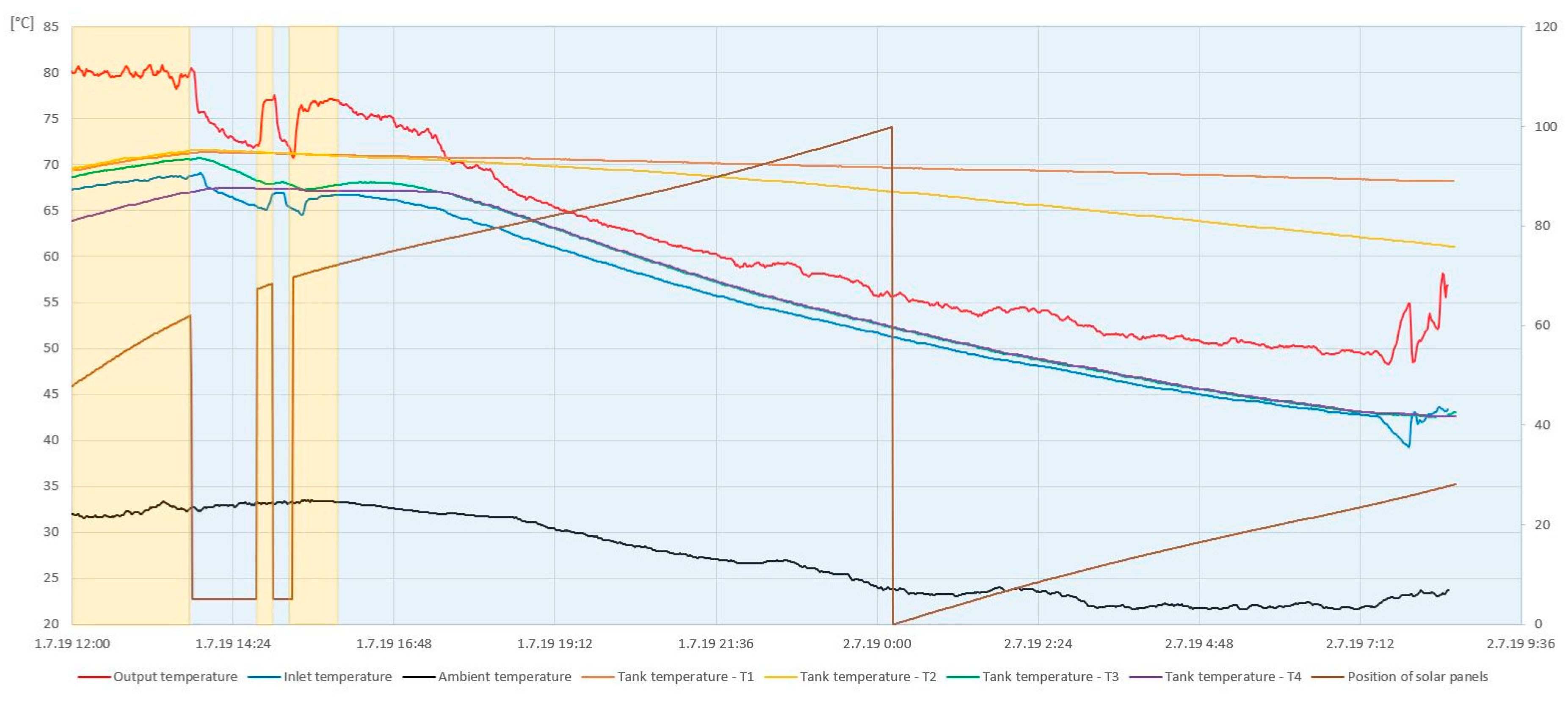
4. Conclusions
There were several options to streamline and maximize the use of the solar potential in solar systems. One possibility is to mount the collector on the tracker construction. This design allows the collector to move and monitor the current position of the sun, making it possible to use more of the incident solar radiation. An important aspect is also to determine the ideal angle of incidence of the sun’s rays on the collector surface. With the ideal tilting and inclination of the collector towards solar radiation, higher temperature gains can be achieved than with a poorly optimized and static system. The threat to any solar system is overheating of the system as a result of a failure or energy saturation when the system may overheat, and stagnation processes may take place. Stagnation can most often occur due to a failure of the circulation pump or insufficient hot water consumption. High temperatures can severely damage the entire solar system and protection systems must be provided to prevent stagnation. In the proposed solar system placed on the tracker construction, no modification of collectors and heat transfer medium is necessary. A suitable option to protect the solar system from stagnation processes is to tilt the collector and reduce the amount of incident solar radiation, thereby lowering the temperature of the medium in the collector. By tilting the collectors, the system temperature decreased by 10% in one hour. Using this process, it is possible to intervene in the already existing stagnation process and lower the temperatures in the system. However, it is more effective to prevent the system from overheating and stagnation. When approaching the critical temperature, the panels tilt away from the incident solar radiation, thus reducing their performance and lowering the system temperature. The advantage of the proposed system is full automation of control and independent decision-making of the system according to the current conditions. The system selects the most appropriate variant of operation for a given time and user intervention is not necessary. In the case of energy saturation of the system, excess heat must be removed from the system, which means that in case of significant accumulation of thermal energy in the storage tanks and assuming a low consumption of hot water, the option is to cool the storage tank. This cooling is carried out by circulating the heat transfer medium throughout the system during the year, thus extracting thermal energy from the storage tank and releasing it to the outside. Measurements have shown that the storage tank can be cooled by circulating the heat transfer medium in the system at night. By doing so, the water temperature in the tank will drop significantly. This preventive solution can be deployed in case of a low hot water consumption during the summer or holiday season. This option is more demanding in terms of time, but it is highly effective in the case of low hot water consumption.