Study on the Formation of Complex Chemical Waveforms by Different Computational Methods

Abstract

Chemical wave is a special phenomenon that presents periodic patterns in space-time domain, and the Belousov–Zhabotinsky (B-Z) reaction is the first well-known reaction-diffusion system that exhibits organized patterns out of a homogeneous environment. In this paper, the B-Z reaction kinetics is described by the Oregonator model, and formation and evolution of chemical waves are simulated based on this model. Two different simulation methods, partial differential equations (PDEs) and cellular automata (CA) are implemented to simulate the formation of chemical waveform patterns, i.e., target wave and spiral wave on a two-dimensional plane. For the PDEs method, reaction caused changes of molecules at different location are considered, as well as diffusion driven by local concentration difference. Specifically, a PDE model of the B-Z reaction is first established based on the B-Z reaction kinetics and mass transfer theory, and it is solved by a nine-point finite difference (FD) method to simulate the formation of chemical waves. The CA method is based on system theory, and interaction relations with the cells nearest neighbors are mainly concerned. By comparing these two different simulation strategies, mechanisms that cause the formation of complex chemical waves are explored, which provides a reference for the subsequent research on complex systems.

1. Introduction

In a reaction-diffusion system, the concentration distribution of its components could exhibit periodic changes in time and space under certain conditions, and this phenomenon is called a chemical wave [1]. Researchers have observed various chemical waves, such as pulse waves along one dimension [2], target waves and spiral waves on a two-dimensional plane [3,4], scroll waves in a three-dimensional space [5]. It is a macroscopic pattern developing from chemical reaction coupling with diffusion [6] and is a typical self-organizing phenomenon [7,8,9]. Self-organization means an ordered structure of the system, which occurs through the internal interaction of the system, and is not directly affected by external directing [10]. There is common understanding regarding the formation of chemical waves [1,6,10,11,12], i.e., when far away from thermodynamic equilibrium, a system is influenced by the interaction among coupling reactions, and the concentration of each location may fluctuate periodically, and together with the influence of diffusion, the system changes from disorder to order, i.e., chemical wave.

The experiment of Belousov–Zhabotinsky (B-Z) reaction is a classic example to study chemical waves [1,2,3,4,6,10,11,12]. Belousov studied this system first [13,14], and then, Zhabotinsky published a paper on its chemical waves [14,15,16]. Before equilibrium is reached, it can be observed that the color of the solution oscillates between red and blue via the action of ferroin indicator [16,17]. In particular, if the reaction takes place in a thin layer reactor, various chemical waves in two-dimensional plane can be obtained [3]. Since this system appears to be violating the 2nd-law of thermodynamics (order evolves from disorder), research efforts are drawn to explain why chemical-waves are thermodynamically possible. Prigogine extended the field of thermodynamics away from equilibrium and developed the theory of dissipative structures [10]. According to his theory, these structures are different from typical equilibrium structures. They maintain a steady state through competing processes. These dynamic processes provide energy to the system to form self-organization and generate chemical waves. Many kinetic models have been developed for B-Z reaction. The most acceptable one is the FKN mechanism proposed by Richard J. Field, Endre Koros, and Richard M. Noyes in 1972 [18]. However, there are 26 variables and 80 coupled chemical equations in their theory, which makes it hard to model mathematically. In 1974, Richard J. Field and Richard M. Noyes proposed a highly idealized model based on FKN, named Oregonator model with only five reactions [19]. It is much simpler to show the chemical waves phenomenon in the B-Z reaction by computer simulation.

To study the formation and evolution of chemical waves without convective motion in a two-dimensional domain at room temperature, a common simulation method is to build a partial differential equations (PDEs) model and solve it [20]. This PDE model can be obtained by describing mass balance at each point in the system. The formation of chemical waves can be obtained by calculating the real-time concentration fluctuations at each point according to PDEs built previously, usually via finite difference (FD) method. Its basic idea is to replace the continuous area with finite discrete points. Specifically, the reaction area is divided into grids by equidistant parallel lines, and then, the area is replaced by grid nodes. At these nodes, the PDEs are transformed into algebraic equations by interpolation methods, such as Lagrange interpolation. Through the Taylor expansion method or other methods, the accuracy of the solution is improved, and a spatiotemporal distribution of concentration is obtained. Although accurate results can be obtained using this method, it requires significant CPU time and memory. It can be explained that there are both time-dependency and spatial dependency considered in the model built by PDEs, which have to be solved simultaneously via FD. If the system can be decomposed into a set of time-dependent sub-systems with information exchanged locally in spatial scale, the computation efficiency can be significantly improved.

Cellular automata (CA) is a spatiotemporal discrete algorithm first proposed by von Neumann (1966) to simulate the self-reproduction phenomenon of cells [21].Its basic idea is to represent the state transition of a system through simple cell change, which follows a specific dynamic mechanism, and cell interaction, which follows local rules. Wolfram was the first to systematically study CA on the basis of a large number of computer experiments, and applied this algorithm to simulate physical and chemical phenomena [22]. Saadia et al. employed CA to study the coupled vegetation growth process, which was previously described by PDEs [23]. In 1990, Gerhardt et al. proposed a two-dimensional CA model to investigate the B-Z reaction and exhibit some typical characteristics of chemical waves [24,25]. However, by their model, the isotropy of waves could not be obtained as in the experiments because the square neighborhood they chose was not enough to reflect the effect of the distance between neighbors and the central cell on the diffusion. Fast and Efimov proposed a weight relationship to improve the spatial isotropy when studying the stability of vortex rotation, but this method is quite time consuming [26]. Weimar et al. studied a large number of discrete approximations to diffusion equations and suggested to replace the calculation of diffusion weights with a fixed matrix, called MASK, by which calculation load can be reduced [27]. It is reasonable to assume that CA method would be efficient for a qualitative study, if MASK can be combined with Gerhardt’s model in the simulation of the chemical waves, while it is still not enough to obtain the concentration of each point in the propagation of chemical waves, which can only be available from the solution of PDE model.

The aim of this work is to compare chemical waveform formation processes by the two above-mentioned simulation methods, and by comparing these two different simulation strategies, mechanisms that cause the formation of complex chemical waves are explored, which provides a reference for the subsequent research on complex systems. The paper is organized as follows: in Section 2, the strategy of using PDE to simulate chemical waves is introduced. Based on B-Z reaction kinetics, the kinetic model of one-point oscillations in the B-Z reaction system is studied without considering diffusion. Then, the PDE model of B-Z reaction is derived by mass transfer theory, and the PDE model is solved by the nine-point FD method. In Section 3, a strategy for simulating chemical waves with CA is addressed. MASK is then introduced to improve the spatial isotropy of CA. In Section 4, the simulation results of two methods are obtained, including two types of chemical waves in B-Z reaction-diffusion system, i.e., target waves and spiral waves. Followed by comparing the two simulation results, the similarities and differences between the two methods are found, which provides a basis for combining the two methods to improve the modeling of complex processes.

2. The B-Z Reaction System: PDE Modeling Strategy for the Simulation of Chemical-Wave

The previously mentioned chemical waves are formed in a two-dimensional B-Z reaction-diffusion system. If attention is paid to a dot, which is assumed small enough in this system, it can be considered as a homogeneous subset, which solely follows the kinetics of the B-Z reaction. In this section, through a detailed discussion of the B-Z reaction kinetics, the parameter range of concentration oscillation in B-Z reaction is explored. Then a PDE model of the reaction-diffusion system is established based on the mass transfer theory and solved by a nine-point FD method for a two-dimensional system.

2.1. The Reaction Kinetics: Generation of Oscillations

Here, the Oregonator model is adopted to explain the B-Z reaction mechanism through a five-step reaction [19,28]. It includes two reactants, D and E, which represent $Br{O}_3^{-}$ and $BrMA$ (MA refers to an organic acid ion), respectively; three intermediate products, A, B, and C, which represent $HBr{O}_2$, Ce(IV), and $B{r}^{-}$, respectively; P represents the product. f is the adjustable stoichiometry, which can be changed according to the experimental environment such as hydrogen ion concentration and temperature, making the model closer to reality. $r_i$ (i = 1, 2, 3, 4, 5) is a label for reaction rate. For calculation purposes, we assume that these reactions are irreversible. The B-Z reaction can be simplified to a reduction reaction of the bromide iron, the overall reaction is D+E→P.

$$\begin{array}{ccc}\mathrm{D}+\mathrm{C}\to \mathrm{A}+\mathrm{P}\hfill & & r_1=k_{1}DC\hfill \\ \mathrm{A}+\mathrm{C}\to 2\mathrm{P}\hfill & & r_2=k_{2}AC\hfill \\ \mathrm{D}+\mathrm{A}\to 2\mathrm{A}+2\mathrm{B}\hfill & & r_3=k_{3}DA\hfill \\ \hfill 2\mathrm{A}\to \mathrm{D}+\mathrm{P}\hfill & & r_4=k_4{A}^2\hfill \\ \mathrm{E}+\mathrm{B}\to \mathrm{fC}\hfill & & r_5=k_{5}EB\hfill \end{array}$$

Three-variable dynamic equations of the Oregonator model are obtained, being dimensionless. Then, an intermediate product C:$B{r}^{-}$ is eliminated according to empirical relationship to obtain a 2-variable Oregonator dimensionless model, as shown in Equation (1). The specific process is proposed by Tyson, so it is also named Tyson type [29].

$$\{\begin{array}{cc}\hfill \frac{da}{dt}={\epsilon }^{-1}(\frac{(q-a)fb}{q+a}+a-a^2)& =f(a,b)\hfill \\ \frac{db}{dt}=a-b\hfill & =g(a,b)\hfill \end{array}$$

(1)

In Equation (1), the variables are defined by $a=\frac{2k_4}{k_{3}D}A$, $b=\frac{k_4{k}_{5}E}{{(k_{3}D)}^2}B$, $c=\frac{k_2}{k_{3}D}C$ and $t=k_{5}E\tau$, and the parameters are obtained by $\epsilon =\frac{k_{5}E}{k_{3}D}$ and $q=\frac{2k_1{k}_4}{k_2{k}_3}$.

From classic thermodynamics, it is assumed that there will be no concentration fluctuations of substances on the macro scale when molecules reach dynamic equilibrium (2nd-law of thermodynamics). However, many reactive systems exhibit complex dynamics, e.g., the concentration of intermediate products in the B-Z reaction can oscillate continuously under certain conditions as shown in Figure 2a.

According to the bifurcation theory [30,31,32], when an equilibrium point is an unstable focus point or center point, a system may exhibit self-oscillatory state trajectories. Specifically, when the real part of all characteristic roots of the Jacobian matrix is negative, three solutions are obtained for the equilibrium point of Equation (1), i.e., one zero solution (0, 0), one negative solution, and one positive solution. The positive one is present in Equation (2). The Jacobian matrix of this equilibrium point is provided in Equations (3).

$$\{\begin{array}{c}{a}_2=\frac{1}{2}\left[(1-f-q)+\sqrt{{(1-f-q)}^2+4q(1+f)}\right]\hfill \\ b_2=\frac{1}{2}\left[(1-f-q)+\sqrt{{(1-f-q)}^2+4q(1+f)}\right]\hfill \end{array}$$

(2)

$$J=\left[\begin{array}{cc}\frac{\partial f}{\partial a}& \frac{\partial f}{\partial b}\\ \frac{\partial g}{\partial a}& \frac{\partial g}{\partial b}\end{array}\right]=\left[\begin{array}{cc}\frac{(1-2a_2){(q+a_2)}^2-2qf{b}_2}{{(q+a_2)}^2\epsilon }& \frac{(q-a_2)f}{(q+a_2)\epsilon }\\ 1& -1\end{array}\right]$$

(3)

According to the Routh–Hurwitz criterion [33,34], the following two conditions need to be satisfied to get negative real parts for characteristic roots of the Jacobian matrix: (a) each coefficient of the characteristic equation (shown in Equation (4)) of the Jacobian matrix is not equal to zero, and (b) the signs of the coefficients are the same. It can be described as Equation (5).

$${\lambda }^2-Tr\lambda +De=0$$

(4)

$$\{\begin{array}{c}Tr<0\\ De>0\end{array}\mathrm{or}\{\begin{array}{c}Tr>0\\ De<0\end{array}$$

(5)

In Equation (4), Tr refers to the trace of the Jacobian matrix (Equation (6)), De stands for determinant value of the matrix (Equation (7)).

$$Tr=\frac{(1-2a){(q+a)}^2-2qfb}{{(q+a)}^2\epsilon }-1$$

(6)

$$De=\frac{1}{\epsilon }(\frac{2qf{b}^{*}-(1-2a^{*}){(q+a^{*})}^2}{{(q+a^{*})}^2}-\frac{(q-a^{*})f}{(q+a^{*})})$$

(7)

There are three parameters here, ε, f, q, where q is only related to the chemical reaction kinetic constant, and the chemical reaction kinetic constant is only related to the temperature. Under the experimental conditions, the temperature is assumed to be constant, so the change of q is not considered and determined q = 0.0008. By definition, ε is a number that is always greater than 0. f is an adjustable parameter ranging from 0 to 3 [19,20]. For the value of De, whether it is greater than 0 depends on the value of f according to Equation (7) as $q$ is a constant and $\epsilon$ is large than 0. 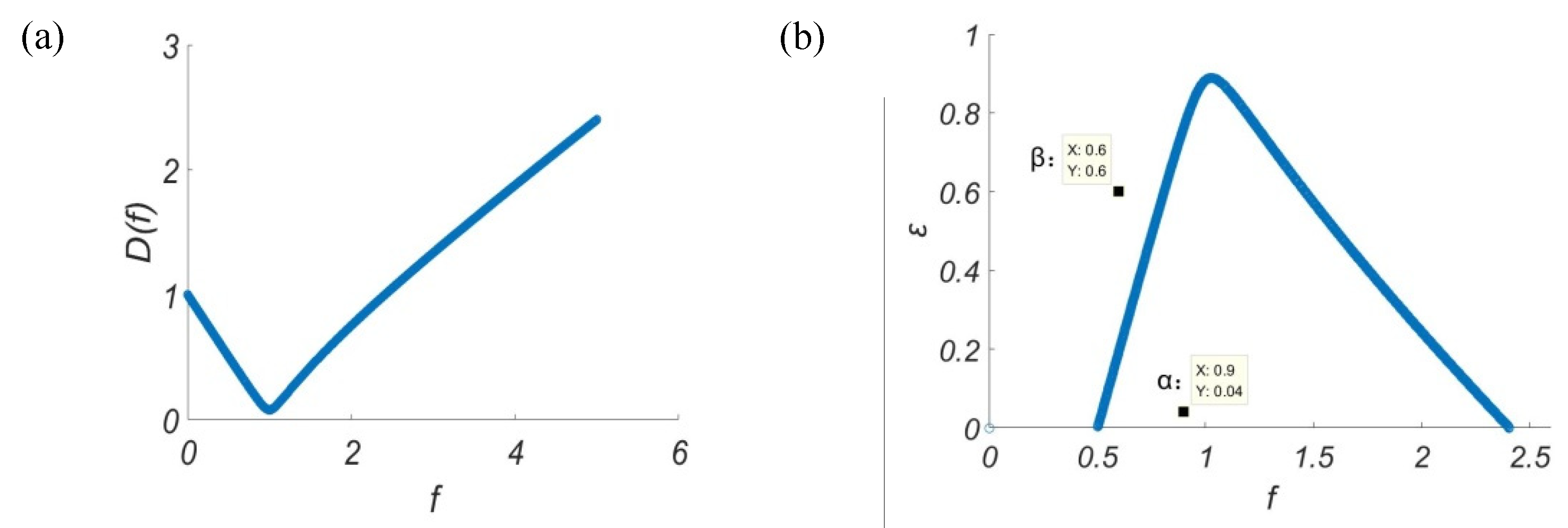Considering De as a function $\mathrm{D}(\mathrm{f})$ about f, by MATLAB plotting in Figure 1a, it is clear that De is always greater than 0 in the range of f values. Therefore, whether the real part of the eigenvalue of the Jacobian matrix is negative depends on the value of Tr. If Tr equal to 0, then the real part of the eigenvalue of the Jacobian matrix is 0, so the critical value relationship between ε and f can be obtained, as shown in Figure 1b.

In Figure 1b, the range of values of ε and f is divided into two parts by the line of their critical values. Above the blue line, the real part of the eigenvalue is positive, and below this line, the real part of the eigenvalue is negative. In this way, the range of parameters that can cause the model to oscillate can be obtained, that is, all corresponding ε and f values in the range enclosed by this line and the x axis. Figure 2 offers a demonstration of the proposed oscillatory criterion: when a point below the blue line (α( f = 0.9, ε = 0.04 )) is selected, oscillatory trajectories can be obtained as shown in Figure 2a, where as a point above the blue line (β( f = 0.6, ε = 0.6 )) is selected, no oscillations will emerge, as shown in Figure 2b. This validates the parameter range obtained previously for oscillation.

2.2. Diffusion Driven Instabilities: Generation of Chemical-Waves in Space-Time

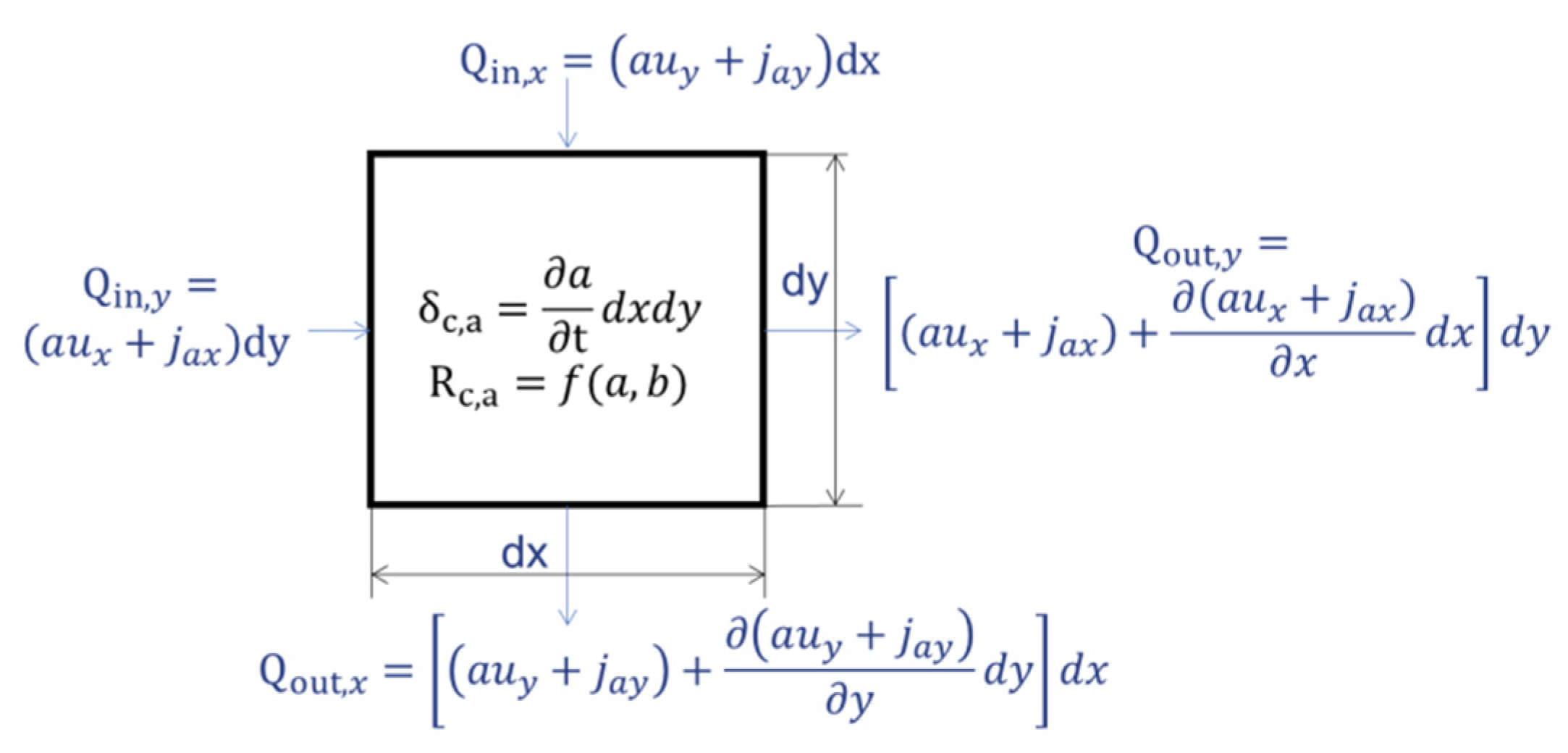
For the reactive-diffusion system, mass balance model can be built through analysis of a dot. Taking component ‘a’ as an example, the mass change of dot is shown in Figure 3.

According to Figure 3, Equation (8) can be obtained as,

$$\frac{\partial (a{u}_x)}{\partial x}+\frac{\partial j_{ax}}{\partial x}+\frac{\partial (a{u}_y)}{\partial y}+\frac{\partial j_{ay}}{\partial y}+\frac{\partial a}{\partial t}-f(a,b)=0$$

(8)

According to Fick’s law (Equation (9), i stands for direction (x, y, z)) and continuity equation of incompressible fluid (Equation (10)); Equation (8) is sorted out, and Equation (11) is obtained.

$$j_{ai}=-D_a\frac{\partial a}{\partial i}$$

(9)

$$\frac{\partial u_x}{\partial x}+\frac{\partial u_y}{\partial y}=0$$

(10)

$$\frac{\partial a}{\partial t}+u_x\frac{\partial a}{\partial x}+u_y\frac{\partial a}{\partial x}=D_a\frac{{\partial }^{2}a}{\partial x^2}+\frac{{\partial }^{2}a}{\partial y^2}+f(a,b)$$

(11)

Since there is no diffusion process of main flow fluid molecules in this process, $u_x$ and $u_y$ are equal to zero. If this relationship is substituted into the Equation (11), the reaction diffusion equation of substance ‘a’ can be represented. Similarly, the reaction diffusion equation of substance ‘b’ can be obtained. Two-variable reaction-diffusion equations for B-Z reaction is shown in Equation (12), where ${\nabla }^{2}a$ and ${\nabla }^{2}b$ represent Laplace operators.

$$\{\begin{array}{c}\frac{\partial a}{\partial t}=D_a\frac{{\partial }^{2}a}{\partial x^2}+\frac{{\partial }^{2}a}{\partial y^2}+f(a,b)=D_a{\nabla }^{2}a+f(a,b)\hfill \\ \frac{\partial b}{\partial t}=D_b\frac{{\partial }^{2}b}{\partial x^2}+\frac{{\partial }^{2}b}{\partial y^2}+g(a,b)=D_b{\nabla }^{2}b+g(a,b)\hfill \end{array}$$

(12)

The equation can be solved by FD method. Here, a nine-point FD method is introduced as follows.

2.3. Solving PDEs by FD Method to Simulate B-Z Reaction

PDE is a common method for modeling process systems. It realizes the simulation of the process system through mathematical description and solving. After so many years of application and improvement, this is one of the most familiar modeling methods for researchers.

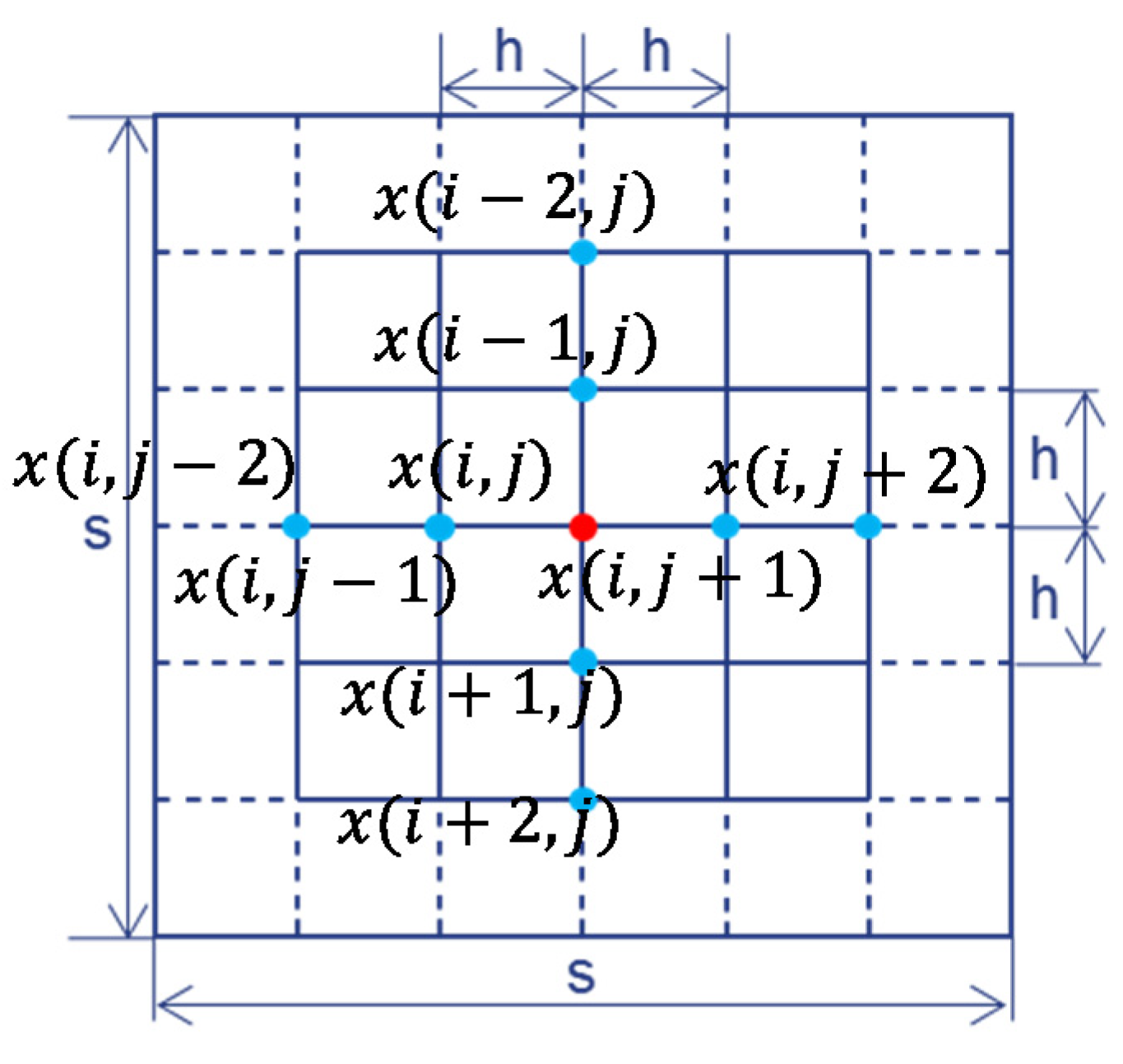
The Laplace operator part and time part in Equation (12) are discretized into two algebraic equations, Equations (13) and (14); u stands for a or b, by a nine-point FD method (Figure 4) and an ordinary FD method, respectively. This nine-point FD discrete method was first proposed by Zhao et al. to increase the discrete precision by increasing the cutting points [35]. Suppose the space step is h and the time step (∆t) is θ. Substituting Equations (13) and (14) into Equation (12) can transform Equation (12) into Equation (15).

$$\begin{array}{c}{(\frac{{\partial }^{2}u}{\partial i^2}+\frac{{\partial }^{2}u}{\partial j^2})}_{(4)}=\frac{1}{12h^2}(-u_{i-2,j}+16u_{i-1,j}-60u_{i,j}+16u_{i+1,j}-u_{i+2,j}-u_{i,j-2}+\\ 16u_{i,j-1}+16u_{i,j+1}-u_{i,j+2}+\frac{h^4}{45}(\frac{{\partial }^5{u}_{\xi ,j}}{\partial i^5}+\frac{{\partial }^5{u}_{i,\zeta }}{\partial j^5}),i-h<\xi <i+h,j-h<\zeta <j+h\end{array}$$

(13)

$${(\frac{\partial u}{\partial t})}_{(4)}=\frac{u^{t+1}-u^t}{∆t}+\frac{\theta }{2}\frac{{\partial }^2{u}^{\delta }}{\partial t^2}, t<\delta <t+\theta$$

(14)

$$\{\begin{array}{c}a(x_i,y_i){}^{t+1}=a(x_i,y_i){}^t+\theta [D_a\frac{1}{12h^2}(-a{(x_{i+2},y_i)}^t+16a{(x_{i+1},y_i)}^t\\ -30a{(x_i,y_i)}^t+16a{(x_{i-1},y_i)}^t-a{(x_{i-2},y_i)}^t-a{(x_i,y_{i+2})}^t+16a{(x_i,y_{i+1})}^t\\ -30a{(x_i,y_i)}^t+16a{(x_i,y_{i-1})}^t-a{(x_i,y_{i-2})}^t+{\epsilon }^{-1}f(a{(x_i,y_i)}^t,b{(x_i,y_i)}^t)\\ b(x_i,y_i){}^{t+1}=b(x_i,y_i){}^t+\theta [D_b\frac{1}{12h^2}(-b{(x_{i+2},y_i)}^t+16b{(x_{i+1},y_i)}^t\\ -30b{(x_i,y_i)}^t+16b{(x_{i-1},y_i)}^t-b{(x_{i-2},y_i)}^t-b{(x_i,y_{i+2})}^t+16b{(x_i,y_{i+1})}^t\\ -30b{(x_i,y_i)}^t+16b{(x_i,y_{i-1})}^t-b{(x_i,y_{i-2})}^t+g(a{(x_i,y_i)}^t,b{(x_i,y_i)}^t)]\end{array}$$

(15)

The truncation error, $L_{i,j}$, of Equation (15) is shown in Equation (16). When the value of $\theta$ and h approach 0, $L_{i,j}$ also approaches 0, so Equation (15) is convergent [36]. This means that the difference scheme is conditionally stable. When the value of $\frac{\theta D}{h^2}$ is less than 3, this difference scheme (Equation (15)) is stable. See Reference [36] for detailed difference format stability and convergence analysis procedures. These results prove that it is feasible to use this difference scheme to simulate the B-Z reaction.

$$L_{i,j}=-\frac{\theta }{2}\frac{{\partial }^2{u}^t}{\partial t^2}+\frac{h^{4}D\theta }{45}(\frac{{\partial }^5{u}_{\xi ,j}}{\partial i^5}+\frac{{\partial }^5{u}_{i,\zeta }}{\partial j^5})$$

(16)

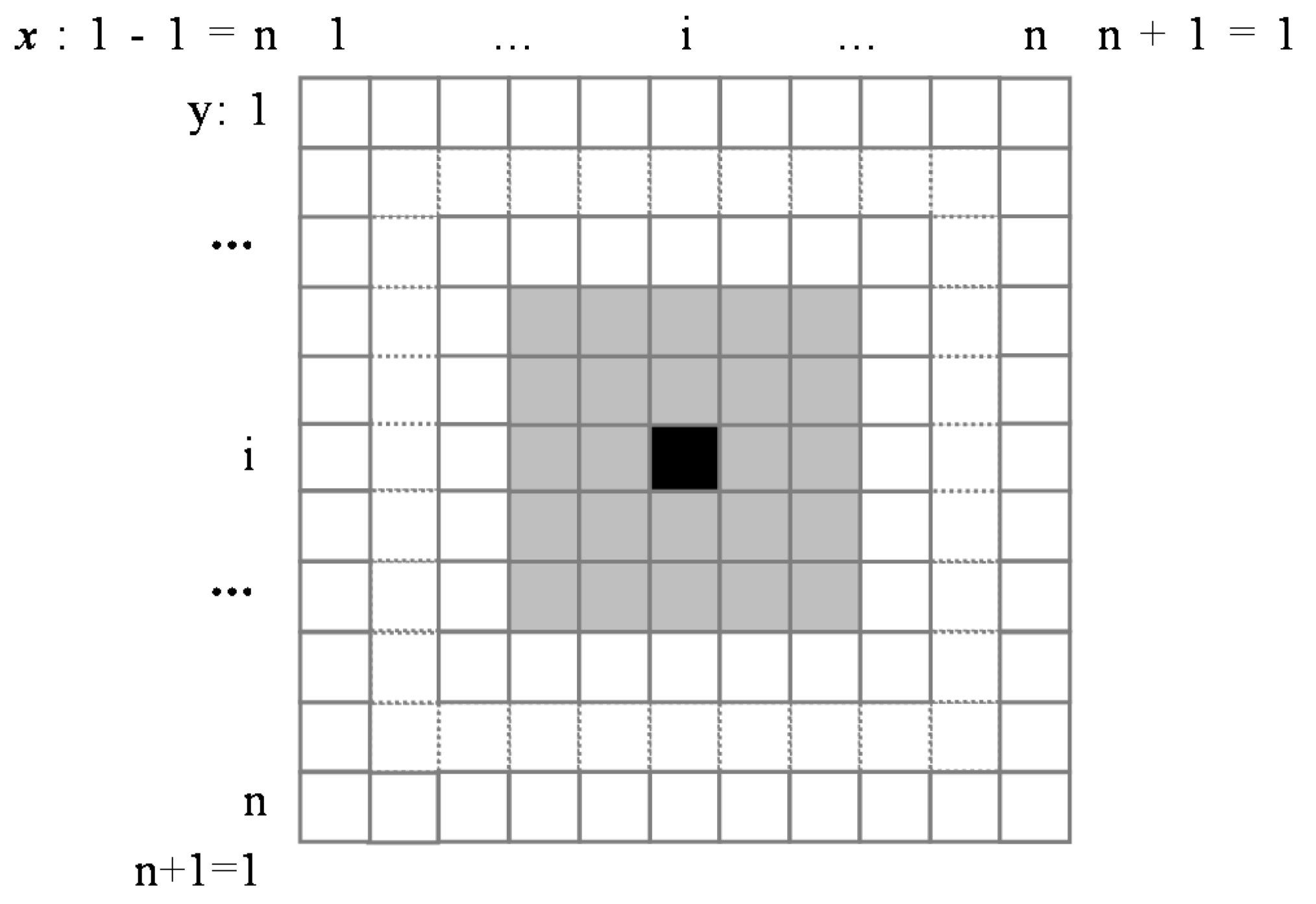
The boundary condition is set to the cyclic boundary condition, which means when $x_i$ or $y_i$ is out of the boundary, it reappears on the other side (as shown in Figure 5, although Figure 5 is about the neighborhood model and boundary conditions of CA, the boundary conditions of the two methods are the same). In this way, the B-Z reaction can be simulated by PDE modeling strategy.

3. The B-Z Reaction System: CA Modeling Strategy for the Simulation of Chemical-Wave

To further explore the mechanism of chemical wave formation in the B-Z reaction process, another method, CA, is used to simulate it. In this method, Gerhardt’s CA model is combined with Weimar’s ideas, i.e. adding MASK to the local rule to represent the effect of distance on diffusion. The specific simulation process is shown in below.

3.1. CA modeling Strategy to Simulation B-Z Reaction

A CA algorithm consists of four parts [22,37]: cells, cellular space, neighbor, and local rule. Cells are the most basic component of CA. Cellular space is a set of spatial grids in which cells are distributed. There is information exchange between neighbor grids according to certain local rule, which is employed to determine the dynamic function of the state of a cell at the next moment according to the current state of the cell and its neighbor state.

As mentioned in Section 1, the process simulation by CA is conducted through changing the state of the cell. For the B-Z reaction-diffusion system, the change of cell state is affected by both reaction and diffusion. The reaction is represented by the state change of the cell itself, and the diffusion is represented by local rules. For a system in an excitable medium, a cell needs three states to simulate the chemical waves according to diffusion theory (chemical waves can propagate not only in a stationary medium but also in a partially restored medium) [24,25], the excited state, the recovered state, and the stationary state. Those states are controlled by two variables, the excitation variable ‘a’ and the recovery variable ‘b’. Without being affected by local rules, the state change rules of a specific cell should be obtained based on phase diagram analysis of Tyson model. More analysis can be found in Reference [24]. The specific change of cell state can be shown below.

$$\{\begin{array}{c} if a_t=0 , then b_{t+1}=max\left\{b_t-g_{down},b_{min}\right\}\hfill \\ if a_t=1 , then b_{t+1}=min\left\{b_t+g_{up},b_{max}\right\}\hfill \\ if a_t=1 , then b_{t+1}=min\left\{b_t+g_{up},b_{max}\right\}\hfill \end{array}$$

To facilitate the expression and display on the computer, two-dimensional square cells are selected to form the cellular space, and the boundary is periodic. This means that i, j can be used to locate each cell in the cellular space, for example, i = 1 and j = 1 represent a cell in the first row and first column in the cellular space. When i + 1 exceeds the range of cellular space, there is i + 1 = 1. The neighbor rule is extended Moor type [27] as shown in Figure 5. It means the cells within the radius r of a center of cell belong to its neighbors, and in this model, there is r = 2.

The local rule of this work is a bit complicated, and it is also the main difference from Gerhardt’s CA model [24,25], which will be explained in the next section.

3.2. Using MASK to Increase Spatial Isotropy

The local rule of CA algorithm here reflects that diffusion is affected by distance [37], and the isotropy is improved by combining the ideas of Fast et al. and Weimar et al [26,27]. The relationship between diffusion and distance can be described by an exponential equation [26]. Then this equation is discretized and replaced by a matrix MASK [27,36,37] (Equation (17)).

$$\mathit{MASK}=\left[\begin{array}{cc}\begin{array}{cc}4& 5\\ 5& 7\end{array}& \begin{array}{ccc}6& 5& 4\\ 8& 7& 5\end{array}\\ \begin{array}{cc}6& 8\\ 5& 7\\ 4& 5\end{array}& \begin{array}{ccc}9& 8& 6\\ 8& 7& 5\\ 6& 5& 4\end{array}\end{array}\right]$$

(17)

For a stationary cell, the information that it receives from its neighbors is represented by an excitation value $E_{(x,y)}$. It is obtained through a two-step calculation, as shown in Equation (18), where the * sign represents the multiplication of the elements at the corresponding positions of the two $\mathrm{n}\times \mathrm{n}$ matrices, and its result is still an $\mathrm{n}\times \mathrm{n}$ matrix. The first step is to multiply each element in the neighbor’s state matrix by another element at the corresponding position in the MASK to form a new matrix. The second step is to sum each element in the newly obtained matrix to get $E_{(x,y)}$. When ${\mathrm{E}}_{(\mathrm{x},\mathrm{y})}$ exceeds the excitation threshold ($k_{exci}$), it is considered that the state of this cell becomes excited by sufficient stimulation of information from neighbors. ${\mathrm{k}}_{\mathrm{exci}}$ should be related to the state of the cell itself [22,23], which is specifically calculated by Equation (19).

$$E_{(x,y)}={\displaystyle \sum }_{i=1}^5{\displaystyle \sum }_{j=1}^5(MASK*N)$$

(18)

$$k_{exci}=k_{exci}(b_{min})+(k_{exci}(b_{exci})-k_{exci}(b_{min}))\frac{b-b_{min}}{b_{exci}-b_{min}}$$

(19)

In Equation (19), $k_{exci}(b_{min})$ is determined by the actual reaction [25]. $k_{exci}{b}_{exci}$ can be calculated by Equation (20).

$$k_{exci}{b}_{exci}={\displaystyle \sum }_{i=1}^5{\displaystyle \sum }_{j=1}^5(MASK*\left[\begin{array}{cc}\begin{array}{cc}1& 1\\ 1& 1\end{array}& \begin{array}{ccc}1& 1& 1\\ 1& 1& 1\end{array}\\ \begin{array}{cc}0& 0\\ 0& 0\\ 0& 0\end{array}& \begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\end{array}\right])$$

(20)

Similarly, the information from neighbors to the central excited state cell is integrated by a recovery value $R_{(x,y)}$. It can be obtained by Equation (21) and corresponds to a recovery threshold ($k_{reco}$) that can be calculated by Equation (23). In Equation (23), $k_{reco}(b_{max})$ is determined by the actual reaction. $k_{reco}{b}_{reco}$ can be calculated by Equation (24).

$$R={\displaystyle \sum }_{i=1}^5{\displaystyle \sum }_{j=1}^5(MASK*I)-E$$

(21)

$$I=\left[\begin{array}{cc}\begin{array}{cc}1& 1\\ 1& 1\end{array}& \begin{array}{ccc}1& 1& 1\\ 1& 1& 1\end{array}\\ \begin{array}{cc}1& 1\\ 1& 1\\ 1& 1\end{array}& \begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}\end{array}\right]$$

(22)

$$k_{reco}=K_{reco}(b_{reco})-(k_{reco}(b_{reco})-k_{reco}(b_{max}))\frac{b-b_{reco}}{b_{reco}-b_{max}}$$

(23)

$$k_{reco}{b}_{reco}={\displaystyle \sum }_{i=1}^5{\displaystyle \sum }_{j=1}^5(MASK*\left[\begin{array}{cc}\begin{array}{cc}0& 0\\ 0& 0\end{array}& \begin{array}{ccc}0& 0& 0\\ 0& 0& 0\end{array}\\ \begin{array}{cc}1& 1\\ 1& 1\\ 1& 1\end{array}& \begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}\end{array}\right])$$

(24)

4. Simulation Results of the Chemical-Wave Patterns

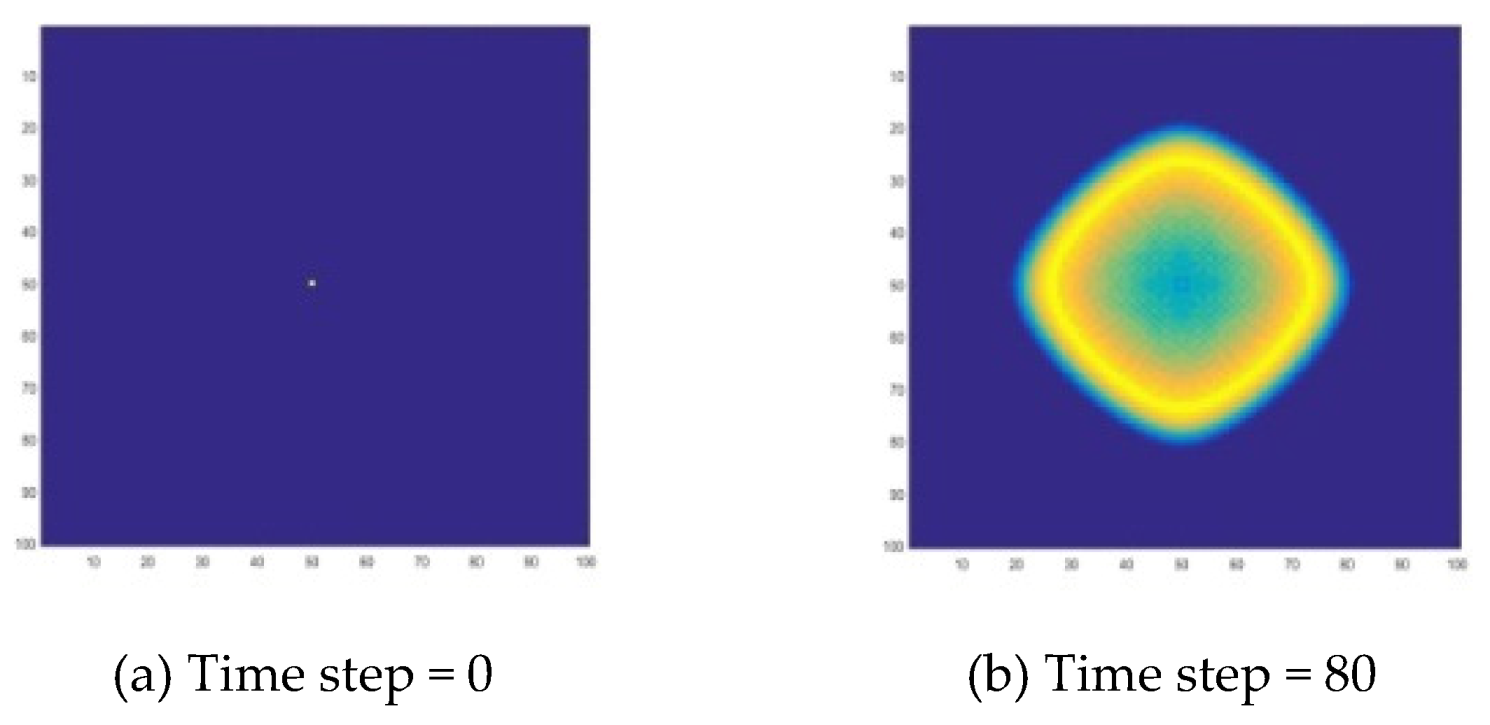
Two methods are employed to simulate the B-Z reaction Oregonator model by MATLAB. 100 × 100 nodes are considered in MATLAB. The target waves and spiral waves formed by the B-Z reaction are simulated on a two-dimensional plane and are detailed in following.

4.1. Target Waves in B-Z Reaction

4.1.1. FD Method to Solve PDE Model

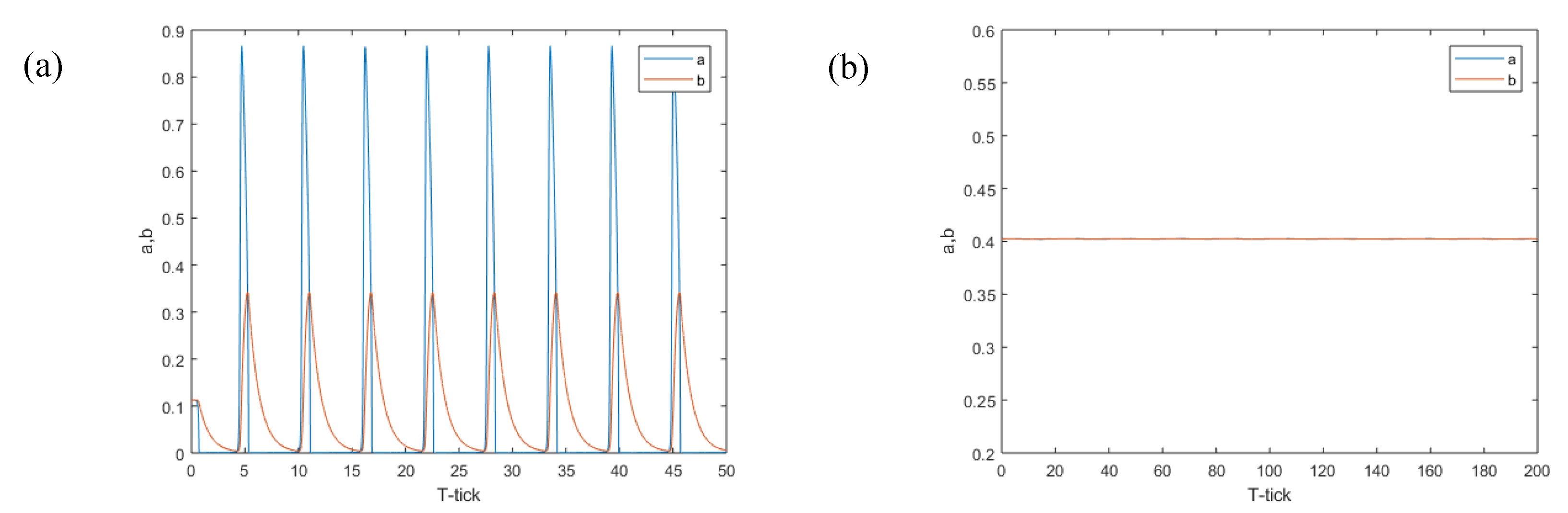
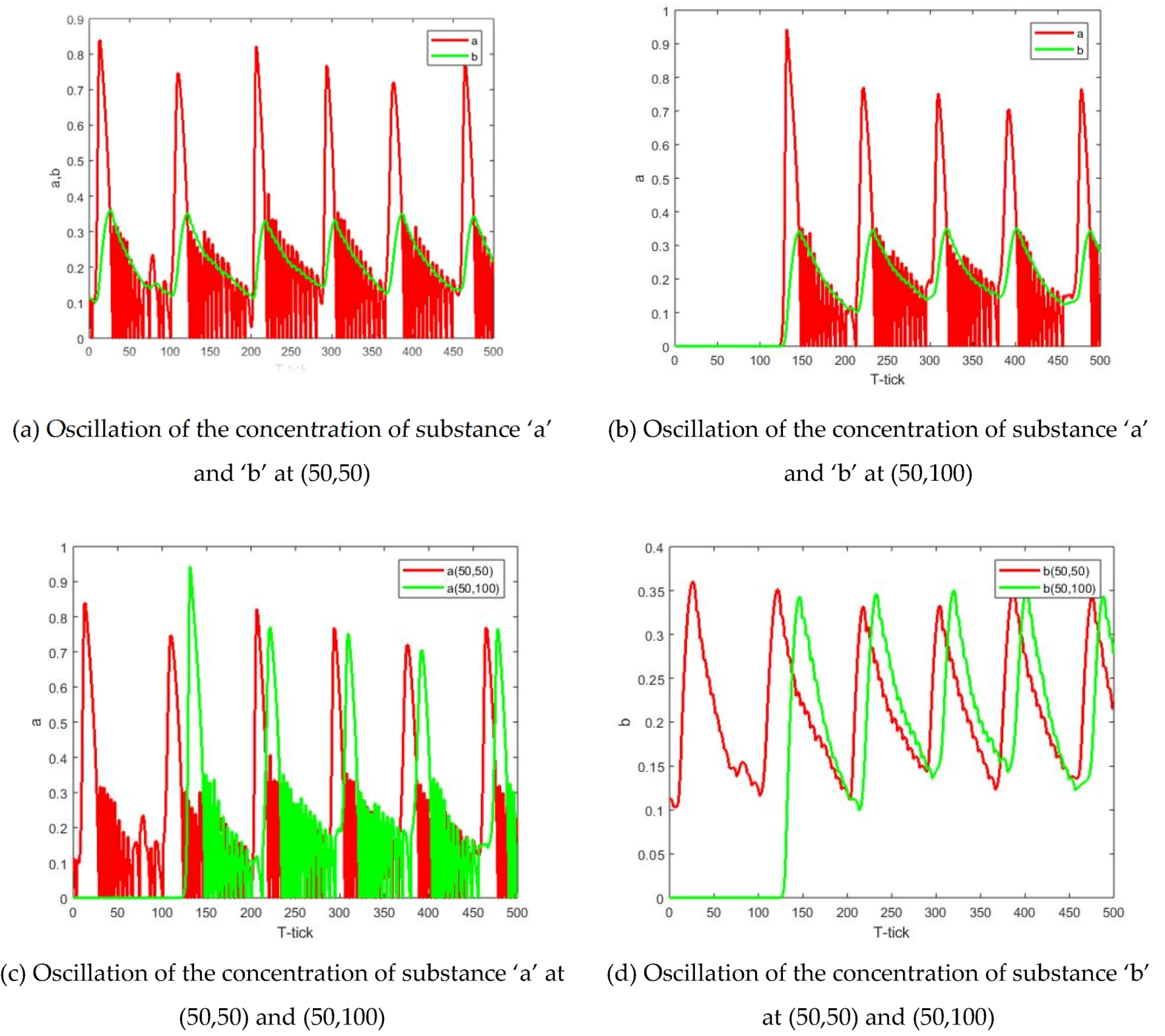
The initial value of ‘a’ and ‘b’ concentration at all nodes is 0, except for the initial value of the middle node (50, 50). Its value is a random number that serves as a starting point for chemical wave generation. The parameters are selected within the oscillation range calculated in the Section 2, which are α: $\theta =0.04$, $D_a=2$, $D_b=0$, $h=1$, $\epsilon =0.04$, $f=0.9$, $q=0.0008$. The simulation results are shown in Figure 6. The concentration changes at the two points of the reaction zone (50, 50) and (50, 100) are shown in Figure 7. 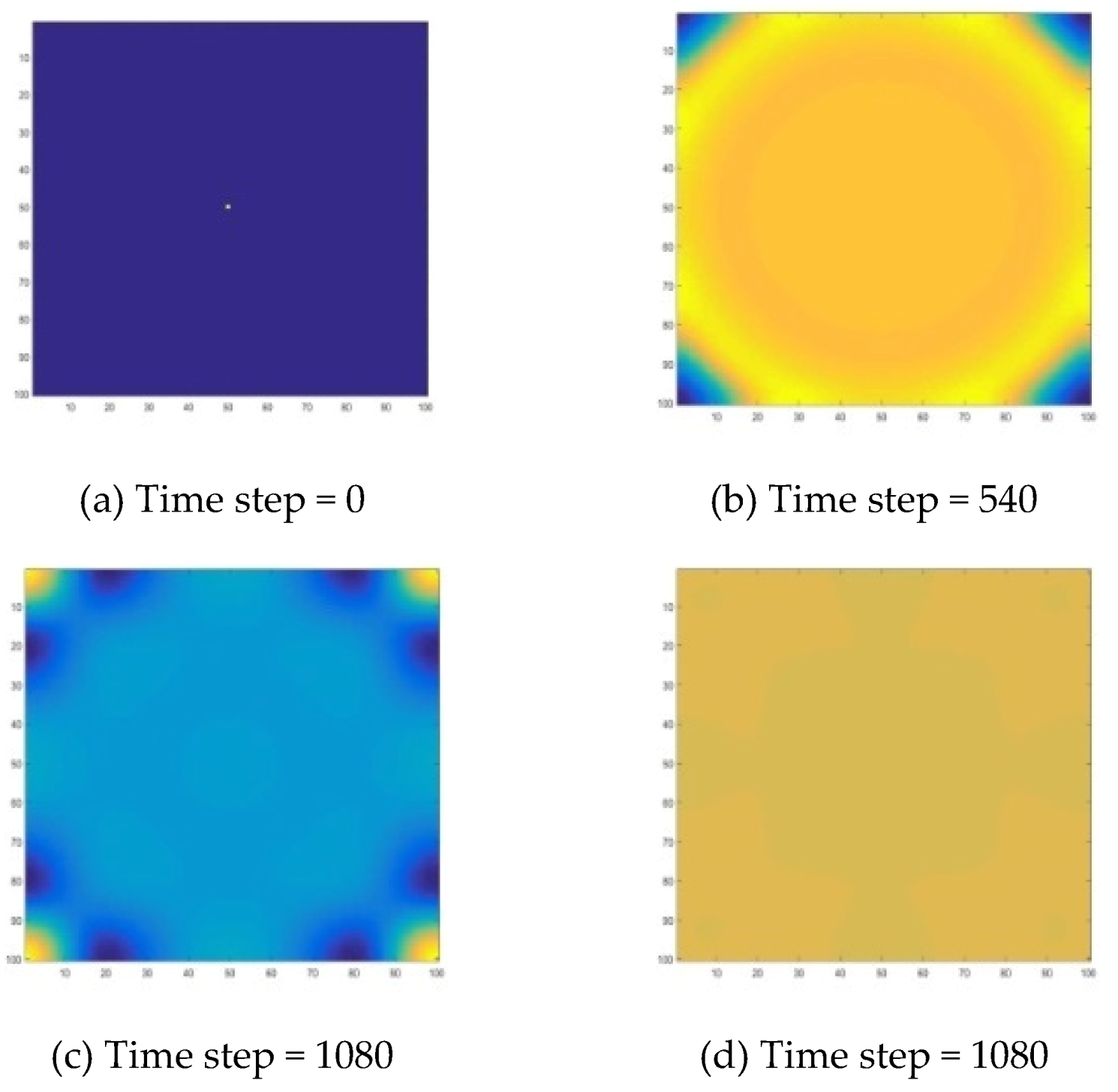In Figure 6, the target wave of the B-Z reaction can be well presented, and it is formed from the center in a series of rings of diffusion.

When the parameters are selected outside the oscillation range calculated in the Section 2, i.e. the parameters are β: $\mathsf{\theta }=0.04$, ${\mathrm{D}}_{\mathrm{a}}=2$, ${\mathrm{D}}_{\mathrm{b}}=0$, $\mathrm{h}=1$, $\mathsf{\epsilon }=0.6$, $\mathrm{f}=0.6$, $\mathrm{q}=0.0008$. The simulation results are shown in Figure 8. The concentrations of ‘a’ and ‘b’ all became 0.4024 in the whole reaction domain, and this concentration is exactly the equilibrium point concentration.

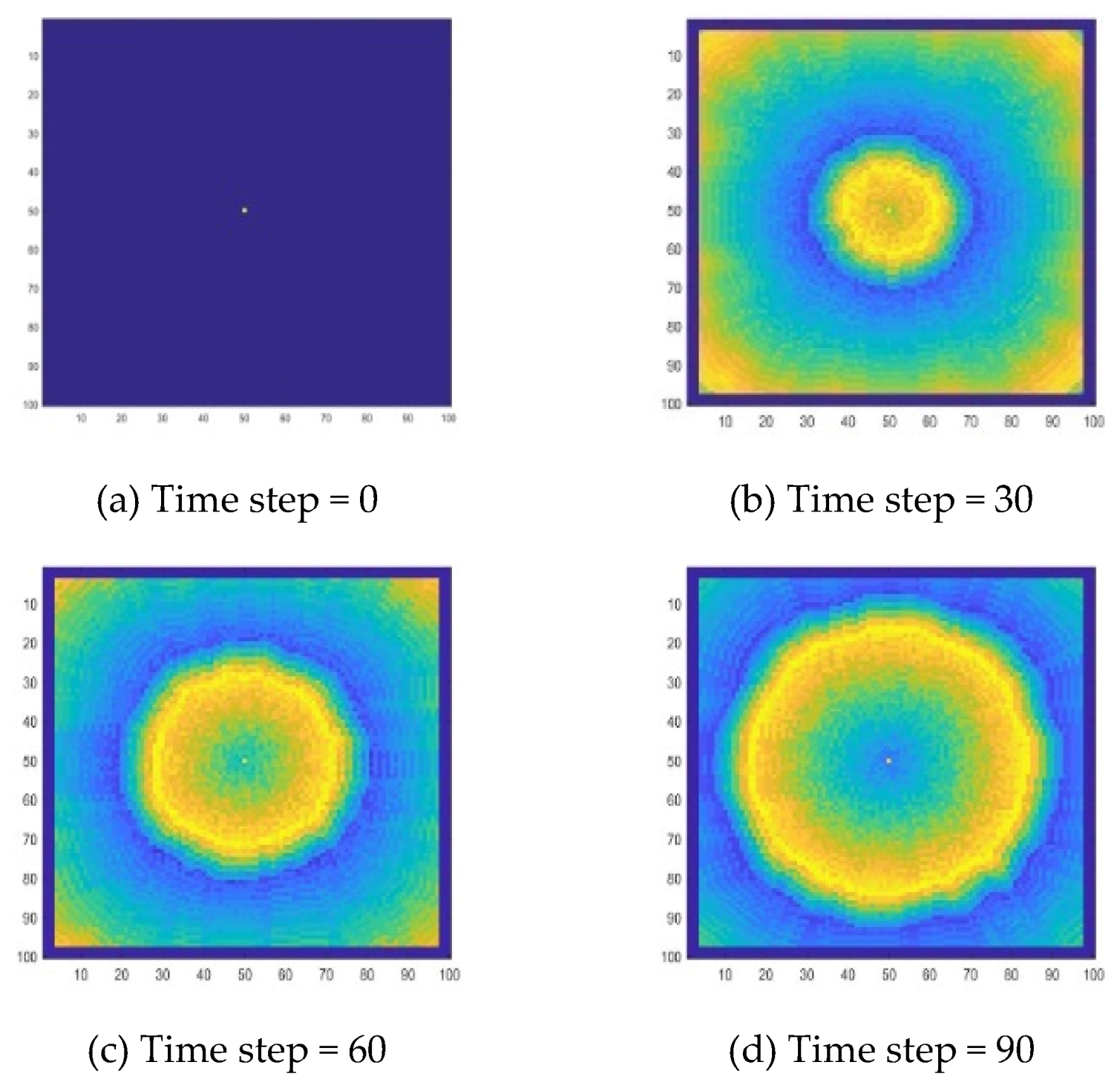
4.1.2. Add MASK to Improve CA Model

The initial value selection is the same as the PDE method. The remaining parameters refer to Reference [25]. There are ${\mathrm{g}}_{\mathrm{up}}=13$, ${\mathrm{g}}_{\mathrm{down}}=3$, ${\mathrm{K}}_{\mathrm{exci}}({\mathrm{b}}_{\min })=3$, ${\mathrm{k}}_{\mathrm{reco}}({\mathrm{b}}_{\max })=9$, ${\mathrm{b}}_{\mathrm{exci}}=60$, ${\mathrm{b}}_{\mathrm{reco}}=93$. The simulation results are shown in Figure 9. The target wave of the B-Z reaction also can be well simulated. It can be seen that the target wave simulated by this method is closer to a circle. This shows that it has better spatial isotropy.

4.2. Spiral Waves in B-Z Reaction

4.2.1. FD Method to Solve PDE Model

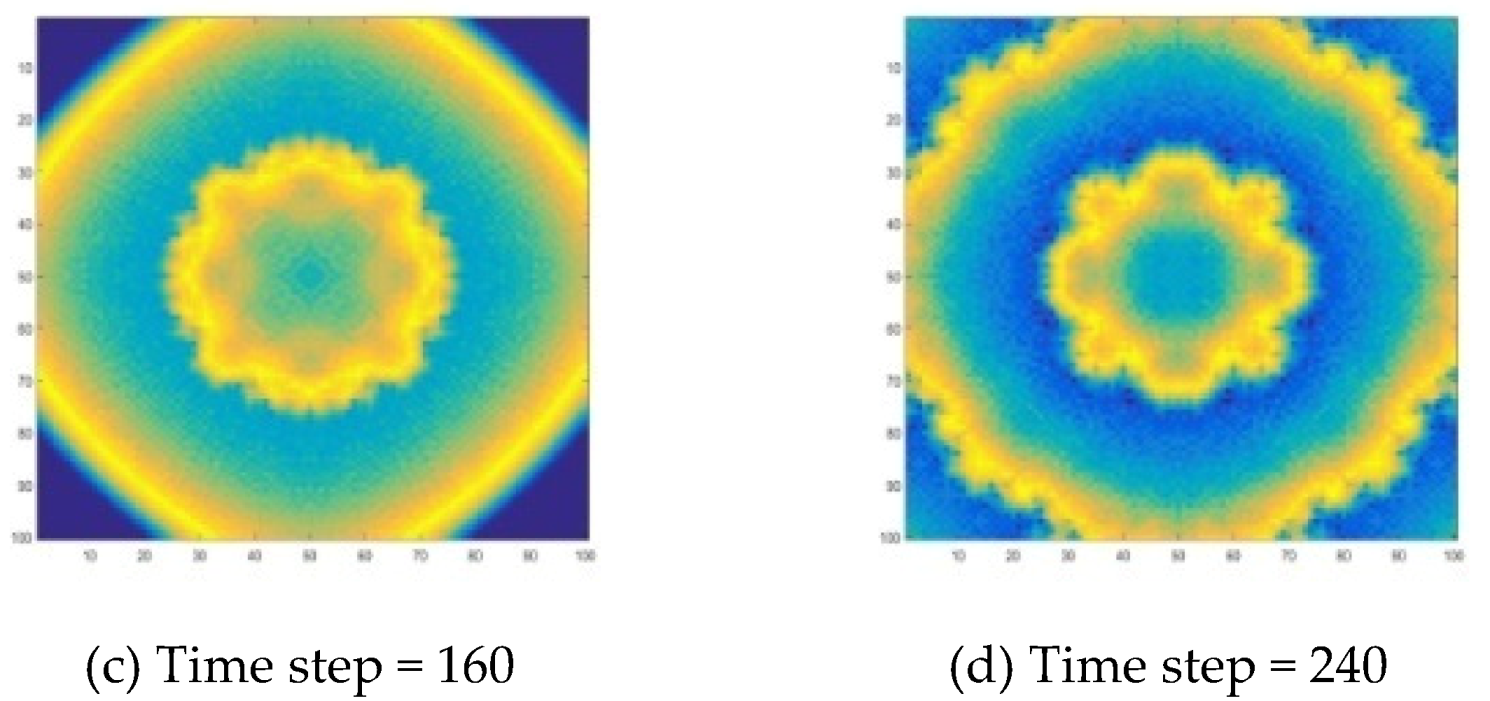
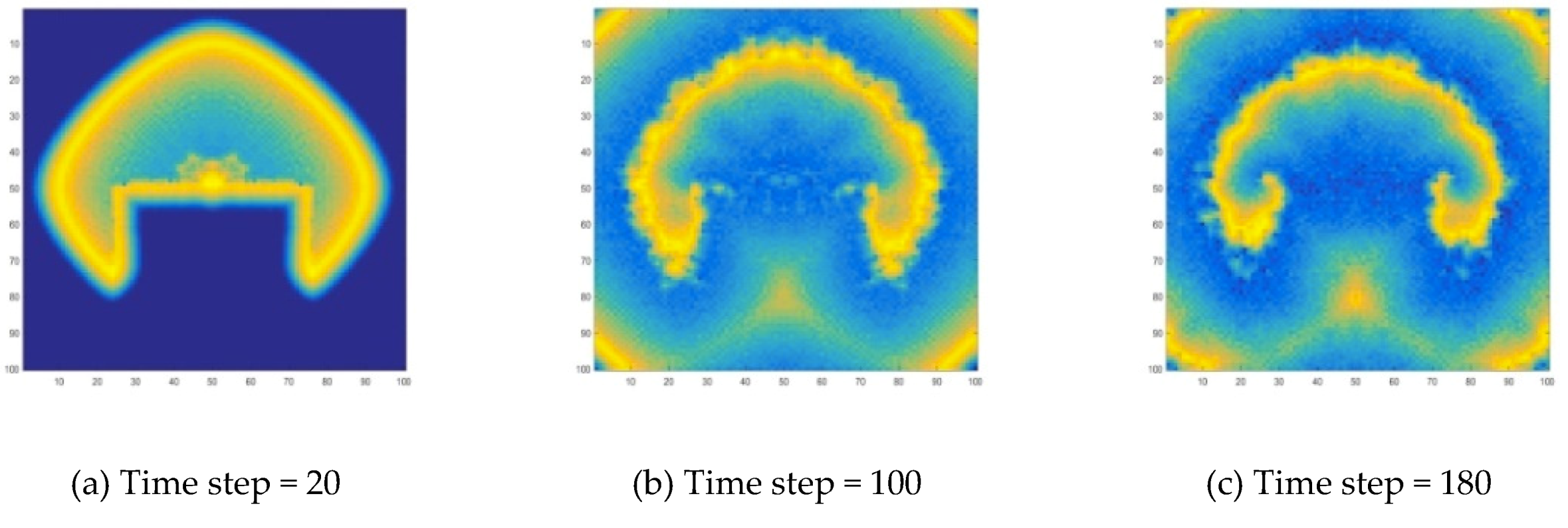
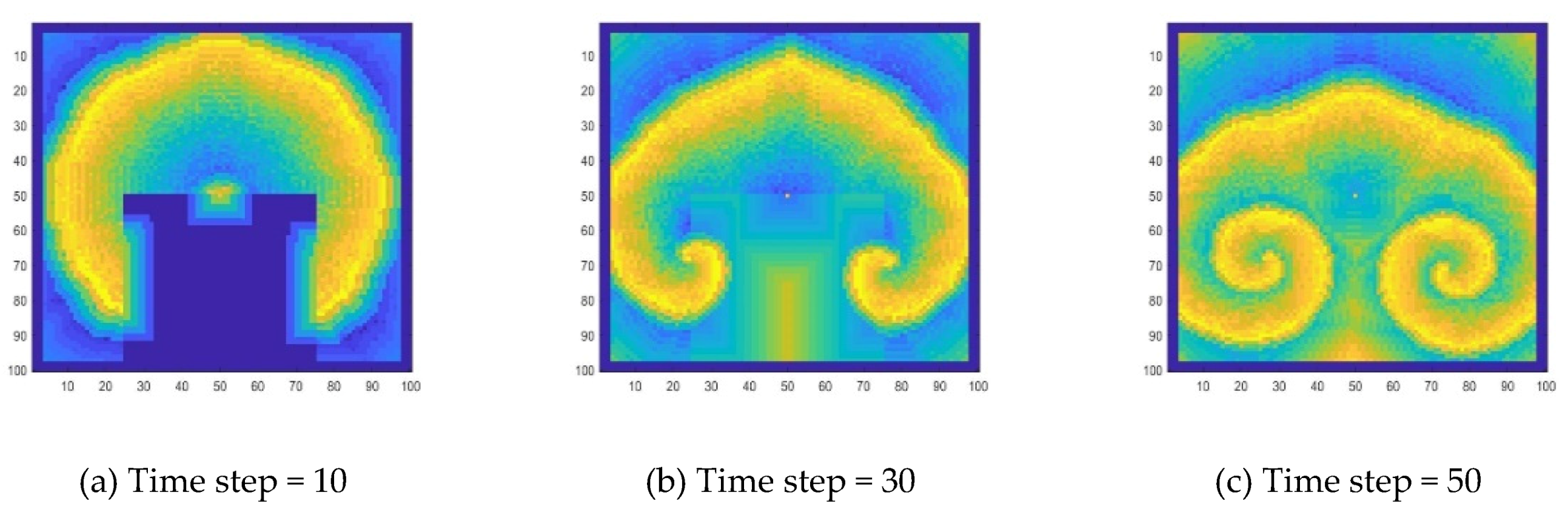
During the development of target wave, its propagation is interrupted by adding a disturbance. Here, the specific method is to make the concentration values of a part of the wave become zero, and the target wave will develop into a spiral wave, as shown in Figure 10.

In order to be clearer regarding how the target wave is transformed into a spiral wave, the concentration changes of ‘b’ at the two points, (80, 25) and (70, 20) are shown in Figure 11. These two positions are (80, 25), the end point of the wave after interference, and (70, 20), the adjacent point of (80, 25) on the same wave band when the disturbance comes.

In Figure 11, the concentration change processes of the target wave and the spiral wave at a certain position are compared. Comparing Figure 11a,b, when there is no interference (target wave), the two concentration change lines coincide better, which means they are in the same wave band. After being disturbed (spiral wave), the two points of the concentration change line separated, indicating that the wave band has deviated. Comparing Figure 11c,d, it can be seen that the influence of the disturbance causes the peak of the concentration oscillation to be delayed, and the further away from the location of the disturbance, the smaller the delay.

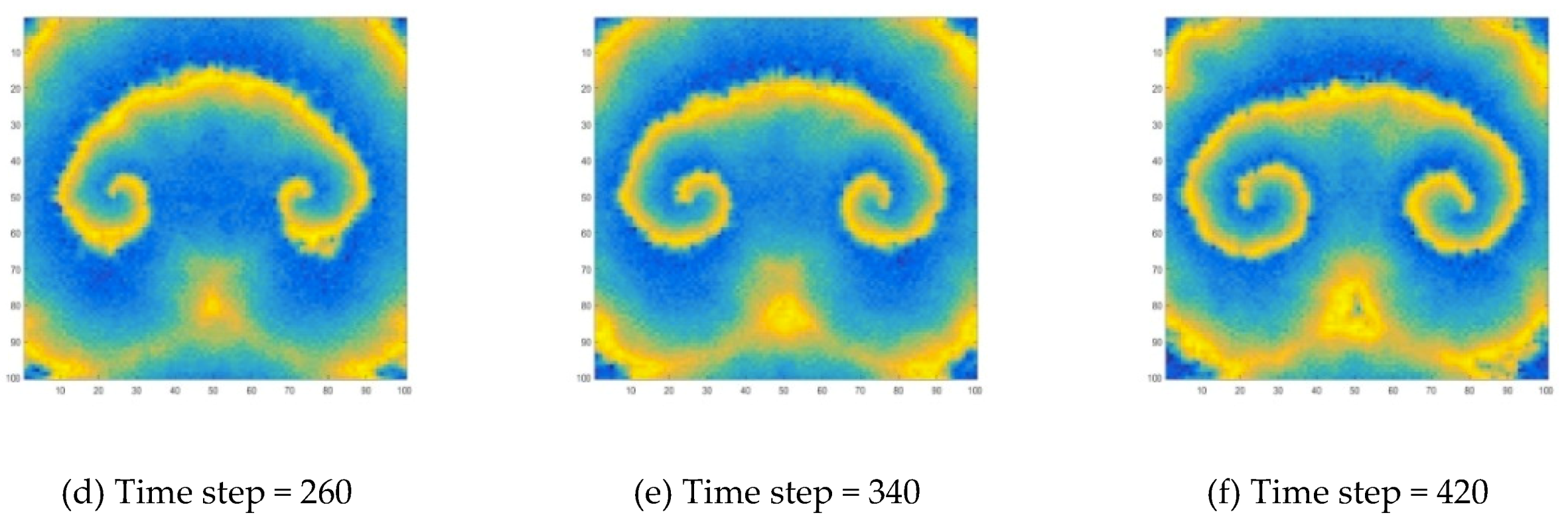
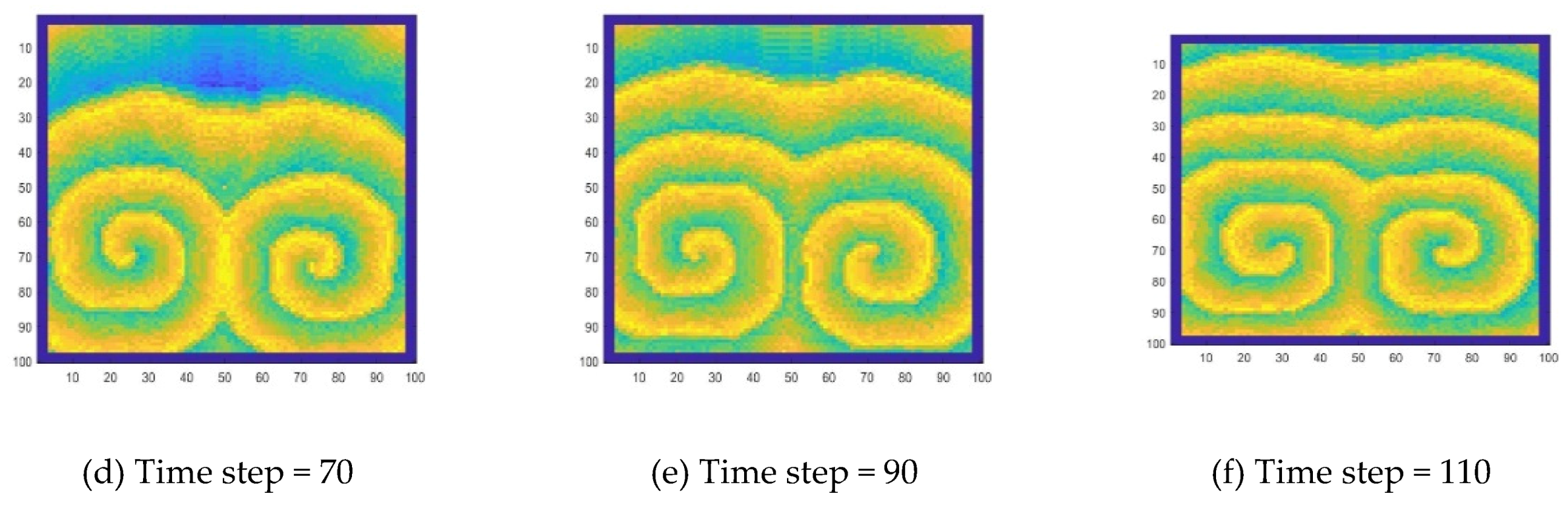
4.2.2. Add MASK to Improve CA Model

Similarly, the target wave simulated by CA is perturbed to obtain a spiral wave. The specific method is to make the excited cells in a certain range into a stationary state. The spiral wave of the B-Z reaction can be well simulated, as shown in Figure 12.

4.3. Result and Discussion

Two methods are employed to simulate the formation of chemical waves in B-Z reactions. What these two methods have in common is that they have the same function. They can be used to demonstrate the characteristics of complex systems, such as self-organization, and to simulate chemical waves, i.e., target waves and spiral waves in B-Z reactions. From the common points, the formation mechanism of the target wave and the spiral wave can be observed. The oscillating reaction system is affected by diffusion, forcing the system to produce regular changing patterns, i.e., chemical waves.

Specifically, for a target wave as shown in Figure 6 and Figure 7 and Figure 9, substances at the center point diffuse to the surrounding area, forming a circle and growing up. Due to the diffusion and reaction, the concentration in the center decreases, so that the circle disappears from the center, and the wave forms a ring-like propagation. When the concentration in the center drops to a certain level, the concentration oscillation will cause the concentration to rise again, thereby generating new waves. A spiral wave as shown in Figure 10 and Figure 12 is generated because a wave is disturbed during the propagation process. In this work, this disturbance is manifested by the disappearance of wave segment. At the end of the wave near the vanishing part, the wave velocity is lower. As the wave moves forward, the position of the endpoint lags. This lag causes the target wave to bend near the endpoint, and a target wave gradually becomes a spiral wave, as shown in Figure 11.

At the same time, there are also certain differences between them. The most obvious is that the simulation strategies of these two methods are developed from different angles. The FD method or other numerical methods are used to solve the PDE, and the concentration at the next moment is obtained to simulate the propagation process of the chemical wave. This method is the most common way to simulate a process. It has high reliability, and all the information in the process can be simulated by it, but it costs a lot of time on calculation. Occasionally, the calculation fails due to mathematical problems, such as the instability of the difference format caused by error accumulation.

One important characteristic of CA is its capability to decompose the two coupled processes of reaction and diffusion into two parts: simple unit change and interaction between units. When it is applied to simulate chemical waves, the mathematical solution process in the PDE method is avoided, and the simulation results can be obtained by changing the state of cells according to a simple local rule. Therefore, the application of this method on simulation is characterized by fast calculation speed and low requirement for computer hardware, but concentration information of each position in the system cannot be specified. Compared with the former method, it is a method to improve simulation speed by compromising quantitative information.

In summary, it is hard to tell which method, CA or PDE, is more suitable for simulating complex-process systems. Each method has its own characteristics and can be used separately according to the needs of the phenomenon under study. Simulation using the CA method is suitable for qualitative research on process systems. In this way, one can get the general situation of the process. The use of the PDE method for simulation is suitable for quantitative studies of process systems. In this way, the specific concentration in the process can be obtained. At the same time, using these two simulation methods from different angle methods, on the one hand, can prove each other to explain the accuracy of the simulation results; on the other hand, the simulation results and the specific situation of the system can be quickly obtained.

5. Conclusions

As a study of complex systems, two different strategy methods were used to simulate the B-Z reaction, and the causes of chemical waves were discussed. Based on the results obtained in this work, one can conclude that different aspects and information are pursued by these two methods. Even though both methods are capable of simulating the formation of chemical wave patterns, PDE and its solution are more suitable for the investigation of quantitative information, and CA is more convenient for the study of overall system evolution, especially, the mechanism that causes formation of a chemical wave. It is concluded that the cells (or every dot) in the complex system exhibit self-oscillatory dynamics, leading to the pattern formation out of a homogeneous system. As the study on complex systems can be much diversified, the comparison provided here can be a reference for future study in this area.