On Parameter Stability Region of LADRC for Time-Delay Analysis with a Coupled Tank Application
Abstract
:1. Introduction
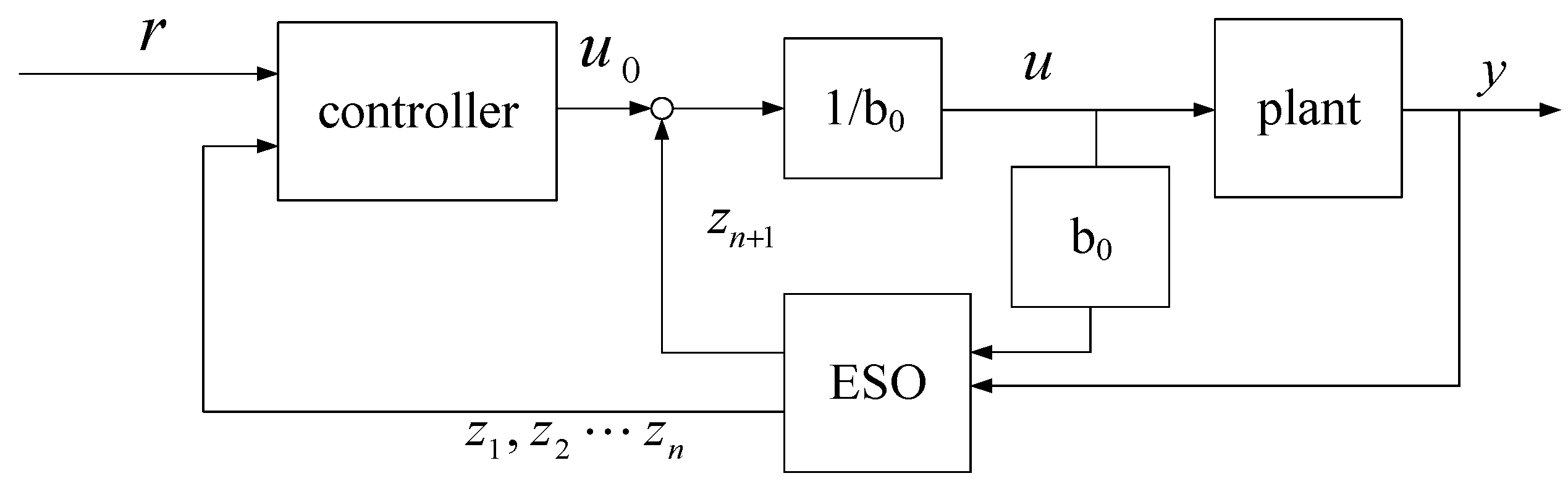
2. Linear Active Disturbance Rejection Control (LADRC)
3. Parameter Stability Region Determination of LADRC
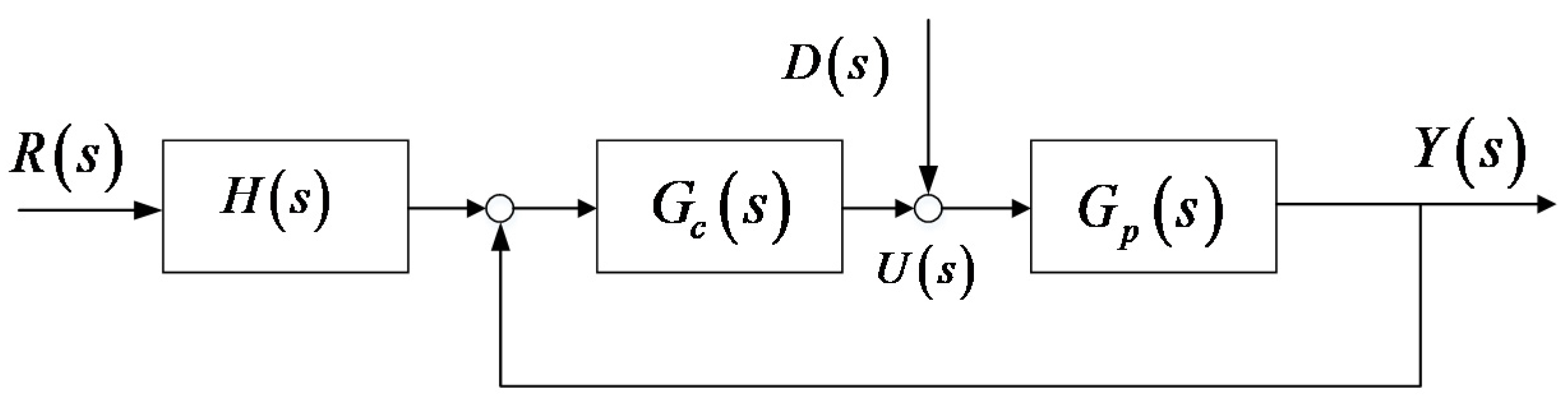
3.1. Principle of Dual-Locus Diagram Method
3.2. Parameter Stability Region Determination Method of LADRC
- (a)
- The steady-state gain , time constants and , and delay time are given explicitly.
- (b)
- The appropriate bandwidth ratio in the designed LADRC is given explicitly.
- (1)
- If the open-loop transfer function of the system has no poles in the right half plane and the Nyquist curve of and do not intersect, the system is stable.
- (2)
- If a positive real root satisfiesand the phase angle ofis larger than that ofat their intersection frequency, the closed-loop system is stable and the stability region of the controller bandwidthcan be calculated accurately as follows:where and are the phase angles of and , respectively.
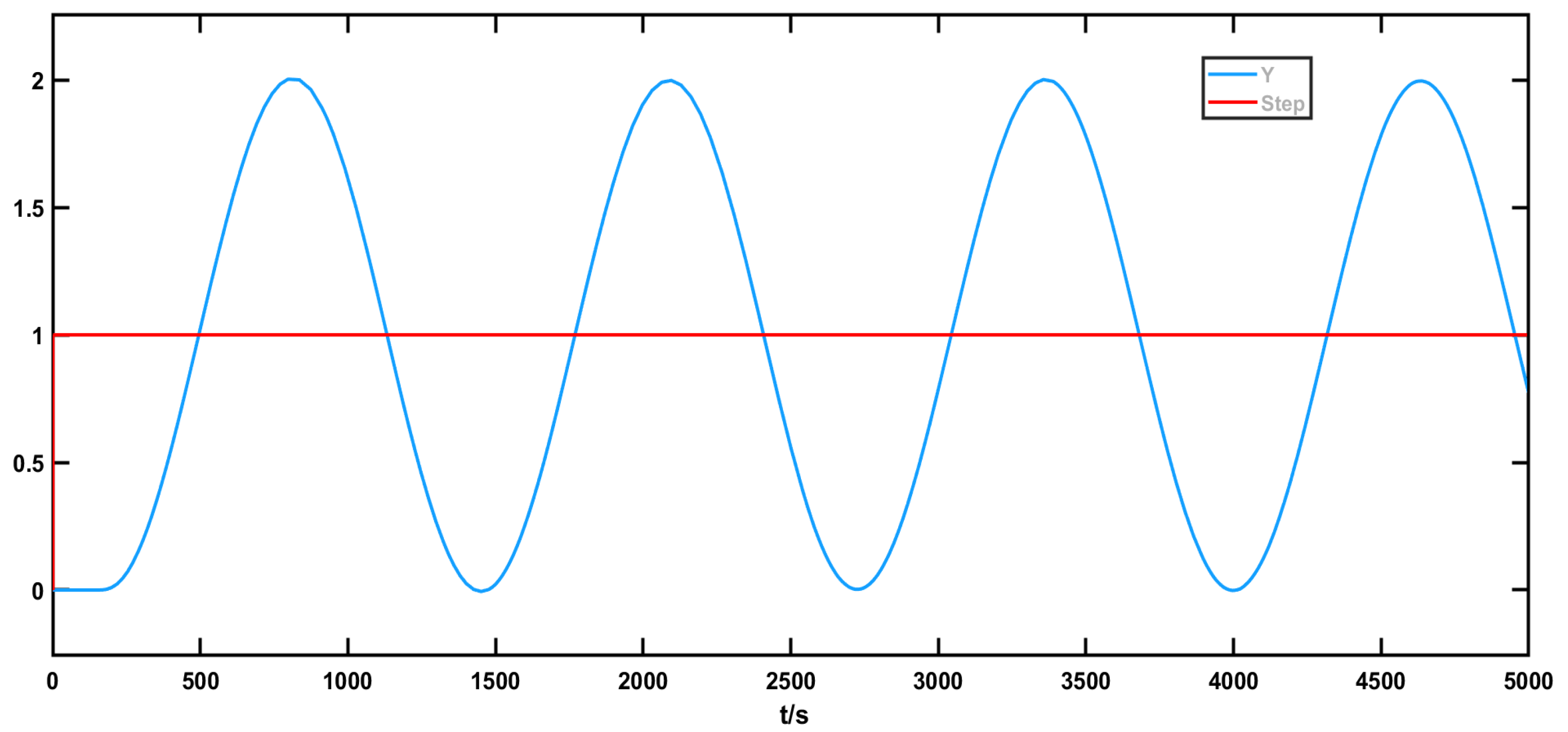
4. Verification of Dual-Locus Diagram Method
4.1. For First-Order Time-Delay Systems
4.1.1. Construction of Extended State Observer for First-Order Systems
4.1.2. Discretization of Extended State Observer
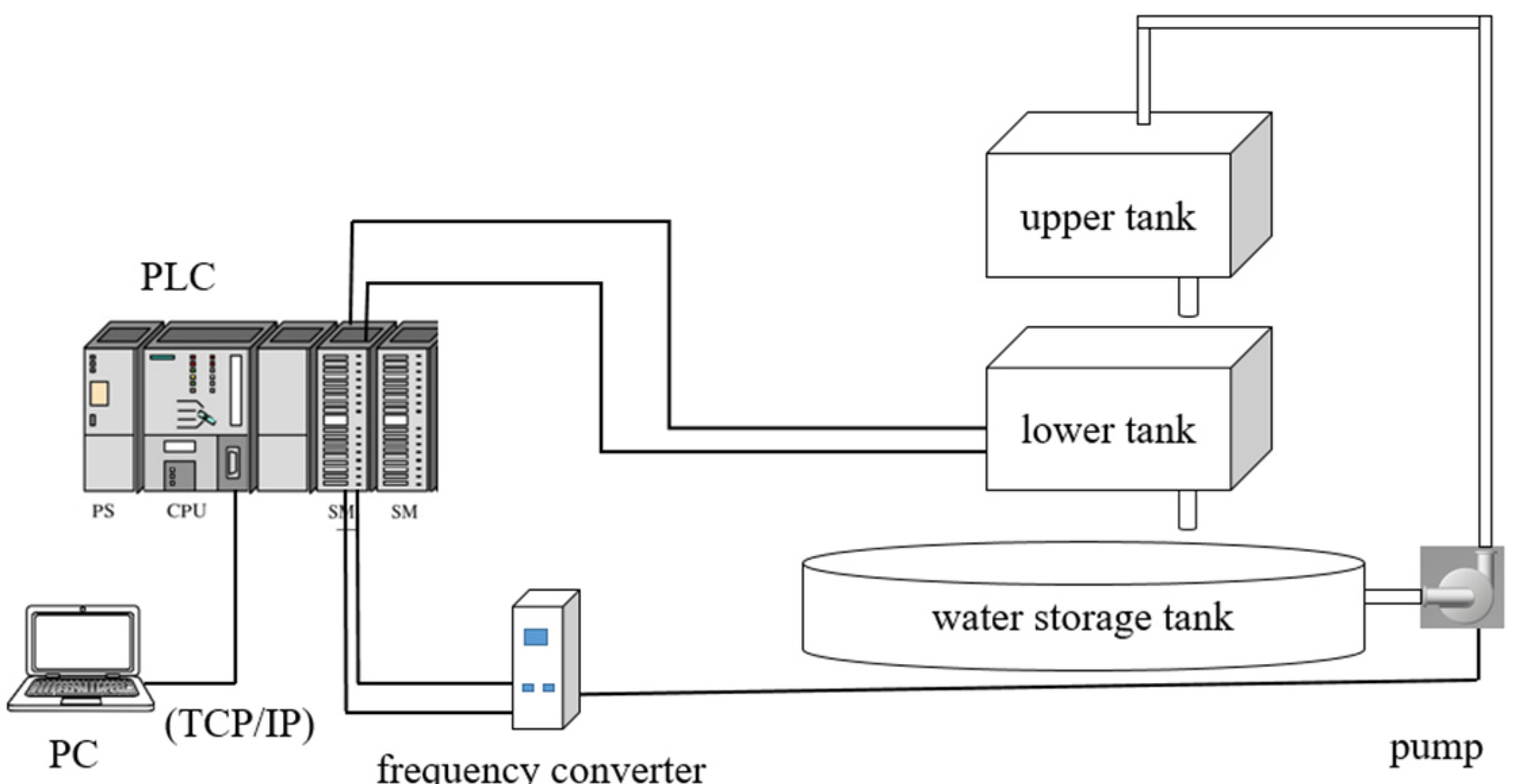
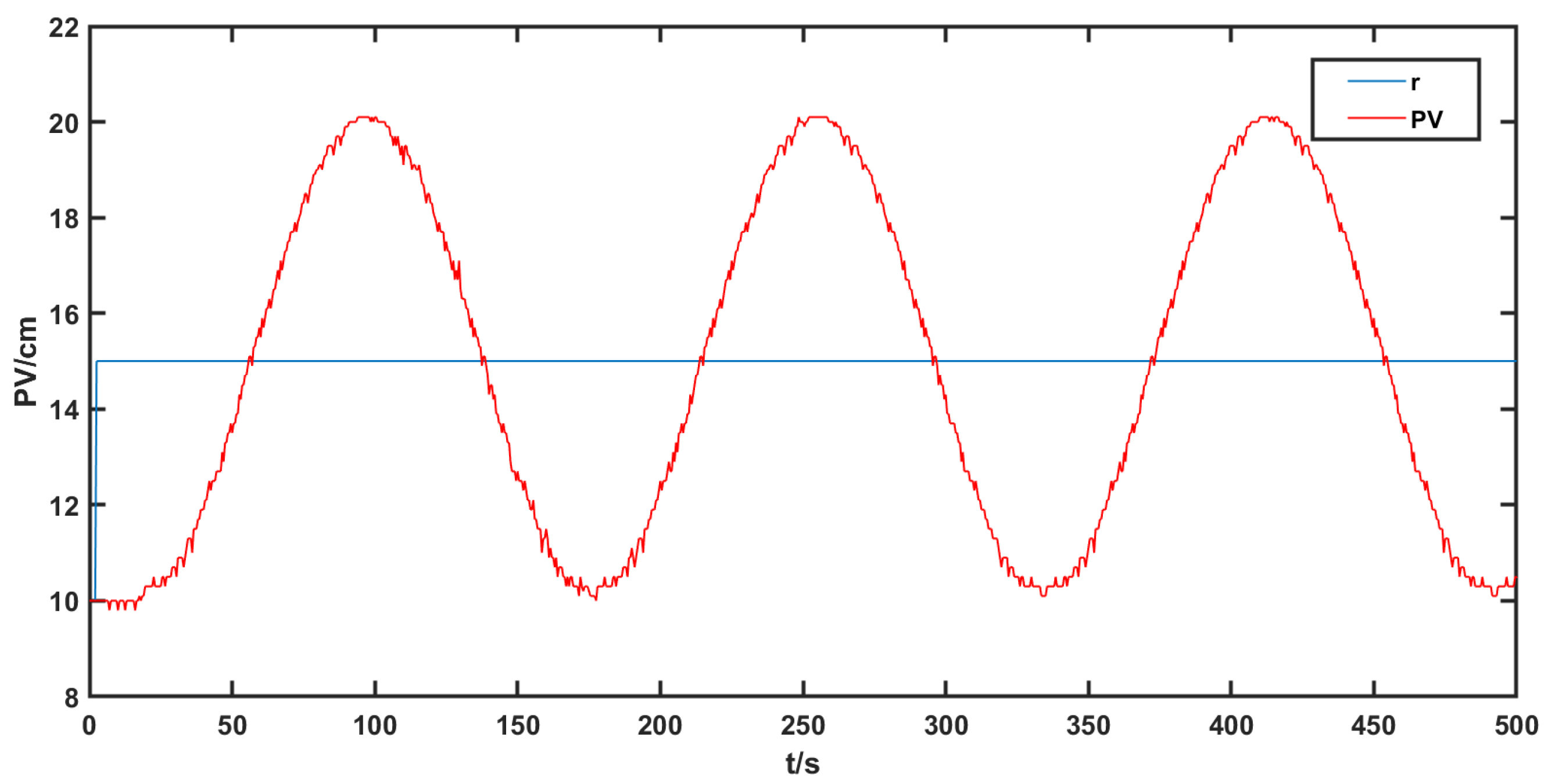
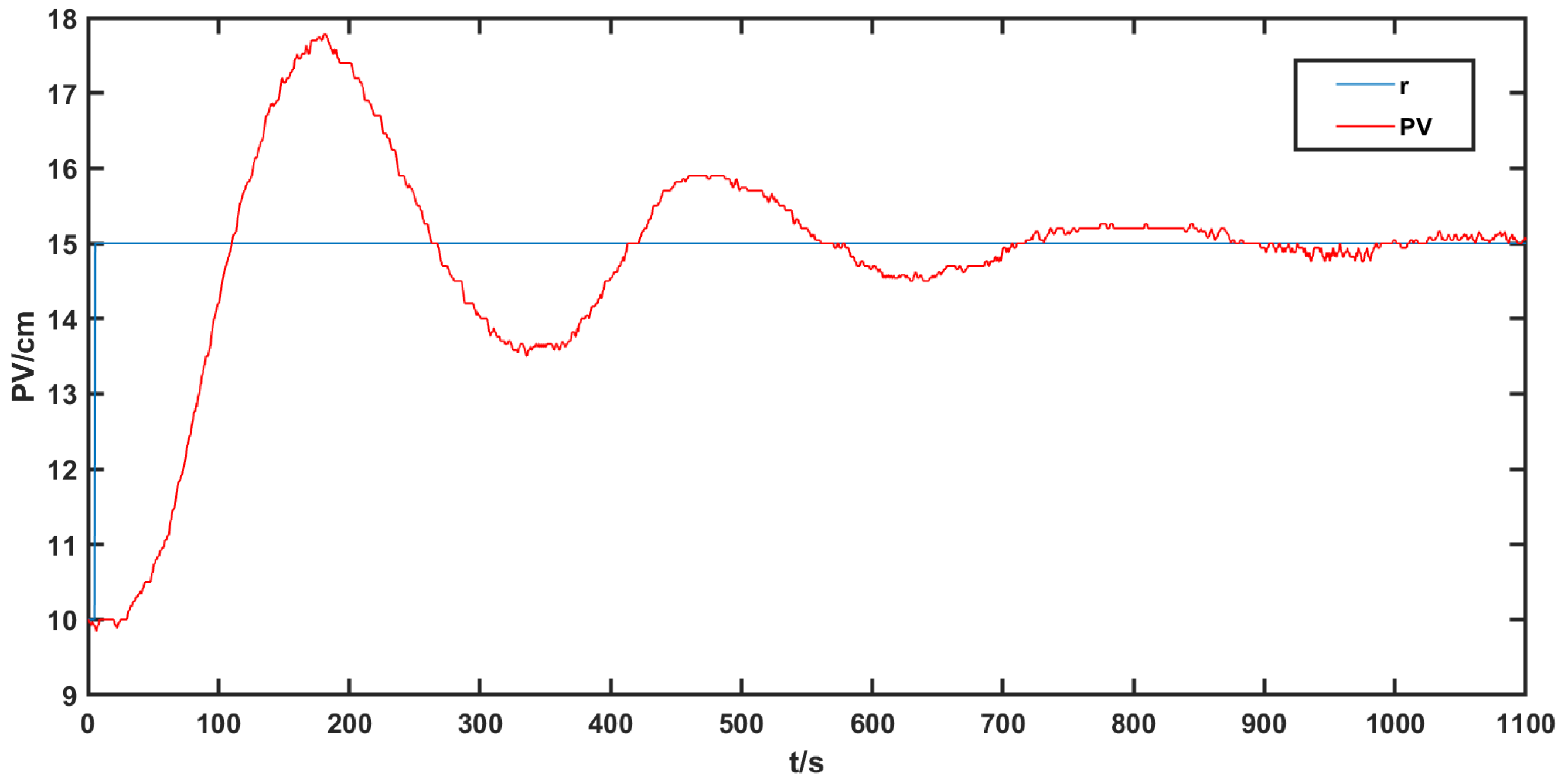
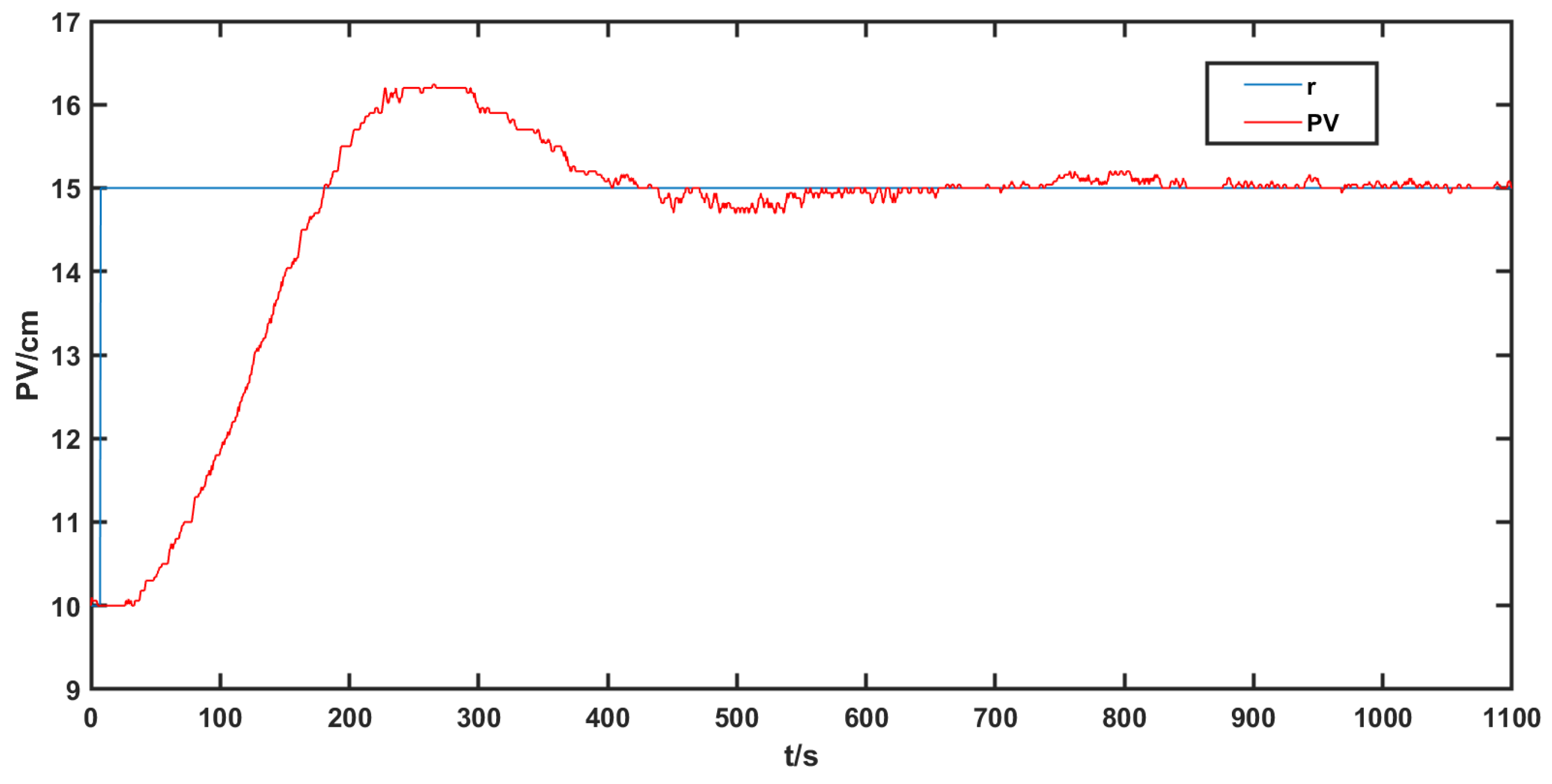
4.1.3. Analysis of Experiment Results
4.2. For Second-Order Time-Delay Systems
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, L.; Tang, G.J. Stability Analysis of a Type of Gas Generator. Aeronaut. Comput. Tech. 2012, 4, 1–5. [Google Scholar]
- Rao, X.K.; Jia, B.L.; Lu, L. Research and Development of Coagulation Dosage Control System for a Water Based on Artificial Neural Network. J. Yangtze River Sci. Res. Inst. 2017, 34, 135–140. [Google Scholar]
- Rajkumar, S.M.; Chakraborty, S.; Dey, R.; Deb, D. Online Delay Estimation and Adaptive Compensation in Wireless Networked System: An Embedded Control Design. Int. J. Control Autom. Syst. 2019. Available online: http://dx.doi.org/10.1007/s12555-018-0612-x (accessed on 4 January 2020).
- Åström, K.J.; Hägglund, T. PID Controllers: Theory, Design and Tuning; Instrument Society of America: Research Triangle, NC, USA, 1995. [Google Scholar]
- Han, J.Q. Active Disturbance Rejection Control Technique; National Defense Industry Press: Beijing, China, 2008; pp. 243–246. [Google Scholar]
- Han, J.Q. Control Theory, Is It A Model Analysis Approach or A Direct Control Approach. J. Syst. Sci. Math. Sci. 1989, 9, 328–335. [Google Scholar]
- Han, J.Q. The “Extended State Observer” of A Class of Uncertain Systems. JCD 1995, 10, 85–88. [Google Scholar]
- Zhao, Z.L.; Guo, B.Z. On Convergence of Nonlinear Active Disturbance Rejection Control for SISO Nonlinear Systems. J. Dyn. Control Syst. 2016, 22, 385–412. [Google Scholar] [CrossRef]
- Chen, Z.Q.; Sun, M.W.; Yang, R.G. On the Stability of Linear Active Disturbance Rejection Control. JAC 2013, 39, 574–580. [Google Scholar] [CrossRef]
- Tian, G.; Gao, Z.Q. Frequency Response Analysis of Active Disturbance Rejection Based Control System. In Proceedings of the 16th IEEE International Conference on Control Applications, Singapore, 1–3 October 2007; pp. 1595–1599. [Google Scholar]
- Wu, D.; Chen, K. Frequency-domain Analysis of Nonlinear Active Disturbance Rejection Control via the Describing Function Method. IEEE Trans. Ind. Electron. 2013, 60, 3906–3914. [Google Scholar] [CrossRef]
- Huang, Y.; Xue, W.C. Active Disturbance Rejection Control: Methodology and Theoretical Analysis. ISA Trans. 2014, 53, 963–976. [Google Scholar] [CrossRef] [PubMed]
- Madonski, C.; Shao, S.; Zhang, H.; Gao, Z.Q.; Li, S. General error-based active disturbance rejection control for swift industrial implementations. Control Eng. Pract. 2019, 84, 218–229. [Google Scholar] [CrossRef]
- Huang, C.Z.; Du, B.; Zheng, Q. Design and Implementation of PLC Based Linear Active Disturbance Rejection Control Approach. Control Eng. China. 2017, 24, 171–177. [Google Scholar]
- Li, D.Z.; Li, Z.; Gao, Z.Q.; Jin, Q.B. Active Disturbance Rejection-Based High-Precision Temperature Control of a Semibatch Emulsion Polymerization Reactor. Ind. Eng. Chem. Res. 2014, 53, 3210–3221. [Google Scholar] [CrossRef]
- Sun, L.; Li, D.H.; Hu, K.T.; Lee, K.Y.; Pan, F.P. On Tuning and Practical Implementation of Active Disturbance Rejection Controller: A Case Study from a Regenerative Heater in a 1000 MW Power Plant. Ind. Eng. Chem. Res. 2016, 55, 6686–6695. [Google Scholar]
- Li, X.Y.; Ai, W.; Tian, S.P. ADRC with Feedfoward Control For Time-Delay Systems. In Proceedings of the IEEE 7th Data Driven Control and Learning Systems Conference, Enshi, China, 25−27 May 2018; pp. 736–742. [Google Scholar]
- Fu, C.F.; Tan, W. Control of unstable processes with time delays via ADRC. ISA Trans. 2017, 71, 530–541. [Google Scholar] [CrossRef] [PubMed]
- Li, D.Z.; Yu, W.L.; Jin, Q.B. Stability Region Analysis of Linear Active Disturbance Rejection Controllers for First Order Systems with Time Delay. J. Contl. Theor. Appl. 2017, 34, 1244–1249. [Google Scholar]
- Li, D.Z.; Wang, Z.; Yu, W.L.; Li, Q.S.; Jin, Q.B. Application of LADRC with Stability Region for A Hydrotreating Back-flushing Process. Control Eng. Pract. 2018, 79, 185–194. [Google Scholar] [CrossRef]
- Ou, L.L.; Tang, Y.C.; Gu, D.Y.; Zhang, W.D. Stability analysis of PID controllers for integral processes with time delay. In Proceedings of the American Control Conference, Portland, OR, USA, 8–10 June 2005; pp. 4247–4252. [Google Scholar]
- Gao, Z.Q. Scaling and bandwidth parameterization based controller tuning. In Proceedings of the American Control Conference, New York, NY, USA; 2003; pp. 4989–4996. [Google Scholar]
- Hu, S.S. Automatic Control Theory; Science Press: Beijing, China, 2013; pp. 201–209. [Google Scholar]
- Patel, R.; Gojiya, A.; Deb, D. Failure Reconfiguration of Pumps in Two Reservoirs Connected to Overhead Tank. Adv. Intell. Syst. Comput. 2019, 757, 81–92. [Google Scholar]
- Zhu, B. Introduction to Active Disturbance Rejection Control; Beihang University Press: Beijing, China, 2017; pp. 47–50. [Google Scholar]
- Zhou, X.Y.; Gao, H.; Zhao, B.L.; Zhao, L.B. A GA-based parameters tuning method for an ADRC controller of ISP for aerial remote sensing applications. ISA Trans. 2018, 81, 318–328. [Google Scholar] [CrossRef] [PubMed]


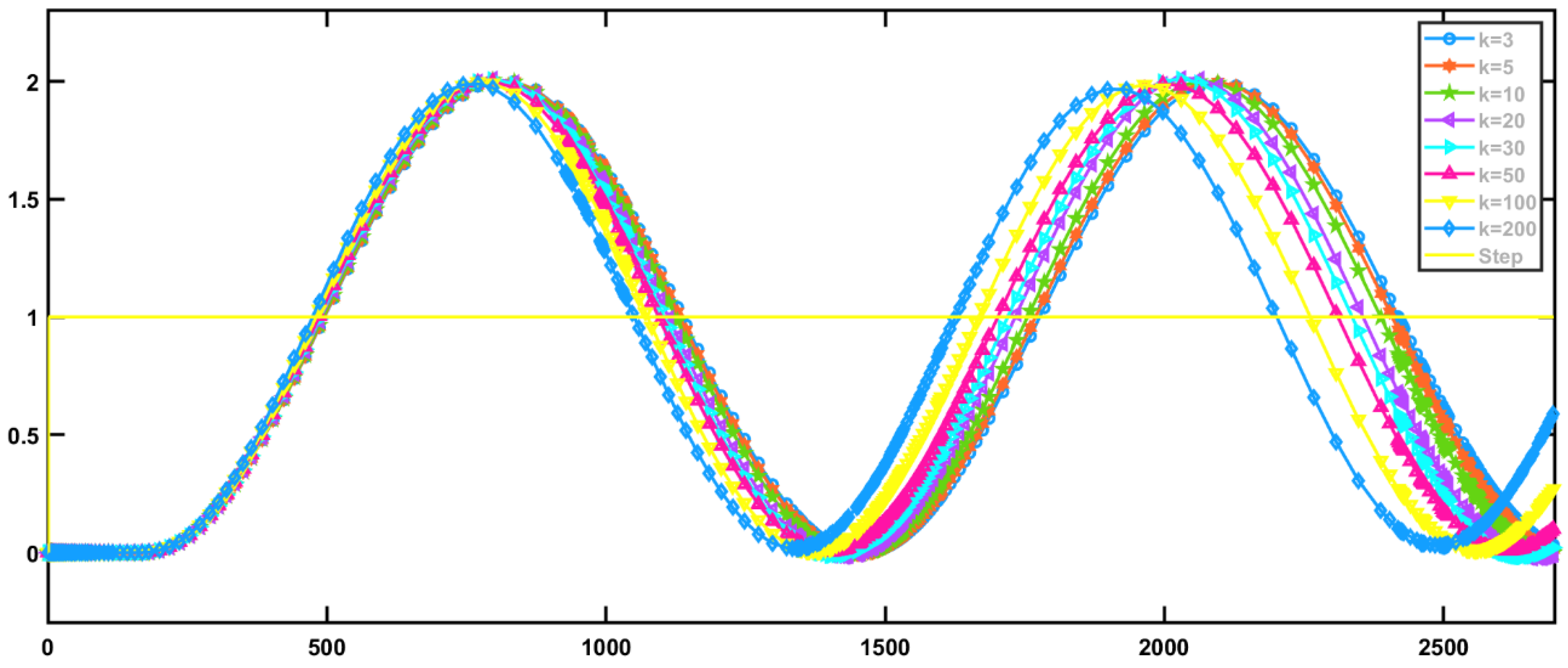
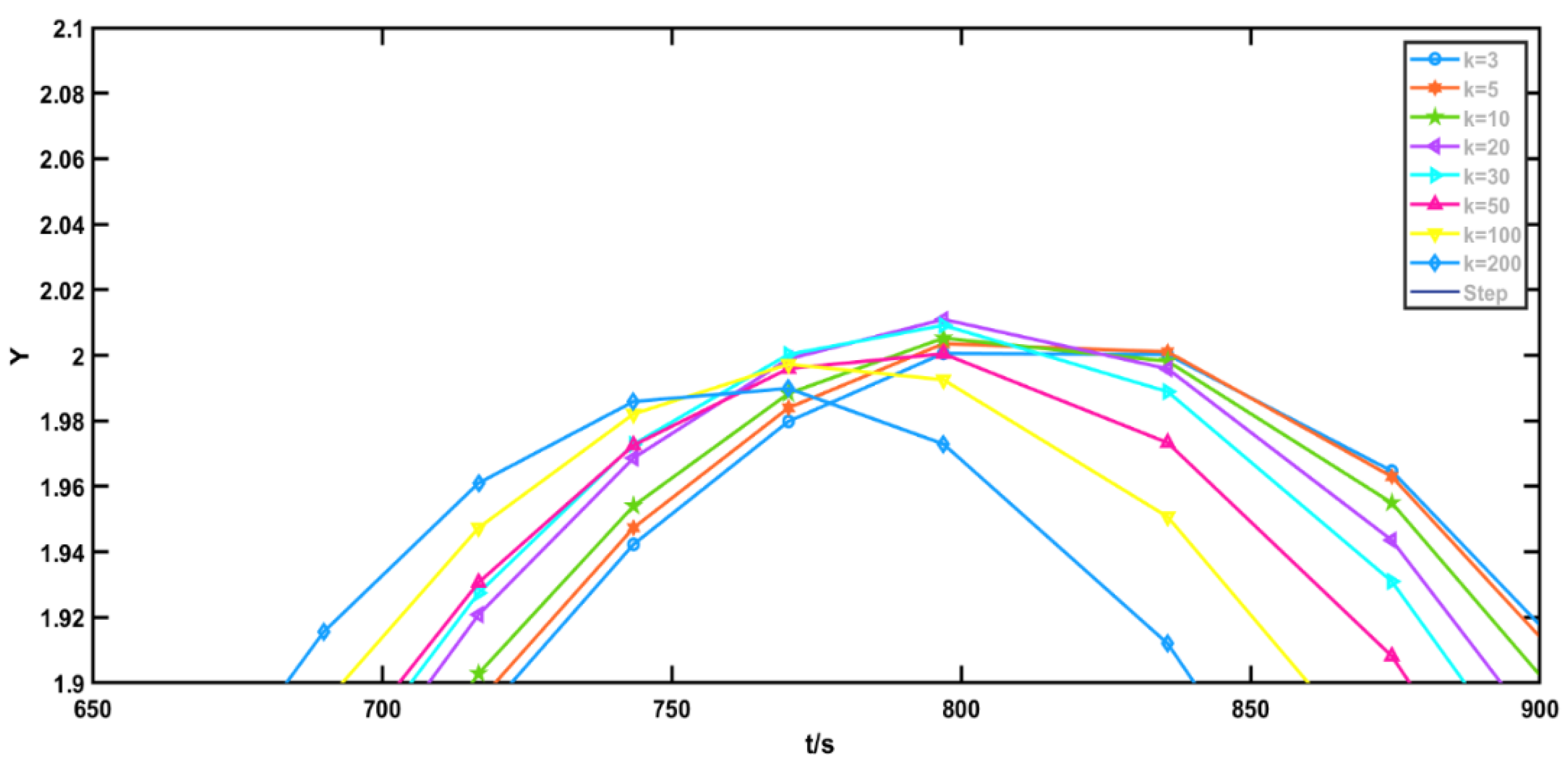
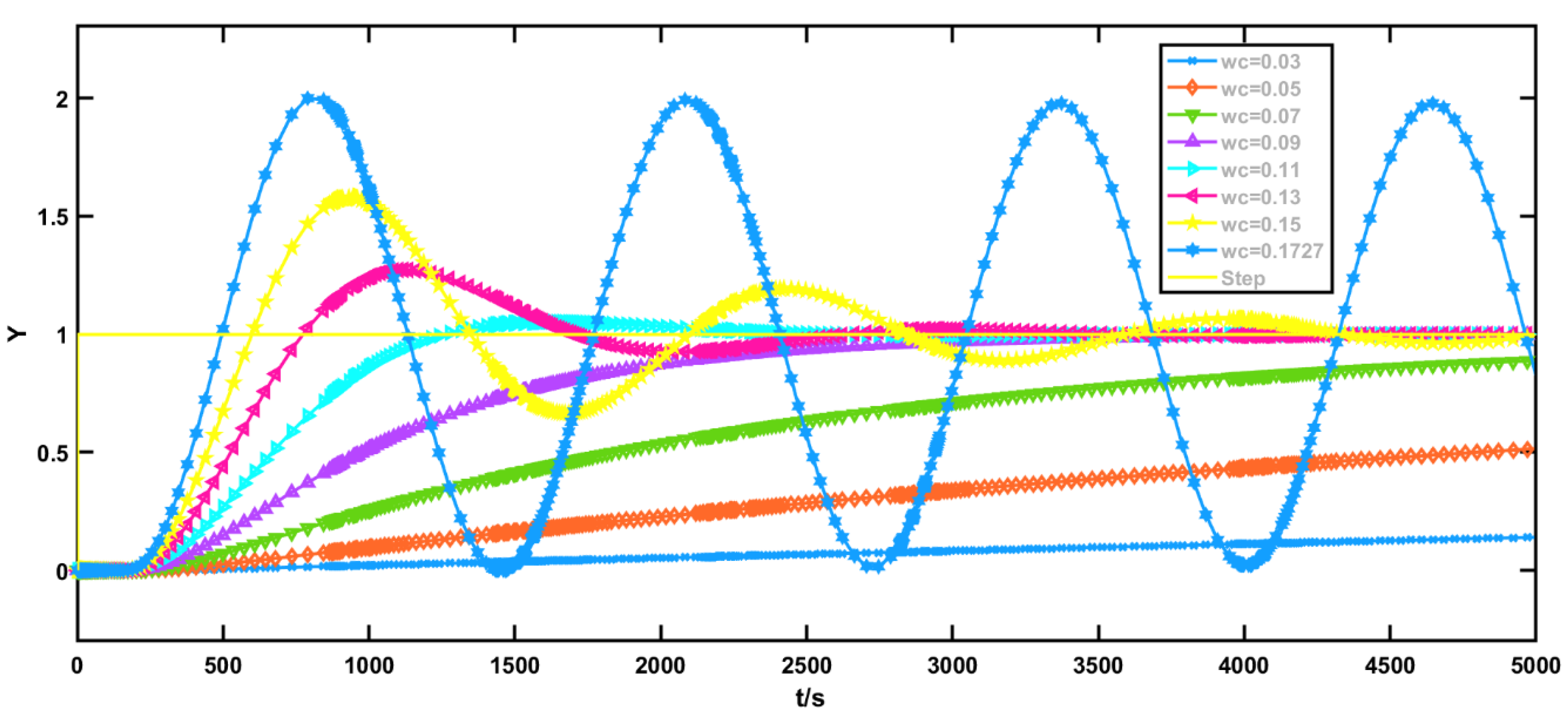
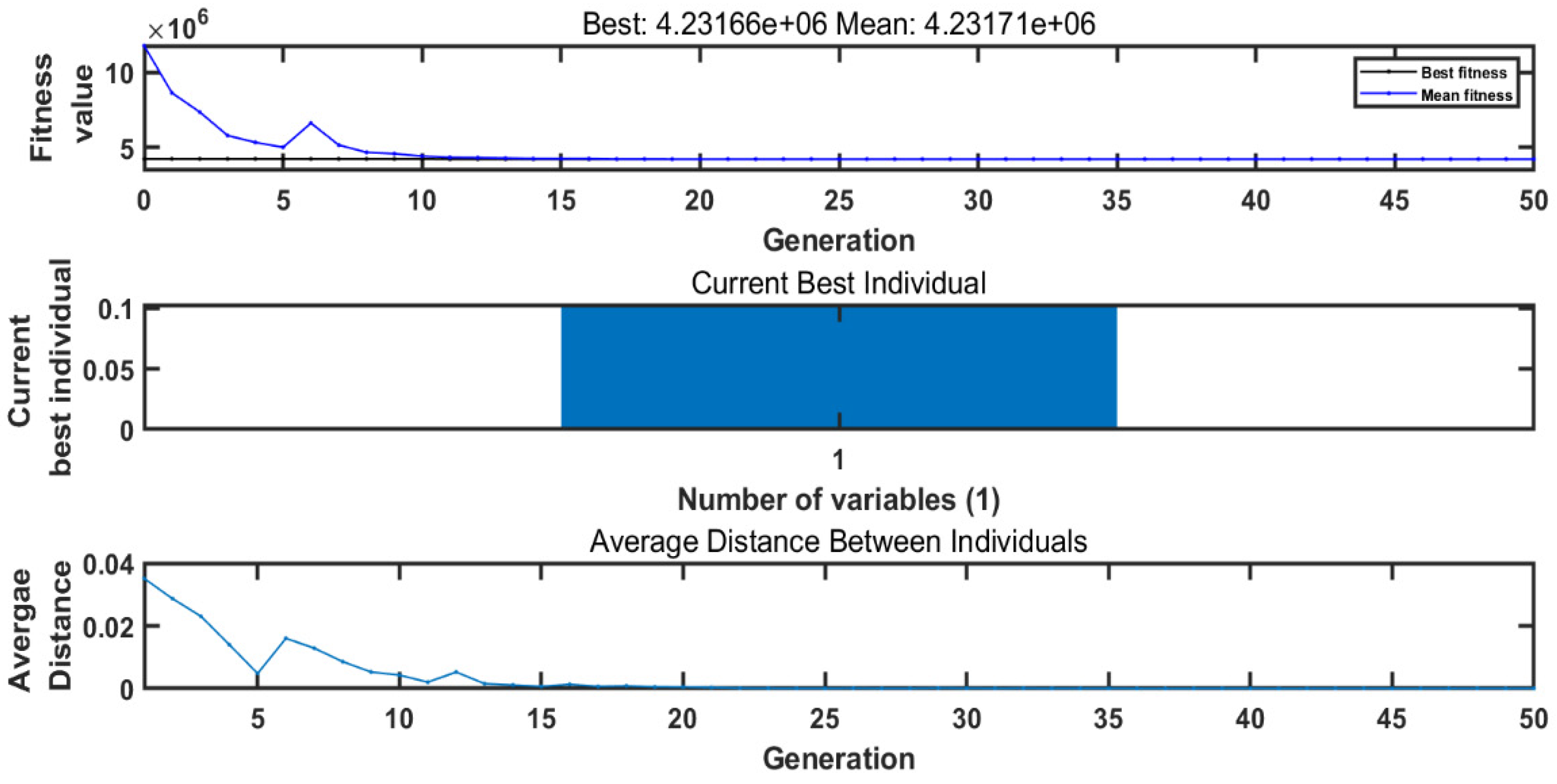
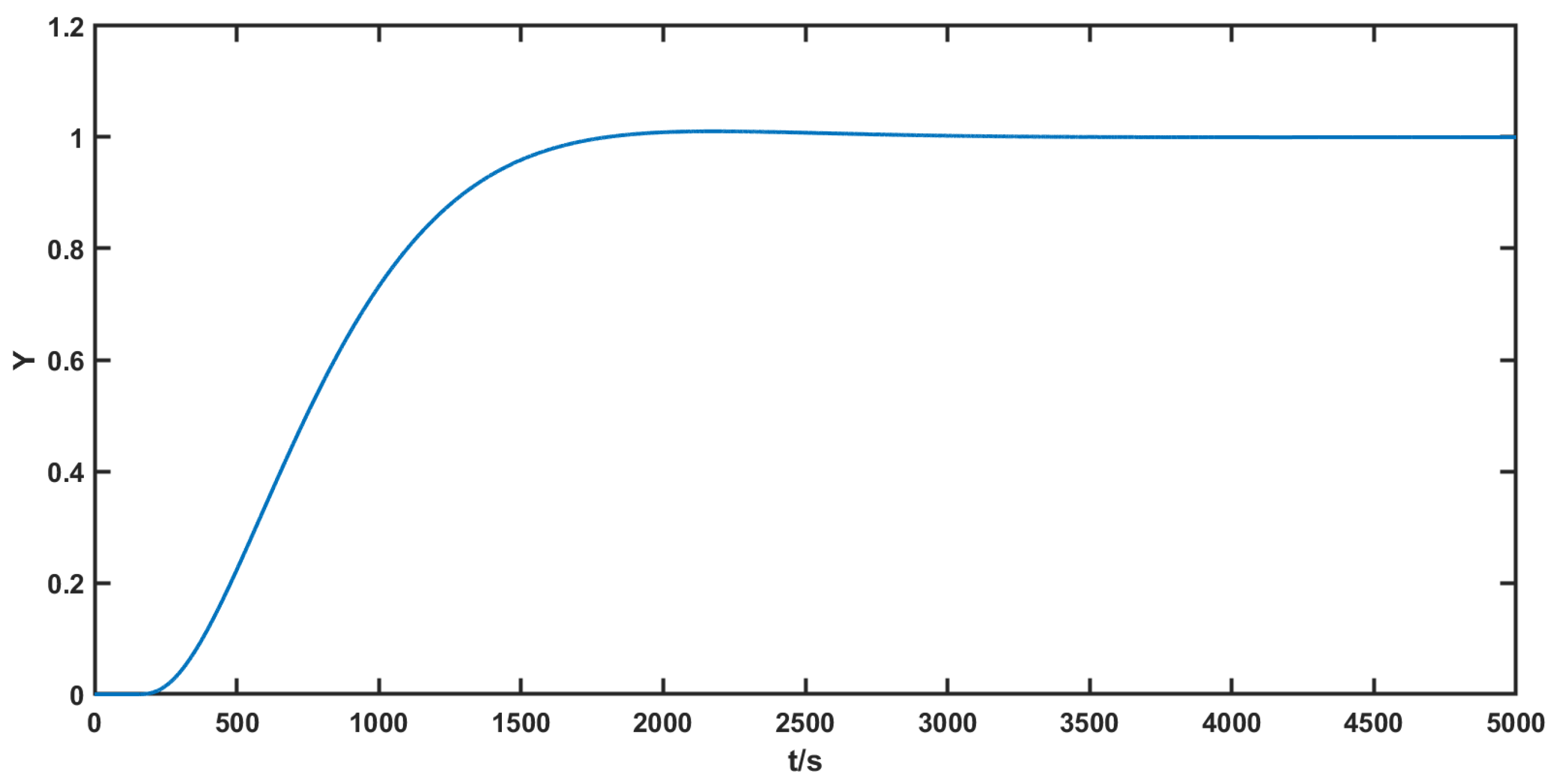

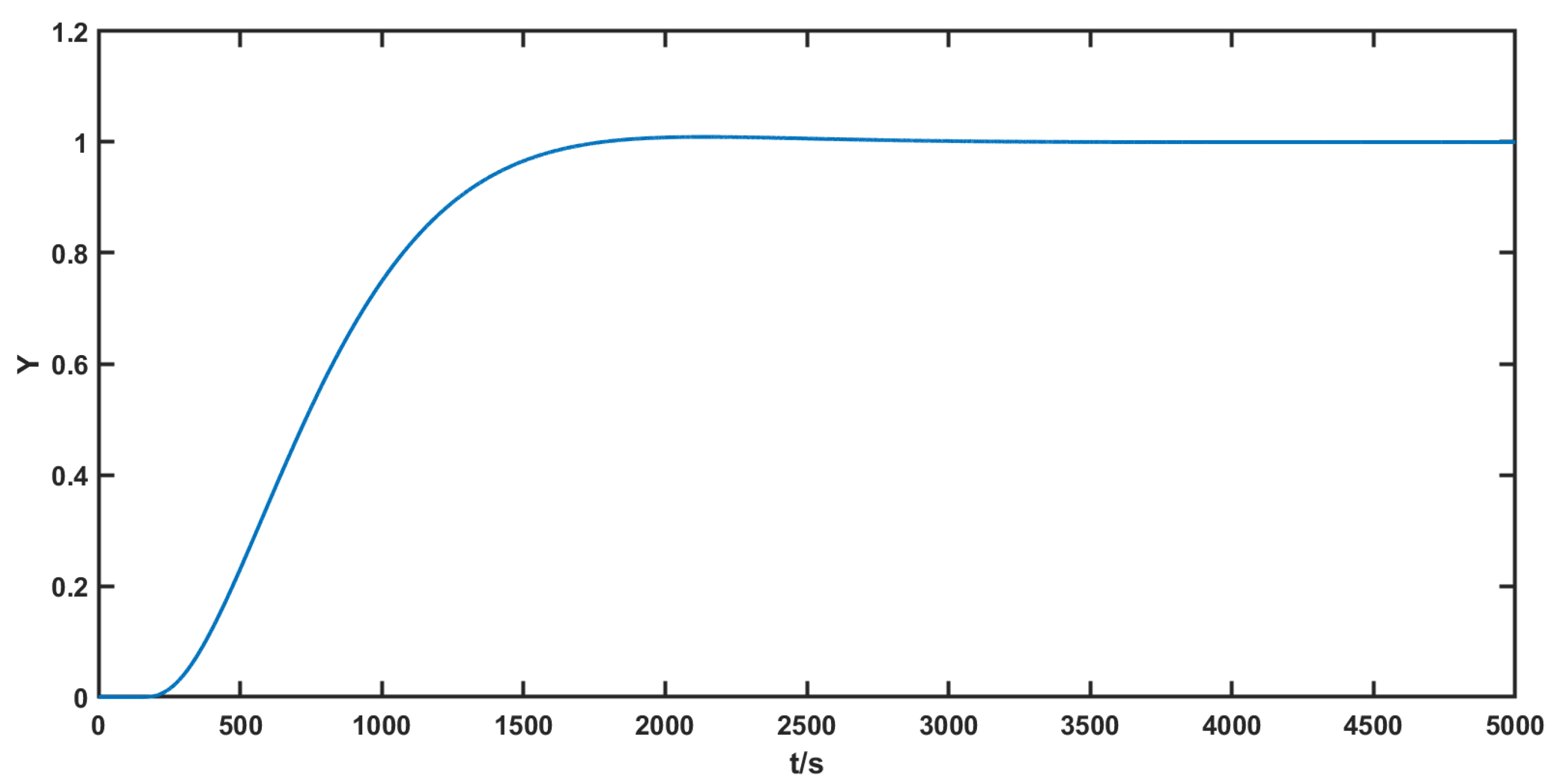
| 3 | 5 | 10 | 20 | 30 | 50 | 100 | 200 | |
|---|---|---|---|---|---|---|---|---|
| ωc | 0.2164 | 0.1727 | 0.1308 | 0.1016 | 0.0882 | 0.0741 | 0.05905 | 0.0473 |
| ωo | 0.6492 | 0.8635 | 1.308 | 2.032 | 2.646 | 3.705 | 5.905 | 9.46 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, D.; Chen, X.; Zhang, J.; Jin, Q. On Parameter Stability Region of LADRC for Time-Delay Analysis with a Coupled Tank Application. Processes 2020, 8, 223. https://doi.org/10.3390/pr8020223
Li D, Chen X, Zhang J, Jin Q. On Parameter Stability Region of LADRC for Time-Delay Analysis with a Coupled Tank Application. Processes. 2020; 8(2):223. https://doi.org/10.3390/pr8020223
Chicago/Turabian StyleLi, Dazi, Xun Chen, Jianqing Zhang, and Qibing Jin. 2020. "On Parameter Stability Region of LADRC for Time-Delay Analysis with a Coupled Tank Application" Processes 8, no. 2: 223. https://doi.org/10.3390/pr8020223
APA StyleLi, D., Chen, X., Zhang, J., & Jin, Q. (2020). On Parameter Stability Region of LADRC for Time-Delay Analysis with a Coupled Tank Application. Processes, 8(2), 223. https://doi.org/10.3390/pr8020223





