The Application of a New PID Autotuning Method for the Steam/Water Loop in Large Scale Ships
Abstract
1. Introduction
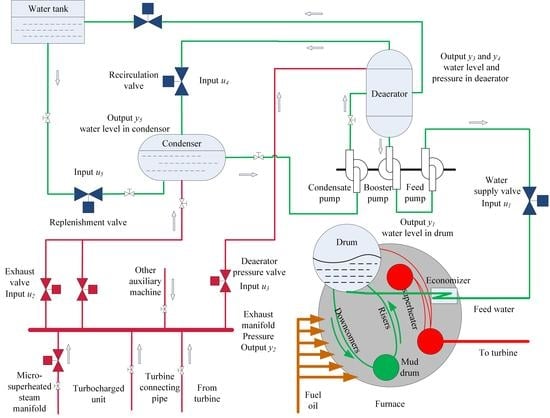
- when the water turns between steam and liquid, the false water level phenomenon appears for reason of the shrink and swell in the water, which makes the drum water level control loop a non-minimum phase system [2].
- the water in the condenser goes to the deaerator, hence, strong interactions exist in the water control loops of the deaerator and the condenser.
- the steam required in the deaerator is from the exhaust manifold, which leads to strong coupling in the pressure control loops of the deaerator and exhaust manifold.
- the amount of required steam in the deaerator changes with the feedwater flow rate. Hence, the water level and the pressure are two strong coupling variables in the deaerator.
2. Introduction of the Steam/Water Loop
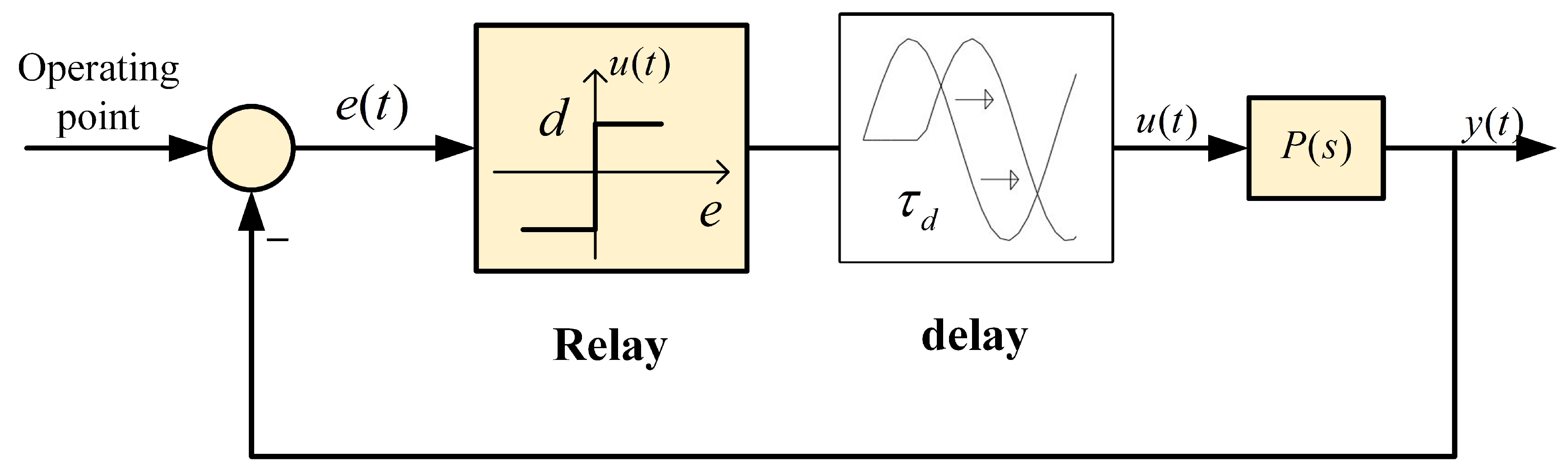
3. Detailed Theory of KC Autotuning Method
- (1)
- Obtain the critical frequency of the system ( is usually critical frequency, but might be different);
- (2)
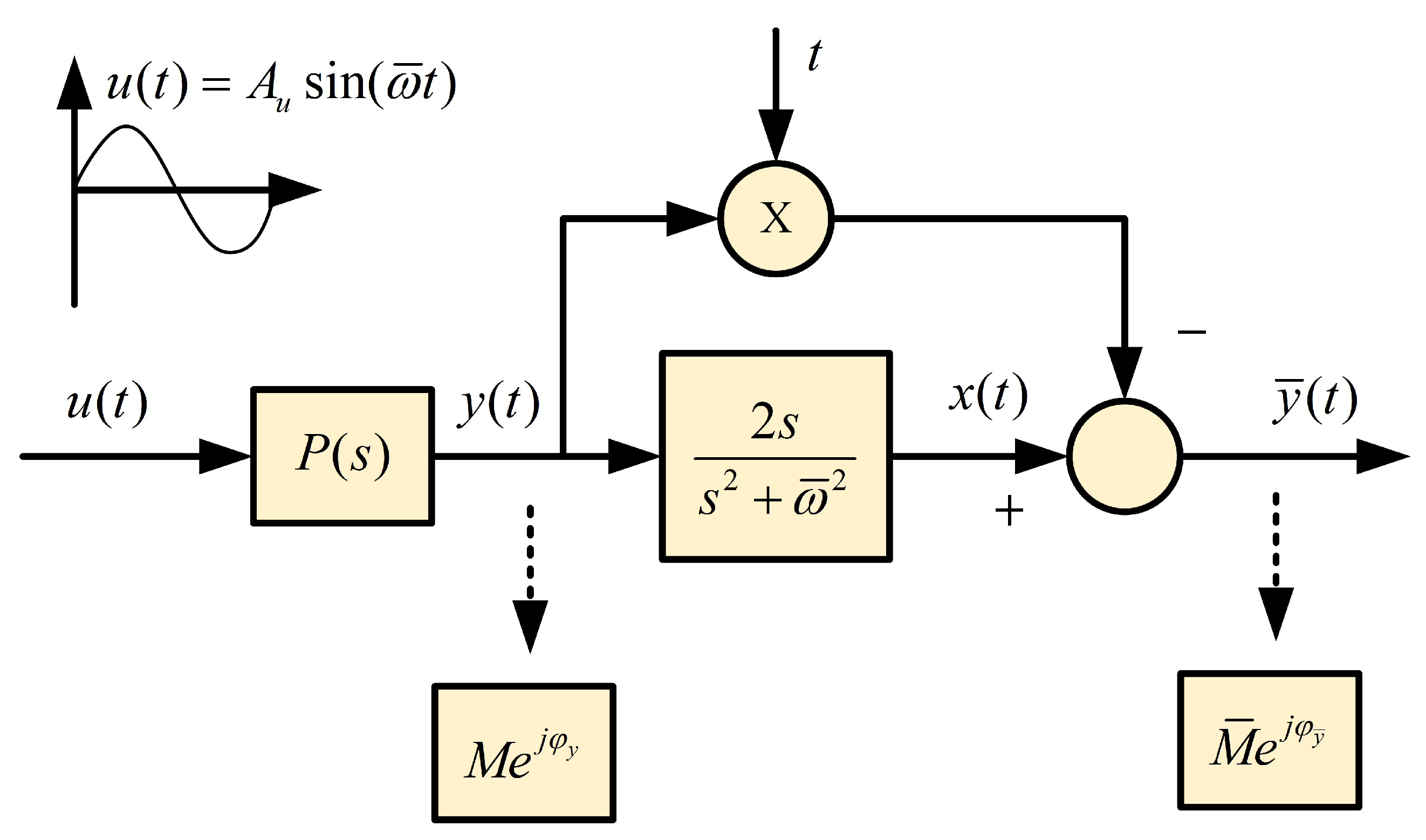
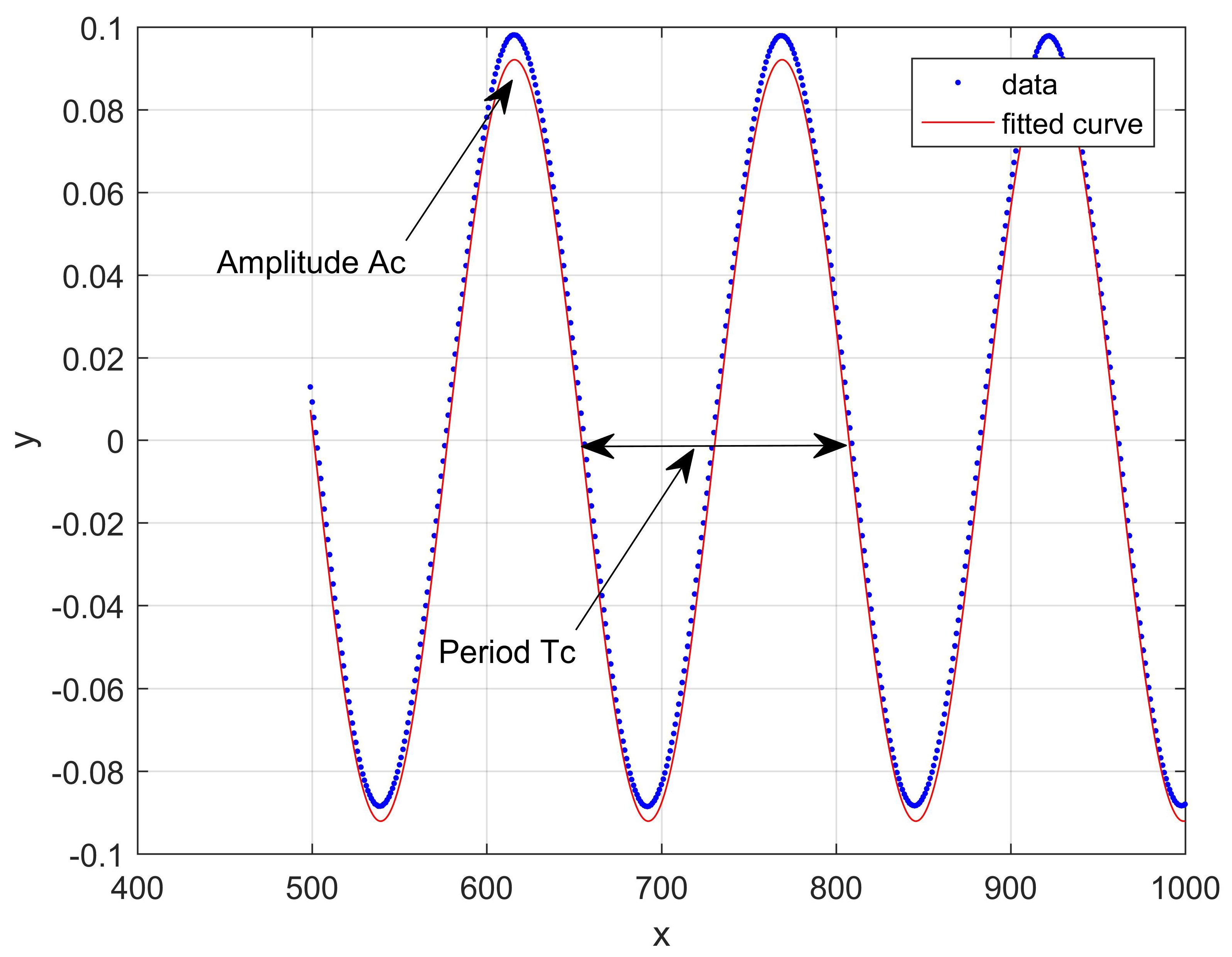
- Conduct sine tests around the operating points on the steam/water loop;
- (3)
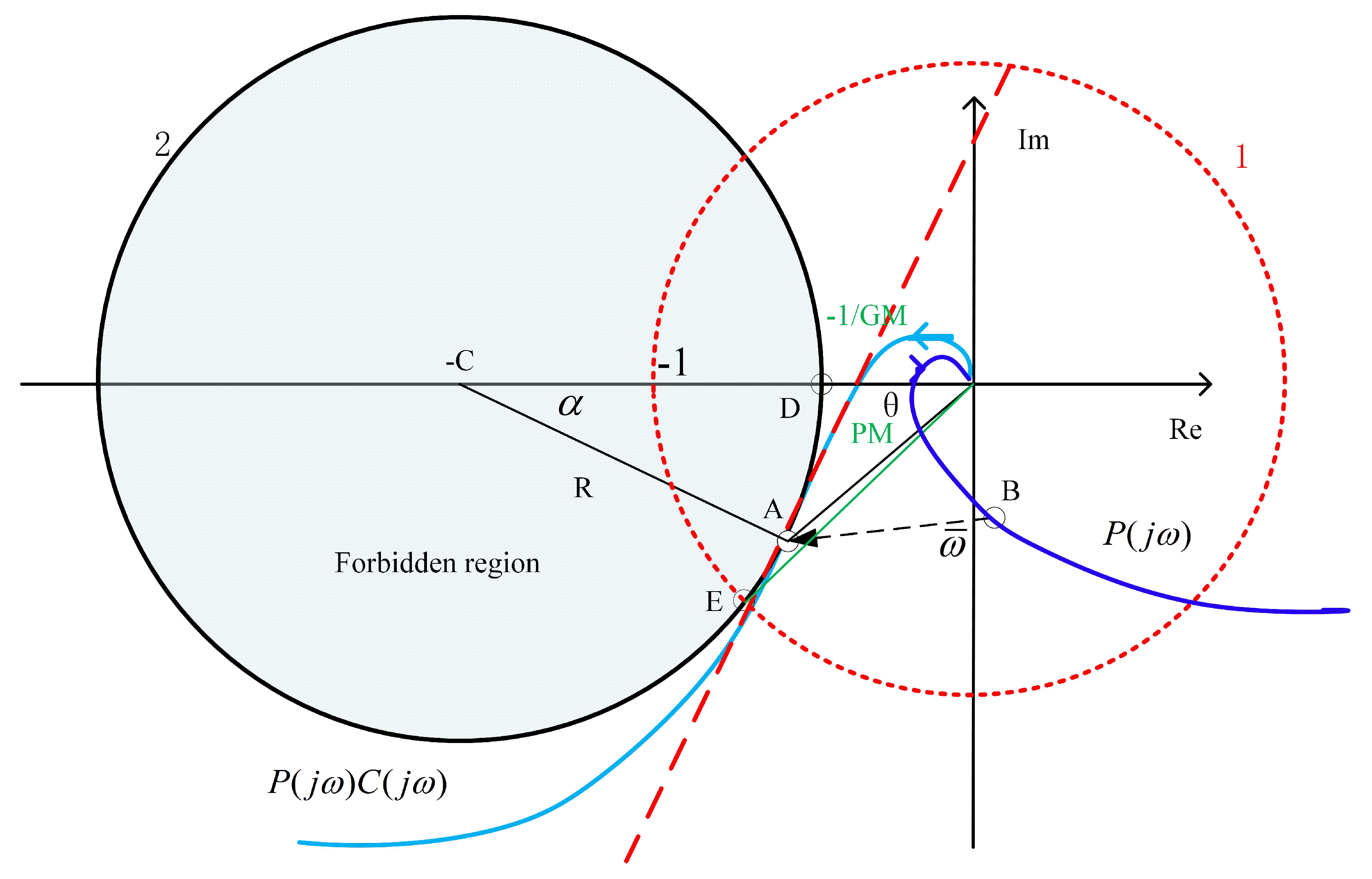
- According to the loop margin requirements, calculate a ‘forbidden region’ on the Nyquist plane;
- (4)
- Calculate parameters for the PID controller for the points on the region edge (for from to );
- (5)
- Search for the point, where the slope of the loop is the same with the slope of the ‘forbidden region’;
- (6)
- The parameters for the PID controller are obtained from step 5).
3.1. Slope of the ‘Forbidden Region’
3.2. Slope of the Loop
3.2.1. Calculation for and Its Derivation
3.2.2. Calculation for and Its Derivation
3.3. Application to Mimo System
- (1)
- Apply sine test around the operating points on one of the sub-loops, while keeping other sub-loops to work at their own operating points. And the controller parameters can be calculated for the selected loop, with the magnitude and phase obtained from the sine test;
- (2)
- Keep the previous sub-loop working at its operating point with the obtained PID control, and conduct a new sine test on one the other sub-loops. The magnitude and phase can be obtained for the new sub-loop and the controller can be calculated;
- (3)
- Repeat step 2 for each sub-loop until the output magnitude and phase do not change significantly between consecutive tests.
- (4)
- The parameters for the PID controller can be obtained for all the sub-loops after step 3 is completed.
4. A Brief Introduction of Other PID Autotuners
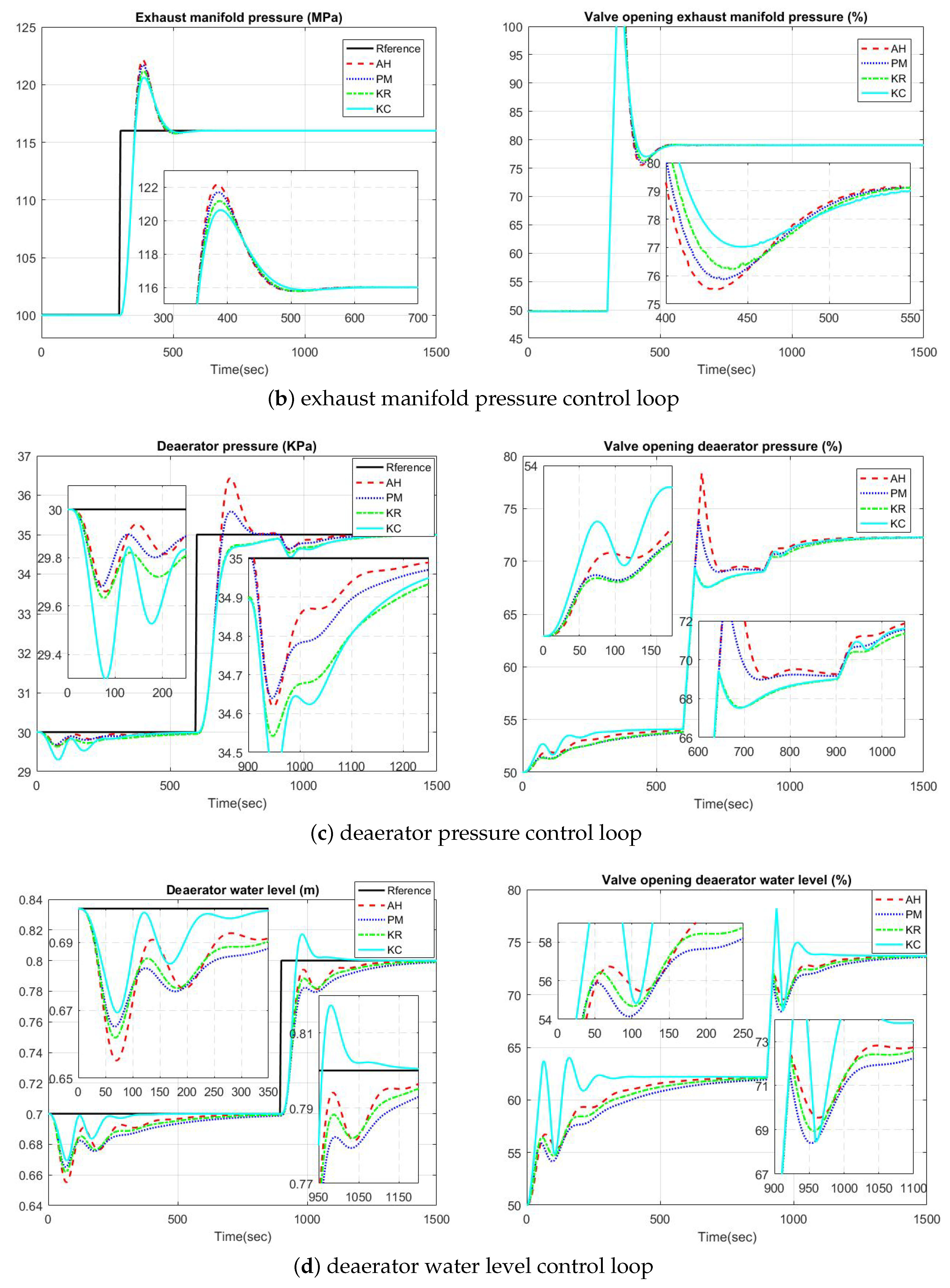
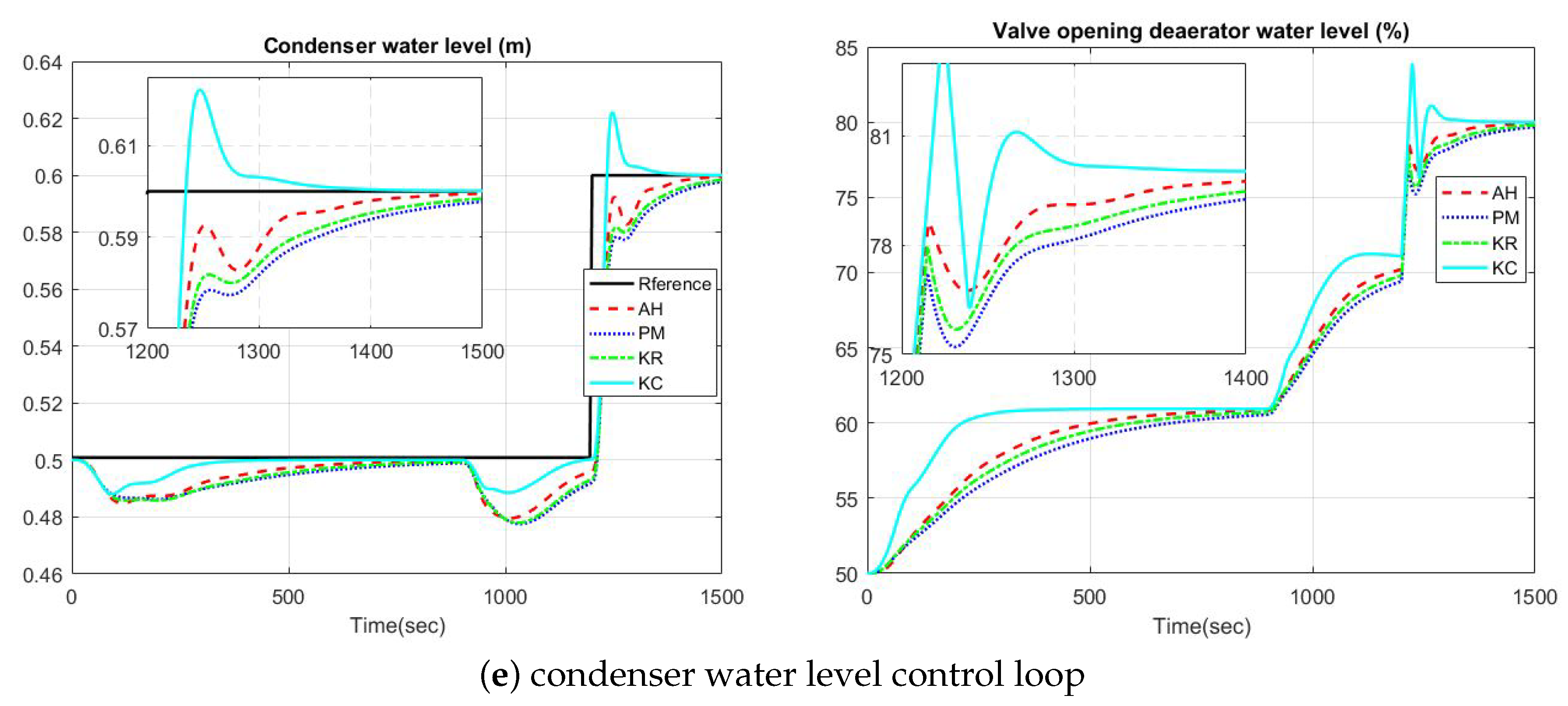
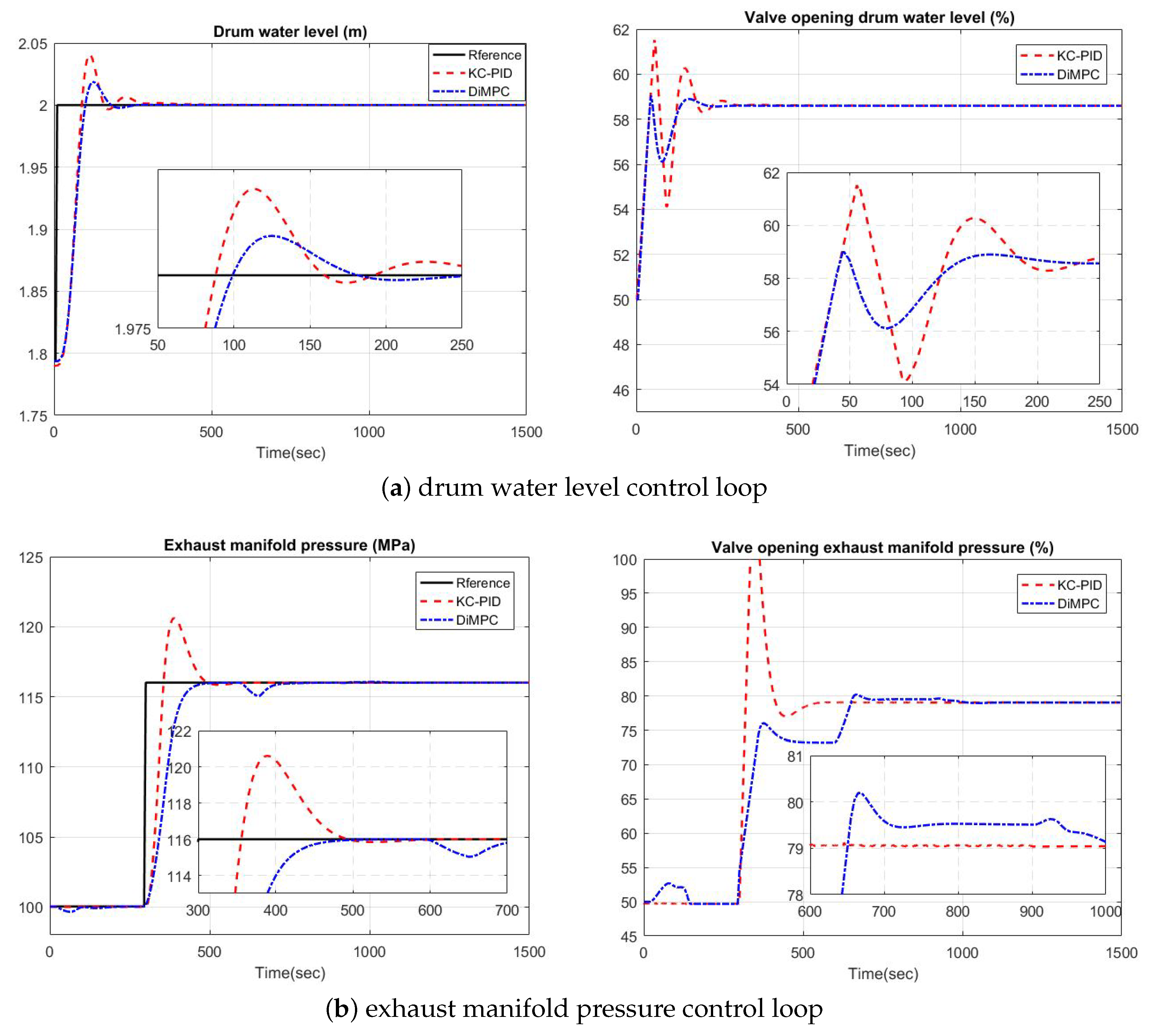
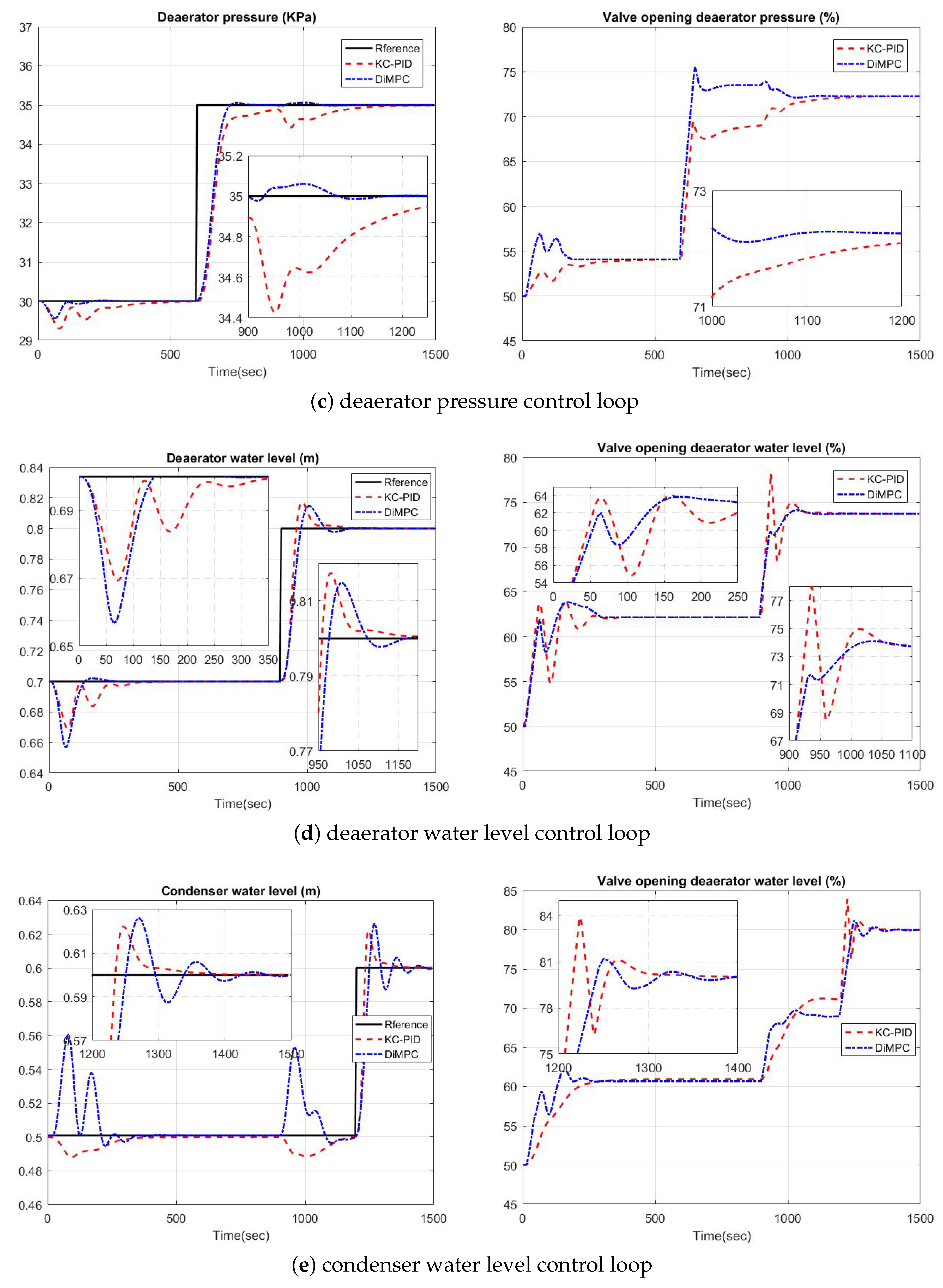
5. Experiments and Results Analyses
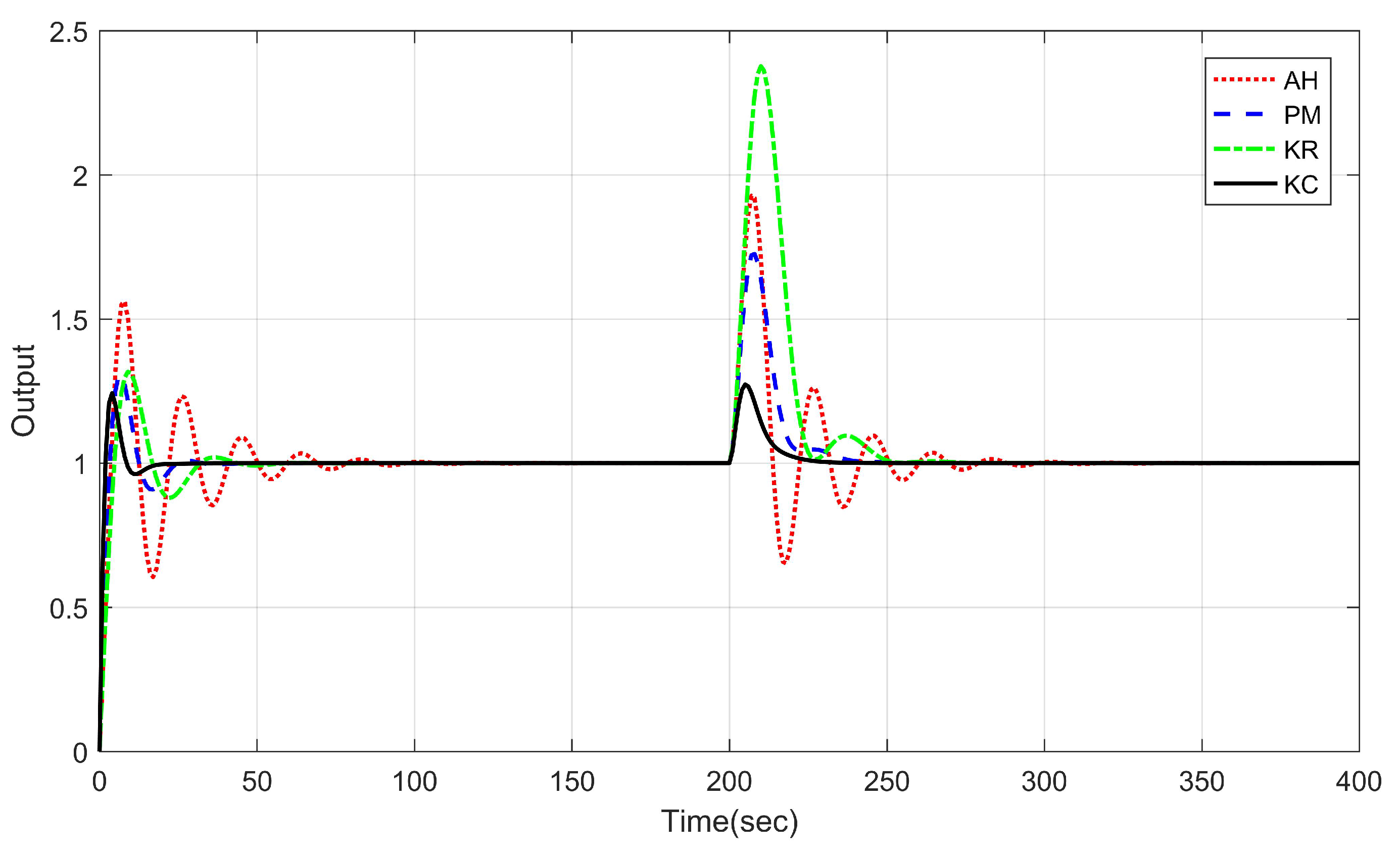
5.1. A Simple Single Input Single Output System Example
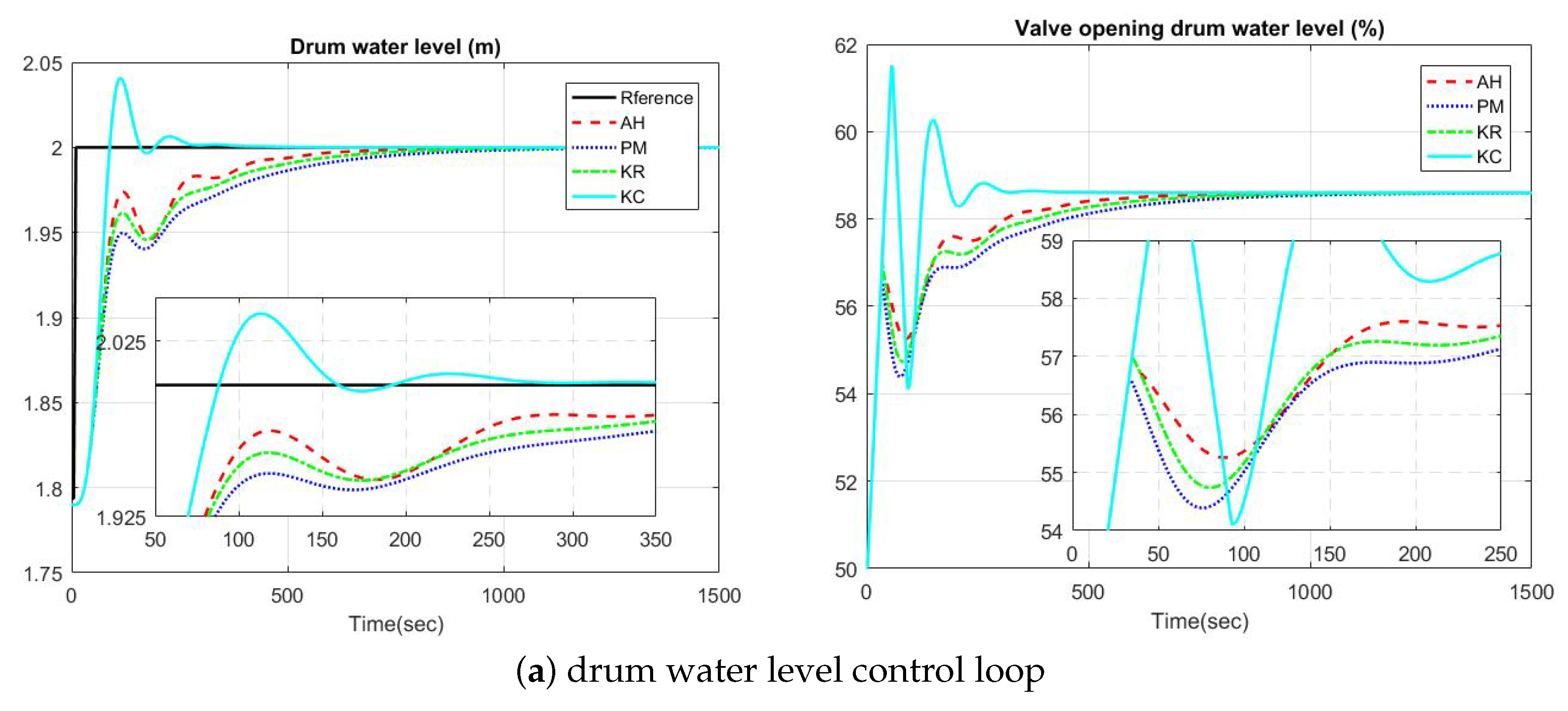
5.2. Simulation on Steam/Water Loop in Large Scale Ships
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Drbal, L.; Westra, K.; Boston, P. Power Plant Engineering; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Åström, K.J.; Bell, R.D. Drum-boiler dynamics. Automatica 2000, 36, 363–378. [Google Scholar] [CrossRef]
- Xia, Y.; Liu, B.; Fu, M. Active disturbance rejection control for power plant with a single loop. Asian J. Control 2012, 14, 239–250. [Google Scholar] [CrossRef]
- Yu, N.; Ma, W.; Su, M. Application of adaptive Grey predictor based algorithm to boiler drum level control. Energy Convers. Manag. 2006, 47, 2999–3007. [Google Scholar] [CrossRef]
- Cheng, Q.M.; Zheng, Y.; Du, X. Three-element Drum Water-level Cascade Control System Featuring a Self-disturbance-resistant Controller. J. Eng. Therm. Energy Power 2008, 23, 69. [Google Scholar]
- Moradi, H.; Saffar-Avval, M.; Bakhtiari-Nejad, F. Sliding mode control of drum water level in an industrial boiler unit with time varying parameters: A comparison with H∞-robust control approach. J. Process Control 2012, 22, 1844–1855. [Google Scholar] [CrossRef]
- Aliakbari, S.; Ayati, M.; Osman, J.H.; Sam, Y.M. Second-order sliding mode fault-tolerant control of heat recovery steam generator boiler in combined cycle power plants. Appl. Therm. Eng. 2013, 50, 1326–1338. [Google Scholar] [CrossRef]
- Ghabraei, S.; Moradi, H.; Vossoughi, G. Multivariable robust adaptive sliding mode control of an industrial boiler–turbine in the presence of modeling imprecisions and external disturbances: A comparison with type-I servo controller. ISA Trans. 2015, 58, 398–408. [Google Scholar] [CrossRef]
- Liu, X.; Cui, J. Economic model predictive control of boiler-turbine system. J. Process Control 2018, 66, 59–67. [Google Scholar] [CrossRef]
- Liu, X.; Kong, X. Nonlinear fuzzy model predictive iterative learning control for drum-type boiler–turbine system. J. Process Control 2013, 23, 1023–1040. [Google Scholar] [CrossRef]
- Liu, X.; Guan, P.; Chan, C. Nonlinear multivariable power plant coordinate control by constrained predictive scheme. IEEE Trans. Control Syst. Technol. 2009, 18, 1116–1125. [Google Scholar] [CrossRef]
- Wu, X.; Shen, J.; Li, Y.; Lee, K.Y. Fuzzy modeling and predictive control of superheater steam temperature for power plant. ISA Trans. 2015, 56, 241–251. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Cajo, R.; De Keyser, R.; Liu, S.; Ionescu, C.M. Nonlinear predictive control applied to steam/water loop in large scale ships. In Proceedings of the 12th IFAC Symposium on Dynamics and Control of Process Systems, including Biosystems, Florianópolis, Brazil, 23–26 April 2019; pp. 868–873. [Google Scholar]
- Wei, L.; Fang, F.; Shi, Y. Adaptive backstepping-based composite nonlinear feedback water level control for the nuclear U-tube steam generator. IEEE Trans. Control Syst. Technol. 2013, 22, 369–377. [Google Scholar] [CrossRef]
- Bolek, W.; Sasiadek, J.; Wisniewski, T. Adaptive backstepping control of a power plant station model. IFAC Proc. Vol. 2002, 35, 215–220. [Google Scholar] [CrossRef]
- Sun, L.; Hua, Q.; Shen, J.; Xue, Y.; Li, D.; Lee, K.Y. Multi-objective optimization for advanced superheater steam temperature control in a 300 MW power plant. Appl. Energy 2017, 208, 592–606. [Google Scholar] [CrossRef]
- Sun, L.; Li, D.; Hu, K.; Lee, K.Y.; Pan, F. On tuning and practical implementation of active disturbance rejection controller: A case study from a regenerative heater in a 1000 MW power plant. Ind. Eng. Chem. Res. 2016, 55, 6686–6695. [Google Scholar] [CrossRef]
- Lu, J.; Chen, L.; Zhao, S.; Wu, Y. Multivariable Fuzzy PID Control System for Deaerator’s and Condenser’s Levels in a Thermal Powerunit. Cybern. Syst. 2002, 33, 483–506. [Google Scholar]
- Wang, P.; Meng, H.; Dong, P.; Dai, R.-H. Decoupling control based on PID neural network for deaerator and condenser water level control system. In Proceedings of the 2015 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015; pp. 3441–3446. [Google Scholar]
- Liao, Y.F.; Guo, S.D.; Yang, G.; Ma, X.Q. Fuzzy Control of Deaerator Water-Level in Nuclear Power Station Based on MATLAB/Simulink. Appl. Mech. Mater. 2013, 291, 2397–2402. [Google Scholar] [CrossRef]
- Wang, P.; Meng, H.; Ji, Q.Z. Application of PID neural network decoupling control in deaerator pressure and deaerator water level control system. In Asian Simulation Conference; Springer: Berlin/Heidelberg, Germany, 2014; pp. 15–25. [Google Scholar]
- Olin, P.M. A Mean-Value Model for Estimating Exhaust Manifold Pressure in Production Engine Applications; Technical Report, SAE Technical Paper; IEEE: San Francisco, CA, USA, 2008. [Google Scholar]
- Grondin, O.; Moulin, P.; Chauvin, J. Control of a turbocharged diesel engine fitted with high pressure and low pressure exhaust gas recirculation systems. In Proceedings of the 48h IEEE Conference on Decision and Control (CDC) held jointly with 2009 28th Chinese Control Conference, Shanghai, China, 15–18 December 2009; pp. 6582–6589. [Google Scholar]
- Ionescu, C.M.; Copot, D. Hands-on MPC tuning for industrial applications. Bull. Pol. Acad. Sci. Tech. Sci. 2019, 67, 925–945. [Google Scholar]
- Cajo, R.; Agila, W. Evaluation of algorithms for linear and nonlinear PID control for Twin Rotor MIMO System. In Proceedings of the 2015 Asia-Pacific Conference on Computer Aided System Engineering, Quito, Ecuador, 14–16 July 2015; pp. 214–219. [Google Scholar]
- Copot, D.; Ghita, M.; Ionescu, C.M. Simple Alternatives to PID-Type Control for Processes with Variable Time-Delay. Processes 2019, 7, 146. [Google Scholar] [CrossRef]
- Maxim, A.; Ferracuti, R.; Ionescu, C.M. A Theoretical Framework to Determine RHP Zero Dynamics in Sequential Interacting Sub-Systems. Algorithms 2019, 12, 102. [Google Scholar] [CrossRef]
- Haemers, M.; Derammelaere, S.; Rosich, A.; Ionescu, C.M.; Stockman, K. Towards a generic optimal co-design of hardware architecture and control configuration for interacting subsystems. Mechatronics 2019, 63, 102275. [Google Scholar] [CrossRef]
- Ionescu, C.M.; Caruntu, C.F.; Cajo, R.; Ghita, M.; Crevecoeur, G.; Copot, C. Multi-Objective Predictive Control Optimization with Varying Term Objectives: A Wind Farm Case Study. Processes 2019, 7, 778. [Google Scholar] [CrossRef]
- Starr, K.D. Single Loop Control Methods, 1st ed.; ABB Inc.: Westerville, OH, USA, 2015. [Google Scholar]
- Zhao, S.; Maxim, A.; Liu, S.; De Keyser, R.; Ionescu, C.M. Distributed model predictive control of steam/water loop in large scale ships. Processes 2019, 7, 442. [Google Scholar] [CrossRef]
- Samad, T. A survey on industry impact and challenges thereof [technical activities]. IEEE Control Syst. Mag. 2017, 37, 17–18. [Google Scholar]
- Wu, Z.; Li, D.; Xue, Y. A New PID Controller Design with Constraints on Relative Delay Margin for First-Order Plus Dead-Time Systems. Processes 2019, 7, 713. [Google Scholar] [CrossRef]
- Cajo, R.; Zhao, S.; Ionescu, C.M.; De Keyser, R.; Plaza, D.; Liu, S. IMC based PID control applied to the Benchmark PID 18. In Proceedings of the 3rd IFAC Conference in Advances in Proportional-Integral-Derivative Control, Ghent, Belgium, 9–11 May 2018; pp. 728–732. [Google Scholar]
- Zhao, S.; Cajo, R.; Ionescu, C.M.; De Keyser, R.; Liu, S.; Plaza, D. A Robust PID Autotuning Method Applied to the Benchmark PID18. In Proceedings of the 3rd IFAC Conference in Advances in Proportional-Integral-Derivative Control, Ghent, Belgium, 9–11 May 2018; pp. 521–526. [Google Scholar]
- De Keyser, R.; Ionescu, C.M.; Muresan, C.I. Comparative evaluation of a novel principle for PID autotuning. In Proceedings of the 2017 11th Asian Control Conference (ASCC), Gold Coast, QLD, Australia, 17–20 December 2017; pp. 1164–1169. [Google Scholar]
- De Keyser, R.; Muresan, C.I.; Ionescu, C.M. Universal direct tuner for loop control in industry. IEEE Access 2019, 7, 81308–81320. [Google Scholar] [CrossRef]
- Zhao, S.; Maxim, A.; Liu, S.; De Keyser, R.; Ionescu, C. Effect of Control Horizon in Model Predictive Control for Steam/Water Loop in Large-Scale Ships. Processes 2018, 6, 265. [Google Scholar] [CrossRef]
- De Keyser, R.; Muresan, C.I.; Ionescu, C.M. A novel auto-tuning method for fractional order PI/PD controllers. ISA Trans. 2016, 62, 268–275. [Google Scholar] [CrossRef]
- De Keyser, R.; Muresan, C.I.; Ionescu, C.M. Autotuning of a robust fractional order PID controller. IFAC-PapersOnLine 2018, 51, 466–471. [Google Scholar] [CrossRef]
- Copot, C.; Muresan, C.; Ionescu, C.M.; Vanlanduit, S.; De Keyser, R. Calibration of UR10 robot controller through simple auto-tuning approach. Robotics 2018, 7, 35. [Google Scholar] [CrossRef]
- Juchem, J.; Muresan, C.; De Keyser, R.; Ionescu, C.M. Robust fractional-order auto-tuning for highly-coupled MIMO systems. Heliyon 2019, 5, e02154. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Ionescu, C.M.; De Keyser, R.; Liu, S. A Robust PID Autotuning Method for Steam/Water Loop in Large Scale Ships. In Proceedings of the 3rd IFAC Conference in Advances in Proportional-Integral-Derivative Control, Ghent, Belgium, 9–11 May 2018; pp. 462–467. [Google Scholar]
- Åström, K.J.; Hägglund, T. Automatic tuning of simple regulators with specifications on phase and amplitude margins. Automatica 1984, 20, 645–651. [Google Scholar] [CrossRef]

| System Outputs | Operating Points | Range | Units |
|---|---|---|---|
| Drum water level | 1.79 | [1.39–2.19] | m |
| Exhaust manifold pressure | 100.03 | [87.03–133.8] | MPa |
| Deaerator pressure | 30 | [24.9–43.86] | KPa |
| Deaerator water level | 0.7 | [0.49–0.89] | m |
| Condenser water level | 0.5 | [0.32–0.63] | m |
| PID | |||
|---|---|---|---|
| AH | 85.42 | 6.81 | 1.70 |
| PM | 100.66 | 10.46 | 2.62 |
| KR | 52.86 | 12.67 | 3.17 |
| KC | 257.76 | 8.49 | 2.12 |
| Time (s) | 2–300 | 300–600 | 600–900 | 900–1200 | 1200–1500 |
|---|---|---|---|---|---|
| Drum Water Level (m) | 2 | 2 | 2 | 2 | 2 |
| Exhaust Manifold Pressure (MPa) | 100.03 | 116 | 116 | 116 | 116 |
| Deaerator Pressure (KPa) | 30 | 30 | 35 | 35 | 35 |
| Deaerator Water Level (m) | 0.7 | 0.7 | 0.7 | 0.8 | 0.8 |
| Condenser Water Level (m) | 0.5 | 0.5 | 0.5 | 0.5 | 0.6 |
| Loop 1 | Loop 2 | Loop 3 | Loop 4 | Loop 5 | ||
|---|---|---|---|---|---|---|
| AH | 0.83 | 0.28 | 0.27 | 2.77 | 2.87 | |
| 76.62 | 20.48 | 42.00 | 57.77 | 31.69 | ||
| 19.16 | 5.12 | 10.50 | 14.44 | 7.92 | ||
| PM | 0.98 | 0.31 | 0.32 | 3.26 | 3.39 | |
| 117.76 | 24.14 | 49.56 | 88.79 | 48.70 | ||
| 29.44 | 6.03 | 12.39 | 22.20 | 12.17 | ||
| KR | 0.98 | 0.29 | 0.29 | 3.28 | 3.50 | |
| 102.64 | 29.99 | 63.33 | 76.60 | 46.92 | ||
| 25.66 | 7.50 | 15.83 | 19.15 | 11.73 | ||
| KC | 2.47 | 0.33 | 0.31 | 8.34 | 8.67 | |
| 96.24 | 31.48 | 64.56 | 72.02 | 39.50 | ||
| 24.06 | 7.87 | 16.14 | 18.01 | 9.88 |
| Index | Autotuners | Loop 1 | Loop 2 | Loop 3 | Loop 4 | Loop 5 |
|---|---|---|---|---|---|---|
| AH | 2.2063 | 1.5750 | 2.7951 | 3.6710 | 4.9961 | |
| PM | 2.9400 | 1.5464 | 2.6325 | 4.7586 | 6.3090 | |
| KR | 2.5294 | 1.5087 | 3.1779 | 4.0973 | 5.9431 | |
| KC | 1.2606 | 1.4744 | 3.2924 | 2.0025 | 2.8126 | |
| AH | 0.0288 | 1.0234 | 0.1766 | 0.2405 | 2.9971 | |
| PM | 0.0425 | 0.9210 | 0.1799 | 0.2934 | 2.9572 | |
| KR | 0.0345 | 0.8095 | 0.2205 | 0.2586 | 2.9566 | |
| KC | 0.0204 | 0.7241 | 0.2043 | 0.1284 | 2.6393 |
| Index | loops | AH vs. PM | AH vs. KR | AH vs. KC | PM vs. KR | PM vs. KC | KR vs. KC |
|---|---|---|---|---|---|---|---|
| loop 1 | 0.7504 | 0.8723 | 1.7502 | 1.1623 | 2.3322 | 2.0064 | |
| loop 2 | 1.0185 | 1.0440 | 1.0683 | 1.0250 | 1.0488 | 1.0233 | |
| loop 3 | 1.0618 | 0.8795 | 0.8490 | 0.8284 | 0.7996 | 0.9652 | |
| loop 4 | 0.7715 | 0.8960 | 1.8332 | 1.1614 | 2.3763 | 2.0461 | |
| loop 5 | 0.7919 | 0.8406 | 1.7763 | 1.0616 | 2.2431 | 2.1130 | |
| loop 1 | 0.6768 | 0.8342 | 1.4100 | 1.2325 | 2.0834 | 2.0834 | |
| loop 2 | 1.1112 | 1.2643 | 1.4134 | 1.1377 | 1.2720 | 1.2720 | |
| loop 3 | 0.9813 | 0.8007 | 0.8645 | 0.8159 | 0.8810 | 0.8810 | |
| loop 4 | 0.8199 | 0.9301 | 1.8739 | 1.1344 | 2.2855 | 2.2855 | |
| loop 5 | 1.0135 | 1.0137 | 1.1356 | 1.0002 | 1.1205 | 1.1205 | |
| J | 0.8997 | 0.9375 | 1.3974 | 1.0559 | 1.6442 | 1.5796 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, S.; Liu, S.; De Keyser, R.; Ionescu, C.-M. The Application of a New PID Autotuning Method for the Steam/Water Loop in Large Scale Ships. Processes 2020, 8, 196. https://doi.org/10.3390/pr8020196
Zhao S, Liu S, De Keyser R, Ionescu C-M. The Application of a New PID Autotuning Method for the Steam/Water Loop in Large Scale Ships. Processes. 2020; 8(2):196. https://doi.org/10.3390/pr8020196
Chicago/Turabian StyleZhao, Shiquan, Sheng Liu, Robain De Keyser, and Clara-Mihaela Ionescu. 2020. "The Application of a New PID Autotuning Method for the Steam/Water Loop in Large Scale Ships" Processes 8, no. 2: 196. https://doi.org/10.3390/pr8020196
APA StyleZhao, S., Liu, S., De Keyser, R., & Ionescu, C.-M. (2020). The Application of a New PID Autotuning Method for the Steam/Water Loop in Large Scale Ships. Processes, 8(2), 196. https://doi.org/10.3390/pr8020196