CFD Simulation of Forced Recirculating Fired Heated Reboilers
Abstract
1. Introduction
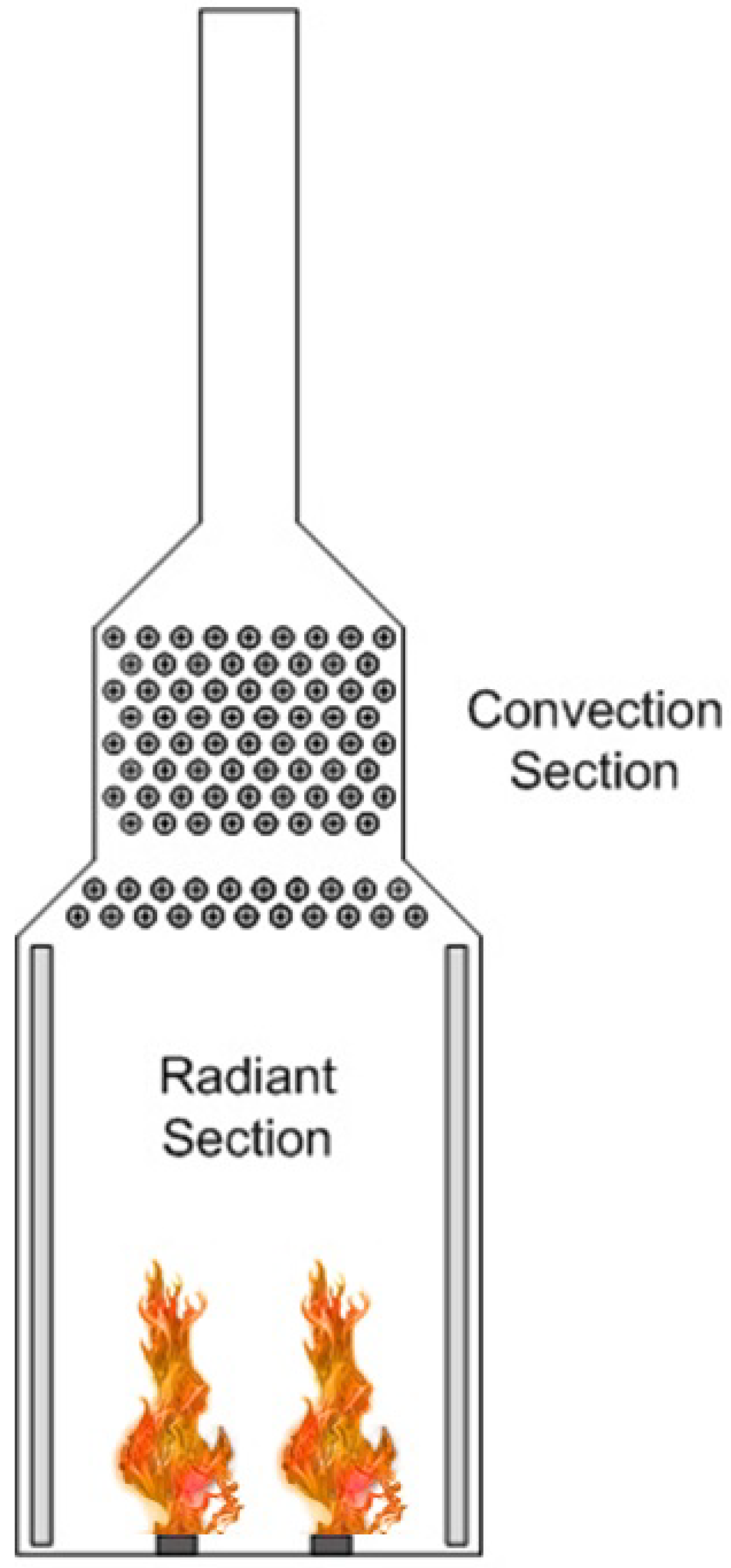
1.1. Fired Heated Furnaces
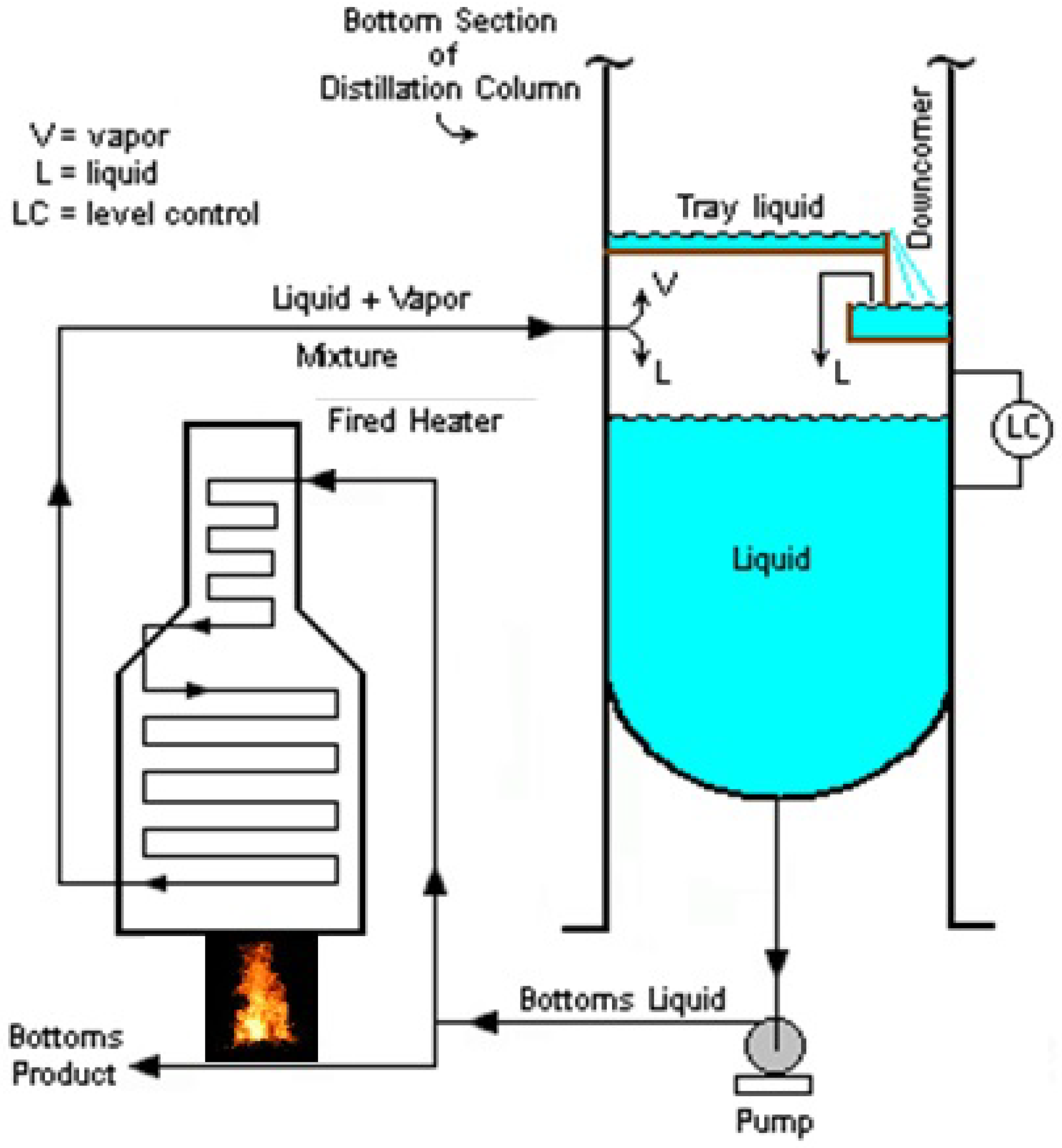
1.2. Reboiler
- (1)
- Forced Recirculation Reboiler
- (2)
- Thermosiphon Natural Circulation Reboiler
- (3)
- Kettle type
- (4)
- Forced Recirculating Fired Heated Reboiler (see Figure 2)
1.3. Two-Phase Flow Heat Transfer Inside the Reboiler
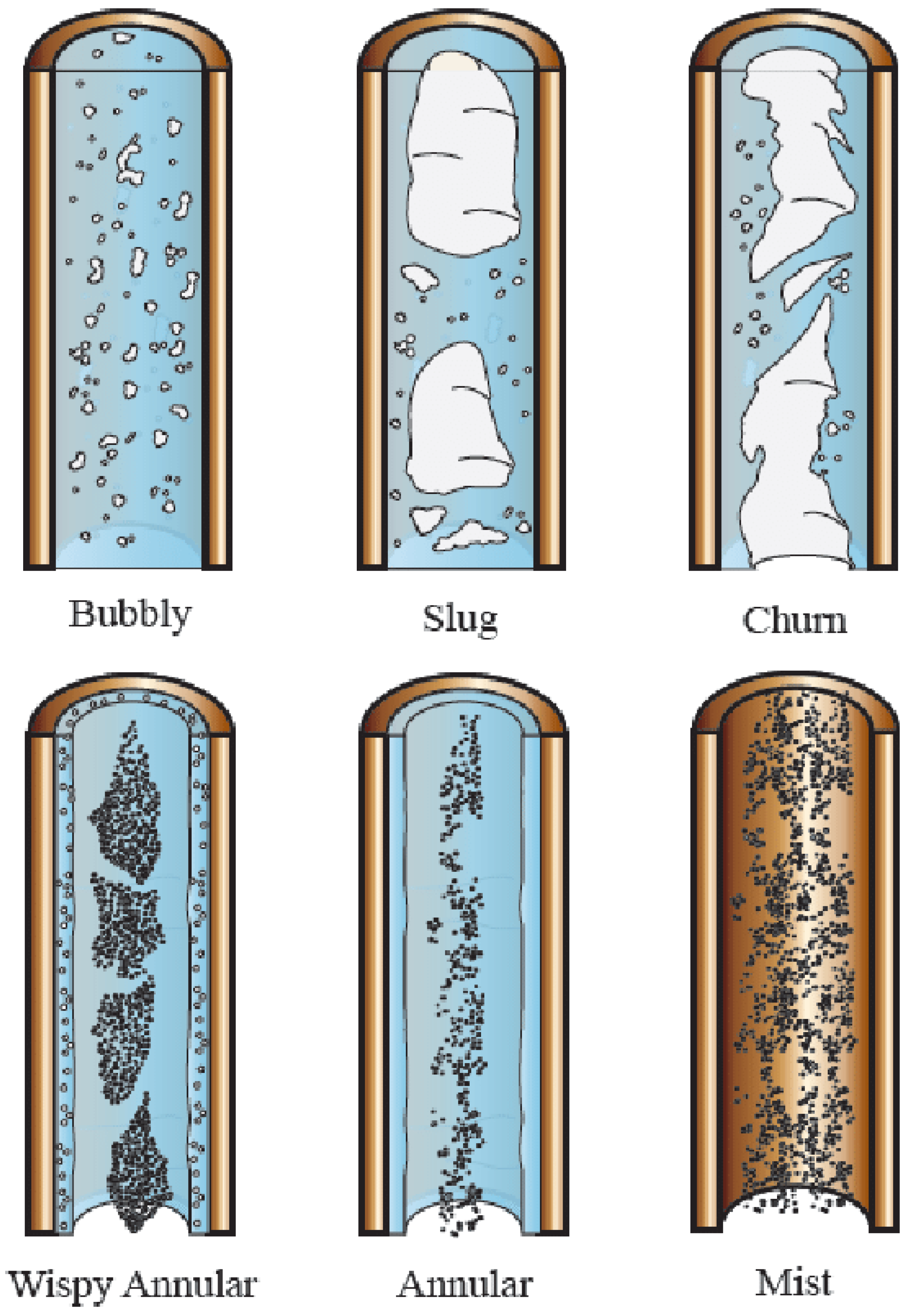
The Definition of Flow Regimes
- (1)
- Bubble flow—the bubbles dispersed in a continuum of liquid
- (2)
- Slug or plug flow—as the concentration of bubbles increases, the bubble coalescence occurs and, progressively, the bubble diameter approaches that of the tube. Once this occurs, the bubble is bullet-shaped.
- (3)
- Churn Flow—as the gas flow is increased and the velocity of the slug-flow bubbles increased, the break-down of these bubbles occurs, leading to unstable regime. For narrow-bore tubes the oscillations may not occur and a smoother transition between the slug and annular flow may be observed.
- (4)
- Annular flow—in this regime, the liquid flows on the wall of the tubes as a film and the gas phase flows in the center. Some of the liquid phase is entrained as small droplets in the gas core.
- (5)
- Wispy annular flow—for high mass velocity flows, the droplet concentration in the gas core of annular flow increases and, ultimately droplet coalescence occurs, leading to streaks or “wisps” of liquid occurring in the gas core.
2. Materials and Methods
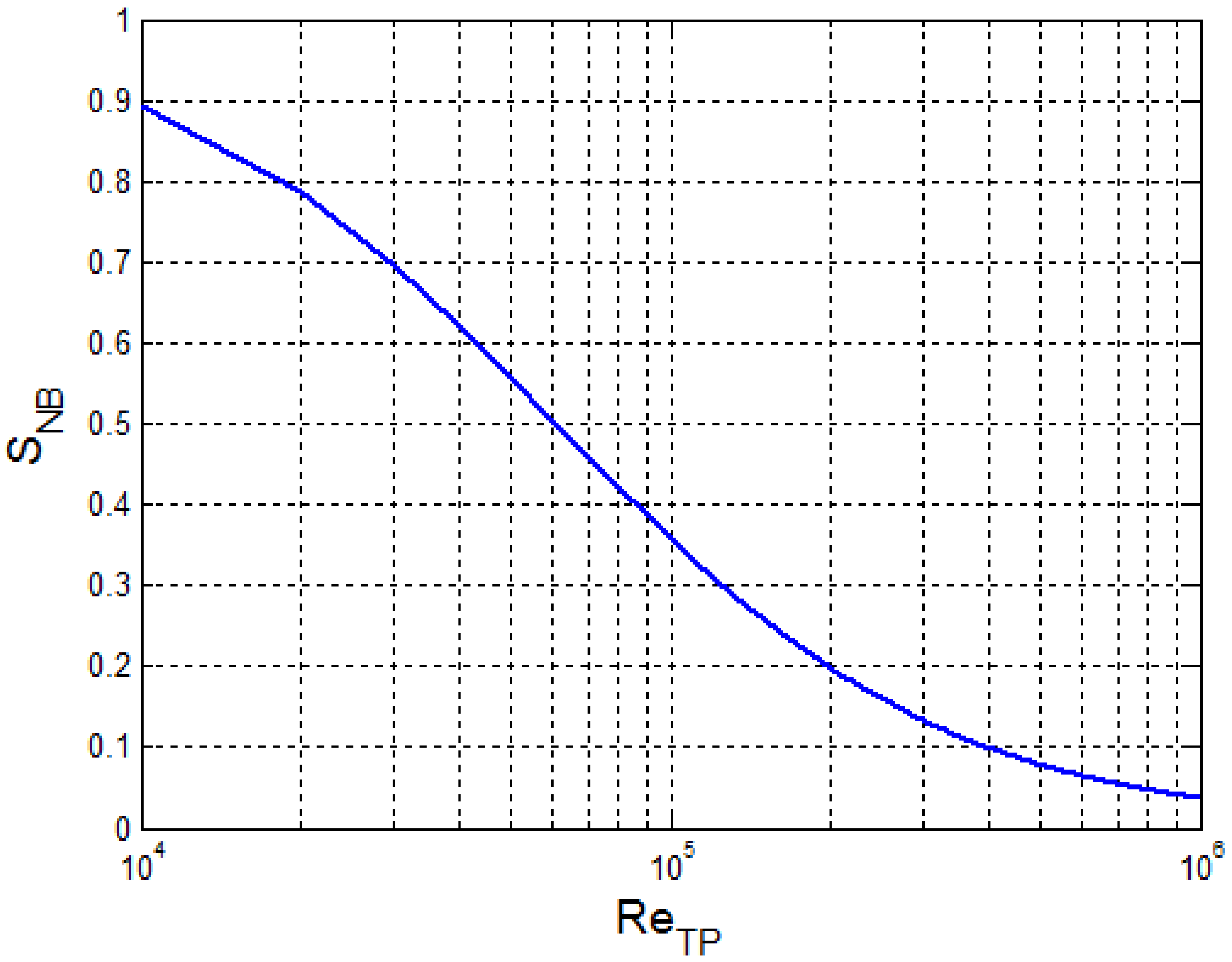
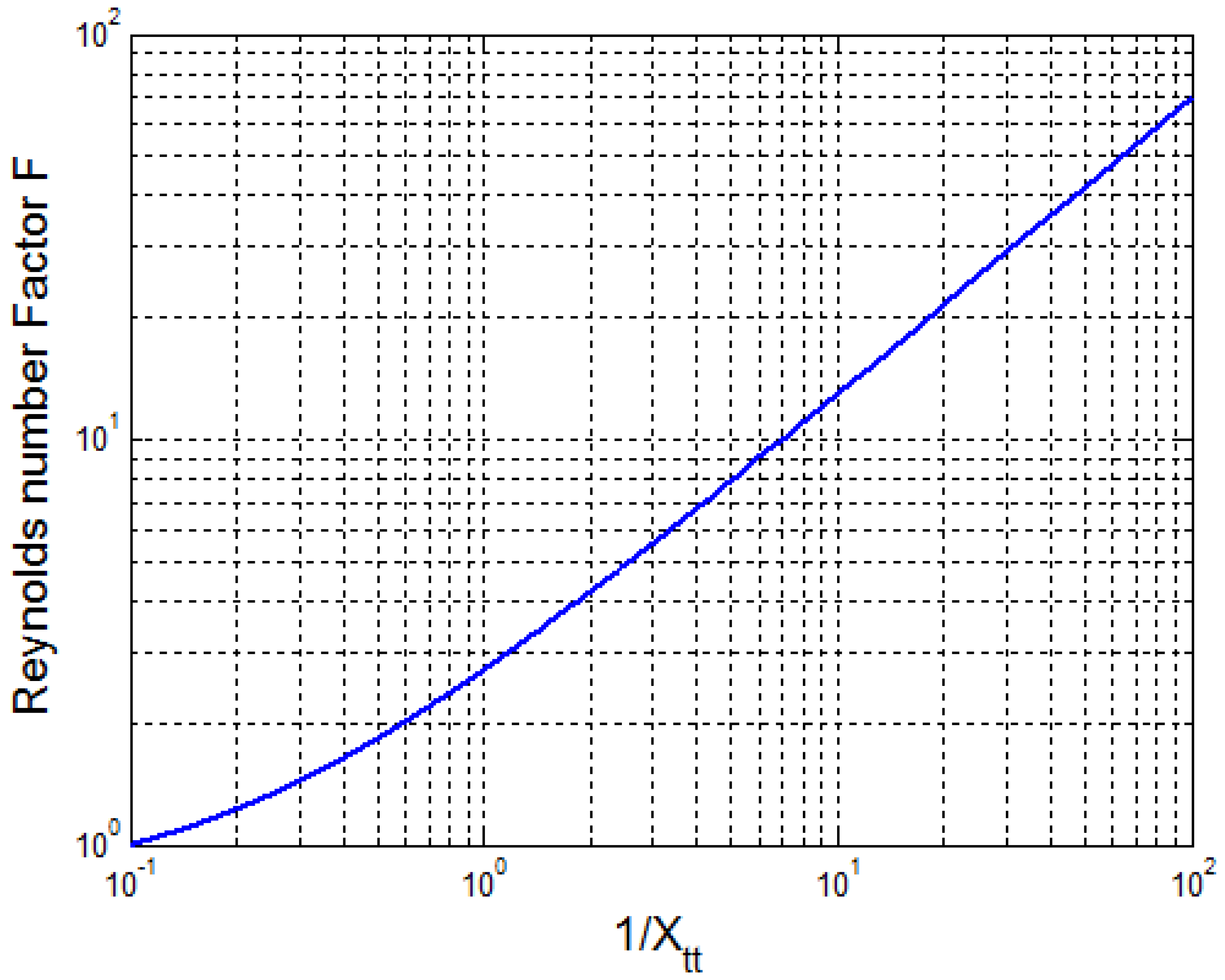
2.1. Calculation of Nucleate Boiling Convective Coefficient
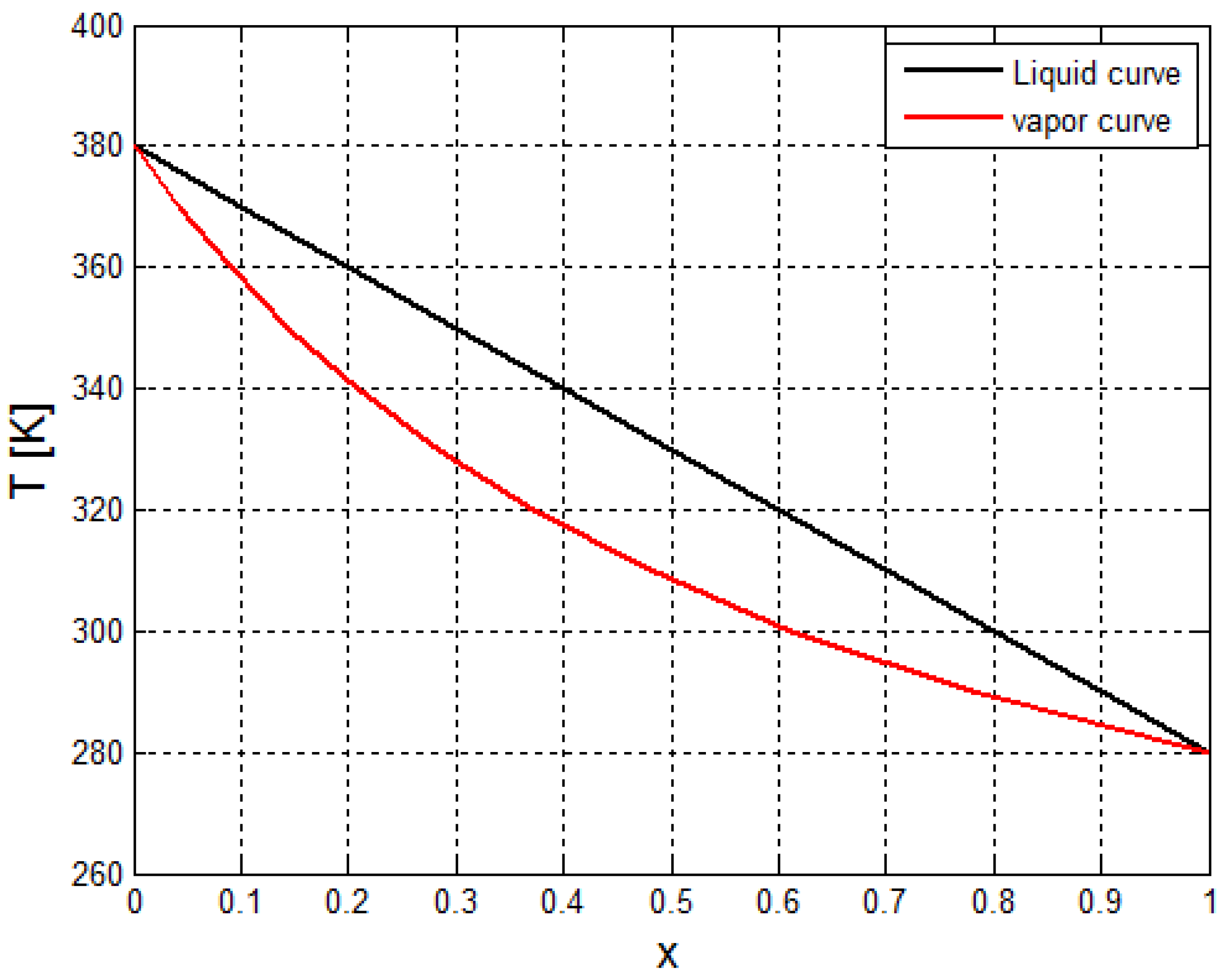
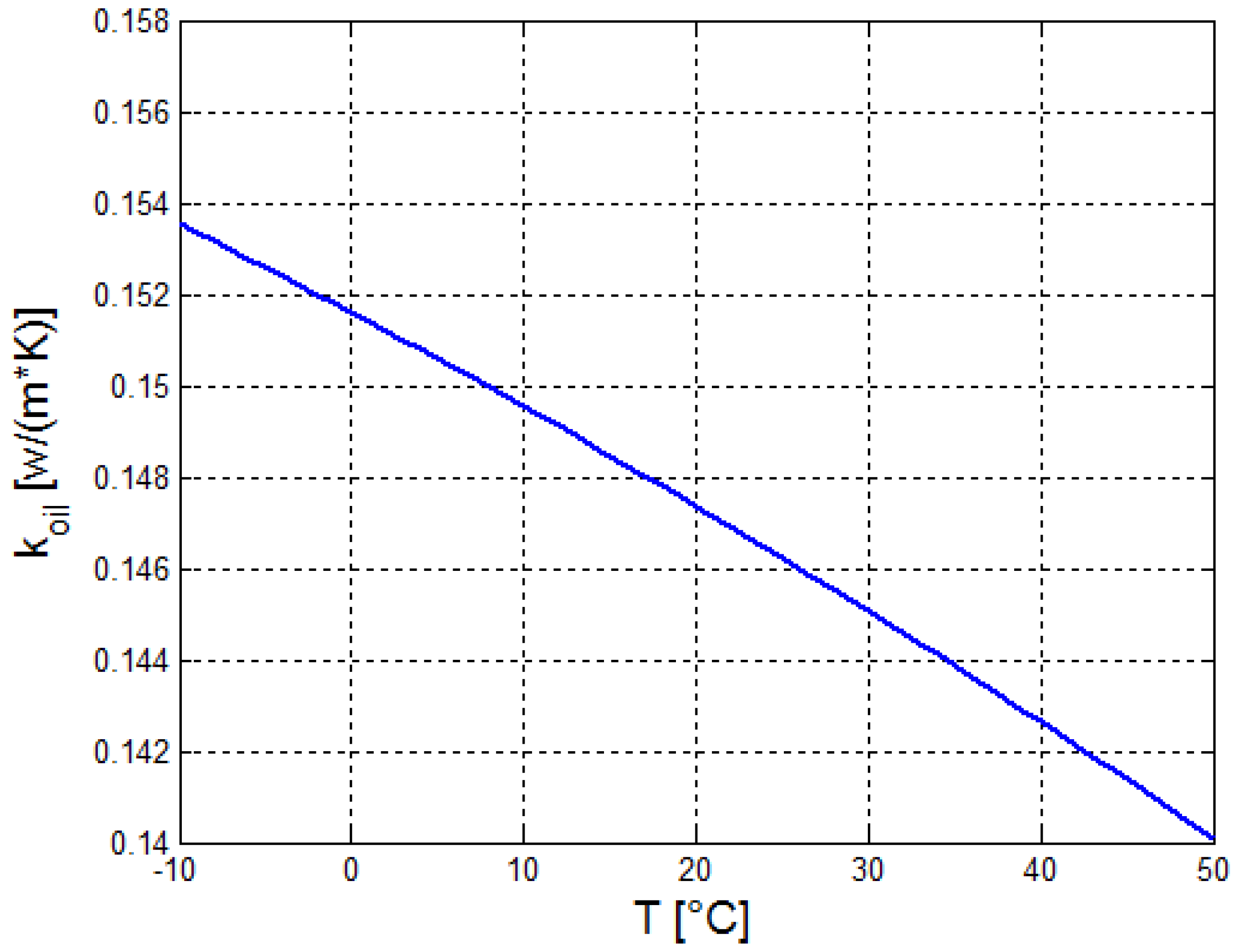
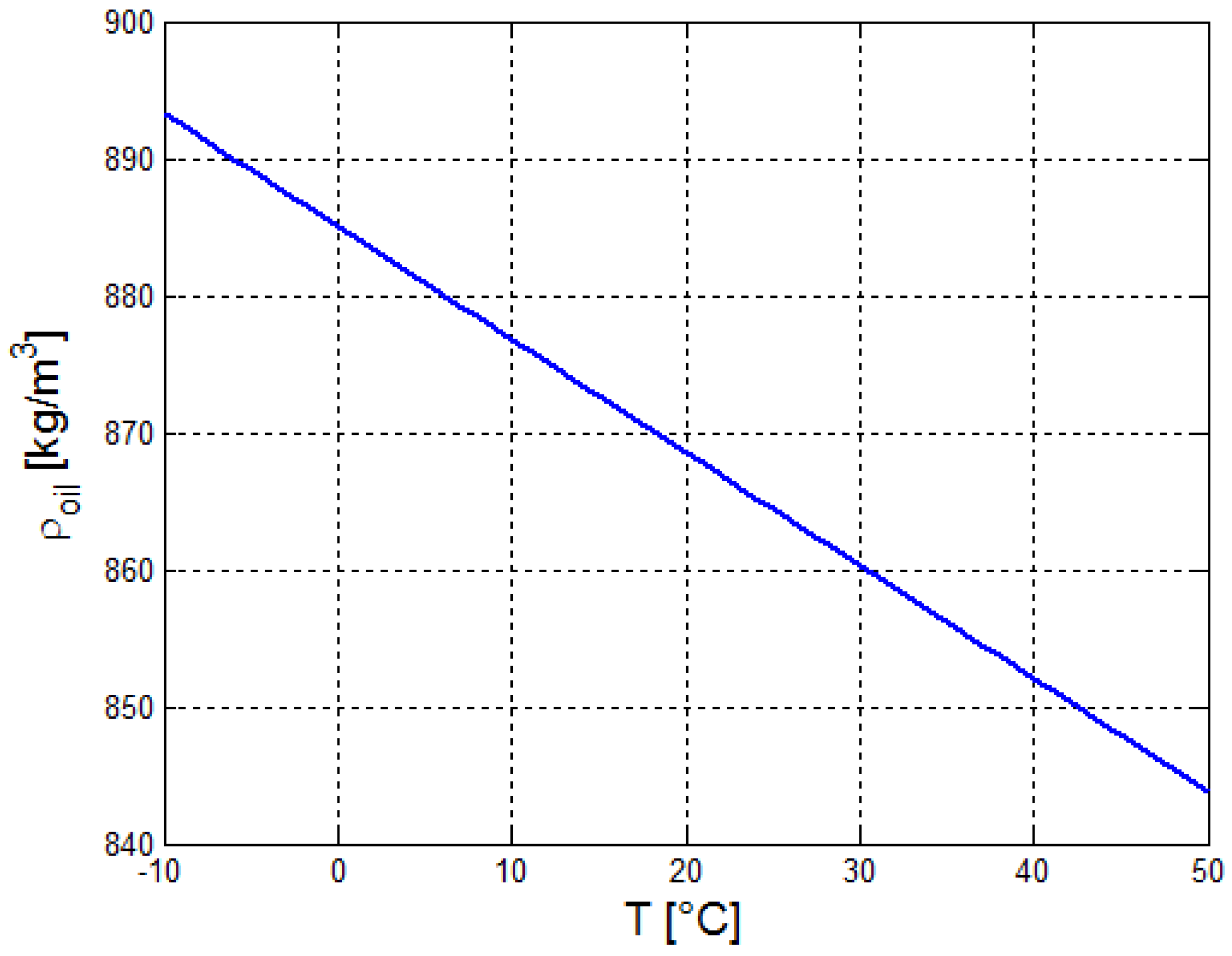
2.2. Estimation of the Thermo-Physical Properties of the Crude Oil
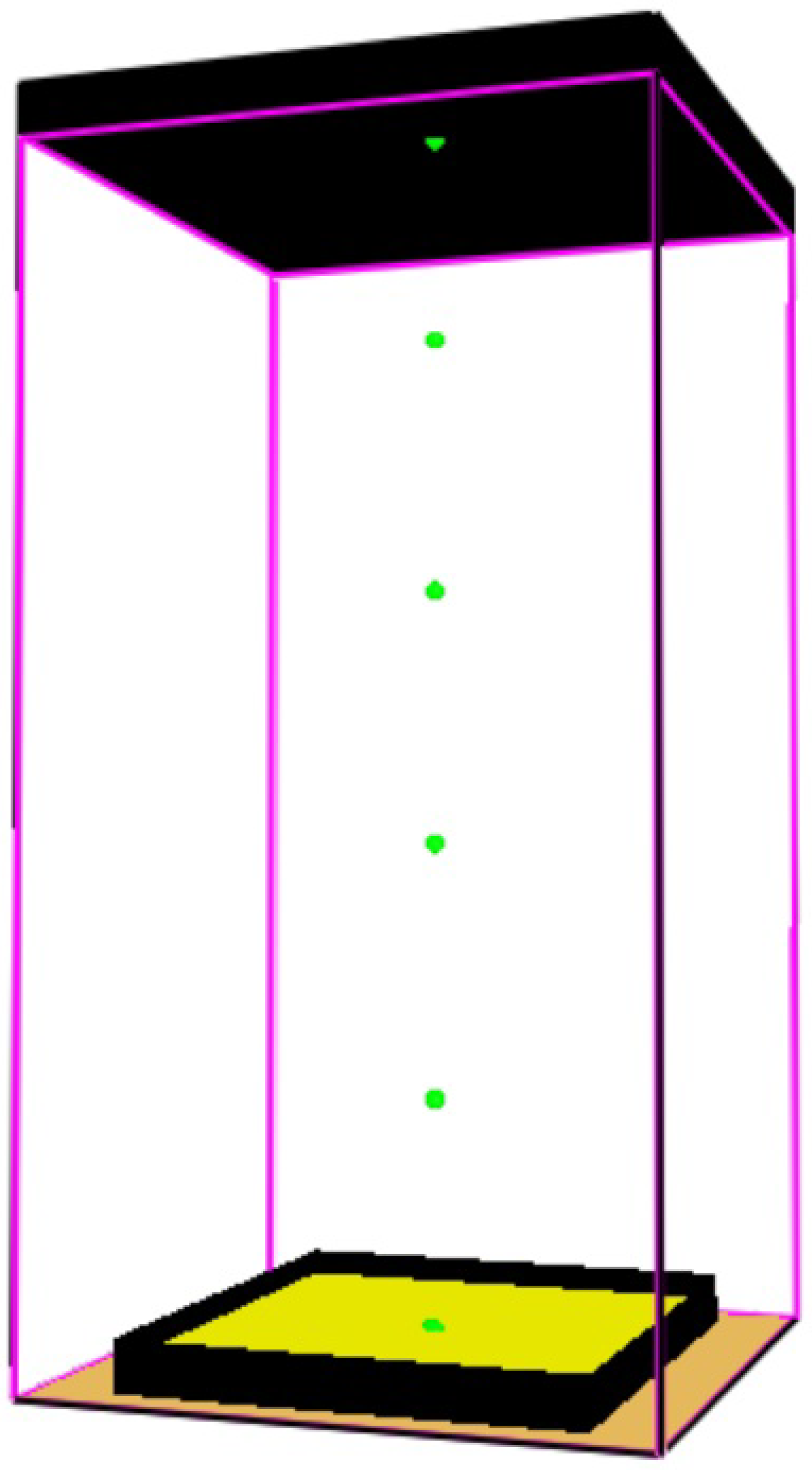
2.3. Fire Dynamic Simulation (FDS) Modeling of the Fired Heater
2.4. Governing Transport Equations of FDS Software
2.4.1. Mass and Species Transport Equations
2.4.2. Momentum Transport Equation
2.4.3. Large Eddy Simulation (LES) Turbulence Method
2.4.4. Energy Transport Equation
2.4.5. Equation of State
2.4.6. Fire Dynamics Simulation (FDS) Modeling of the Heptane Burner
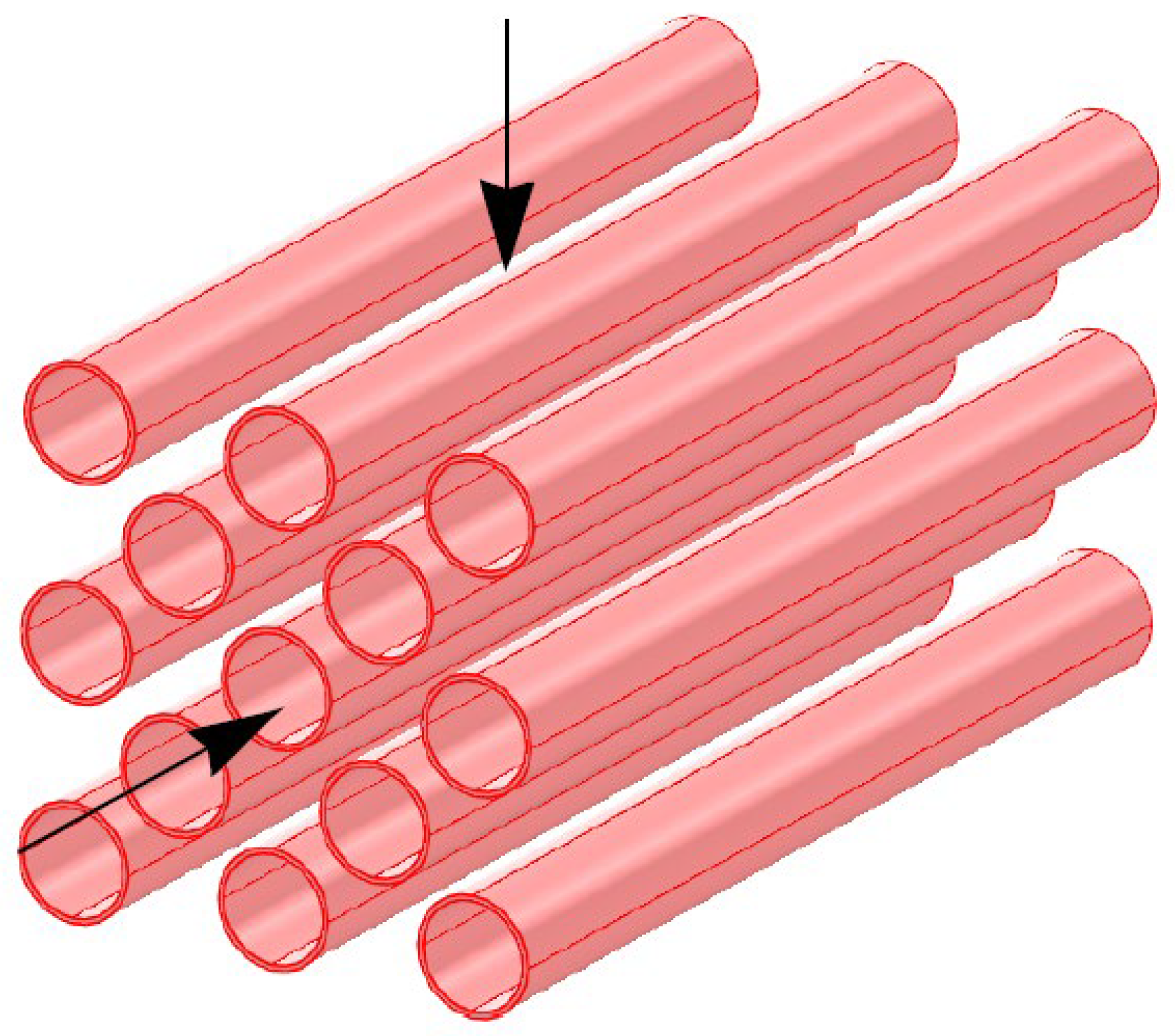
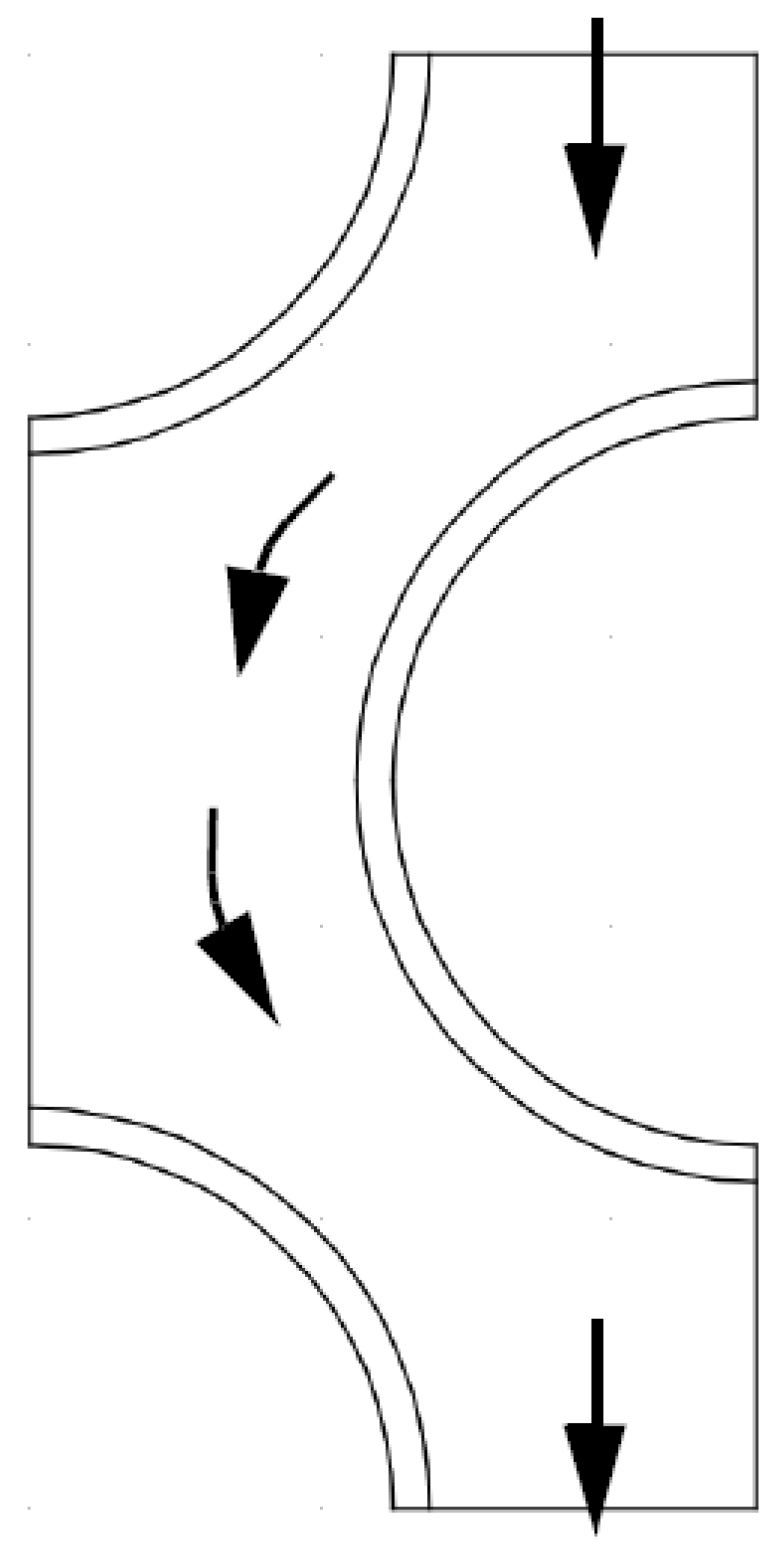
2.5. Turbulent Flow through Reboiler tube bundle
2.6. Convective Heat Transfer across Banks of Tubes
2.7. Calcaulation of the Radiative Heat Flux Emitted by the Mixture Flue Gaseous and the Soot Particles
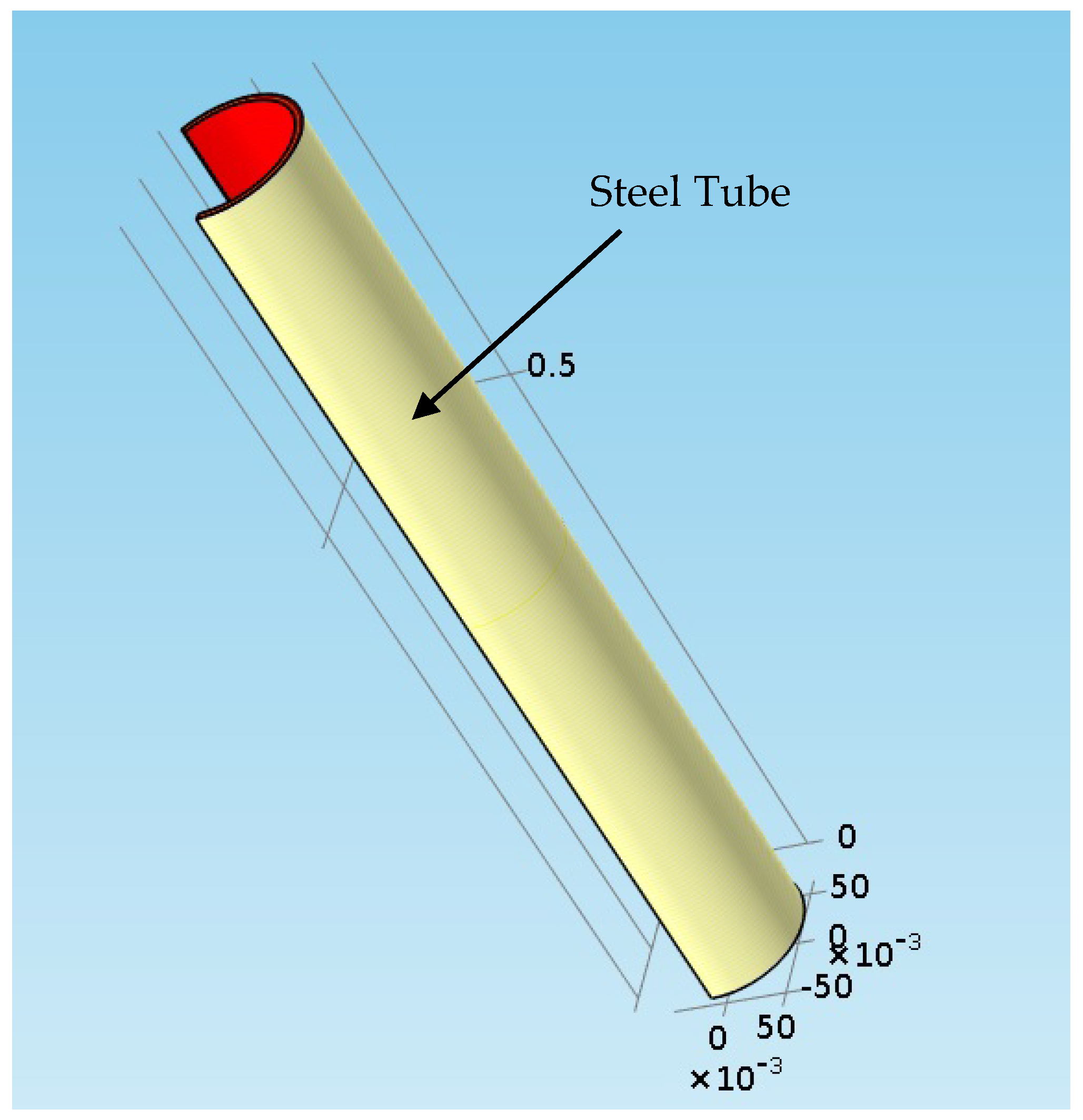
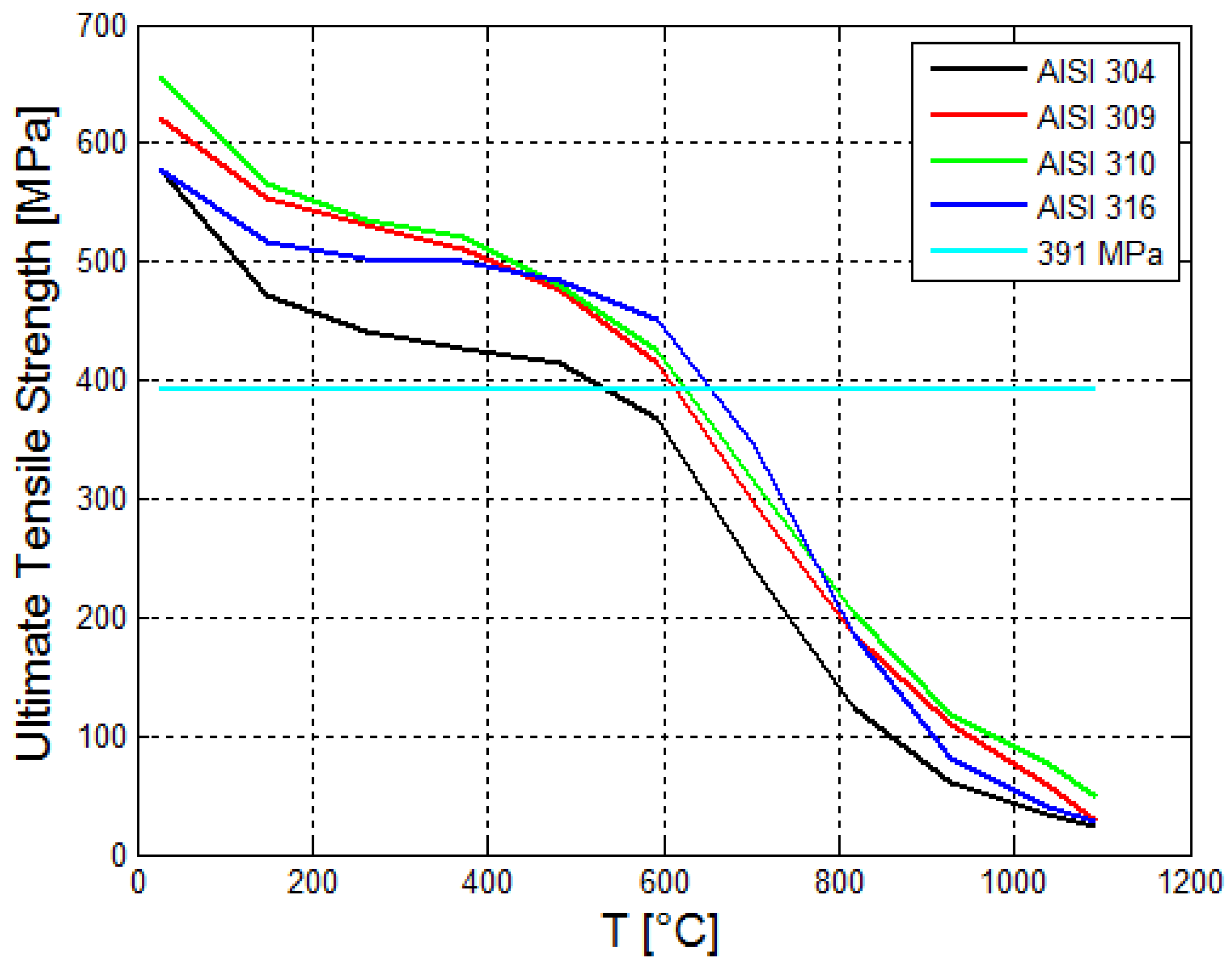
2.8. Thermal Structural Analysis—Reboiler Steel Tube
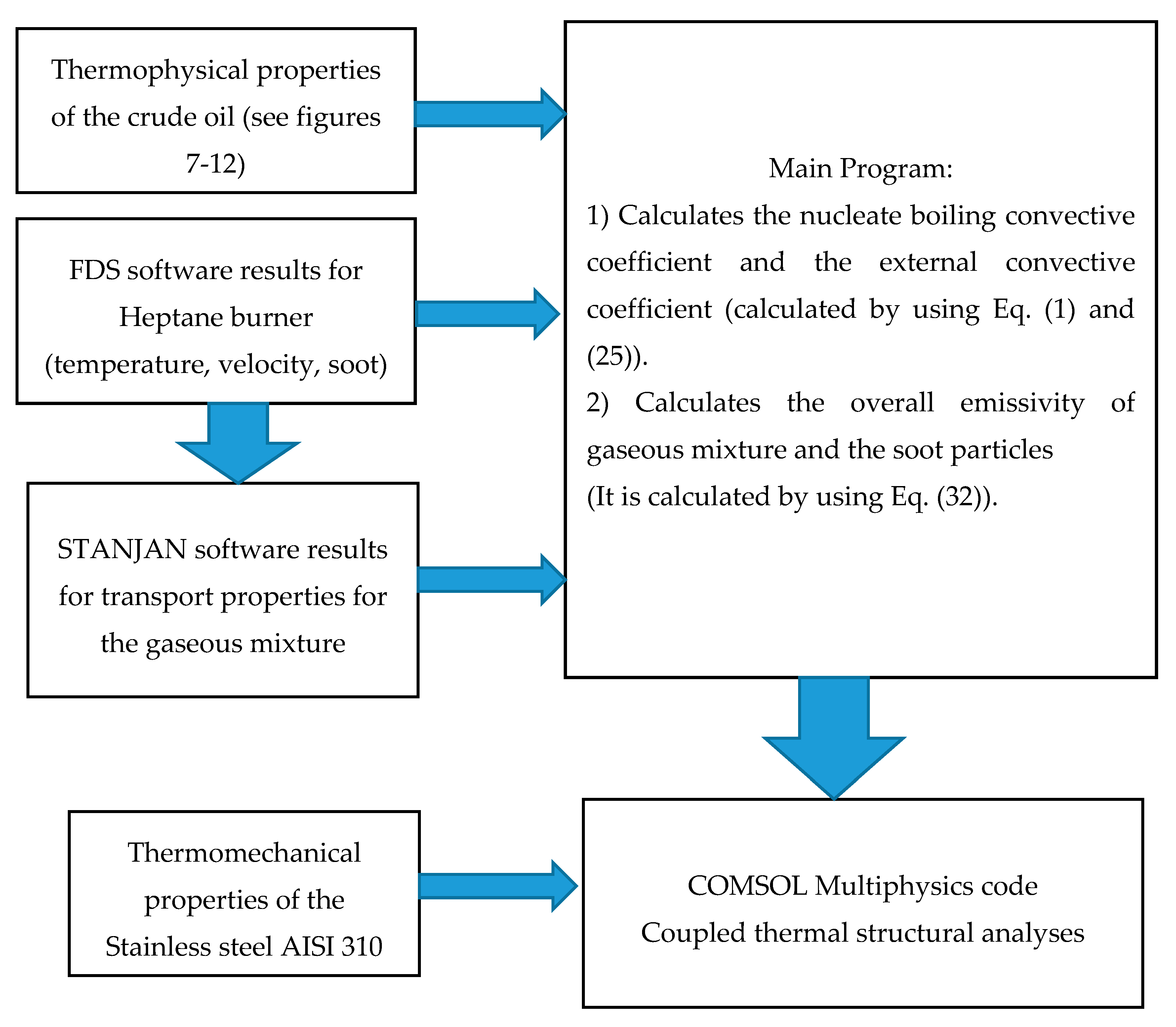
2.9. Structure of the Compoutation Process
3. Results.
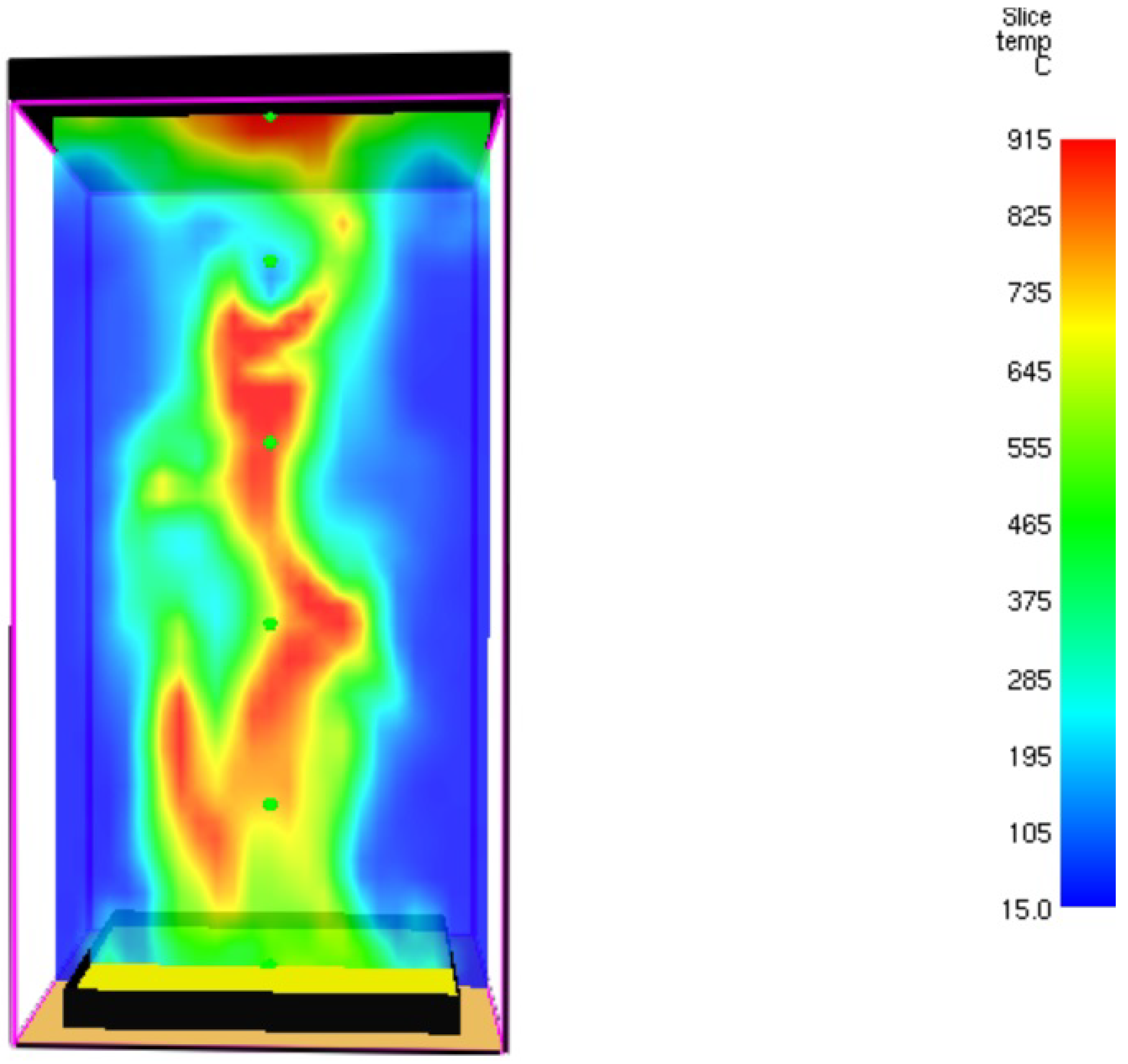
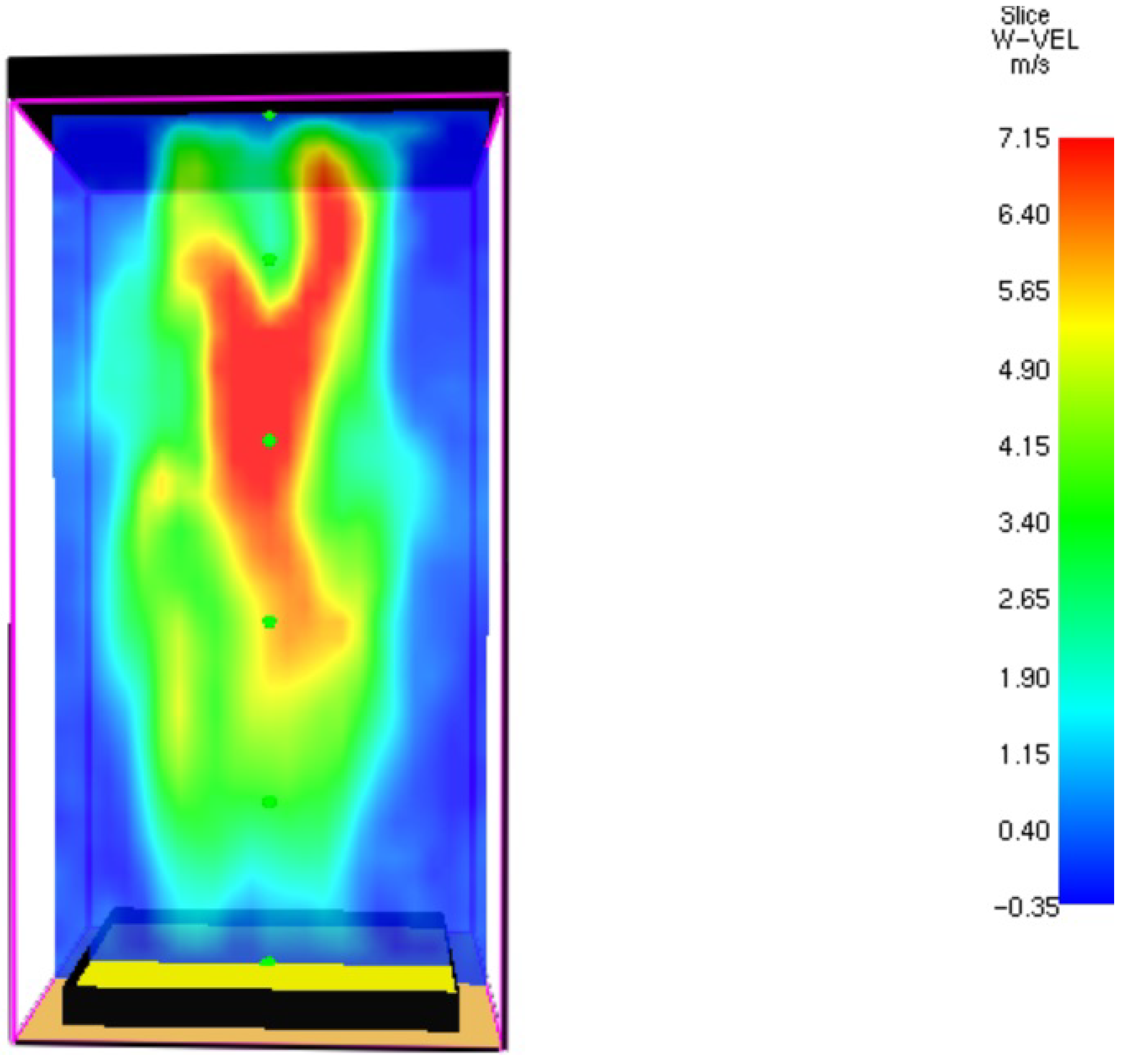
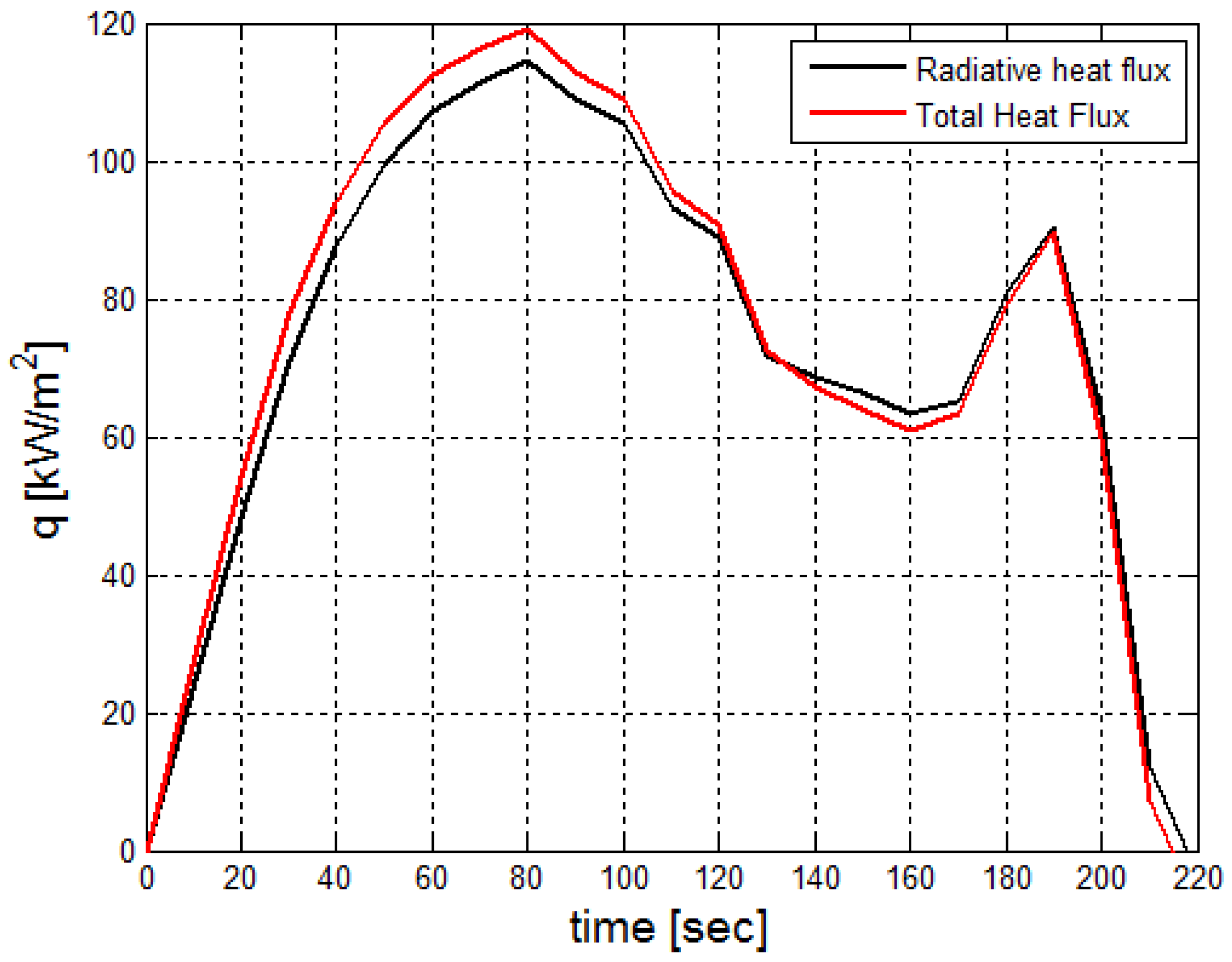
3.1. Fire Dynamics Simulator Software Results for Heptane Burner
3.2. Calculation and Validation Results for the Nucleate Boiling Convective Coefficient
3.3. Thermal Structural Analyses Results for the Reboiler Tube
4. Discussion
5. Conclusions
Funding
Conflicts of Interest
References
- Sciance, C.T. Pool Boiling Heat Transfer to Liquefied Hydrocarbon Gases. Ph.D. Thesis, College of Chemical Engineering, University of Oklahoma, Norman, OA, USA, 1966. [Google Scholar]
- Noyes, R.C. An Experimental Study of Sodium Pool Boiling Heat Transfer. J. Heat Transf. 1963, 85, 125. [Google Scholar] [CrossRef]
- Zhu, M. Large Eddy Simulation of Thermal Cracking in Petroleum Industry. Ph.D. Thesis, Institute National Polytechnique de Toulouse, Toulouse, France, 2015. [Google Scholar]
- Walker, W.H.; Lewis, W.K.; McAdams, W.H.; Gilliland, E.R. Principles of Chemical Engineering; McGraw-Hill Book Company, Inc.: New York, NY, USA, 1937. [Google Scholar]
- Pludek, V.R. Design and Corrosion Control; The Macmillan Press Ltd.: London, UK, 1977. [Google Scholar]
- Dowtherm, A. Heat Transfer Fluid, Product Technical Tool. Available online: http://www.dow.com/heattrans (accessed on 4 February 2017).
- Chechetkin, A.V. High Temperature Heat Carriers; Sinclair, F.A., Ed.; The Macmillan Press Ltd.: New-York, NY, USA, 1963. [Google Scholar]
- Sharar, D.; Jankowski, N.; Bar Cohen, A. Two Phase Fluid Selection for High Temperature Automotive Platforms; ARL-TR-6171; U.S Army Research Laboratory (ARL): Adelphi, MD, USA, 2012.
- Davidy, A. Proposal of an Alternative UAV Engine Organic Coolants; MDPI: Basel, Switzerland, 2018. [Google Scholar] [CrossRef]
- Garg, A. Get the Most from Your Fired Heaters, Chemical Engineering; McGraw Hill Book Company Incorporated then Chemical Week Publishing: New York, NY, USA, 2004. [Google Scholar]
- Mullinger, P.; Jenkins, B. Industrial and Process Furnaces Principles, Design and Operation, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2014. [Google Scholar]
- Lewis, B.; Von Elbe, G. Combustion Flames and Explosion of Gases, 2nd ed.; Academic Press Inc.: New York, NY, USA; London, UK, 1961. [Google Scholar]
- Heywood, J.B. Internal Combustion Engine Fundamentals; McGraw-Hill Book Company: New York, NY, USA, 1988. [Google Scholar]
- Davidy, A. CFD Simulation of Ethanol Steam Reforming System for Hydrogen Production. ChemEngineering 2018, 2, 34. [Google Scholar] [CrossRef]
- Whalley, P.B.; Hewitt, G.F. Multiphysics Science and Technology; Chapter 4: Reboilers in Hewitt, G.F. Delhaye, G.M. Zuber, N.; Springer-Verlag: Berlin/Heidelberg, Germany, 1986. [Google Scholar]
- Hewitt, G.F. Chapter 2: Flow Patterns in Butterworth, D. & Hewitt, G.F. In Two Phase Flow and Heat Transfer; Oxford University Press: Oxford, UK, 1977. [Google Scholar]
- Chen, J.C. A Correlation for Boiling Heat Transfer to Saturated Fluids in Convective Flow. ASME paper 63-HT-34; 1963. Available online: https://www.osti.gov/biblio/4636495-correlation-boiling-heat-transfer-saturated-fluids-convective-flow (accessed on 18 August 2019).
- Todreas, N.E.; Kazimi, M.S. Nuclear Systems I Thermal Hydraulic Fundamentals; Taylor & Francis: Boca Raton, FL, USA, 1993. [Google Scholar]
- Forster, K.; Zuber, N. Dynamics of Vapor Bubbles and Boiling Heat Transfer. AIChE J. 1955, 1, 531–535. [Google Scholar] [CrossRef]
- McCabe, W.L.; Smith, J.C.; Harriott, P. Unit Operations of Chemical Engineering, 2nd ed.; McGraw-hill Book Company: New York, NY, USA, 1967. [Google Scholar]
- Stephan, K.; Preusser, P. Heat Transfer in Natural Convection Boiling of Polynary Mixtures. In Proceedings of the 6th International Heat Transfer Conference, Toronto, ON, Canada, 7–11 August 1978. [Google Scholar]
- Fahim, M.A.; Al-Sahhaf, T.A.; Elkiani, A.S. Fundamentals of Petroleum Refining, 1st ed.; Elsevier: Oxford, UK, 2010. [Google Scholar]
- Ancheyta, J. Modelling and Simulation of Catalytic Reactors for Petroleum Refining; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Das, D.K.; Nerella, S.; Kulkarni, D. Thermal Properties of Petroleum and Gas-to-liquid Products. Pet. Sci. Technol. 2007, 25, 415–425. [Google Scholar] [CrossRef]
- United States Department of Commerce. Thermal properties of Petroleum Products; United States Government Printing Office: Washington, WA, USA, 1929.
- Abdul-Majeed, G.H.; Abu Al-Soof, N.B. Estimation of gas–oil surface Tension. J. Pet. Sci. Eng. 2000, 27, 197–200. [Google Scholar] [CrossRef]
- Riazi, M.R.; Al-Sahhaf, T.A. Physical properties of heavy petroleum fractions and crude oils. Fluid Phase Equilib. 1996, 117, 217–224. [Google Scholar] [CrossRef]
- McGrattan, K. Fire Dynamics Simulator (Version 5)—Technical Reference Guide Volume 1: Mathematical Model; NIST Special Publication 1018; National Institute of Standards and Technology, U.S. Department of Commerce: Gaithersburg, MD, USA, 2010.
- McGrattan, K.; Forney, G.P. Fire Dynamics Simulator (Version 5)—User’s Guide; NIST Special Publication 1019; National Institute of Standards and Technology, U.S. Department of Commerce: Gaithersburg, MD, USA, 2010.
- McGrattan, K. Numerical Simulation of the Caldecott Tunnel Fire, April 1982; NISTIR 7231; National Institute of Standards and Technology, U.S. Department of Commerce: Gaithersburg, MD, USA, 2005.
- Furnace Improvements. Fired Heaters for General Refinery Service API 560 Standard—1986–2016. 2017. Available online: https://static1.squarespace.com/static/5659c9cde4b05079e4b0c3d9/t/5bbc865a0852296a3725ed62/1539081888920/API560-Comparison-All-in-One-05.12.17-Rev+C.pdf (accessed on 18 August 2019).
- Iqbal, N.; Salley, M.H. Fire Dynamics Tools (FDTs) Quantitative Fire Hazard Analysis Methods for the U.S. Nuclear Regulatory Commission Fire Protection Inspection Program, NUREG-1805; Prepared for Division of Systems Safety and Analysis Office of Nuclear Reactor Regulation: Washington, DC, USA, 2003.
- Thermal Conductivity of Heptane. Available online: https://www.engineeringtoolbox.com/thermal-conductivity-liquids-d_1260.html (accessed on 18 August 2019).
- Specific Heat of Heptane. Available online: https://www.engineeringtoolbox.com/specific-heat-fluids-d_151.html (accessed on 18 August 2019).
- Desity of Heptane. Available online: https://www.engineeringtoolbox.com/liquids-densities-d_743.html (accessed on 18 August 2019).
- Staffansson, L. Selecting Design Fires; Lund University: Lund, Sweden, 2010. [Google Scholar]
- Grimison, E.D. Correlation and Utilization of New Data on Flow Resistance and Heat Transfer for Cross Flow of Gases Over Tube Banks. Trans. ASME 1937, 59, 583–594. [Google Scholar]
- Incropera, F.P.; Dewitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 6th ed.; John Wiley and Sons: New York, NY, USA, 2007. [Google Scholar]
- Transport Property Evaluation Website, Colorado State University Bioanalytical Microfluidics Program Chemical and Biological Engineering. Available online: http://navier.engr.colostate.edu/code/code-2/index.html (accessed on 30 September 2019).
- Beer, J.M. Methods for Calculating Radiative Heat Transfer from Flames in Combustors and Furnaces, Chapter 2 in Heat Transfer in Flames; Afgan, N.H., Beer, J.M., Eds.; Scripta Book Company: Washington, WA, USA, 1974. [Google Scholar]
- COMSOL Multiphysics—Modeling Guide, Version 4.3b. Comsol AB, Tegnérgatan 23 SE-111 40 Stockholm Sweden. 2013. Available online: https://cdn.comsol.com/doc/4.3b/COMSOL_ReleaseNotes.pdf (accessed on 18 August 2019).
- Mostinski, I.L. Calculation of boiling heat transfer coefficients, based on the law of corresponding states. Teploenergetika 4, 66; English abstract in Brit. Chem. Eng. 1963, 8, 580. [Google Scholar]
- American Iron and Steel Institute. High. Temperature Characteristics of Stainless Steels, A Designer’s Handbook Series, No. 9004; AISI: Washington, WA, USA, 2011. [Google Scholar]
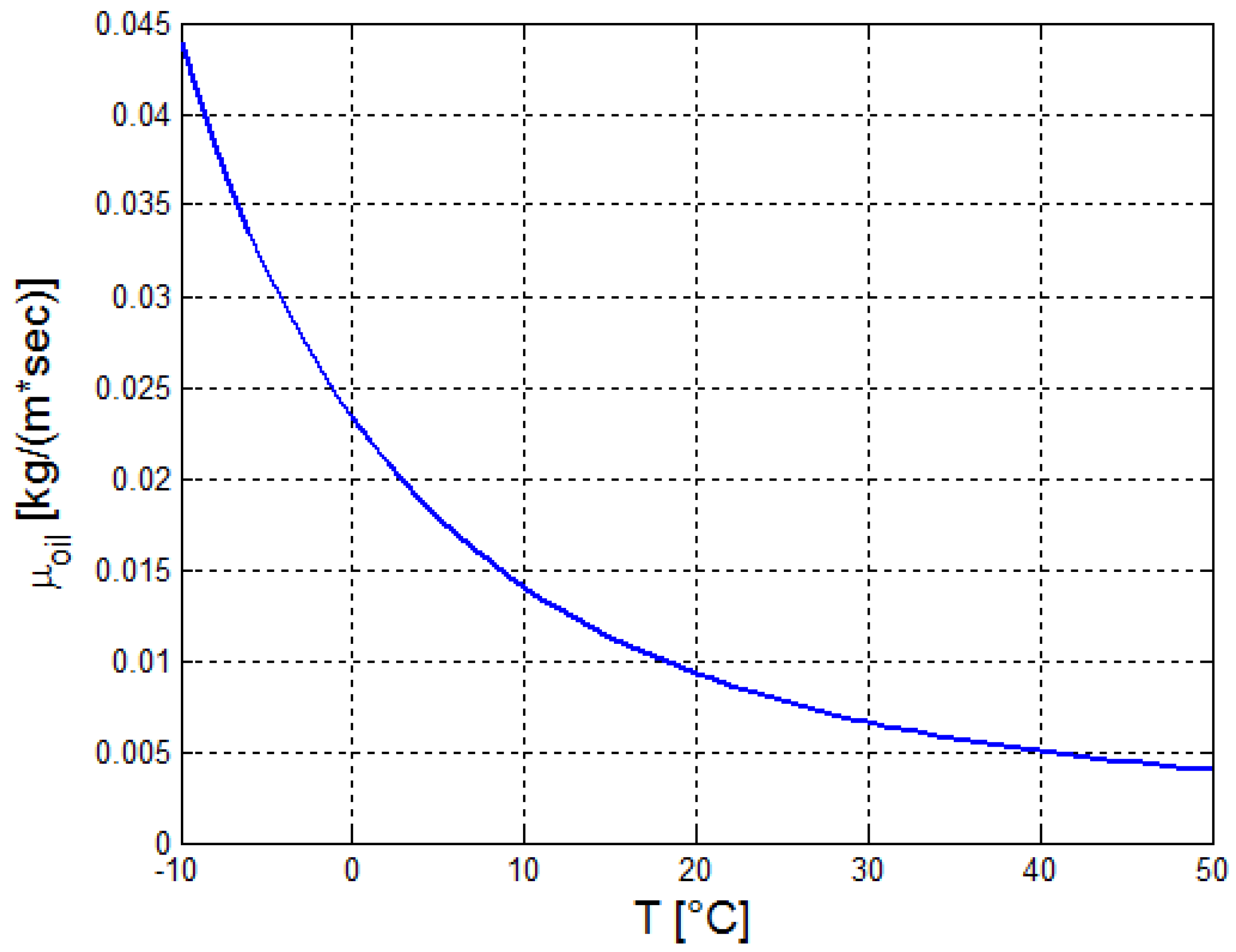
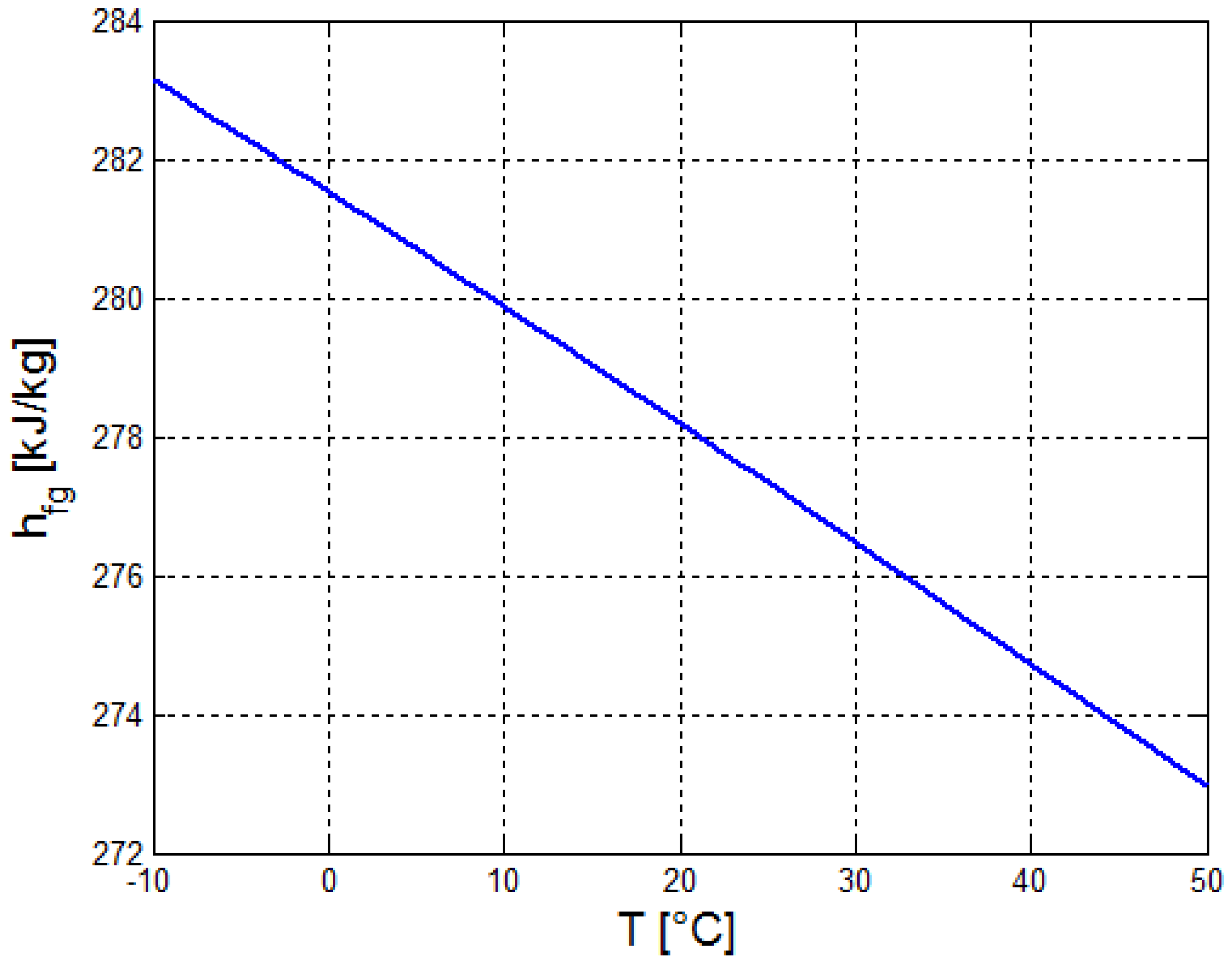
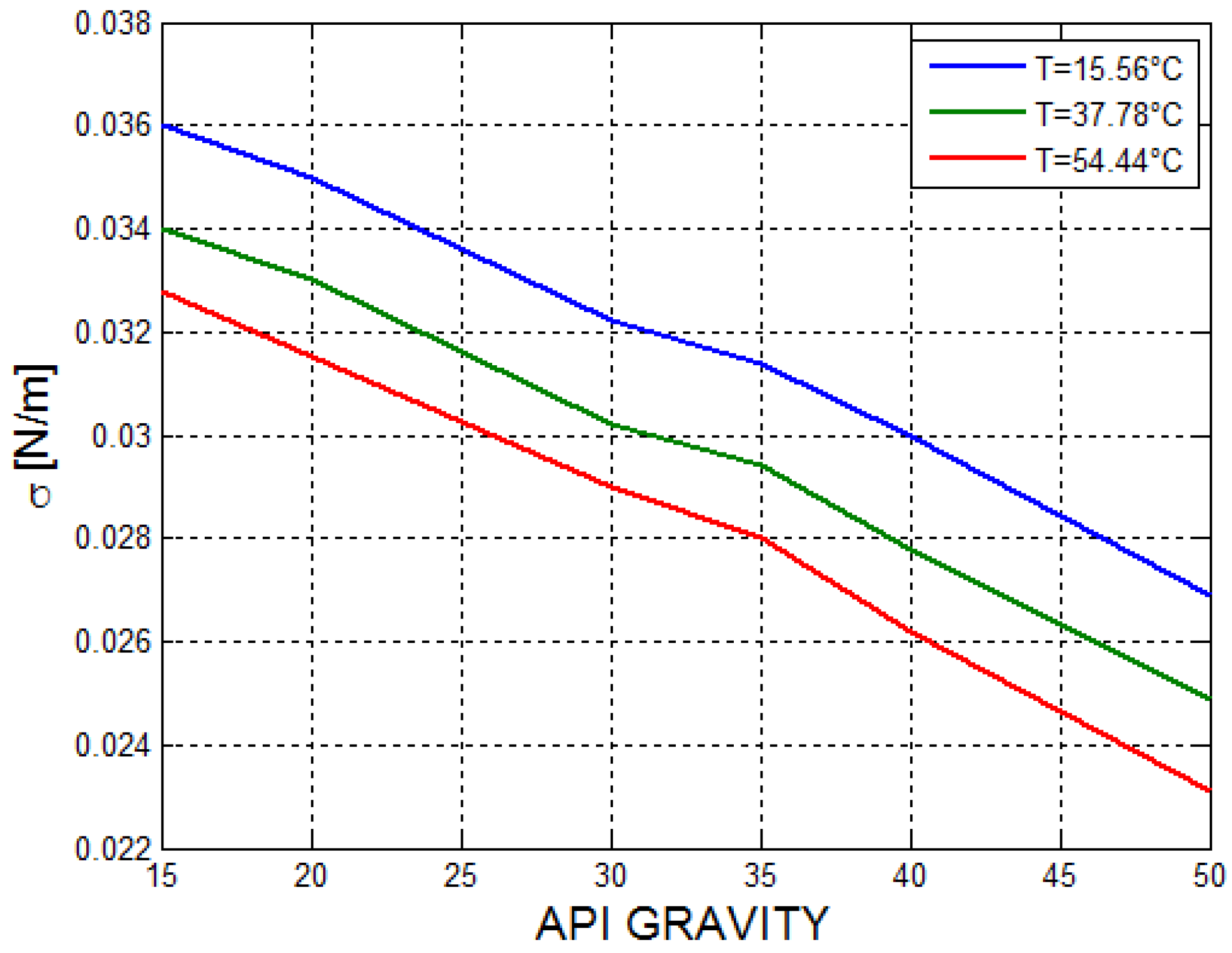
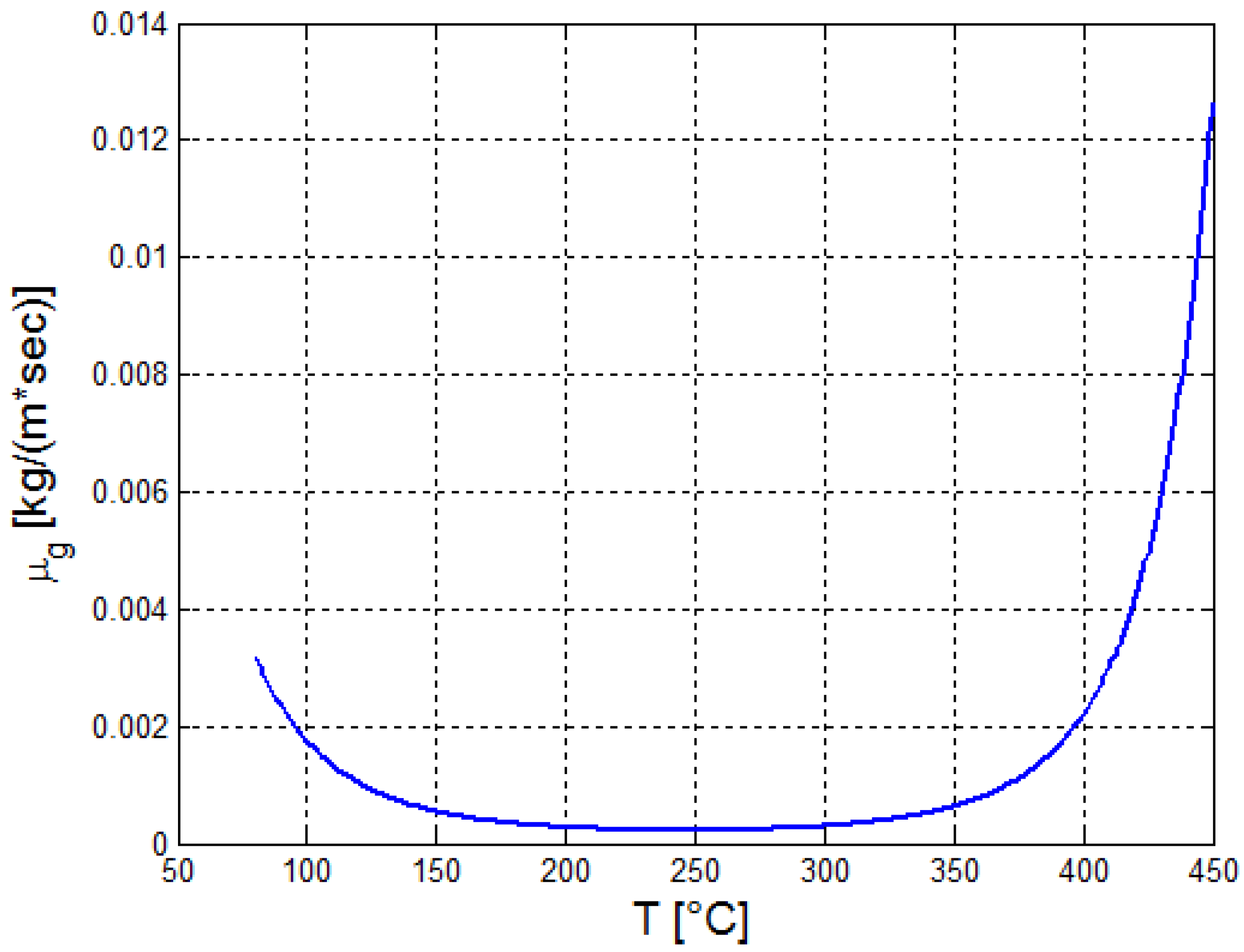

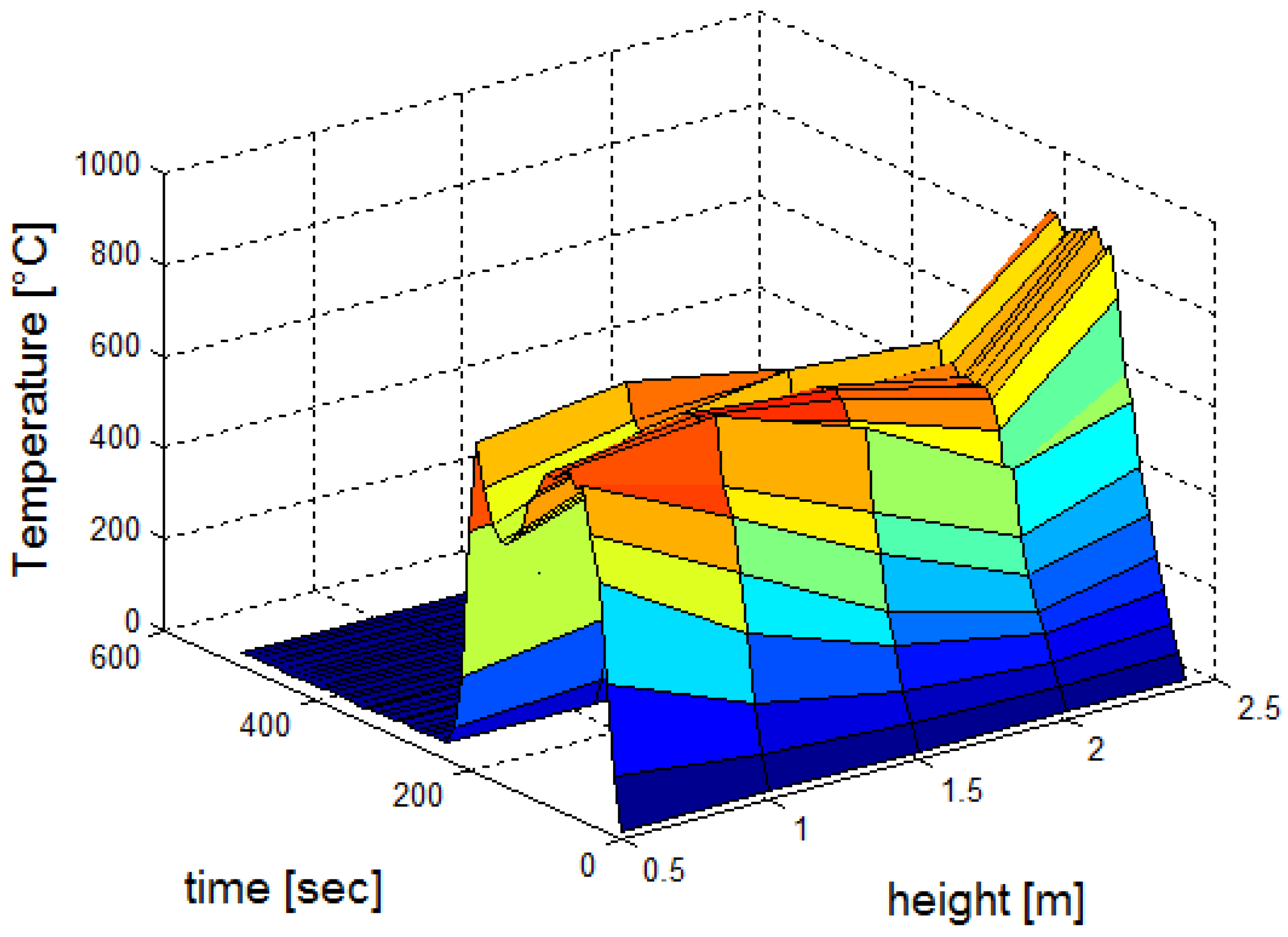
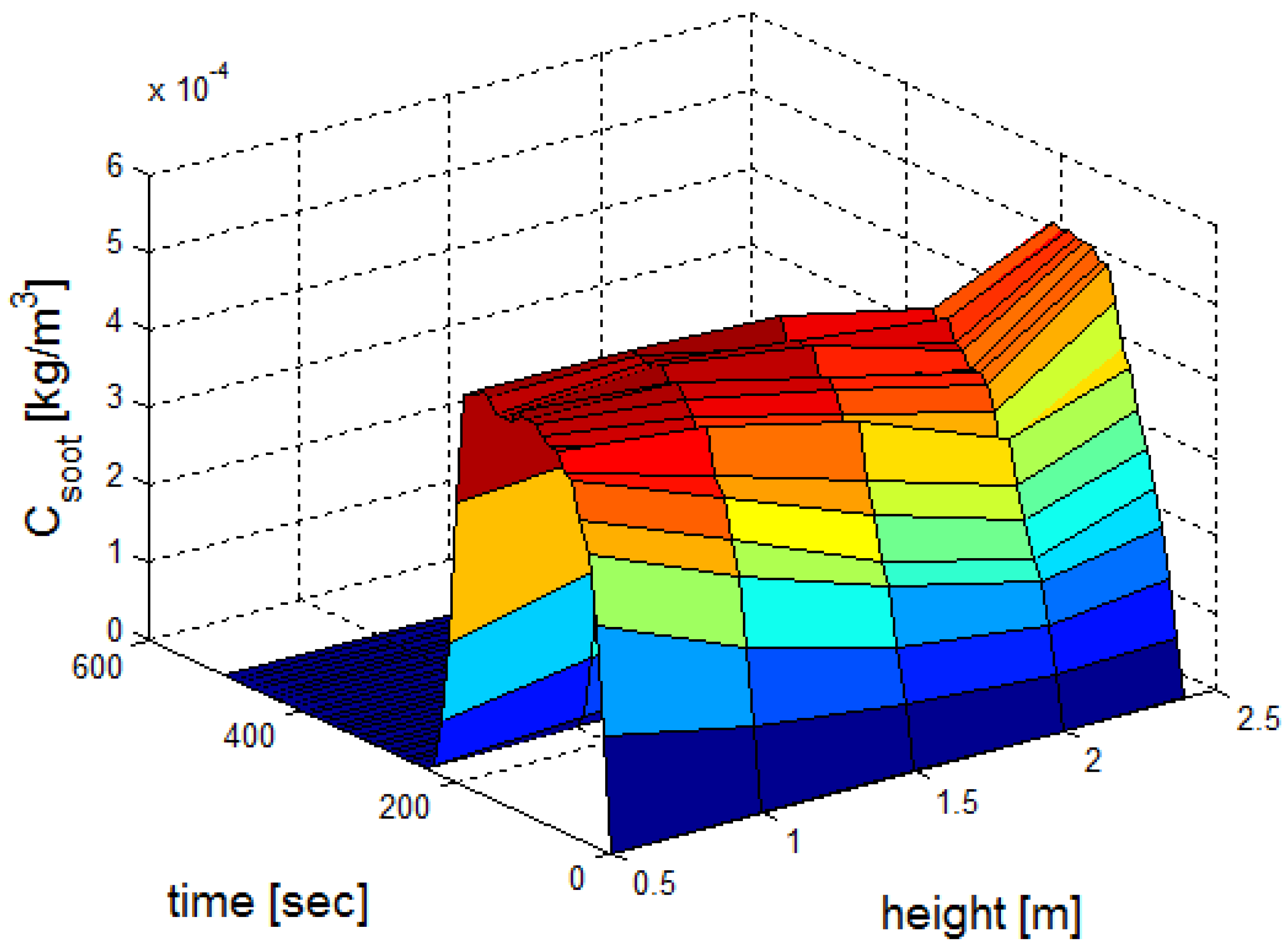
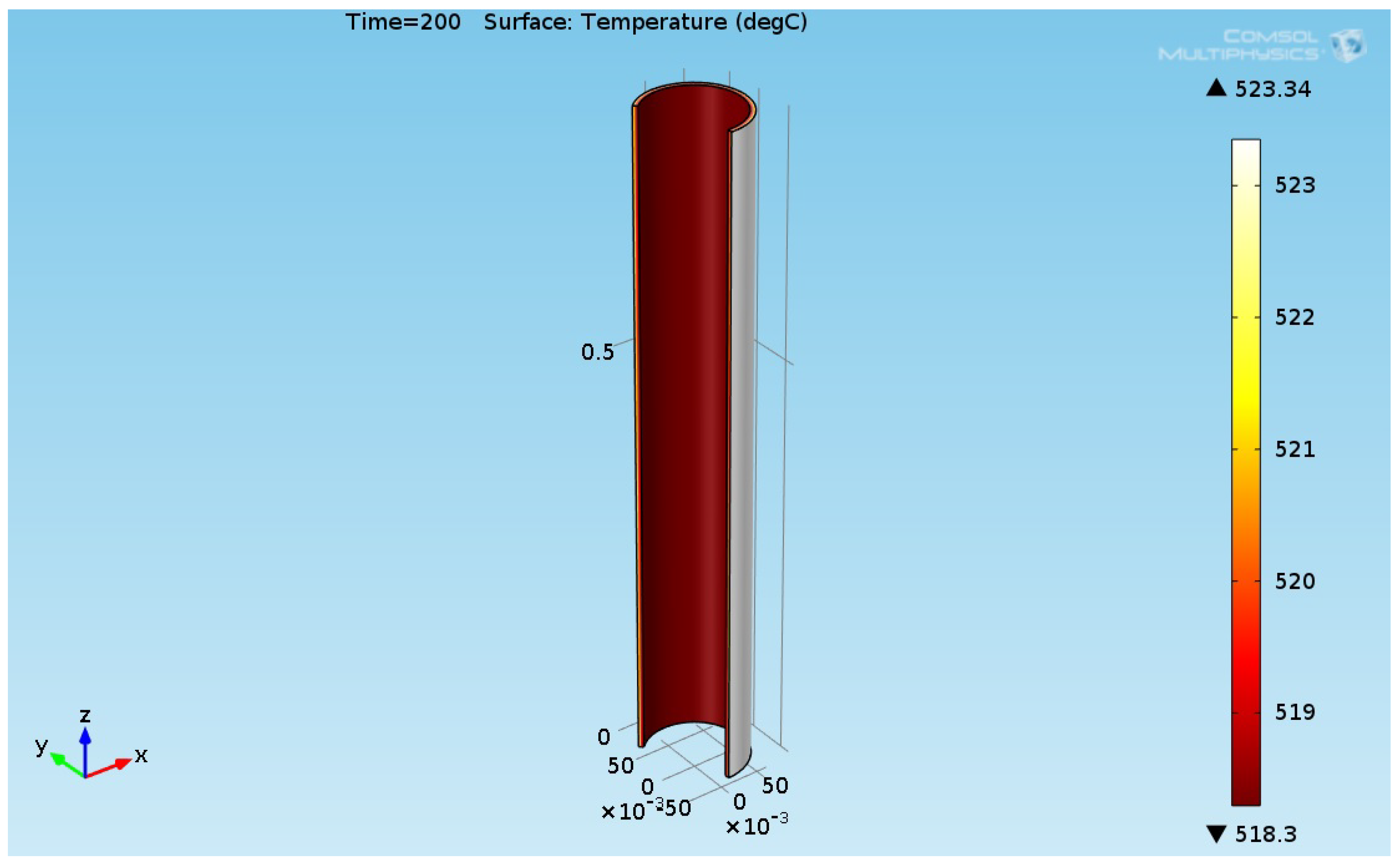
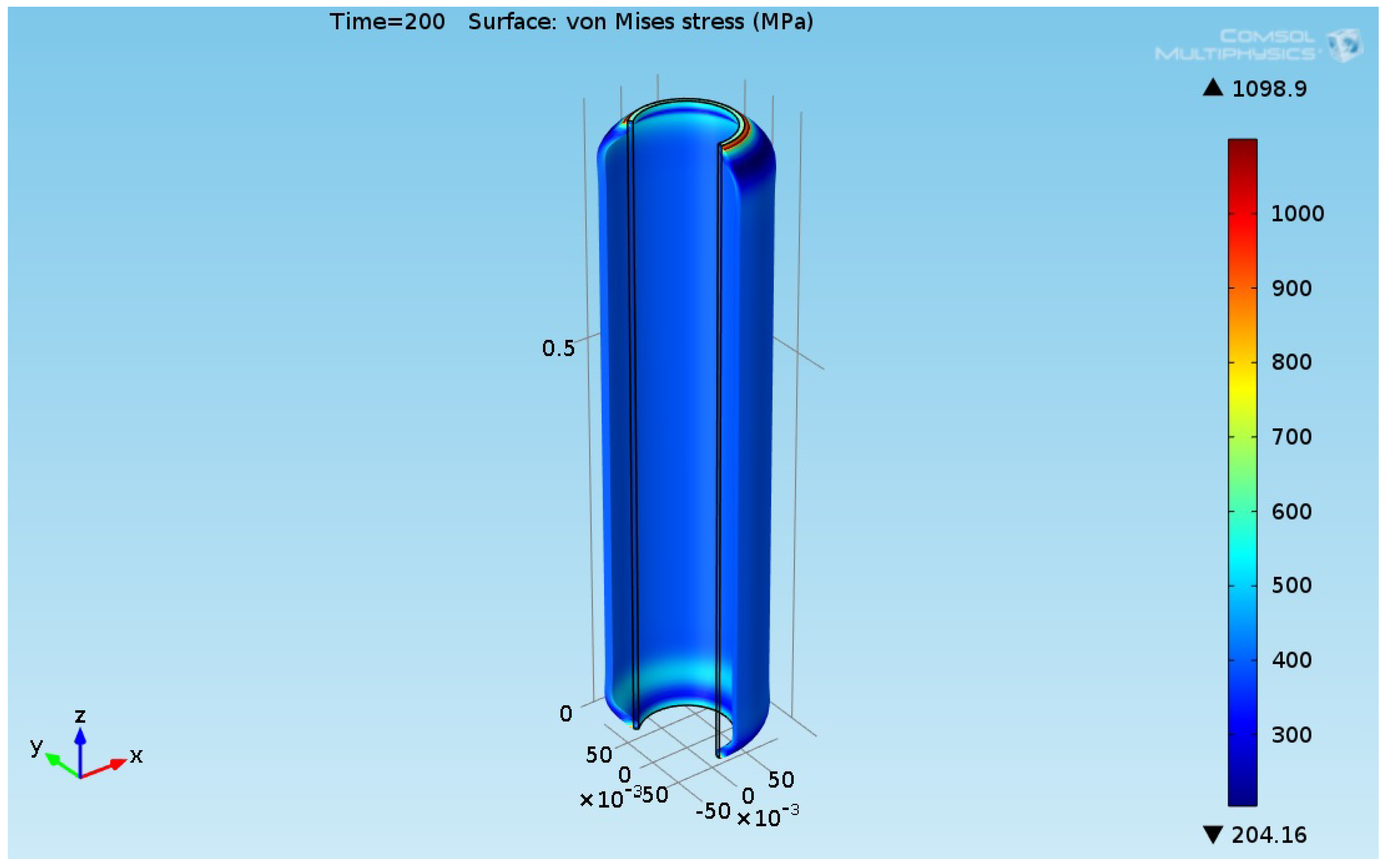
| a | b | c | ||
|---|---|---|---|---|
| 1080 | 6.97996 | 0.01964 | 0.67 | |
| SG | 1.07 | 3.56073 | 2.93886 | 0.1 |
| 0 | 6.34492 | 0.72390 | 0.3 |
| Symbol | Value |
|---|---|
| 0.335 [kg/m3] | |
| 1.90 × 10−4 (m2/s) | |
| 1.28 × 10−4 (m2/s) | |
| 0.102 [w/(m·K)] |
| n | ||||
|---|---|---|---|---|
| 1 | 0.130 | 0.000265 | 0 | 3460 |
| 2 | 0.595 | −0.000150 | 0.835 | 960 |
| 3 | 0.275 | −0.00115 | 26.25 | 960 |
| Value [m] | |
|---|---|
| D (outer diameter) | 0.121 |
| w (tube thickness) | 0.006 |
| Material Property | Value |
|---|---|
| E(Young Modulus) | 196 × 109 [Pa] |
| nu (Poisson ratio) | 0.305 |
| (Density) | 7850 [kg/m3] |
| (Coefficient of Thermal Expansion) | 15.7 × 10-6 [1/°C] |
| Cp (Heat capacity) | 480 [J/(kg·°C)] |
| k (Thermal conductivity) | 11.7 [W/(m·°C)] |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Davidy, A. CFD Simulation of Forced Recirculating Fired Heated Reboilers. Processes 2020, 8, 145. https://doi.org/10.3390/pr8020145
Davidy A. CFD Simulation of Forced Recirculating Fired Heated Reboilers. Processes. 2020; 8(2):145. https://doi.org/10.3390/pr8020145
Chicago/Turabian StyleDavidy, Alon. 2020. "CFD Simulation of Forced Recirculating Fired Heated Reboilers" Processes 8, no. 2: 145. https://doi.org/10.3390/pr8020145
APA StyleDavidy, A. (2020). CFD Simulation of Forced Recirculating Fired Heated Reboilers. Processes, 8(2), 145. https://doi.org/10.3390/pr8020145




