An Integrated Approach to the Design of Centralized and Decentralized Biorefineries with Environmental, Safety, and Economic Objectives
Abstract
1. Introduction
2. Problem Statement
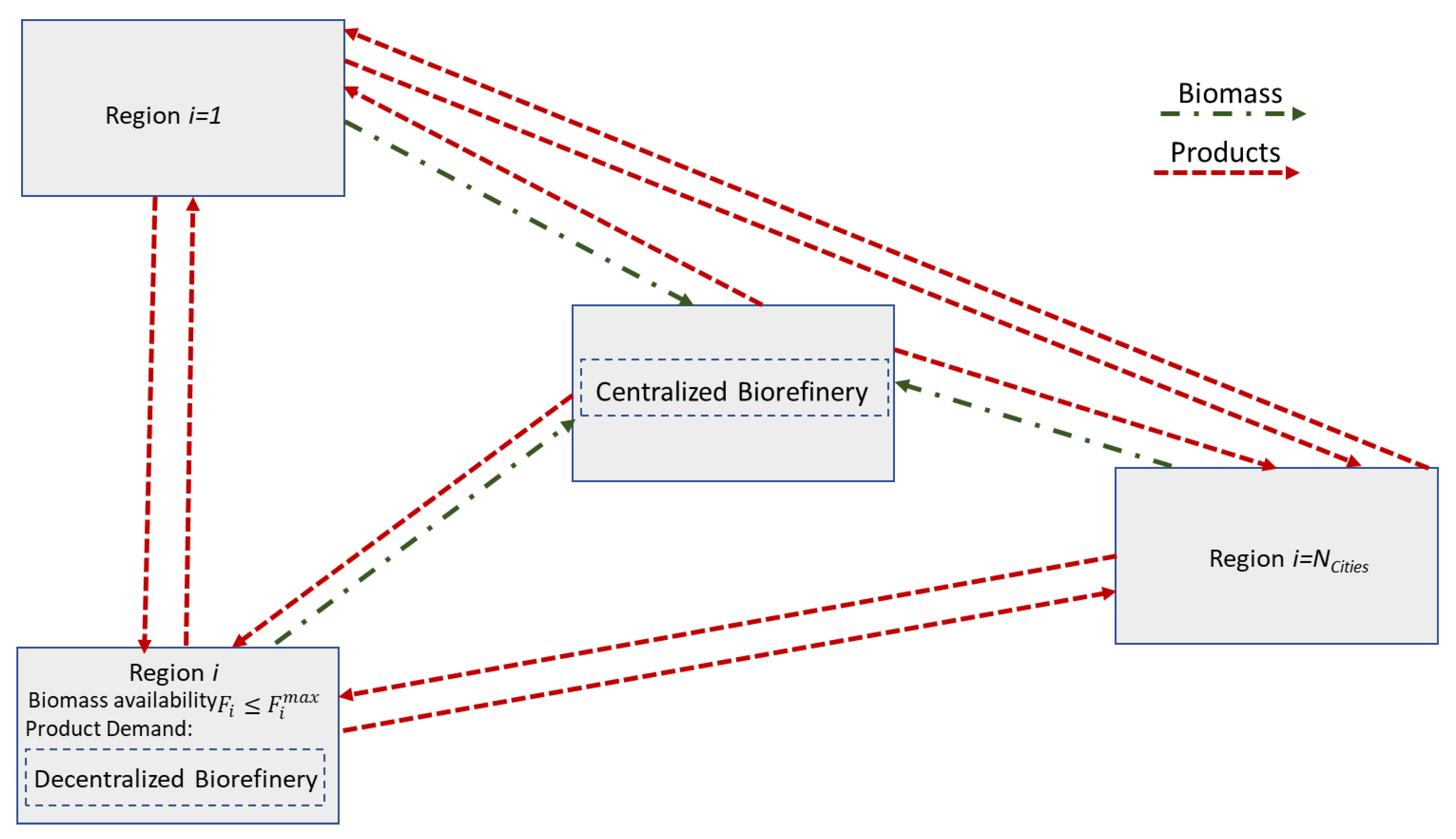
- A set of cities/regions: {i|i = 1, 2, …, NCities}. Each city/region has a supply of available biomass with known flowrate (Fi), composition of Ncomponents, and price (Costi, USD/tonne).
- A proposed location for a centralized facility, which is given the index i = NCities+1.
- A set of monetization technologies {j|j = 1, 2, …, NTech} that may be used to convert the biomass to a set of value-added chemicals and fuels {p|p = 1, 2, …, NProducts}. The selling price of each product is referred to as Cp.
- A set of transportation options for biomass and for products with known cost (USD/tonne·mile).
- Market demand and selling price for each product.
- Should the biomass be processed in centralized facilities with industrial symbiosis or in decentralized facilities?
- Which technologies should be used?
- What is the capacity of each facility?
- What are the economic, environmental, and safety roles of transporting biomass to the biorefineries and the products to consumers?
- How should the economic, environmental, and safety objectives for the integrated systems be evaluated and reconciled?
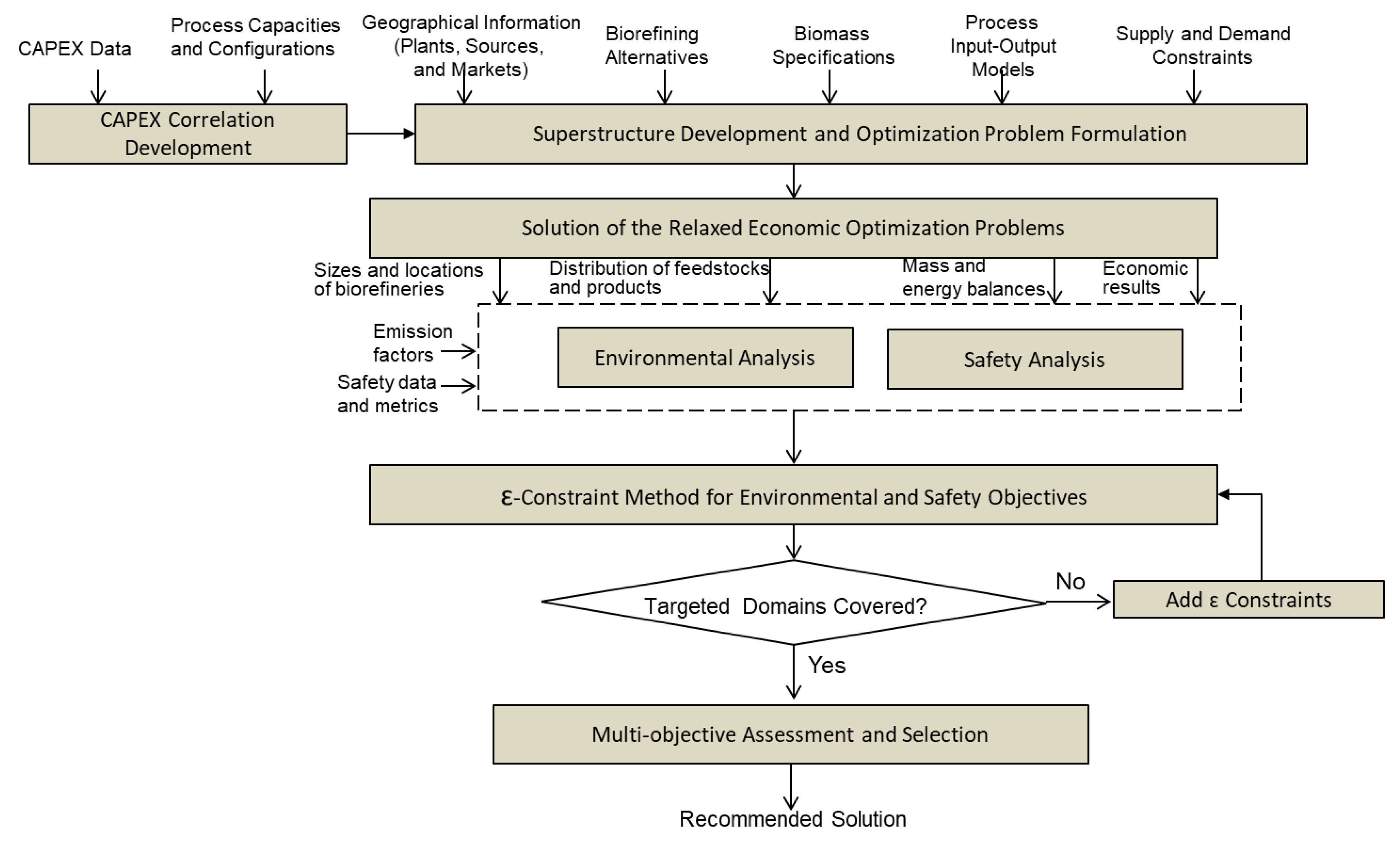
3. Methodology
- Development of superstructure and optimization formulation;
- Development of a correlation for capital cost to be used in the economic optimization;
- Life cycle analysis of the proposed pathways;
- Safety analysis of the proposed pathways;
- Reconciliation of economic, environmental, and safety objectives.
3.1. Development of Superstructure and Optimization Formulation
3.2. Capital Cost Estimation
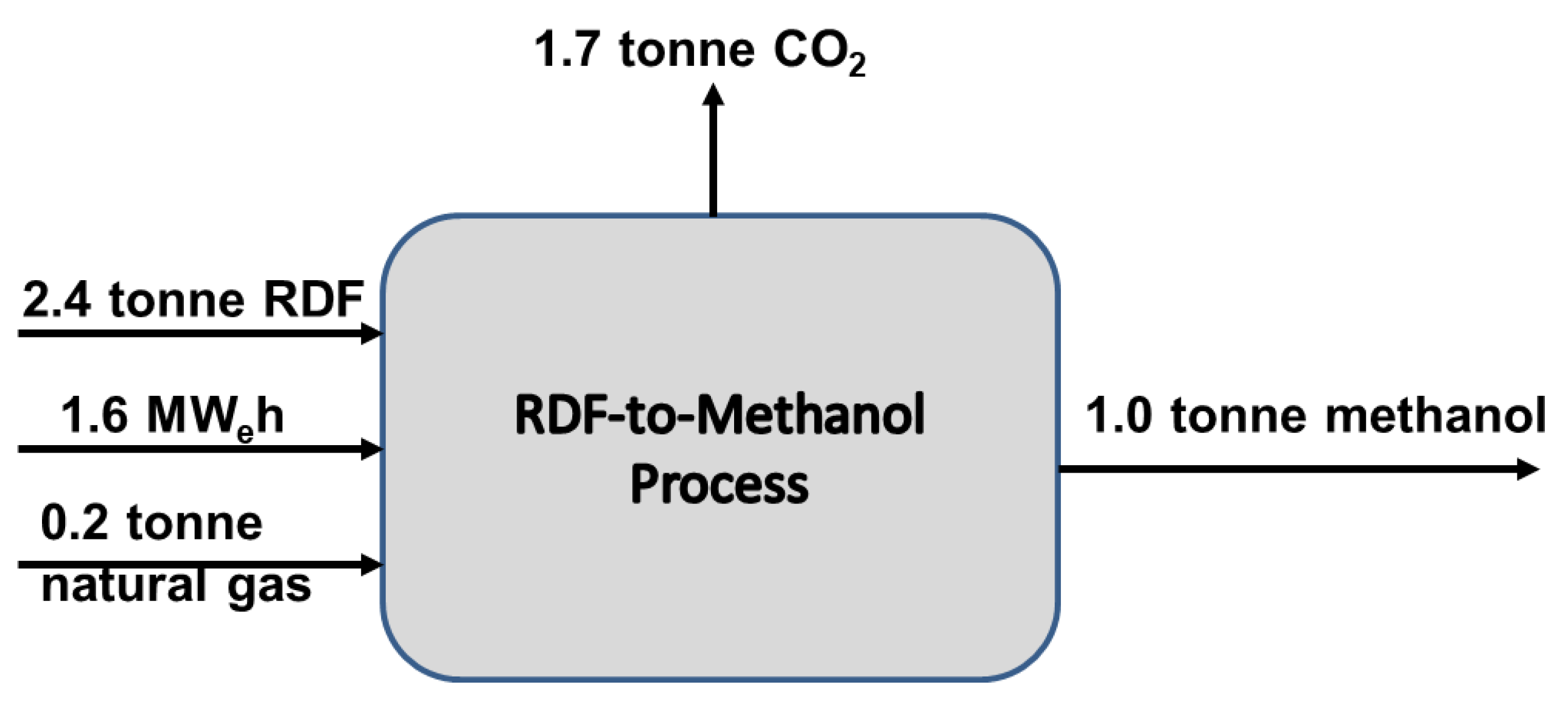
3.3. Life Cycle for RDF to Methanol Process
3.4. Safety Analysis
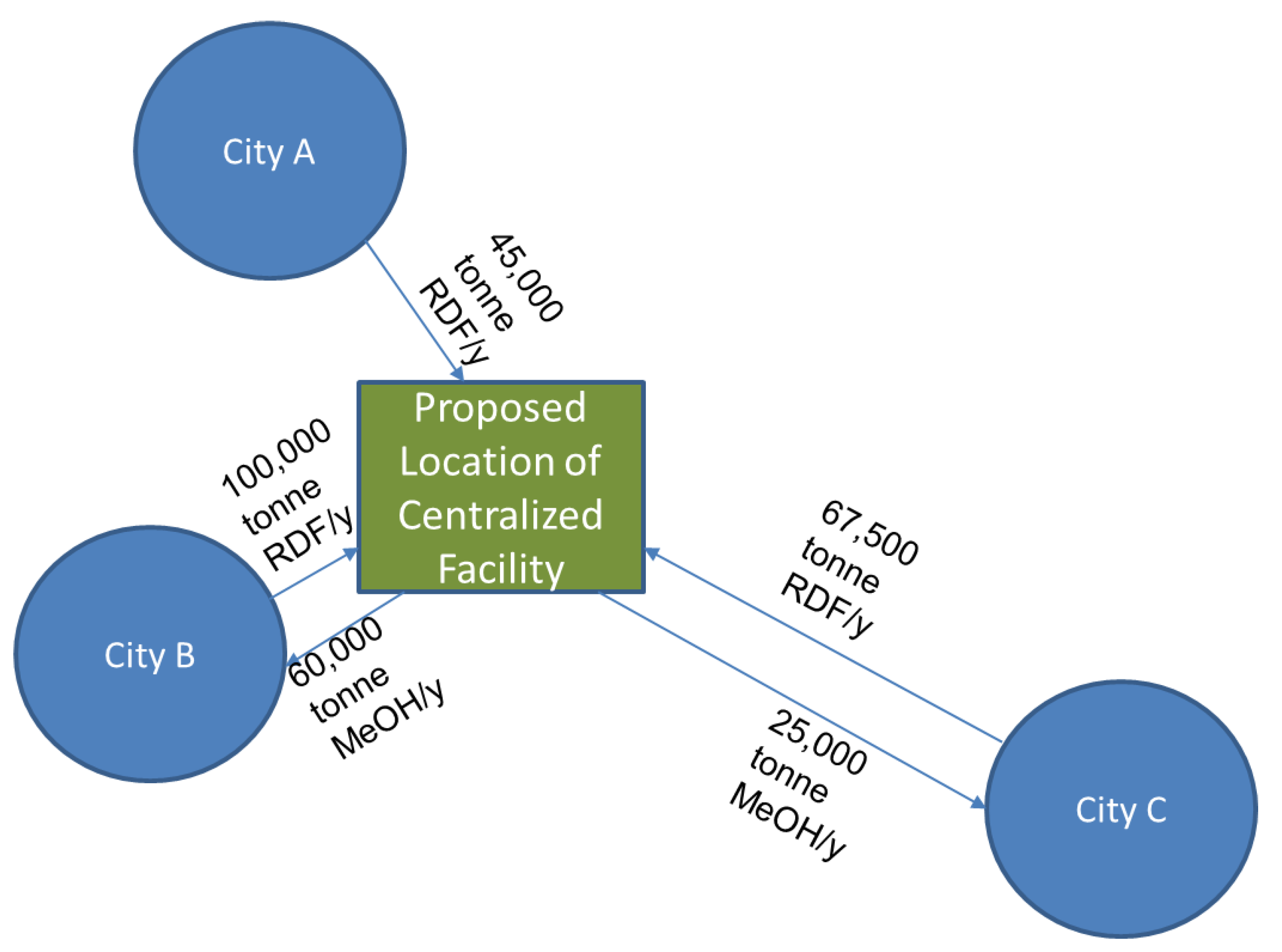
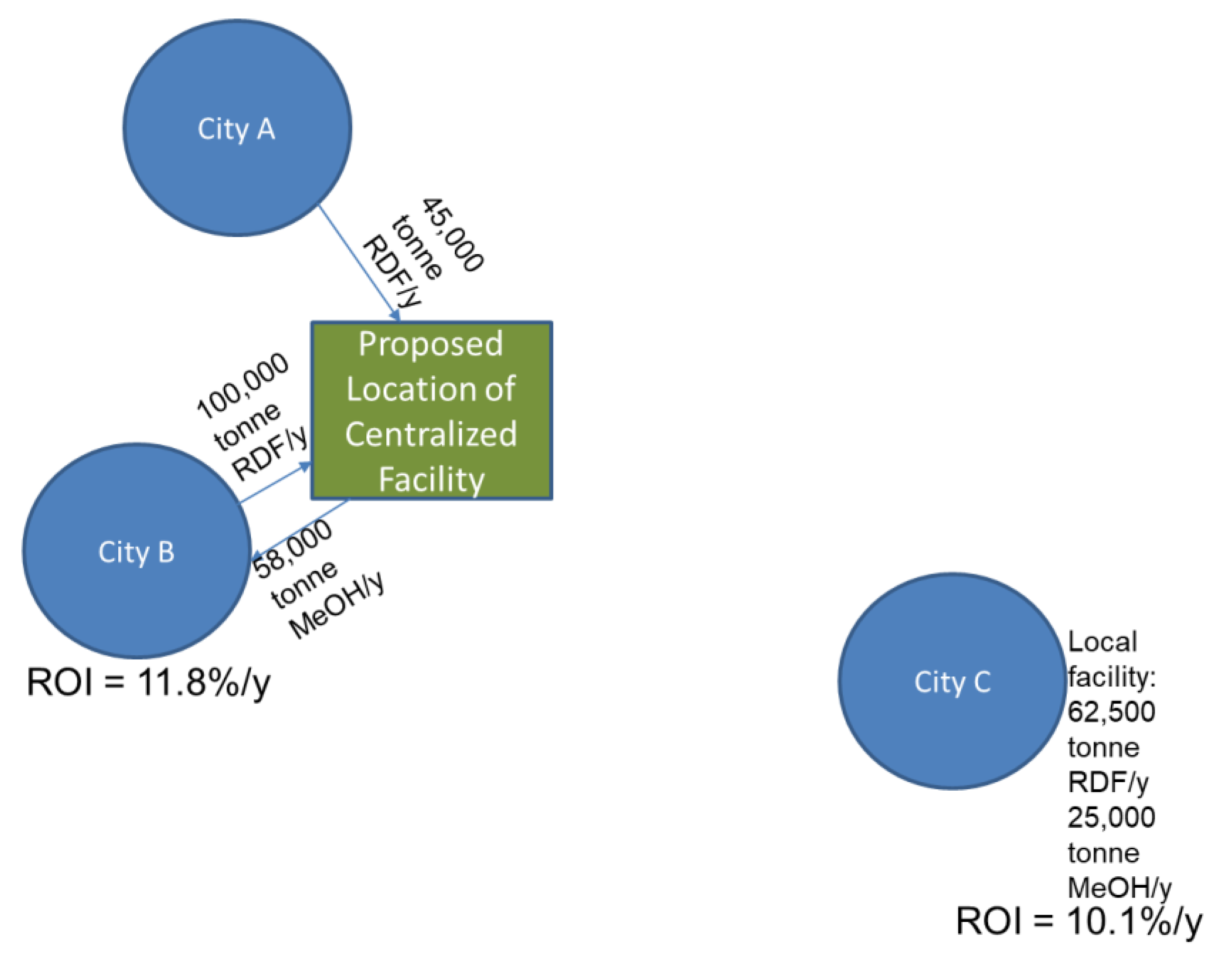
4. Case Study: Centralized vs. Decentralized Conversion of MSW to Methanol
Life Cycle Assessment for RDF to Methanol Process
5. Results and Discussion
6. Conclusions and Recommendations for Future Research
- Inclusion of multiple environmental metrics—while the case study in this paper focused on GHG emissions, other environmental metrics may be used, such as land use change, water usage and discharge, pollutant discharge, acidification, and eutrophication;
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Cp | Selling price of product p |
| Costi | Cost of biomass in city i |
| Process production capacity | |
| Reference process capacity | |
| EM | Environmental metric |
| Fi | Flowrate of biomass available in city i |
| Maximum flowrate of biomass available in city i | |
| Flowrate of biomass assigned to city i and technology j to produce product p | |
| Flowrate of biomass assigned from city i to city i’ and technology j to produce product p | |
| FCI | Fixed capital investment |
| Gi, p | Net production of product p in the plant in city i |
| Gi,j,p | Production capacity of product p in the plant in city i using technology j |
| Net amount of product p shipped out of city i | |
| HPSI | Hazardous process stream index |
| Smallest HPSI value of reference process | |
| Highest HPSI value of reference process | |
| i | Index for cities/regions |
| Ii,j,p | Binary integer variable that takes the value of 1 when product p is produced in city i using technology j. |
| Flash point indicator | |
| Heat of combustion indicator | |
| Molar flow indicator | |
| Pressure indicator | |
| Density indicator | |
| j | Index for technologies |
| NCities | Total number of cities/regions |
| NTech | Total number of technologies |
| P | Index for products |
| Individual risk of process streams | |
| Total process risk | |
| RM | Risk metric |
| TCI | Total capital investment |
| HPSE scaling factor | |
| WCI | Working capital investment |
| Greek | |
| A process yield function that relates products to reactants | |
References
- Santibañez-Aguilar, J.E.; González-Campos, J.B.; Ponce-Ortega, J.M.; Serna-González, M.; El-Halwagi, M.M. Optimal planning and site selection for distributed multiproduct biorefineries involving economic, environmental and social objectives. J. Clean. Prod. 2014, 65, 270–294. [Google Scholar] [CrossRef]
- Ubando, A.T.; Felix, C.B.; Chen, W.-H. Biorefineries in circular bioeconomy: A comprehensive review. Bioresour. Technol. 2020, 299, 122585. [Google Scholar] [CrossRef] [PubMed]
- Pyrgakis, K.; Kokossis, A.C.; Kokossis, A.C. A Total Site Synthesis approach for the selection, integration and planning of multiple-feedstock biorefineries. Comput. Chem. Eng. 2019, 122, 326–355. [Google Scholar] [CrossRef]
- Ng, D.K.; Tan, R.R.; Foo, D.C.; El-Halwagi, M.M. Process Design Strategies for Biomass Conversion Systems; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Sengupta, D.; Pike, R.W. Chemicals from Biomass: Integrating Bioprocesses into Chemical Production Complexes for Sustainable Development; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Stuart, P.; El-Halwagi, M.M. (Eds.) Integrated Biorefineries: Design, Analysis, and Optimization; Taylor and Francis/CRC: Boca Raton, FL, USA, 2013. [Google Scholar]
- Sadhukhan, J.; Kok, S.N.; Martinez, E. Biorefineries and Chemical Processes. Design, Integration and Sustainability Analysis; John Wiley & Sons: West Sussex, UK, 2014. [Google Scholar]
- El-Halwagi, A.M.; Rosas, C.; Ponce-Ortega, J.M.; Jiménez-Gutiérrez, A.; Mannan, M.S.; El-Halwagi, M.M. Multiobjective optimization of biorefineries with economic and safety objectives. AIChE J. 2013, 59, 2427–2434. [Google Scholar] [CrossRef]
- Conrad, K.; Wang, J. On the Design of Incentive Mechanisms in Environmental Policy. In Economic Incentives and Environmental Policies; Springer Science and Business Media LLC: Berlin, Germany, 1994; pp. 69–85. [Google Scholar]
- Cruce, J.R.; Quinn, J.C. Economic viability of multiple algal biorefining pathways and the impact of public policies. Appl. Energy 2019, 233, 735–746. [Google Scholar] [CrossRef]
- Lohman, L.D.S. Economic Incentives in Environmental Policy: Why are They White Ravens? In Economic Incentives and Environmental Policies; Springer Science and Business Media LLC: Berlin, Germany, 1994; pp. 55–67. [Google Scholar]
- Parry, I.W.; Heine, M.D.; Lis, E.; Li, S. Getting Energy Prices Right: From Principle to Practice; International Monetary Fund: Washington, DC, USA, 2014. [Google Scholar]
- Clements, M.B.J.; Coady, D.; Fabrizio, M.S.; Gupta, M.S.; Alleyne, M.T.S.C.; Sdralevich, M.C.A. Energy Subsidy Reform: Lessons and Implications; International Monetary Fund: Washington, DC, USA, 2014. [Google Scholar]
- Greene, D.L.; Patterson, P.D.; Singh, M.; Li, J. Feebates, rebates and gas-guzzler taxes: A study of incentives for increased fuel economy. Energy Policy 2005, 33, 757–775. [Google Scholar] [CrossRef]
- Aune, F.R.; Dalen, H.M.; Hagem, C. Implementing the EU renewable target through green certificate markets. Energy Econ. 2012, 34, 992–1000. [Google Scholar] [CrossRef]
- Brown, T.R.; Thilakaratne, R.; Brown, R.C.; Hu, G. Regional differences in the economic feasibility of advanced biorefineries: Fast pyrolysis and hydroprocessing. Energy Policy 2013, 57, 234–243. [Google Scholar] [CrossRef]
- SDGs Kenya Forum: Vision 2030s Medium Term Plan as a Framework for Implementation of the Sustainable Development Goals, SDGs Kenya Forum for Sustainable Development. Available online: http://www.developlocal.org/wp-content/uploads/2016/04/ImplementingTheSDGs.pdf (accessed on 1 August 2020).
- Sadhukhan, J.; Martinez-Hernandez, E.; Murphy, R.J.; Ng, D.K.; Hassim, M.H.; Ng, K.S.; Kin, W.Y.; Jaye, I.F.M.; Hang, M.Y.L.P.; Andiappan, V. Role of bioenergy, biorefinery and bioeconomy in sustainable development: Strategic pathways for Malaysia. Renew. Sustain. Energy Rev. 2018, 81, 1966–1987. [Google Scholar] [CrossRef]
- Sánchez, E.N.; Ojeda, K.; Elhalwagi, M.M.; Kafarov, V. Biodiesel from microalgae oil production in two sequential esterification/transesterification reactors: Pinch analysis of heat integration. Chem. Eng. J. 2011, 176–177, 211–216. [Google Scholar] [CrossRef]
- Dickinson, S.; Mientus, M.; Frey, D.; Amini-Hajibashi, A.; Ozturk, S.; Shaikh, F.; Sengupta, D.; El-Halwagi, M.M. A review of biodiesel production from microalgae. Clean Technol. Environ. Policy 2016, 19, 637–668. [Google Scholar] [CrossRef]
- Ng, R.T.L.; Ng, D.K.; Tan, R.R.; El-Halwagi, M.M. Disjunctive fuzzy optimisation for planning and synthesis of bioenergy-based industrial symbiosis system. J. Environ. Chem. Eng. 2014, 2, 652–664. [Google Scholar] [CrossRef]
- Ng, L.Y.; Andiappan, V.; Chemmangattuvalappil, N.G.; Ng, D.K. A systematic methodology for optimal mixture design in an integrated biorefinery. Comput. Chem. Eng. 2015, 81, 288–309. [Google Scholar] [CrossRef]
- Liew, W.H.; Hassim, M.H.; Ng, D.K.S. Review of evolution, technology and sustainability assessments of biofuel production. J. Clean. Prod. 2014, 71, 11–29. [Google Scholar] [CrossRef]
- Alamia, A.; Gardarsdottir, S.O.; Larsson, A.; Normann, F.; Thunman, H. Efficiency Comparison of Large-Scale Standalone, Centralized, and Distributed Thermochemical Biorefineries. Energy Technol. 2017, 5, 1435–1448. [Google Scholar] [CrossRef]
- Lan, K.; Ou, L.; Park, S.; Kelley, S.S.; Yao, Y. Life Cycle Analysis of Decentralized Preprocessing Systems for Fast Pyrolysis Biorefineries with Blended Feedstocks in the Southeastern United States. Energy Technol. 2020, 8. [Google Scholar] [CrossRef]
- Roni, M.S.; Thompson, D.N.; Hartley, D.S. Distributed biomass supply chain cost optimization to evaluate multiple feedstocks for a biorefinery. Appl. Energy 2019, 254, 113660. [Google Scholar] [CrossRef]
- Psycha, M.; Kapnisi, M.; Kokossis, A.C. Extended Value Chain Synthesis towards the Design of Multi-Feedstock Algae Biorefineries. In Computer Aided Chemical Engineering; Elsevier BV: Amsterdam, The Netherlands, 2018; Volume 43, pp. 645–650. [Google Scholar]
- Bao, B.; Ng, D.K.; Tay, D.H.; Jiménez-Gutiérrez, A.; El-Halwagi, M.M. A shortcut method for the preliminary synthesis of process-technology pathways: An optimization approach and application for the conceptual design of integrated biorefineries. Comput. Chem. Eng. 2011, 35, 1374–1383. [Google Scholar] [CrossRef]
- Tay, D.H.S.; Ng, D.K.; Kheireddine, H.; El-Halwagi, M.M. Synthesis of an integrated biorefinery via the C–H–O ternary diagram. Clean Technol. Environ. Policy 2011, 13, 567–579. [Google Scholar] [CrossRef]
- Tay, D.H.S.; Kheireddine, H.; Ng, D.K.S.; El-Halwagi, M.M.; Tan, R.R. Conceptual Synthesis of Gasification-Based Biorefineries Using Thermodynamic Equilibrium Optimization Models. Ind. Eng. Chem. Res. 2011, 50, 10681–10695. [Google Scholar] [CrossRef]
- Meramo-Hurtado, S.-I.; González-Delgado, Á.D. Biorefinery synthesis and design using sustainability parameters and hierarchical/3D multi-objective optimization. J. Clean. Prod. 2019, 240, 118134. [Google Scholar] [CrossRef]
- Parada, M.P.; Osseweijer, P.; Posada, J. Sustainable biorefineries, an analysis of practices for incorporating sustainability in biorefinery design. Ind. Crops Prod. 2017, 106, 105–123. [Google Scholar] [CrossRef]
- Andiappan, V.; Ko, A.S.Y.; Lau, V.W.S.; Ng, L.Y.; Ng, R.T.L.; Chemmangattuvalappil, N.G.; Ng, D.K. Synthesis of sustainable integrated biorefinery via reaction pathway synthesis: Economic, incremental environmental burden and energy assessment with multiobjective optimization. AIChE J. 2014, 61, 132–146. [Google Scholar] [CrossRef]
- Roy, N.; Eljack, F.; Jiménez-Gutiérrez, A.; Zhang, B.; Thiruvenkataswamy, P.; El-Halwagi, M.; Mannan, M.S. A review of safety indices for process design. Curr. Opin. Chem. Eng. 2016, 14, 42–48. [Google Scholar] [CrossRef]
- Park, S.; Xu, S.; Rogers, W.; Pasman, H.; El-Halwagi, M.M. Incorporating inherent safety during the conceptual process design stage: A literature review. J. Loss Prev. Process. Ind. 2020, 63, 104040. [Google Scholar] [CrossRef]
- Bowling, I.M.; Ponce-Ortega, J.M.; El-Halwagi, M.M. Facility Location and Supply Chain Optimization for a Biorefinery. Ind. Eng. Chem. Res. 2011, 50, 6276–6286. [Google Scholar] [CrossRef]
- Piñas, J.A.V.; Venturini, O.; Lora, E.E.S.; Del Olmo, O.A.; Roalcaba, O.D.C. An economic holistic feasibility assessment of centralized and decentralized biogas plants with mono-digestion and co-digestion systems. Renew. Energy 2019, 139, 40–51. [Google Scholar] [CrossRef]
- Tay, D.H.; Ng, D.K.; Sammons, N.E., Jr.; Eden, M.R. Fuzzy optimization approach for the synthesis of a sustainable integrated biorefinery. Ind. Eng. Chem. Res. 2011, 50, 1652–1665. [Google Scholar] [CrossRef]
- Ponce-Ortega, J.M.; Pham, V.; El-Halwagi, M.M.; El-Baz, A.A. A Disjunctive Programming Formulation for the Optimal Design of Biorefinery Configurations. Ind. Eng. Chem. Res. 2012, 51, 3381–3400. [Google Scholar] [CrossRef]
- Sun, O.; Fan, N. A Review on Optimization Methods for Biomass Supply Chain: Models and Algorithms, Sustainable Issues, and Challenges and Opportunities. Process. Integr. Optim. Sustain. 2020, 4, 203–226. [Google Scholar] [CrossRef]
- El-Halwagi, M.M. Sustainable Design through Process Integration: Fundamentals and Applications to Industrial Pollution Prevention, Resource Conservation, and Profitability Enhancement, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Zhang, C.; El-Halwagi, M.M. Estimate the Capital Cost of Shale-Gas Monetization Projects. Chem. Eng. Prog. 2017, 113, 28–32. [Google Scholar]
- Chouinard-Dussault, P.; Bradt, L.; Ponce-Ortega, J.M.; El-Halwagi, M.M. Incorporation of process integration into life cycle analysis for the production of biofuels. Clean Technol. Environ. Policy 2010, 13, 673–685. [Google Scholar] [CrossRef]
- EPA (Environmental Protection Agency). Emission Factors for Greenhouse Gas Inventories. 2020. Available online: https://www.epa.gov/sites/production/files/2020-04/documents/ghg-emission-factors-hub.pdf (accessed on 4 June 2020).
- López-Molina, A.; Huerta-Martínez, Á.A.; Gómez-Castro, F.I.; Conde-Mejía, C. A novel approach to identify hazards in non-conventional/intensified biofuels production processes. Chem. Eng. Process. Process. Intensif. 2020, 157, 108139. [Google Scholar] [CrossRef]
- Park, J.; Cho, J.; Lee, Y.; Park, M.-J.; Lee, W.B. Practical Microkinetic Modeling Approach for Methanol Synthesis from Syngas over a Cu-Based Catalyst. Ind. Eng. Chem. Res. 2019, 58, 8663–8673. [Google Scholar] [CrossRef]
- Ramzan, N.; Ashraf, A.; Naveed, S.; Malik, A. Simulation of hybrid biomass gasification using Aspen plus: A comparative performance analysis for food, municipal solid and poultry waste. Biomass-Bioenergy 2011, 35, 3962–3969. [Google Scholar] [CrossRef]
- Salladini, A.; Agostini, E.; Borgogna, A.; Spadacini, L.; Annesini, M.; Iaquaniello, G. Analysis on High Temperature Gasification for Conversion of RDF into Bio-Methanol. Gasif. Low-grade Feedstock 2018, 143. [Google Scholar] [CrossRef]
- Julián-Durán, L.; Ortiz-Espinoza, A.P.; El-Halwagi, M.M.; Jiménez-Gutiérrez, A. Techno-economic assessment and environmental impact of shale gas alternatives to methanol. ACS Sustain. Chem. Eng. 2014, 2, 2338–2344. [Google Scholar] [CrossRef]
- Ehlinger, V.M.; Gabriel, K.J.; Noureldin, M.M.B.; El-Halwagi, M.M. Process Design and Integration of Shale Gas to Methanol. ACS Sustain. Chem. Eng. 2014, 2, 30–37. [Google Scholar] [CrossRef]
- Alsuhaibani, A.S.; Afzal, S.; Challiwala, M.; Elbashir, N.O.; El-Halwagi, M.M. The impact of the development of catalyst and reaction system of the methanol synthesis stage on the overall profitability of the entire plant: A techno-economic study. Catal. Today 2020, 343, 191–198. [Google Scholar] [CrossRef]
- Shehzad, A.; Bashir, M.J.; Sethupathi, S. System analysis for synthesis gas (syngas) production in Pakistan from municipal solid waste gasification using a circulating fluidized bed gasifier. Renew. Sustain. Energy Rev. 2016, 60, 1302–1311. [Google Scholar] [CrossRef]
- Leo, D. Process Modelling and Simulation of a Methanol Synthesis Plant Using Syngas Streams Obtained from Biomass. Master’s Thesis, Politecnico di Milano, Milan, Italy, 2018. Available online: https://www.politesi.polimi.it/bitstream/10589/142748/3/2018_10_Leo.pdf (accessed on 4 June 2020).
- Lücking, L.E. Methanol Production from Syngas: Process Modelling and Design Utilising Biomass Gasification and Integrating Hydrogen Supply. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 2017. Available online: http://repository.tudelft.nl/ (accessed on 4 June 2020).
- Iaquaniello, G.; Centi, G.; Salladini, A.; Palo, E.; Perathoner, S.; Spadaccini, L. Waste-to-methanol: Process and economics assessment. Bioresour. Technol. 2017, 243, 611–619. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Nguyen, C.; Eljack, F.; Linke, P.; El-Halwagi, M.M. Integration of Safety in the Optimization of Transporting Hazardous Materials. Process. Integr. Optim. Sustain. 2018, 2, 435–446. [Google Scholar] [CrossRef]
- El-Halwagi, M.M. A return on investment metric for incorporating sustainability in process integration and improvement projects. Clean Technol. Environ. Policy 2017, 19, 611–617. [Google Scholar] [CrossRef]
- El-Halwagi, M.M.; Sengupta, D.; Pistikopoulos, E.N.; Sammons, J.; Eljack, F.; Kazi, M.-K. Disaster-Resilient Design of Manufacturing Facilities Through Process Integration: Principal Strategies, Perspectives, and Research Challenges. Front. Sustain. Food Syst. 2020, 1. [Google Scholar] [CrossRef]
- Guillen-Cuevas, K.; Ortiz-Espinoza, A.P.; Ozinan, E.; Jiménez-Gutiérrez, A.; Kazantzis, N.K.; El-Halwagi, M.M. Incorporation of Safety and Sustainability in Conceptual Design via a Return on Investment Metric. ACS Sustain. Chem. Eng. 2018, 6, 1411–1416. [Google Scholar] [CrossRef]
- Ortiz-Espinoza, A.P.; Jiménez-Gutiérrez, A.; El-Halwagi, M.M.; Kazantzis, N.K.; Kazantzi, V. Comparison of safety indexes for chemical processes under uncertainty. Process. Saf. Environ. Prot. 2021, 148, 225–236. [Google Scholar] [CrossRef]
- Moreno-Sader, K.; Jain, P.; Tenorio, L.C.B.; Mannan, M.S.; El-Halwagi, M.M. Integrated Approach of Safety, Sustainability, Reliability, and Resilience Analysis via a Return on Investment Metric. ACS Sustain. Chem. Eng. 2019, 7, 19522–19536. [Google Scholar] [CrossRef]
- Al-Douri, A.; Kazantzi, V.; Eljack, F.T.; Mannan, M.S.; El-Halwagi, M.M. Mitigation of operational failures via an economic framework of reliability, availability, and maintainability (RAM) during conceptual design. J. Loss Prev. Process. Ind. 2020, 67, 104261. [Google Scholar] [CrossRef]
- El-Halwagi, M.M. A Shortcut Approach to the Multi-scale Atomic Targeting and Design of C–H–O Symbiosis Networks. Process. Integr. Optim. Sustain. 2017, 1, 3–13. [Google Scholar] [CrossRef]
- Noureldin, M.M.; El-Halwagi, M.M. Synthesis of C-H-O Symbiosis Networks. AIChE J. 2015, 61, 1242–1262. [Google Scholar] [CrossRef]
- Mukherjee, R.; Asani, R.R.; Boppana, N.; El-Halwagi, M.M. Performance evaluation of shale gas processing and NGL recovery plant under uncertainty of the feed composition. J. Nat. Gas Sci. Eng. 2020, 83, 103517. [Google Scholar] [CrossRef]

| Total Process Risk (RT) | Risk Level |
|---|---|
| 0.0–0.2 | Very Low Risk |
| 0.2–0.4 | Low Risk |
| 0.4–0.6 | Medium Risk |
| 0.6–0.8 | High Risk |
| 0.8–1.0 | Very High Risk |
| RDF (Refuse-Derived Fuel) | Electric Energy Needed | Cost of Electric Energy (Assuming USD0.05/kWh) | Demineralized Water Needed | Cost of Water (Assuming USD3/Tonne) | Produced Methanol | Value of Methanol (Assuming USD350/Tonne) |
|---|---|---|---|---|---|---|
| 1 tonne | 500 kWh | 25 | 0.15 tonne | USD0.45 | 0.4 tonne | USD140 |
| Item | CO2 Factor Tonne/MWh | CH4 Factor Tonne/MWh | N2O Factor Tonne/MWh |
|---|---|---|---|
| US Average Energy Mix | 0.65 | 5.30 × 10−5 | 0.77 × 10−5 |
| Item | MMBtu per Tonne of Natural Gas (LNG Factor Used) | CO2 Factor (kg CO2/MMBtu) | CH4 Factor (g CH4/MMBtu) | N2O Factor (g N2O/MMBtu) |
|---|---|---|---|---|
| Steam and Heat (from Natural Gas) | 51.7 | 53.06 | 1.0 | 0.10 |
| Solution | Risk Factor by City | Highway | Railroad |
|---|---|---|---|
| Optimal | Transporting methanol to city B | 207.27 | 128.08 |
| Transporting methanol to city C | 426.87 | 673.17 | |
| Total risk factor from centralized facility | 634.14 | 801.24 | |
| Suboptimal | Transporting methanol to city B | 200.39 | 297.13 |
| Solution | Total GHG Emissions (Tonnes CO2eq/year) | Process Risk (HPSI) | Lower Transportation Risk Factor |
|---|---|---|---|
| Optimal with Maximum ROI (11.8%) | 290,877 Total (104,061 from electricity, 39,659 from natural gas, 144,500 from process emissions, 2269 from raw material transport, 388 from product transport) | 0.75 (High Risk) | 554.9 (using the highway to transport methanol to city B and using railroad to transport methanol to city C) |
| Suboptimal Solution | 282,760 Total (101,613 from electricity, 38,726 from natural gas, 141,100 from process emissions, 993 from raw material transport, 329 from product transport) | 0.50 (Medium Risk) | 200.4 (using the highway to transport methanol to city B) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
López-Molina, A.; Sengupta, D.; Shi, C.; Aldamigh, E.; Alandejani, M.; El-Halwagi, M.M. An Integrated Approach to the Design of Centralized and Decentralized Biorefineries with Environmental, Safety, and Economic Objectives. Processes 2020, 8, 1682. https://doi.org/10.3390/pr8121682
López-Molina A, Sengupta D, Shi C, Aldamigh E, Alandejani M, El-Halwagi MM. An Integrated Approach to the Design of Centralized and Decentralized Biorefineries with Environmental, Safety, and Economic Objectives. Processes. 2020; 8(12):1682. https://doi.org/10.3390/pr8121682
Chicago/Turabian StyleLópez-Molina, Antioco, Debalina Sengupta, Claire Shi, Eman Aldamigh, Maha Alandejani, and Mahmoud M. El-Halwagi. 2020. "An Integrated Approach to the Design of Centralized and Decentralized Biorefineries with Environmental, Safety, and Economic Objectives" Processes 8, no. 12: 1682. https://doi.org/10.3390/pr8121682
APA StyleLópez-Molina, A., Sengupta, D., Shi, C., Aldamigh, E., Alandejani, M., & El-Halwagi, M. M. (2020). An Integrated Approach to the Design of Centralized and Decentralized Biorefineries with Environmental, Safety, and Economic Objectives. Processes, 8(12), 1682. https://doi.org/10.3390/pr8121682







