Abstract
In addition to proper physicochemical properties, low toxicity is also desirable when seeking suitable ionic liquids (ILs) for specific applications. In this context, machine learning (ML) models were developed to predict the IL toxicity in leukemia rat cell line (IPC-81) based on an extended experimental dataset. Following a systematic procedure including framework construction, hyper-parameter optimization, model training, and evaluation, the feedforward neural network (FNN) and support vector machine (SVM) algorithms were adopted to predict the toxicity of ILs directly from their molecular structures. Based on the ML structures optimized by the five-fold cross validation, two ML models were established and evaluated using IL structural descriptors as inputs. It was observed that both models exhibited high predictive accuracy, with the SVM model observed to be slightly better than the FNN model. For the SVM model, the determination coefficients were 0.9289 and 0.9202 for the training and test sets, respectively. The satisfactory predictive performance and generalization ability make our models useful for the computer-aided molecular design (CAMD) of environmentally friendly ILs.
1. Introduction
Ionic liquids (ILs) are known as molten salts, consisting solely of organic cation and inorganic or organic anion. ILs present several unique and benign characteristics, such as low melting point, low volatility, and high thermal stability. For these reasons, ILs have attracted extensive attention in both academia and industry as alternatives to traditional organic solvents. In fact, they have been used in many chemical processes [1,2,3,4] to meet specific requirements while improving the process efficiency. In spite of their superior properties and large application prospects, many ILs present potential negative effects on the ecosystem, which could also impact human health. Therefore, toxicity is a significant factor that should be considered in IL selection, and therefore the toxicological assessment of ILs is essential for the development of a sustainable IL-based chemical process.
In order to find ILs showing desired low toxicity, experimental measurement is the most direct and effective way. However, the number of new IL structures is increasing rapidly due to numerous feasible cation–anion combinations. This makes the experimental measurement a time-consuming, resource-intensive, and even impractical method. In contrast, mathematical modeling methods based on existing IL structures and toxicity data become efficient substitutes. Researchers have built mathematical models for predicting various properties of ILs, including electrical conductivity [5], thermal decomposition temperature [6], critical properties [7], and water solubility [8]. These models are regressed from experimental property data and can provide satisfying predictions on the properties of new ILs that are not used in model training. Such well-established property models have been widely used in the computer-aided molecular design (CAMD) of IL solvents [9,10,11,12,13,14], where optimal ILs possessing desirable properties are identified based on the property models. Unfortunately, up to now, mathematical models for the toxicity properties of ILs have been explored more scarcely in comparison to other IL properties.
In literature, the mortality of leukemia rat cell line (IPC-81) is frequently used to quantitatively indicate the toxicity of ILs [15,16]. A few researchers have developed models to predict the toxicity of ILs against IPC-81 from IL structures. Based on a dataset of 173 experimental samples, Yan et al. [17] established a structure–activity relationship model for an IL to predict its toxicity against IPC-81 using multiple linear regression (MLR) and topological descriptors. The mean absolute error (MAE) was 0.226. Later, Sosnowska et al. [18] constructed a larger IPC-81 dataset containing 304 experimental samples, and on this basis, they used structure-related descriptors to develop another MLR model where the MAE was 0.3779. Due to the utilization of a larger database, this model, in principle, shows improved applicability. Based on this updated dataset, Wu et al. [19] recently reported another MLR model using IL fingerprint descriptors, which resulted in an improved predictive accuracy (MAE = 0.34). Despite the effectiveness of MLR, there is still a large potential for the further improvement of model accuracy.
As proven by many studies [20,21,22,23,24,25], machine learning (ML) is an efficient and promising approach for building quantitative structure–property relationship (QSPR) models to predict various properties for chemical compounds. Until now, ML techniques have obtained wide applications and great successes in predicting IL properties, including melting point [26], CO2 solubility [27], viscosity [28], etc. Despite its popularity, there is still a lack of accurate ML models for predicting IL toxicity.
Considering the above aspects, we herein explore ML models to predict the toxicity of ILs against IPC-81 by applying a systematic procedure covering model framework construction, hyper-parameter optimization, training, and evaluation. Since ML is a data-driven method, an extended experimental dataset is always preferred for building a reliable ML model. In this work, we first collect experimental toxicity data for 355 ILs. Two different ML models are then developed, one using the feedforward neural network (FNN) algorithm and the other using the support vector machine (SVM) algorithm. The structures of ML models, characterized by their hyper-parameters, are optimized with the five-fold cross validation to improve the model robustness. The corresponding models are then established with the training dataset, followed by an evaluation with an external test set to measure their generalization abilities.
2. Experimental Data
A dataset of the toxicity of 355 ILs against the IPC-81 was collected from the literature [18,29]. The toxicity was evaluated in terms of the logarithm of the half maximal effective concentration (logEC50), and the IL structures were depicted by SMILES (simplified molecular-input line-entry system) strings obtained from PubChem [30]. Therefore, the logEC50 dataset for the 355 ILs was used for predictive modeling. The detailed data are tabulated in Table S1 (Supporting Information) accompanied with the corresponding IL full name and SMILES strings.
To translate the text-form IL structure (i.e., SMILES string) into a ML-acceptable type (i.e., numerical values), the IL descriptors were created by a feature extraction algorithm [31] to characterize the IL structure. Specifically, an IL was treated as a molecule in which the cation and anion are connected with each other, and its SMILES string was parsed by the RDKit cheminformatics tool [32] to obtain detailed structural and chemical information. A set of substructures (subgroups) were defined as descriptors, and their appearance frequencies in the IL molecule were used as model inputs to characterize the structure of ILs. After analyzing the structures of the 355 ILs, a total of 42 structural descriptors were resulted, including 9 cation descriptors, 9 anion descriptors, and 24 general descriptors. These structural descriptors and their occurrence frequencies in each IL are provided in Tables S2 and S3 (Supporting Information), respectively.
To develop the ML models for IL toxicity prediction, a systematic procedure covering framework construction (step A), hyper-parameter optimization (step B), model establishment (step C), and model evaluation (step D) was deployed (see Figure 1). The full dataset was randomly divided into two parts, a training set (80% of the dataset, 284 samples) to develop the ML model and a test set (20% of the dataset, 71 samples) to evaluate the predictive accuracy of the developed model on unseen data.
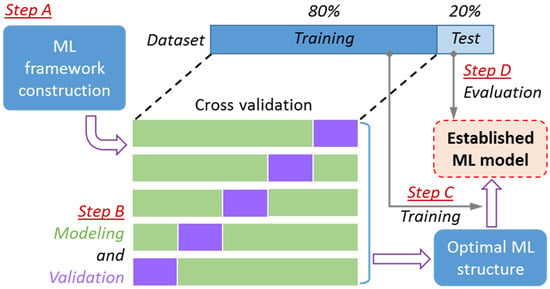
Figure 1.
Systematic procedure for machine learning (ML)-assisted ionic liquid (IL) toxicity predictive modeling.
To obtain a ML model with high robustness, cross validation should be employed to optimize the structural parameters (i.e., hyper-parameters). Herein, the five-fold cross validation strategy was adopted to determine the optimal hyper-parameters (Step B in Figure 1). First, the training set was equally divided into five parts. Then, for each combination of different hyper-parameters, the modeling process was performed five times based on the selected four parts (marked green in Figure 1), and the validation process was also carried out five times on the remaining part (marked yellow). Optimal hyper-parameters could be determined from the variation of the averaged error of the validation results. Finally, for the fixed hyper-parameters, the ML models were developed using the entire training set (Step C) and evaluated with the test set (Step D in Figure 1). The ILs in the randomly divided training and test sets are provided in Table S1 (Supporting Information).
3. ML Modeling
3.1. FNN Modeling
Artificial neural networks are probably the most widespread ML technique in mathematical modeling, image recognition, process control, etc. due to their flexible and configurable structures and connections. Therein, a feedforward neural network (FNN) is a common type, which presents the regular layer structure and one-directional transmission of information. Due to its simpler structure and less adjustable parameters, a FNN is computationally efficient in learning and making predictions, compared to other neural networks, such as the convolutional neural network and recurrent neural network. Moreover, it is more suitable for handling one-dimensional time-independent input data, as is the case in this work.
In this section, a two-hidden-layer FNN (see Figure 2) is constructed to correlate the logEC50 values with the IL structures. The appearance frequencies of the 42 subgroups are loaded into the neurons in the input layer, and after being processed by two adjacent hidden layers, the predicted logEC50 is given by the output layer. The activation functions, namely “sigmoid” and “softplus”, are assigned for the two hidden layers to achieve the non-linear data transformations, enabling the FNN to model complex mathematical relationships.
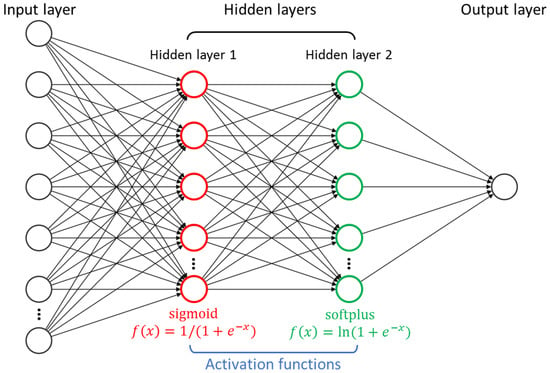
Figure 2.
Structure of the two-hidden-layer feedforward neural network (FNN) with activation functions.
The FNN framework was implemented with the PyTorch [33] toolkit in Python. The root mean square error (RMSE) was employed as the loss function to monitor the model performance. Moreover, Adam optimizer [34] was used to adjust the learning rate and model parameters, coupling with the back-propagation algorithm [35] that computes the gradient of the loss function and guides the optimization process.
Since the number of hidden layers was pre-defined, the number of neurons in each layer is an important hyper-parameter in the FNN structure that determines the model performance. The number of neurons in the input layer depends on the dimension of the used descriptors (42 in this work), and the neuron number of the output layer equals one, corresponding to the scalar logEC50. In this case, the number of neurons in the two hidden layers needed to be optimized by the five-fold cross validation. As can be seen in Figure 3, the lowest average RMSE (0.5696) of the five-round independent validations was obtained when 10 and 6 neurons were used in hidden layer 1 and 2, respectively. This means that this FNN structure was the most robust and promising one in predicting the toxicity of ILs against IPC-81.
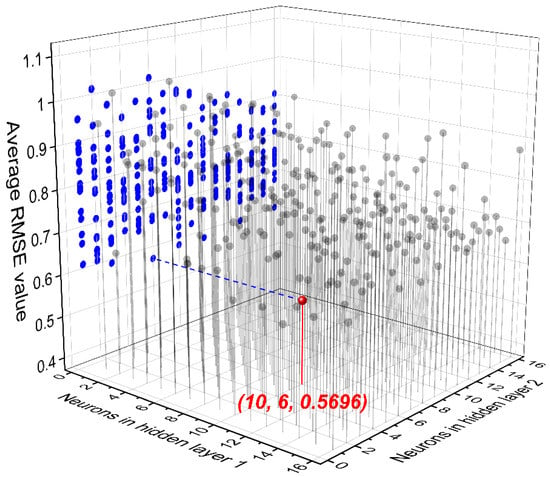
Figure 3.
Average root mean square error (RMSE) values in the five-fold cross validation for the FNN model.
After the numbers of neurons in the two hidden layers were determined, the FNN model was established with all of the training samples and then evaluated with the test samples. Figure 4 plots the predicted logEC50 of samples in the training and test sets against the corresponding experimental logEC50. In addition to the RMSE, mean absolute error (MAE) and coefficient of determination (R2) were also used to quantify the performance of the FNN model. The RMSE, MAE, and R2 were 0.2906, 0.2111, and 0.9227 for the training set, and 0.3732, 0.3028, and 0.8917 for the test set, respectively. The satisfying and close metrics obtained for the training and test sets indicate a generally good predictive performance of the obtained model for the prediction of the toxicity of ILs against IPC-81. For the established FNN model, prediction results are provided in Table S1, and weight and bias values in each layer are summarized in Table S4 (Supporting Information).
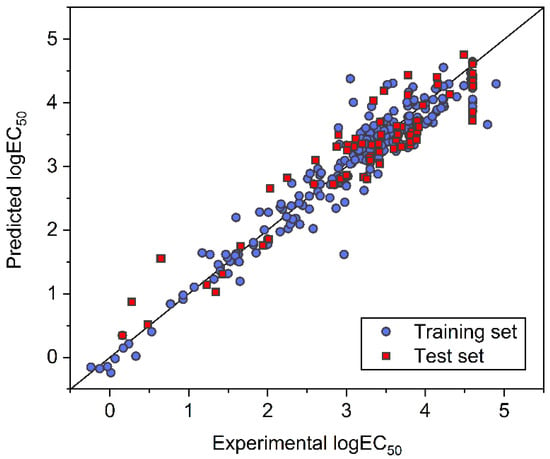
Figure 4.
Comparison between experimental and FNN-predicted logEC50 for ILs in the training and test datasets.
3.2. SVM Modeling
A support vector machine (SVM) is another popular ML algorithm in data analysis and predictive modeling. In terms of the regression task, the SVM algorithm is able to fit the training data by creating hyperplanes in the high-dimensional descriptor space. An accurate SVM model makes samples stay as close as possible to these hyperplanes.
The SVM framework was implemented with the scikit-learn [36] toolkit in Python. Gaussian radial basis function was adopted as the kernel function to map input descriptors into a high-dimensional space for complex nonlinear modeling. The RMSE was used again as the loss function to measure the model’s predictive capability. Two important hyper-parameters in the SVM algorithm, regularization parameter C and tolerance ε, were optimized by the five-fold cross validation. As shown in Figure 5, the lowest average RMSE value (0.4591) of the five independent validations was achieved by the SVM algorithm when the regularization parameter C and tolerance ε were 30 and 0.11, respectively.
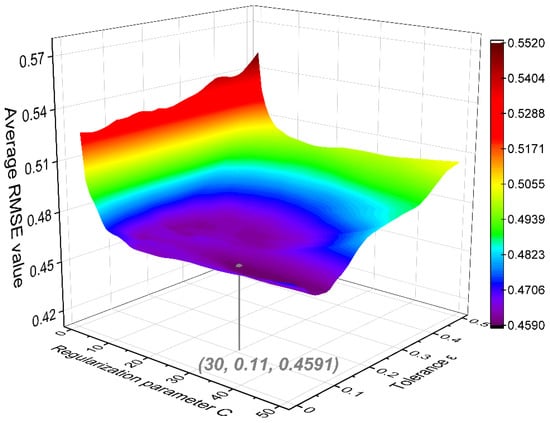
Figure 5.
Average RMSE values in the five-fold cross validation for the support vector machine (SVM) model.
Based on the optimized hyper-parameters highlighted in Figure 5, the final SVM model was developed with all the training samples and then evaluated with the test samples. The comparison between experimental and SVM-predicted logEC50 is shown in Figure 6. Except for a few outliers, most of the samples exhibited low deviations. The determined RMSE, MAE, and R2 were 0.2787, 0.1762, and 0.9289 for the training set, and 0.3204, 0.2628, and 0.9202 for the test set, respectively. These statistical indicators demonstrate a good predictive capability of the SVM model. For the established SVM model, prediction results are also provided in Table S1, and model parameters are summarized in Tables S5 and S6 (Supporting Information).
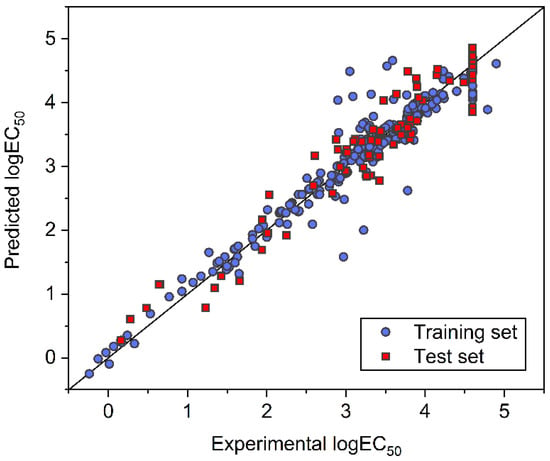
Figure 6.
Comparison between experimental and SVM-predicted logEC50 for ILs in the training and test datasets.
4. Model Comparison
Both the FNN and SVM models showed good predictive performances, as proven by the statistical results. Sorted in ascending order, the absolute errors between ML-predicted and experimental logEC50 for the 71 ILs in the test dataset are shown in Figure 7. As indicated, the SVM model exhibited smaller absolute errors, revealing its higher predictive accuracy for IL toxicity.
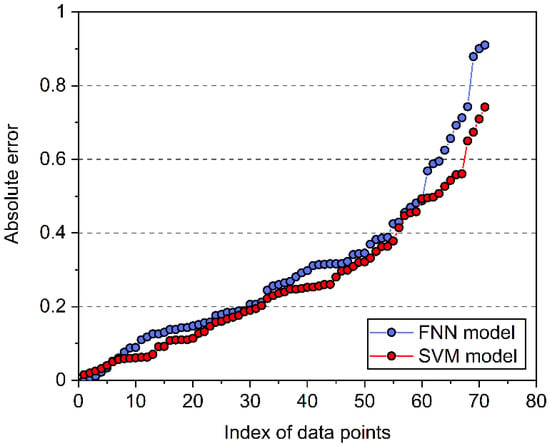
Figure 7.
Absolute errors between model-predicted and experimental logEC50 for the 71 ILs in the test dataset.
The two ML models established in this work were compared with the reported models developed by Sosnowska et al. [18] and Wu et al. [19]. As shown in Table 1, the FNN and SVM models presented much lower RMSE and MAE as well as a much higher R2 value than the two previous models, indicating their higher predictive accuracy. Moreover, they have improved applicability due to the extended dataset used in the model development. Comparing the two models developed in this work, it was found that the SVM model presented relatively lower RMSE and MAE as well as a higher R2 than the FNN model. Therefore, the SVM model can generally provide more accurate predictions on the toxicity of ILs against IPC-81, which confirms the conclusion obtained from Figure 7.

Table 1.
Statistical comparisons of different models in predicting the toxicity of ILs. MLR: multiple linear regression.
5. Conclusions
In this work, a dataset of 355 IL experimental logEC50 values was constructed to quantify the toxicity of ILs against IPC-81. Structural descriptors were generated with a feature extraction algorithm based on the SMILES strings of the ILs. Two ML frameworks (FNN and SVM) were built, and their structural parameters were optimized with five-fold cross validation. After determining the best set of structural parameters, the ML models were regressed using the training dataset, and the established models were evaluated with the test data. It was observed that the SVM model performed slightly better than the FNN model. However, compared with previously reported models, both models presented better predictive performance and improved applicability. Considering the satisfactory predictions on IL toxicity, the established ML models can be incorporated into computer-aided molecular design (CAMD) frameworks in order to identify suitable ILs that show low toxicity while meeting other requirements defined by the specific applications.
Supplementary Materials
The following are available online at https://www.mdpi.com/2227-9717/9/1/65/s1: Table S1: Details of the employed dataset and ML prediction results. Table S2: Structural descriptors of ILs for ML model development. Table S3: Occurrence frequencies of the descriptors in IL molecules. Table S4: Weight and bias values of the FNN model. Table S5: Support vectors of the SVM model. Table S6: Fitting parameters of the SVM model.
Author Contributions
Conceptualization: T.Z.; Methodology: T.Z. and Z.W.; Investigation: Z.W.; Writing—Original Draft Preparation: Z.W.; Writing—Review and Editing: Z.S. and T.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Acknowledgments
Zihao Wang acknowledges the support from the International Max Planck Research School (IMPRS) for Advanced Methods in Process and Systems Engineering, Magdeburg, Germany.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Watanabe, M.; Thomas, M.L.; Zhang, S.; Ueno, K.; Yasuda, T.; Dokko, K. Application of ionic liquids to energy storage and conversion materials and devices. Chem. Rev. 2017, 117, 7190–7239. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zhang, X.; Dong, H.; Zhao, Z.; Zhang, S.; Huang, Y. Carbon capture with ionic liquids: Overview and progress. Energy Environ. Sci. 2012, 5, 6668–6681. [Google Scholar] [CrossRef]
- Song, Z.; Hu, X.; Zhou, Y.; Zhou, T.; Qi, Z.; Sundmacher, K. Rational design of double salt ionic liquids as extraction solvents: Separation of thiophene/n-octane as example. AIChE J. 2019, 65, e16625. [Google Scholar] [CrossRef]
- Song, Z.; Zhou, T.; Qi, Z.; Sundmacher, K. Systematic method for screening ionic liquids as extraction solvents exemplified by an extractive desulfurization process. ACS Sustain. Chem. Eng. 2017, 5, 3382–3389. [Google Scholar] [CrossRef]
- Gharagheizi, F.; Sattari, M.; Ilani-Kashkouli, P.; Mohammadi, A.H.; Ramjugernath, D.; Richon, D. A “non-linear” quantitative structure–property relationship for the prediction of electrical conductivity of ionic liquids. Chem. Eng. Sci. 2013, 101, 478–485. [Google Scholar] [CrossRef]
- Gharagheizi, F.; Sattari, M.; Ilani-Kashkouli, P.; Mohammadi, A.H.; Ramjugernath, D.; Richon, D. Quantitative structure—property relationship for thermal decomposition temperature of ionic liquids. Chem. Eng. Sci. 2012, 84, 557–563. [Google Scholar] [CrossRef]
- Huang, Y.; Dong, H.; Zhang, X.; Li, C.; Zhang, S. A new fragment contribution-corresponding states method for physicochemical properties prediction of ionic liquids. AIChE J. 2013, 59, 1348–1359. [Google Scholar] [CrossRef]
- Zhou, T.; Chen, L.; Ye, Y.; Chen, L.; Qi, Z.; Freund, H.; Sundmacher, K. An overview of mutual solubility of ionic liquids and water predicted by COSMO-RS. Ind. Eng. Chem. Res. 2012, 51, 6256–6264. [Google Scholar] [CrossRef]
- Song, Z.; Zhang, C.; Qi, Z.; Zhou, T.; Sundmacher, K. Computer-aided design of ionic liquids as solvents for extractive desulfurization. AIChE J. 2018, 64, 1013–1025. [Google Scholar] [CrossRef]
- Chong, F.K.; Eljack, F.T.; Atilhan, M.; Foo, D.C.; Chemmangattuvalappil, N.G. A systematic visual methodology to design ionic liquids and ionic liquid mixtures: Green solvent alternative for carbon capture. Comput. Chem. Eng. 2016, 91, 219–232. [Google Scholar] [CrossRef]
- Chong, F.K.; Foo, D.C.Y.; Eljack, F.T.; Atilhan, M.; Chemmangattuvalappil, N.G. A systematic approach to design task-specific ionic liquids and their optimal operating conditions. Mol. Syst. Des. Eng. 2016, 1, 109–121. [Google Scholar] [CrossRef]
- Zhou, T.; Shi, H.; Ding, X.; Zhou, Y. Thermodynamic modeling and rational design of ionic liquids for pre-combustion carbon capture. Chem. Eng. Sci. 2021, 229, 116076. [Google Scholar] [CrossRef]
- Zhou, T.; McBride, K.; Linke, S.; Song, Z.; Sundmacher, K. Computer-aided solvent selection and design for efficient chemical processes. Curr. Opin. Chem. Eng. 2020, 27, 35–44. [Google Scholar] [CrossRef]
- Shi, H.; Zhang, X.; Zhou, T.; Sundmacher, K. Model-based optimal design of phase change ionic liquids for efficient thermal energy storage. Green Energy Environ. 2021. [Google Scholar] [CrossRef]
- Ranke, J.; Stolte, S.; Störmann, R.; Arning, J.; Jastorff, B. Design of sustainable chemical products the example of ionic liquids. Chem. Rev. 2007, 107, 2183–2206. [Google Scholar] [CrossRef]
- Stolte, S.; Matzke, M.; Arning, J.; Böschen, A.; Pitner, W.R.; Welz-Biermann, U.; Jastorff, B.; Ranke, J. Effects of different head groups and functionalised side chains on the aquatic toxicity of ionic liquids. Green Chem. 2007, 9, 1170–1179. [Google Scholar] [CrossRef]
- Yan, F.; Xia, S.; Wang, Q.; Ma, P. Predicting the toxicity of ionic liquids in leukemia rat cell line by the quantitative structure–activity relationship method using topological indexes. Ind. Eng. Chem. Res. 2012, 51, 13897–13901. [Google Scholar] [CrossRef]
- Sosnowska, A.; Grzonkowska, M.; Puzyn, T. Global versus local QSAR models for predicting ionic liquids toxicity against IPC-81 leukemia rat cell line: The predictive ability. J. Mol. Liq. 2017, 231, 333–340. [Google Scholar] [CrossRef]
- Wu, T.; Li, W.; Chen, M.; Zhou, Y.; Zhang, Q. Estimation of Ionic Liquids Toxicity against Leukemia Rat Cell Line IPC-81 based on the Empirical-like Models using Intuitive and Explainable Fingerprint Descriptors. Mol. Inf. 2020, 39, 2000102. [Google Scholar] [CrossRef]
- Varnek, A.; Baskin, I. Machine learning methods for property prediction in chemoinformatics: Quo vadis? J. Chem. Inf. Model. 2012, 52, 1413–1437. [Google Scholar] [CrossRef]
- Liu, Q.; Zhang, L.; Tang, K.; Liu, L.; Du, J.; Meng, Q.; Gani, R. A machine learning-based atom contribution method for the prediction of charge density profiles and solvent design. AIChE J. 2020, e17110. [Google Scholar] [CrossRef]
- Zhang, L.; Mao, H.; Liu, L.; Du, J.; Gani, R. A machine learning based computer-aided molecular design/screening methodology for fragrance molecules. Comput. Chem. Eng. 2018, 115, 295–308. [Google Scholar] [CrossRef]
- Su, Y.; Wang, Z.; Jin, S.; Shen, W.; Ren, J.; Eden, M.R. An architecture of deep learning in QSPR modeling for the prediction of critical properties using molecular signatures. AIChE J. 2019, 65, e16678. [Google Scholar] [CrossRef]
- Wang, Z.; Su, Y.; Shen, W.; Jin, S.; Clark, J.H.; Ren, J.; Zhang, X. Predictive deep learning models for environmental properties: The direct calculation of octanol-water partition coefficients from molecular graphs. Green Chem. 2019, 21, 4555–4565. [Google Scholar] [CrossRef]
- Zhou, T.; Jhamb, S.; Liang, X.; Sundmacher, K.; Gani, R. Prediction of acid dissociation constants of organic compounds using group contribution methods. Chem. Eng. Sci. 2018, 183, 95–105. [Google Scholar] [CrossRef]
- Venkatraman, V.; Evjen, S.; Knuutila, H.K.; Fiksdahl, A.; Alsberg, B.K. Predicting ionic liquid melting points using machine learning. J. Mol. Liq. 2018, 264, 318–326. [Google Scholar] [CrossRef]
- Song, Z.; Shi, H.; Zhang, X.; Zhou, T. Prediction of CO2 solubility in ionic liquids using machine learning methods. Chem. Eng. Sci. 2020, 223, 115752. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhang, X.; Deng, L.; Zhang, S. Prediction of viscosity of imidazolium-based ionic liquids using MLR and SVM algorithms. Comput. Chem. Eng. 2016, 92, 37–42. [Google Scholar] [CrossRef]
- Zhao, Y.; Zhao, J.; Huang, Y.; Zhou, Q.; Zhang, X.; Zhang, S. Toxicity of ionic liquids: Database and prediction via quantitative structure-activity relationship method. J. Hazard. Mater. 2014, 278, 320–329. [Google Scholar] [CrossRef]
- Kim, S.; Chen, J.; Cheng, T.; Gindulyte, A.; He, J.; He, S.; Li, Q.; Shoemaker, B.A.; Thiessen, P.A.; Yu, B.; et al. PubChem 2019 update: Improved access to chemical data. Nucleic Acids Res. 2019, 47, D1102–D1109. [Google Scholar] [CrossRef]
- Wang, Z.; Su, Y.; Jin, S.; Shen, W.; Ren, J.; Zhang, X.; Clark, J.H. A novel unambiguous strategy of molecular feature extraction in machine learning assisted predictive models for environmental properties. Green Chem. 2020, 22, 3867–3876. [Google Scholar] [CrossRef]
- RDKit: Open-Source Cheminformatics Software. Available online: https://www.rdkit.org/ (accessed on 14 October 2020).
- PyTorch. Available online: https://pytorch.org/ (accessed on 14 October 2020).
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).