Answer Set Programming for Computing Constraints-Based Elementary Flux Modes: Application to Escherichia coli Core Metabolism
Abstract
1. Introduction
2. Results
2.1. Application on the E. coli core Model
2.2. Model Modifications
3. Discussion
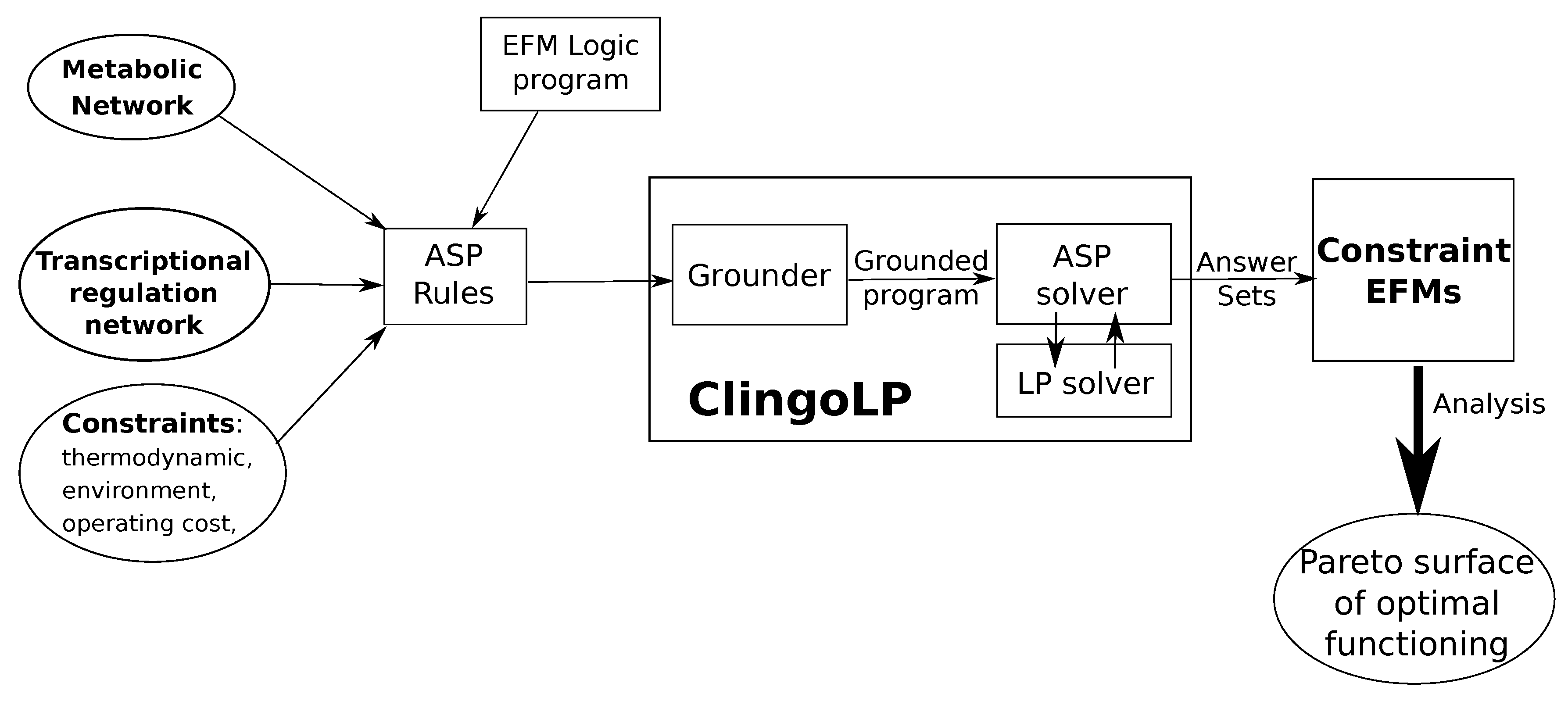
4. Materials and Methods
4.1. Answer Set Programming
4.2. Problem Formulation of EFMs Computation
4.3. Constraints’ Formulation
4.4. Pareto Surface of Optimal Functioning
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| EFM | Elementary Flux Mode |
| EFMA | Elementary Flux Modes Analysis |
| FBA | Flux Balance Analysis |
| DD | Double Description |
| ASP | Answer Set Programming |
| LP | Linear Programming |
| SMT | Satisfiability Modulo Theories |
| MCFM | Minimal Constrained Flux Mode |
| MILP | Mixed Integer Linear Program |
Appendix A. Pareto Optimal Pathways of E. coli
Appendix B. E. coli Biomass Modifications
Appendix C. Pareto Optimal Pathways of E. coli with the Adjusted Biomass
| Standard Regulation | No Formate Regulation | ||
|---|---|---|---|
| Processing | Aerobic conditions | 4273 EFMs [2362 s] | 16,411 EFMs [8005 s] |
| Anaerobic conditions | 930 EFMs [469 s] | ||
| Post-processing | Filtered out MCFMs | 36 MCFMs | 137 MCFMs |
| Pareto optimal in biomass yield | 5 EFMs | 9 EFMs | |
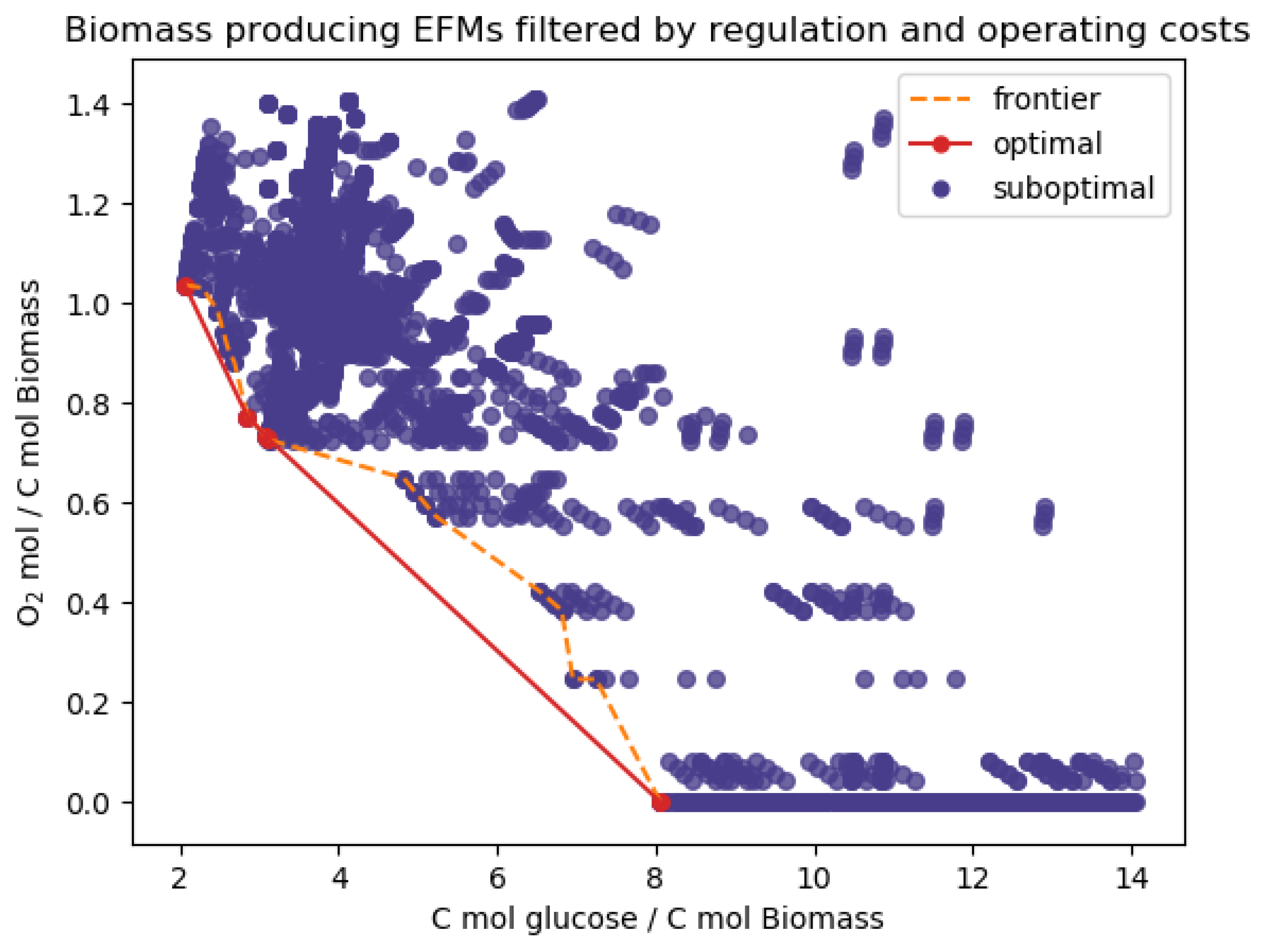
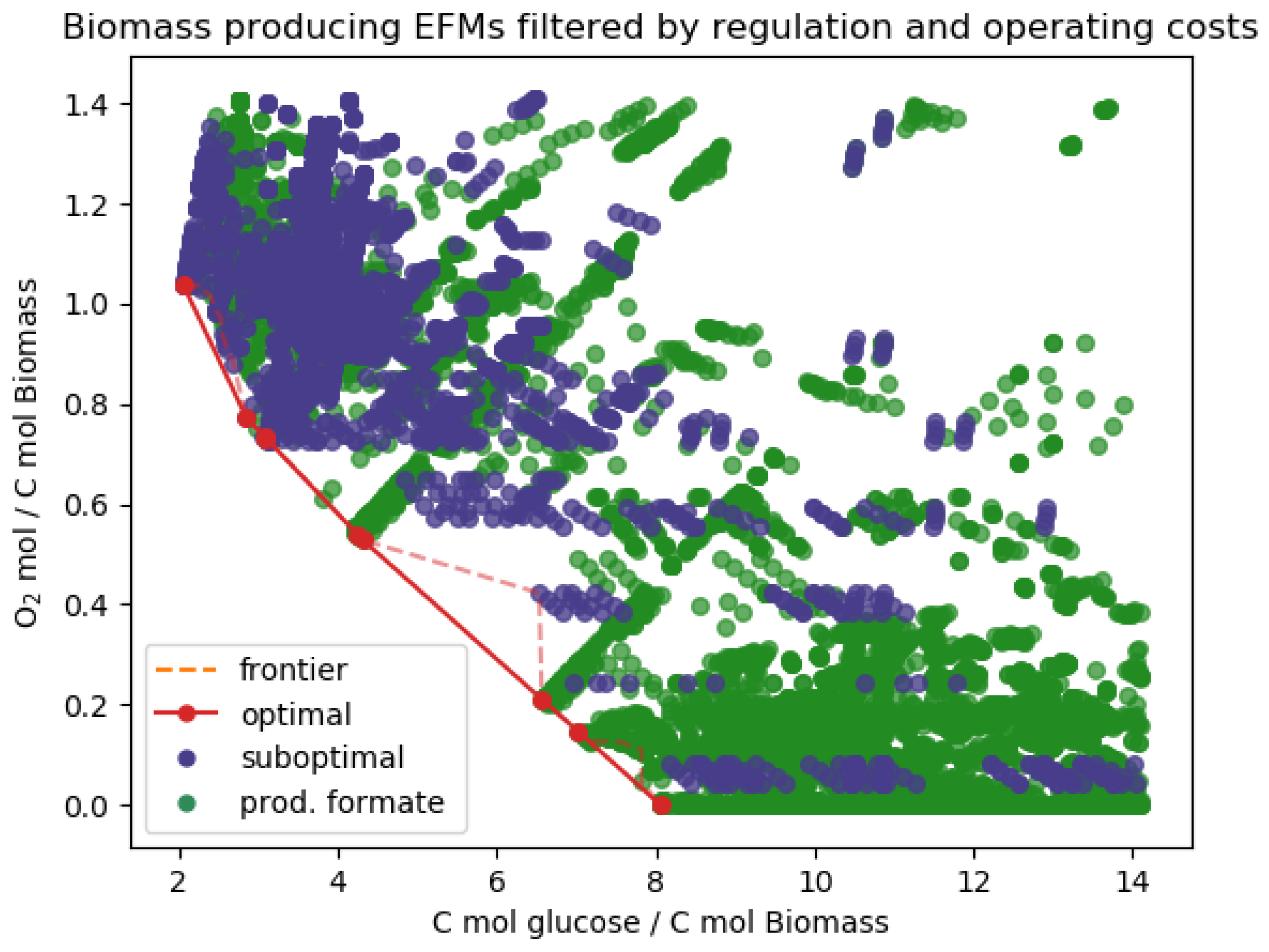
Appendix D. Additional Results
| Constraints | Filtered out MCFMs | EFMs and MCFMs | ||||
|---|---|---|---|---|---|---|
| With regulation and environment | O2 | No O2 | Formate | O2 | No O2 | Formate |
| No additional constraints | 0 | 0 | 0 | 4027 [1314 s] | 1459 [602 s] | 28,256 [5572 s] |
| Biomass-producing | 0 | 0 | 0 | 2746 [833 s] | 1355 [436 s] | 24,324 [6281 s] |
| Biomass-producing Thermodynamic data | 0 | 0 | 0 | 2746 [901 s] | 1355 [471 s] | 24,324 [6843 s] |
| Biomass-producing Yields (O2 < 0.7) (C < 7) | 39 | 0 | 119 | 1157 [560 s] | 363 [220 s] | 11,136 [4884 s] |
| Biomass-producing Thermo and Yields | 39 | 0 | 119 | 1157 [542 s] | 363 [232 s] | 11,136 [5318 s] |
| Constraints | Filtered out MCFMs | EFMs and MCFMs | |||||
|---|---|---|---|---|---|---|---|
| With regulation and environment | O2 | No O2 | Formate | O2 | No O2 | Formate | |
| ATPM | No additional constraints | 0 | 0 | 0 | 8354 [2518 s] | 1260 [473 s] | 33,499 [6676 s] |
| Biomass-producing | 3 | 0 | 3 | 7076 [2939 s] | 1156 [428 s] | 29,570 [8697 s] | |
| No ATPM | No additional constraints | 0 | 0 | 0 | 7735 [2337s] | 1228 [428s] | 32,098 [6474s] |
| Biomass-producing | 3 | 0 | 3 | 6656 [2948 s] | 1140 [441 s] | 28,795 [8664 s] | |
| BP Thermodynamic data | 3 | 0 | 3 | 6656 [3027 s] | 1140 [458 s] | 28,795 [8744 s] | |
| BP Yields (O2 < 1.4) (C < 14) | 36 | 0 | 137 | 4309 [2369 s] | 930 [473 s] | 16,548 [7904 s] | |
| BP Thermo and yields | 36 | 0 | 137 | 4309 [2362 s] | 930 [469 s] | 16,548 [8005 s] | |
Appendix E. ASP Encoding
- representing the flux values for every reaction r. These are theory atoms valued during the solving by clingo[LP]. The vector composed of all values contained in the flux atoms of a solution is a flux vector.
- representing active reactions, reactions r such that . There is no atom support(r) for reactions r for which . In this way, the set of all support atoms represents the support of the solution flux vector .
Appendix F. ASP Programs
- solve[LP].lp4 : Program implementing the computation of EFMs under constraints. Works with any network and constraints encoded in ASP as presented in Appendix E.
- orth_ecoli_core.lp4 : ASP translation of the network, using the encoding established above.
- orth_ecoli_core_atp.lp4 : ASP translation of the network with modified biomass.
- ecoli_core_regul.lp4 : Full translation of the E. coli core transcriptional regulation network.
- ecoli_core_additional_constraints.lp4 : Additional constraints for the E. coli core network, including environments, thermodynamic constraints and operating costs constraints.
Appendix G. Additional Python Code
References
- Schuster, S.; Hilgetag, C. On Elementary Flux Modes in Biochemical Reaction Systems at Steady State. J. Biol. Syst. 1994, 2, 165–182. [Google Scholar] [CrossRef]
- Schuster, S.; Fell, D.; Dandekar, T. A General Definition of Metabolic Pathways Useful for Systematic Organization and Analysis of Complex Metabolic Networks. Nat. Biotechnol. 2000, 18, 326–332. [Google Scholar] [CrossRef] [PubMed]
- Behre, J.; Wilhelm, T.; von Kamp, A.; Ruppin, E.; Schuster, S. Structural Robustness of Metabolic Networks with Respect to Multiple Knockouts. J. Theor. Biol. 2008, 252, 433–441. [Google Scholar] [CrossRef] [PubMed]
- Gerstl, M.P.; Klamt, S.; Jungreuthmayer, C.; Zanghellini, J. Exact Quantification of Cellular Robustness in Genome-Scale Metabolic Networks. Bioinformatics 2015, 32, 730–737. [Google Scholar] [CrossRef] [PubMed]
- Jungreuthmayer, C.; Nair, G.; Klamt, S.; Zanghellini, J. Comparison and Improvement of Algorithms for Computing Minimal Cut Sets. BMC Bioinform. 2013, 14, 318. [Google Scholar] [CrossRef] [PubMed]
- Jungreuthmayer, C.; Ruckerbauer, D.E.; Gerstl, M.P.; Hanscho, M.; Zanghellini, J. Avoiding the Enumeration of Infeasible Elementary Flux Modes by Including Transcriptional Regulatory Rules in the Enumeration Process Saves Computational Costs. PLoS ONE 2015, 10, e0129840. [Google Scholar] [CrossRef]
- Trinh, C.T.; Unrean, P.; Srienc, F. Minimal Escherichia Coli Cell for the Most Efficient Production of Ethanol from Hexoses and Pentoses. Appl. Environ. Microbiol. 2008, 74, 3634–3643. [Google Scholar] [CrossRef]
- Hädicke, O.; Klamt, S. Computing Complex Metabolic Intervention Strategies Using Constrained Minimal Cut Sets. Metab. Eng. 2011, 13, 204–213. [Google Scholar] [CrossRef]
- Carlson, R.; Srienc, F. Fundamental Escherichia Coli Biochemical Pathways for Biomass and Energy Production: Identification of Reactions. Biotechnol. Bioeng. 2004, 85, 1–19. [Google Scholar] [CrossRef]
- Carlson, R.P. Metabolic Systems Cost-Benefit Analysis for Interpreting Network Structure and Regulation. Bioinformatics 2007, 23, 1258–1264. [Google Scholar] [CrossRef]
- Carlson, R.P. Decomposition of Complex Microbial Behaviors into Resource-Based Stress Responses. Bioinformatics 2009, 25, 90–97. [Google Scholar] [CrossRef] [PubMed]
- Carlson, R.P.; Taffs, R.L. Molecular-Level Tradeoffs and Metabolic Adaptation to Simultaneous Stressors. Curr. Opin. Biotechnol. 2010, 21, 670–676. [Google Scholar] [CrossRef] [PubMed]
- Beck, A.; Hunt, K.; Bernstein, H.; Carlson, R. Chapter 15—Interpreting and Designing Microbial Communities for Bioprocess Applications, from Components to Interactions to Emergent Properties. In Biotechnology for Biofuel Production and Optimization; Eckert, C.A., Trinh, C.T., Eds.; Elsevier: Amsterdam, The Netherlands, 2016; pp. 407–432. [Google Scholar] [CrossRef]
- Folsom, J.P.; Carlson, R.P. Physiological, Biomass Elemental Composition and Proteomic Analyses of Escherichia Coli Ammonium-Limited Chemostat Growth, and Comparison with Iron- and Glucose-Limited Chemostat Growth. Microbiology 2015, 161, 1659–1670. [Google Scholar] [CrossRef] [PubMed]
- Folsom, J.P.; Parker, A.E.; Carlson, R.P. Physiological and Proteomic Analysis of Escherichia coli Iron-Limited Chemostat Growth. J. Bacteriol. 2014, 196, 2748–2761. [Google Scholar] [CrossRef] [PubMed]
- Müller, S.; Regensburger, G.; Steuer, R. Enzyme Allocation Problems in Kinetic Metabolic Networks: Optimal Solutions Are Elementary Flux Modes. J. Theor. Biol. 2014, 347, 182–190. [Google Scholar] [CrossRef]
- Wortel, M.; Noor, E.; Ferris, M.; Bruggeman, F.; Liebermeister, W. Metabolic Enzyme Cost Explains Variable Trade-Offs between Microbial Growth Rate and Yield. PLoS Comput. Biol. 2018, 14, 1–21. [Google Scholar] [CrossRef]
- Provost, A.; Bastin, G. Dynamic Metabolic Modelling under the Balanced Growth Condition. J. Process Control 2004, 14, 717–728. [Google Scholar] [CrossRef]
- Kim, J.I.; Varner, J.D.; Ramkrishna, D. A Hybrid Model of Anaerobic E. Coli GJT001: Combination of Elementary Flux Modes and Cybernetic Variables. Biotechnol. Prog. 2008, 24, 993–1006. [Google Scholar] [CrossRef]
- Motzkin, T.; Raiffa, H.; Thompson, G.; Thrall, R. The Double Description Method. In Contributions to Theory of Games, Volume 2; Kuhn, H., Tucker, A., Eds.; Princeton University Press: Princeton, NJ, USA, 1953. [Google Scholar]
- Fukuda, K.; Prodon, A. Double Description Method Revisited. In Proceedings of the Combinatorics and Computer Science; Deza, M., Euler, R., Manoussakis, I., Eds.; Springer: Berlin/Heidelberg, Germany, 1996; pp. 91–111. [Google Scholar] [CrossRef]
- Pfeiffer, T.; Sanchez-Valdenebro, I.; Nuno, J.C.; Montero, F.; Schuster, S. METATOOL: For Studying Metabolic Networks. Bioinformatics 1999, 15, 251–257. [Google Scholar] [CrossRef]
- Terzer, M.; Stelling, J. Large-Scale Computation of Elementary Flux Modes with Bit Pattern Trees. Bioinformatics 2008, 24, 2229–2235. [Google Scholar] [CrossRef]
- Hunt, K.A.; Folsom, J.P.; Taffs, R.L.; Carlson, R.P. Complete Enumeration of Elementary Flux Modes through Scalable Demand-Based Subnetwork Definition. Bioinformatics 2014, 30, 1569–1578. [Google Scholar] [CrossRef] [PubMed]
- Jungreuthmayer, C.; Ruckerbauer, D.E.; Zanghellini, J. regEfmtool: Speeding up Elementary Flux Mode Calculation Using Transcriptional Regulatory Rules in the Form of Three-State Logic. Biosystems 2013, 113, 37–39. [Google Scholar] [CrossRef] [PubMed]
- Peres, S.; Jolicœur, M.; Moulin, C.; Dague, P.; Schuster, S. How Important Is Thermodynamics for Identifying Elementary Flux Modes? PLoS ONE 2017, 12, 1–20. [Google Scholar] [CrossRef] [PubMed]
- Gerstl, M.P.; Jungreuthmayer, C.; Zanghellini, J. tEFMA: Computing Thermodynamically Feasible Elementary Flux Modes in Metabolic Networks. Bioinformatics 2015, 31, 2232–2234. [Google Scholar] [CrossRef]
- Gerstl, M.P.; Ruckerbauer, D.E.; Mattanovich, D.; Jungreuthmayer, C.; Zanghellini, J. Metabolomics Integrated Elementary Flux Mode Analysis in Large Metabolic Networks. Sci. Rep. 2015, 5, 8930. [Google Scholar] [CrossRef]
- Peres, S.; Schuster, S.; Dague, P. Thermodynamic Constraints for Identifying the Elementary Flux Modes. Biochem. Soc. Trans. 2018, 46, 641–647. [Google Scholar] [CrossRef]
- Peres, S.; Morterol, M.; Simon, L. SAT-Based Metabolics Pathways Analysis without Compilation. In Lecture Note in Bioinformatics; P. Mendes, J.D., Smallbone, K., Eds.; Springer International Publishing: Berlin/Heidelberg, Germany, 2014; Volume 8859, pp. 20–31. [Google Scholar] [CrossRef]
- Morterol, M.; Dague, P.; Peres, S.; Simon, L. Minimality of Metabolic Flux Modes under Boolean Regulation Constraints. In Proceedings of the Workshop on Constraint-Based Methods for Bioinformatics (WCB), Toulouse, France, 5 September 2016. [Google Scholar]
- de Figueiredo, L.F.; Podhorski, A.; Rubio, A.; Kaleta, C.; Beasley, J.E.; Schuster, S.; Planes, F.J. Computing the Shortest Elementary Flux Modes in Genome-Scale Metabolic Networks. Bioinformatics 2009, 25, 3158–3165. [Google Scholar] [CrossRef]
- Pey, J.; Planes, F.J. Direct Calculation of Elementary Flux Modes Satisfying Several Biological Constraints in Genome-Scale Metabolic Networks. Bioinformatics 2014, 30, 2197–2203. [Google Scholar] [CrossRef][Green Version]
- Vieira, V.; Rocha, M. CoBAMP: A Python Framework for Metabolic Pathway Analysis in Constraint-Based Models. Bioinformatics 2019, 35, 5361–5362. [Google Scholar] [CrossRef]
- Rezola, A.; de Figueiredo, L.F.; Brock, M.; Pey, J.; Podhorski, A.; Wittmann, C.; Schuster, S.; Bockmayr, A.; Planes, F.J. Exploring Metabolic Pathways in Genome-Scale Networks via Generating Flux Modes. Bioinformatics 2010, 27, 534–540. [Google Scholar] [CrossRef][Green Version]
- von Kamp, A.; Klamt, S. Enumeration of Smallest Intervention Strategies in Genome-Scale Metabolic Networks. PLoS Comput. Biol. 2014, 10, 1–13. [Google Scholar] [CrossRef] [PubMed]
- David, L.; Bockmayr, A. Computing Elementary Flux Modes Involving a Set of Target Reactions. IEEE/ACM Trans. Comput. Biol. Bioinform. 2014, 11, 1099–1107. [Google Scholar] [CrossRef] [PubMed]
- Song, H.S.; Goldberg, N.; Mahajan, A.; Ramkrishna, D. Sequential Computation of Elementary Modes and Minimal Cut Sets in Genome-Scale Metabolic Networks Using Alternate Integer Linear Programming. Bioinformatics 2017, 33, 2345–2353. [Google Scholar] [CrossRef] [PubMed]
- Gebser, M.; Schaub, T.; Thiele, S.; Usadel, B.; Veber, P. Detecting Inconsistencies in Large Biological Networks with Answer Set Programming. In Proceedings of the International Conference on Logic Programming, Udine, Italy, 9–13 December 2008; pp. 130–144. [Google Scholar] [CrossRef]
- Razzaq, M.; Paulevé, L.; Siegel, A.; Saez-Rodriguez, J.; Bourdon, J.; Guziolowski, C. Computational Discovery of Dynamic Cell Line Specific Boolean Networks from Multiplex Time-Course Data. PLoS Comput. Biol. 2018, 14, 1–23. [Google Scholar] [CrossRef] [PubMed]
- Frioux, C.; Schaub, T.; Schellhorn, S.; Siegel, A.; Wanko, P. Hybrid Metabolic Network Completion. In Logic Programming and Nonmonotonic Reasoning; Balduccini, M., Janhunen, T., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 308–321. [Google Scholar] [CrossRef]
- Janhunen, T.; Kaminski, R.; Ostrowski, M.; Schaub, T.; Schellhorn, S.; Wanko, P. Clingo Goes Linear Constraints over Reals and Integers. arXiv 2017, arXiv:1707.04053. [Google Scholar] [CrossRef]
- Gebser, M.; Kaminski, R.; Kaufmann, B.; Ostrowski, M.; Schaub, T.; Wanko, P. Theory Solving Made Easy with Clingo 5. In Technical Communications of the 32nd International Conference on Logic Programming (ICLP 2016); Carro, M., King, A., Saeedloei, N., Vos, M.D., Eds.; OpenAccess Series in Informatics (OASIcs); Schloss Dagstuhl–Leibniz-Zentrum fuer Informatik: Dagstuhl, Germany, 2016; Volume 52, pp. 2:1–2:15. [Google Scholar] [CrossRef]
- Orth, J.D.; Fleming, R.M.T.; Palsson, B.Ø. Reconstruction and Use of Microbial Metabolic Networks: The Core Escherichia Coli Metabolic Model as an Educational Guide. EcoSal Plus 2010, 4. [Google Scholar] [CrossRef]
- de Graef, M.R.; Alexeeva, S.; Snoep, J.L.; Teixeira de Mattos, M.J. The Steady-State Internal Redox State (NADH/NAD) Reflects the External Redox State and Is Correlated with Catabolic Adaptation in Escherichia Coli. J. Bacteriol. 1999, 181, 2351–2357. [Google Scholar] [CrossRef]
- Alexeeva, S.; Hellingwerf, K.J.; Teixeira de Mattos, M.J. Requirement of ArcA for Redox Regulation in Escherichia Coli under Microaerobic but Not Anaerobic or Aerobic Conditions. J. Bacteriol. 2003, 185, 204–209. [Google Scholar] [CrossRef]
- Orth, J.D.; Thiele, I.; Palsson, B.Ã. What Is Flux Balance Analysis? Nat. Biotechnol. 2010, 28, 245–248. [Google Scholar] [CrossRef]
- Peres, S.; Fromion, V. Thermodynamic Approaches in Flux Analysis. In Methods in Molecular Biology; Analysis, M.F., Ed.; Springer: Berlin/Heidelberg, Germany, 2019; Chapter 17. [Google Scholar]
- Klamt, S.; Gagneur, J.; von Kamp, A. Algorithmic Approaches for Computing Elementary Modes in Large Biochemical Reaction Networks. IEE Proc. Syst. Biol. 2005, 152, 249–255. [Google Scholar] [CrossRef]
- Olivier, B.G.; Bergmann, F.T. SBML Level 3 Package: Flux Balance Constraints Version 2. J. Integr. Bioinform. 2018, 15, 1–39. [Google Scholar] [CrossRef] [PubMed]
- King, Z.A.; Lu, J.; Dräger, A.; Miller, P.; Federowicz, S.; Lerman, J.A.; Ebrahim, A.; Palsson, B.O.; Lewis, N.E. BiGG Models: A Platform for Integrating, Standardizing and Sharing Genome-Scale Models. Nucleic Acids Res. 2016, 44, D515–D522. [Google Scholar] [CrossRef] [PubMed]
- Schuster, S.; Dandekar, T.; Fell, D. Detection of Elementary Modes in Biochemical Networks: A Promising Tool for Pathway Analysis and Metabolic Engineering. Trends Biotechnol. 1999, 17, 53–60. [Google Scholar] [CrossRef]
- Lifschitz, V. What Is Answer Set Programming? In Proceedings of the AAAI 2008, Chicago, IL, USA, 13–17 July 2008; Volume 8, pp. 1594–1597. [Google Scholar]
- Gebser, M.; Kaufmann, B.; Schaub, T. Conflict-Driven Answer Set Solving: From Theory to Practice. Artif. Intell. 2012, 187–188, 52–89. [Google Scholar] [CrossRef]
- Gebser, M.; Kaminski, R.; Kaufmann, B.; Lindauer, M.; Ostrowski, M.; Romero, J.; Schaub, T.; Thiele, S.; Wanko, P. Potassco User Guide, 2nd ed.; University of Potsdam: Potsdam, Germany, 2019. [Google Scholar]
- Covert, M.W.; Palsson, B.O. Constraints-Based Models: Regulation of Gene Expression Reduces the Steady-State Solution Space. J. Theor. Biol. 2003, 221, 309–325. [Google Scholar] [CrossRef]
- King, Z.A.; Dräger, A.; Ebrahim, A.; Sonnenschein, N.; Lewis, N.E.; Palsson, B.O. Escher: A Web Application for Building, Sharing, and Embedding Data-Rich Visualizations of Biological Pathways. PLoS Comput. Biol. 2015, 11, e1004321. [Google Scholar] [CrossRef] [PubMed]
- Kluyver, T.; Ragan-Kelley, B.; Pérez, F.; Granger, B.; Bussonnier, M.; Frederic, J.; Kelley, K.; Hamrick, J.; Grout, J.; Corlay, S.; et al. Jupyter Notebooks—A Publishing Format for Reproducible Computational Workflows; Loizides, F., Schmidt, B., Eds.; Positioning and Power in Academic Publishing: Players, Agents and Agendas; IOS Press: Amsterdam, The Netherlands, 2016; pp. 87–90. [Google Scholar]

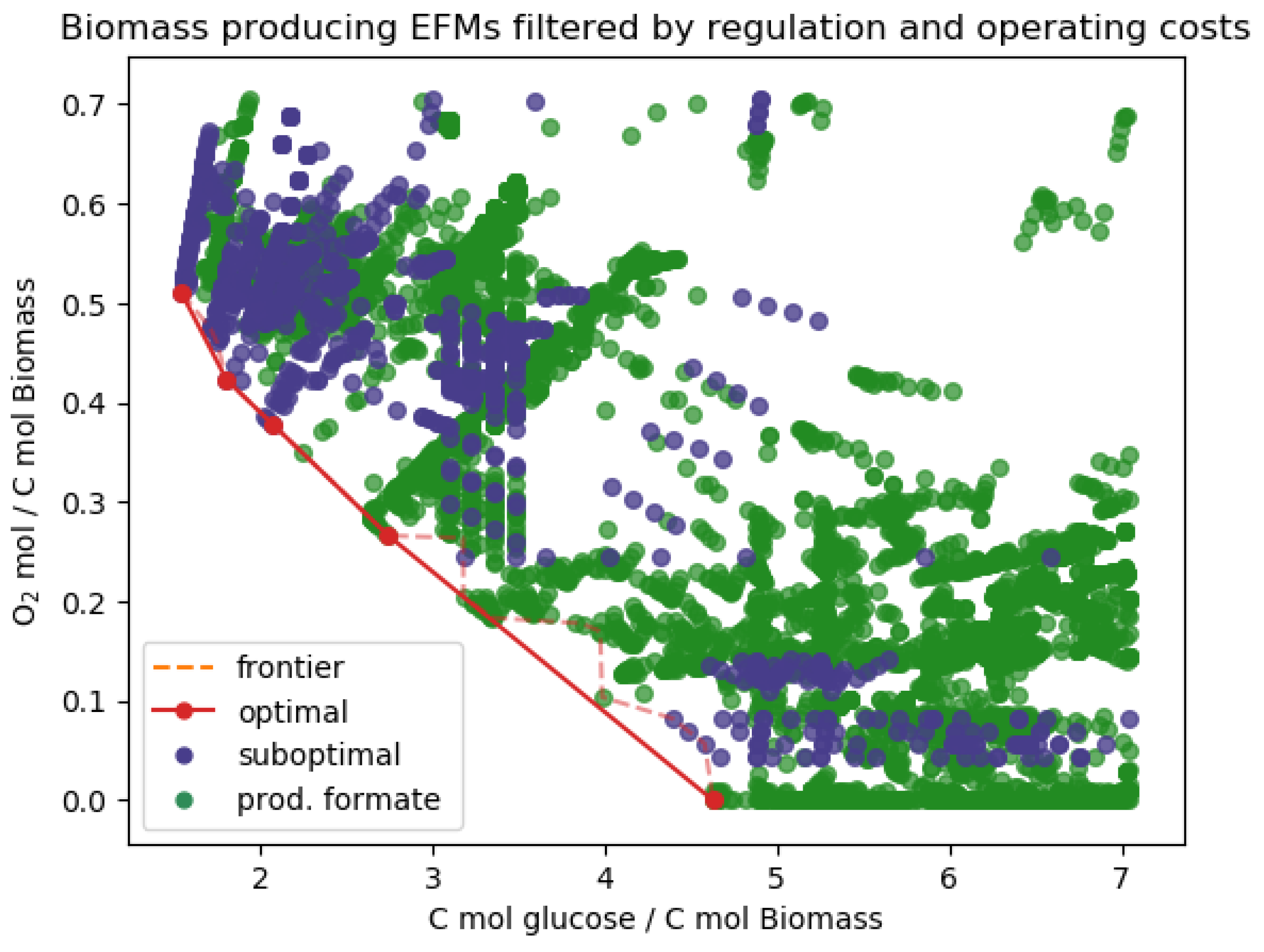
| Standard Regulation | No Formate Regulation | ||
|---|---|---|---|
| Processing | Aerobic conditions | 1118 EFMs [542 s] | 11,017 EFMs [5318 s] |
| Anaerobic conditions | 363 EFMs [232 s] | ||
| Post-processing | Filtered out MCFMs | 39 MCFMs | 119 MCFMs |
| Pareto optimal in biomass yield | 4 EFMs | 5 EFMs | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahout, M.; Carlson, R.P.; Peres, S. Answer Set Programming for Computing Constraints-Based Elementary Flux Modes: Application to Escherichia coli Core Metabolism. Processes 2020, 8, 1649. https://doi.org/10.3390/pr8121649
Mahout M, Carlson RP, Peres S. Answer Set Programming for Computing Constraints-Based Elementary Flux Modes: Application to Escherichia coli Core Metabolism. Processes. 2020; 8(12):1649. https://doi.org/10.3390/pr8121649
Chicago/Turabian StyleMahout, Maxime, Ross P. Carlson, and Sabine Peres. 2020. "Answer Set Programming for Computing Constraints-Based Elementary Flux Modes: Application to Escherichia coli Core Metabolism" Processes 8, no. 12: 1649. https://doi.org/10.3390/pr8121649
APA StyleMahout, M., Carlson, R. P., & Peres, S. (2020). Answer Set Programming for Computing Constraints-Based Elementary Flux Modes: Application to Escherichia coli Core Metabolism. Processes, 8(12), 1649. https://doi.org/10.3390/pr8121649







