Hybrid Modeling for Simultaneous Prediction of Flux, Rejection Factor and Concentration in Two-Component Crossflow Ultrafiltration
Abstract
1. Introduction
2. Materials and Methods
2.1. Equipment and Chemicals
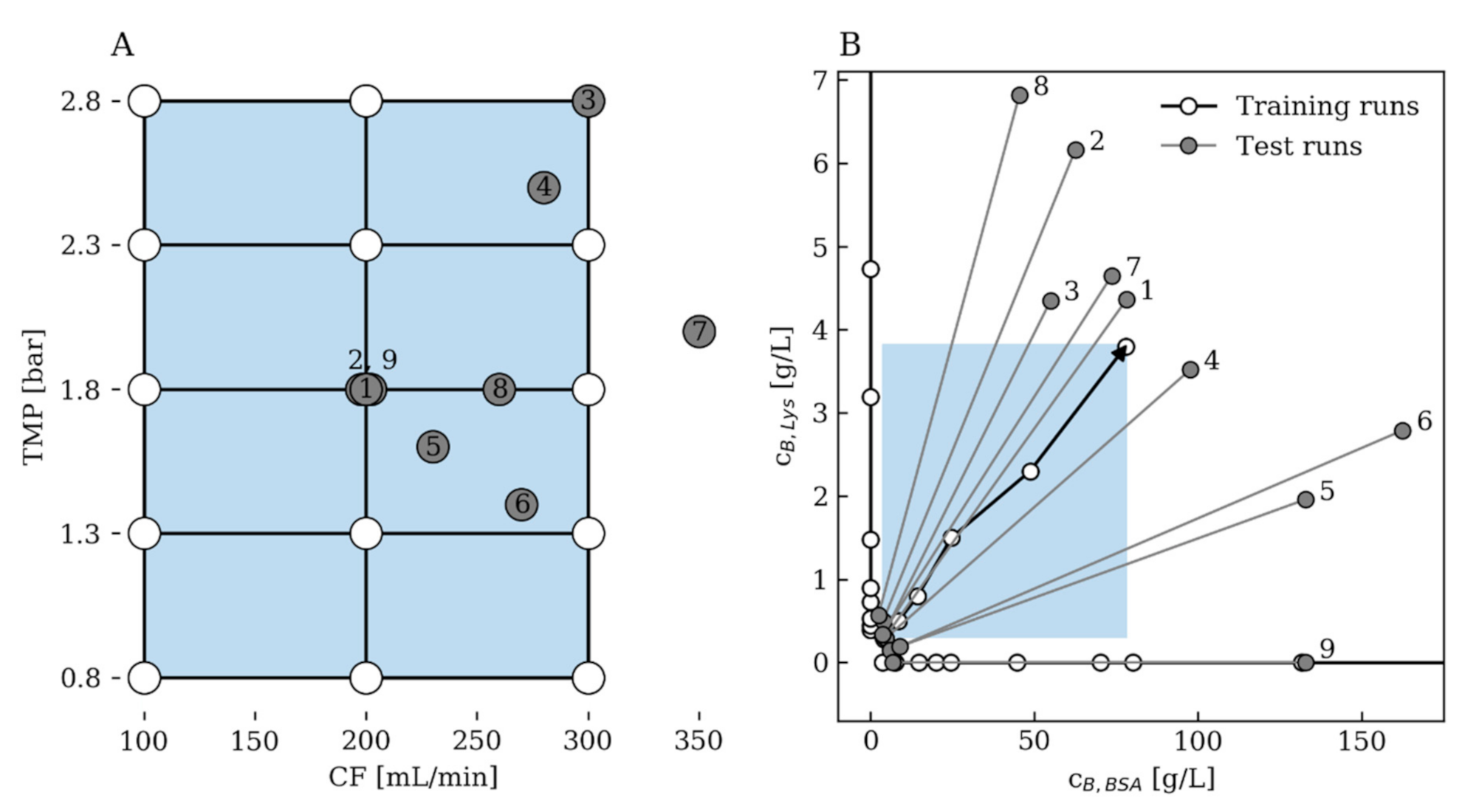
2.2. Training and Test Data Generation
2.3. Concentration Polarization Correction
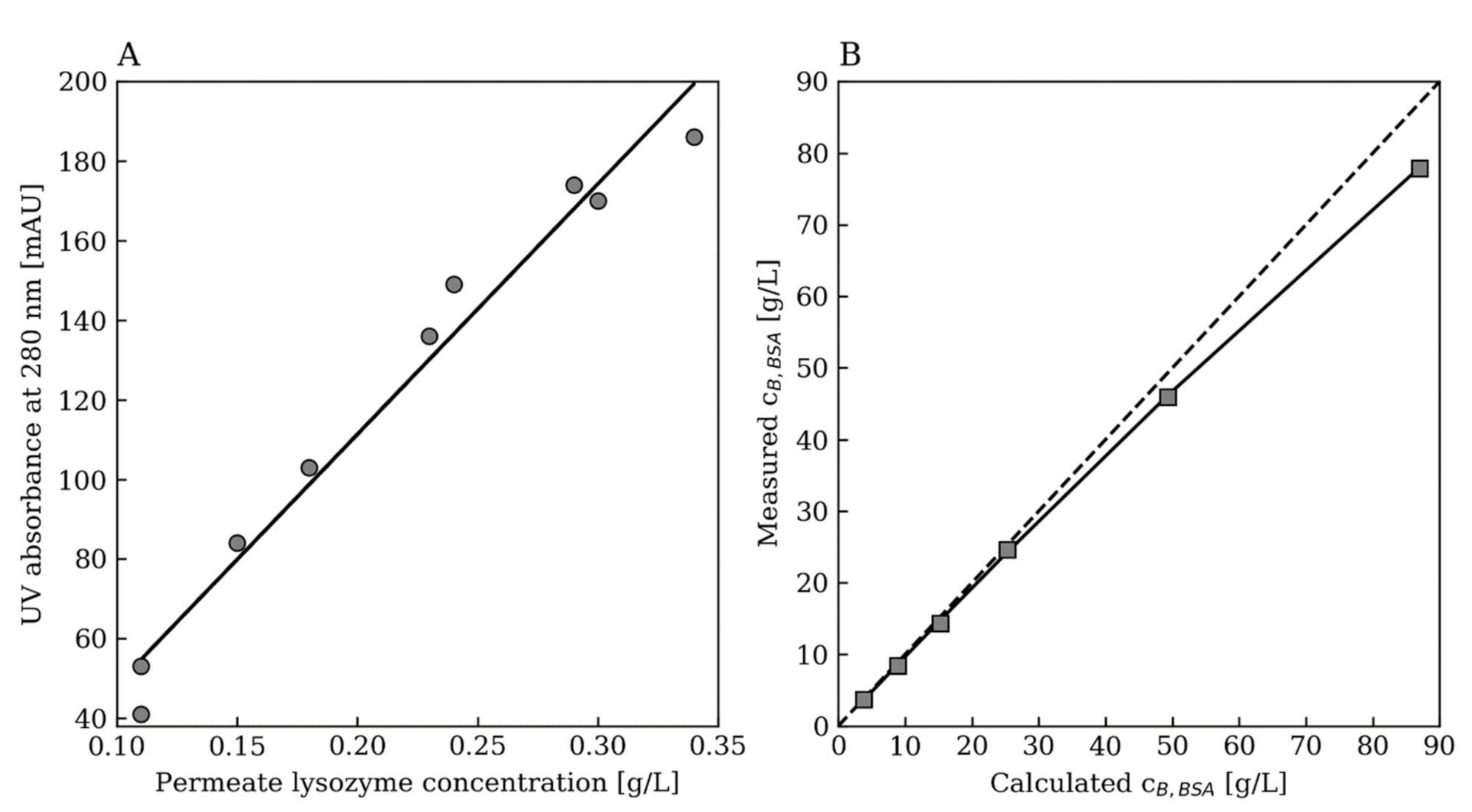
2.4. Protein Quantification
2.5. Hybrid Modeling
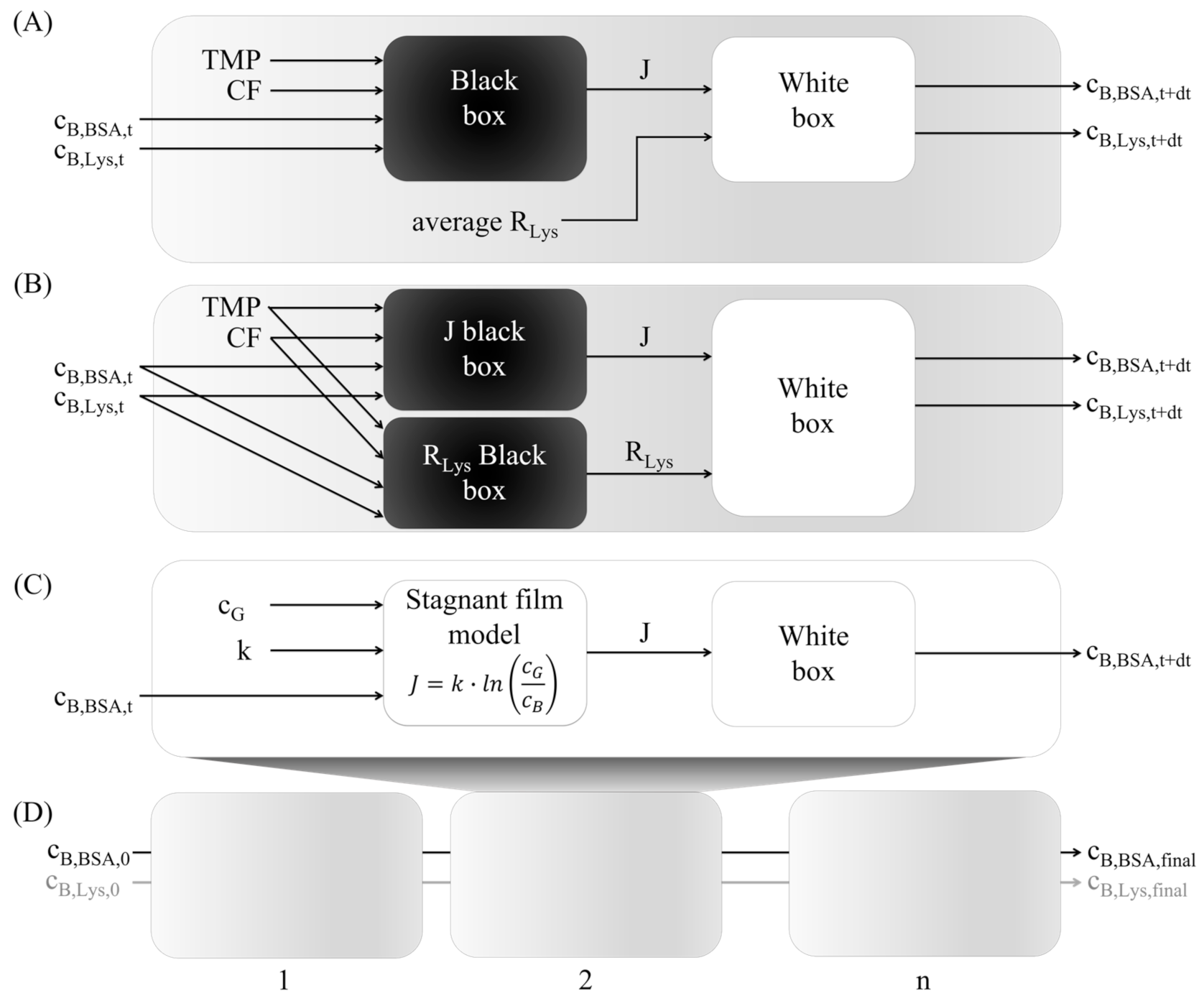
2.5.1. Black Box Model
2.5.2. White Box Model
2.5.3. Training and Test Data
2.5.4. Multistep-Ahead Hybrid Model
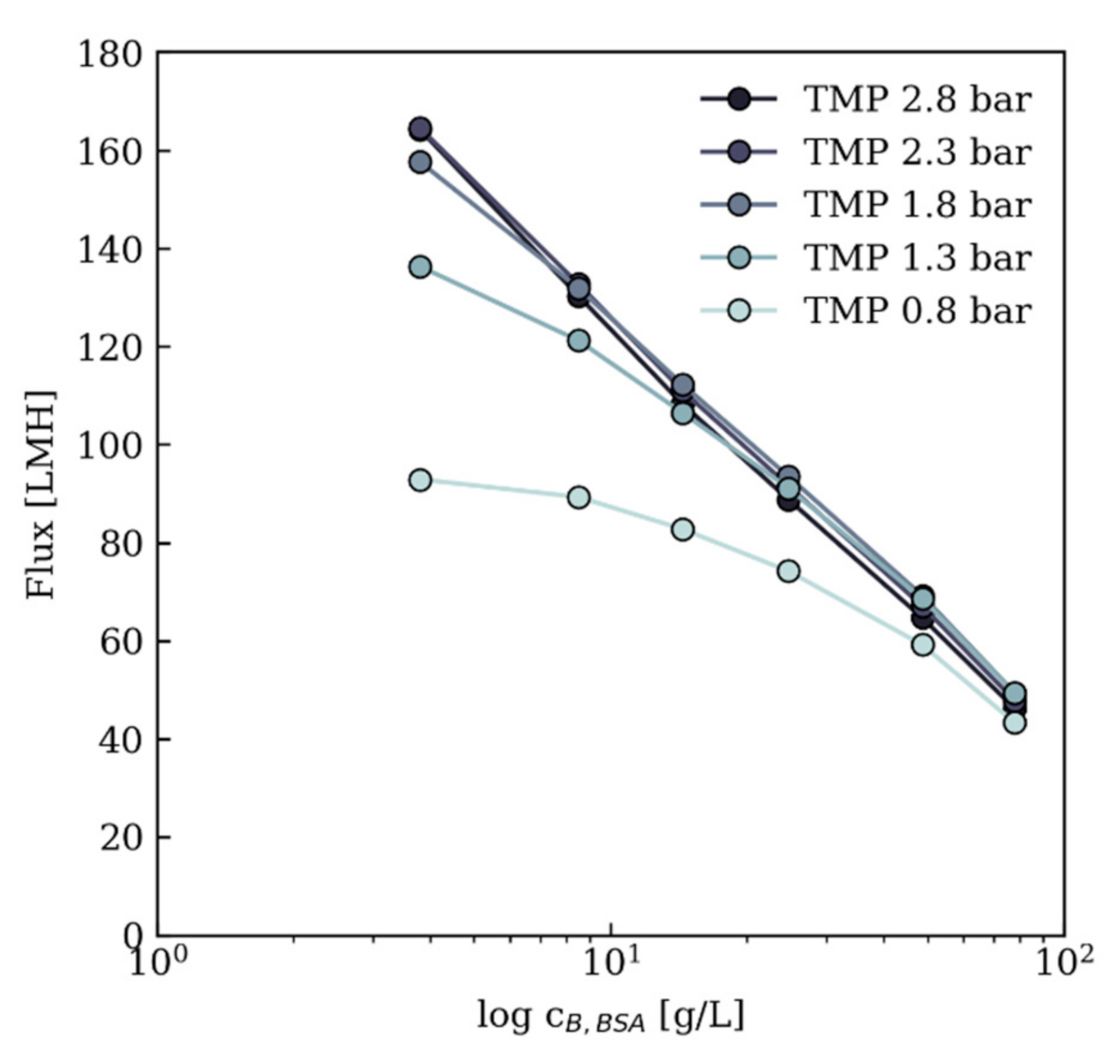
2.5.5. Stagnant Film Theory
3. Results and Discussion
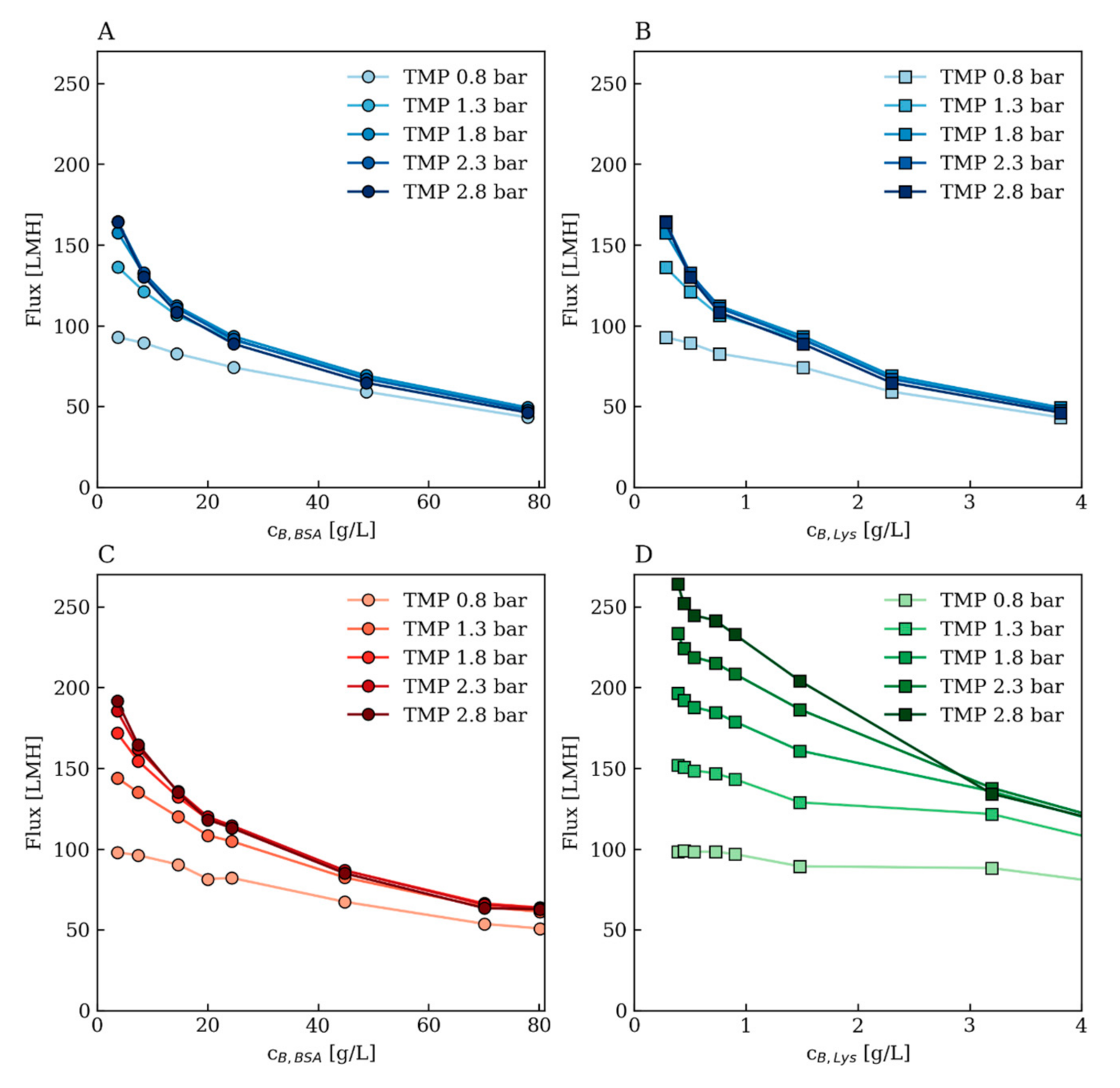
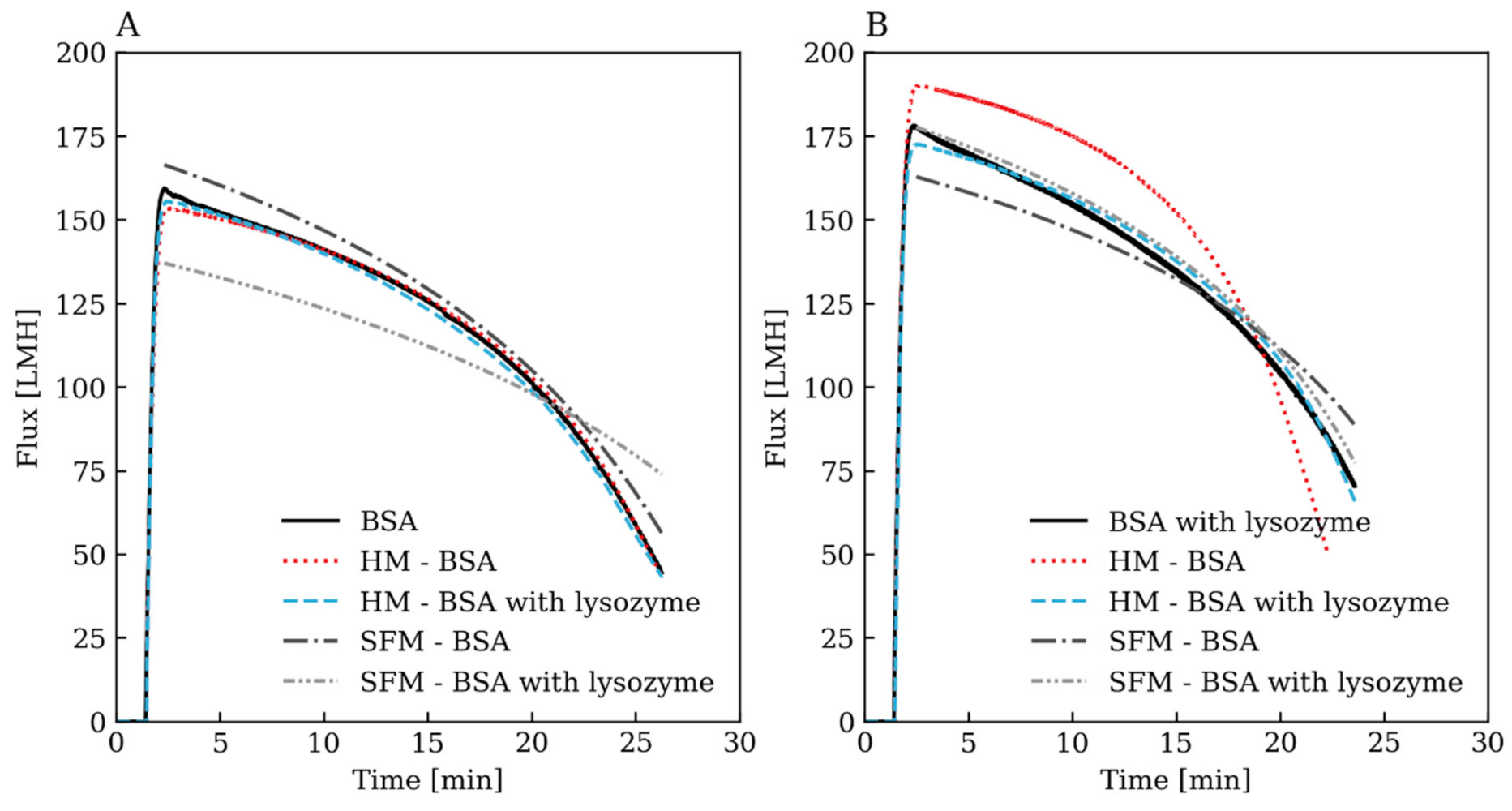
3.1. Training Data Description
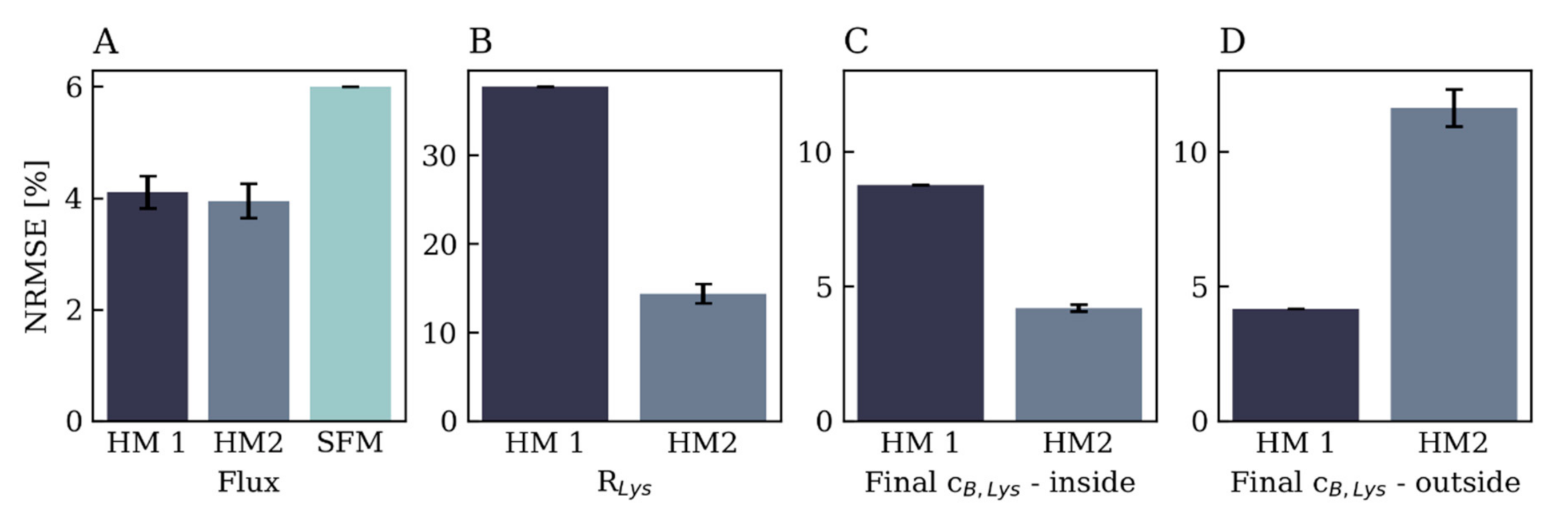
3.2. Comparison of the Hybrid Models to the Stagnant Film Theory
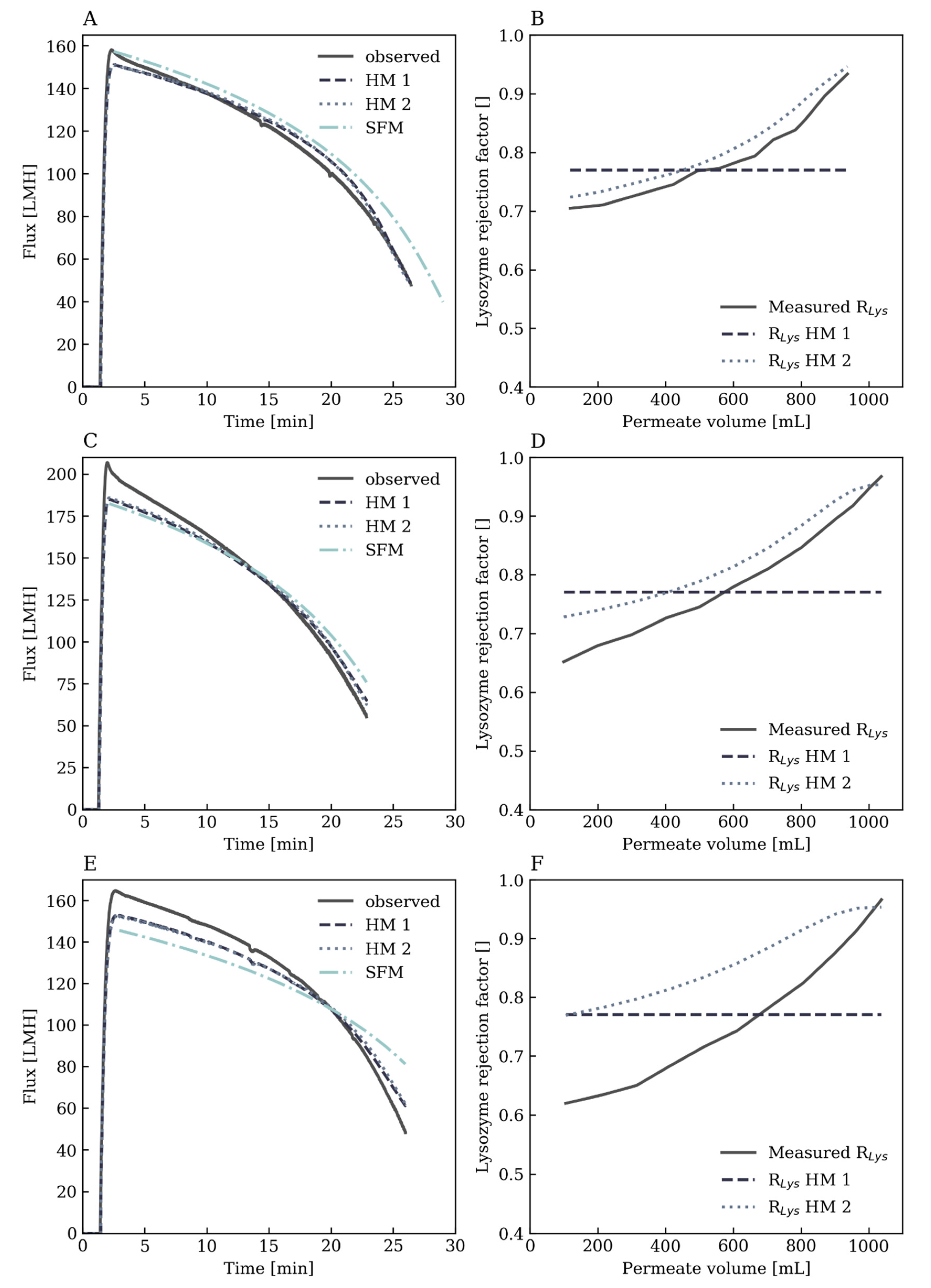
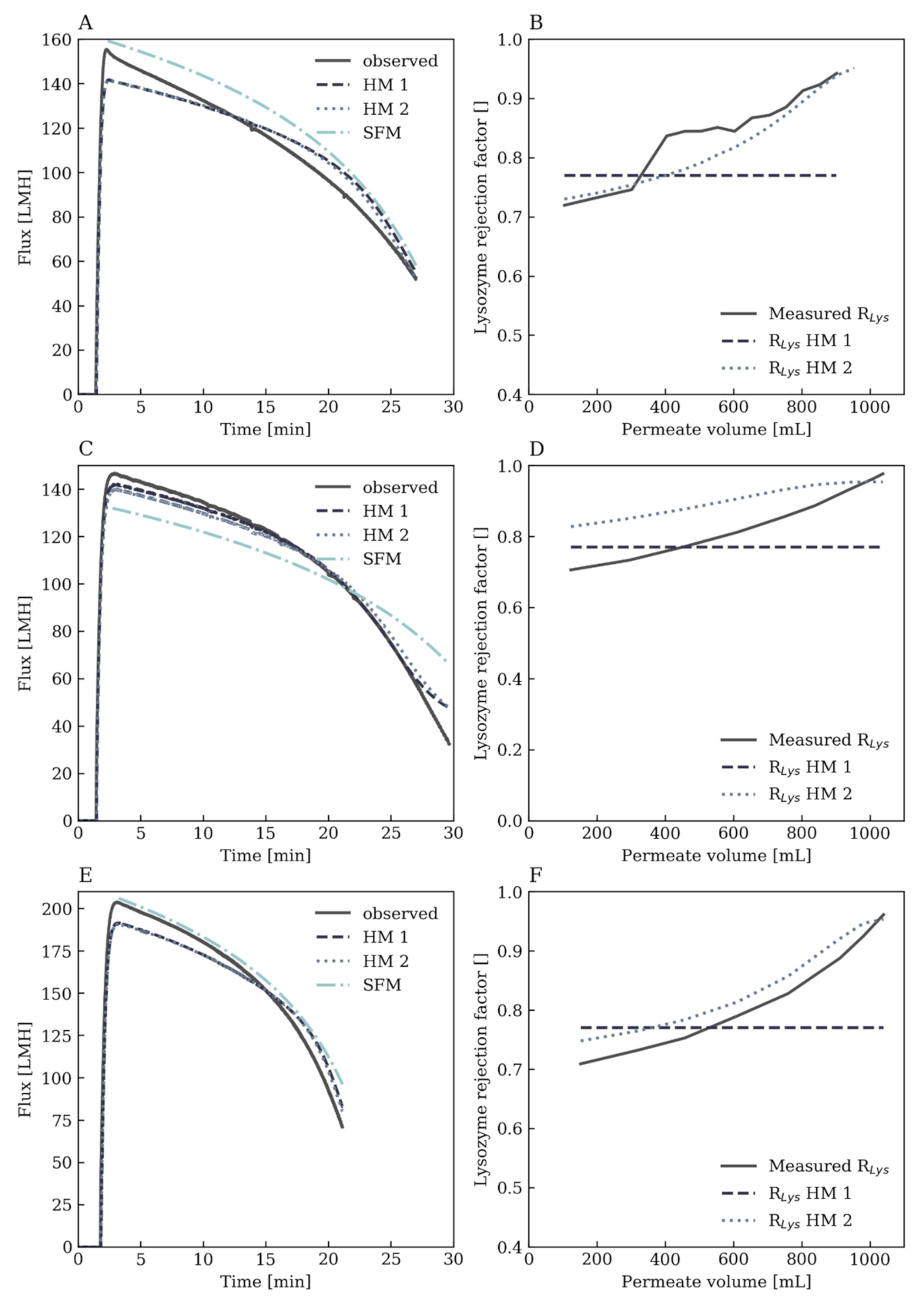
3.3. Comparison of Hybrid Model Performance
3.3.1. Flux Prediction
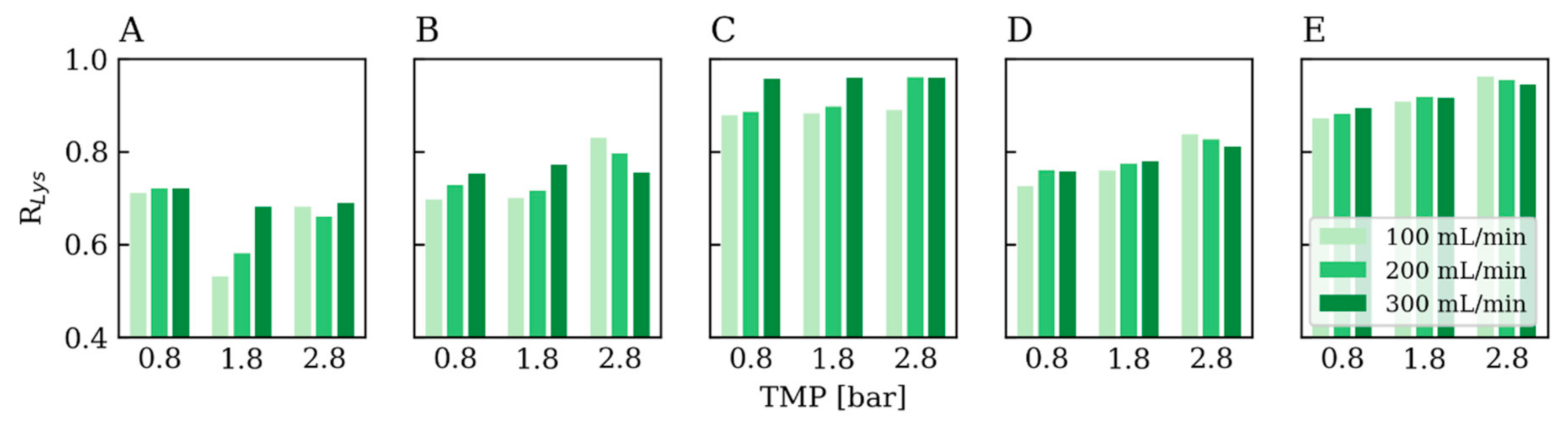
3.3.2. Rejection Factor Prediction for Lysozyme
Hybrid Model 1: Constant Lysozyme Rejection Factor
Hybrid Model 2: Dynamic Lysozyme Rejection Factor
3.3.3. Endpoint Bulk Concentration
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Symbols and Abbreviations
| ANN | artificial neural network |
| BSA | bovine serum albumin |
| CF | cross-flow velocity |
| CP | concentration polarization |
| HM | hybrid model |
| MWCO | molecular weight cutoff |
| NRMSE | normalized root-mean-squared error |
| SEC | size exclusion chromatography |
| SFM | stagnant film model |
| TMP | transmembrane pressure |
| UF | ultrafiltration |
| A | membrane area [m2] |
| cB | bulk concentration [g/L] |
| cG | gel layer concentration [g/L] |
| cP | permeate concentration [g/L] |
| cR | retentate concentration [g/L] |
| dt | time increment [s] |
| J | permeate flux [LMH] or [m/s] |
| k | mass transfer coefficient [LMH] |
| RLys | lysozyme retention coefficient [-] |
| VB | bulk/reservoir volume [mL] |
| Vp | permeate volume [mL] |
Appendix A
Appendix A.1. Neural Network Model Optimization
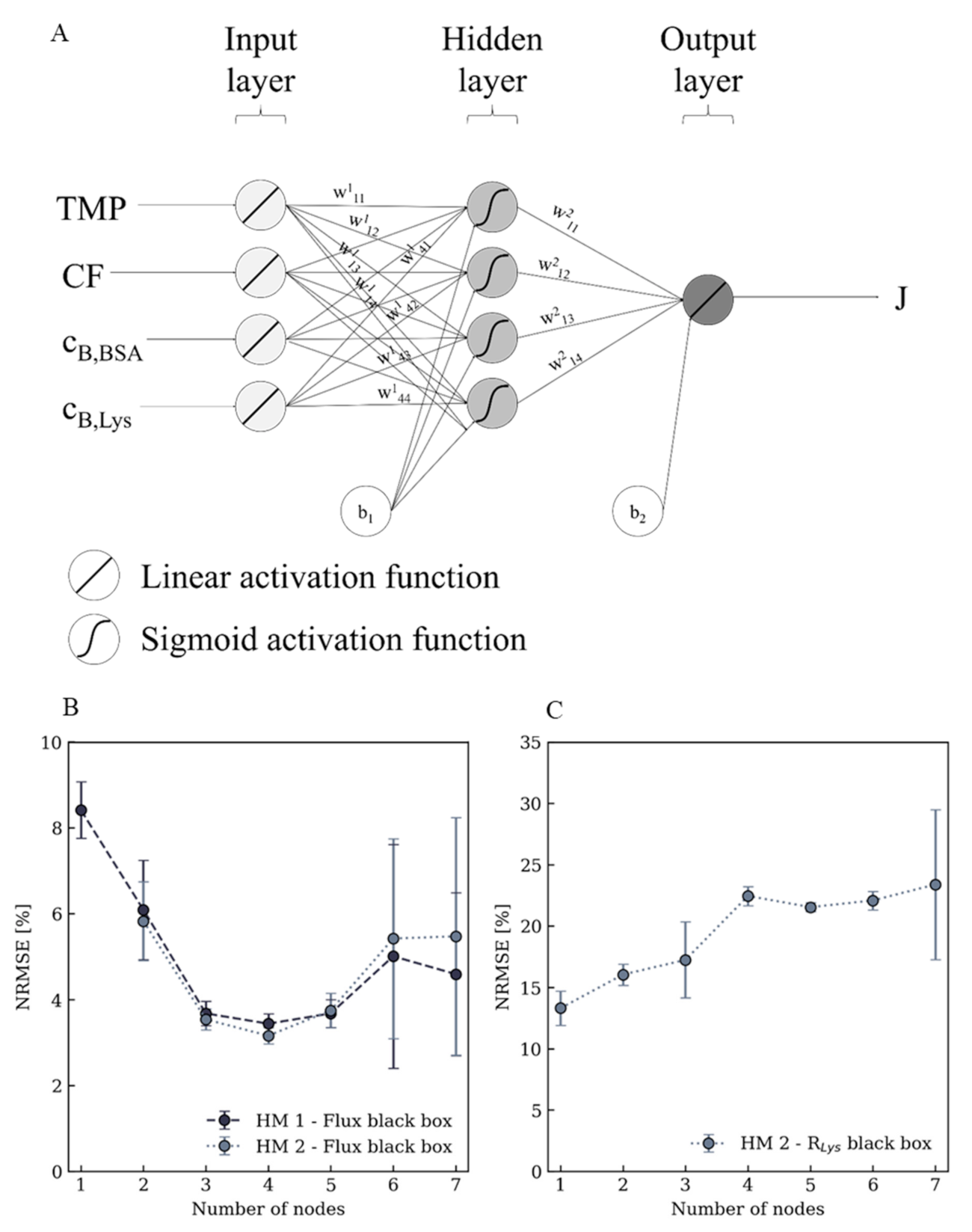
Appendix A.2. Experimental Data Summary
| Training Set | Observation | cB,Lys [g/L] | cB,BSA [g/L] | Flux at TMP 0.8 bar [LMH] | Flux at TMP 1.3 bar [LMH] | Flux at TMP 1.8 bar [LMH] | Flux at TMP 2.3 bar [LMH] | Flux at TMP 2.8 bar [LMH] |
|---|---|---|---|---|---|---|---|---|
| 1 | 100 | 0.28 | 3.77 | 87.6 | 113.3 | 121.0 | 121.5 | 119.1 |
| 0.5 | 8.48 | 78.0 | 93.3 | 96.3 | 95.6 | 93.4 | ||
| 0.76 | 14.38 | 70.1 | 80.5 | 81.6 | 80.0 | 77.7 | ||
| 1.51 | 24.68 | 60.7 | 67.5 | 67.5 | 65.9 | 63.9 | ||
| 2.3 | 48.72 | 46.8 | 50.7 | 50.1 | 48.6 | 47.1 | ||
| 3.81 | 77.93 | 34.0 | 36.6 | 36.2 | 35.1 | 34.0 | ||
| 200 | 0.28 | 3.77 | 92.9 | 136.3 | 157.6 | 164.5 | 164.2 | |
| 0.5 | 8.48 | 89.3 | 121.2 | 131.9 | 132.7 | 130.3 | ||
| 0.76 | 14.38 | 82.8 | 106.5 | 112.3 | 111 | 108.3 | ||
| 1.51 | 24.68 | 74.2 | 91.1 | 93.5 | 91.6 | 88.8 | ||
| 2.3 | 48.72 | 59.2 | 68.6 | 69.2 | 67.1 | 64.7 | ||
| 3.81 | 77.93 | 43.3 | 49.3 | 49.4 | 47.8 | 46.2 | ||
| 300 | 0.28 | 3.77 | 92.0 | 143.4 | 178.3 | 194.8 | 199.8 | |
| 0.5 | 8.48 | 90.2 | 133.8 | 155.6 | 161.5 | 161.1 | ||
| 0.76 | 14.38 | 85.6 | 121.5 | 135.2 | 136.9 | 134.7 | ||
| 1.51 | 24.68 | 78.8 | 106.2 | 114.0 | 113.4 | 110.7 | ||
| 2.3 | 48.72 | 65.1 | 82.2 | 85.1 | 83.2 | 80.6 | ||
| 3.81 | 77.93 | 48.4 | 59.2 | 60.4 | 58.9 | 56.9 | ||
| 2a | 100 | 3.19 | - | 97.6 | 150.1 | 195.1 | 232.6 | 260.6 |
| 4.73 | - | 97.9 | 146.5 | 186.1 | 218.2 | 244.8 | ||
| 8.11 | - | 97.6 | 144.7 | 181.1 | 209.5 | 235.8 | ||
| 11.99 | - | 96.8 | 142.2 | 176.8 | 205.2 | 231.8 | ||
| 23.79 | - | 95.0 | 137.5 | 171.0 | 199.1 | 221.8 | ||
| 32.95 | - | 85.7 | 124.9 | 152.3 | 172.4 | 187.2 | ||
| 200 | 0.39 | - | 98.3 | 151.9 | 196.6 | 233.6 | 264.2 | |
| 0.44 | - | 99 | 150.8 | 192.2 | 224.3 | 252.4 | ||
| 0.53 | - | 98.3 | 148.7 | 187.9 | 218.9 | 244.8 | ||
| 0.72 | - | 98.3 | 146.9 | 184.7 | 215.3 | 241.6 | ||
| 0.9 | - | 96.8 | 143.3 | 178.9 | 208.4 | 232.9 | ||
| 1.48 | - | 89.3 | 128.9 | 160.9 | 186.5 | 204.1 | ||
| 300 | 3.19 | - | 97.2 | 152.28 | 198.36 | 236.52 | 267.84 | |
| 4.73 | - | 97.56 | 150.84 | 195.48 | 229.68 | 258.12 | ||
| 8.11 | - | 96.84 | 149.4 | 192.24 | 225 | 252.36 | ||
| 11.99 | - | 96.84 | 148.32 | 189.36 | 222.12 | 249.84 | ||
| 23.79 | - | 96.12 | 145.08 | 183.6 | 215.28 | 240.84 | ||
| 32.95 | - | 86.76 | 129.96 | 165.6 | 192.6 | 212.76 | ||
| 2b | 100 | 3.19 | - | 86.0 | 113.8 | 121.0 | 115.6 | 105.5 |
| 4.73 | - | 67.3 | 81.0 | 84.2 | 82.4 | 79.9 | ||
| 8.11 | - | 59.8 | 69.8 | 71.6 | 70.6 | 68.8 | ||
| 11.99 | - | 55.1 | 62.6 | 63.4 | 61.9 | 60.5 | ||
| 23.79 | - | 45.7 | 50.0 | 49.7 | 47.9 | 46.8 | ||
| 32.95 | - | 36.0 | 37.8 | 36.4 | 35.3 | 34.2 | ||
| 200 | 3.19 | - | 88.2 | 121.7 | 135.7 | 137.9 | 134.3 | |
| 4.73 | - | 74.5 | 96.1 | 105.8 | 108.4 | 108.0 | ||
| 8.11 | - | 67.7 | 85.7 | 92.9 | 94.3 | 93.6 | ||
| 11.99 | - | 63.0 | 78.5 | 83.9 | 84.2 | 82.8 | ||
| 23.79 | - | 54.0 | 64.8 | 67.0 | 65.5 | 63.4 | ||
| 32.95 | - | 43.9 | 50.0 | 49.7 | 47.9 | 46.8 | ||
| 300 | 3.19 | - | 85.0 | 121.0 | 140.0 | 148.7 | 151.2 | |
| 4.73 | - | 74.9 | 102.6 | 117.7 | 125.6 | 128.5 | ||
| 8.11 | - | 69.5 | 93.2 | 105.8 | 111.6 | 113.0 | ||
| 11.99 | - | 65.5 | 87.5 | 97.6 | 100.8 | 100.8 | ||
| 23.79 | - | 57.2 | 73.8 | 79.2 | 79.6 | 78.1 | ||
| 32.95 | - | 50.0 | 62.6 | 64.8 | - | - | ||
| 3a | 100 | - | 3.65 | 90.8 | 119.6 | 131.9 | 136.5 | 138.3 |
| - | 7.45 | 84.9 | 106.8 | 114.8 | 117.4 | 117.2 | ||
| - | 14.65 | 76.6 | 92.4 | 97.0 | 97.3 | 96.4 | ||
| - | 20.06 | 68.2 | 82.1 | 85.5 | 85.1 | 83.3 | ||
| - | 24.4 | 67.2 | 78.7 | 82.0 | 82.0 | 80.8 | ||
| - | 44.78 | 53.2 | 61.4 | 63.2 | 62.9 | 61.6 | ||
| 200 | - | 3.65 | 97.9 | 144 | 171.7 | 185.4 | 191.5 | |
| - | 7.45 | 96.1 | 135 | 154.4 | 162 | 164.5 | ||
| - | 14.65 | 90.4 | 119.9 | 132.1 | 135.7 | 135 | ||
| - | 20.06 | 81.4 | 108.4 | 118.4 | 119.9 | 118.1 | ||
| - | 24.4 | 82.1 | 104.8 | 113 | 114.5 | 113 | ||
| - | 44.78 | 67.3 | 82.4 | 86.8 | 86.8 | 85 | ||
| 300 | - | 3.65 | 98.4 | 151.4 | 190.8 | 214.9 | 228.5 | |
| - | 7.45 | 98.6 | 147.2 | 178.4 | 194.4 | 201.0 | ||
| - | 14.65 | 93.8 | 134.4 | 155.9 | 164.9 | 167.2 | ||
| - | 20.06 | 87.5 | 124.9 | 143.4 | 149.2 | 149.0 | ||
| - | 24.4 | 87.6 | 120.8 | 136.0 | 141.1 | 141.3 | ||
| - | 44.78 | 74.6 | 97.9 | 106.1 | 107.9 | 106.8 | ||
| 3b | 100 | - | 70.12 | 40.7 | 46.4 | 47.3 | 46.6 | 45.5 |
| - | 80.15 | 39.4 | 45.5 | 46.9 | 46.6 | 45.8 | ||
| - | 131.69 | 24.0 | 28.8 | 29.9 | 29.6 | 29.0 | ||
| - | 179.95 | 13.6 | 18.1 | 19.6 | 19.7 | 19.7 | ||
| - | 231.67 | 6.3 | 10.9 | 13.1 | 13.8 | 13.7 | ||
| - | 277.25 | 0.0 | 5.5 | 7.7 | 8.8 | 9.4 | ||
| 200 | - | 70.12 | 53.6 | 64.1 | 66.2 | 65.5 | 63.4 | |
| - | 80.15 | 50.8 | 61.2 | 63.7 | 63.4 | 62.6 | ||
| - | 131.69 | 31.8 | 38.9 | 40.3 | 40 | 39.2 | ||
| - | 179.95 | 17.3 | 23.5 | 25.7 | 26 | 25.7 | ||
| - | 231.67 | 7.2 | 13.8 | 16.3 | 17.4 | 17.5 | ||
| - | 277.25 | 5.9 | 9.4 | 10.8 | - | - | ||
| 300 | - | 70.12 | 62.6 | 79.0 | 83.3 | 82.6 | 63.5 | |
| - | 80.15 | 58.2 | 73.3 | 78.0 | 78.3 | 62.5 | ||
| - | 131.69 | 37.1 | 46.8 | 49.5 | 49.3 | 39.2 | ||
| - | 179.95 | 19.5 | 27.5 | 30.3 | 30.9 | 25.7 | ||
| - | 231.67 | - | - | - | - | 17.5 | ||
| - | 277.25 | - | - | - | - | - |
| Test Set Number | TMP [bar] | CF [mL/min] | Initial cB,BSA [g/L] | Final cB,BSA [g/L] | Initial cB,Lys [g/L] | Final cB,Lys [g/L] |
|---|---|---|---|---|---|---|
| 1 | 1.8 | 200 | 4.00 | 78.11 | 0.28 | 4.36 |
| 2 | 1.8 | 200 | 3.79 | 62.48 | 0.50 | 6.16 |
| 3 | 2.8 | 300 | 3.82 | 54.95 | 0.32 | 4.35 |
| 4 | 2.5 | 280 | 4.56 | 97.59 | 0.28 | 3.52 |
| 5 | 1.6 | 230 | 5.97 | 132.81 | 0.15 | 1.96 |
| 6 | 1.4 | 270 | 8.80 | 162.45 | 0.19 | 2.79 |
| 7 | 2.0 | 350 | 3.62 | 73.62 | 0.34 | 4.65 |
| 8 | 1.8 | 260 | 2.38 | 45.42 | 0.57 | 6.82 |
| 9 | 1.8 | 200 | 6.68 | 132.70 | 0.00 | 0.00 |
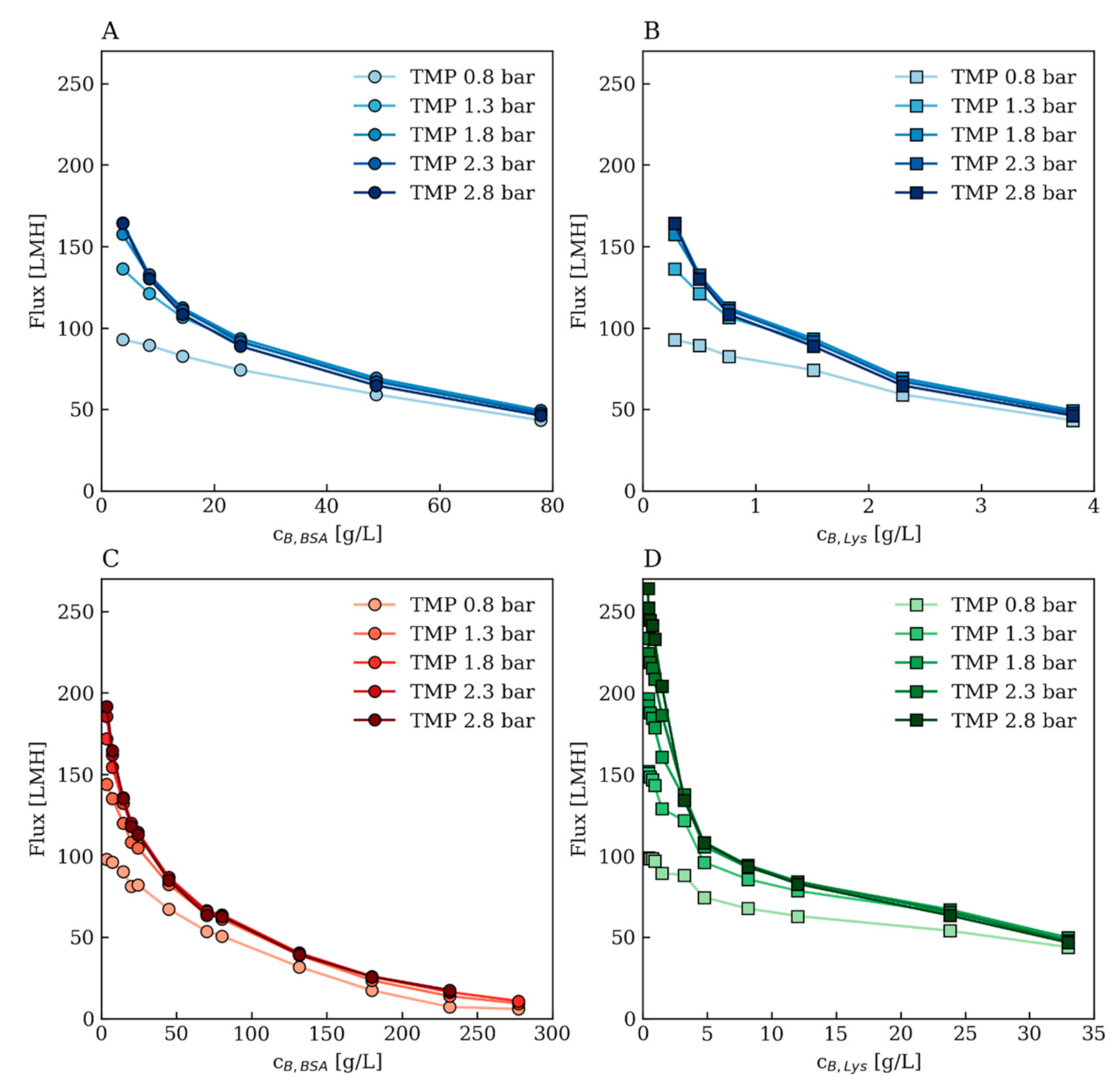
Appendix A.3. Further Modeling Results
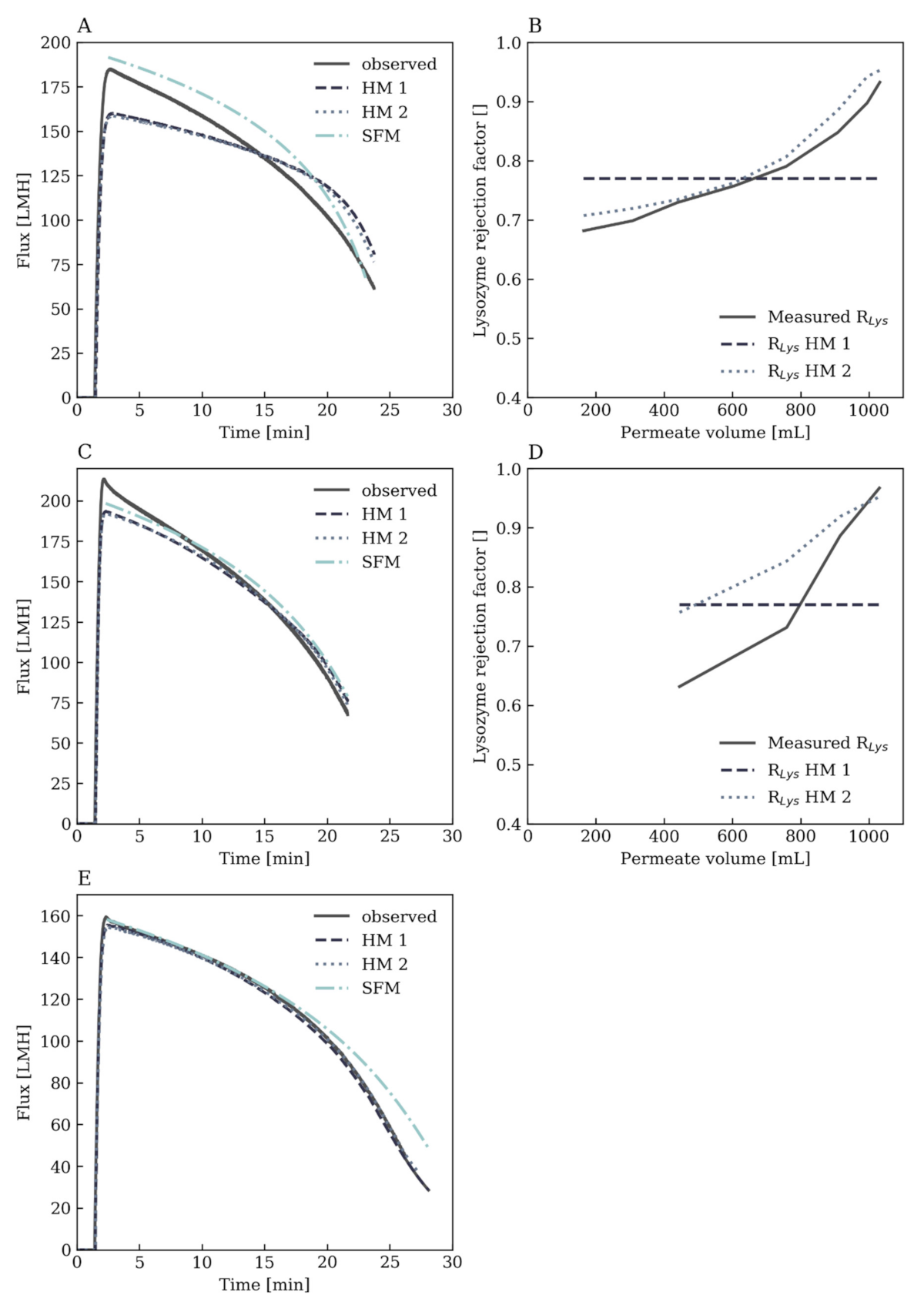
| Test Set Number | NRMSE Flux [%] | NRMSE RLys [%] | NRMSE final cB,Lys [%] | NRMSE Final cB,BSA [%] | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| HM 1 | HM 2 | SFM | HM 1 | HM 2 | HM 1 | HM 2 | HM 1 | HM 2 | SFM | |
| 1 | 2.3 ± 0.3 | 2.1 ± 0.3 | 5.3 | 32.5 ± 0.0 | 6.2 ± 0.2 | 7.4 ± 0.0 | 4.1 ± 0.0 | 4.6 | 4.6 | 4.6 |
| 2 | 4.3 ± 0.2 | 4.1 ± 0.1 | 7.2 | 39.7 ± 0.0 | 14.7 ± 2.2 | 7.9 ± 0.0 | 4.9 ± 0.3 | 3.8 | 3.8 | 3.8 |
| 3 | 3.6 ± 0.2 | 3.2 ± 0.2 | 3.0 | 40.3 ± 0.0 | 20.4 ± 0.5 | 13.0 ± 0.0 | 4.3 ± 0.0 | 2.2 | 2.2 | 2.2 |
| 4 | 3.9 ± 0.3 | 3.7 ± 0.2 | 5.0 | 34.9 ± 0.0 | 6.9 ± 0.6 | 6.7 ± 0.0 | 3.4 ± 0.2 | 0.7 | 0.7 | 0.7 |
| 5 | 4.8 ± 0.3 | 4.9 ± 0.4 | 8.5 | 32.6 ± 0.0 | 25.7 ± 1.3 | 3.2 ± 0.0 | 11.9 ± 0.5 | 8.7 | 8.7 | 8.7 |
| 6 | 3.4 ± 0.3 | 3.3 ± 0.5 | 9.3 | 45.3 ± 0.0 | 24.5 ±1.3 | 7.6 ± 0.0 | 12.1 ± 0.4 | 0.1 | 0.1 | 0.1 |
| 7 | 4.7 ± 0.3 | 4.5 ± 0.4 | 4.4 | 40.6 ± 0.0 | 6.2 ±0.7 | 3.9 ± 0.0 | 9.4 ± 0.3 | 6.6 | 6.6 | 6.6 |
| 8 | 8.2 ± 0.2 | 8.0 ± 0.3 | 6.3 | 35.6 ± 0.0 | 10.0 ±2.0 | 1.9 ± 0.0 | 13.0 ± 1.6 | 7.2 | 7.2 | 7.2 |
| 9 | 1.7 ± 0.5 | 1.7 ± 0.4 | 4.9 | 0.0 | 0.0 | 0.0 | 0.0 | 4.6 | 4.6 | 4.6 |
| Test Run Number | NRMSE Final cB,Lys [%] | NRMSE RLys [%] | NRMSE Flux [%] | |||
|---|---|---|---|---|---|---|
| 1-node ANN | MLR | 1-node ANN | MLR | 1-node ANN | MLR | |
| 1 | 4.1 | 5.7 | 6.2 | 9.9 | 2.1 | 2.3 |
| 2 | 4.9 | 6.4 | 14.7 | 26.9 | 4.1 | 3.9 |
| 3 | 4.3 | 4.3 | 20.4 | 20.9 | 3.2 | 3.3 |
| 4 | 3.4 | 4.7 | 6.9 | 21.1 | 3.7 | 3.8 |
| 5 | 11.9 | 6.4 | 25.7 | 34.5 | 4.9 | 5.1 |
| 6 | 12.1 | 11.6 | 24.5 | 69.4 | 3.3 | 3.5 |
| 7 | 9.4 | 16.1 | 6.2 | 20.0 | 4.5 | 4.4 |
| 8 | 13.0 | 38.4 | 10.0 | 55.5 | 8.0 | 7.5 |
| Average | 7.9 | 11.7 | 14.3 | 32.3 | 3.9 | 4.0 |
| k based on BSA | k based on BSA with lysozyme | ||||||||
| Feedflow [mL/min] | Feedflow [mL/min] | ||||||||
| 100 | 200 | 300 | 100 | 200 | 300 | ||||
| TMP [bar] | 0.8 | 47.36 | 36.23 | 31.63 | TMP [bar] | 0.8 | 17.61 | 33.84 | 14.03 |
| 1.3 | 54.67 | 41.97 | 32.33 | 1.3 | 25.03 | 36.12 | 27.92 | ||
| 1.8 | 54.51 | 42.14 | 30.13 | 1.8 | 27.59 | 36.75 | 39.06 | ||
| 2.3 | 53.40 | 41.63 | 28.99 | 2.3 | 28.11 | 38.22 | 44.73 | ||
| 2.8 | 53.75 | 42.97 | 27.95 | 2.8 | 27.70 | 38.58 | 46.84 | ||
| cG based on BSA | cG based on BSA with lysozyme | ||||||||
| Feedflow [mL/min] | Feedflow [mL/min] | ||||||||
| 100 | 200 | 300 | 100 | 200 | 300 | ||||
| TMP [bar] | 0.8 | 277.83 | 303.41 | 279.25 | TMP [bar] | 0.8 | 665.40 | 280.12 | 4421.42 |
| 1.3 | 302.79 | 330.45 | 323.30 | 1.3 | 355.06 | 312.56 | 887.24 | ||
| 1.8 | 322.39 | 345.88 | 355.30 | 1.8 | 288.49 | 277.52 | 419.22 | ||
| 2.3 | 332.29 | 353.74 | 369.46 | 2.3 | 264.69 | 273.21 | 304.56 | ||
| 2.8 | 323.99 | 327.45 | 378.28 | 2.8 | 256.72 | 252.80 | 263.97 | ||
References
- Kelley, B. Downstream Processing of monoclonal Antibodies: Current practice and future opportunities. In Process Scale Purification of Antibodies; John Wiley & Sons: Hoboken, NJ, USA, 2017; pp. 1–21. [Google Scholar]
- Benner, S.W.; Welsh, J.P.; Rauscher, M.A.; Pollard, J.M. Prediction of lab and manufacturing scale chromatography performance using mini-columns and mechanistic modeling. J. Chromatogr. A 2019, 1593, 54–62. [Google Scholar] [CrossRef] [PubMed]
- Hebbi, V.; Roy, S.; Rathore, A.S.; Shukla, A. Modeling and prediction of excipient and pH drifts during ultrafiltration/diafiltration of monoclonal antibody biotherapeutic for high concentration formulations. Sep. Purif. Technol. 2020, 238, 116392. [Google Scholar] [CrossRef]
- Baek, Y.; Singh, N.; Arunkumar, A.; Zydney, A. Ultrafiltration behavior of an Fc-fusion protein: Filtrate flux data and modeling. J. Membr. Sci. 2017, 528, 171–177. [Google Scholar] [CrossRef]
- Berg, G.V.D.; Smolders, C. Concentration polarization phenomena during dead-end ultrafiltration of protein mixtures. The influence of solute-solute interactions. J. Membr. Sci. 1989, 47, 1–24. [Google Scholar] [CrossRef]
- Borujeni, E.E.; Zydney, A.L. Membrane fouling during ultrafiltration of plasmid DNA through semipermeable membranes. J. Membr. Sci. 2014, 450, 189–196. [Google Scholar] [CrossRef]
- Jim, K.; Fane, A.; Fell, C.; Joy, D. Fouling mechanisms of membranes during protein ultrafiltration. J. Membr. Sci. 1992, 68, 79–91. [Google Scholar] [CrossRef]
- Haribabu, M.; Dunstan, D.E.; Martin, G.J.; Davidson, M.R.; Harvie, D.J.E. Simulating the ultrafiltration of whey proteins isolate using a mixture model. J. Membr. Sci. 2020, 613, 118388. [Google Scholar] [CrossRef]
- Namila, F.; Zhang, D.; Traylor, S.; Nguyen, T.; Singh, N.; Wickramasinghe, R.; Qian, X.; Wickramasinghe, S.R. The effects of buffer condition on the fouling behavior of MVM virus filtration of an Fc-fusion protein. Biotechnol. Bioeng. 2019, 116, 2621–2631. [Google Scholar] [CrossRef]
- Saksena, S.; Zydney, A.L. Influence of protein-protein interactions on bulk mass transport during ultrafiltration. J. Membr. Sci. 1997, 125, 93–108. [Google Scholar] [CrossRef]
- Matsuyama, H.; Shimomura, T.; Teramoto, M. Formation and characteristics of dynamic membrane for ultrafiltration of protein in binary protein system. J. Membr. Sci. 1994, 92, 107–115. [Google Scholar] [CrossRef]
- Iritani, E.; Mukai, Y.; Murase, T. Separation of binary protein mixtures by ultrafiltration. Filtr. Sep. 1997, 34, 967–973. [Google Scholar] [CrossRef]
- Teng, M.-Y.; Lin, S.-H.; Wu, C.-Y.; Juang, R.-S. Factors affecting selective rejection of proteins within a binary mixture during cross-flow ultrafiltration. J. Membr. Sci. 2006, 281, 103–110. [Google Scholar] [CrossRef]
- Müller, C.; Agarwal, G.; Melin, T.; Wintgens, T. Study of ultrafiltration of a single and binary protein solution in a thin spiral channel module. J. Membr. Sci. 2003, 227, 51–69. [Google Scholar] [CrossRef]
- Chen, H.; Kim, A.S. Prediction of permeate flux decline in crossflow membrane filtration of colloidal suspension: A radial basis function neural network approach. Desalination 2006, 192, 415–428. [Google Scholar] [CrossRef]
- Melcher, M.; Scharl, T.; Spangl, B.; Luchner, M.; Cserjan, M.; Bayer, K.; Leisch, F.; Striedner, G. The potential of random forest and neural networks for biomass and recombinant protein modeling in Escherichia coli fed-batch fermentations. Biotechnol. J. 2015, 10, 1770–1782, 2015. [Google Scholar] [CrossRef] [PubMed]
- Glassey, J.; Von Stosch, M. Hybrid Modeling in Process Industries, 1st ed.; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Bayer, B.; von Stosch, M.; Striedner, G.; Duerkop, M. Comparison of Modeling Methods for DoE-Based Holistic Upstream Process Characterization. Biotechnol. J. 2020, 15, 1900551. [Google Scholar] [CrossRef] [PubMed]
- Díaz, V.H.G.; Prado-Rubio, O.A.; Willis, M.J.; Von Stosch, M. Dynamic Hybrid Model for Ultrafiltration Membrane Processes; Elsevier: Amsterdam, The Netherlands, 2017; Volume 40, pp. 193–198. [Google Scholar]
- Chew, C.M.; Aroua, M.K.T.; Hussain, M.A. A practical hybrid modelling approach for the prediction of potential fouling parameters in ultrafiltration membrane water treatment plant. J. Ind. Eng. Chem. 2017, 45, 145–155. [Google Scholar] [CrossRef]
- Van Can, H.J.L.; Braake, H.A.B.T.; Dubbelman, S.; Hellinga, C.; Luyben, K.C.A.M.; Heijnen, J.J. Understanding and applying the extrapolation properties of serial gray-box models. AIChE J. 1998, 44, 1071–1089. [Google Scholar] [CrossRef]
- Krippl, M.; Dürauer, A.; Duerkop, M. Hybrid modeling of cross-flow filtration: Predicting the flux evolution and duration of ultrafiltration processes. Sep. Purif. Technol. 2020, 248, 117064. [Google Scholar] [CrossRef]
- Zydney, A.L. Stagnant film model for concentration polarization in membrane systems. J. Membr. Sci. 1997, 130, 275–281. [Google Scholar] [CrossRef]
- Van den Berg, G.B.; Smolders, C.A. Flux decline in ultrafiltration processes. Desalination 1990, 77, 101–133. [Google Scholar] [CrossRef]
- Berg, G.V.D.; Smolders, C. The boundary-layer resistance model for unstirred ultrafiltration. A new approach. J. Membr. Sci. 1989, 40, 149–172. [Google Scholar] [CrossRef][Green Version]
- Berg, G.V.D.; Racz, I.; Smolders, C. Mass transfer coefficients in cross-flow ultrafiltration. J. Membr. Sci. 1989, 47, 25–51. [Google Scholar] [CrossRef]
- Thiess, H.; Leuthold, M.; Grummert, U.; Strube, J. Module design for ultrafiltration in biotechnology: Hydraulic analysis and statistical modeling. J. Membr. Sci. 2017, 540, 440–453. [Google Scholar] [CrossRef]
- Iritani, E. A Review on Modeling of Pore-Blocking Behaviors of Membranes During Pressurized Membrane Filtration. Dry. Technol. 2013, 31, 146–162. [Google Scholar] [CrossRef]
- Kujundzic, E.; Greenberg, A.R.; Fong, R.; Hernandez, M. Monitoring Protein Fouling on Polymeric Membranes Using Ultrasonic Frequency-Domain Reflectometry. Membranes 2011, 1, 195–216. [Google Scholar] [CrossRef] [PubMed]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krippl, M.; Bofarull-Manzano, I.; Duerkop, M.; Dürauer, A. Hybrid Modeling for Simultaneous Prediction of Flux, Rejection Factor and Concentration in Two-Component Crossflow Ultrafiltration. Processes 2020, 8, 1625. https://doi.org/10.3390/pr8121625
Krippl M, Bofarull-Manzano I, Duerkop M, Dürauer A. Hybrid Modeling for Simultaneous Prediction of Flux, Rejection Factor and Concentration in Two-Component Crossflow Ultrafiltration. Processes. 2020; 8(12):1625. https://doi.org/10.3390/pr8121625
Chicago/Turabian StyleKrippl, Maximilian, Ignasi Bofarull-Manzano, Mark Duerkop, and Astrid Dürauer. 2020. "Hybrid Modeling for Simultaneous Prediction of Flux, Rejection Factor and Concentration in Two-Component Crossflow Ultrafiltration" Processes 8, no. 12: 1625. https://doi.org/10.3390/pr8121625
APA StyleKrippl, M., Bofarull-Manzano, I., Duerkop, M., & Dürauer, A. (2020). Hybrid Modeling for Simultaneous Prediction of Flux, Rejection Factor and Concentration in Two-Component Crossflow Ultrafiltration. Processes, 8(12), 1625. https://doi.org/10.3390/pr8121625








