Abstract
We use a system biology approach to translate the interaction of Bacillus Calmette-Gurin (BCG) + interleukin 2 (IL-2) for the treatment of bladder cancer into a mathematical model. The main goal of this research is to predict the outcome of BCG + IL-2 treatment combinations. We examined whether the delay effect caused by the proliferation of tumor antigen-specific effector cells after the immune system destroys BCG-infected urothelium cells after BCG and IL-2 immunotherapy influences success in bladder cancer treatment. To do this, we introduce a system of differential equations where the variables are the main participants in the immune response after BCG installations to fight cancer: the number of tumor cells, BCG cells, immune cells, and cytokines involved in the tumor-immune response. The relevant parameters describing the dynamics of the system are taken from a variety of biological, clinical literature and estimated using the mathematical models. We examine the local stability analysis of non-negative equilibrium states of the model. In theory, treatment could improve system stability, and we analyze the stability of all equilibria using the method of Lyapunov functionals construction and the method of linear matrix inequalities (LMIs). Our results prove that the period for the proliferation of tumor antigen-specific effector cells does not influence to the success of the non-responsive patients after an intensified combined BCG + IL-2 treatment.
1. Introduction
Bladder cancer (BC) is the fourth most common cancer in males [1] and the 11th most common cancer in women [2]. The global prevalence of BC is estimated at more than one million and is steadily increasing [1]. The risks of BC appear to vary across world regions, correlating with smoking and occupational exposures to carcinogens [3].
The long-term nature of BC is similar to that of many chronic diseases and often requires invasive and careful long-term follow-up, and in some cases, adjuvant treatment. This translates into high patient costs, making BC one of the most expensive cancers to treat. The preferred treatment for BC depends on its grade at diagnosis. Transurethral resection (TURBT) is the standard primary treatment for BC low-grade (stages Ta, T1 and carcinoma in situ), where cancer growth occurs superficially on the inner surface of the bladder in the form of a polyp but does not extend to the muscle. After TURBT, in malignant case, the treatment is either chemotherapy or immunotherapy for eradication of any residual cancer cells. Chemotherapeutic agents such as mitomycin C, doxorubicin, and epirubicin have long been used as intravesical therapies for BC [3,4].
Immunotherapy, BCG, a live attenuated strain of Mycobacterium bovis, has been shown to reduce both recurrence and progression of BC, and therefore represents an important tool in the treatment of BC [5]. BCG was first introduced as an intravesical therapy for BC in 1976 year by Morales and associates [6]. However, despite BCG favorable effects, a significant proportion of patients do not respond to BCG or tolerate treatment. Therefore, research has been pursued and efforts made to improve BCG therapy. During the past decades, cytokine-based therapies have been developed [7]. To date, multiple cytokines, such as IFN-, IL-2 and IL-12 [8,9], have been evaluated, alone, or in combination with BCG for the treatment of BC.
This research is based on the model of BC immunotherapy [10], focusing on the clinical use of BCG and IL-2. During this treatment, the malignant cells are attacked by the patient’s own immune system rather than through external chemical or surgical intervention. BCG is introduced into the bladder where it adheres to the damaged regions of the bladder wall. The cascade of immune response induced by intravesical BCG + IL-2 instillation consists of 2 phases:
I. BCG infects tumor cells, and stimulates the patient’s immune response, which mainly targets BCG infected tumor cells and may potentially eliminate the remaining tumor. At the same time, BCG infection stimulates the antigen (Ag)-presenting cells (APCs) to produce cytotoxic T-lymphocytes (CTL) associated with bacteria Ag. This causes the presentation of bacterial Ag on the tumor surface, which attracts APCs that ingest these cells.
II. Once a tumor cell has been ingested, tumor Ag’s are presented by the APCs. Due to the aforementioned inflammatory environment, created by the bacterial infection, APCs cause the effector cells (the most CTL cells) to either mature and capture tumor cells according to their tumor-associated-antigen (TAA) [11].
In other words, two CTL populations can destroy tumor cells—either via the TAA mechanism (uninfected tumor cells) or via bacteria-associated Ag (infected tumor cells). The addition of IL-2 is expected to create an inflammatory environment that stimulates the maturation of either CTL population [12]. During the second phase of the immune response, there is a delay in the entry of CTL cells into the bladder, because the CTL maturation cells process can take until 7 days. The modeling of biological systems with delays is based on differential equations with delay (Delay Differential Equations—DDE), where the derivative of an unknown function depends on the past states of the system [13,14].
The purpose of the current research is to analyze the stability of BCG model in DDE. Stability of equilibria is analyzed using the classical Lyapunov-Krasovskii functionals method together with the Kolmanovskii-Shaikhet general method of Lyapunov functionals construction [15,16] and the method of linear matrix inequalities (LMIs) [17,18,19,20]. The considered BCG-model is described by a system of nonlinear differential equations with delays. A stability investigation of systems of this type can be reduced to stability investigation of the linear part of a nonlinear system. The obtained sufficient conditions for asymptotic stability of the zero solution of an auxiliary linear system, at the same time, are sufficient conditions for the local stability of the corresponding equilibrium of the initial nonlinear system. Here standard definitions of stability are used (see, for instance [21]).
2. Description of the Model
The model that we analyze in this work describes interactions between BCG, the immune system and tumor cells within the bladder during combined BCG + IL-2 treatment (see Figure 1). BCG induces tumor removal by attaching to the urothelium and causing an inflammatory response there. The inflamed area attracts innate immune cells, which in turn attract CTLs and natural killer cells that attack tumor cells [22]. There are key variables interest us in the BCG + IL-2 treatment’s model: BCG and IL-2, APCs not activate and activated, effector T lymphocytes, tumor cells and tumor cells infected with BCG, transforming growth factor-beta (TGF-).
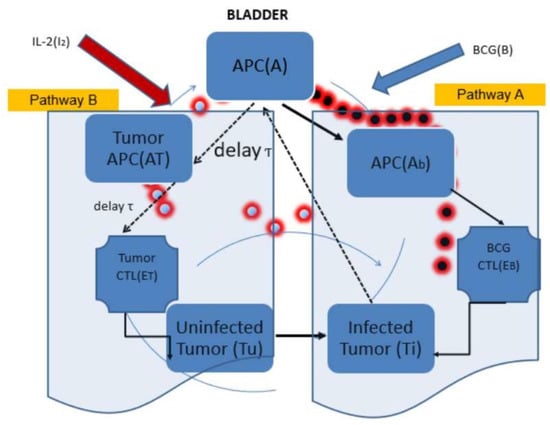
Figure 1.
BCG (denoted by B) invade the APCs (denoted by A) present ed in the urothelium. Bacterial infection stimulates APCs to produce inflammatory cytokines such as IL-2. At the same time, bacteria infect residual cancer cells after surgery designated as . As a result of infection, bacterial Ag appears on the surface of tumor cells, attracting APC (designated as ). engulf tumor infected cells () and transfer the tumor agent to APC (denoted by ). Due to the inflammatory environment created by the bacterial infection, cause CTLs to either mature and track bacterial Ag, denoted as (Pathway A), or mature and invade tumor cells according to their tumor Ag, starting with a delay (it is indicated by a broken line) due to the time it takes to form the CTL population, designated by (Pathway B). Two CTL populations can destroy tumor cells and ; and IL-2 will stimulate the maturation of the CTL cell population.
On basis of these key variables we build the equations in the system (1), described rates of change in concentrations of molecules or cell populations using the following notations:
- -
- BCG bacteria within the bladder as B;
- -
- APCs (dendritic cells (DCs) and macrophages) as A;
- -
- activated/matured APC’s after BCG internalization and processing as ;
- -
- activated/matured APC’s specific to tumor Ag as ;
- -
- effector T lymphocytes consisting mostly of CTLs that react to BCG as ;
- -
- effector T lymphocytes consisting mostly of CTLs that react to tumor Ags as ;
- -
- IL-2 units injected inside the bladder as ;
- -
- tumor cells infected with BCG as ;
- -
- tumor cells not infected by BCG as ;
- -
- transforming growth factor-beta (TGF-) denotes as .
Mathematical and biological interpretation of every equation from the system (1) are examined below:
BCG dynamics:
where is the dynamical rate of BCG level changes with time. It is comprised of a positive term corresponding to BCG instillations, and of negative terms corresponding to the elimination of BCG by antigen-presenting cells (APCs) according to the rate coefficient , BCG tumor cell infection at a rate coefficient , and bacteria cell death with rate coefficient . A quantity b of BCG is instilled into the bladder via a catheter inserted through the urethra once in a week during 6–8 weeks. In this study, we have chosen to simplify the problem by assuming that BCG is introduced into the bladder at a constant rate b.
Dynamics of non-activated APC:
where dynamic of is governed by two positive terms and three negative terms. The first positive term describes the normal influx of APCs to the tumor at a constant rate . The second positive term describes the recruitment of APCs due to bacterial infection at a rate coefficient . The first negative term describes the activation of APCs by BCG at the rate coefficient . The second negative term is natural cell death at the rate coefficient . The last negative term accounts for the two-stage elimination of tumor cells, according to recent knowledge, first by effector CTL activity upon BCG-infected tumor cells, which leads to lysis of these cells and flooding of the tumor micro-environment with tumor antigens. Activation of APC cells with tumor-specific antigens occurs with a delay of after the destruction of infected tumor cells. The localized inflammatory response then attracts APCs, such as macrophages, which in turn eliminate uninfected tumor cells, according to the rate .
Dynamics of APC activated by BCG:
where dynamic of is described by one positive term and two negative terms. The positive term is proportional to the numbers of non-activated APCs as well as BCG bacteria, with rate coefficient . The first negative term is the migration of the infected, activated APCs to the draining lymphoid tissues, at a rate of coefficient . The second negative term is the death of activated APCs at a rate of coefficient .
Dynamics of tumor-Ag-activated APC (TAA-APC):
where the dynamic TAA-APC is comprised of one positive term and three negative terms. The positive term describes the APCs which were activated by tumor antigen after eradication of infected tumor cells with the same delay function. The first negative term represents the tumor-Ag-activated APCs cells which destroy the uninfected tumor cells, with a rate coefficient after delay. This term is multiplied by an IL-2-dependent parameter with a saturation constant , to propose that in the absence of IL-2, production ceases, while in the presence of external IL-2, the production term is close to 1. The second negative term describes the migration of TAA-APC to the draining lymphoid tissues at a rate of coefficient . The third negative term denotes the natural death of TAA-APC at a rate coefficient .
Dynamics of effector CTLs that react to BCG infection:
where dynamic of is comprised of their migration rate, determined by their creation in the lymph node and subsequent migration to the bladder, inactivation rate, and their death rate. The migration element is proportional to and IL-2, with a maximal rate of coefficient . This rate is brought to saturation by large numbers of , using a Michaelis-Menten saturation function, with Michaelis parameter g. The first negative term is inactivation of effector CTLs via their encounter with infected tumor cells () at a success rate coefficient . The second negative term corresponds to the BCG-effector CTL () cells’ natural death rate .
Dynamics of effector CTLs that react to tumor Ag:
where is the dynamic of effector cells reacting to tumor Ag after delay time due to the eradication of infected tumor cells. It is comprised of their migration rate, inactivation rate, and death rate. The migration element is proportional to and IL-2 with a maximal rate coefficient . This rate is brought to saturation by large numbers of using a Michaelis-Menten saturation function, with Michaelis parameter g. The first negative term describes the inactivation of effector CTLs via their encounter with uninfected tumor cells (), at success rate coefficient . The second negative term describes the natural death rate, with a rate coefficient .
IL-2 dynamics:
where IL-2 dynamic is driven by a natural source (with constant rate coefficient ), an external source , as well as sink and degradation courses. is consumed by APCs and CTLs with rate. The consumption depends on and is limited in a Michaelis-Menten fashion, with the Michaelis constant . degradates with rate of .
Infected tumor cells:
where dynamic of depend on two mechanisms: the rate of bacterial infection of uninfected tumor cells, (), according to rate coefficient ; and the elimination of infected tumor cells by their interaction with BCG-CTL effector cells (represented by ), at rate coefficient .
Uninfected tumor cells:
where dynamic of is comprised of three processes: natural tumor growth, tumor infection by bacteria and tumor elimination by immune cells. The natural tumor growth is characterized by a maximal growth rate coefficient, r, which is limited by the maximal tumor cell number, K. The first negative term, due to bacterial infection, is characterized by a coefficient rate of . The second negative term is attributed both to the capture and elimination of cells by APCs cells, which were activated by tumor-Ag at rate coefficient , and to the activity of TAA-CTL effectors, (), which destroy uninfected tumor cells, (), at a rate coefficient . Two these processes take place after delay . The dependence in the equation of on is decreasing from 1to with Michaelis constant [23]. And then there is a multiplication of those terms by an -dependent Michaelis-Menten term, with Michaelis parameter , to propose that in the absence of , cellular death does not occur. Since the tumor produces a variety of mechanisms in the biological settings that curtail the success of effector cell activity, they multiply by , to denote the inversely proportional reduction in effector cell activity rate, such that when the term is equal to 1 and . Note that although this factor can, in principle, nullify the efficacy of CTLs, this is not observed in cases of interest because [24].
Dynamic of a transforming growth factor-beta TGF- is proportional to the tumor cell population, , with and destroyed at a rate of
The model is as follows:
Here it is supposed that the delay is given by the equality , , . So, the delay is decreasing and , . is a time-varying function, representing the delay in immune response following treatment, and expressing the number of effector cells in the cancer region. Delay means that the system in the current time moment t depends on her state in the past, i.e., in the time . In particular, the dynamics of non-activated APC in the moment t depends on (see the first equation in system (1)), dynamics of tumor-Ag-activated APC (TAA-APC) depends on and (see the fourth equation in system (1)) and so on. The delay is measured in reference to the beginning of BCG treatment (), with a maximum delay of approximately 10 days.
The influence of BCG tends towards zero over time.
To use the mathematical model (1), it is important to estimate ranges of parameters that are realistic and consistent with values from the biological and medical literature. In Table 1, we present a list of all the estimated model parameters and the literature for their estimation. Methods for estimating most of the parameters used here are described in [24,25,26].

Table 1.
List of all parameters.
3. Equilibria
The concept of equilibrium refers to the theory of dynamical systems, that is, systems developing in time. Equilibrium means a state of rest in which, in the absence of external influences, the system can be indefinitely. In our case, the investigated dynamic system is the human organism and different equilibria means different state of human health. Equilibria of the model (1) are found by setting all derivatives to zero and solving for B,A,,,,,,, and (where the asterisk indicates that the variables are at their steady state values). The system (1) have several fixed points, we only need to focus on the non-negative equilibria.
Equilibria of the model (1) are defined by the system of the algebraic equations
that follows from (1) by the assumption that are constants.
Note that the solution of the system (2) can be not unique. Let us get some solutions of the system (2) in two different situations: and .
3.1. Equilibrium with ,
Consider the following way to get a solution of the system (2), i.e., an equilibrium of the system (1) for the “tumor-free” case:
- (1)
- From (9’) it follows that one of the possible is .
- (2)
- (10’) it follows (via ).
- (3)
- From (8’) it follows (via ).
- (4)
- From (4’) it follows (via and ).
- (5)
- From (6’) it follows (via and ).
- (6)
- (7)
- From (3’) it follows (via , ).
- (8)
- From (5’) it follows that if then but via (7’) it is impossible. So, from it follows .
- (9)
- From (5’) and (7’) the system for , it follows (via )
with the solution (see Appendix A.2)
As a result we obtain a tumor-free equilibrium
3.2. Equilibria with ,
Consider another way to get equilibria of the system (1):
- (1)
- From (2’) it follows .
- (2)
- From (3’) it follows (via ).
- (3)
- From (5’) it follows (via ).
- (4)
- From (4’) it follows (via ).
- (5)
- From (6’) it follows (via ).
- (6)
- From (1’) it follows (via ).
- (7)
- From (7’) it follows (via ).
- (8)
- From (9’) it follows or (via ).
- (9)
- From (10’) it follows or (via or ).
- (10)
- From (8’) it follows (via ).
As a result we obtain two following equilibria:
- (1)
- tumor-free ()
- (2)
- not tumor-free ()
Remark 1.
Suppose that . Then from the Equations (5’) and (6’) of the system (2) it follows that . From (7’) it follows that . From (3’) it follows that . From (1’) it follows that A cannot be zero by and from (2’) it follows that B is zero by . So, we obtain again the equilibria , .
4. Centralization and Linearization
Calculating the Jacobian matrices and of the initial system (1), we obtain (see Appendix A.3) the linear approximation of this system in the form
where , and are the matrices of dimension , such that
and the nonzero elements and of these matrices respectively are
and
where
5. Stability
The stability of the equilibrium means that small deviations from the equilibrium do not greatly affect the system and allow it to remain at state of rest. Instability of equilibrium means that the slightest deviation from equilibrium does not allow the system to return to this state. In this case, the system can go into one of the other equilibria (if such states there are) or it can be completely destroyed. In our case, the investigated dynamic system is the human organism. The task of physicians is to determine the equilibrium favorable for human health and to organize such treatment in which this equilibrium becomes stable. In [16] stability conditions for the Equation (8) are obtained in the form of nonlinear matrix Riccati equations. Via Schur complement (see Appendix A.4) similarly to [19,20] these conditions can be reformulated in the form of LMIs:
Lemma 1.
Put . If and for some positive definite matrices P and R at least one of the LMIs
holds then the zero solution of the Equation (8) is asymptotically stable.
Corollary 1.
Remark 2.
For LMIs (13) the matrix H has to be the Hurwitz matrix.
In the following examples, we check the stability of E1-E3 using the standard (from Table 1) and reduced (up to one third of the usual dose) BCG dose, taking into account Lamm’s [41] experience in dose reduction to avoid side effects. We distinguished between patients in the examples below using a clinically relevant range of tumor growth rate r.
Example 1.
Let be , , and all other parameters are given in Table 1. Via the LMIs (13) and MATLAB it is shown that the equilibrium is locally asymptotically stable for . In particular, the equilibria
and
are locally asymptotically stable. For and the equilibrium is unstable.
Example 2.
Let be again but , and all other parameters are given in Table 1. Similarly to Example 1 it is shown that the equilibrium is locally asymptotically stable in the same interval . In particular, the equilibria
and
are locally asymptotically stable.
Example 3.
Let be and all other parameters as in Example 1. In this case, the equilibrium is locally asymptotically stable for . In particular, the equilibria
and
are locally asymptotically stable. For and the equilibrium is unstable.
Example 4.
Let be again but , and all other parameters as in Example 3. In this case the equilibrium is locally asymptotically stable for . In particular, the equilibria
and
are locally asymptotically stable.
Remark 3.
To examine the net effect of IL-2 on tumor dynamics we consider the equilibrium without the presence of BCG. We use physiologically acceptable doses of 200,000–250,000 IU per instillation ( units per treatment) [9,24].
Example 5.
By , , and the same values of all other parameters the following two equilibria are unstable:
Remark 4.
If the matrix H is the Hurwitz matrix then . For the equilibria and we have . From (10) it follows that , i.e., all elements of the eighth column of the matrix H are zeros and therefore . It means that the matrix H is not the Hurwitz matrix and the equilibrium and are unstable for all values of the parameters.
6. Discussion and Conclusions
In this work we present the improved model of combined therapy BCG + IL-2 immunotherapy for BC. There are two outcomes in the presented model analysis: (1) analytical analysis of stationary system’s points and (2) examining the delay influence to stability of these stationary system’s points.
A detailed description of the results is presented below:
(1). The current manuscript describes the outcome of analytical methods used to derive the equilibria points and especially the tumor-free equilibrium point, at which cancer cells are effectively eliminated. The model demonstrates several equilibria which depend on biologically related parameters and initial conditions.
In our previous works [10,24,42], we provided a local analysis of the stability of the equilibrium states of the model only in simulation ways, because the model consists of 10 equations, which made the analytical analysis of stationary points very difficult. Using the general method of Lyapunov functionals construction [15,16] and the method of linear matrix inequalities (LMIs) [17,18,19,20] gives a possibility for research of the “big” system’s stability.
The biological system (bladder is in our case) in the presence of cancer cells without treatment is unstable [25]. The clinical importance of steady state stability stems from the uncertainty typically encountered by the clinician in assessing the exact number of tumor and immune cells present at the start of treatment. In theory, treatment could improve system stability. The physician will be interested in the local stable system with great interest. This means that if a tumor can be localized or eradicated, minor violations of its components will not cancel it.
It is shown that the considered system has three equilibria describing the different states of the patient. Only in the equilibrium do get cancer cell eradication (), meaning successful treatment. Stability analysis of the system (1) shows the equilibrium is stable if the BCG dose is reflected in the condition depend on the growth of cancer cells (as indicated in Examples 1–4). In equilibrium we obtain a strong immune response because and that help to arrive at a tumor-free fixed point. By the basic parameters of BCG, maximum tumor size, tumor growth rate, and immune response parameters, we found the BCG dose where will be stable (Examples 1–4). Equilibria and were obtained only for IL-2 therapy. equilibrium do get cancer cell eradication (), but the system is not stable in the equilibrium (as shown in Example 5 and Remark 4). equilibrium do not get cancer cell eradication () and system is not stable in the equilibrium too. Hence, we found that administering only IL-2 did not result in the elimination of tumor cells. The same result we received via simulations in the [24].
(2). In this work, for the first time, we consider the real picture of the immune response in the treatment of BCG + IL-2, taking into account the time of formation of effector cells due to BCG infection, which leads to a delay in the response to the destruction of cancer cells. We investigate this influence using the method of Lyapunov functionals and the method of linear matrix inequalities (LMIs). The delay effect during cancer cell eradication does not influence the stability in the equilibrium . As it is shown in the Remark 3, each element of the matrix D for before the term with delay or equals zero or close enough to zero. It means that dependence on delay is low enough.
We would like to raise awareness in the community of urological-oncological doctors about the possibilities of mathematical modeling and receive quantitative data to improve this model. The ability to plan and predict by calculating a modulated dose of treatment can benefit patients who are unable to take routine treatment because of its serious side effects, as well as to patients who were previously not considered treatable. It is necessary to note also that three equilibria that are investigated in this work are equilibria obtained from the system (2) in an analytical way. So, there is a possibility of continuing stability investigation of the considered model via getting additional equilibria by numerical methods and using additional results of stability theory [16]. Thus, it will be an interest of experts in this direction to the obtained here results and this research will be continued.
Author Contributions
Conceptualization: S.B.-M.; Methodology: L.S.; Investigation and data curation: S.B.-M.; Writing—original draft preparation, S.B.-M. and L.S.; Writing—review and editing, S.B.-M.; Project administration and Funding acquisition: S.B.-M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Appendix A.1. Solution of (3)
Appendix A.2. Solution of (4)
Appendix A.3. Centralization and Linearization of a Nonlinear Equation
Consider the nonlinear delay differential equation
where and the equation has a solution that is an equilibrium of the differential Equation (A1). By virtue of the new variable we centralize the Equation (A1) around the equilibrium
It is clear that stability of the zero solution of the Equation (A2) is equivalent to stability of the equilibrium of the Equation (A1).
Let and be Jacobian matrices of the function with respect to the first and to the second argument respectively. Using Taylor’s expansion in the form
where , is the Euclidean norm in , and the equality , we obtain the linear approximation
of the Equation (A2). So, a condition for asymptotic stability of the zero solution of the Equation (A3) is also a condition for local stability of the equilibrium of the initial Equation (A1).
Appendix A.4. Schur Complement
Schur complement [43]. The symmetric matrix is negative definite if and only if C and are both negative definite.
References
- Kassouf, W.; Traboulsi, S.L.; Kulkarni, G.S.; Breau, R.H.; Zlotta, A.; Fairey, A.; So, A.; Lacombe, L.; Rendon, R.; Aprikian, A.G.; et al. CUA guidelines on the management of non-muscle invasive bladder cancer. Can. Urol. Assoc. J. 2015, 9, 690–704. [Google Scholar] [CrossRef] [PubMed]
- Anastasiadis, A.; de Reijke, T.M. Best practice in the treatment of nonmuscle invasive bladder cancer. Ther. Adv. Urol. 2012, 4, 13–32. [Google Scholar] [CrossRef] [PubMed]
- Bunimovich-Mendrazitsky, S.; Pisarev, V.; Kashdan, E. Modeling and simulation of a low-grade urinary bladder carcinoma. Comput. Biol. Med. 2015, 58, 118–129. [Google Scholar] [CrossRef] [PubMed]
- Adeloye, D.; Harhay, M.O.; Ayepola, O.O.; Dos Santos, J.P.; David, A.R.; Ogunlana, O.O.; Gadanya, M.A.; Osamor, V.C.; Amuta, O.A.; Iweala, E.E.; et al. Estimate of the incidence of bladder cancer in Africa: A systematic review and Bayesian meta-analysis. Int. J. Urol. 2019, 26, 102–112. [Google Scholar] [CrossRef] [PubMed]
- Rodriguez, D.; Sotolongo-Grau, O.; Espinosa, R.; Sotolongo-Costo, R.O.; Miranda, J.A.S.; Antozanz, J.C. Assessment of cancer immunotherapy outcome in terms of the immune response time features. Math. Med. Biol. 2007, 24, 287–300. [Google Scholar] [CrossRef] [PubMed]
- Morales, A.; Eidinger, D.; Bruce, A.W. Intracavity Bacillus Calmette-Guerin in the treatment of superficial bladder tumors. J. Urol. 1976, 116, 180–183. [Google Scholar] [CrossRef]
- Pettenati, C.; Ingersoll, M.A. Mechanisms of BCG immunotherapy and its outlook for bladder cancer. Nat. Rev. Urol. 2018, 15, 615–625. [Google Scholar] [CrossRef]
- Lee, C.F.; Chang, S.Y.; Hsieh, D.S.; Yu, D.S. Immunotherapy for bladder cancer using recombinant bacillus Calmette-Guerin DNA vaccines and interleukin-12 DNA vaccine. J. Urol. 2004, 171, 1343–1347. [Google Scholar] [CrossRef]
- Shapiro, A.; Gofrit, O.; Pode, D. The treatment of superficial bladder tumor with IL-2 and BCG. J. Urol. 2007, 177, 81. [Google Scholar] [CrossRef]
- Guzev, E.; Halachmi, S.; Bunimovich-Mendrazitsky, S. Additional extension of the mathematical model for BCG immunotherapy of bladder cancer and its validation by auxiliary tool. Int. J. Nonlinear Sci. Numer. Simul. 2019, 20, 675–689. [Google Scholar] [CrossRef]
- Kitamura, H.; Tsukamoto, T. Immunotherapy for Urothelial Carcinoma. Current Status and Perspectives. Cancers 2011, 3, 3055–3072. [Google Scholar] [CrossRef] [PubMed]
- Malek, T.R.; Bayer, A.L. Tolerance, not immunity, crucially depends on IL-2. Nat. Rev. Immunol. 2004, 4, 665–674. [Google Scholar] [CrossRef] [PubMed]
- D’onofrio, A.; Gatti, F.; Cerrai, P.; Fresci, L. Delay-induced oscillatory dynamics of tumor-immune system interaction. Math. Comp. Mod. 2010, 51, 572–591. [Google Scholar] [CrossRef]
- Galach, M. Dynamics of the tumor-immune system competition: The effect of time delay. Int. J. Appl. Math. Comp. Sci. 2003, 3, 395–406. [Google Scholar]
- Kolmanovskii, V.; Shaikhet, L. Some peculiarities of the general method of Lyapunov functionals construction. Appl. Math. Lett. 2002, 15, 355–360. [Google Scholar] [CrossRef]
- Shaikhet, L. Lyapunov Functionals and Stability of Stochastic Functional Differential Equations; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Boyd, S.; El Ghaoui, L.; Feron, E.; Balakrishnan, V. Linear Matrix Inequalities in System and Control Theory. In SIAM Studies in Applied Mathematics; SIAM: Philadelphia, PA, USA, 1994. [Google Scholar]
- Xu, S.; Lam, J. A survey of linear matrix inequality techniques in stability analysis of delay systems. Int. J. Syst. Sci. 2008, 39, 1095–1113. [Google Scholar] [CrossRef]
- Shaikhet, L.; Bunimovich-Mendrazitsky, S. Stability analysis of delayed immune response BCG infection in bladder cancer treatment model by stochastic perturbations. Comput. Math. Methods Med. 2018. [Google Scholar] [CrossRef]
- Fridman, E.; Shaikhet, L. Simple LMIs for stability of stochastic systems with delay term given by Stieltjes integral or with stabilizing delay. Syst. Control. Lett. 2019, 124, 83–91. [Google Scholar] [CrossRef]
- Berezansky, L.; Bunimovich-Mendrazitsky, S.; Shklyar, B. Stability and controllability issues in mathematical modeling of the intensive treatment of leukemia. J. Optim. Theory Appl. 2015, 167, 326–341. [Google Scholar] [CrossRef]
- Biot, C.; Rentsch, C.A.; Gsponer, J.R.; Birkhäuser, F.D.; Jusforgues-Saklani, H.; Lemaître, F.; Auriau, C.; Bachmann, A.; Bousso, P.; Demangel, C.; et al. Preexisting BCG-Specific T Cells Improve Intravesical Immunotherapy for Bladder Cancer. Sci. Transl. Med. 2012, 4, 137. [Google Scholar] [CrossRef]
- Kronik, N.; Kogan, Y.; Schlegel, P.G.; Wölfl, M. Improving T-cell immunotherapy for melanoma through a mathematically motivated strategy: Efficacy in numbers? J. Immunother. 2012, 35, 116–124. [Google Scholar] [CrossRef] [PubMed]
- Bunimovich-Mendrazitsky, S.; Halachmi, S.; Kronik, N. Improving bacillus Calmette-Guérin (BCG) immunotherapy for bladder cancer by adding interleukin 2 (IL-2): A mathematical model. Math. Med. Biol. J. IMA 2015, 30, 159–188. [Google Scholar] [CrossRef]
- Bunimovich-Mendrazitsky, S.; Shochat, E.; Stone, L. Mathematical Model of BCG Immunotherapy in Superficial Bladder Cancer. Bull. Math. Biol. 2007, 69, 1847–1870. [Google Scholar] [CrossRef] [PubMed]
- Bunimovich-Mendrazitsky, S.; Gluckman, J.C.; Chaskalovic, J. A mathematical model of combined bacillus calmette-guerin (BCG) and interleukin (IL)-2 immunotherapy of superficial bladder cancer. J. Theor. Biol. 2011, 277, 27–40. [Google Scholar] [CrossRef] [PubMed]
- Ludewig, B.; Krebs, P.; Junt, T.; Metters, H.; Ford, N.J.; Anderson, R.M.; Bocharov, G. Determining control parameters for dendritic cell-cytotoxic T lymphocyte interaction. Eur. J. Immunol. 2004, 34, 2407–2418. [Google Scholar] [CrossRef] [PubMed]
- Marino, S.; Kirschner, D.E. The human immune response to Mycobacterium tuberculosis in lung and lymph node. J. Theor. Biol. 2004, 227, 463–486. [Google Scholar] [CrossRef] [PubMed]
- Yee, C.; Thompson, J.A.; Byrd, D.; Riddell, S.R.; Roche, P.; Celis, E.; Greenberg, P.D. Adoptive T cell therapy using antigen-specific CD8+ T cell clones for the treatment of patients with metastatic melanoma: In vivo persistence, migration, and antitumor effect of transferred T cells. Proc. Natl. Acad. Sci. USA 2002, 99, 16168–16173. [Google Scholar] [CrossRef] [PubMed]
- Archuleta, R.J.; Mullens, P.; Primm, T.P. The relationship of temperature to desiccation and starvation tolerance of the Mycobacterium avium complex. Arch. Microbiol. 2002, 178, 311–314. [Google Scholar] [CrossRef]
- Wigginton, J.; Kirschner, D. A model to predict cell-mediated immune regulatory mechanisms during human infection with Mycobacterium tuberculosis. J. Immunol. 2001, 166, 1951–1967. [Google Scholar] [CrossRef]
- Kuznetsov, V.A.; Makalkin, I.A.; Taylor, M.A.; Perelson, A.S. Nonlinear dynamics of immunogenic tumors: Parameter estimation and global bifurcation analysis. Bull. Math. Biol. 1994, 56, 295–321. [Google Scholar] [CrossRef]
- Vegh, Z.; Mazumder, A. Generation of tumor cell lysate-loaded dendritic cells preprogrammed for IL-12 production and augmented T cell response. Cancer Immunol. Immunother. 2003, 52, 67–79. [Google Scholar] [CrossRef] [PubMed]
- Fikri, Y.; Pastoret, P.P.; Nyabenda, J. Costimulatory molecule requirement for bovine WC1 + gammadelta T cells proliferative response to bacterial superantigens. Scand. J. Immunol. 2002, 55, 373–381. [Google Scholar] [CrossRef] [PubMed]
- Kronin, V.; Fitzmaurice, C.J.; Caminschi, I.; Shortman, K.; Jackson, D.C.; Brown, E.L. Differential effect of CD8(+) and CD8(-) dendritic cells in the stimulation of secondary CD4(+) T cells. Int. Immunol. 2001, 13, 465–473. [Google Scholar] [CrossRef] [PubMed]
- Shochat, E.; Hart, D.; Agur, Z. Using computer simulations for evaluating the efficacy of breast cancer chemotherapy protocols. Math. Model. Methods Appl. Sci. 1999, 9, 599–615. [Google Scholar] [CrossRef]
- Kogan, Y.; Forys, U.; Shukron, O.; Kronik, N.; Agur, Z. Cellular immunotherapy for high grade Gliomas: Mathematical analysis deriving efficacious infusion rates based on patient requirements. SIAM J. Appl. Math. 2010, 70, 1953–1976. [Google Scholar] [CrossRef]
- Kronik, N.; Kogan, Y.; Vainstein, V.; Agur, Z. Improving alloreactive CTL immunotherapy for malignant gliomas using a simulation model of their interactive dynamics. Cancer Immunol. Immunother. 2008, 57, 425–439. [Google Scholar] [CrossRef]
- Klinger, M.; Brandl, C.; Zugmaier, G.; Hijazi, Y.; Bargou, R.C.; Topp, M.S.; Gökbuget, N.; Neumann, S.; Goebeler, M.; Viardot, A.; et al. Immunopharmacologic response of patients with B-lineage acute lymphoblastic leukemia to continuous infusion of T cell engaging CD19/CD3-bispecific BiTE antibody blinatumomab. Blood 2012, 119, 6226–6233. [Google Scholar] [CrossRef]
- Schiphorst, P.P.; Chang, P.C.; Clar, N.; Schoemaker, R.; Osanto, S. Pharmacokinetics of interleukin-2 in two anephric patients with metastatic renal cell cancer. Ann. Oncol. 1999, 10, 1381–1383. [Google Scholar] [CrossRef]
- Lamm, D.L. Improving Patient Outcomes: Optimal BCG Treatment Regimen to Prevent Progression in Superficial Bladder Cancer. Eur. Urol. Suppl. 2006, 5, 654–659. [Google Scholar] [CrossRef]
- Nave, O.; Hareli, S.; Elbaz, M.; Iluz, I.H.; Bunimovich-Mendrazitsky, S. BCG and IL—2 model for bladder cancer treatment with fast and slow dynamics based on S PV F method—Stability analysis. Math. Biosci. Eng. 2019, 16, 5346–5379. [Google Scholar] [CrossRef]
- Haynsworth, E.V. On the Schur Complement. Basel Math. Notes 1968, 20, 17. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).