Mixing in Turbulent Flows: An Overview of Physics and Modelling

1. Introduction

Turbulent flows, common in nature and technology, are still challenging from the standpoint of physical modelling and computation [1]. Further complexity is due to the fact that turbulent flows sometimes feature additional variables, such as the chemical compositions and concentrations of contaminants or admixtures, etc. These are called scalar variables and are governed by their own transport equations that express, basically, the mass balance of species/admixtures in the flow, to be solved jointly with the fluid dynamics [2]. Additionally, the temperature field can sometimes be treated this way, through an appropriate energy balance. In non-uniform scalar fields, either due to initial conditions or when inlets are present, the mixing process will take place [3,4]; it consists of a non-trivial interplay between advection by turbulence and molecular diffusion. An overview of such processes is the main aim of the present work.

Environmental flows with scalars include ocean dynamics with the temperature and salinity gradients, dispersion of contaminants in waters or in the atmosphere [5,6,7], air pollution in urban areas [8,9], cloud microphysics [10,11,12] and numerical weather prediction and climate models [13,14]. On the industrial side, mixing is of utmost importance for various operations and devices in the area of chemical and process engineering [15]. Among those intensely studied because of the ecology, economy and safety concerns are the processes of combustion, including the diffusive flames and the environmentally friendly concept of flameless oxidation [16,17].

Although turbulent flows are governed by a well-known system of macroscopic conservation equations, i.e., the Navier–Stokes (N–S) equations for Newtonian fluids, the detailed solution in terms of the relevant hydrodynamic variables with no simplifying assumptions (unsteady, fully 3D flow) remains computationally costly or even unfeasible for many practical problems involving complex geometry or a wider range of eddying motions. However, this method, called the direct numerical simulation (DNS), is a precious tool to gain fundamental knowledge about turbulence, including the mixing process, and to validate closure proposals; the pioneering studies on fully resolved scalar transport in turbulent flows date back to before the year 2000 [18,19,20,21,22]. The DNS, although limited to simple geometries, is particularly useful in studying turbulent reactive flows. This is due to a sound description of chemical reactions that involves the length scales ranging from the system size down to the smallest ones. Those disipative eddies, of the order of the Kolmogorov length scale, are resolved in DNS but have to be modelled in other methods. Thus, there is still ample room for development and use of numerical models within the scope of a simplified description of turbulence. They represent an alternative to the DNS and provide a partial (approximate) description of the flow. Two such approaches are: the statistical closures, usually formulated in terms of the Reynolds-averaged Navier–Stokes (RANS) equations, and the large eddy simulation (LES) where the subfilter scales are not resolved. Let us note that hybrid RANS-LES models with zonal coupling have undergone a rapid development, in particular for cases when both wall-bounded turbulence (statistically-resolved for computational efficiency) and large vortical structures controlling some flow aspects (resolved by LES) are of importance [23].

Generally speaking, the statistical approach is usually applied for the phenomena (processes) where it is either too expensive or of no interest to gather detailed information about the system under scrutiny. Admittedly, a remarkable exception is quantum physics where the statistical description is the only one possible. Additionally, in turbulence, randomness can be purposefully introduced, even though it is not explicitly present in the governing flow equations. As an alternative to more established Eulerian moment closures (RANS), where averaged equations representing conservation laws are considered, turbulent flow can be described with the use of the one-point probability density for instantaneous velocities of notional fluid elements, and additional scalars. This is the starting point of the probability density function (PDF) method. As discussed in the following, the molecular diffusion persists down to the smallest flow scales (and even becomes dominant there), so the need to model the micro-mixing applies both to the statistical turbulence models and to the LES.

The present review is meant to provide an introduction to the issue of mixing, in particular in turbulent flows, considering some recent developments in the field and addressing both the physics and modelling, with no particular emphasis on combustion though. The account of existing closures for reacting flow and their ramifications for various combustion regimes would require a comprehensive review on its own, beyond the expertise of the authors. For recent work on turbulent combustion models, including the LES and PDF methods, interested readers may refer to [24,25,26,27]. Other specific topics are mixing in non-Newtonian fluids (as in polymer processing), mixing in plasmas [28], dispersed solid-fluid flows (e.g., blending in food industry) and macromixing of components featuring interphasial surfaces, i.e., liquid–liquid or gas–liquid systems [29], that often aims at maximising the interfacial area. Although of importance in various applications, the latter processes involve other physical phenomena such as surface tension (rather than molecular diffusion); they are left out of the present overview.

The paper is organised as follows. In Section 2, we provide a short account of the problem of mixing in turbulent flows, its physical aspects and practical importance. The notion and classification of additional scalar variables in turbulent flows are introduced. Turbulent flows with scalars are considered in Section 3 where the closure problem is presented together with the available models. We introduce the probability density function approach, accompanied by the trajectory (Lagrangian) point of view. In particular, we identify the molecular transport term pertaining to mass diffusion or heat conductivity. It is this so-called micro-mixing term that causes fundamental difficulties in one-point modelling of turbulent flows. This is discussed in a separate section (Section 4) because of the role of micro-mixing both in the statistical turbulence modelling and in the LES. A few mixing models are presented, with more details on the bounded Langevin model; the problem of scalar mixing in isotropic turbulence serves as an illustration. In Section 5, we address the filtered density function (FDF) approach to scalar variables in the context of large-eddy simulations. A short summary is made in Section 6: some emerging trends are reported, as prompted by recent progress in computing technology, and some suggestions are put forward for possible further developments in the modelling of turbulent flows with scalars.

2. Mixing Processes

In a fluid flow, and in a turbulent flow in particular, one may be interested in the evolution of additional variables such as the chemical composition, the concentration of contaminants or admixtures, the temperature field, etc., called scalars for brevity.

In this section, we briefly recall some facts about the mixing processes in the flow. To fix our attention, the starting point is a generic scalar transport equation; the corresponding scalar PDF equation in a turbulent flow will be introduced in Section 3. The evolution equation for a scalar variable $\mathsf{\Phi }=\mathsf{\Phi }(\mathbf{x},t)$ with a generic molecular transport coefficient $\lambda$ (the diffusivity of mass D or thermal diffusivity $\alpha$) has got the structure of an advection–diffusion equation, possibly also containing a source term $\dot{w}\left(\mathsf{\Phi }\right)$. The scalar equation is written in the Cartesian tensor notation (the summation over repeated dummy indices is implied) as

$$\frac{\partial \mathsf{\Phi }}{\partial t}+U_j\frac{\partial \mathsf{\Phi }}{\partial x_j}=\frac{\partial }{\partial x_j}\lambda \frac{\partial \mathsf{\Phi }}{\partial x_j}+\dot{w}\left(\mathsf{\Phi }\right)$$

(1)

where $\mathbf{U}=\mathbf{U}(\mathbf{x},t)$ is the fluid velocity field. In general, scalar variables are classified as passive in case they do not influence the flow dynamics, or active, in case they do. Examples of active scalar are considerable temperature differences that affect the fluid density and/or viscosity. Then, the scalars can be treated as conserved (inert) or reactive, depending on whether the source term (e.g., due to chemical reactions) occurs in their transport equations. In a general multiscalar case, a vector quantity $\mathsf{\Phi }$ appears in Equation (1) and the source term $\dot{\mathbf{w}}\left(\mathsf{\Phi }\right)$ may involve, e.g., the chemical composition of reactive species and the temperature.

The largest length scales of the scalar field are usually determined by the initial conditions (e.g., two layers, or slabs, of width L and different values of $\mathsf{\Phi }$, featuring thus a so-called scalar interface) or the boundary conditions (e.g., two inlets to the flow domain, characterised by a length scale L). Then, in the case of pure molecular diffusion of scalar (no advection), the process is governed by the parabolic-type partial differential equation. The time scale is readily found from the dimensional analysis: ${\tau }_{\mathrm{mix}}=L^2/\lambda$ where L is a characteristic scale (e.g., the width of a slab/lamella). The local uniformity of the scalar field means that it is homogeneous at the molecular level, or well micro-mixed. In contrast, the field can be uniform on a larger scale, i.e., well macro-mixed, which is the case for the often-used benchmark: binary scalar distribution in homogeneous turbulence.

In various situations of process engineering, one is interested in efficient mixing, resulting in a well-micromixed system in a possibly short time. As the molecular diffusion is generally a slow process, except in microfluidics perhaps, a standard practice is to enhance it by engaging the advection term of Equation (1). The general idea has been to promote the occurrence of smaller length scales and to increase the area of scalar interfaces. Basically, the mixing enhancement can be passive or active. In the former case, one designs a specific geometry for the purpose. In a laminar flow, the task is usually more demanding; see a study on serpentine micromixers [30]. As for active mixers, an external energy source is built into the microfluidic system in terms of the electric and magnetic fields or ultrasonic vibrations. The role of such actuators is to produce flow perturbations to make the mixing process more efficient. For recent general reviews on active and passive micromixers in microfluidics, often called lab-on-a-chip devices, see [31,32].

Additionally, the fractal concepts have found their way to enhance mixing. A canonical case is grid turbulence. Fractal grids have been experimentally studied and found to increase the mixing efficiency [33], and the scalar diffusion [34]. Concerning the case of active micromixers, the use of fractal-like blades of impellers has been examined in [35]. As the outcome of their DNS, the authors state that the power consumption of such an impeller with fractally-designed blading is reduced with respect to the standard layout, while a considerably shorter mixing time is observed.

Back to passive mixers, an interesting endeavour has recently been reported in [36] where the specific geometry of flow obstacles or deflectors has been conceived through the adjoint optimisation method, resulting in a fairly complex structure (resembling a porous medium) to promote the occurrence of flow separation zones and enhance the mixing process. Unfortunately, a typical drawback of passive methods featuring extra obstacles or walls is the resulting increased pressure loss.

Often-used configurations to reduce the scalar length scale at the flow inlet are the annular jets with co-flowing streams, such as those of fuel and oxidant, possibly also of hot co-flow, typical of non-premixed combustion [16,17]. Additionally, strong gradients of tangential velocity in the shear layers promote the growth of scalar interfaces due to the Kelvin–Helmholtz instability. Alternatively, a system of many inlet nozzles may be conceived to reduce the inlet length scale of the scalar. An ingenious configuration of this type has been found to result in more efficient mixing than the T-junction system of inlets [37].

Assuming that the Schmidt number $Sc=\nu /\lambda$ is unity, for the scalar structures of the Kolmogorov scale $L={\eta }_K={({\nu }^3/ϵ)}^{1/4}$ one readily finds that ${\tau }_{\mathrm{mix}}=L^2/\lambda ={(\nu /ϵ)}^{1/2}={\tau }_K$; i.e., the mixing time scale is equal to the Kolmogorov time scale, which is expected. For the Schmidt numbers larger than 1, occurring in some liquids, the smallest length scales of the scalar field in a turbulent flow, called the Batchelor scale ${\eta }_B={(\nu {\lambda }^2/ϵ)}^{1/4}$, are smaller than the dissipative eddies: ${\eta }_B/{\eta }_K\sim {\left(Sc\right)}^{-1/2}$. This means, in particular, that for a well-resolved mixing process under such conditions, the DNS mesh should be correspondingly finer.

For a simple experiment using household appliances, a qualitative picture of the mixing process is shown in Figure 1. An initially arranged system consists of three concentric spots of coloured liquids; the blobs get stirred by a rotating central disk (an electric toothbrush is used for the purpose). As the time elapses, thinner and thinner structures appear, as advected and deformed by the flow, and finally disappear due to the prevailing action of molecular diffusion. This very observation seems to be in line with the recent and comprehensive review of Villermaux [38]. He describes a lamellar representation of the mixing problem where a mixture is seen as a set of stretched sheets (in 3D) or lamellae (in 2D). In that paper, the differences between stirring, blending and mixing are clearly explained: in stirring and blending (or macromixing), the length scales of the scalar field decrease through stretching and folding with no substantial diffusion, whereas mixing is perceived as “stretching-enhanced diffusion”. Additionally, a caveat is formulated in [38] that “the sequential vision of the process (stirring, then diffusion) is fundamentally incorrect”, since some molecular diffusion occurs already at larger scales of the scalar field. Another consequence of the scalar interfaces being stretched and folded by the flow, aside from the occurrence of smaller-scale structures, is the increase of scalar gradients [39]. This happens in a way analogous to the increase of local velocity gradients in turbulence, ultimately being destroyed by the action of viscosity.

To reiterate the classification of scalar variables: Dimotakis [3] distinguishes among three levels of mixing: (i) passive scalars, (ii) dynamically active ones with mixing coupled to the dynamics and (iii) mixing that alters the fluid composition and/or density (as it occurs in chemically reactive flows). To the category (i), i.e., scalars that do not affect the flow dynamics, belongs a concentration of tracer species or a small excess in temperature that does not trigger natural convection. The category (ii) includes the buoyancy-affected flows, for example, due to the temperature or salinity gradients in the ocean, the unstable stratification, the breaking of internal waves or the Rayleigh–Taylor instability. That paper also presents considerations on scalar dissipation and mixing as interdependent on the full spectrum of turbulent flow scales. A nontrivial model that mimics scalar evolution at different scales was advanced by Kraichnan [40]. Therein, the velocity in Equation (1) was replaced by a stochastic Gaussian field with a prescribed two-point correlation tensor and with time correlation that decays infinitely rapidly. Although the advecting flow was idealised, that model, exactly solvable, was able to correctly predict scalar mixing at small scales, known for their complex, intermittent behaviour; see also an insightful review paper by Warhaft [41].

In [4], the very concept of mixing is addressed, with its irreversibility and possible emergence of complexity. An interesting perspective on turbulent mixing is offered by Sreenivasan [42]. He analyses the dependencies of the mixing state on the Schmidt and Reynolds numbers, and focuses on the scalar spectra resulting from a large-scale stirring. In [43], the DNS findings are analysed as being relevant to the fine-scale scalar mixing and dissipation. The authors also study the multifractal properties of scalar dissipation which are related to another fascinating topic in turbulence theory, i.e., fractals (see [44]), as some features of turbulence may be assumed this way for further modelling [45,46].

3. Turbulent Flows with Scalar Variables: Statistical Modelling

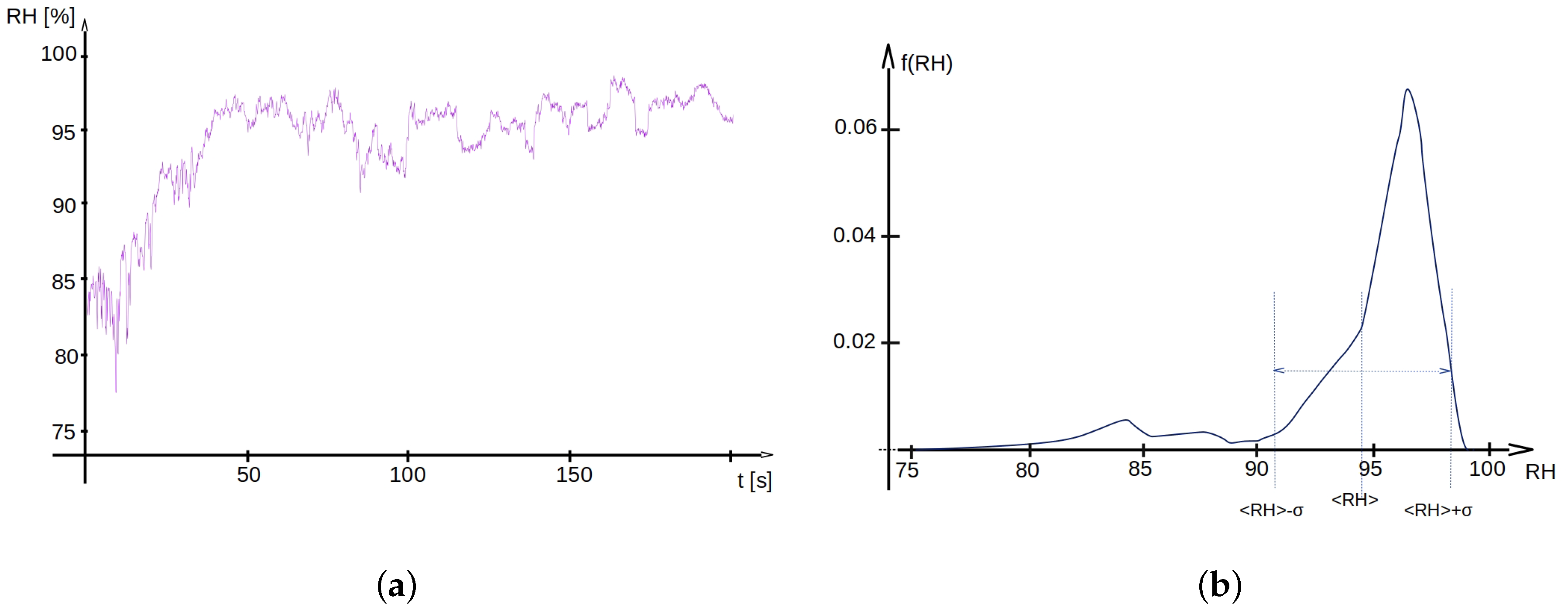
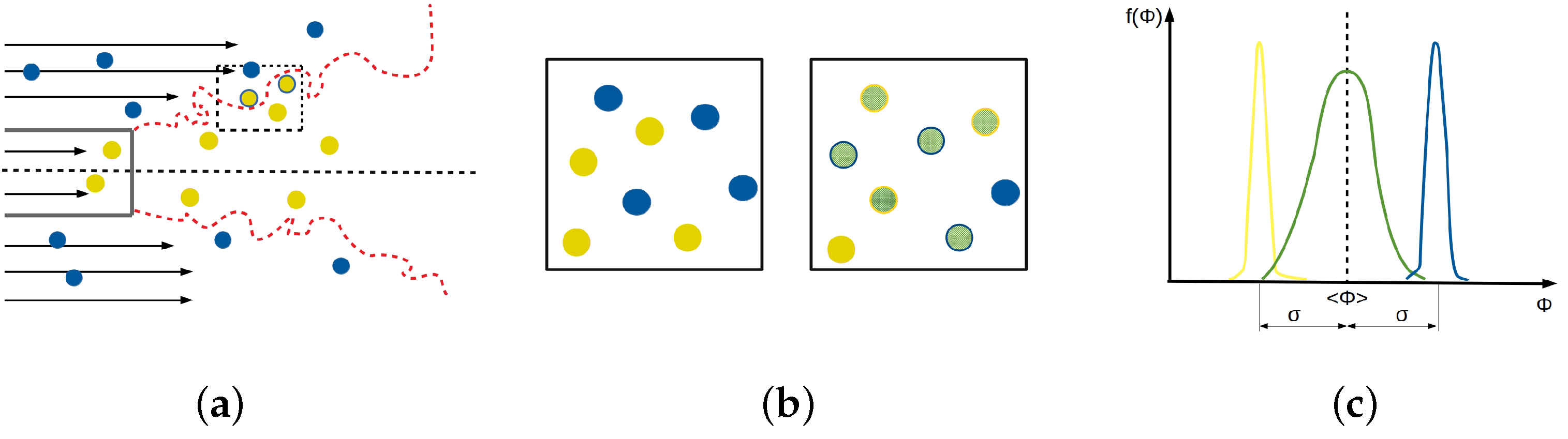
3.1. The PDF and Statistical Description

Apart from empirical studies [41], the physical evidence about the mixing processes can be reconstructed in the DNS, to the extent limited by available computing resources. Otherwise, for most of practical computations, a reduced description needs to be applied. The most common are single-point statistical approaches (with the underlying probability distribution, or PDF, of relevant fluid-dynamical variables). Here, we only briefly recall some fundamental notions; for detailed coverage see [1,47,48].

Given the instantaneous scalar field evolving in a turbulent flow, $\mathsf{\Phi }=\mathsf{\Phi }(\mathbf{x},t)$, the useful statistics are at least the mean and the variance. From the theoretical standpoint, they are the lowest-order moments of the one-point PDF of the scalar variable. The PDF is introduced as $f=f_{\mathsf{\Phi }}(\mathsf{\Psi };\mathbf{x},t)$ meaning that the probability of the event $\mathsf{\Psi }\le \mathsf{\Phi }\le \mathsf{\Psi }+d\mathsf{\Psi }$ at point $(\mathbf{x},t)$ is equal to $f\left(\mathsf{\Psi }\right)d\mathsf{\Psi }$. The sampling space variable $\mathsf{\Psi }$ corresponds to the instantaneous scalar value $\mathsf{\Phi }$, which in this description becomes a random variable, or more precisely, a stochastic process when the time evolution is followed. Then, using the Dirac delta $\delta$, the fine-grained PDF $f^{\prime }$ is introduced as $f^{\prime }(\mathsf{\Psi };\mathbf{x},t)=\delta (\mathsf{\Phi }(\mathbf{x},t)-\mathsf{\Psi })$ to describe a given realisation. Its statistical average yields the PDF: $\langle f^{\prime }(\mathsf{\Psi };\mathbf{x},t)\rangle =f(\mathsf{\Psi };\mathbf{x},t)$. This property is useful when tackling the PDF equations.

Consequently, the scalar mean and variance are defined as

$$\begin{array}{c}\hfill \langle \mathsf{\Phi }(\mathbf{x},t)\rangle ={\int }_{-\infty }^{\infty }\mathsf{\Psi }f(\mathsf{\Psi };\mathbf{x},t)\mathrm{d}\mathsf{\Psi },{\sigma }^2={\int }_{-\infty }^{\infty }{(\mathsf{\Psi }-\langle \mathsf{\Phi }\rangle )}^{2}f(\mathsf{\Psi };\mathbf{x},t)\mathrm{d}\mathsf{\Psi }\end{array}$$

(2)

and the conditional mean value of an arbitrary function $H(\mathbf{x},t)$ satisfies

$$\begin{array}{c}\hfill \langle H(\mathbf{x},t)f^{\prime }(\mathsf{\Psi };\mathbf{x},t)\rangle =\langle H(\mathbf{x},t)|\mathsf{\Phi }(\mathbf{x},t)=\mathsf{\Psi }\rangle f.\end{array}$$

(3)

Except when the PDF form is known a priori (presumed), the mean and the variance are not sufficient to characterise the probability distribution. This is illustrated in Figure 2. The time series of relative humidity ($RH$) was taken from airborne measurements (assuming it is representative of a statistically steady process) [49]. It was then used to construct the PDF, $f\left(RH\right)$, which revealed itself to be non trivial, highly skewed and obviously bounded (as $RH\le 100\%$).

By applying the Reynolds decomposition, $\mathsf{\Phi }=\langle \mathsf{\Phi }\rangle +\varphi$ and $U_i=\langle U_i\rangle +u_i$, to Equation (1), the mean transport equation that constitutes the starting point of the moment closures is obtained. The equation takes the form

$$\frac{\partial \langle \mathsf{\Phi }\rangle }{\partial t}+\langle U_j\rangle \frac{\partial \langle \mathsf{\Phi }\rangle }{\partial x_j}=\frac{\partial }{\partial x_j}\lambda \frac{\partial \langle \mathsf{\Phi }\rangle }{\partial x_j}-\frac{\partial }{\partial x_j}\langle u_j\varphi \rangle +\langle \dot{w}\left(\mathsf{\Phi }\right)\rangle ;$$

(4)

the unknown turbulent transport term of scalar fluctuations $\langle u_i\varphi \rangle$ and the mean source term $\langle \dot{w}\left(\mathsf{\Phi }\right)\rangle$ have to be closed. A note on moment closures for the turbulent scalar flux is given in Section 3.3 below. A closure of the source term, particularly important for reactive flows, is generally difficult, as $\dot{w}\left(\mathsf{\Phi }\right)$ is usually a highly nonlinear function of its arguments, and consequently $\langle \dot{w}\left(\mathsf{\Phi }\right)\rangle \ne \dot{w}\left(\langle \mathsf{\Phi }\rangle \right)$. Indeed, $\mathsf{\Phi }$ is often taken as a vector of chemical composition and the reaction rate is expressed through the Arrhenius law (see [2], Ch. 5). In a special case of infinitely fast reactions in a non-premixed configuration, a mixture fraction can be introduced as a conserved scalar (hence no source term will appear).

3.2. The PDF Equation of Scalar Transport

Again, as in Section 3.1, the aim here is not to provide a self-contained introduction to the PDF methods for turbulent flows ([1,47,50,51]), but mostly to identify the micro-mixing term that will be in focus in Section 4.

Consider now the PDF equation corresponding to the generic transport equation, Equation (1). The exact transport equation for f can be derived using the fine-grained PDF $f^{\prime }(\mathsf{\Psi };\mathbf{x},t)$ which is governed by

$$\frac{\partial f^{\prime }}{\partial t}+\frac{\partial }{\partial x_j}\left(f^{\prime }{U}_j\right)+\frac{\partial }{\partial \mathsf{\Psi }}\left(\frac{d\mathsf{\Phi }}{dt}{f}^{\prime }\right)=0.$$

(5)

Please note that in the scalar PDF formulation, used here, the velocity is not an independent variable; hence $U_j$ must be acted upon by the spatial derivative operator. After averaging and substituting for the material derivative of the scalar variable from Equation (1), the exact transport equation for f is derived (see Equation 12.322 in [1]):

$$\frac{\partial f}{\partial t}+\frac{\partial f\langle U_j\rangle }{\partial x_j}+\frac{\partial }{\partial x_j}\langle u_j{f}^{\prime }\rangle =-\frac{\partial }{\partial \mathsf{\Psi }}\left[\langle \lambda \frac{{\partial }^2\mathsf{\Phi }}{\partial x_j\partial x_j}|\mathsf{\Phi }=\mathsf{\Psi }\rangle f\right]-\frac{\partial }{\partial \mathsf{\Psi }}\left[f\dot{w}\left(\mathsf{\Psi }\right)\right].$$

(6)

The third LHS term of Equation (6), i.e., the turbulent diffusion term, is rewritten using Equation (3)

$$\langle u_j\delta (\mathsf{\Phi }(\mathbf{x},t)-\mathsf{\Psi })\rangle =\langle u_j|\mathsf{\Phi }=\mathsf{\Psi }\rangle f.$$

(7)

Then, the RHS term of Equation (6) involving $\lambda$ is further rearranged to yield

$$\frac{\partial f}{\partial t}+\frac{\partial f\langle U_j\rangle }{\partial x_j}+\frac{\partial }{\partial x_j}\left[f\langle u_j|\mathsf{\Phi }=\mathsf{\Psi }\rangle \right]=\lambda \frac{{\partial }^{2}f}{\partial x_j\partial x_j}-\frac{{\partial }^2}{\partial {\mathsf{\Psi }}^2}\left[f\langle \lambda \frac{\partial \mathsf{\Phi }}{\partial x_j}\frac{\partial \mathsf{\Phi }}{\partial x_j}|\mathsf{\Phi }=\mathsf{\Psi }\rangle \right]-\frac{\partial }{\partial \mathsf{\Psi }}\left[f\dot{w}\left(\mathsf{\Psi }\right)\right].$$

(8)

This way, the molecular diffusion term in the physical space ($\lambda {\nabla }^{2}f$) that is exact and requires no closure becomes separated from the scalar mixing (or micromixing) term which is the second RHS term of Equation (8); the latter is unclosed and is further discussed in Section 4. As to the turbulent convective flux (appearing in the third LHS term of Equation (8), a gradient diffusion hypothesis is usually applied: $f\langle \mathbf{u}|\mathsf{\Psi }\rangle =-{\lambda }_t\nabla f$, so the closure is shifted to the turbulent diffusivity ${\lambda }_t$. Another important quantity is the scalar dissipation rate (here: conditional) appearing in the micromixing term.

From the PDF of $\mathsf{\Phi }$, all statistical moments of the distribution are readily computed. Of particular importance is the variance of scalar fluctuations $\langle {\varphi }^2\rangle ={\sigma }^2$—see Equation (2)—which serves as a useful measure of local mixedness. A separate transport equation for the variance can also be written and solved in the Eulerian approach without explicitly introducing the PDF f; see Section 3.3. However, for some applications such as the dispersion of hazardous admixtures, the prediction of extreme events is of importance rather than just the fields of the scalar mean or variance [38]. An example is pollutant concentration following dispersion from the source (as in an accident scenario) in human-populated areas where the probability of peak concentrations above some threshold value (possibly also their residence time) are of interest [8]. In that work, a joint velocity-scalar PDF approach was adopted to predict dispersion in an urban street canyon.

Although the topic is beyond the scope of the present overview, the joint approach uses the PDF in the form $f=f_{\mathsf{\Phi }\mathbf{U}}(\mathsf{\Psi },\mathbf{V};\mathbf{x},t)$ with $\mathbf{V}$ being the sample-space variable for velocity. The subject is vast, as comprehensively presented in the landmarking paper by Pope [47]; see also [2,52]. The joint velocity-scalar PDF approach offers access, without modelling, to other statistics such as the turbulent flux of scalar, yet it is more complex and computationally expensive than the scalar PDF only. For example, considerable difficulties need to be overcome to properly implement the velocity PDF approach in wall-bounded turbulence, including either the wall function formulation or explicit accounting for the molecular viscosity with the down-to-the-wall integration [1]. The tools known from the Eulerian RANS approach, such as the elliptic relaxation in near-wall regions, have been successfully applied in the PDF solution with the viscous sublayer [8,53]. Additionally, the joint velocity-scalar PDF has been attempted to predict the near-wall temperature field [54], and for modelling of thermal fluctuations in conjugate heat transfer [55]. The FDF variant of the joint velocity-scalar approach, in the LES setting, will be briefly presented in Section 5.

Following the presentation of the velocity PDF approach by Pope in his textbook [1], Fox [2] developed a theoretical framework for turbulent reacting flows based on the joint PDF. In a series of papers, Minier and coworkers extended the Lagrangian PDF formalism to dispersed two-phase turbulent flows; see the review [56] (its title bears a clear parallel to the seminal work [47]).

The scalar PDF methods were historically used first, especially for turbulent combustion problems [50], and often coupled with Eulerian flow solvers. Given the maturity of the Eulerian CFD and the availability of software, hybrid methods have been proposed where the velocity field predicted by the PDF equation is further made consistent with the mean field computed from an Eulerian code [51,57]. The hybrid PDF-CFD methods have been intensely developed [57] and applied to cutting-edge industrial problems [58,59]. A disadvantage is still the use of the gradient diffusion hypothesis for turbulent transport, yet the computational cost is considerably reduced.

The formulation for the scalar PDF only is less computationally expensive. As mentioned above, an alternative approach is based on the joint velocity-scalar PDF equation, yet it is not detailed here, as the main focus of this review is the turbulent mixing, which needs to be closed in either PDF approach.

The PDF transport equation is a partial differential equation (PDE). In principle, it could be solved with a Eulerian method, on a computational grid. However, the main challenge of such an approach is the high dimensionality of the PDF, in particular in cases of multi-scalar simulations. Numerical algorithms for such high-dimensional problems have recently been developed in [60] and are based on reduction of the joint PDF equation of many variables to a sequence of low-dimensional problems.

After a proper closure of the micromixing term (Section 4), for practical computations the Lagrangian PDF approach is applied to solve Equation (8). In the Lagrangian setting, the relevant fields are represented by a set of notional particles [1,47]. The particles carry the evolving values of the scalar variable (and possibly also velocity in the joint PDF model). This is a crucial step that has made the PDF method computationally feasible. Without presenting the actual particle evolution equations, let us imagine a bi-modal distribution of the scalar variable. In reality, it may result from a macro-mixing process in the shear layer (nota bene, often called the mixing layer) as in a jet with co-flow, schematically represented in Figure 3a and discretised with the particles. Due to advection by turbulence, the ”scalar particles” of both streams undergo macro-mixing (stirring) that does not affect the value of the scalar variable they carry (“the colour”). The particles only change their colour due to molecular diffusion; see plots in (b). These changes are reflected in the evolution of the local scalar PDF shown in the plot in (c).

3.3. A Note on Moment Closures for Scalar Transport

Turbulent flows with scalar variables are often tackled within the Eulerian RANS approach. Various models have been developed over the years and continue to be used in practical applications, including for turbulent heat transfer. As the topic is definitely mature, the Eulerian moment closures are only briefly recalled here for the sake of completeness, but also in view of parameterising the turbulent mixing time needed in one-point micromixing models (Section 4). The main types of closures recalled here are the algebraic ones using the turbulent Prandtl or Schmidt numbers, and the one or two-equation closures where additional modelled PDEs are solved for some statistics of scalar fluctuations. A common feature of these closures, unlike the second-order models (with transport equations for turbulent scalar flux), is that the turbulent transport coefficients for momentum and for the scalar variable, ${\nu }_t$ and ${\lambda }_t$, are introduced in the standard way, respectively, from the Boussinesq assumption for the turbulent (Reynolds) stresses and from the gradient hypothesis for the turbulent scalar flux:

$$\langle u_i{u}_j\rangle =-{\nu }_t\left(\frac{\partial \langle U_i\rangle }{\partial x_j}+\frac{\partial \langle U_j\rangle }{\partial x_i}\right)+\frac{2}{3}k{\delta }_{ij},\langle u_j\varphi \rangle =-{\lambda }_t\frac{\partial \langle \mathsf{\Phi }\rangle }{\partial x_j}$$

(9)

where $k=\langle u_i{u}_i\rangle /2$ is the turbulence kinetic energy. Hence, Equation (4) is written as (the source term will henceforth be skipped)

$$\frac{\partial \langle \mathsf{\Phi }\rangle }{\partial t}+\langle U_j\rangle \frac{\partial \langle \mathsf{\Phi }\rangle }{\partial x_j}=\frac{\partial }{\partial x_j}\left[\left(\lambda +{\lambda }_t\right)\frac{\partial \langle \mathsf{\Phi }\rangle }{\partial x_j}\right].$$

(10)

In a known mean velocity field, Equation (10) can be solved for given ${\lambda }_t$. In algebraic (or zero-equation) models, no additional transport equations are formulated and the expressions for turbulent Prandtl or Schmidt numbers (often semi-empirical) are used instead. The molecular and turbulent Prandtl numbers, when the scalar considered is the temperature and $\lambda =\alpha$, are defined as $\mathrm{Pr}=\nu /\lambda$ and ${\mathrm{Pr}}_t={\nu }_t/{\lambda }_t$. The respective Schmidt numbers for the mass diffusivity (when $\lambda =D$) are defined analogously. At the lowest closure level, the turbulent Prandtl number ${\mathrm{Pr}}_t$ is often assumed as ${\mathrm{Pr}}_t=1$ from the so-called Reynolds analogy. However, depending on the flow configuration, actual values of ${\mathrm{Pr}}_t$ can deviate considerably from this estimate. Examples are the near-wall flows; see [61], or flows in turbulent plumes. In the latter case, under certain assumptions the value ${\mathrm{Pr}}_t=3/5$ was determined theoretically in reference [62]. Moreover, predictions of ${\mathrm{Pr}}_t$ with the use of the renormalisation group theory are reported in reference [63].

The turbulent viscosity ${\nu }_t$ can be determined either from algebraic mixing-length type formulae or from a standard expression based on the turbulent kinetic energy k and its dissipation rate $ϵ$

$${\nu }_t=C_{\mu }{f}_{\mu }\frac{k^2}{ϵ}$$

(11)

where $C_{\mu }=0.09$ and $f_{\mu }$ is a damping function meant to reduce ${\nu }_t$ in the near-wall region. In one and two-equation closures, additional transport equations for the scalar statistics are formulated, independently of the model applied for the dynamics of turbulence (be it k–$ϵ$ or $R_{ij}$–$ϵ$).

The exact equation for the fluctuating scalar variance $\langle {\varphi }^2\rangle$ is derived from Equations (1) and (4). It has the form (see [64] for the context of near-wall heat transfer modelling):

$$\frac{\partial \langle {\varphi }^2\rangle }{\partial t}+\langle U_j\rangle \frac{\partial \langle {\varphi }^2\rangle }{\partial x_j}=\lambda \frac{{\partial }^2\langle {\varphi }^2\rangle }{\partial x_j\partial x_j}-\frac{\partial }{\partial x_j}\langle u_j{\varphi }^2\rangle +2{\mathcal{P}}_{\varphi }-2{ϵ}_{\varphi }.$$

(12)

The structure of Equation (12) is similar to the well known transport equation for k: the first and second RHS terms represent the molecular and turbulent diffusion; ${\mathcal{P}}_{\varphi }$ and ${ϵ}_{\varphi }$ respectively stand for the production and destruction rate of scalar fluctuations:

$${\mathcal{P}}_{\varphi }=-\langle u_j\varphi \rangle \frac{\partial \langle \mathsf{\Phi }\rangle }{\partial x_j},{ϵ}_{\varphi }=\lambda \langle \frac{\partial \varphi }{\partial x_j}\frac{\partial \varphi }{\partial x_j}\rangle .$$

(13)

In the turbulent combustion community, this latter quantity (the scalar dissipation rate) is of utmost importance in modelling. It the simplest setting, it may be assumed proportional to the scalar variance; see [24].

In one-equation closures, one solves Equation (12) supplied with a model for the turbulent diffusion and an algebraic formula for ${ϵ}_{\varphi }$. It can be expressed through the dissipation rate of the kinetic turbulent energy $ϵ$, assuming that the dynamic and scalar time scales are proportional: $k_{\varphi }/{ϵ}_{\varphi }=C_{\varphi }k/ϵ$ with usually $C_{\varphi }=1.5÷2.5$ and $k_{\varphi }=\langle {\varphi }^2\rangle /2$.

In two-equation models, an additional transport equation for ${ϵ}_{\varphi }$ is formulated. It is symbolically written as

$$\frac{\partial {ϵ}_{\varphi }}{\partial t}+\langle U_j\rangle \frac{\partial {ϵ}_{\varphi }}{\partial x_j}=\mathrm{RHS}.$$

(14)

The RHS of Equation (14) contains only small-scale statistics such as products of fluctuating velocity and scalar gradients; for the actual form, see Section 3.3.4. in Ref. [2]. For this reason, the whole RHS of ${ϵ}_{\varphi }$ equation requires modelling, similarly to the case of $ϵ$ equation. Moreover, dynamical parameters used in the modelling have their scalar counterparts, e.g., $k/ϵ$ and $k_{\varphi }/{ϵ}_{\varphi }$, or $\mathcal{P}/ϵ$ and ${\mathcal{P}}_{\varphi }/{ϵ}_{\varphi }$, so in the closure variants for scalar statistics there are more combinations of different expressions to be considered.

When the two-equation model is used for scalar variable, then the turbulent mixing time can naturally be determined as ${\tau }_{\varphi }=k_{\varphi }/{ϵ}_{\varphi }$, alleviating a part of the difficulties in the formulation of micromixing models.

Finally, let us note some alternatives to the closure for turbulent scalar fluxes using the gradient hypothesis with a turbulent diffusivity ${\lambda }_t$, Equation (9). The first are generalised gradient hypotheses involving a tensorial form of the turbulent diffusivity so that the scalar flux vector $\langle \varphi \mathbf{u}\rangle$ no longer has to be colinear with the mean scalar gradient $\nabla \langle \mathsf{\Phi }\rangle$. Another alternative, avoiding the use of such diffusivity coefficients altogether, is to formulate and close additional evolution equations for the scalar fluxes $\langle \varphi u_j\rangle$. However, as it is typically the case in turbulence modelling with a hierarchy of moment closures, such a procedure makes a number of new terms appear that need to be closed.

4. Lagrangian Modelling of Scalar Micromixing

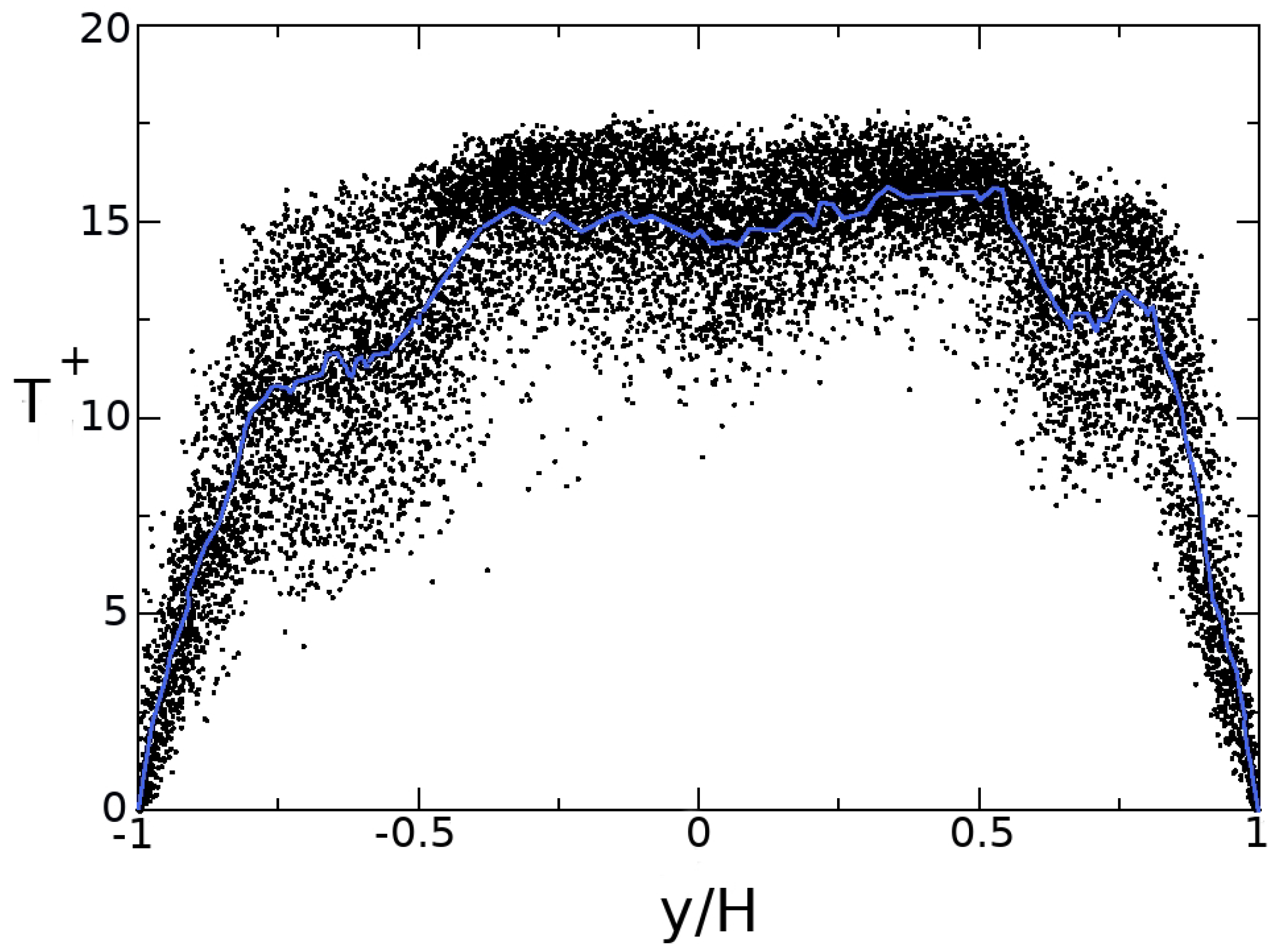
4.1. Generalities

In flows with additional scalar variables, the system is supplemented by a suitable process to model the scalar evolution. However, in all one-point statistical descriptions of turbulent flows with scalars, the so-called micro-mixing term in Equation (8) remains unclosed and has to be modelled [65]. A number of works provide descriptions, at various depth, and surveys of micromixing models; see [1,2,39,47,50,51,66,67,68,69,70,71]. As already noted, due to important applications of flows with chemical species or flows with temperature variations, the modelling of the scalar mixing term in the one-point PDF methods for turbulent flows remains a crucial issue.

The micromixing term describes the so-called negative diffusion, or antidiffusion in the phase space of the scalar variable. The antidiffusion is (unlike the diffusion) a two-point process. Therefore, in the Lagrangian particle methods, the mixing appears as a two-particle process; in other words, it involves a change of the scalar value associated with a fluid element (in reality) or a notional particle (in models) due to its interaction with neighbouring elements/particles. Roughly speaking, the modelling is inherently difficult because it should account for diffusion in the physical space (that can be represented by a random walk) and antidiffusion in the phase space of the scalar [72]. Hence, several particle interaction models have been proposed with a varying degree of success, yet the mixing is often modelled as a one-point process through modification of a particle scalar variable with respect to the local mean scalar value, which is more efficient from the computational standpoint. Therefore, in the one-point PDF approach, the most popular are closures based on the particle-field formulation.

In the following, we consider the scalar micromixing in its simplest setting of homogeneous turbulence with no source terms. Then, Equation (8) reduces to that for the PDF $f=f_{\varphi }(\psi ;t)$ of the fluctuating scalar variable $\varphi$:

$$\frac{\partial f}{\partial t}=-\frac{{\partial }^2}{\partial {\psi }^2}\left[\langle \lambda \frac{\partial \varphi }{\partial x_k}\frac{\partial \varphi }{\partial x_k}|\varphi =\psi \rangle f\right]$$

(15)

where $\psi$ stands for the sampling-space variable that corresponds to $\varphi$.

However, the homogeneity assumption does not limit the universality of reasoning; in general turbulent flows, additional terms, left out of Equation (8), are simply added again.

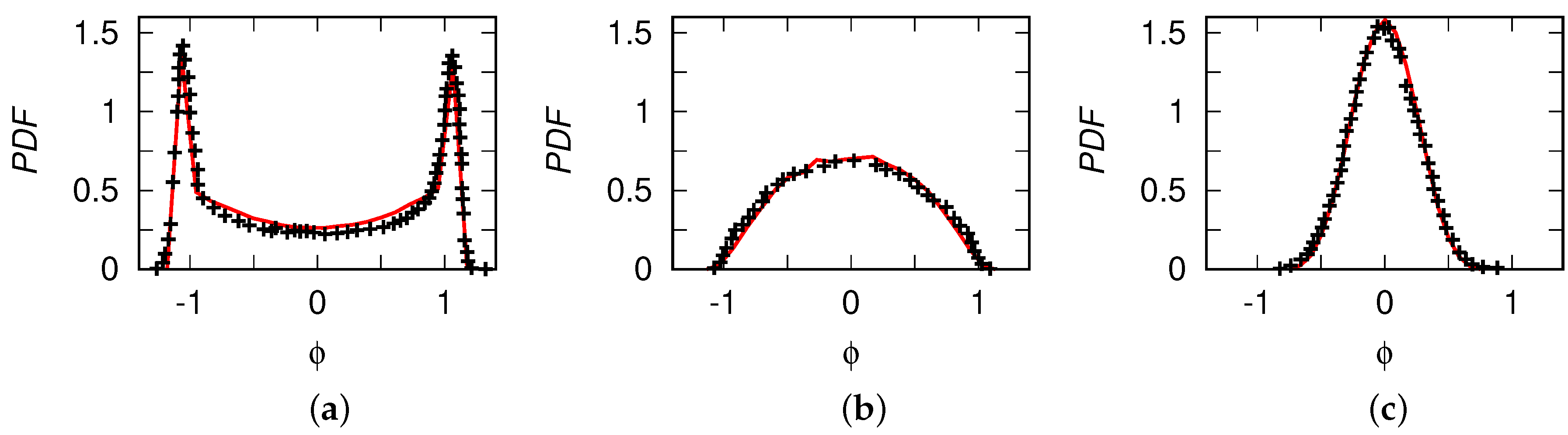
4.2. One-Point Scalar Mixing Models: IEM and Langevin

We first recall the IEM (interaction by exchange with the mean) mixing model, originally proposed by Villermaux and Devillon, and then Dopazo and O’Brien (cited in [1]). The model is also known as the LMSE (linear mean square estimation), and is arguably the simplest and robust closure for the scalar mixing. In terms of the PDF it is represented by

$$\frac{\partial f}{\partial t}=\frac{\partial }{\partial \mathsf{\Psi }}\left[\frac{1}{{\tau }_{\varphi }}\left(\mathsf{\Psi }-\langle \mathsf{\Phi }\rangle \right)f\right].$$

(16)

The IEM model is readily understood from the Lagrangian standpoint as the particle model of the relaxation type. The corresponding scalar evolution equation

$$d{\mathsf{\Phi }}^{}=-\frac{\mathsf{\Phi }-\langle \mathsf{\Phi }\rangle }{{\tau }_{\varphi }}dt$$

(17)

implies a deterministic relaxation of scalar values $\mathsf{\Phi }$ to their local mean $\langle \mathsf{\Phi }\rangle \left(\mathbf{x}\right)$ with a local scalar mixing time scale ${\tau }_{\varphi }$. In the original version of the IEM model, ${\tau }_{\varphi }$ is related to the turbulent time scale (or turbulent frequency $\omega =ϵ/k$):

$${\tau }_{\varphi }=\frac{2}{C_{\varphi }}\frac{k}{ϵ}=\frac{2}{C_{\varphi }\omega }$$

(18)

where the model constant $C_{\varphi }$, usually taken as 2, is meant to represent the turbulent-to-scalar time scale ratio. It is certainly not universal in various flow types (see [47], §5.7.3). The IEM model, although very simple, can provide good results in some flow cases, such as the thermal mixing layer studied in [73]. Moreover, its formulation is reduced to the interaction of the particle scalar value with the mean field; no particle–particle interactions that tend to make the model more computationally demanding are involved. One of the IEM faults, however, is that it unphysically preserves the form of the initial PDF. For example, in binary mixing, it yields two persisting delta-peaks of decaying variance and no relaxation to a Gaussian-like shape; cf., Figure 3c.

The coalescence/dispersion (CD) model, originally proposed by Curl [74], has a simple explanation in terms of particle representation. Let every fluid particle in a given flow region (a computational cell, say) take a scalar value ${\varphi }^{\left(i\right)}$, $i=1...N$. A number $n_m$ of them mix at each time step $∆t$. The scalar values ${\varphi }^{\left(p\right)}$ and ${\varphi }^{\left(q\right)}$ of two particles (selected randomly) become identical according to:

$${\varphi }^{\left(q\right)}(t+∆t)={\varphi }^{\left(p\right)}(t+∆t)=\frac{1}{2}({\varphi }^{\left(p\right)}\left(t\right)+{\varphi }^{\left(q\right)}\left(t\right)).$$

(19)

The number $n_m$ equals $n_m=N∆t/{\tau }_{\varphi }$ where ${\tau }_{\varphi }$ is a characteristic time scale. The remaining $N-n_m$ particles preserve their scalar values at time $t+∆t$. It is, by construction, a two-particle model, yet it is not local in the scalar space.

The mapping closure (MC) model, first proposed by Pope [75], utilises a transformation (mapping) that starts from a reference Gaussian field with known conditional scalar gradient statistics appearing in the micromixing term. The MC model is local in the scalar space; it has been successfully tested on the benchmark of [18] and applied in reactive flow cases.

An extension of the IEM model, Equation (17), is the Langevin model (see Equation 5.52 in [47]) where a white noise term is added:

$$d\mathsf{\Phi }=-G{\omega }_{\varphi }\left(\mathsf{\Phi }-\langle \mathsf{\Phi }\rangle \right)dt+\sqrt{B{\omega }_{\varphi }\langle {\varphi }^2\rangle }dW.$$

(20)

Here, ${\omega }_{\varphi }$ is the mixing frequency or the inverse of the scalar time scale; G and B are model constants; and $d{W}_{}$ is an independent increment of the Wiener process; for a general introduction to stochastic processes, see [48]. The Langevin model for scalar variables, Equation (20), tends to correctly relax the PDF shape (e.g., to a Gaussian), but its main disadvantage is that it violates the principle of boundedness (unless the scalar values are unlimited). The Gaussian random numbers $\xi$ used in the discrete increment of the Wiener process, $∆W=\xi \sqrt{∆t}$, can be arbitrarily large, and so can the whole diffusion term. Although fundamentally unsatisfactory from the theoretical viewpoint, this property of the mixing model is arguably of minor importance in flows where instantaneous scalar values are unlikely to attain their bounds (and this is indeed the case in the wall-function formulation considered in [54]). However, the violation may represent a serious problem when the evolution of the bounded scalar likely to approach its bounds (like the species concentration or the mixture fraction) is to be modelled.

4.3. Binomial Langevin Model for Scalar Mixing Revisited: Bounded Langevin Model

As argued above, the IEM model for scalar micromixing, Equation (17), has the advantage of simplicity, but it unphysically preserves the initial PDF. On the other hand, the Langevin model, Equation (20), tends to correctly relax the initial PDF shape, but violates the principle of boundedness (where relevant). An attempt to improve over the undesirable behaviour of the IEM, while keeping the scalar values bounded, was the binomial sampling model of Valiño and Dopazo [76] that belongs to the class of stochastic jump processes. In a practical simulation of a bimodal scalar field evolving in homogeneous turbulence, this model produced a persisting initial spikes in the scalar PDF. A natural idea to correct that deficiency is to propose a stochastic diffusion process instead. However, this was done in the discrete formulation from the outset and resulted in the binomial Langevin model of Valiño and Dopazo [77], later formally written by Valiño (1994, private communication) as a stochastic differential equation (SDE). The binomial model made use of particle-dependent binomially distributed random numbers rather than Gaussian ones. Both these features, as presented by those authors, were necessary to preserve the scalar boundedness. Here, we briefly summarise some of the findings of [78] where the binomial Langevin model has been revisited with both of the constraints relaxed.

We rewrite the original binomial Langevin model [77] in continuous time (for infinitesimally small time increments). Thus, it becomes a true stochastic diffusion process, represented by the Langevin equation for the fluctuating (or instantaneous) scalar value. We will tentatively call it the bounded Langevin model (BLM), represented by

$$d\varphi =A_{\varphi }dt+\sqrt{B_{\varphi }}d{W}_{\varphi }.$$

(21)

Above, $A_{\varphi }$ is a drift term and $B_{\varphi }$ is a diffusion term; they are specified as:

$$A_{\varphi }=-\varphi \left[1+K_0\left(1-\langle {\varphi }^2\rangle )/{\varphi }_B^2\right)\right]{\omega }_{\varphi }/2,B_{\varphi }=K_0{\omega }_{\varphi }\left(1-{\varphi }^2/{\varphi }_B^2\right)\langle {\varphi }^2\rangle$$

(22)

where ${\omega }_{\varphi }$ is the mixing frequency and $K_0$ is a model constant; ${\varphi }_B$ is equal to the higher scalar bound ${\varphi }_{max}$ whenever $\varphi$ is greater than zero, and otherwise $-{\varphi }_B$ equals the lower scalar bound ${\varphi }_{min}$; ${\varphi }_{max}$ and ${\varphi }_{min}$ are respectively the maximum and minimum fluctuations allowed. For the sake of simplicity, we limit ourselves here to the symmetric scalar PDFs. In this case, ${\varphi }_B$ stands for a local magnitude of scalar fluctuations (scalar bound). The question arises of how to predefine (or determine dynamically in the course of computations) the scalar bounds ${\varphi }_{min}$ and ${\varphi }_{max}$ in the general flow case. For the often-considered validation test of initially-segregated (bimodal) scalar in homogeneous turbulence (described below), the bounds are readily defined since there is no dependence of scalar statistics on the location in space.

We emphasise the fact that $dW$ in Equation (21) is an increment of the Wiener process, $\langle {\left(dW\right)}^2\rangle =dt$. In the discrete version it becomes $∆W=\xi \sqrt{∆t}$ where $\xi$ is a random number from the standard Gaussian distribution, and not a binomially-distributed random variable as used by Valiño and Dopazo [77] in their original proposal.

It is readily seen that the BLM encompasses IEM as a limit case (for $K_0=0$), so the considerations presented in the following remain valid for the IEM. This fact provides the prescription for the mixing frequency in Equation (22): ${\omega }_{\varphi }=C_{\varphi }ϵ/k$.

By virtue of the equivalence of SDE and the Fokker–Planck equation [79], the BLM, Equation (21), written in terms of particle evolution, corresponds to the following closure of the scalar micromixing term in the PDF equation for scalar fluctuation: $f=f_{\varphi }(\psi ,t)$

$$\frac{\partial f}{\partial t}=-\frac{{\partial }^2}{\partial {\psi }^2}\left[\langle \lambda \frac{\partial \varphi }{\partial x_k}\frac{\partial \varphi }{\partial x_k}|\varphi =\psi \rangle f\right]=\frac{\partial }{\partial \psi }\left(A_{\varphi }f\right)+\frac{{\partial }^2}{\partial {\psi }^2}\left(B_{\varphi }f\right).$$

(23)

The BLM, Equation (21), satisfies the scalar boundedness property, and a suitable numerical integration scheme for the SDE (respecting the boundedness also on the discrete level) can be put forward. Both have been done in [78]. The discrete scheme is briefly recalled.

The SDE, Equation (21), respects the scalar bounds (if any), yet a simple discretisation with the first-order explicit Euler scheme no longer possesses this property, unless the discrete increments of the Wiener process are artificially limited (clipped). One of the possibilities to deal with the scalar boundedness in a correct way at the discrete simulation level is to introduce an unbounded function of the scalar variable, $\chi =\chi \left(\varphi \right)$, say, through a suitable transformation. The SDE is transformed to the corresponding SDE for $\chi$ using the Ito theorem [79]:

$$d\chi =A_{\varphi }{\chi }^{\prime }\left(\varphi \right)dt+\frac{1}{2}{B}_{\varphi }{\chi }^{″}\left(\varphi \right)dt+\sqrt{B_{\varphi }}{\chi }^{\prime }\left(\varphi \right)d{W}_{\chi }$$

(24)

where ${\chi }^{\prime }\left(\varphi \right)=d\chi /d\varphi$. Upon some reflection, accompanied by a series of trials and errors, we decided to go for a particular transformation

$$\chi =\varphi {\left({\varphi }_B^2-{\varphi }^2\right)}^{-1/2}.$$

(25)

It assures a one-to-one correspondence between the interval $-{\varphi }_B\le \varphi \le +{\varphi }_B$ and the real $\chi$-axis. Interestingly, the form of Equation (25) reminds one of the expression for the conditional scalar PDF in lamellar structures that stems from the 1D diffusion equation; see [2]. Relationship (25) applied to Equation (24) yields the following transformed SDE:

$$d\chi =\frac{{\varphi }_B^2}{{({\varphi }_B^2-{\varphi }^2)}^{3/2}}\left[A_{\varphi }+\frac{3\varphi B_{\varphi }}{2({\varphi }_B^2-{\varphi }^2)}\right]dt+\sqrt{B_{\varphi }}\frac{{\varphi }_B^2}{{({\varphi }_B^2-{\varphi }^2)}^{3/2}}d{W}_{\chi }.$$

(26)

We note that Pope and Chen (see Section 12.5.2 in Ref. [1]) proposed a somewhat similar procedure to deal with the equation for the turbulent frequency $\omega$.

They assumed the log-normal distribution of $\omega$; hence, a natural transformation to a Gaussian variable was possible, allowing for the analytical solution of a resulting SDE (which is not the case here).

We performed a well-known fundamental test of scalar mixing in a homogeneous stationary turbulence. For this case, the DNS data are available for the evolution of the PDF and its moments [18]. The initial distribution of the scalar is close to bimodal. Actually, for the sake of convenient numerical handling in the DNS, it has been slightly smoothed around $\pm {\varphi }_B$. The bounded Langevin model, Equation (21), has been applied together with the transformation of variables, Equation (25), to guarantee the scalar boundedness also at the discrete level. The initial condition for the scalar has been taken as in the DNS. The shape of the evolving PDF is shown in Figure 4. The chosen time instants are characteristic of the scalar evolution. At an early time, the distribution is still close to bimodal. As micromixing proceeds, the PDF changes its form and a central peak develops; cf., Figure 3c. At later times, the scalar PDF becomes closer and closer to Gaussian (but still bounded). This is also confirmed by the moments of the distribution, and especially the flatness coefficient (not shown here) that correctly tends to its ultimate Gaussian value of 3. A very good overall agreement with the DNS data is noticed.

Apart from the homogeneous turbulence case presented above, the BLM has also been tested, along with two other micro-mixing models. It has been applied for computation using a standalone joint PDF of velocity, turbulent frequency and scalar. The case considered was the thermal mixing layer generated by a temperature step in a grid turbulence, studied experimentally in [80]. Numerical results [73] have been obtained for transport and mixing of temperature as a passive inert scalar variable. Computed statistics included moments (up to the fourth order) of the temperature distribution and velocity-temperature correlations. The overall agreement with experimental data was satisfactory.

4.4. More Models of Scalar Mixing

The micromixing models presented so far are the oldest, and arguably, also most often used. As already discussed, they have a number of drawbacks each, not satisfying at least some of the theoretically established criteria—hence a continuing quest for better formulations that at the same time should be computationally tractable. We mention here some comparative studies of micromixing models (mostly from the area of turbulent combustion) and some more recent proposals, including those for multiscalar mixing.

Subramanian and Pope [81] have proposed a mixing model based on Euclidean minimum spanning trees (EMST) that accounts for the locality of interaction in the scalar space. Among other closures, [82] made the scalar mixing time scale variable, accounting for its multiscale fluctuations. In a series of papers, Kerstein and coworkers (see [83] and references therein), developed the so-called linear eddy model (or one-dimensional turbulence); it features some 1D representation of the turbulent stirring effect on the scalar field to mimic the action of stretching and folding. The shadow position micromixing model of Pope [84] is formulated based on a number of physical observations, including that the mean scalar field at high $Re$ should not be affected by molecular diffusion.

There are a number of comparative studies of micromixing models, either in a binary scalar setup, or in real flames. As for the former, a selection of commonly used closures are assessed in [39]. An example of the latter is [70], wherein three different models (IEM, MC and EMST) were studied, including for the case of the $H_2$-air system. The results for the mixture fraction PDF and for the temperature field were found there to depend on the choice of the micromixing model. Another work is [69] for the case of turbulent diffusion flame with a bluff-body stabilisation. The flow is solved with the second-moment closure coupled with the joint scalar PDF and the mixing models studied are the modified Curl and the EMST. The authors state that the model’s choice may become visible in non-equilibrium situations such as a local flame extinction or reignition. The micromixing models in the PDF simulation of premixed flames have recently been studied in [71]. To handle the turbulence-chemistry interaction and to better predict the MILD combustion regime, in [16] a selection of expressions for the mixing time scale were analysed, both constant and variable (dynamic), in the case of jet in hot coflow flames.

Another comprehensive study on scalar mixing models, including both a review and future prospects, is [67]. The models are detailed there and a comparative analysis of their performance is presented. As for the outlook, interesting thoughts are formulated into the Lagrangian coherent structures and their potential use in the development of mixing models. A comprehensive study [68] explored the DNS data in isotropic turbulence and in a premixed flame to get better insights into mixing for modelling purposes. The evolution of the scalar PDF and its moments is related to the geometrical description in terms of scalar isosurfaces, their transport by turbulent convection and molecular diffusion.

For the case of multiple scalars like several chemical species, a vector quantity $\mathsf{\Phi }$ appears in Equation (6); the name of thermochemical state vector is sometimes used, gathering the mass fraction of chemical species, temperature and possibly pressure. The main implication of $\mathsf{\Phi }$ becoming a vector is that multiscalar mixing models need to be developed. For multiple scalars, the molecular diffusivity is often assumed identical for each species. In practice, the differential diffusion effects may become significant, in particular in turbulent flames. Ideally, a micromixing model should account for different mixing time scales of individual species. Along these lines, in [85] the modified Curl and IEM models are presented. Another approach to treat differential diffusion has been proposed in [86] and applied to the IEM and EMST mixing models.

One of the difficulties in extending the micromixing models for the multiple scalar case stems from the fact that such models represent a coupled effect of molecular diffusion and convective stirring at non-resolved length scales. Interestingly, the linear eddy modelling (LEM) concept of Kerstein, mentioned above, allows one to decouple the two agents, as the molecular diffusion is implemented there in a deterministic way and depends on the actual Schmidt or Prandtl number, whereas the convective stirring is represented as a stochastic rearrangement of a scalar profile (identical for all scalars). Therefore, the LEM may naturally treat differential diffusion effects [87].

As far as reacting flows are concerned in general, a very interesting paper by Pope [26] puts the issue of mixing into a broader perspective of turbulent combustion physics. According to the Author, the principal challenges are: the presence of small scales, the many chemical species (like in hydrocarbon combustion), and the coupled processes of diffusion and reaction.

The turbulent mixing of multiple scalars has been studied far less than the mixing process of a single scalar variable. It is a difficult yet important topic that certainly merits a separate review on its own; it is just signalled here. The method of multiple mapping conditioning [88] combines the advantages of the PDF and CMC methods; it is based on a generalisation of the mapping closure (MC) concept. The approach implicitly provides a mixing model that extends the MC to multiple scalar variables. Another advantage is that a number of constraints are respected, such as the boundedness, linearity, independence and the Gaussian limiting behaviour. In [89], a further study is reported on coupling the BLM with the multiple mapping conditioning (MMC) of [88]. The authors advocate the use of mixture fraction statistics in MMC to outperform other approaches, including those based on LES. In [90], a bivariate generalisation of the beta-PDF is proposed. Based on the DNS data examination, it has been found to be suitable for a two-scalar mixture, yet a further generalisation to the multiscalar case remains an open issue.

5. Filtered Density Function Approach to Scalars in Turbulence

5.1. The FDF Basics

In the statistical methods, presented in Section 3, moments of fluctuating scalar variables and the mean reaction rate are calculated. However, the one-point PDF provides only limited description of turbulent field. In particular, information on the spatial structure of turbulence is missing. This poses a problem if one recalls that turbulence is the flow regime characterised by a myriad of eddies, of different lengths and time scales, strongly interacting with each other. Resolving all these scales is still beyond current computing capacities for most of physically complex flows of industrial interest or turbulent flows in the atmosphere.

Hence, the idea of the large eddy simulation approach is to resolve the largest energy-containing eddy structures and to model the influence of the smaller scales, which are removed by a low-pass filtering procedure. The filtering can also be understood as a type of spatial average. For further purposes we will only consider homogeneous and non-negative filter functions $G(\mathbf{x}-{\mathbf{x}}^{\prime })$. Filtering of a scalar variable $\mathsf{\Phi }$ is represented mathematically as a convolution [1]

$${\langle \mathsf{\Phi }(\mathbf{x},t)\rangle }_L={\int }_{\mathsf{\Omega }}\mathsf{\Phi }({\mathbf{x}}^{\prime },t)G(\mathbf{x}-{\mathbf{x}}^{\prime })d{\mathbf{x}}^{\prime }$$

(27)

where ${\langle ·\rangle }_L$ denotes a smoothed (large scale) quantity and $\mathsf{\Omega }$ is the computational domain. The characteristic length of the spatial filter, ${∆}_G$, specifies the minimal size of eddies that are resolved (the cutoff length scale). The filter function is normalised

$${\int }_{\mathsf{\Omega }}G(\mathbf{x}-{\mathbf{x}}^{\prime })d{\mathbf{x}}^{\prime }=1;$$

(28)

linear, i.e., ${\langle F+H\rangle }_L={\langle F\rangle }_L+{\langle H\rangle }_L$; and commutes with differentiation with respect to time and space.

The two classical filters in LES are the top-hat filter

$$\begin{array}{c}\hfill G(\mathbf{x}-{\mathbf{x}}^{\prime })=\left\{\begin{array}{cc}\frac{1}{{∆}_G},\hfill & \mathrm{if}|\mathbf{x}-{\mathbf{x}}^{\prime }|\le \frac{{∆}_G}{2},\hfill \\ 0,\hfill & \mathrm{otherwise}\hfill \end{array}\right.\end{array}$$

(29)

and Gaussian filters

$$\begin{array}{c}\hfill G(\mathbf{x}-{\mathbf{x}}^{\prime })={\left(\frac{\gamma }{\pi {∆}_G^2}\right)}^{3/2}exp\left(-\frac{\gamma |\mathbf{x}-{\mathbf{x}}^{\prime }{|}^2}{{∆}_G^2}\right).\end{array}$$

(30)

where $\gamma$ is a scale parameter: for $\gamma =6$ the size of Gaussian filter (the standard deviation) is equal to half-width of the top-hat filter. The 1D filters can be extended to 3D by a proper extension of the formulae and choosing proper normalisation constants. The characteristic length scale ${∆}_G$ is usually much larger than the dissipative Kolmogorov scales ${∆}_G\gg {\eta }_K$.

When the filtering operation is applied to the scalar transport, Equation (1), the following filtered transport equation is obtained:

$$\frac{\partial {\langle \mathsf{\Phi }\rangle }_L}{\partial t}+{\langle U_j\rangle }_L\frac{\partial {\langle \mathsf{\Phi }\rangle }_L}{\partial x_j}=\lambda \frac{{\partial }^2{\langle \mathsf{\Phi }\rangle }_L}{\partial x_j\partial x_j}-\frac{\partial }{\partial x_j}\left({\langle U_j\mathsf{\Phi }\rangle }_L-{\langle U_j\rangle }_L{\langle \mathsf{\Phi }\rangle }_L\right)+{\langle \dot{w}\left(\mathsf{\Phi }\right)\rangle }_L;$$

(31)

The subgrid scalar flux ${\langle U_j\mathsf{\Phi }\rangle }_L-{\langle U_j\rangle }_L{\langle \mathsf{\Phi }\rangle }_L$ and the filtered reaction terms are analogous to those appearing in the statistical approach; see Equation (4). The most popular closure for the subgrid scalar flux is the Smagorinsky model (cited, e.g., by [1]) where the Boussinesq hypothesis is employed

$${\langle U_j\mathsf{\Phi }\rangle }_L-{\langle U_j\rangle }_L{\langle \mathsf{\Phi }\rangle }_L=-\frac{{\nu }_r}{S{c}_r}\frac{\partial {\langle \mathsf{\Phi }\rangle }_L}{\partial x_j}$$

(32)

where $S{c}_r$ is the subgrid Schmidt number (typically of $\mathcal{O}\left(1\right)$ order) and ${\nu }_r$ is the eddy viscosity of residual motions, which is expressed by

$${\nu }_r={\left(C_s{∆}_G\right)}^2{\langle \mathcal{S}\rangle }_L;$$

(33)

with ${\langle \mathcal{S}\rangle }_L=2{\left({\langle S_{ij}\rangle }_L{\langle S_{ij}\rangle }_L\right)}^{1/2}$. The term ${\langle S_{ij}\rangle }_L$ is the filtered rate of strain tensor, which is defined as

$${\langle S_{ij}\rangle }_L=\frac{1}{2}\left(\frac{\partial {\langle U_i\rangle }_L}{\partial x_j}+\frac{\partial {\langle U_j\rangle }_L}{\partial x_i}\right).$$

As follows from a priori studies, the values of the Smagorinsky coefficient $C_s$ in Equation (33) vary considerably in space and time [1]. Hence, a good add-on to the Smagorinsky model is the dynamic procedure proposed by Germano which determines the value of $C_s$ locally. The Germano model is based on a double filtering, where an additional coarser filter ${\widetilde{∆}}_G>{∆}_G$ is used to determine local energy transport between the scales and the function $C_s(\mathbf{x},t)$. For details of the procedure, as well as other modelling approaches for the subgrid stress term, the reader is referred to textbooks on turbulence, e.g., [1].

Here, of particular interest is the extension of the PDF methods towards large eddy models. This extension is called the filtered density function model and its concept dates back to the early work of S.B. Pope [47], although it was named differently therein. The idea was further developed in [91] and implemented numerically; see [92,93].

The filtered density function is defined as

$$\begin{array}{c}\hfill f_L(\mathsf{\Psi };\mathbf{x},t)={\int }_{\mathsf{\Omega }}\delta (\mathsf{\Psi }-\mathsf{\Phi }({\mathbf{x}}^{\prime },t))G\left({\mathbf{x}-\mathbf{x}}^{\prime }\right)d{\mathbf{x}}^{\prime }.\end{array}$$

(34)

As is seen, while the PDF considered in Section 3 is the ensemble-average of the fine-grained PDF (the Dirac delta), here the averaging is replaced by the filtering operation. The function $f_L$ has all the properties of the probability density function. That is, it is normalised

$${\int }_{-\infty }^{\infty }{f}_L(\mathsf{\Psi };\mathbf{x},t)d\mathsf{\Psi }={\int }_{-\infty }^{\infty }{\int }_{\mathsf{\Omega }}\delta (\mathsf{\Psi }-\mathsf{\Phi }({\mathbf{x}}^{\prime },t))G\left({\mathbf{x}-\mathbf{x}}^{\prime }\right)d{\mathbf{x}}^{\prime }d\mathsf{\Psi }={\int }_{\mathsf{\Omega }}G\left({\mathbf{x}-\mathbf{x}}^{\prime }\right)d{\mathbf{x}}^{\prime }=1$$

(35)

and non-negative, provided that the filter function G is non-negative too. Moreover, the filtered scalar ${\langle \mathsf{\Phi }\rangle }_L$ and the residual (subgrid-scale) scalar variance ${\sigma }_r^2={\langle {\mathsf{\Phi }}^2\rangle }_L-{\langle \mathsf{\Phi }\rangle }_L^2$ are calculated as the first and second-order moments of the FDF

$$\begin{array}{c}\hfill {\langle \mathsf{\Phi }(\mathbf{x},t)\rangle }_L={\int }_{-\infty }^{\infty }\mathsf{\Psi }{f}_L(\mathsf{\Psi };\mathbf{x},t)\mathrm{d}\mathsf{\Psi },{\sigma }_r^2={\int }_{-\infty }^{\infty }{\mathsf{\Psi }}^2{f}_L(\mathsf{\Psi };\mathbf{x},t)\mathrm{d}\mathsf{\Psi }-{\langle \mathsf{\Phi }\rangle }_L^2.\end{array}$$

(36)

The conditional filtered value of an arbitrary function $H(\mathbf{x},t)$ satisfies

$$\begin{array}{c}\hfill {\langle H(\mathbf{x},t)\delta (\mathsf{\Phi }(\mathbf{x},t)-\mathsf{\Psi })\rangle }_L={\langle H(\mathbf{x},t)|\mathsf{\Phi }(\mathbf{x},t)=\mathsf{\Psi }\rangle }_L{f}_L,\end{array}$$

(37)

which can be compared directly to Equation (3) for the PDF counterpart.

5.2. The FDF Equation of Scalar Transport

The exact FDF transport equation is derived analogously as in the PDF case, Equation (8). The time derivative of the FDF reads

$$\begin{array}{c}\hfill \frac{\partial f_L}{\partial t}=-{\int }_{\mathsf{\Omega }}\frac{\partial \mathsf{\Phi }}{\partial t}\frac{\partial f^{\prime }(\mathsf{\Psi };{\mathbf{x}}^{\prime },t)}{\partial \mathsf{\Psi }}G\left({\mathbf{x}-\mathbf{x}}^{\prime }\right)\mathrm{d}{\mathbf{x}}^{\prime }.\end{array}$$

(38)

With the use of the generic transport equation for the passive scalar, Equation (1), one obtains

$$\begin{array}{c}\hfill \frac{\partial f_L}{\partial t}={\int }_{\mathsf{\Omega }}\left(\frac{\partial U_i\mathsf{\Phi }}{\partial x_i}-\lambda \frac{{\partial }^2\mathsf{\Phi }}{\partial x_i\partial x_i}-\dot{w}\left(\mathsf{\Psi }\right)\right)\frac{\partial f^{\prime }}{\partial \mathsf{\Psi }}G(\mathbf{x}-{\mathbf{x}}^{\prime })\mathrm{d}{\mathbf{x}}^{\prime }.\end{array}$$

(39)

After employing properties of FDF and Equations (34) and (37), the following exact transport equation is obtained:

$$\begin{array}{ccc}\hfill \frac{\partial f_L}{\partial t}+{\langle U_i\rangle }_L\frac{\partial f_L}{\partial x_i}=& -& \frac{\partial ({\langle U_i|\mathsf{\Psi }\rangle }_L-{\langle U_i\rangle }_L)f_L}{\partial x_i}+\lambda \frac{{\partial }^2{f}_L}{\partial x_i\partial x_i}-\lambda \frac{\partial {\langle \mathsf{\Phi }\rangle }_L}{\partial x_i}\frac{\partial {\langle \mathsf{\Phi }\rangle }_L}{\partial x_i}\frac{{\partial }^2{f}_L}{\partial {\mathsf{\Psi }}^2}\hfill \\ \hfill & -& \lambda \frac{{\partial }^2}{\partial {\mathsf{\Psi }}^2}\left[{\langle \frac{\partial \mathsf{\Phi }}{\partial x_i}\frac{\partial \mathsf{\Phi }}{\partial x_i}|\mathsf{\Psi }\rangle }_L{f}_L-\frac{\partial {\langle \mathsf{\Phi }\rangle }_L}{\partial x_i}\frac{\partial {\langle \mathsf{\Phi }\rangle }_L}{\partial x_i}{f}_L\right]-\frac{\partial }{\partial \mathsf{\Psi }}\left[f_L\dot{w}\left(\mathsf{\Psi }\right)\right]\hfill \end{array}$$

(40)

where ${\langle U_i\rangle }_L$ denotes the filtered velocity which can be computed from separate LES simulations (e.g., performed with an Eulerian code). Alternatively, the joint velocity-scalar FDF method, as proposed in [93], can be used. In this approach also the first RHS term in Equation (40) is closed. If only the scalar FDF is considered, all terms with conditional averages in Equation (40) require modelling. In [92], it was proposed to replace the convective flux of the subgrid scales by

$$\begin{array}{c}\hfill ({\langle U_i|\mathsf{\Psi }\rangle }_L-{\langle U_i\rangle }_L)f_L=-{\lambda }_r\frac{\partial f_L}{\partial x_i}\end{array}$$

(41)

where ${\lambda }_r={\nu }_r/S{c}_r$ denotes the subgrid (or residual) diffusivity. Equation (41) corresponds to the standard gradient diffusion models in the Eulerian LES and in the scalar PDF approach; see the text below Equation (8).

The fourth RHS term of Equation (40) represents the effect of subgrid mixing, and by analogy with the micromixing term in Equation (8), it needs a closure. It is possible to provide the FDF analogy of the micromixing models introduced in Section 4. In particular, the equivalent of the IEM approach for LES reads [92]

$$\begin{array}{c}\hfill -\lambda \frac{{\partial }^2}{\partial {\mathsf{\Psi }}^2}\left[{\langle \frac{\partial \mathsf{\Phi }}{\partial x_i}\frac{\partial \mathsf{\Phi }}{\partial x_i}\rangle }_L{f}_L-\frac{\partial {\langle \mathsf{\Phi }\rangle }_L}{\partial x_i}\frac{\partial {\langle \mathsf{\Phi }\rangle }_L}{\partial x_i}{f}_L\right]\Rightarrow \frac{\partial }{\partial \mathsf{\Psi }}\left[{\mathsf{\Omega }}_m(\mathsf{\Psi }-{\langle \mathsf{\Phi }\rangle }_L)f_L\right]\end{array}$$

(42)

where

$${\mathsf{\Omega }}_m=\frac{C_{\mathsf{\Omega }}}{{∆}_G^2}(\lambda +{\lambda }_r)$$

(43)

is the subgrid mixing frequency and $C_{\mathsf{\Omega }}$ is a model constant. Similarly, analogies to the Langevin and bounded Langevin models can be provided.

In reference [94] concentrations of reactive scalars are calculated with the FDF approach. Therein, it was argued that the stand-alone IEM closure fails to correctly reproduce transport in the concentration space. Hence, in a yet another model proposed in [94], a Langevin-type equation is solved for the scalar concentration, with the drift and diffusion coefficients determined from comparison with time series of simulated concentrations. This method is called the time series (TS) mixing model. It is found that the best results are obtained for a mixing model being a linear combination of TS and the IEM closure.

The third RHS term in Equation (40), with gradients of the filtered scalar, does not contain conditional averages; however, it also requires a closure due to its anti-diffusive nature. This term was omitted in [92]; however, such an approach is not always justified. The molecular transport terms are regarded as negligibly small in RANS or PDF computations far from walls, but they are usually accounted for in well-resolved LES and so should be the case in the FDF approach. It was proposed in reference [95] to replace this term by

$$\frac{1}{{\tau }_L}\frac{\partial }{\partial \mathsf{\Psi }}\left[(\mathsf{\Psi }-{\langle \mathsf{\Phi }\rangle }_L)f_L\right],\mathrm{where}\frac{1}{{\tau }_L}=\frac{\lambda }{{\sigma }_r^2}\left(\frac{\partial {\langle \mathsf{\Phi }\rangle }_L}{\partial x_i}\frac{\partial {\langle \mathsf{\Phi }\rangle }_L}{\partial x_i}\right).$$

(44)

The term ${\sigma }_r^2$ above is the residual scalar variance, see Equation (36).

After the closure, the FDF equation is solved by a Lagrangian method, with equations analogous to those presented in Section 4. The filtered properties are calculated by averaging over the particles contained within a certain area of characteristic size ${∆}_L$, where in general ${∆}_L\ne {∆}_G$. For the illustration, Figure 5 presents a scatter plot representing values of a scalar (here: the temperature of stochastic particles) in a flow between two parallel, cooled walls; see [95]. The profile of filtered temperature calculated from the particle properties is also plotted in Figure 5 (solid line).

The Lagrangian FDF method can also be coupled with other low-order models for velocity, instead of LES. An example is an approach based on the proper orthogonal decomposition (POD), which allows for more efficient simulations of velocity field of the most energetic eddy structures. In reference [96] conjugate heat transfer was studied with the use of such a low-order dynamical system for velocity coupled with the FDF method for temperature considered as a dynamically passive scalar variable. Reduced-order approaches seem suitable for the simulations of turbulent flows in near-wall geometries, where a substantial grid refinement necessary for LES makes that method computationally expensive, especially if it is coupled with a Lagrangian solver for inertial solid particles [97,98]. Results of Lagrangian particle tracking in the velocity field generated by POD-based low-order systems are reported in [99].

It turns out that the Lagrangian approach is also advantageous in the study of droplets’ motion in turbulent cloud systems. In [100], the stochastic FDF approach was used to model fluctuations of the turbulent velocity and supersaturation. Although the model for velocity was simplified, it was shown that the subgrid motions alter the droplet size distribution by broadening of their spectra, which affects subsequent rain formation processes.

Still concerning the dispersed flows: as an extension of the formalism presented in this Section, the two-phase FDF has been proposed [101] to address spray combustion modelling in LES.

6. Conclusions and Perspectives

In this paper, we recalled the salient features of turbulent mixing and presented the modelling approaches for scalar variables with an emphasis on the Lagrangian PDF and FDF formulations. Despite a number of closures proposed to date, the micro-mixing models for scalars still represent a challenge. In particular, a further pursuit of models for the multiscalar mixing is of importance for reactive flows. The issue of scalar mixing is also relevant for flows in near-wall regions where molecular transport effects become dominant. A persistent difficulty is a physically sound estimation of the ratio of scalar to dynamical time scales (more too often taken as a constant) in various turbulent flows. The zonal coupling of the PDF/FDF approaches to an Eulerian code remains another direction of research. The local coupling should be performed according to a well-determined criterion to provide more detailed flow information in regions of interest. Arguably, with such a coupling the full value of the PDF method could manifest itself in practical applications for physically complex flows in a non-trivial geometry.

Apart from the scalar PDF/FDF open issues, there are a number of recent ideas beyond the topics discussed in the present overview. In particular, new trends in algorithm development are prompted by the recent advances in computing technology. In [27], progress in LES of reacting flows is addressed together with some emerging trends in computational combustion. According to the authors, uncertainties in simulation need to be estimated for practical use of LES. Then, on even more practical side, the authors notice that a new generation of approaches are needed to explore and utilise a vast amount of data collected during the operation of combustors. They are tentatively called “heterogeneous, data driven environment,” enabling better efficiency, lower emissions, operational safety, and reduced maintenance. Some information on data-driven modelling is provided in that paper. A related (and increasingly fashionable) topic is deep learning, in its various possible applications. As far as the presumed PDF models for LES are concerned, the DNS evidence is used to develop training data and different algorithms are evaluated in [102]. Another paper, directly related to turbulent mixing, is [103]. Using deep learning ideas, the authors propose a framework to deduce models from the experimental measurements of the PDF.

For several years now, high performance computing (HPC) has been increasingly implemented using graphic processing units (GPU) for massively parallel code execution. In parallel (nomen omen), a shift in paradigm is noticed: the numerical methods to solve a particular problem are purposefully chosen, and further developed, to better utilise the hardware capabilities and its specific architecture. In this respect, the statement of John Argyris (the title of his famous lecture in 1965): “The computer shapes the theory” remains of ever more evident actuality. In other words: the available hardware may, and does, impact the choice of numerical solution procedure or even physical models. As an example from the general CFD, consider computational methods (otherwise quite mature) for incompressible flow. The weakly compressible (WC) approach to solve otherwise zero-divergence velocity fields becomes a method of interest to avoid the elliptic solver of the Poisson equation for the pressure correction in truly incompressible approaches. The main reason is that the numerical schemes that are explicit in time and local in space may be tremendously efficient when run on GPU (even despite the restrictions on the allowable time step), as recently demonstrated for a wall-bounded turbulent flow case [104]. The Lagrangian PDF approach readily lends itself for parallel computing as well. An example of massively parallel, GPU-accelerated computation of turbulent mixing is described in [105]. The DNS of mixing at high Schmidt numbers is reported: different grid resolutions are used, as the scalar fluctuations persist down to scales smaller than ${\eta }_K$. Consequently, the Fourier pseudospectral method for velocity has been used together with the compact finite difference scheme for the scalar. The core of the paper is very technical, focusing on HPC issues with GPU-specific programming, but the overall message of [105] is clear: the software developments successfully accompany the progress on the hardware side, resulting in highly efficient simulations. Another example of GPU-accelerated computation for environmental application is the paper of Kristóf and Papp [9]. They performed a LES study of dispersion, referred to as a virtual (numerical) wind tunnel. The urban boundary layer (UBL) was solved, and the inlet BC were suitably chosen to mimic the mean velocity and turbulent intensity profiles of the UBL. The GPU-based simulation was aimed to estimate the urban air quality and to study possible options to mitigate high pollution conditions.

A technological breakthrough is looming on the horizon: the advent of quantum computers. Before it becomes reality, quantum algorithms (QA) must be tested and run on classical computers. To the best of the authors’ knowledge, the works in the CFD domain are still rare. A recent example is [106] (see also Supplementary Information to that paper, available online) where a QA is conceived to solve a simplified N–S equation in a transonic nozzle. The results agree well with the reference solution and a significant speed-up with respect to classical algorithms is reported to be possible. Then, definitely relevant for the topic of the present overview, [107] deals with turbulent mixing: a QA is advocated that accelerates the computation of the transported PDF and its moments. The computational efficiency is illustrated with the binary scalar mixing problem using a family of C-D micromixing models. The work is rooted in the recent interest in QA to speed up the Monte Carlo techniques.

As the bottom line of this overview: there has been significant progress to date, ranging from the understanding of physical aspects of the turbulent mixing process, through the fully resolved simulations able to provide a wealth of data to feed the models of practical applicability, up to impressive full-fledged computations of advanced systems such as combustion devices. Despite this enormous progress, there is still room for improvements concerning physically-sound and computationally efficient micromixing closures, in particular for multiple scalars, and efficient hybrid formulations, such as coupled LES/FDF approaches. Additionally, a vigilant eye should be kept on new, emerging software and hardware opportunities, such as machine learning, GPU-acceleration and possibly quantum computing.